Complete Generalization of the Equations for the Stress–Strain Curves of Concrete under Uniaxial Compression
Abstract
1. Introduction
2. Materials and Methods
2.1. Generalized Extreme Value Distribution
2.2. Fractional Calculus
2.2.1. Introduction
2.2.2. Definition of Fractional-Order Integral
2.2.3. Fractional Calculus and Constitutive Models
3. Process of Generalization of Concrete Stress–Strain Equations
3.1. Introduction
3.2. First Generalization: Fractional Hooke’s Law
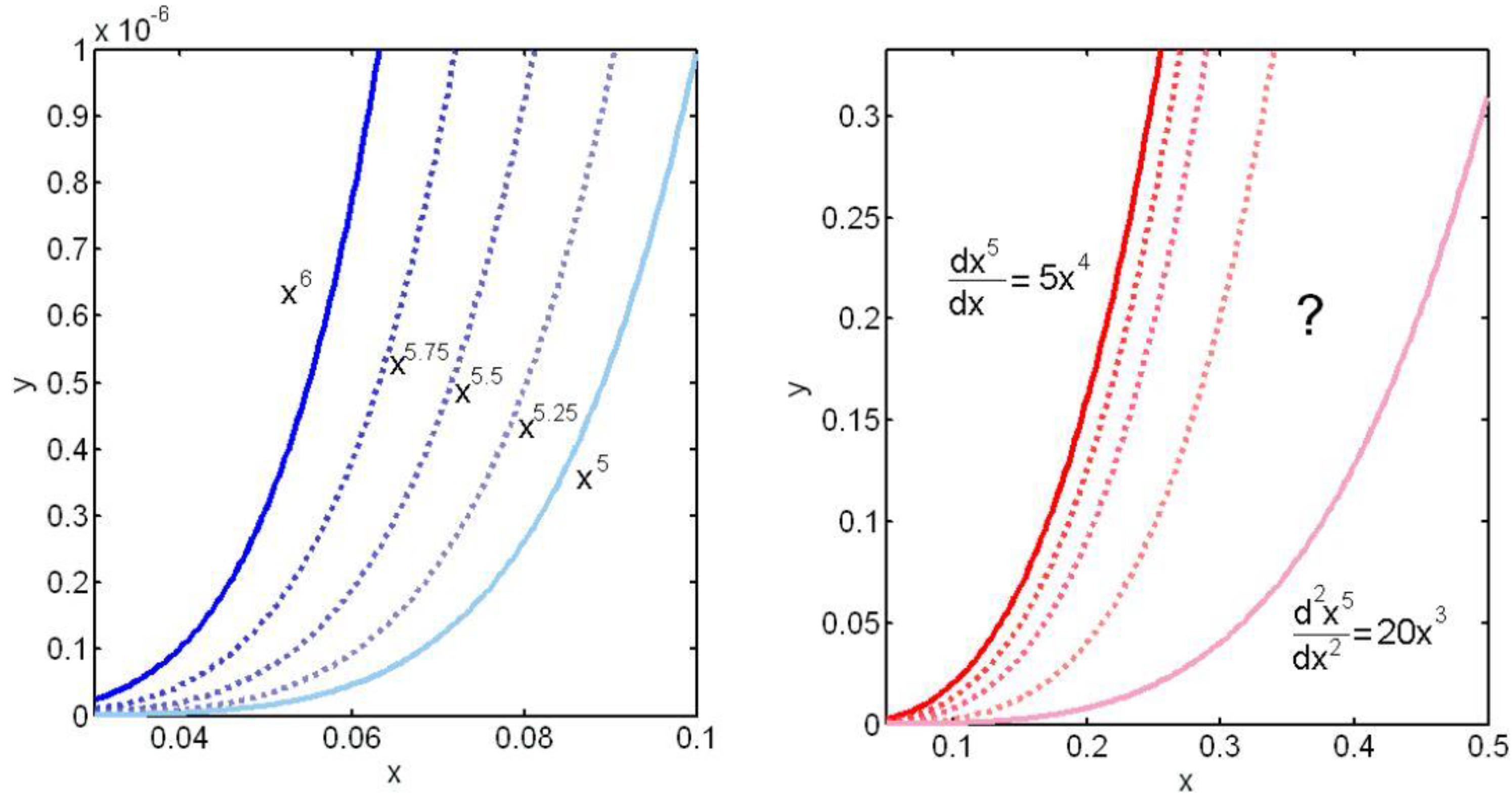
3.3. Second Generalization: Exponent m
3.4. Third Generalization: Generalized Extreme Value Distribution
3.5. Formulation of the Stress–Strain Equation: Restricted Form
3.6. Complete Stress–Strain Curves
3.7. General Form of the Equation
4. Experimental Verification of the Results
4.1. Results for the Low-Strength Concrete Test Specimens
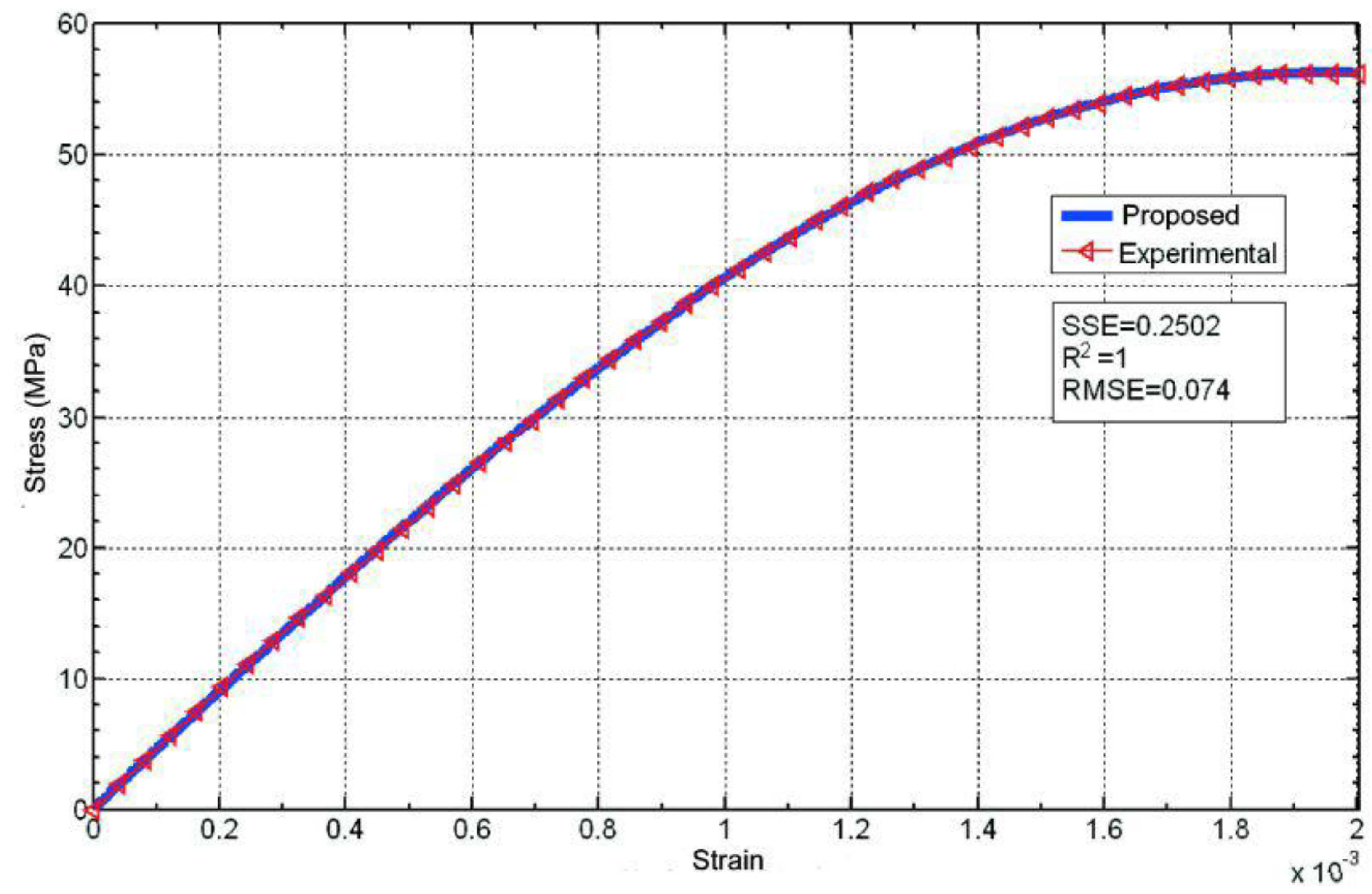
4.2. Results for the Medium-Strength Concrete Test Specimens
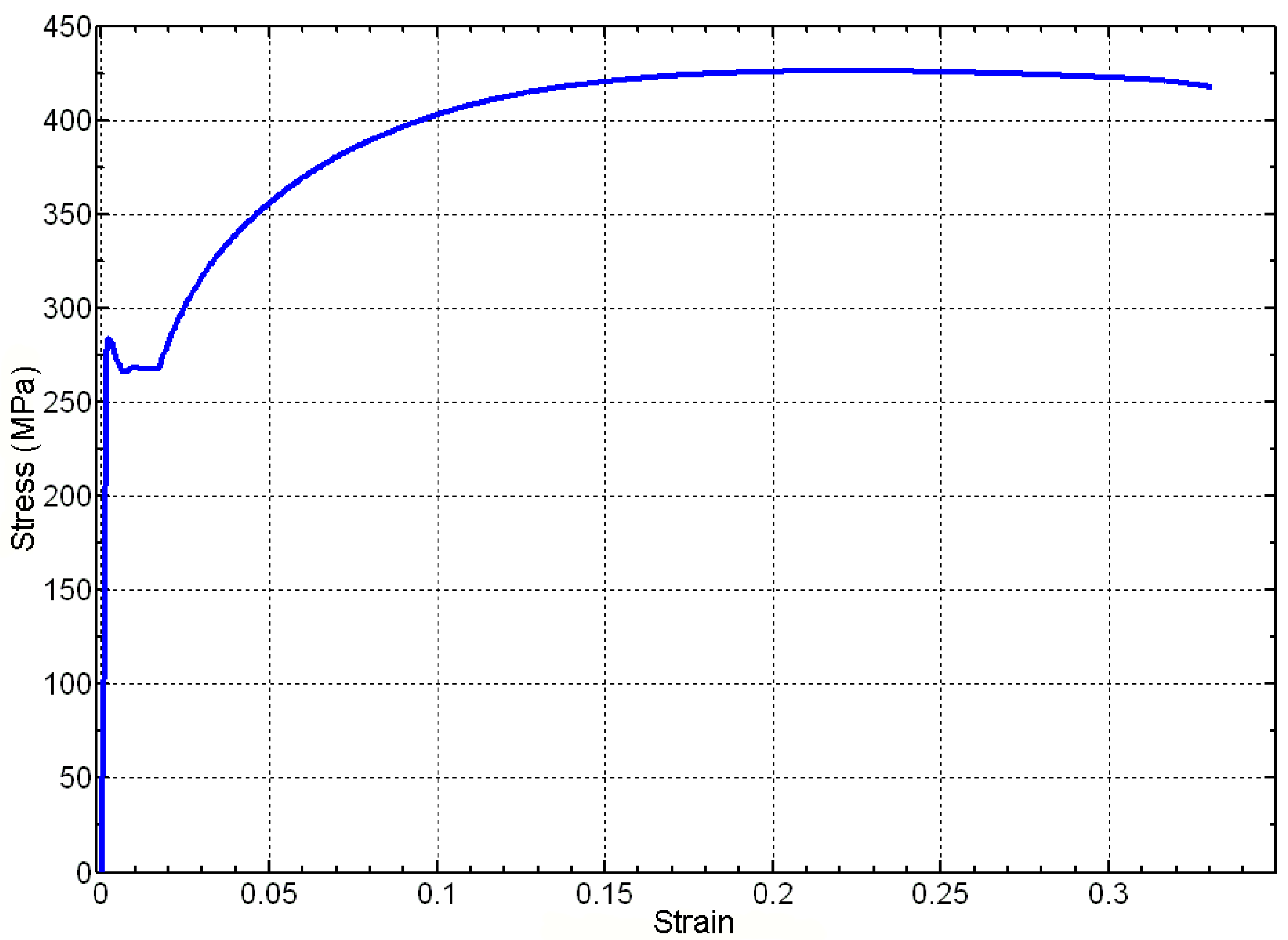
4.3. Results for the High-Strength Concrete Test Specimens
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bach, J.C.V. Untersuchungen von Granit in Bezug auf Zug-, Druck-, Biegungs-und Schubfestigkeit, sowie in Hinsicht auf Zug-, Druck- und Biegungselastizität. Z. Ver. Dtsch. Ing. 1897, 41, 248. [Google Scholar]
- Ritter, K.W. Die Bauweise Hennebique. Schweiz. Bauztg. 1899, XXXIII, 59–61. [Google Scholar]
- Smith, G.M.; Young, L.E. Ultimate flexural analysis on stress-strain curves for cylinders. ACI J. Proc. 1956, 53, 597–609. [Google Scholar]
- Yip, W.K. Generic form of stress-strain equations for concrete. Cem. Concr. Res. 1997, 28, 499–508. [Google Scholar] [CrossRef]
- Desayi, P.; Krishnan, S. Equation for the stress-strain curve of concrete. ACI J. Proc. 1964, 61, 345–350. [Google Scholar]
- Saenz, L.P. Discussion of “Equation for the stress-strain curve of concrete” by P. Desayi and S. Krishnan. ACI J. Proc. 1964, 61, 1229–1235. [Google Scholar]
- Alexander, S. A single equation for the stress-strain curve of concrete. Indian Concr. J. 1965, 39, 247–277. [Google Scholar]
- Sinha, B.P.; Gerstle, K.H.; Tulin, L.G. Stress-strain relations for concrete under cyclic loading. ACI J. 1964, 61, 195–211. [Google Scholar]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Carreira, D.J.; Chu, K.-H. Stress-strain Relationship for plain concrete in compression. ACI J. Proc. 1985, 82, 797–804. [Google Scholar]
- Tsai, W.T. Uniaxial compressional stress-strain relation of concrete. J. Struc. Eng. 1988, 14, 2133–2136. [Google Scholar] [CrossRef]
- Collins, M.P.; Mitchell, D.; MacGregor, J.G. Structural design considerations for highstrengthconcrete. Concr. Int. Des. Constr. 1933, 15, 27–34. [Google Scholar]
- Tasnimi, A.A. Mathematical model for complete stress-strain curve prediction ofnormal, light-weight and high-strength concretes. Mag. Concr. Res. 2004, 56, 23–34. [Google Scholar] [CrossRef]
- Sargin, M. Stress-Strain Relationships for Concrete and the Analysis of Structural Concrete Sections; Solid Mechanics Division, University of Waterloo: Waterloo, ON, Canada, 1971. [Google Scholar]
- Wang, P.T.; Shah, S.P.; Naaman, A.E. Stress-strain curves of normal and light weight concrete in compression. ACI J. Proc. 1978, 75, 603–611. [Google Scholar]
- Comité Euro-International du Béton. CBE-FIP Model Code 90; Thomas Telford: London, UK, 1991. [Google Scholar]
- Sargin, M.; Handa, V. A general formulation for the stress-strain properties of concrete. In Solid Mechanics Division, Report no. 3; University of Waterloo: Waterloo, ON, Canada, 1969; pp. 1–27. [Google Scholar]
- CEB Working Group on HSC/HPC. High performance concrete, Recommended Extensions to the MC 90 Research Needs. Bull. D’Inf. CEB 1995, 228, 1–60. [Google Scholar]
- Van Gysel, A.; Taerwe, L. Analytical formulation of the complete stress-strain curvefor high strength concrete. Mater. Struct. 1996, 29, 529–533. [Google Scholar] [CrossRef]
- Kachanov, L.M. On the time to rupture under creep conditions. Izv. Akad. Nauk SSSR. Otd. Tekhn. Nauk. 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. A Mechanism of a Long Time Failure, in Creep Problems in Structural Members; USSR Academy of Sci. Publ.: Moscow, Russia, 1959. [Google Scholar]
- Janson, J. Fracture mechanics and damage mechanics: A combined approach. J. Mécanique Appliquée 1977, 1, 69–84. [Google Scholar]
- Krajcinovic, D.; Fonseca, G.U. The continuous damage theory of brittle materials. Part I: General theory. J. Appl. Mech. 1981, 48, 809–815. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Mazars, J.J.; Pijaudier-Cabot, G. Continuum damage theory-Application to concrete. J. Eng. Mech. 1989, 115, 345–365. [Google Scholar] [CrossRef]
- Shah, S.P.; Winter, G. Inelastic behavior and fracture of concrete. ACI J. Proc. 1966, 63, 925–930. [Google Scholar]
- Weibull, W. A statistical theory of the strength of materials. Ing. Vetensk. Akad. 1939, 151, 1–45. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. Trans. ASME 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Phil. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar]
- Smekal, A. Bruchtheorie spröder körper. Z. Phys. A-Hadron Nucl. 1936, 103, 495–525. (In German) [Google Scholar]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc. R. Soc. Lond. A 1934, 145, 362–387. [Google Scholar]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part II. Comparison with observation. Proc. R. Soc. Lond. A 1934, 145, 388–404. [Google Scholar]
- Taylor, G.I. A theory of plasticity of crystals. Z. Krist. Cryst. Mater. 1934, 89, 375–385. [Google Scholar] [CrossRef]
- Blechman, I. Stage model of stress-strain relationship for concrete under short-termload. Part 1: Ascending branch. Cem. Concr. Res. 1988, 18, 863–873. [Google Scholar] [CrossRef]
- Blechman, I. Stage model of stress-strain relationship for concrete under short-termload. Part 2: Nature of concrete atrophy. Cem. Concr. Res. 1989, 19, 7–15. [Google Scholar] [CrossRef]
- Blechman, I. Stage model of stress-strain relationship for concrete under short-termload. Part 3: Descending branch. Cem. Concr. Res. 1989, 19, 203–215. [Google Scholar] [CrossRef]
- Ferretti, E. Modellazione del Comportamento del Cilindrofasciato in Compressione. Ph. D. Thesis, Universisity of Lecce, Lecce, Italy, 2001. (In Italian). [Google Scholar]
- Ferretti, E.; Di Leo, A. Cracking and creep role in displacements at constant load: Concrete solids in compression, Computers. Mater. Contin. 2008, 7, 59–79. [Google Scholar]
- Fréchet, M. Sur la loi de probabilité de l’ecartmaximum. Ann. Soc. Pol. Math. 1927, 6, 93–116. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frecuency distribution of thelargest or smallest members of a sample. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Gnedenko, B.V. Sur la distribution limit´e du terme maximum d’unesériealéatoire. Ann. Math. 1943, 44, 423–453. [Google Scholar] [CrossRef]
- Gumbel, E. Statistical Theory of Extreme Values and some Practical Application. In Journal Applied Mathematics Series 33; National Bureau of Standards: Washington, DC, USA; U.S. Department of Commerce: Washington, DC, USA, 1954. [Google Scholar]
- Liouville, J. M´emoire sur quelquesquestion de g´eometrie et de m´ecanique et sur un nouveaugenre de calculpourresoudre ces questions. J. L’´Ec. 1832, 13, 1–69. [Google Scholar]
- Malinin, N.N. Applied Theory of Plasticity and Creep; Mashinostroine: Moscow, Russia, 1975. [Google Scholar]
- Sobotka, Z. Reology of Materials and Construction; Academia: Prague, Czech Republic, 1981. [Google Scholar]
- Blair, G.W.S. Limitations of the Newtonian time scale in relation to non-equibrium rheological states and a theory of quasi-propierties. Proc. R. Soc. Lond. A 1947, 189, 69–87. [Google Scholar]
- Blair, G.W.S. The role of psycophysics in rheology. J. Colloid Sci. 1947, 2, 21–32. [Google Scholar] [CrossRef]
- Gerasimov, A.N.N. A generalizationof linear laws of deformation and its application to inner friction problems. Prikt. Mat. Mek. 1948, 12, 251–259. [Google Scholar]
- Slonimsky, G.L. On the law of deformation of highly elastic polymeric bodies. Dokl. Akad. Nauk. SSSR 1961, 140, 343–346. [Google Scholar]
- Nutting, P.G. A new general law of deformation. J. Frankl. Inst. 1921, 191, 679–685. [Google Scholar] [CrossRef]
- Nonnemnacher, T.F. Fractional relaxation equations for viscoelasticity and relatedphenomena. Lect. Notes Phys. 1991, 381, 309–320. [Google Scholar]
- Yip, W.K.; Kong, F.K.; Chan, K.S.; Lim, M.K. A statistical model of microcrackingof concrete under uniaxial compression. Theor. Appl. Fract. Mech. 1995, 22, 17–27. [Google Scholar] [CrossRef]
- Yip, W.K. New damage variable in failure analysis of concrete. J. Mater. Civ. Eng. 1996, 8, 184–188. [Google Scholar] [CrossRef]
- Basu, B.; Tiwari, D.; Kundu, D.; Prasad, R.R. Is the Weibull distribution the mostappropiate statistical strength distribution for brittle materials? Ceram. Int. 2009, 35, 237–246. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distributions. Aust. N. Z. J. Stat. 1999, 41, 173–188. [Google Scholar] [CrossRef]
- Salguero, F.; Romero, S.; Prat, F.; Arribas, R.; Moreno, F. Universal Stress-Strain Equation for Metallic Materials. J. Mater. Civ. Eng. 2014, 26, 040140030(1)–040140030(9). [Google Scholar] [CrossRef]
- Salgero, F. Sobre las Curvas Tensión-Deformación de Hormigones y Otros Materiales Sometidos a Ensayos de Tensión Uniaxial. Ph. D. Thesis, University of Huelva, Huelva, Spain, 2012. (In Spanish). [Google Scholar]
- Kato, B.; Aoki, H.; Yamanouchi, H. Standarized mathematical expression for stress-strain relations of structural steel under monotonic and uniaxial tension loading. Mater. Struct. 1990, 23, 47–58. [Google Scholar] [CrossRef]











| Initial Distribution F(x) | Limit Distribution for the Maxima G(x) |
|---|---|
| Exponential | Type I GEVD (Gumbel) |
| Gamma | Type I GEVD (Gumbel) |
| Normal | Type I GEVD (Gumbel) |
| Log-normal | Type I GEVD (Gumbel) |
| Pareto | Type II GEVD (Fréchet) |
| Cauchy | Type II GEVD (Fréchet) |
| Burr | Type II GEVD (Fréchet) |
| Log-gamma | Type II GEVD (Fréchet) |
| Uniform | Type III GEVD (Weibull) |
| Beta | Type III GEVD (Weibull) |
| Test Specimen | CEM (kg/m3) | W/C | CA (kg/m3) | FA (kg/m3) | SF (kg/m3) | WR(kg/m3) | f′c (MPa) |
|---|---|---|---|---|---|---|---|
| L2 | 250 | 0.65 | 975.41 | 1056.46 | - | - | 32.35 |
| M1 | 375 | 0.44 | 925.76 | 995.71 | 4.69 | - | 56.18 |
| M2 | 375 | 0.44 | 925.76 | 995.71 | 4.69 | - | 50.06 |
| H2 | 500 | 0.23 | 907.80 | 982.26 | 25.00 | 12.5 | 105.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domínguez-Cartes, V.; Ramos-Cabeza, D.; de la Torre, M.L.; Salguero-Andújar, F. Complete Generalization of the Equations for the Stress–Strain Curves of Concrete under Uniaxial Compression. Materials 2023, 16, 3387. https://doi.org/10.3390/ma16093387
Domínguez-Cartes V, Ramos-Cabeza D, de la Torre ML, Salguero-Andújar F. Complete Generalization of the Equations for the Stress–Strain Curves of Concrete under Uniaxial Compression. Materials. 2023; 16(9):3387. https://doi.org/10.3390/ma16093387
Chicago/Turabian StyleDomínguez-Cartes, Vanesa, Daniel Ramos-Cabeza, María Luisa de la Torre, and Francisco Salguero-Andújar. 2023. "Complete Generalization of the Equations for the Stress–Strain Curves of Concrete under Uniaxial Compression" Materials 16, no. 9: 3387. https://doi.org/10.3390/ma16093387
APA StyleDomínguez-Cartes, V., Ramos-Cabeza, D., de la Torre, M. L., & Salguero-Andújar, F. (2023). Complete Generalization of the Equations for the Stress–Strain Curves of Concrete under Uniaxial Compression. Materials, 16(9), 3387. https://doi.org/10.3390/ma16093387





