Electronic Structure and Hole Transfer of All B-DNA Dimers and Homopolymers, via the Fishbone-Wire Model
Abstract
1. Introduction
2. System and Methods
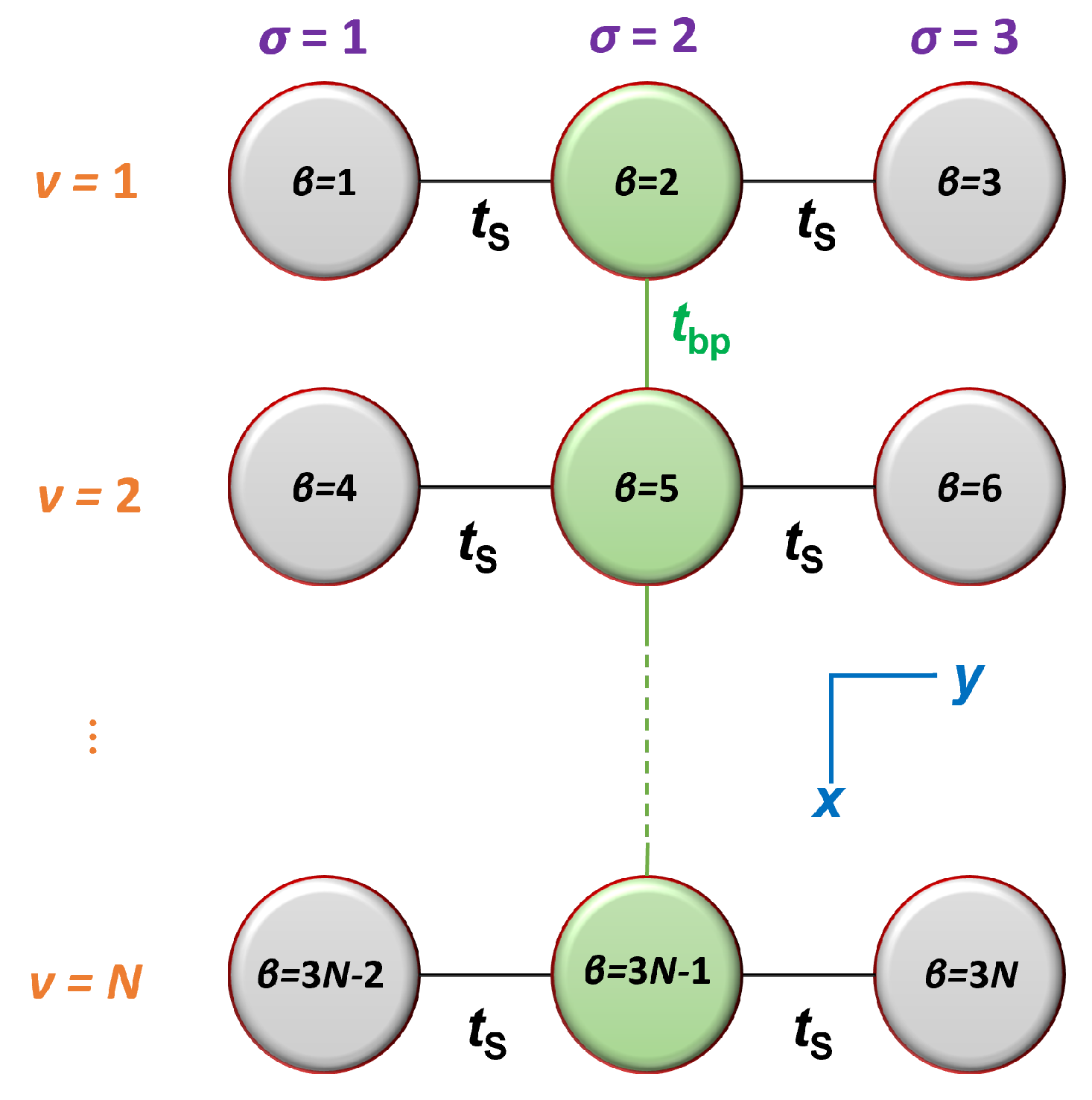
2.1. Hamiltonian
2.2. Time-Independent Problem
2.3. Density of States
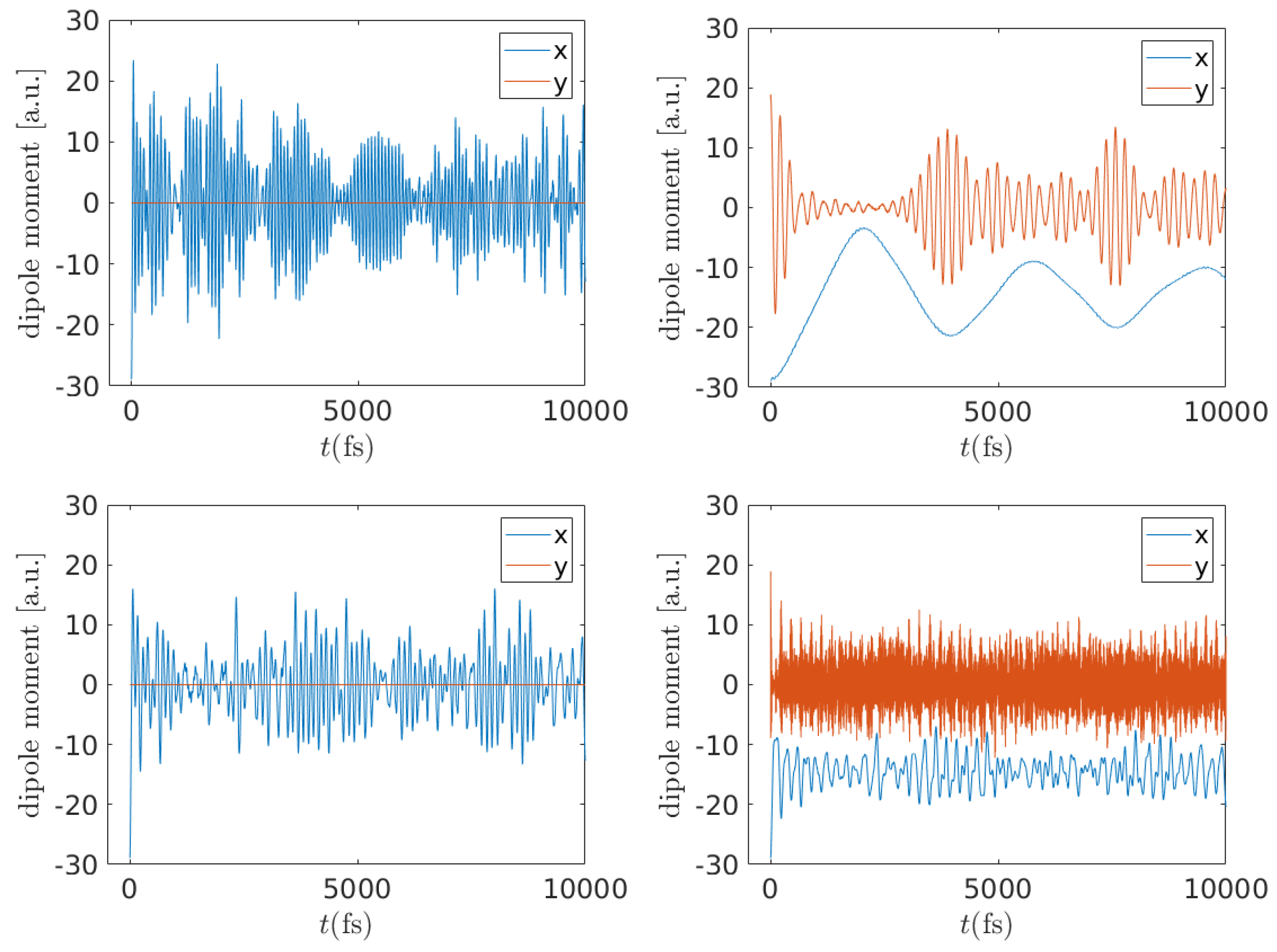
2.4. Time-Dependent Problem
3. Results and Discussion
3.1. Homopolymers
3.1.1. Eigenspectra
3.1.2. Density of States
3.1.3. Mean-over-Time Probabilities
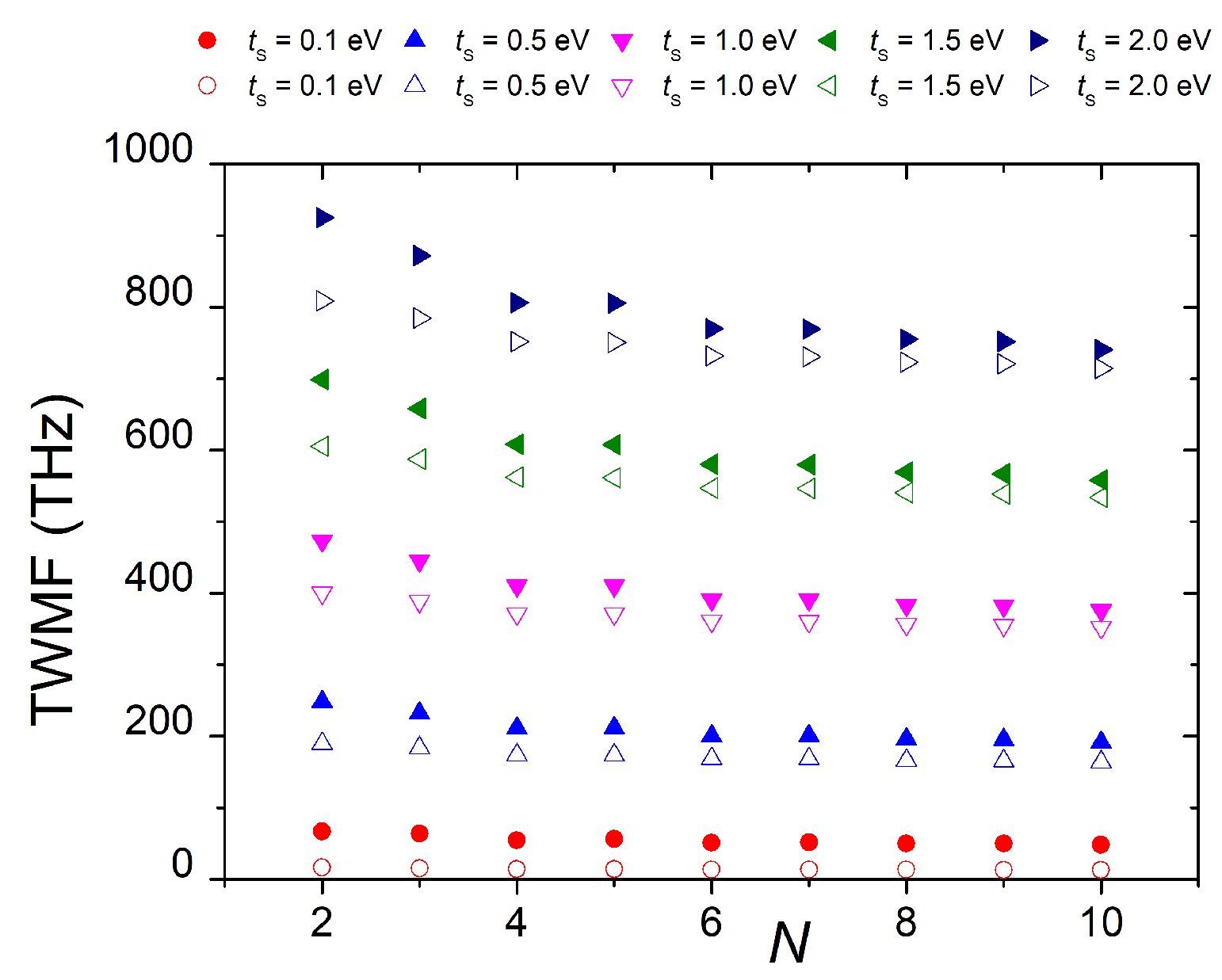
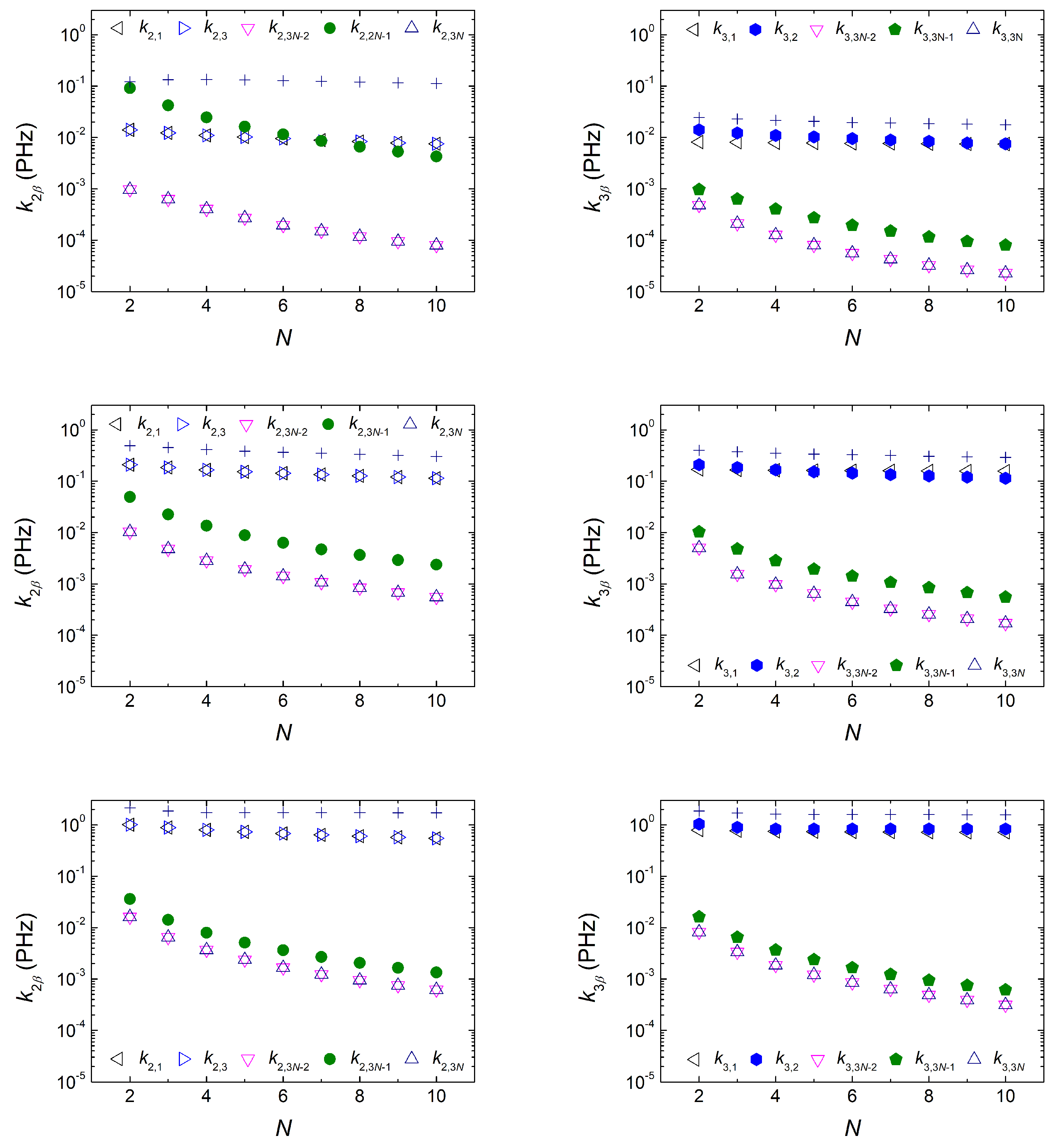
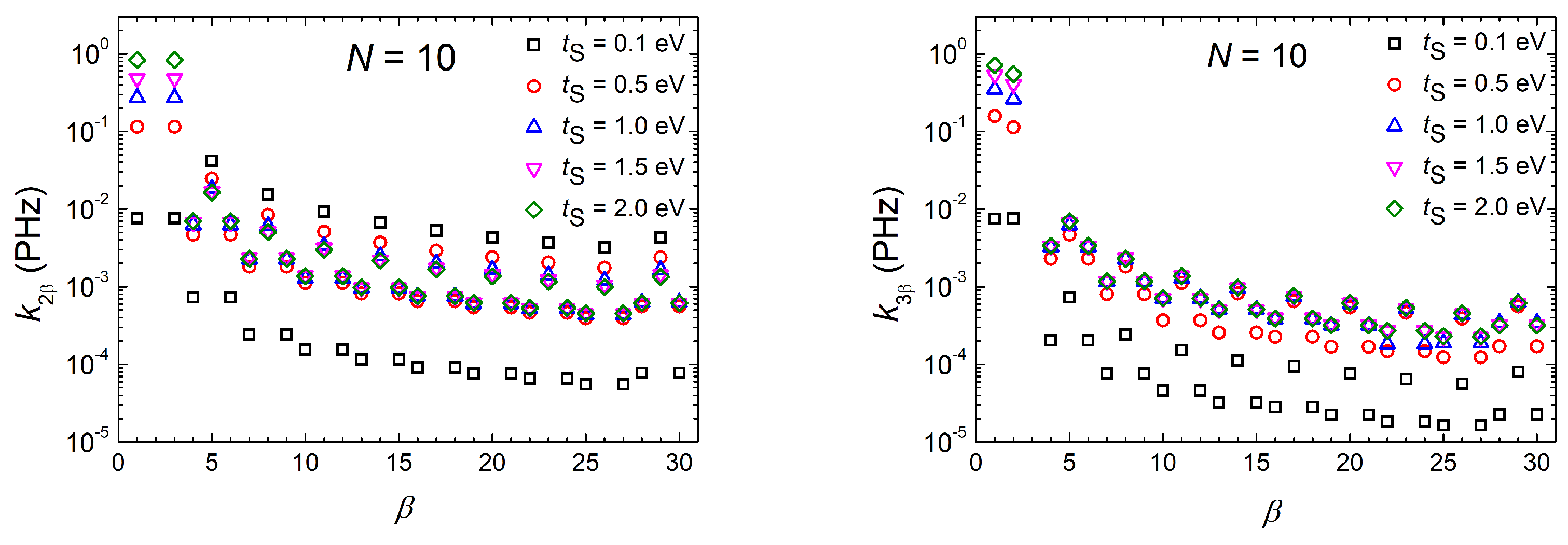
3.1.4. Frequency Content
3.1.5. Mean Transfer Rates
3.2. Dimers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TB | Tight Binding |
| FWM | Fishbone-Wire Model |
| DOS | Density of States |
| HOMO | Highest Occupied Molecular Orbital |
| LUMO | Lowest Unoccupied Molecular Orbital |
| WMF | Weighted Mean Frequency |
| TWMF | Total Weighted Mean Frequency |
Appendix A. Results for All Dimer Types
Appendix A.1. Dimers Made of Identical Monomers with Purine on Purine

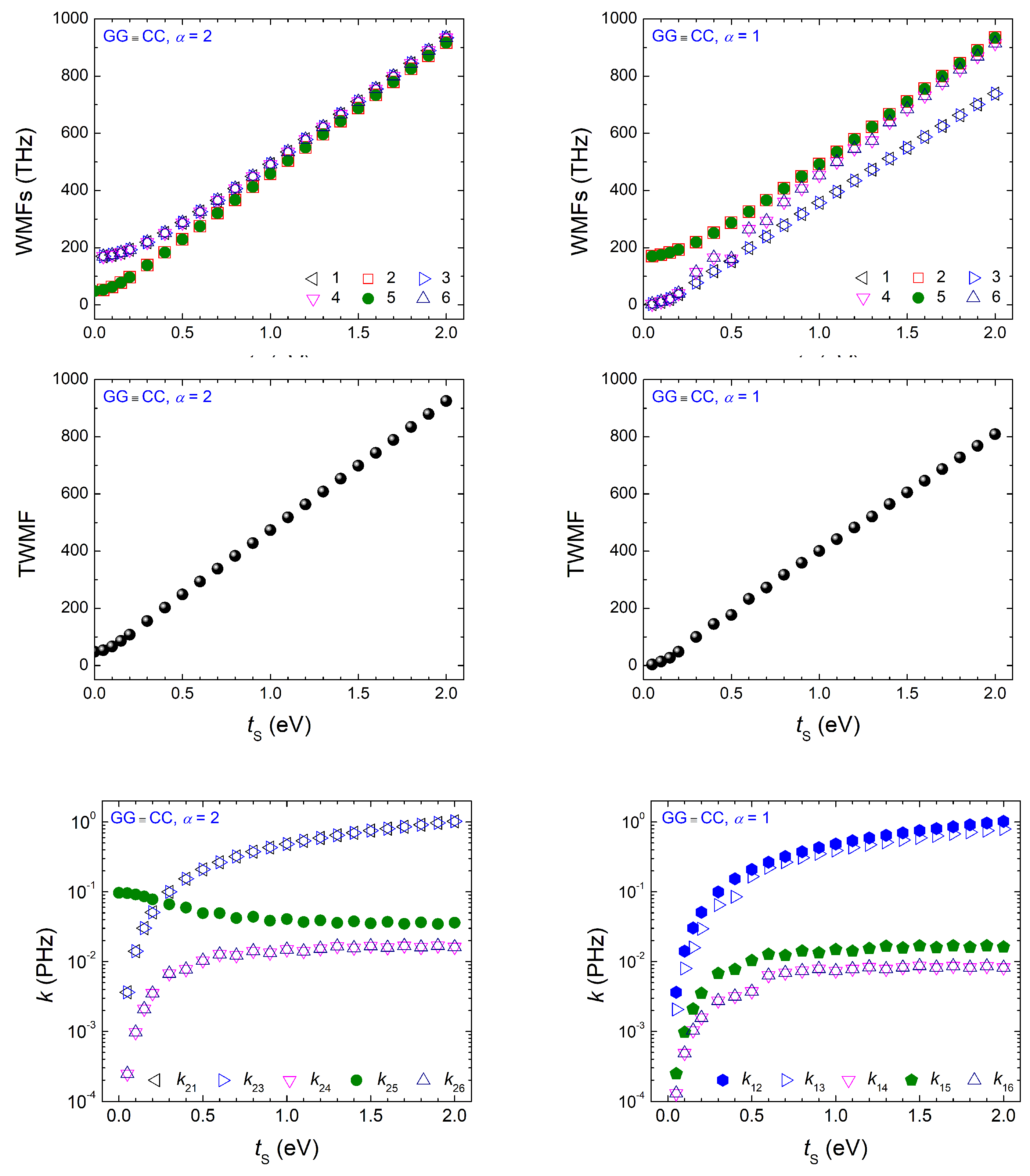
Appendix A.2. Dimers Made of Identical Monomers with Purine on Pyrimidine


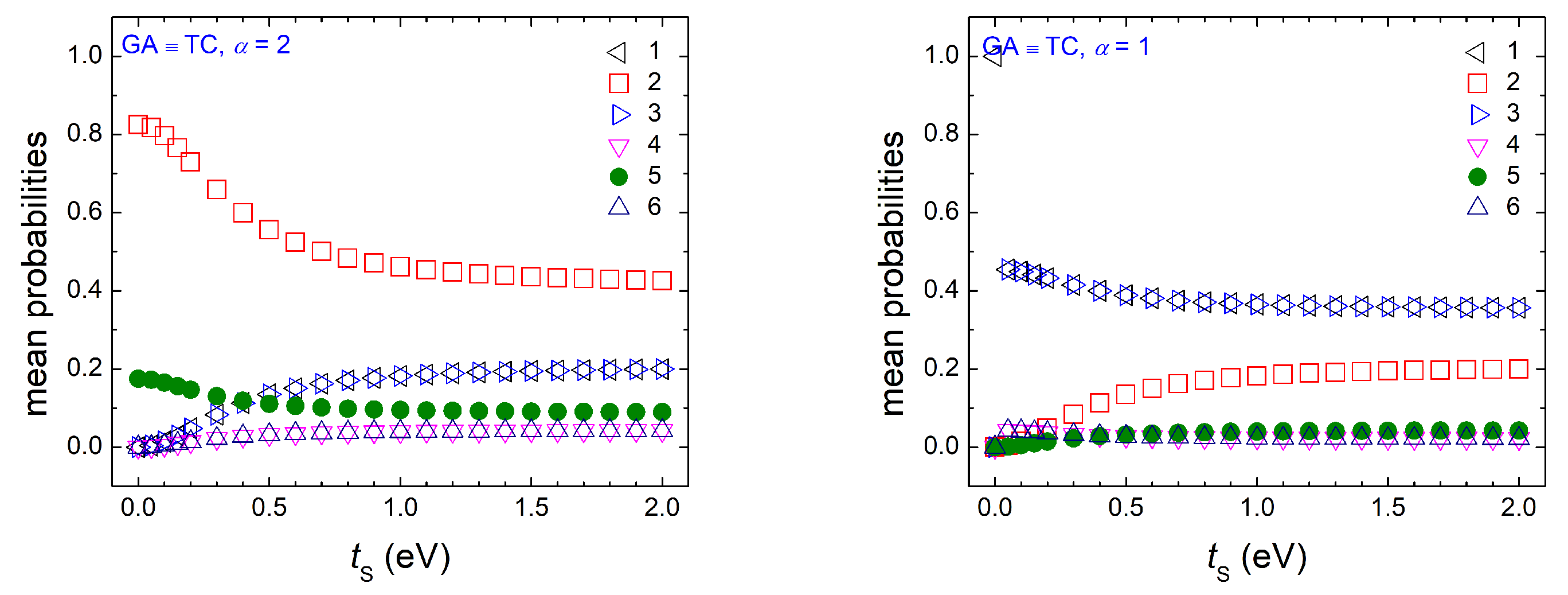
Appendix A.3. Dimers Made of Different Monomers

References
- Klotsa, D.; Roemer, R.A.; Turner, M.S. Electronic Transport in DNA. Biophys. J. 2005, 89, 2187–2198. [Google Scholar] [CrossRef] [PubMed]
- Cuniberti, G.; Craco, L.; Porath, D.; Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 2002, 65, 241314. [Google Scholar] [CrossRef]
- Zhong, J.X. Effects of backbone disorder on electronic transport in DNA molecules. In Proceedings of the 2003 Nanotechnology Conference and Trade Show-Nanotech 2003, San Francisco, CA, USA, 23–27 February 2003; Volume 2, pp. 105–108, ISBN 0972842209. Available online: https://www.ornl.gov/~webworks/cppr/y2001/pres/115736.pdf (accessed on 28 March 2023).
- Shih, C.T.; Roche, S.; Römer, R.A. Point-Mutation Effects on Charge-Transport Properties of the Tumor-Suppressor Gene p53. Phys. Rev. Lett. 2008, 100, 018105. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.T.; Wells, S.A.; Hsu, C.L.; Cheng, Y.Y.; Römer, R.A. The interplay of mutations and electronic properties in disease-related genes. Sci. Rep. 2012, 2, 272. [Google Scholar] [CrossRef] [PubMed]
- Joe, Y.S.; Lee, S.H.; Hedin, E.R.; Kim, Y.D. Temperature and Magnetic Field Effects on Electron Transport Through DNA Molecules in a Two-Dimensional Four-Channel System. J. Nanosci. Nanotechnol. 2013, 13, 3889–3896. [Google Scholar] [CrossRef] [PubMed]
- Jalilvand, S.; Sepahvand, R.; Mousavi, H. Electronic behavior of randomly dislocated RNA and DNA nanowires: A multi-model approach. Eur. Phys. J. Plus 2022, 137, 928. [Google Scholar] [CrossRef]
- Kurnia Suhendro, D.; Yudiarsah, E.; Saleh, R. Effect of phonons and backbone disorder on electronic transport in DNA. Phys. B Condens. Matter 2010, 405, 4806–4811. [Google Scholar] [CrossRef]
- Kundu, S.; Karmakar, S.N. Electronic specific heat of DNA: Effects of backbones and disorder. Phys. Lett. A 2015, 379, 1377–1383. [Google Scholar] [CrossRef]
- Páez, C.J.; Schulz, P.A.; Wilson, N.R.; Römer, R.A. Robust signatures in the current-voltage characteristics of DNA molecules oriented between two graphene nanoribbon electrodes. New J. Phys. 2012, 14, 093049. [Google Scholar] [CrossRef]
- Al-mebir, A.A.K.; Al-Saidi, S.A.A. Theoretical Investigation of Base Pairs-Dependent Electron Transport in DNA System. J. Phys. Conf. Ser. 2020, 1530, 012147. [Google Scholar] [CrossRef]
- Ojeda, J.H.; Orellana, P.A. DNA Molecule as a Spintronic Device. J. Supercond. Nov. Magn. 2013, 26, 2227–2230. [Google Scholar] [CrossRef]
- Walet, N.R.; Zakrzewski, W.J. A simple model of the charge transfer in DNA-like substances. Nonlinearity 2005, 18, 2615–2636. [Google Scholar] [CrossRef]
- Sarmento, R.G.; Albuquerque, E.L.; Sesion, P.D.; Fulco, U.L.; de Oliveira, B.P.W. Electronic transport in double-strand poly(dG)–poly(dC) DNA segments. Phys. Lett. A 2009, 373, 1486–1491. [Google Scholar] [CrossRef]
- Malakooti, S.; Hedin, E.R.; Kim, Y.D.; Joe, Y.S. Enhancement of charge transport in DNA molecules induced by the next nearest-neighbor effects. J. Appl. Phys. 2012, 112, 094703. [Google Scholar] [CrossRef]
- Malakooti, S.; Hedin, E.; Joe, Y. Tight-binding approach to strain-dependent DNA electronics. J. Appl. Phys. 2013, 114, 014701. [Google Scholar] [CrossRef]
- Hawke, L.G.D.; Kalosakas, G.; Simserides, C. Electronic Parameters for charge transfer along DNA. Eur. Phys. J. E 2010, 32, 291–305. [Google Scholar] [CrossRef]
- Simserides, C. A systematic study of electron or hole transfer along dimers, trimers and polymers. Chem. Phys. 2014, 440, 31–41. [Google Scholar] [CrossRef]
- Joe, Y.S.; Lee, S.H.; Hedin, E.R. Electron transport through asymmetric DNA molecules. Phys. Lett. A 2010, 374, 2367–2373. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Chatzieleftheriou, M.; Morphis, A.; Kaklamanis, K.; Theodorakou, M.; Simserides, C. Unbiased charge oscillations in B-DNA: Monomer polymers and dimer polymers. Phys. Rev. E 2015, 92, 032725. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Chatzieleftheriou, M.; Morphis, A.; Kaklamanis, K.; Lopp, R.; Theodorakou, M.; Tassi, M.; Simserides, C. Electronic structure and carrier transfer in B-DNA monomer polymers and dimer polymers: Stationary and time-dependent aspects of a wire model versus an extended ladder model. Phys. Rev. E 2016, 94, 062403. [Google Scholar] [CrossRef]
- Ghosh, D.; Golan, A.; Takahashi, L.K.; Krylov, A.I.; Ahmed, M. A VUV Photoionization and Ab Initio Determination of the Ionization Energy of a Gas-Phase Sugar (Deoxyribose). J. Phys. Chem. Lett. 2012, 3, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. Electronic structure and transport properties of double-stranded Fibonacci DNA. Phys. Rev. B 2006, 74, 245105. [Google Scholar] [CrossRef]
- Maciá, E.; Roche, S. Backbone-induced effects in the charge transport efficiency of synthetic DNA molecules. Nanotechnology 2006, 17, 3002. [Google Scholar] [CrossRef]
- Endres, R.G.; Cox, D.L.; Singh, R.R.P. Colloquium: The quest for high-conductance DNA. Rev. Mod. Phys. 2004, 76, 195–214. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Jortner, J.; Bixon, M.; Rösch, N. Electronic coupling between Watson-Crick pairs for hole transfer and transport in desoxyribonucleic acid. J. Chem. Phys. 2001, 114, 5614–5620. [Google Scholar] [CrossRef]
- Migliore, A.; Corni, S.; Varsano, D.; Klein, M.L.; Di Felice, R. First Principles Effective Electronic Couplings for Hole Transfer in Natural and Size-Expanded DNA. J. Phys. Chem. B 2009, 113, 9402–9415. [Google Scholar] [CrossRef]
- Kubar, T.; Woiczikowski, P.B.; Cuniberti, G.; Elstner, M. Efficient Calculation of Charge Transfer Matrix Elements for Hole Transfer in DNA. J. Phys. Chem. B 2008, 112, 7937–7947. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, A.; Shushkov, P.; Rösch, N. Systematic Study of the Influence of Base Step Parametres on the Electronic Coupling between Base Pair Dimers: Comparison of A-DNA and B-DNA Forms. J. Phys. Chem. A 2008, 112, 7106–7114. [Google Scholar] [CrossRef] [PubMed]
- Mantela, M.; Morphis, A.; Lambropoulos, K.; Simserides, C.; Di Felice, R. Effects of Structural Dynamics on Charge Carrier Transfer in B-DNA: A Combined MD and RT-TDDFT Study. J. Phys. Chem. B 2021, 125, 3986–4003. [Google Scholar] [CrossRef]
- Mantela, M.; Simserides, C.; Di Felice, R. LCAO Electronic Structure of Nucleic Acid Bases and Other Heterocycles and Transfer Integrals in B-DNA, including Structural Variability. Materials 2021, 14, 4930. [Google Scholar] [CrossRef]
- Bagci, V.M.K.; Krokhin, A.A. Metal-insulator transition in DNA molecules induced by long-range correlations in the sequence of nucleotides. Chaos Solitons Fractals 2007, 34, 104–111. [Google Scholar] [CrossRef]
- González, J.E.; Cruz-Irisson, M.; Sánchez, V.; Wang, C. Thermoelectric transport in poly(G)-poly(C) double chains. J. Phys. Chem. Solids 2020, 136, 109136. [Google Scholar] [CrossRef]
- Orfanaki, E. Charge Transfer in DNA Polymers: Fishbone Description at the Base-Pair Level. BSc Diploma Thesis, National and Kapodistrian University of Athens, Athens, Greece, 2023. Available online: http://users.uoa.gr/~csimseri/OrfanakiEBScDiplomaThesis.pdf (accessed on 28 March 2023). (In Greek).
- Kawai, K.; Takada, T.; Tojo, S.; Majima, T. Kinetics of Weak Distance-Dependent Hole Transfer in DNA by Adenine-Hopping Mechanism. J. Am. Chem. Soc. 2003, 125, 6842–6843. [Google Scholar] [CrossRef] [PubMed]
- Margariti, N. Hole Transfer in DNA Dimers: Fishbone-Wire Model Description. BSc Diploma Thesis, National and Kapodistrian University of Athens, Athens, Greece, 2022. Available online: http://users.uoa.gr/~csimseri/MargaritiNBScDiplomaThesis.pdf (accessed on 28 March 2023). (In Greek).




| Dimer | t | Dimer | t | Dimer | t | Dimer | t |
|---|---|---|---|---|---|---|---|
| AA≡TT | 20 | GG≡CC | 100 | ||||
| AT | −35 | GC | −10 | AG≡CT | 30 | TC≡GA | 110 |
| TA | −50 | CG | 50 | AC≡GT | −10 | TG≡CA | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simserides, C.; Orfanaki, A.; Margariti, N.; Lambropoulos, K. Electronic Structure and Hole Transfer of All B-DNA Dimers and Homopolymers, via the Fishbone-Wire Model. Materials 2023, 16, 3200. https://doi.org/10.3390/ma16083200
Simserides C, Orfanaki A, Margariti N, Lambropoulos K. Electronic Structure and Hole Transfer of All B-DNA Dimers and Homopolymers, via the Fishbone-Wire Model. Materials. 2023; 16(8):3200. https://doi.org/10.3390/ma16083200
Chicago/Turabian StyleSimserides, Constantinos, Aikaterini Orfanaki, Neokleia Margariti, and Konstantinos Lambropoulos. 2023. "Electronic Structure and Hole Transfer of All B-DNA Dimers and Homopolymers, via the Fishbone-Wire Model" Materials 16, no. 8: 3200. https://doi.org/10.3390/ma16083200
APA StyleSimserides, C., Orfanaki, A., Margariti, N., & Lambropoulos, K. (2023). Electronic Structure and Hole Transfer of All B-DNA Dimers and Homopolymers, via the Fishbone-Wire Model. Materials, 16(8), 3200. https://doi.org/10.3390/ma16083200






