Multi-Scale Topology Optimization of Femoral Stem Structure Subject to Stress Shielding Reduce
Abstract
1. Introduction
- Considering the mechanical characteristics and structural composition of the femoral stem and the flexibility variation amplitude of the femoral stem structure, multi-scale parallel topology optimization is proposed;
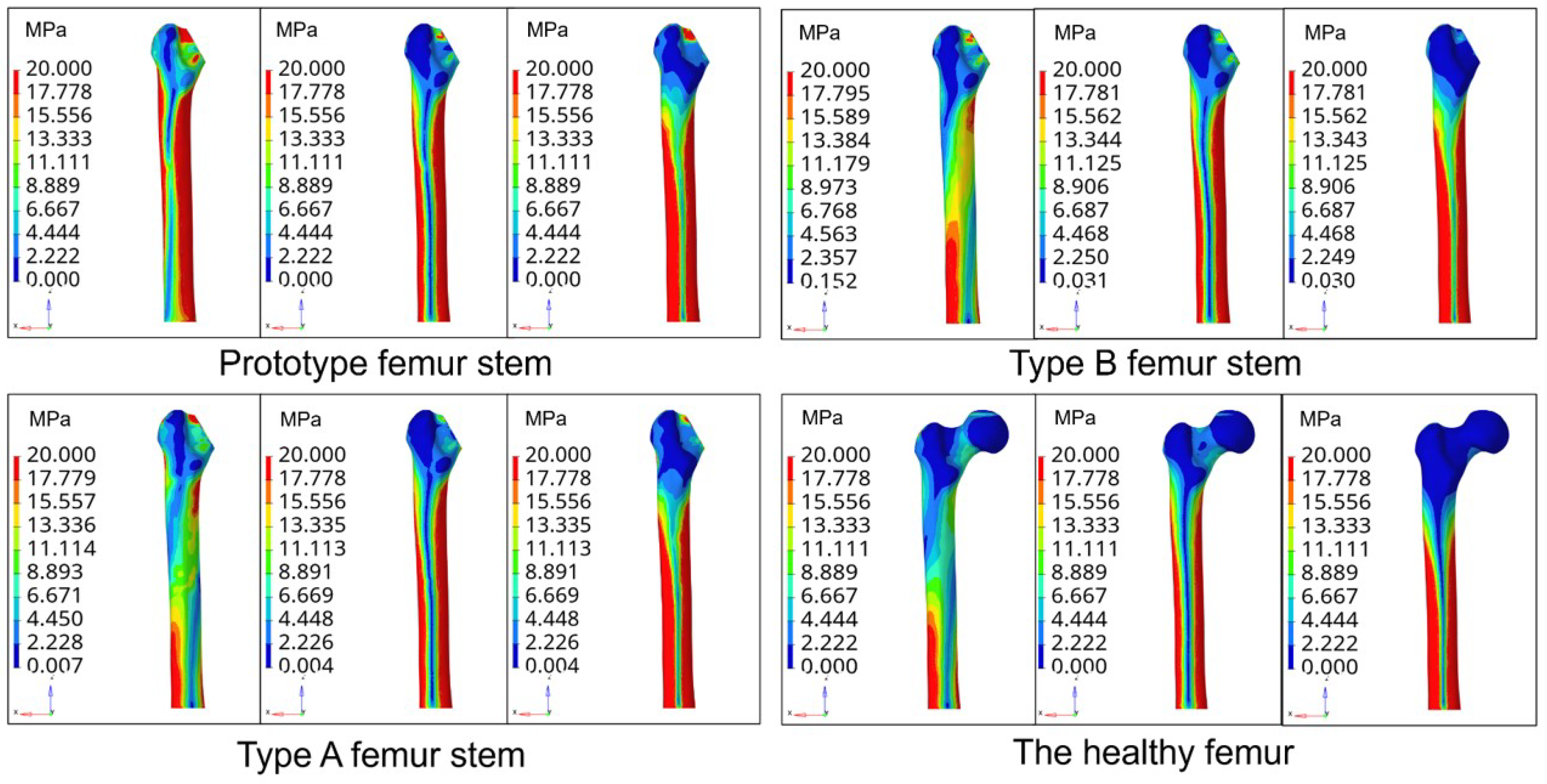
- Compared with the traditional topology optimization method (SIMP), the average stress of the type B femoral stem is MPa and the stress shielding reduction is ;
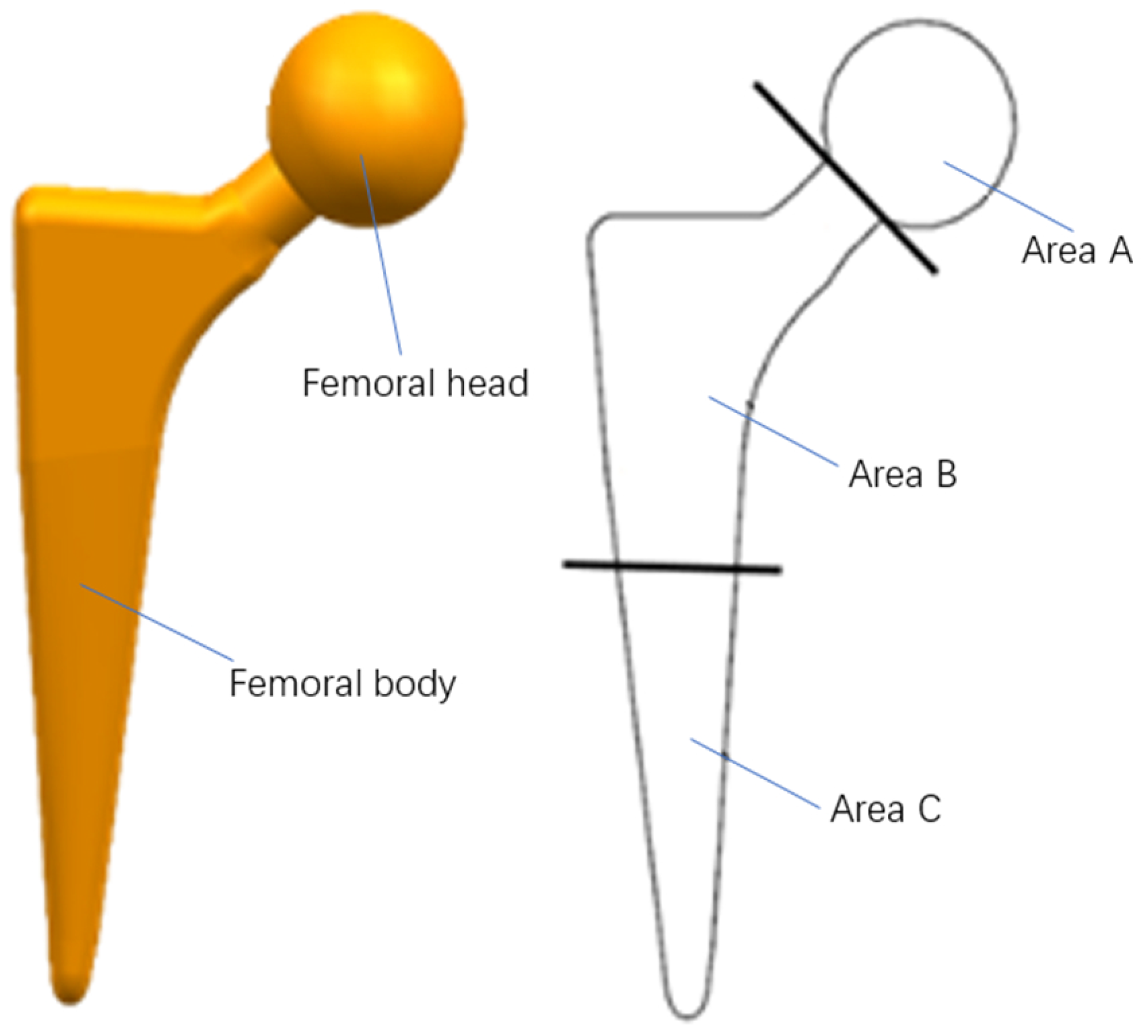
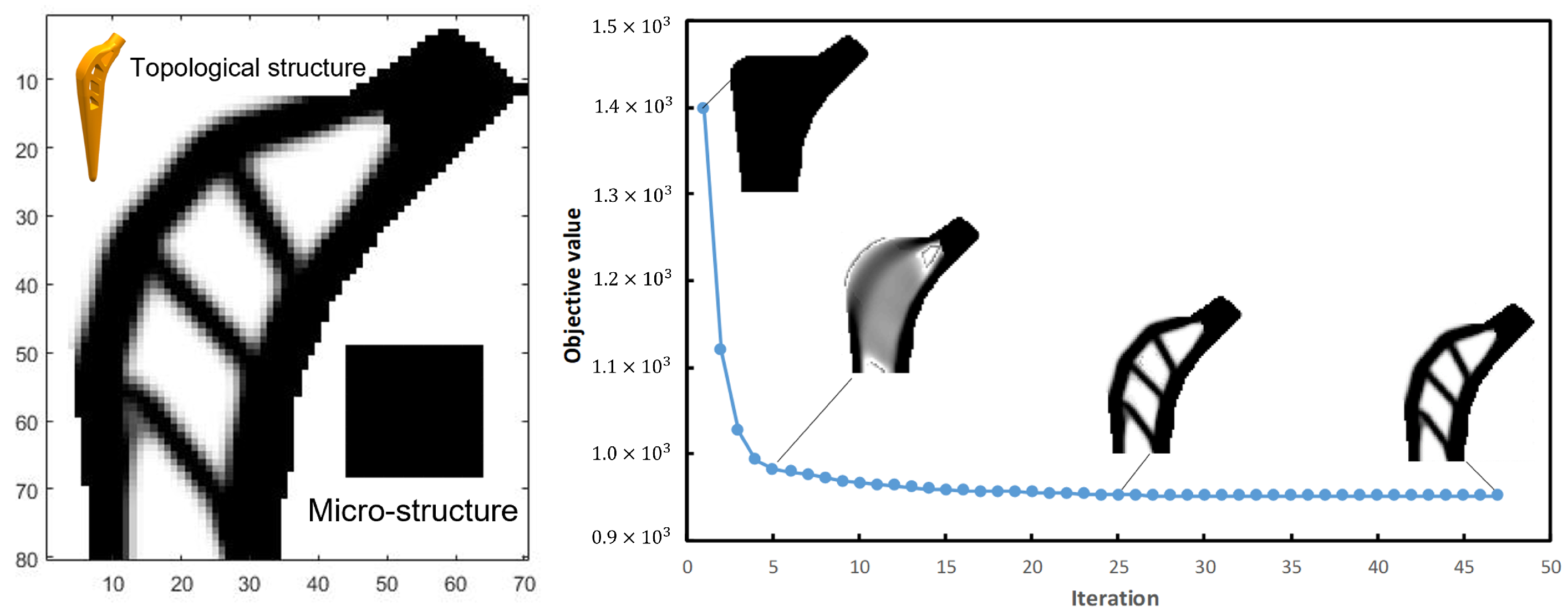
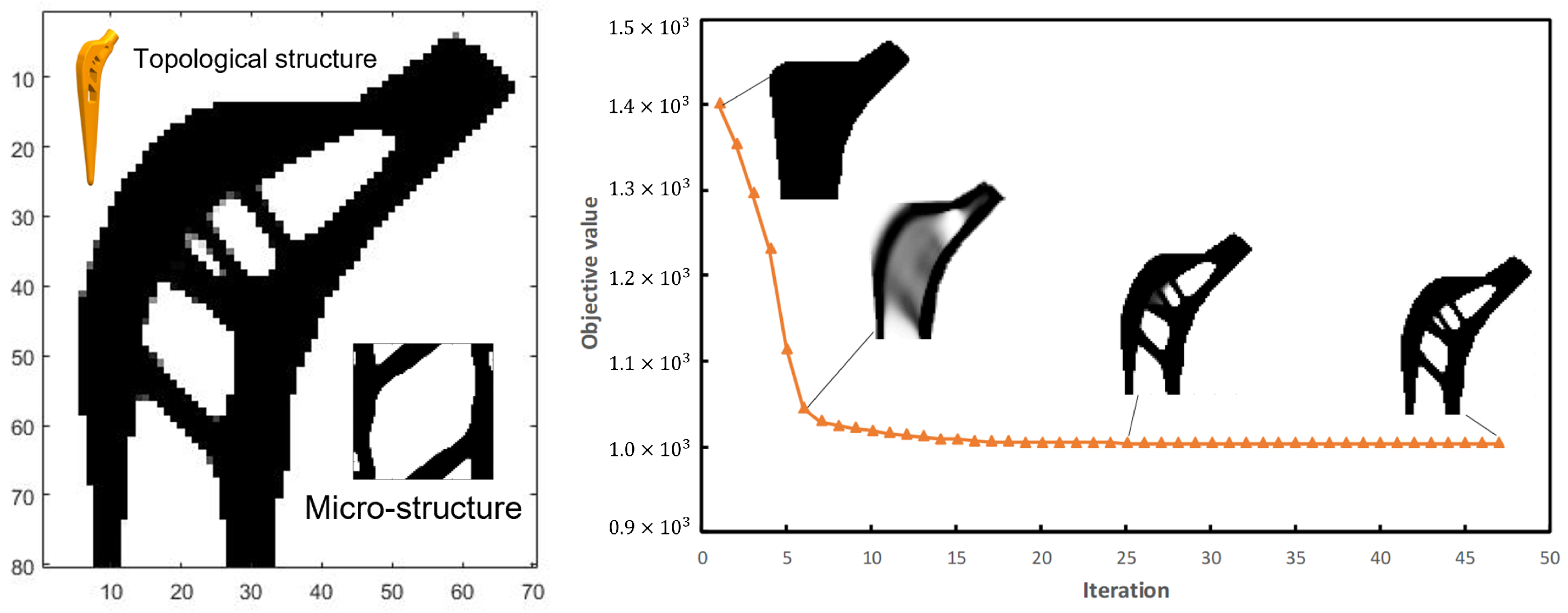
2. Method Description and Topological Model
3. Design of Prosthetic Femoral Stem
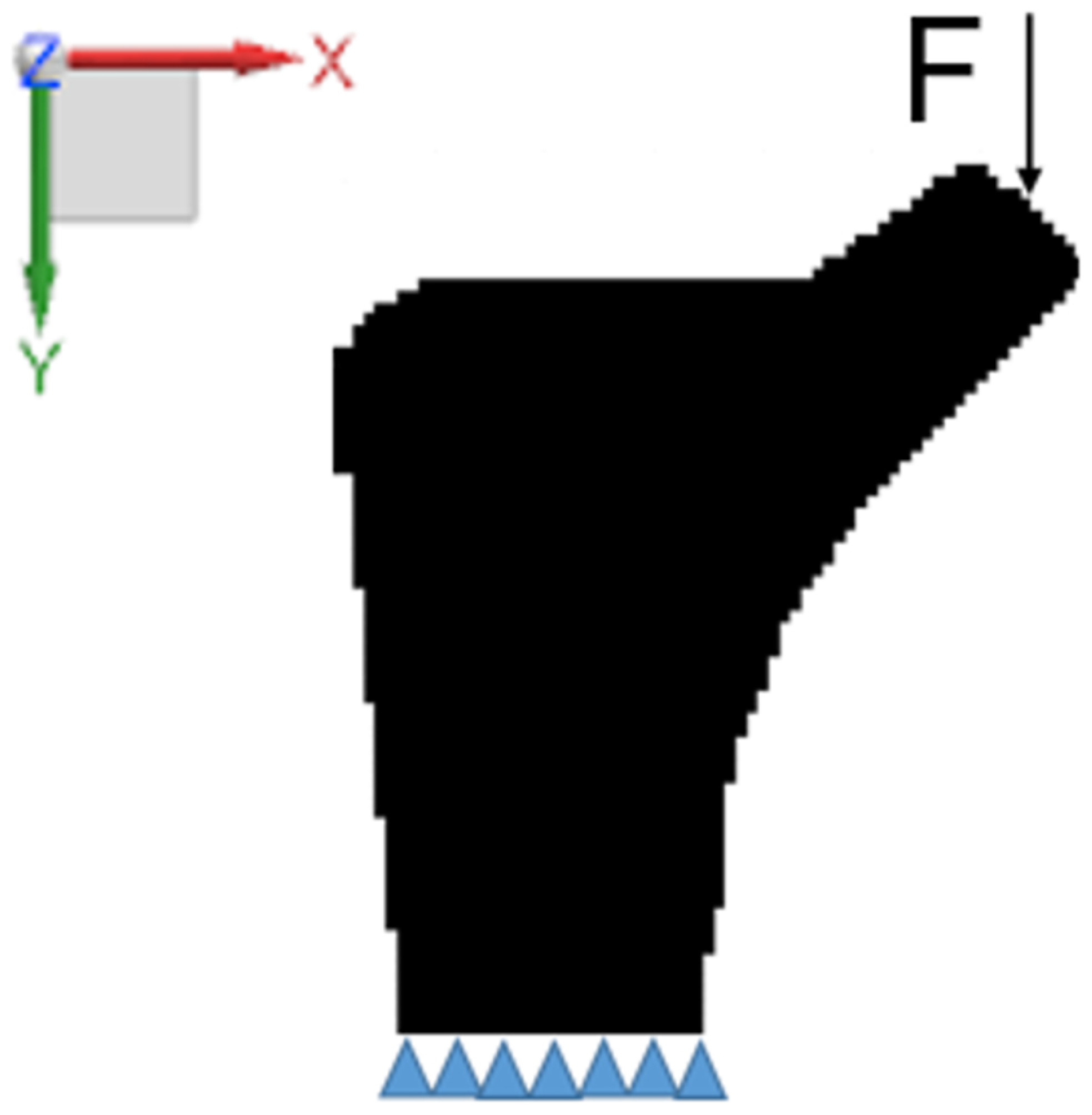
4. Simulations
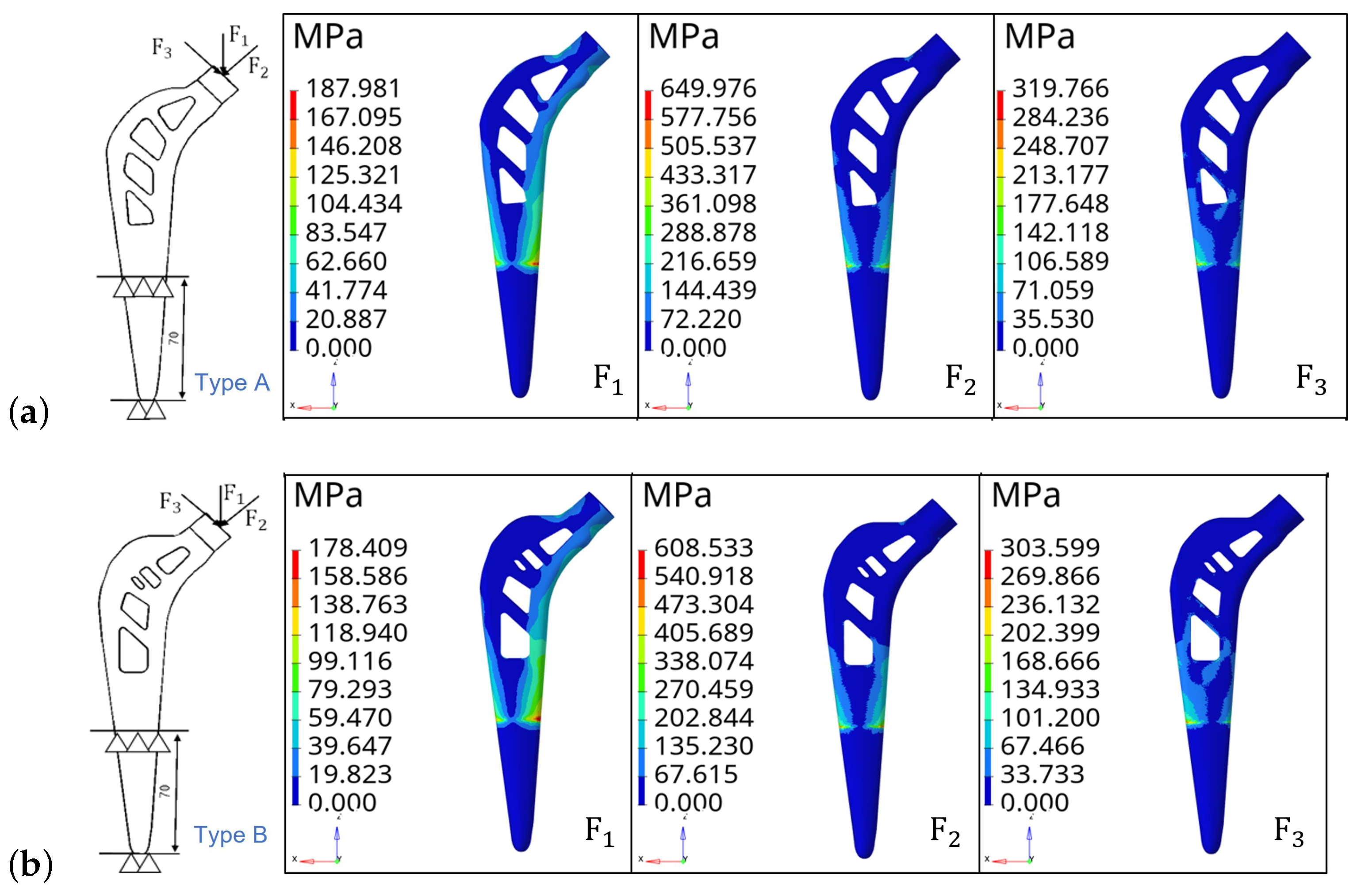
4.1. Effect of Load Direction Change on Structure
4.2. Stress Analysis with Multi-Condition
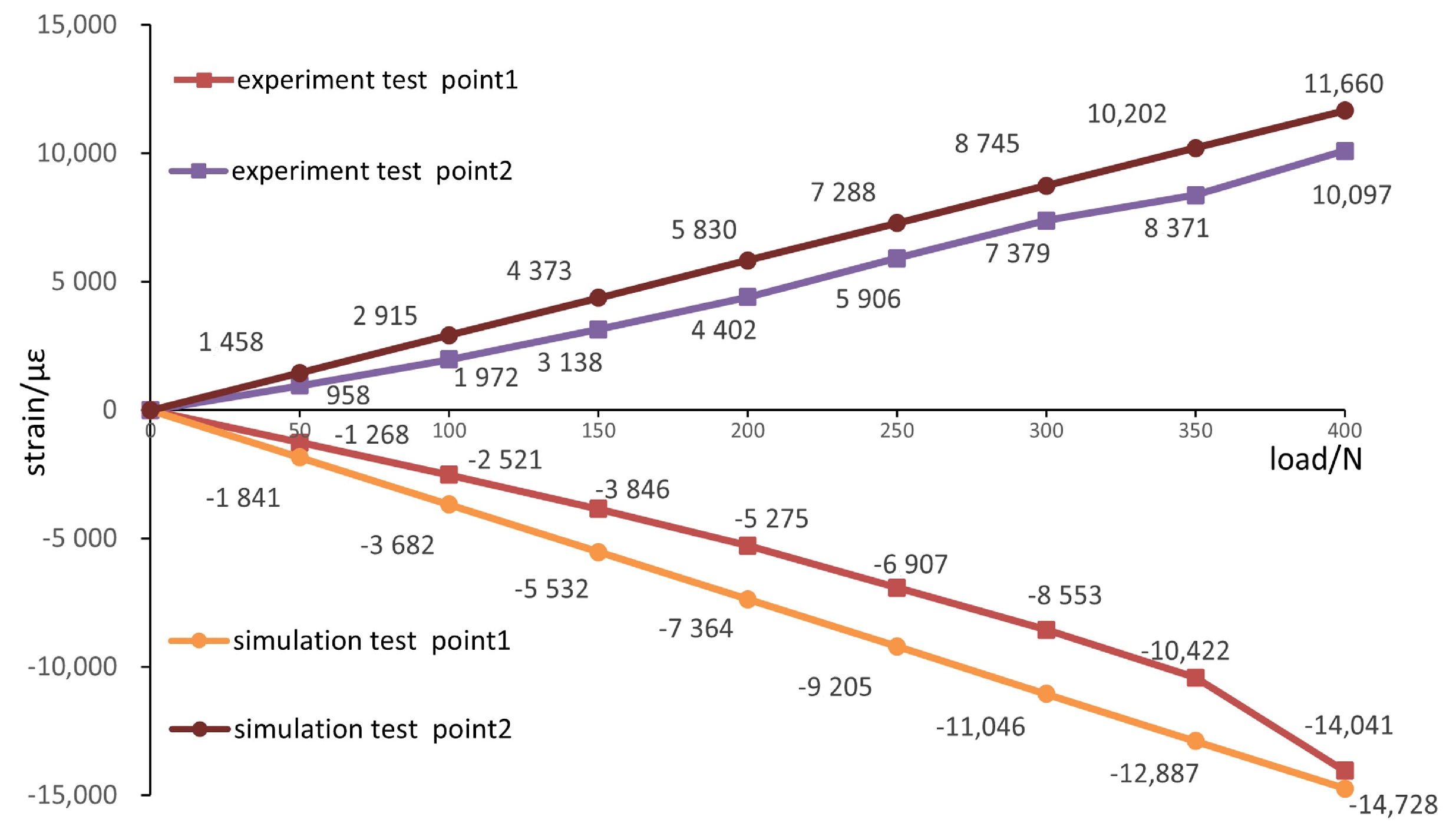
5. Experiments
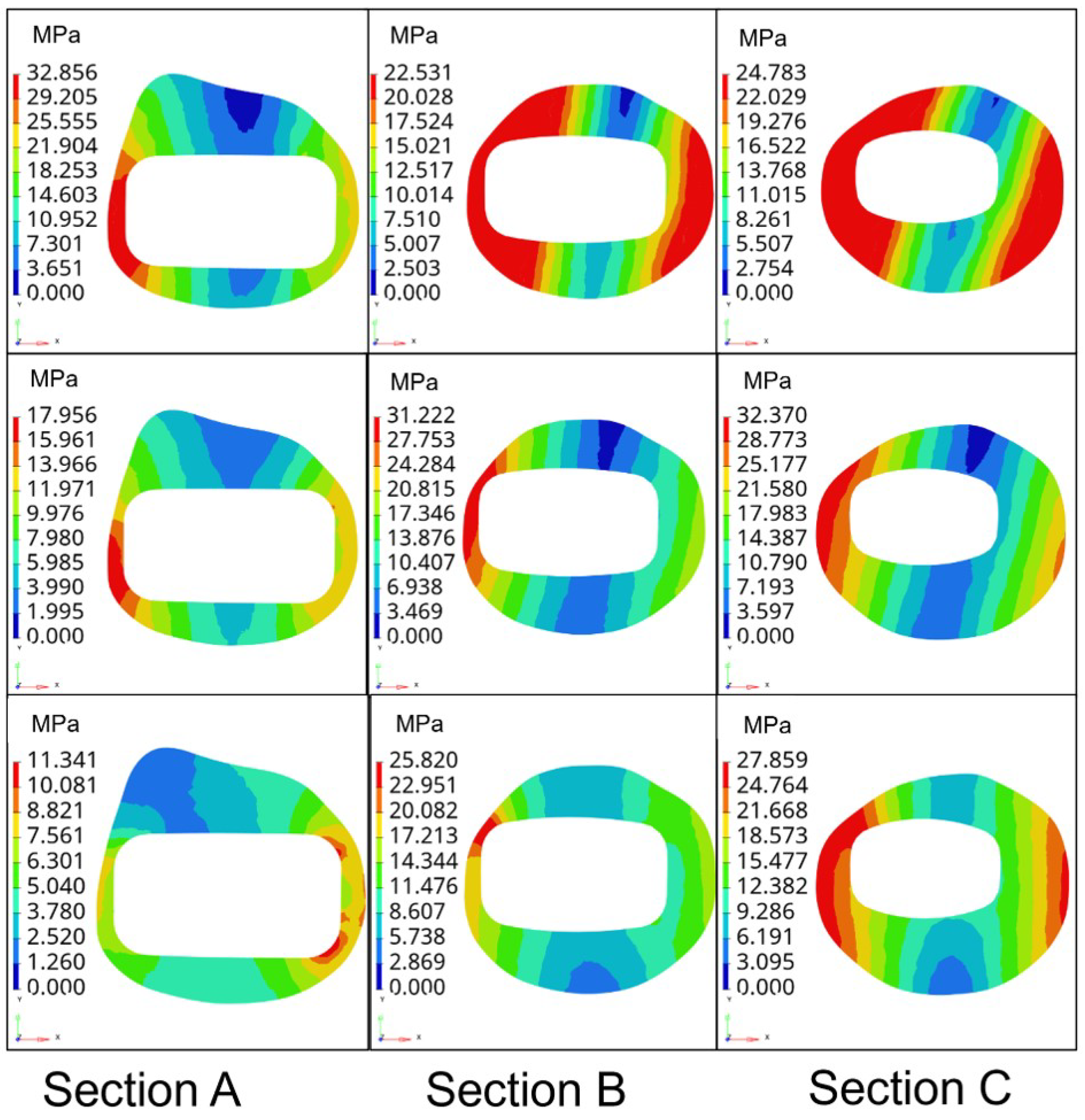
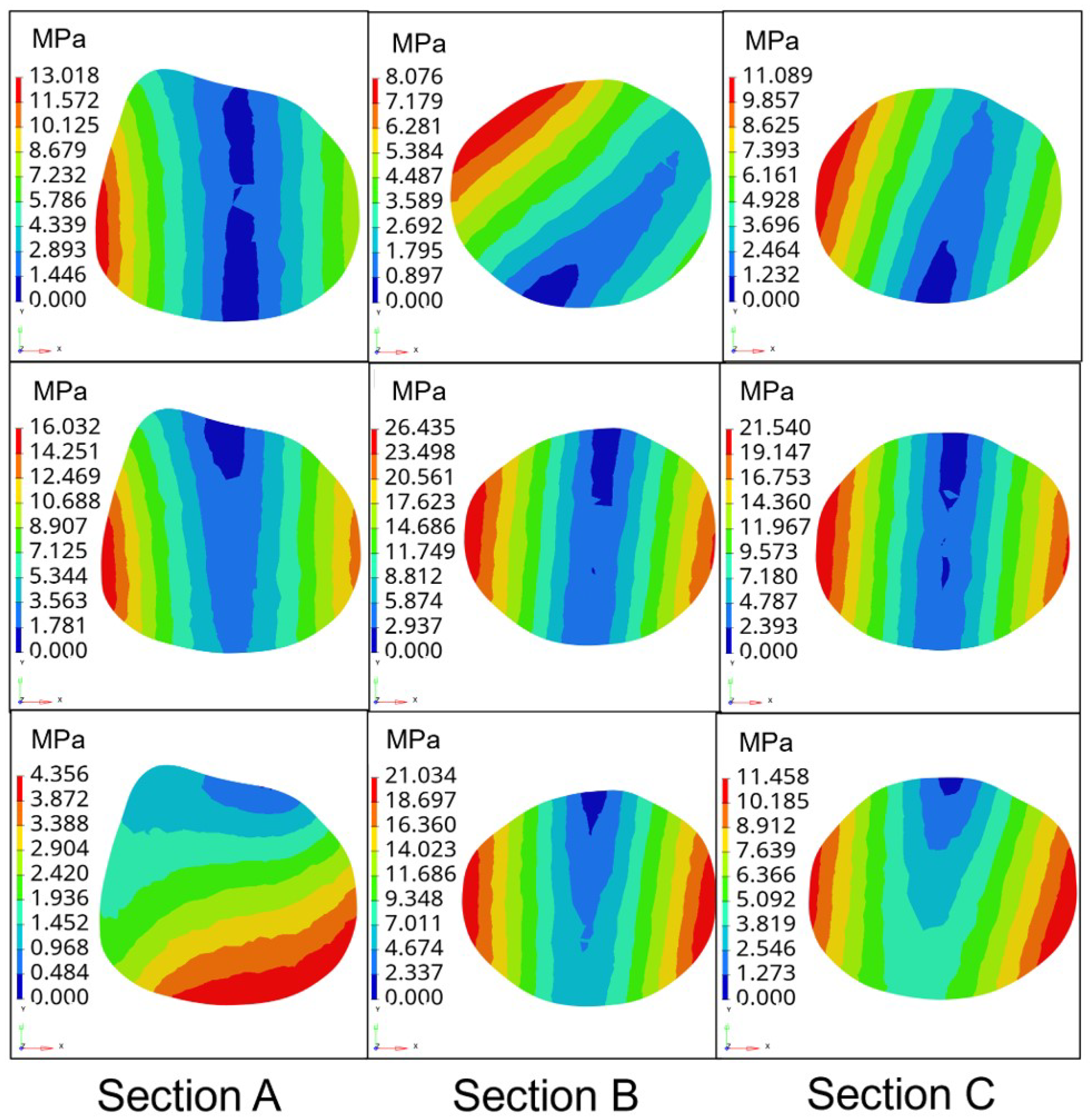
5.1. Experimental Process and Results
5.2. Finite Element Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.H.; Money, B.F.; An, K.N.; Luo, Z.P. Bone remodeling characteristics of a short-stemmed total hip replacement. J. Arthroplast. 2009, 24, 945–950. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.Y.; Naghavi, S.A.; Wang, Z.Q.; Varma, S.N.; Han, Z.W.; Yao, Z.W.; Wang, L.; Wang, L.Q.; Liu, C.Z. On the design evolution of hip implants: A review. Mater. Des. 2022, 216, 110552. [Google Scholar] [CrossRef]
- Shubnyakov, I.I.; Riahi, A.; Shubnyakov, M.I.; Denisov, A.O.; Khujanazarov, I.E.; Tikhilov, R.M. Cementless hip implants: History and current status of the issue. Traumatol. Orthop. Russ. 2020, 26, 160–179. [Google Scholar] [CrossRef]
- Acosta-Sinchez, L.A.; Botello-Arredondo, A.I.; Moya-Bencomo, M.D.; Zúñiga-Aguilar, E.S. Porous lattice structure of femoral stem for total hip arthroplasty. Rev. Mex. Ing. Biomed. 2020, 41, 69–79. [Google Scholar]
- Sun, C.N.; Wang, L.; Kang, J.F.; Li, D.C.; Jin, Z.M. Biomechanical optimization of elastic modulus distribution in porous femoral stem for artificial hip joints. J. Bionic Eng. 2020, 15, 693–702. [Google Scholar] [CrossRef]
- Jette, B.; Brailovski, V.; Dumas, M.; Simoneau, C.; Terriault, P. Femoral stem incorporating a diamond cubic lattice structure: Design, manufacturing and testing. J. Mech. Behav. Biomed. 2018, 77, 58–72. [Google Scholar] [CrossRef] [PubMed]
- Jette, B.; Brailovski, V.; Simoneau, C.; Dumas, M.; Terriault, P. Development and in vitro validation of a simplified numerical model for the design of a biomimetic femoral stem. J. Mech. Behav. Biomed. 2018, 77, 539–550. [Google Scholar] [CrossRef]
- Alkhatib, S.E.; Tarlochan, F.; Mehboob, H.; Singh, R.; Kadirgama, K.; Harun, W.S.B. Finite element study of functionally graded porous femoral stems incorporating body-centered cubic structure. Artif. Organs. 2019, 43, E152–E164. [Google Scholar] [CrossRef]
- Al Zoubi, N.F.; Tarlochan, F.; Mehboob, H.; Jarrar, F. Design of titanium alloy femoral stem cellular structure for stress shielding and stem stability: Computational analysis. Appl. Sci. 2022, 12, 1548. [Google Scholar] [CrossRef]
- Al Zoubi, N.F.; Tarlochan, F.; Mehboob, H. Mechanical and fatigue behavior of cellular structure Ti-6AL-4V alloy femoral stems: A finite element analysis. Appl. Sci. 2022, 12, 4197. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, X.; Liu, L.L.; Shi, Z.A.; Hao, Y.Q. On the design and properties of porous femoral stems with adjustable stiffness gradient. Med. Eng. Phys. 2020, 81, 30–38. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.W.; Gong, H. Biomechanical effects of tibial stems with different structures on human knee joint after total knee arthroplasty: A finite element analysis. J. Bionic Eng. 2022, 19, 197–208. [Google Scholar] [CrossRef]
- Mehboob, H.; Tarlochan, F.; Mehboob, A.; Chang, S.H. Finite element modelling and characterization of 3D cellular microstructures for the design of cementless biomimetic porous hip stem. Mater. Des. 2018, 149, 101–112. [Google Scholar] [CrossRef]
- Ghavidelnia, N.; Bodaghi, M.; Hedayati, R. Femur auxetic meta-implants with tuned micromotion distribution. Materials 2021, 14, 114. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.S.; Zhao, Y.H.; Wang, M.; Liu, Z.Y.; Liu, C.Z. Parametric design of hip implant with gradient porous structure. Front. Bioeng. Biotech. 2022, 10, 850184. [Google Scholar] [CrossRef]
- Liu, B.L.; Wang, H.Z.; Zhang, M.; Liu, J.W.; Zhang, N.Z.; Luan, Y.C.; Fang, C.H.; Cheng, C.K. Capability of auxetic femoral stems to reduce stress shielding after total hip arthroplasty. J. Orthop. Transl. 2023, 38, 220–228. [Google Scholar] [CrossRef]
- Liu, B.L.; Wang, H.Z.; Zhang, N.Z.; Zhang, M.; Cheng, C.K. Femoral stems with porous lattice structures: A review. Front. Bioeng. Biotech. 2022, 9, 772539. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.Y.; Yan, X.C.; Yin, S.; Liu, L.L.; Liu, X.; Zhao, G.R.; Ma, W.Y.; Qi, W.Z.; Ren, Z.M.; Liao, H.L.; et al. Influence of the pore size and porosity of selective laser melted Ti6Al4V ELI porous scaffold on cell proliferation osteogenesis and bone ingrowth. Mat. Sci. Eng. C Mater. 2020, 106, 110289. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.C.; Wu, L.F.; He, Y.L. Three-dimensional force decoupling soft sensor with topological elastomer. Mathematics 2023, 11, 396. [Google Scholar] [CrossRef]
- Hazlehurst, K.B.; Wang, C.J.; Stanford, M. The potential application of a cobalt chrome molybdenum femoral stem with functionally graded orthotropic structures manufactured using laser melting technologies. Med. Hypotheses 2013, 81, 1096–1099. [Google Scholar] [CrossRef]
- Messina, C.; Usuelli, F.G.; Maccario, C.; Di Silvestri, C.A.; Gitto, S.; Cortese, M.C.; Albano, D.; Sconfienza, L.M. Precision of Bone Mineral Density Measurements Around Total Ankle Replacement Using Dual Energy X-ray Absorptiometry. J. Clin. Densitom. 2020, 23, 656–663. [Google Scholar] [CrossRef]
- Nandi, S.; Shah, A.; Joukar, A.; Becker, K.; Crutchfield, C.; Goe, V. Short-wedge stems have higher risk of periproshetic fracture than other cementless stem designs in Dorr type A femurs: A finite element analysis. Hip. Int. 2022, 32, 298–303. [Google Scholar] [CrossRef]
- Wang, M.N. Optimization of femoral prosthesis based on comprehensive evaluation of structure and material properties. J. Mech. Med. Biol. 2016, 16, 1640013. [Google Scholar] [CrossRef]
- Avila, J.D.; Bandyopadhyay, Z. Zirconia-toughened alumina coated Ti6Al4V via additive manufacturing. Mater. Lett. 2021, 291, 129577. [Google Scholar] [CrossRef] [PubMed]
- Da Costa, R.R.C.; de Almeida, F.R.B.; da Silva, A.A.X.; Domiciano, S.M.; Vieira, A.F.C. Design of a polymeric composite material femoral stem for hip joint implant. Polimeros 2019, 29, e2019057. [Google Scholar] [CrossRef]
- Maji, P.K.; Roychowdhury, A.; Datta, D. Minimizing stress shielding effect of femoral stem-a review. J. Med. Imaging Health Inform. 2013, 3, 171–178. [Google Scholar] [CrossRef]
- Liang, K.X.; Zhu, D.C.; Liu, J. Topology optimization of a spatial compliant parallel mechanism based on constant motion transmission characteristic matrix. Mech. Mach. Theory 2023, 180, 105125. [Google Scholar] [CrossRef]
- Hennicke, N.S.; Saemann, M.; Kluess, D.; Bader, R.; Sander, M. Subject specific finite element modelling of periprosthetic femoral fractures in different load cases. J. Mech. Behav. Biomed. 2022, 126, 105059. [Google Scholar] [CrossRef] [PubMed]
- Metzner, F.; Neupetsch, C.; Carabello, A.; Pietsch, M.; Wendler, T.; Drossel, W.-G. Biomechanical validation of additively manufactured artificial femoral bones. BMC Biomed. Eng. 2022, 4, 6. [Google Scholar] [CrossRef]
- Sun, C.N.; Kang, J.F.; Wang, L.; Jin, Z.M.; Liu, C.Z.; Li, D.C. Stress-dependent design and optimization methodology of gradient porous implant and application in femoral stem. Comput. Methods Biomech. Biomed. Eng. 2022. [Google Scholar] [CrossRef]
- Gungorurler, M.; Gursan, O.; Havitcioglu, H. Computational analysis of the effects of interprosthetic distance on normal and reduced cortical thickness femur models. Proc. Inst. Mech. Eng. Part J. Eng. Med. 2022, 236, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Tan, N.; van Aekel, R.J. Topology optimisation for compliant hip implant design and reduced strain shielding. Materials 2021, 14, 7184. [Google Scholar] [CrossRef]
- Cheng, C.; Dai, N.; Huang, J.; Zhuang, Y.H.; Tang, T.; Yang, M.N. Topological optimization design for a multiscale femoral prosthesis model based on homogenization method. Sci. Program. 2022, 2022, 4243476. [Google Scholar] [CrossRef]
- Nomura, J.; Takezawa, A.; Zhang, H.; Kitamura, M. Design optimization of functionally graded lattice infill total hip arthroplasty stem for stress shielding reduction. Proc. Inst. Mech. Eng. Part J. Eng. Med. 2022, 236, 515–525. [Google Scholar] [CrossRef] [PubMed]
- Xue, H.W.; Bai, H.T.; Zhou, R.Q.; Wang, J.C.; Zhou, B.; Wang, X.A.; Luo, W.B.; Zhao, X. Novel design of the compound sleeve and stem prosthesis for treatment of proximal femur bone defects based on topology optimization. Front. Bioeng. Biotech. 2022, 10, 938337. [Google Scholar] [CrossRef]




| Condition | Joint Contact Force | Abductor Muscles |
|---|---|---|
| Stand | 2317 N | 703 N |
| Outreach | 1158 N | 351 N |
| Adduction | 1548 N | 468 N |
| Section | One Leg Stand | Abduction | Adduction | |
|---|---|---|---|---|
| Type A | A | 20.68 | 15.78 | 8.92 |
| B | 15.42 | 24.56 | 15.56 | |
| C | 8.32 | 27.31 | 26.34 | |
| Prototype | A | 21.78 | 15.24 | 7.98 |
| B | 18.53 | 25.61 | 17.36 | |
| C | 17.22 | 28.93 | 25.84 | |
| Type B | A | 10.33 | 16.19 | 7.23 |
| B | 12.54 | 22.13 | 16.57 | |
| C | 9.82 | 24.46 | 25.71 | |
| Healthy fermur | A | 10.61 | 13.76 | 3.24 |
| B | 6.21 | 20.52 | 16.23 | |
| C | 9.95 | 19.13 | 8.83 |
| Load/N | Strain/ | Load/N | Strain/ | ||
|---|---|---|---|---|---|
| 50 | 50 | 958 | |||
| 100 | 100 | 1972 | |||
| 150 | 150 | 3138 | |||
| 200 | 200 | 4402 | |||
| 250 | 250 | 5906 | |||
| 300 | 300 | 7379 | |||
| 350 | −10,422 | 350 | 8371 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Wu, L.; Wu, W.; Tang, R.; Dai, J.; Zhu, D. Multi-Scale Topology Optimization of Femoral Stem Structure Subject to Stress Shielding Reduce. Materials 2023, 16, 3151. https://doi.org/10.3390/ma16083151
Xiao Z, Wu L, Wu W, Tang R, Dai J, Zhu D. Multi-Scale Topology Optimization of Femoral Stem Structure Subject to Stress Shielding Reduce. Materials. 2023; 16(8):3151. https://doi.org/10.3390/ma16083151
Chicago/Turabian StyleXiao, Zhongmin, Longfei Wu, Wenqiang Wu, Ruizhi Tang, Jietao Dai, and Dachang Zhu. 2023. "Multi-Scale Topology Optimization of Femoral Stem Structure Subject to Stress Shielding Reduce" Materials 16, no. 8: 3151. https://doi.org/10.3390/ma16083151
APA StyleXiao, Z., Wu, L., Wu, W., Tang, R., Dai, J., & Zhu, D. (2023). Multi-Scale Topology Optimization of Femoral Stem Structure Subject to Stress Shielding Reduce. Materials, 16(8), 3151. https://doi.org/10.3390/ma16083151






