Optimization of the Cross-Sectional Geometry of Auxetic Dowels for Furniture Joints
Abstract
1. Introduction
- ▪
- Analyzing the system;
- ▪
- Identifying constraints;
- ▪
- Identifying variables;
- ▪
- Introducing the target (target function selection);
- ▪
- Choosing the most appropriate optimization method;
- ▪
- Control of the system.
- ▪
- Size optimization: in other words, it can be described as sizing optimization, which deals with the cross-sectional areas of structures or cross-sectional areas of members of structures as the design variables;
- ▪
- Shape optimization: Additionally, it can be described as configuration optimization, which deals with the nodal coordinates of structures as the design variables;
- ▪
- Topology optimization: this optimization is the aim to delete needless structural members to reach the optimum design values;
- ▪
- Multi-objective optimization: using two or more of the above optimization methods at the same time to produce better optimization results.
2. Materials and Methods
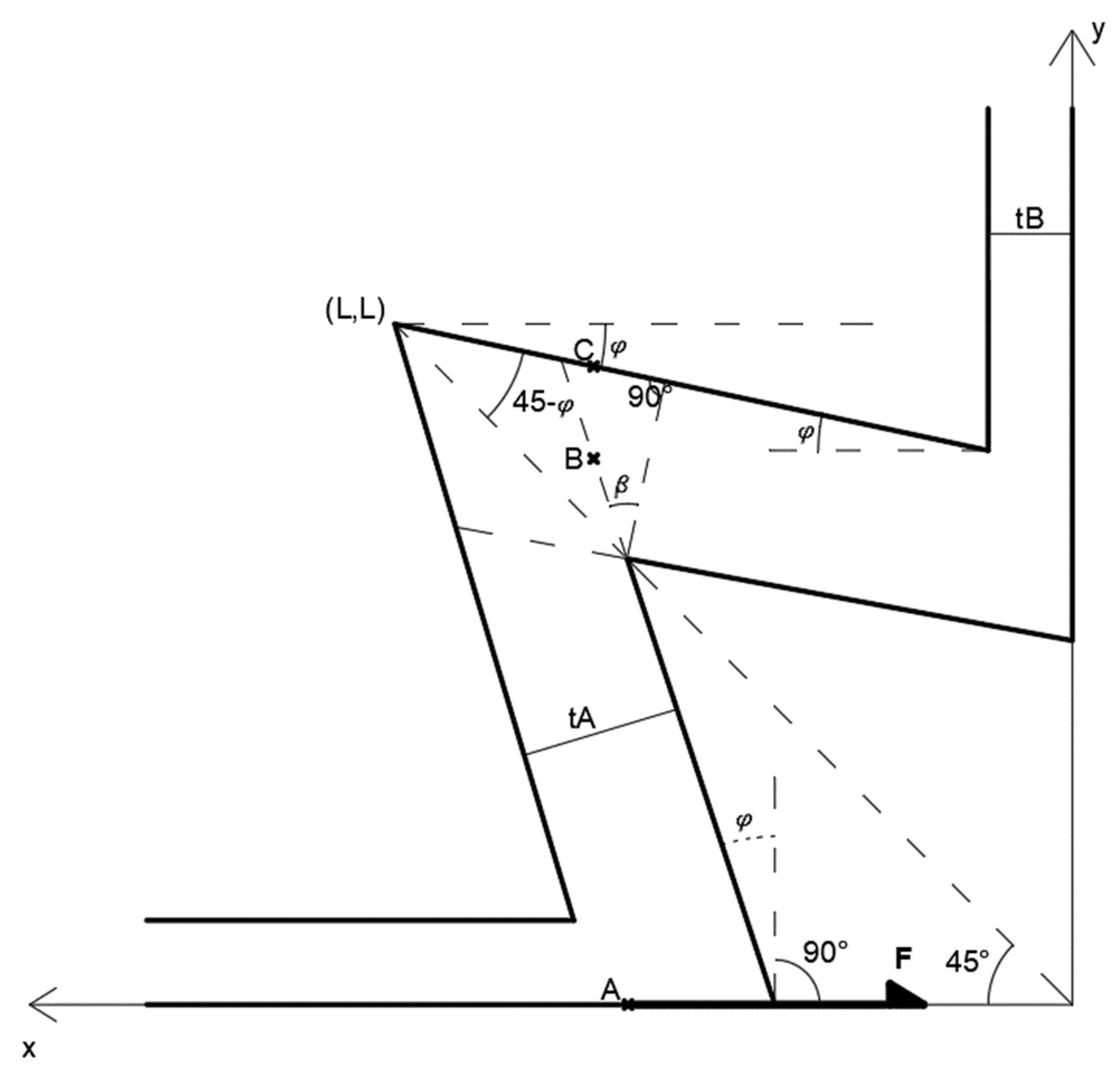
2.1. Design of the Auxetic Dowels
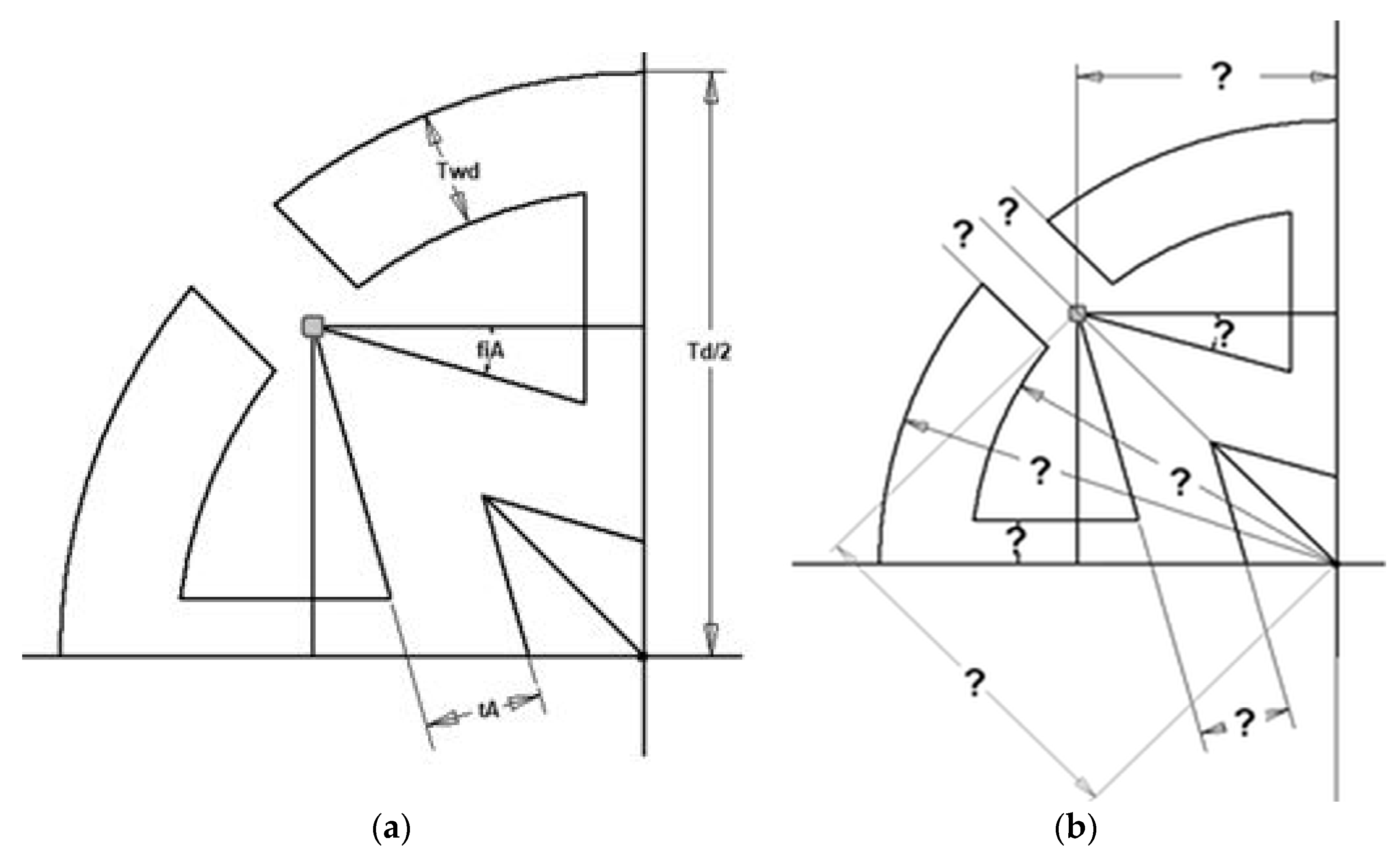
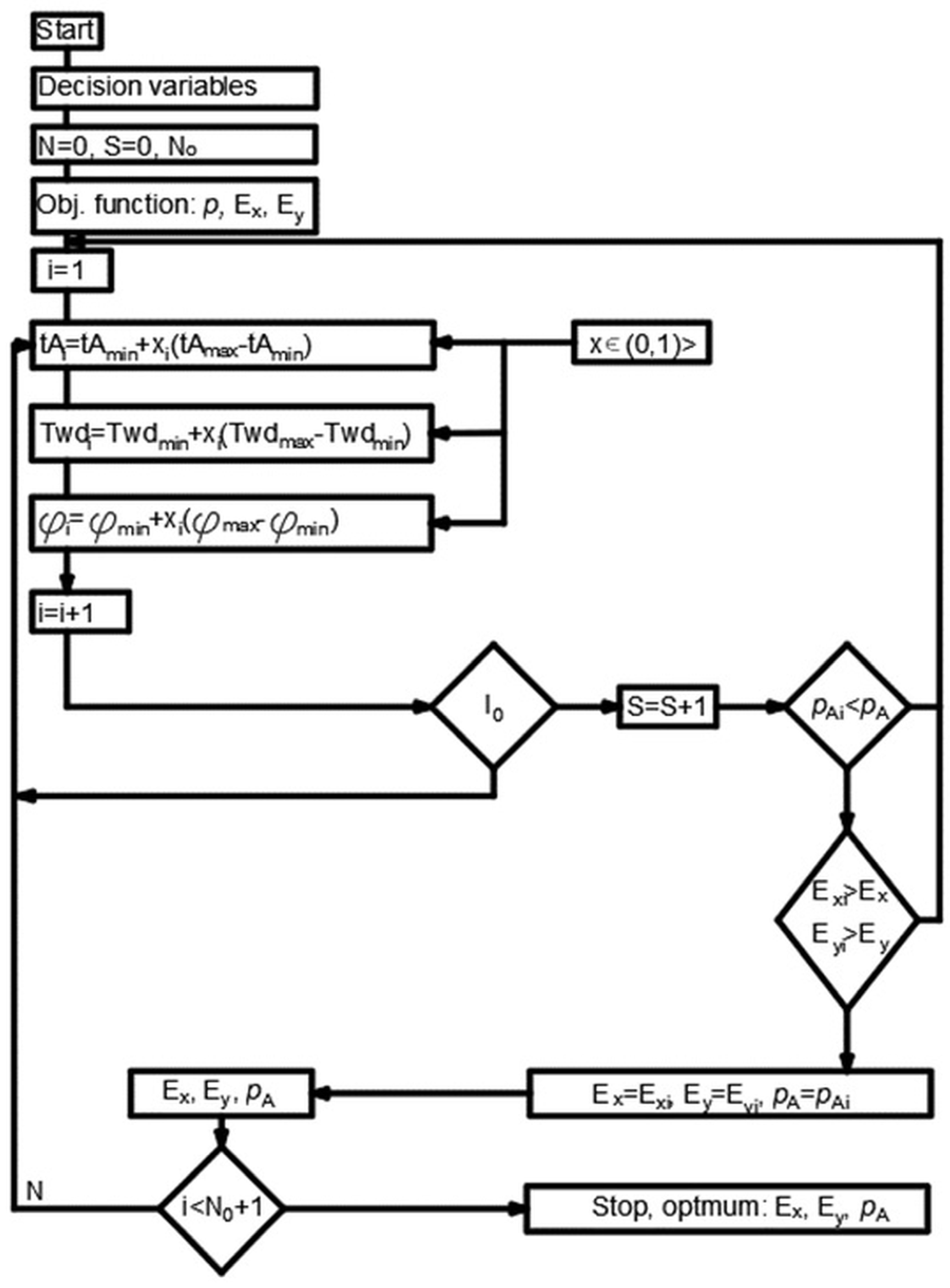
2.2. Optimization of the Cross-Sectional Geometry of Auxetic Dowels
2.3. Numerical Model and Analyses of Auxetic Dowels
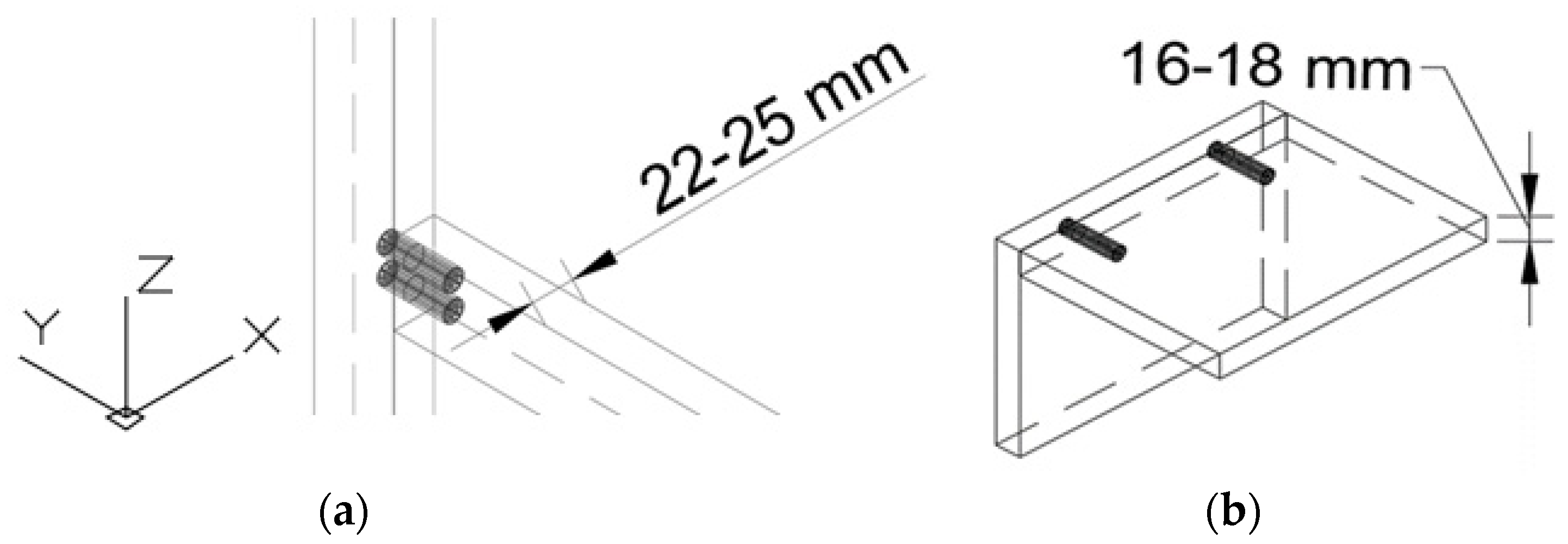
2.4. Production and Experimental Tests of the Dowels
3. Results and Discussion
3.1. Optimization Results for Cross-Section of Auxetic Dowels
3.2. Comparison of the Experimental Results, Numerical Analyses and Analytical Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasal, A.; Kuşkun, T.; Smardzewski, J. Experimental and Numerical Study on Withdrawal Strength of Different Types of Auxetic Dowels for Furniture Joints. Materials 2020, 13, 4252. [Google Scholar] [CrossRef] [PubMed]
- Smardzewski, J.; Rzepa, B.; Kiliç, H. Mechanical Properties of Externally Invisible Furniture Joints Made of Wood-Based Composites. BioResources 2016, 11, 1224–1239. [Google Scholar] [CrossRef]
- Podskarbi, M.; Smardzewski, J. Numerical Modelling of New Demountable Fasteners for Frame Furniture. Eng. Struct. 2019, 185, 221–229. [Google Scholar] [CrossRef]
- Krzyżaniak, Ł.; Smardzewski, J. Modeling of Externally Invisible Cabinet Furniture Joints. In Proceedings of the 28th International Conference on Wood Modification and Technology, Zagreb, Croatia, 7–8 December 2017; pp. 191–197. [Google Scholar]
- Krzyżaniak, Ł.; Smardzewski, J. Strength and Stiffness of New Designed Externally Invisible and Demountable Joints for Furniture Cases. Eng. Struct. 2019, 199, 109674. [Google Scholar] [CrossRef]
- Krzyżaniak, Ł.; Kuşkun, T.; Kasal, A.; Smardzewski, J. Analysis of the Internal Mounting Forces and Strength of Newly Designed Fastener to Joints Wood and Wood-Based Panels. Materials 2021, 14, 7119. [Google Scholar] [CrossRef] [PubMed]
- Kuşkun, T.; Smardzewski, J.; Kasal, A. Experimental and Numerical Analysis of Mounting Force of Auxetic Dowels for Furniture Joints. Eng. Struct. 2021, 226, 111351. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496. [Google Scholar] [CrossRef]
- Kolpakov, A.G. Determination of the Average Characteristics of Elastic Frameworks. J. Appl. Math. Mech. 1985, 49, 739–745. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant Thermodynamic Tension Monte Carlo Studies of Elastic Properties of a Two-Dimensional System of Hard Cyclic Hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Cabras, L.; Brun, M. Auxetic Two-Dimensional Lattices with Poisson’s Ratio Arbitrarily Close to 1. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E. Auxetic Polymers: A New Range of Materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chirima, G.; Ravirala, N.; Zied, K.M. The In-Plane Linear Elastic Constants and out-Ofplane Bending of 3-Coordinated Ligament and Cylinder-Ligament Honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar]
- Lorato, A.; Innocenti, P.; Scarpa, F.; Alderson, A.; Alderson, K.L.; Zied, K.M.; Ravirala, N.; Miller, W.; Smith, C.W.; Evans, K.E. The Transverse Elastic Properties of Chiral Honeycombs. Compos. Sci. Technol. 2010, 70, 1057–1063. [Google Scholar] [CrossRef]
- Smardzewski, J. Elastic Properties of Cellular Wood Panels with Hexagonal and Auxetic Cores. Holzforschung 2013, 67, 87–92. [Google Scholar] [CrossRef]
- Smardzewski, J.; Jasinska, D. Mathematical Models and Experimental Data for HDF Based Sandwich Panels with Dual Corrugated Lightweight Core. Holzforschung 2017, 71, 265–273. [Google Scholar] [CrossRef]
- Smardzewski, J.; Wojciechowski, K.W.; Pozniak, A. Auxetic Lattice Truss Cores Fabricated of LayWood. BioResources 2018, 13, 8823–8838. [Google Scholar] [CrossRef]
- Smardzewski, J.; Wojciechowski, W.K. Response of Wood-Based Sandwich Beams with Three-Dimensional Lattice Core. Compos. Struct. 2019, 216, 340–349. [Google Scholar] [CrossRef]
- Smardzewski, J. Wooden Sandwich Panels with Prismatic Core–Energy Absorbing Capabilities. Compos. Struct. 2019, 230, 111535. [Google Scholar] [CrossRef]
- Smardzewski, J. Experimental and Numerical Analysis of Wooden Sandwich Panels with an Auxetic Core and Oval Cells. Mater. Des. 2019, 183, 108159. [Google Scholar] [CrossRef]
- Patiballa, S.K.; Krishnan, G. Qualitative Analysis and Conceptual Design of Planar Metamaterials with Negative Poisson’s Ratio. J. Mech. Robot. 2018, 10, 021006. [Google Scholar] [CrossRef]
- Balan, P.M.; Mertens, A.J.; Bahubalendruni, M.V.A.R. Auxetic Mechanical Metamaterials and Their Futuristic Developments: A State-of-Art Review. Mater. Today Commun. 2023, 34, 105285. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic Metamaterials and Structures: A Review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Smardzewski, J. Auxetic Springs for Seating. Turk. J. Agric. For. 2013, 37. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic Nail: Design and Experimental Study. Compos. Struct. 2018, 184, 288–298. [Google Scholar] [CrossRef]
- Rajput, S.P.S.; Datta, S. A Review on Optimization Techniques Used in Civil Engineering Material and Structure Design. Mater. Today Proc. 2020, 26, 1482–1491. [Google Scholar]
- Mei, L.; Wang, Q. Structural Optimization in Civil Engineering: A Literature Review. Buildings 2021, 11, 66. [Google Scholar] [CrossRef]
- Zavala, G.R.; Nebro, A.J.; Luna, F.; Coello, C.A.C. A Survey of Multi-Objective Metaheuristics Applied to Structural Optimization. Struct. Multidiscip. Optim. 2014, 49, 537–558. [Google Scholar]
- Kazaz, A.; Ulubeyli, S. Physical Factors Affecting Productivity of Turkish Construction Workers. In Proceedings of the 22nd Annual ARCOM Conference, Birmingham, UK, 4–6 September 2006; pp. 29–37. [Google Scholar]
- Choi, S.W.; Oh, B.K.; Park, H.S. Design Technology Based on Resizing Method for Reduction of Costs and Carbon Dioxide Emissions of High-Rise Buildings. Energy Build. 2017, 138, 612–620. [Google Scholar] [CrossRef]
- Horta, I.M.; Camanho, A.S.; Johnes, J.; Johnes, G. Performance Trends in the Construction Industry Worldwide: An Overview of the Turn of the Century. J. Product. Anal. 2013, 39, 89–99. [Google Scholar] [CrossRef]
- Xu, G.; Wang, W. China’s Energy Consumption in Construction and Building Sectors: An Outlook to 2100. Energy 2020, 195, 117045. [Google Scholar] [CrossRef]
- Tsiptsis, I.N.; Liimatainen, L.; Kotnik, T.; Niiranen, J. Structural Optimization Employing Isogeometric Tools in Particle Swarm Optimizer. J. Build. Eng. 2019, 24, 100761. [Google Scholar] [CrossRef]
- Gagg, C.R. Cement and Concrete as an Engineering Material: An Historic Appraisal and Case Study Analysis. Eng. Fail. Anal. 2014, 40, 114–140. [Google Scholar] [CrossRef]
- Afzal, M.B.; Liu, Y.; Cheng, J.C.P.; Gan, V.J.L. Reinforced Concrete Structural Design Optimization: A Critical Review. J. Clean. Prod. 2020, 260, 120623. [Google Scholar]
- Xiao, A.; Wang, B.; Jin, Y. Evolutionary Truss Layout Optimization Using the Vectorized Structure Approach. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2879–2886. [Google Scholar]
- Dapogny, C.; Faure, A.; Michailidis, G.; Allaire, G.; Couvelas, A.; Estevez, R. Geometric Constraints for Shape and Topology Optimization in Architectural Design. Comput. Mech. 2017, 59, 933–965. [Google Scholar] [CrossRef]
- Smardzewski, J.; Gawroński, T. FEM Algorithm for Chair Optimisation. Electron. J. Polish Agric. Univ. 2001, 4. Available online: http://www.ejpau.media.pl/new/volume4/issue2/wood/abs-1.html (accessed on 6 March 2023).
- Smardzewski, J.; Prekrat, S. Optimisation of a Sofa Frame in the Integrated CAD-CAE Environment. Electron. J. Pol. Agric. Univ. 2009, 12. Available online: http://www.ejpau.media.pl/volume12/issue4/abs-01.html (accessed on 6 March 2023).
- Hu, W.; Liu, N.; Guan, H. Optimal Design of a Furniture Frame by Reducing the Volume of Wood. Drewno 2019, 62, 85–97. [Google Scholar] [CrossRef]
- Ke, Q.; Lin, L.; Chen, S.; Zhang, F.; Zhang, Y. Optimization of L-Shaped Corner Dowel Joint in Pine Using Finite Element Analysis with Taguchi Method. Wood Res. 2016, 61, 243–254. [Google Scholar]
- Hu, W.; Fu, W.L.; Guan, H.Y. Optimal Design of Stretchers Positions of Mortise and Tenon Joint Chair. Wood Res. 2018, 63, 505–516. [Google Scholar]
- Güray, E.; Ceylan, E.; Kasal, A. Weight-Strength Optimization of Wooden Household Chairs Based on Member Section Size. Maderas. Cienc. Tecnol. 2022, 24, 1–24. [Google Scholar] [CrossRef]
- Kalos, M.H.; Whitlock, P.A. Monte Carlo Methods; WILEY-VCH Verlag GmbH&Co. KGaA.: Weinheim, Germany, 2008. [Google Scholar]
- Efron, B.; Diaconis, P. Computer-Intensive Methods in Statistics. Sci. Am. 1983, 248, 116–131. [Google Scholar]
- Simon, J.L.; Bruce, P. Resampling: A Tool for Everyday Statistical Work. Chance 1991, 4, 22–32. [Google Scholar] [CrossRef]
- Ferson, S. What Monte Carlo Methods Cannot Do. Hum. Ecol. Risk Assess. 1996, 2, 990–1007. [Google Scholar] [CrossRef]
- Kelkar, P.U.; Kim, H.S.; Cho, K.H.; Kwak, J.Y.; Kang, C.Y.; Song, H.C. Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors 2020, 20, 3132. [Google Scholar] [CrossRef] [PubMed]
- Garlotta, D. A Literature Review of Poly(Lactic Acid). J. Polym. Environ. 2019, 9, 63–84. [Google Scholar] [CrossRef]

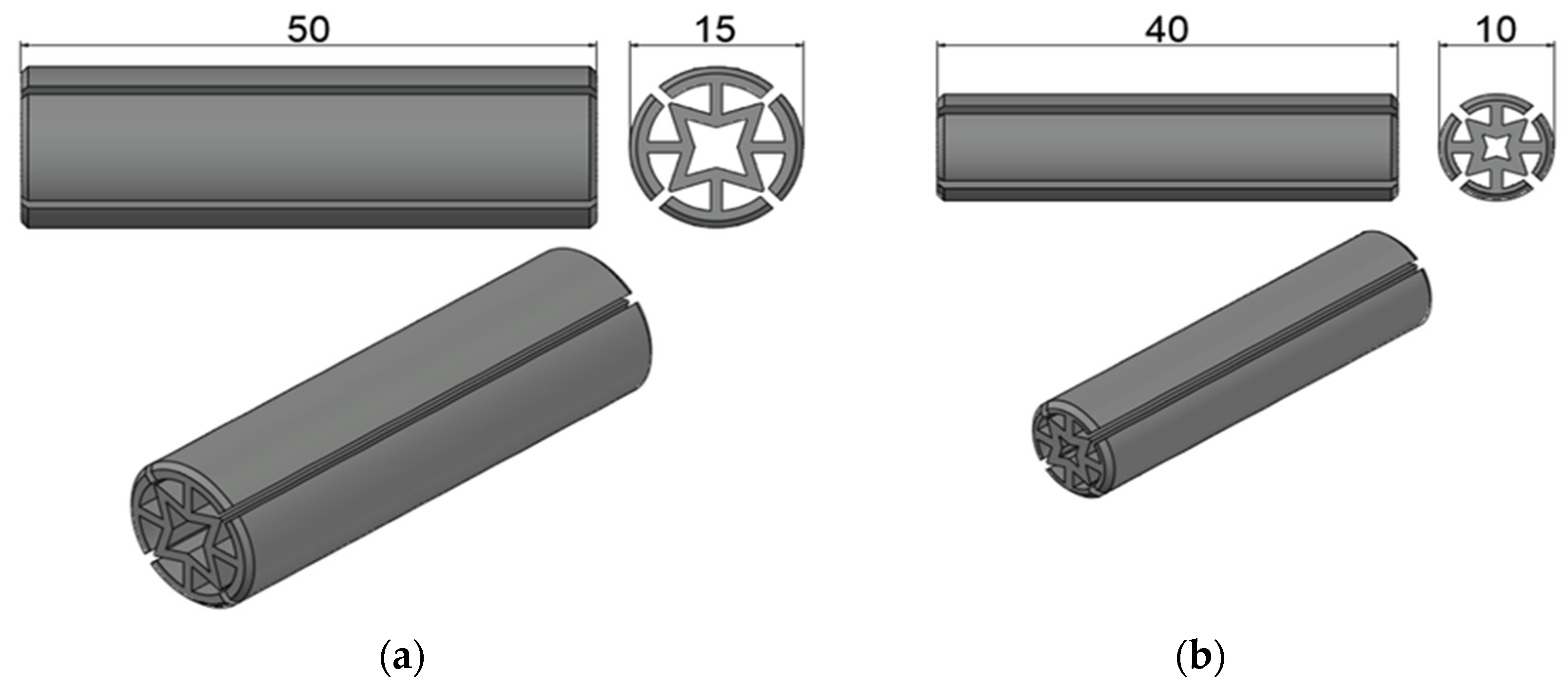


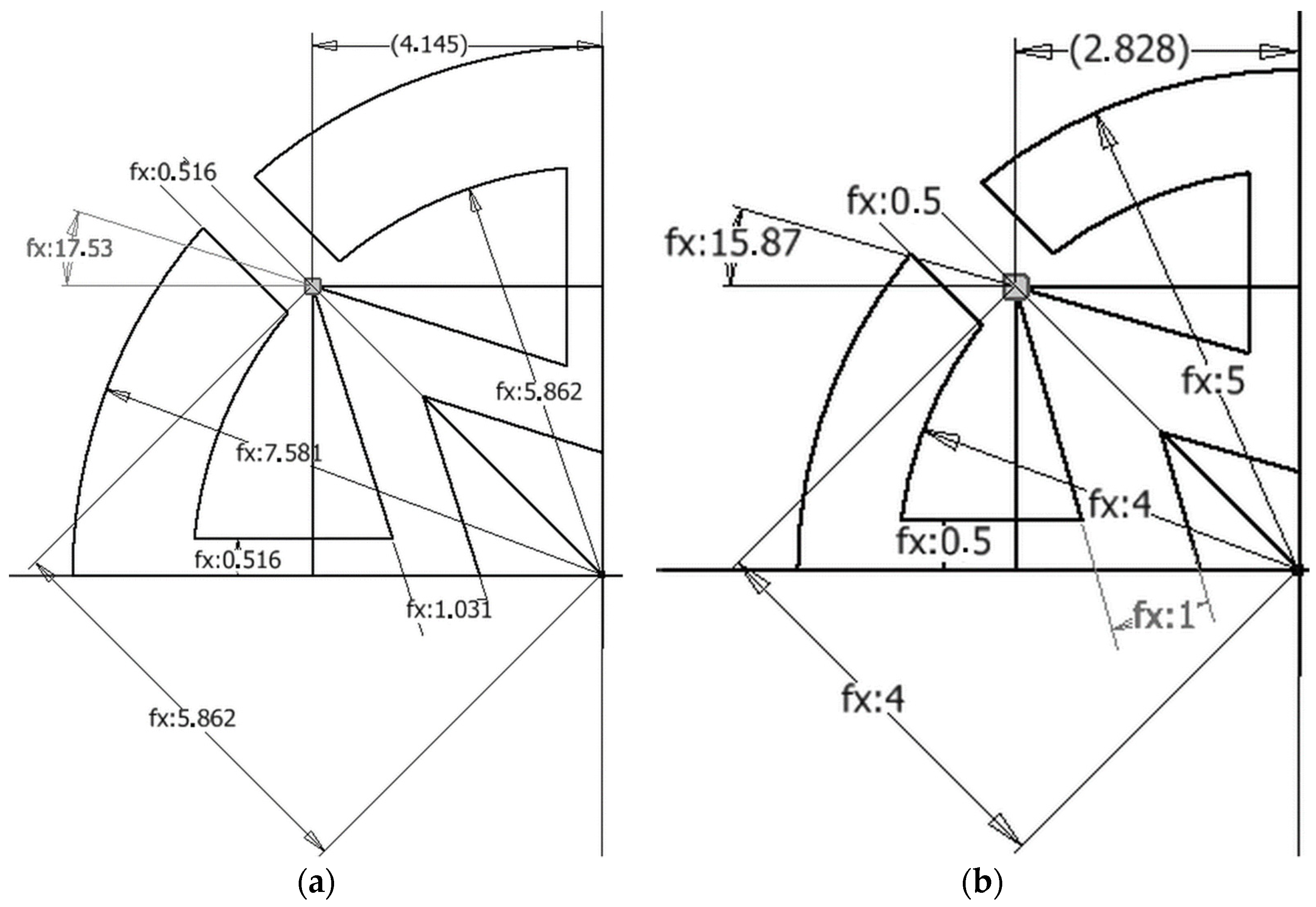
| Parameters | 1st Dowel Type | 2nd Dowel Type | ||
|---|---|---|---|---|
| Minimum Level | Maximum Level | Minimum Level | Maximum Level | |
| 1 mm | 2 mm | 1 mm | 2 mm | |
| 15° | 40° | 15° | 40° | |
| 1 mm | 2 mm | 1 mm | 2 mm | |
| 15 mm | 10 mm | |||
| Length | 50 mm | 40 mm | ||
| Parameters | 1st Dowel Type | 2nd Dowel Type |
|---|---|---|
| 1.03 mm | 1 mm | |
| 17.53° | 15.87° | |
| 1.72 mm | 1 mm | |
| 15 mm | 10 mm | |
| Length | 50 mm | 40 mm |
| Dowel Type | Dowel Diameter (mm) | Dowel Length (mm) | Poisson’s Ratios | MOE (MPa) | ||
|---|---|---|---|---|---|---|
| Experimental | Numerical | Analytical | ||||
| 1st type | 15 | 50 | −0.273 (0.054) * | −0.309 | −0.302 | 155.54 |
| 2nd type | 10 | 40 | −0.287 (0.065) | −0.313 | −0.341 | 436.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuşkun, T.; Kasal, A.; Çağlayan, G.; Ceylan, E.; Bulca, M.; Smardzewski, J. Optimization of the Cross-Sectional Geometry of Auxetic Dowels for Furniture Joints. Materials 2023, 16, 2838. https://doi.org/10.3390/ma16072838
Kuşkun T, Kasal A, Çağlayan G, Ceylan E, Bulca M, Smardzewski J. Optimization of the Cross-Sectional Geometry of Auxetic Dowels for Furniture Joints. Materials. 2023; 16(7):2838. https://doi.org/10.3390/ma16072838
Chicago/Turabian StyleKuşkun, Tolga, Ali Kasal, Gökhan Çağlayan, Erkan Ceylan, Murat Bulca, and Jerzy Smardzewski. 2023. "Optimization of the Cross-Sectional Geometry of Auxetic Dowels for Furniture Joints" Materials 16, no. 7: 2838. https://doi.org/10.3390/ma16072838
APA StyleKuşkun, T., Kasal, A., Çağlayan, G., Ceylan, E., Bulca, M., & Smardzewski, J. (2023). Optimization of the Cross-Sectional Geometry of Auxetic Dowels for Furniture Joints. Materials, 16(7), 2838. https://doi.org/10.3390/ma16072838







