Abstract
Ceramic Foam Filters (CFF) are frequently used during the filtration of aluminum (Al) melts to produce high-quality products. In the present study, the physical and hydraulic characteristics of alumina (Al2O3)-based CFF from three different suppliers (A, B and C) have been thoroughly investigated. The filters’ porosity and pore diameter, i.e., Window and Cell Feret diameters, were measured and the permeability of the different filters calculated based on pressure drop experiments. The comparison of the classification systems of CFF, i.e., Grade and PPI (Pore Per Inch) numbers, using statistical analysis of permeability and Window Feret diameter showed significant variations between the morphological and hydraulic properties of some CFFs of identical Grade and PPI numbers. Moreover, the Fanning friction factor was plotted as a function of interstitial Reynolds numbers (Rei), and laminar, transient, and turbulent flow regimes were identified. The relationship between the Fanning friction factor and the interstitial Reynolds numbers of all the filter samples investigated was processed using regression analysis, and a model equation developed to calculate the pressure drop over the CFF using the Window Feret diameter. The correlation between the experimental pressure drop values and the derived model equation indicates that empirical expressions for calculating the pressure drop over CFFs should be derived based on experimental measurements carried out at the velocity range of the application of the CFF, which is about 10 mm·s−1 for aluminum filtration.
1. Introduction
The filtration of aluminum (Al) using alumina (Al2O3) Ceramic Foam Filters (CFF) has been an approach extensively used in Al cast houses since their invention in 1974 [1]. Through the filtration process, particles/inclusions, i.e., metallic, and non-metallic impurities, are collected on or in the filter [2]. CFFs are, however, wetted unfavorably by molten Al, so a metallic static head is required to prime the filters, i.e., the force needed to push the air inside the tortuous structure of the filters out, and subsequently infiltrate the porous material [1,3]. The filter capacity depends on the type and size of the particles collected [4]. The filtration modes, i.e., cake and/or depth filtration, as well as the flow velocity, play significant roles in the removal of the particles [5]. Depth filtration, i.e., removal of particles on the filter walls, is more desired than cake filtration, especially if the size of the particles is larger, as they may clog the filter [6]. Larger particles, as well as the number of oxide films present in the molten metal, can be reduced both in size and amount through a pre-refining process, i.e., fluxing, degassing, or filtration using Fiber glass cloth filters in the launder, making it possible to efficiently use cake filtration [7].
Interception and gravity are the main collision mechanisms through which the particles are trapped on the walls of the CFF [8]. Due to the higher interfacial tension of the filter material relative to the melt, the collection efficiency is not equal to the collision efficiency, and particles are partly collected and later re-entrained in the melt [9]. This phenomenon escalates with a more significant pressure drop and/or velocity [5], and the optimum conditions for molten metal filtration should, therefore, be considered through which the re-entrainment forces, i.e., viscous drag and inertial forces, are less than the restraining forces [2].
Through the semi-continuous casting process of Al, i.e., through Direct Chill (DC) casting, the filtration is performed at flow rates from 5 to 1200 kg·min−1 (≈10 mm·s−1) for filters of Grade 10–80 [1]. The different flow regimes induced in the CFF relative to the flow velocity, i.e., laminar, transient, and turbulent flow regimes, can affect the filtration efficiency as the transition from one flow regime to another, e.g., from laminar to the transient flow regime, persuade inertial forces on the trapped particles that may result in re-entrainment of the particles into the flow of molten metal [2]. Therefore, estimating the onset of the transient flow regime through the CFF of various Grades or Pores Per Inch (PPI) is essential to define the induced forces on the particles. Nevertheless, the studies that have been performed to characterize and determine the hydraulic properties of alumina CFF for aluminum filtration applications have been performed in the velocity ranges >> 15 mm·s−1 [10,11,12,13,14,15]. In addition, the CFF from various suppliers are named according to two different systems, i.e., Grade and PPI. The PPI number is traditionally used to characterize the CFF [1]. In a grading system, a CFF Grade 20 has a pore (Cell) size of approximately half that of a CFF Grade 10, and a CFF Grade 40 is half of a CFF Grade 20, etc. [16]. The general idea is that a CFF of, for instance, Grade 30 is equivalent to 30 PPI. However, due to different characterization methods, the morphology characteristics, hydraulic properties, and filtration efficiency would not be necessarily identical. In this regard, a thorough investigation of the different CFFs available for Al filtration is needed to define the flow regimes through the filters, i.e., for CFF of different Grades/PPI numbers. By establishing the characteristic length scales of the different filters, i.e., the Cell and Window sizes, as well as the permeability and the form drag coefficient, a uniform grading of the filters should be possible to obtain.
The main objective of the present work is, therefore, to perform a fundamental characterization study of commercial CFF used in the Al filtration process. In view of this, the present study investigates the morphological characteristics and the pressure gradient of CFF of various Grades/PPI numbers from three different suppliers, as well as determines the dominating flow regimes within the different filters. An empirical equation was derived by correlation between experimentally obtained permeability values and the interstitial Reynolds numbers (Rei) to determine the pressure drop of different CFFs using the morphology characteristics, i.e., Windows’ mean Feret diameter, of the CFFs.
2. Theory
The present study uses the Re number, a dimensionless number expressing the inertia ratio to viscous forces, to identify the laminar, transition, and turbulent flow regimes in conduits [17]. By analogy, Reynolds number is also defined for flow through porous media [17]:
where d is the length dimension of the porous media (m), ρ the fluid density (kg·m−3), u the superficial velocity (m·s−1), and µ the dynamic viscosity (Pa·s). The mean grain diameter is often taken as the length dimension (characteristic length scale) in unconsolidated porous media such as packed beds [18]. However, in CFFs with a network structure of polyhedral cells, it is customary to take the mean of the characteristic length scales, i.e., of the Cell (dC), Window (dw), and Strut (ds), as the length dimension [18,19], see Figure 1. Continuing the analogy with the flow in conduits, the flow in porous media could be expressed using a relationship between different friction factors and Re number [17]. The most common friction factor relations in cylindrical pipes are the Darcy–Weisbach and Fanning friction factors [17]:
where f is the friction factor (dimensionless), d the diameter of the pipe (m), ΔP·L−1 the pressure loss per unit length (Pa·m−1), ρ the fluid density (kg·m−3), and u the mean flow velocity (m·s−1).
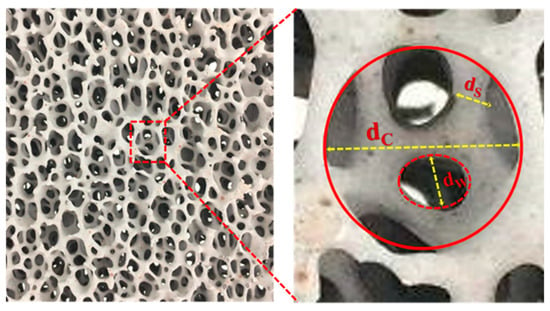
Figure 1.
An uncut surface of a CFF of Grade 30, and the characteristic length scales, i.e., Cell (dc), Window (dw), and Strut (ds), which are indicated by the large solid circle, dotted circle, and double line arrow, respectively, in the enlarged section of image.
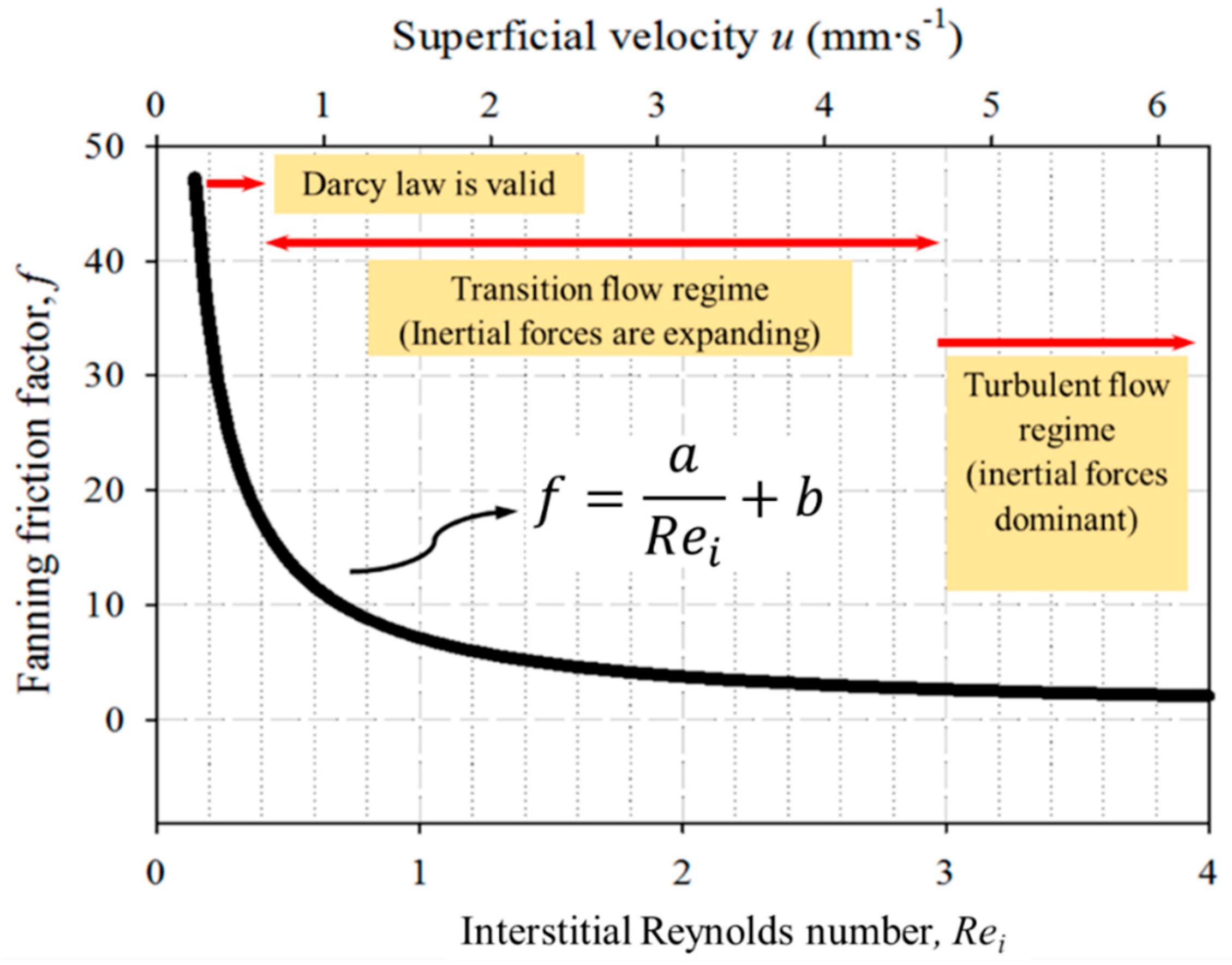
When considering flows through a porous medium, d is the same representative length as in Equation (1), and u the superficial velocity. The friction factor can be calculated using pressure drop experiments and plotting the result as a function of interstitial Reynolds number (Rei)) and the superficial velocity will generate a graph in which the existence of three different flow regions can be distinguished. Figure 2 illustrates a schematic of this graph with the three flow regions as follows [17]:
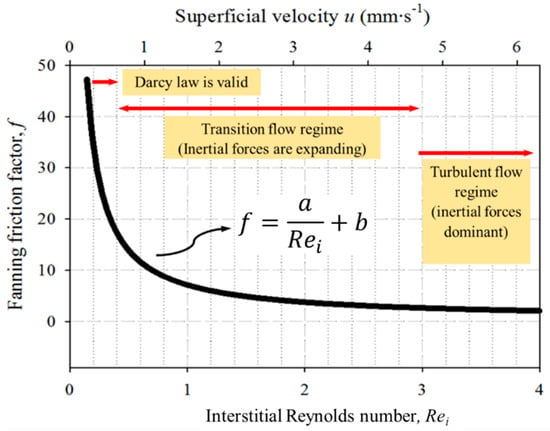
Figure 2.
Schematic classification of the flow through a porous medium. Based on reference [17].
- The first region (Darcy law) is the Darcian flow regime at extremely low (<1 mm·s−1) fluid velocities—there is a linear relationship between the friction factor and Rei, and viscous forces are predominant.
- At the upper end of the Darcian flow regime, the transition flow starts and the linear relation between the friction factor and Rei starts to bend, and the viscous forces are not predominant anymore.
- The third region (Turbulent flow) is the Forchheimer or turbulent flow regime, where the form drag forces are dominant. The Fanning friction factor gets close to zero at the upper end of the transition zone, and the curve becomes almost horizontal.
An equation on the form f = a/Rei + b (where a and b are constants) can express the equality between the Fanning friction factor and Rei:
This relation is just another form of the Forchheimer equation describing the fluid transport of a single-phase fluid through a porous medium when the pressure gradient changes with the average fluid velocity [20,21]:
where k is the intrinsic permeability (m2) and relates to the effective surface length of the solid porous matrix, and β the form drag coefficient (m−1). The second term of Equations (4) and (5) illustrates the deviation of the pressure drop from the linearity where the drag forces become dominant over the viscous forces [22,23]. Both the permeability (k) and the form drag coefficient (β) relate the energy dissipation in a porous medium to structural characteristics such as pore geometry and porosity [17].
Ergun and Orning introduced a semi-empirical equation based on the structural characteristics of packed beds of spheres and adapted the Forchheimer equation to define the pressure gradient [24]:
where ϕ is the total porosity (dimensionless) and dp the spherical particle diameter (m). The porosity is the ratio of the pore space to the bulk volume, and the pore space is either the effective or the non-effective flow through the porous medium. In view of this, the effective porosity is defined as the ratio of the interconnected (effective) pore space (Vev) to the bulk volume (Vb) [17]:
The non-effective porosity is, however, the non-interconnected pores in the form of triangular holes in the struts that remained after burning out the impregnated foam, see Figure 3, which is the main disadvantage of the CFF manufacturing method as it diminishes the strength of the CFF [1].

Figure 3.
Scanning Electron Microscopy (SEM) micrograph of a triangular pore in a CFF that remained after burning out the impregnated foam.
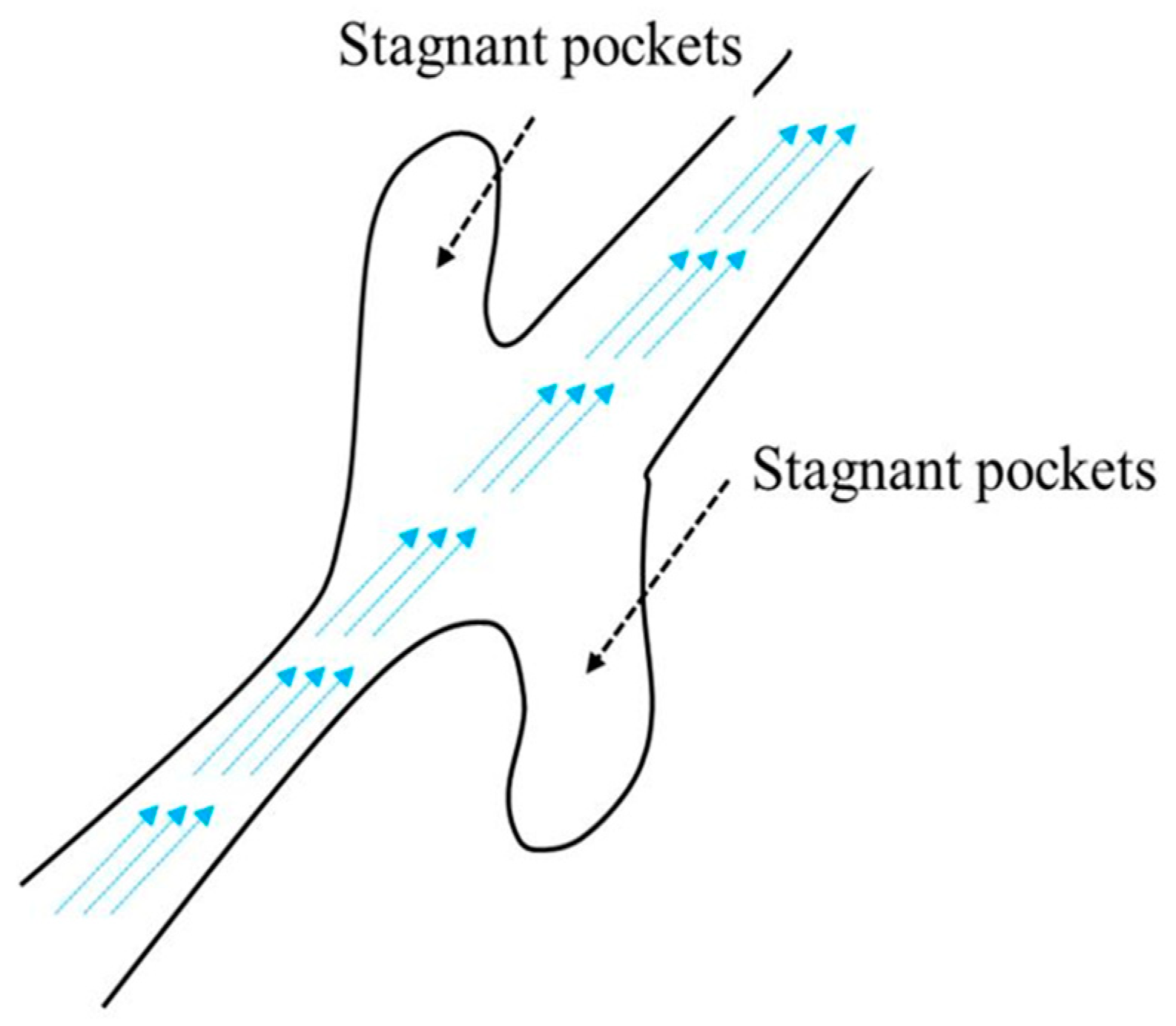
The dead-end pores and stagnant pockets are considered as non-effective spaces because they contribute very little to the flow in the porous medium. Figure 4 illustrates the schematic of stagnant pockets in a porous medium where the fluid is almost static in such pores [17].
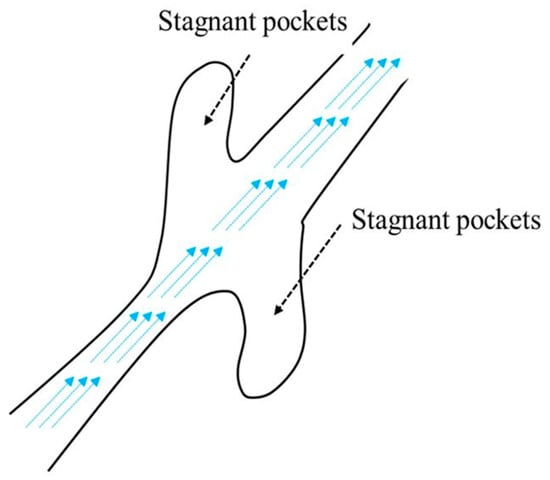
Figure 4.
Schematic representation of stagnant pocket pores in a porous medium. Based on Ref. [17].
The dissociation of non-effective pores from effective pores is not straightforward, and, therefore, the absolute or total porosity is often measured using Equation (8) [17]:
where Vv and Vs are the voids and solid matrix volume, respectively. In this definition, Vv is the total void space, regardless of whether the pores are interconnected.
Equation (6), or a modified version, has been extensively used to evaluate the pressure drop over open foams, including CFFs [19,21,25,26]. Kennedy et al. [19], however, proposed a modified version of Ergun’s equation to determine the pressure gradient over CFF for applications in aluminum filtration:
where dc is the mean Cell diameter for CFF of Grades 30–80 in the water velocity range of 30–800 mm·s−1. A deviation between the calculated pressure gradient and the experimental results of ~30% was obtained. Water was used as the fluid medium as its dynamic viscosity is comparable to molten Al at its casting temperature, i.e., ~ 1003 K (730 °C). However, since the constants of the viscous and form drag terms (23.4 and 2.00) were defined from pressure drop experiments at highly turbulent flow regimes, a more significant error would be expected when calculating the pressure drops at fluid velocities in the range of Darcy, transient, and the onset of turbulent flow regimes.
3. Materials and Methods
Commercial Al2O3-based CFF of various Grades/PPI numbers were supplied from three different manufacturers, see Table 1. The name of the CFF suppliers has not been disclosed due to confidentiality agreements, and they are therefore only referred to as manufacturers A, B, and C.

Table 1.
The dimensions and Grade/PPI numbers of the CFF used in the present study.
3.1. Sample Preparation
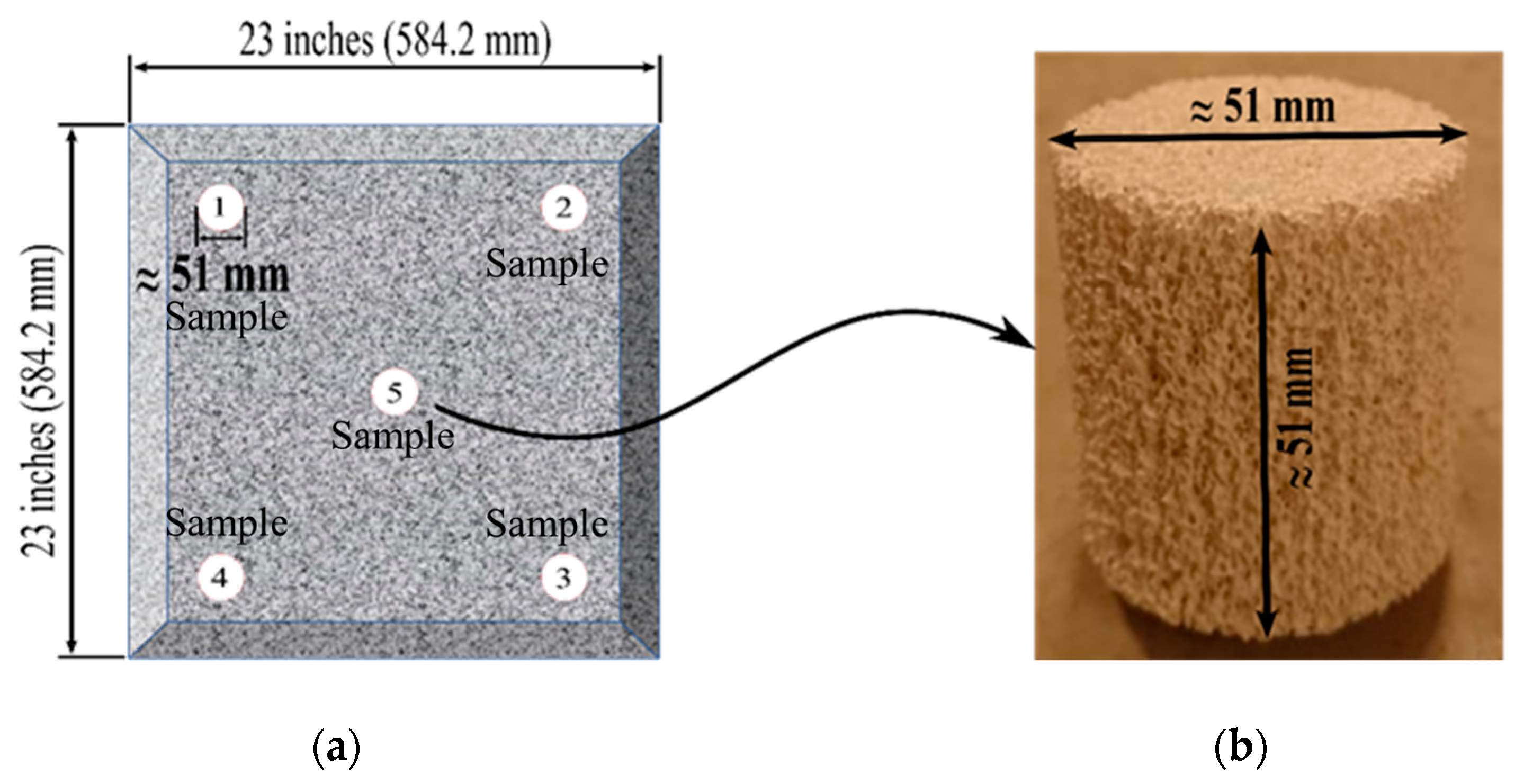
Three CFF blocks of every Grade/PPI numbers were used to secure the samples to be used in the pressure drop experiments. In total, five cylindrical samples were drilled from each filter block, i.e., from the center and the corners, see Figure 5a. In Figure 5b, a secured cylindrical sample from a CFF of Grade 50 is presented.
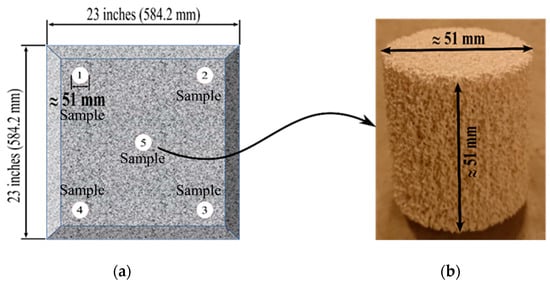
Figure 5.
(a) Schematics of a Ceramic Foam Filer (CFF) block and the locations where the five samples were taken, (b) a cylindrical sample drilled from a CFF of Grade 50.
The actual diameter and height of the samples were measured using a digital caliper from Mitutoyo, model CD-15DAX, (Kanagawa, Japan), with a resolution of 0.01 mm, and the weight using a scale from Mettler Toledo, model ME204, (Greifensee, Switzerland), with a readability of 0.1 mg and a maximum capacity of 220 g. The uncut surface of the cylindrical CFF samples was scanned using a Perfection V330 Photo Scanner from Seiko Epson Corporation, ( Tokyo, Japan), with a resolution of 2400. The captured images were used to determine the characteristic length scale of each CFF sample, i.e., the Cell diameter (dC) and the Window diameter (dw).
A thin layer (1–2 mm) of a sealing glue (Casco SuperFix, Sika Group, Baar, Switzerland) was overlaid on the outer wall of the samples and dried at room temperatures for at least 24 h before the surplus dried glue was removed so that the sample would fit in the sample holder shown in Figure 6.
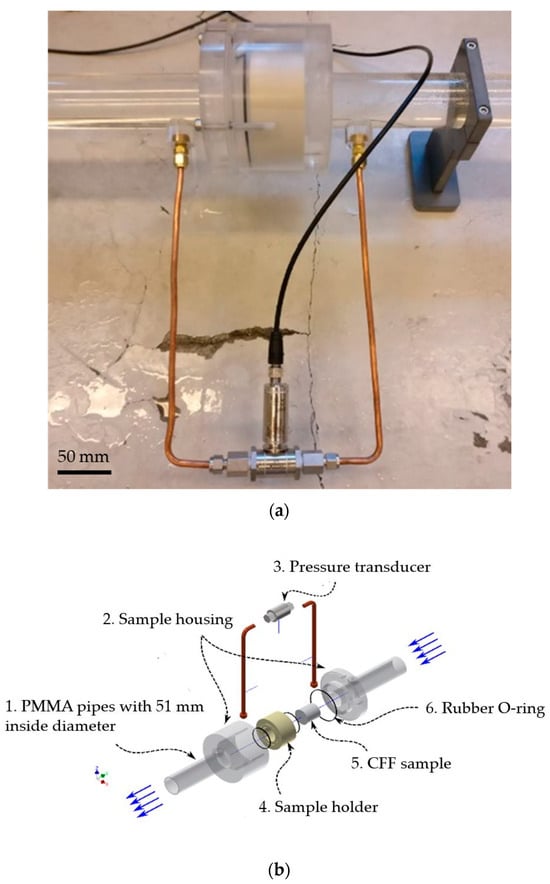
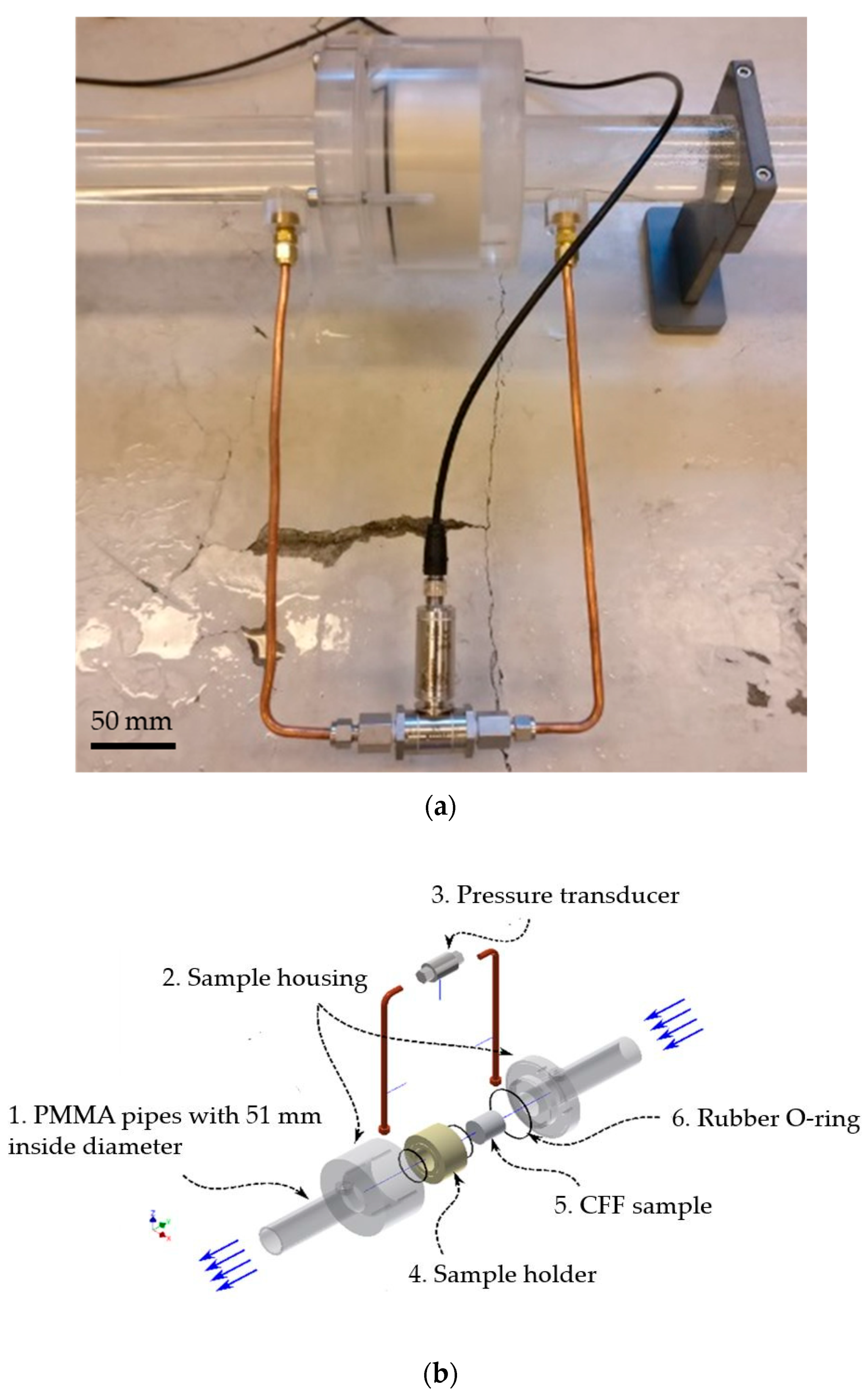
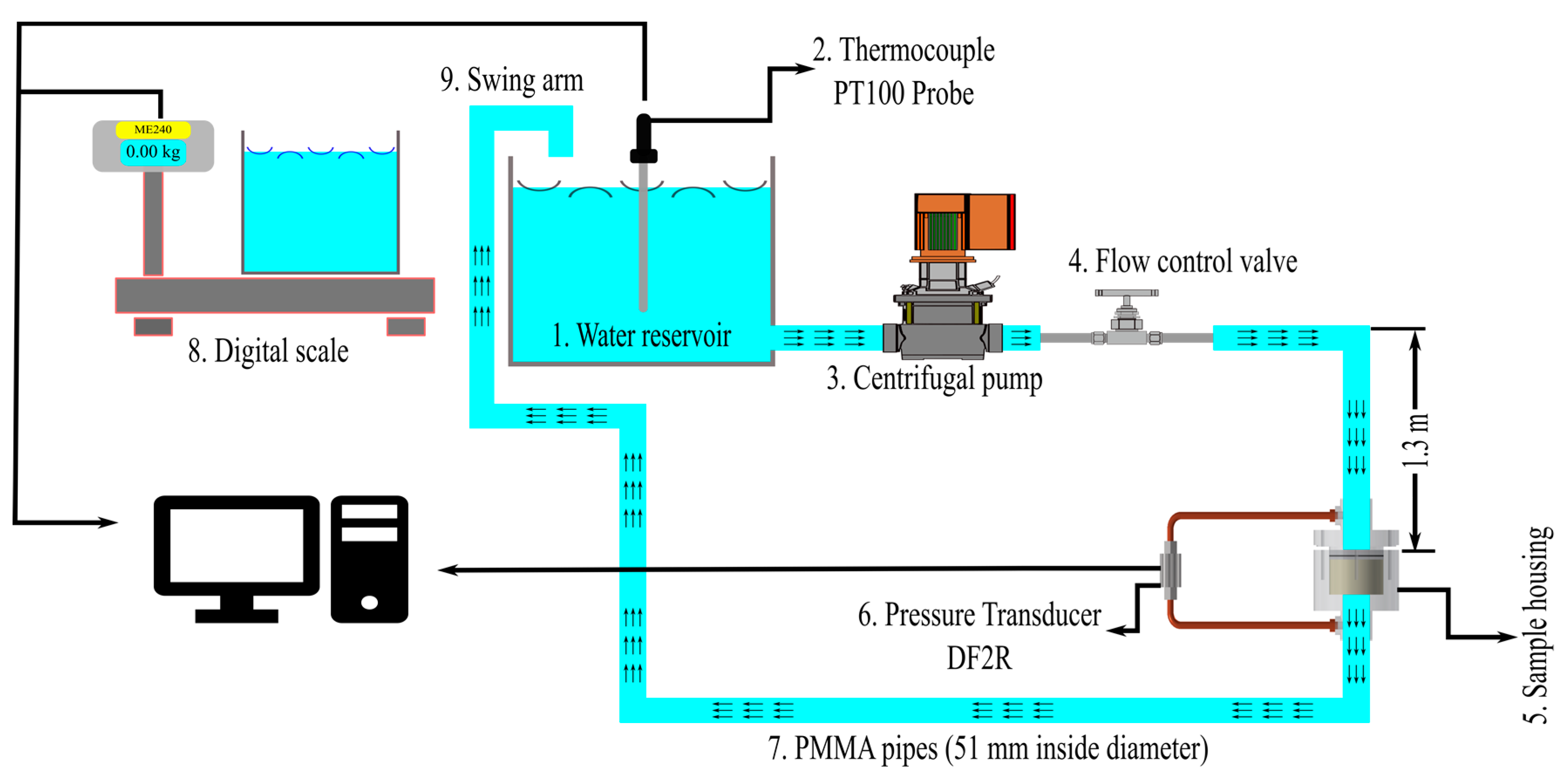
Figure 6.
The sample housing in more detail. (a) setup for holding the CFF sample and measuring the pressure drop using a transducer. (b) The exploded 3D CAD drawing of the sample housing: (1) PMMA (Poly Methyl Methacrylate) pipes to transport the water in the system, (2) Plexiglas housing to hold the CFF sample holder in place throughout the experiment, (3) Pressure transducer, (4) sample holder encompassing the sample to make a straight-through filter design, (5) CFF sample, and (6) Rubber O-rings used to prevent water bypass between the sample holder and the housing.
Before pushing the sample into the holder, the inner wall of the holder was covered by high-viscosity silicone grease to smoothen the surface and prevent bypassing of water. The sample holder and the interior sample were then inserted inside the housing, and the two parts were tightened using screws. Highly sensitive pressure transducer from AEP, model DF2R 100 mbar, (Modena, Italy), with a resolution of 0.001 V and ±0.03 % expanded uncertainty, were used to measure the pressure drop over the filters. The output voltage signal from the pressure transducer was data-logged using a multimeter from FLUKE, model 289 TRUE RMS, (Everett, WA, USA), with a resolution of 0.001 mV and an expanded uncertainty of 0.025% mV.
3.2. Total Porosity
The total porosity of the CFF samples was calculated using Equation (8). The bulk volume (Vb) was naturally determined using the dimensions of the samples, as well as the volume of the solid matrix (VS), i.e., using the sample’s weight and the true particle density of the CFF material. The particle density of the different CFF samples was obtained using the gas expansion method (Pycnometry), a standard method to measure the volume and absolute density of a porous material matrix. Accordingly, a fully automatic gas displacement Pycnometer from the Micromeritics Instrument Corporation, AccuPyc II 1340, Norcross, GA, USA, was used, and the average true density of the CFF samples measured.
3.3. Physical Morphology
The mean diameter of the Cells and Windows of the CFF samples was determined using the images secured from scanning the uncut surfaces of the filters. An average area of ~4 cm2 was assigned to the CFF samples, and the characteristic length scales (Cells and Windows) were determined using an image analysis software, i.e., the i-Solution DT software, from IMT i-Solution Inc., (Tempe, AZ, USA). The principle of the method was based on manipulating the threshold to contrast the Cells or Windows from the rest of the geometry and thereby automatically measure the Feret diameter of each sample from which the mean and standard deviation could be derived.
3.4. Pressure Drop Test
In Figure 7, a schematic illustration of the pressure drop setup used in the present study is shown. The water reservoir with a capacity of 700 L was filled with tap water at 283 ± 3 K (10 ± 3 °C) with a viscosity of 0.0013 Pa·s which is equal to viscosity of molten aluminum at its casting temperature 993–1003 K (720–730 °C). Water is an excellent physical analogue to Al, and it can be used to study molten Al fluid dynamics.
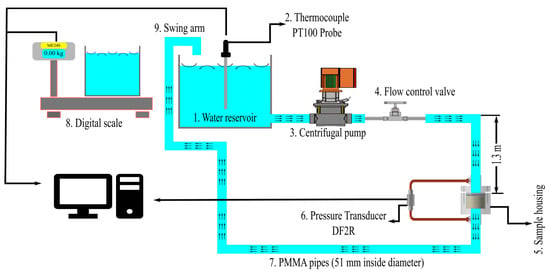
Figure 7.
Schematic drawing of the experimental pressure drop setup.
The different parts of the setup have been numbered and are explained below:
- The water reservoir.
- The thermocouple Probe PT100 and data logger GMH3750 from GHM Group, Remscheid, Germany) to measure the water temperature. The thermocouple was factory-calibrated to an expanded uncertainty of ±0.22 °C with a coverage factor of 2. The software (GSOFT 3050, GHM Group, Remscheid, Germany) was used to transfer data from the logger to the PC.
- The vertical multistage centrifugal pump (GRUNDFOS, Bjerringbro, Denmark) with integrated frequency converter, maximum 10 bar pressure and 20.5 m3·h−1.
- The stainless-steel needle valve regulates the flow of water through the system allowing adjustment of the velocity.
- The sample housing.
- The differential pressure transducers DF2R.
- Poly Methyl Methacrylate (PMMA) pipes used to transport the water in the system. The inlet pipe was 1.3 m long to secure a fully developed laminar flow in the low water velocity range. This length was calculated using Equation (10) where D is the pipe diameter (m), LE the entrance length (m), and ReD the Reynolds number of the pipes calculated from the defined flow rate (dimensionless), i.e., 10 mm·s−1,:
- The digital scale model ME204, METTLER TOLEDO, Switzerland, with the readability of 0.1 mg and a maximum capacity of 220 g. The scale was equipped with a LAB-it View software (version 5.0.1), for computer data storage.
- The swingarm that was part of the piping system.
Due to some temperature fluctuations in the experiments, the exact viscosity and density of water were calculated using the following relationships [27,28]:
where T is the temperature (K), µ the dynamic viscosity (kg∙m−1∙s−1), and A, B, and C constants with a magnitude of 4.5318, −220.57, and 149.39, respectively, in the temperature range 276 – 380 K (3 – 107 °C). The water temperature was measured and logged using the OMEGA thermocouple PT100 from GHM Group (Remscheid, Germany), connected to the control software GSOFT3050 V3.6.
The air in the pipes and the CFF samples had to be eliminated to secure stable conditions throughout the experiments. Accordingly, a loop for the water to circulate at high pressure before entering the experimental setup was established. The loop was interrupted by turning the moving part of the piping system, i.e., the swingarm shown in Figure 7, over the container placed on the digital scale. The water accumulation was measured and logged using the digital scale. A constant flow rate was established, and the corresponding pressure drop, and accumulation rate of water were logged for 30–60 s. Ten to twenty different velocities and their corresponding pressure drop were data-logged for each CFF sample. The superficial velocity (u) was determined from the mass of the accumulated water, the density of the water, and the measured cross-sectional area of the CFF samples. The permeability was later determined using measured data for the pressure drop through the filter, the sample dimensions, the water viscosity, and the superficial velocity.
4. Results and Discussion
4.1. Porosity
The true particle density of the CFF samples and their average are summarized in Table 2. As can be seen from the table, the average true particle density for the CFFs from suppliers A and B were relatively similar and slightly higher than those of the CFFs from supplier C.

Table 2.
The true particle density of CFFs from suppliers A, B, and C.
The porosity of the CFF samples was calculated using Equation (8), and the average values for the different Grades/PPI numbers are summarized in Table 3 and the results for each of the individual CFF samples can be found in Table A1, Table A2, Table A3 and Table A4. As can be seen from the table, the high-Grade/PPI number CFFs (65 and 80) from suppliers A and B showed slightly lower porosity than the low-Grade/PPI number CFFs (30). However, this trend was not observed for the CFFs from supplier C. The reason for this is believed to be directly linked to the uneven cylindrical shape of the samples secured from the 50 PPI and 60 PPI CFF blocks from supplier C which later also gave an increased uncertainty in measuring the sample dimensions. Nevertheless, the obtained result clearly indicated that the porosity of the different CFF samples was somewhat similar.

Table 3.
The average porosity of CFF from suppliers A, B, and C.
4.2. Mean Feret Diameter of the Cell and the Window
To better understand the differences between the CFF samples in view of their physical morphologies, the mean Feret diameter of the Cells and Windows of each Grade/PPI number was calculated and presented together with the pooled standard deviations and the number of counts (sample population) within each Grade/PPI number, see Table 4 (the mean Feret diameter of the Cells and Windows of each of the individual CFF samples can be found in Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12). As can be seen from the table, the deviations between the measured Feret diameter of the Windows proved to be less than in the case of the Cells. This is believed to be due to how they were measured, i.e., the circumferences of the Windows were identified through thresholding with a higher degree of precision than in the case of the Cells. It can also be seen from the Table 4 that CFF samples of corresponding Grade/PPI number clearly have different values for the Feret diameter of the Cells and Windows. In some cases, the values are significantly different, e.g., the average CFF Window diameter of Grade 30 from supplier A was 27% less than that of the 30 PPI from supplier C. It should be noted that in the grading system, the Cell Feret diameter defines the range of each CFF Grade. However, as the Windows Feret diameter can be measured with more precision, it is believed that it can substitute the Cell size in the grading system.

Table 4.
The mean Feret diameter of the Cell and Window of CFF from suppliers A, B, and C.
4.3. Permeability
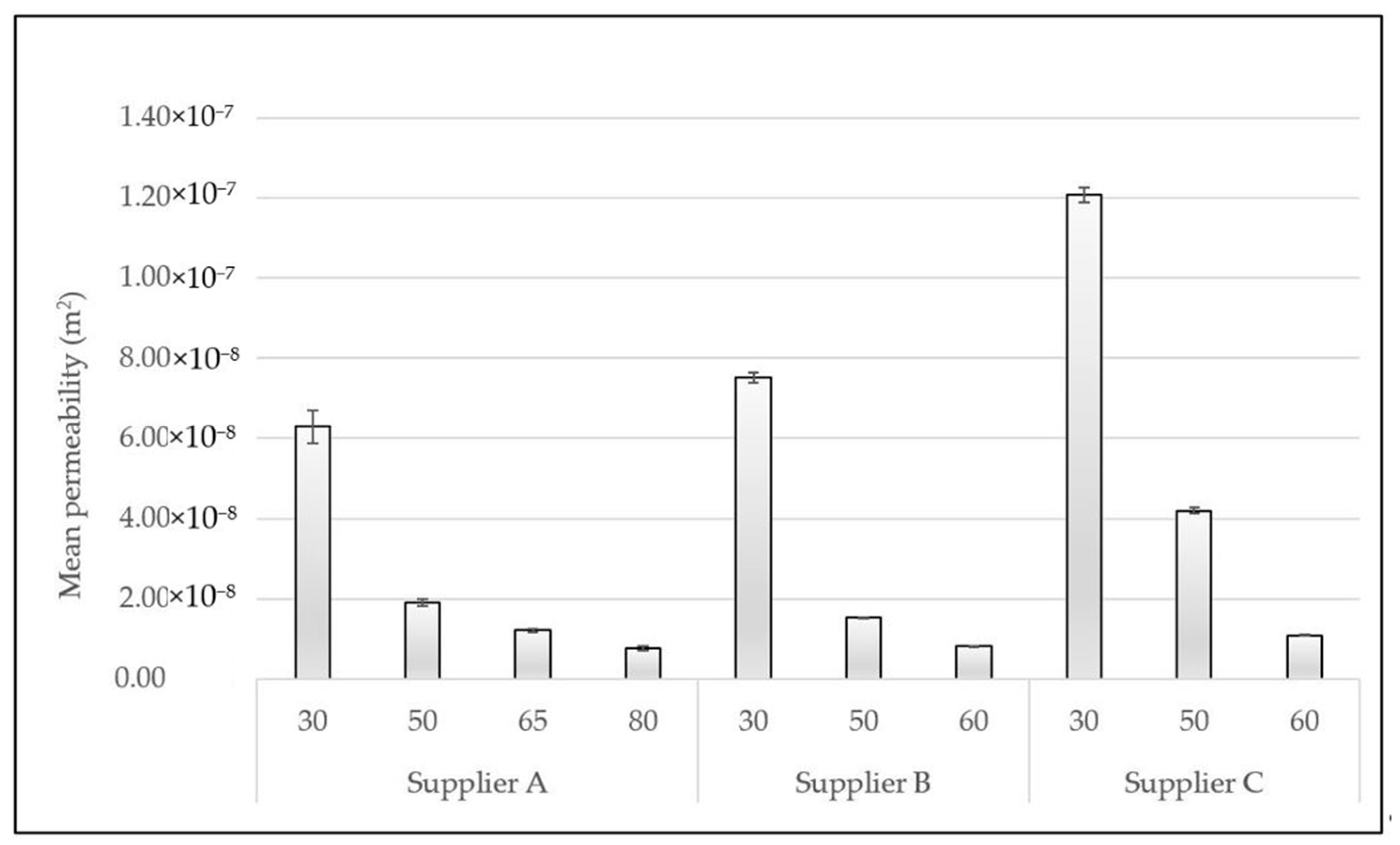
The CFF sample permeability was measured based on pressure drop experiments performed at the velocity range ≤ 10 mm·s−1. In Figure 8 the calculated mean permeability of all the investigated CFFs is presented. The permeability of each of the individual CFF samples within each Grade/PPI number can be found in Table A13, Table A14, Table A15 and Table A16.
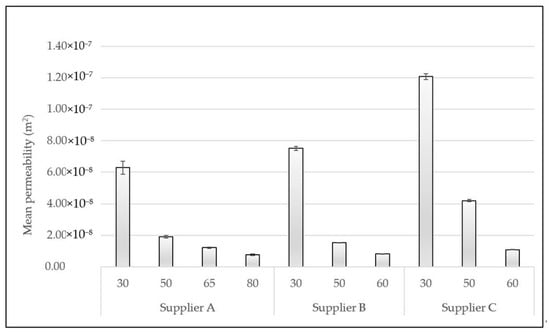
Figure 8.
Mean permeability of CFFs of various Grades/PPI numbers from suppliers A, B, and C.
As can be seen from Figure 8, the permeability of CFF 30 PPI and CFF 50 PPI from supplier C is significantly higher than the corresponding CFFs from suppliers A and B, i.e., Grade 30 and Grade 50 from supplier A, as well as 30 PPI and 50 PPI from supplier B, which, as previously mentioned, is believed to be linked to the disparity of their structural morphologies, see Table 4. This observation indicates that the permeability of the CFFs of a specific class can be relatively different in view of their structural morphologies and fluid flow properties when originating from different suppliers.
The permeability or morphological characteristics of the samples investigated in the present study, i.e., of the CFFs within each Grade/PPI, were defined using the statistical two-sample t-test with a 95% confidence interval. Before executing the t-test, the equality of the variances between the two datasets was tested to identify what assumption, i.e., equal, or unequal variances, should be practiced for the unpaired t-test. The test was accomplished by performing a two-sample F-test with a 95% confidence interval and by assuming equal variances for each pair of the dataset, i.e., the Null hypothesis. In Table 5, the results from the statistical analysis in view of identifying the variations in the mean sample permeability of CFFs Grade 30 from supplier A and 30 PPI from supplier B are presented. As can be seen from the table, the Null hypothesis could not be rejected, concluding that the variation of the mean permeability of CFFs Grade 30 from supplier A and CFFs 30 PPI from supplier B was not statistically significant.

Table 5.
The descriptive statistics of the F-Test, examining the equality of the variances of the permeabilities of the CFF samples and subsequently testing the significance of the variation of their mean permeability using the t-test. The CFFs tested were Grade 30 from supplier A and 30 PPI from supplier B.
An identical statistical analysis was performed to identify the corresponding CFF from suppliers B and supplier C to CFF from supplier A. A summary of the results is shown in Table 6 correlating the identical CFF using colored boxes. The results in Table 6 are valid for statistical analysis of both permeability and the Feret diameter of the Window and confirm/highlight the lack of a systematic way of sorting CFFs as there are two different classification systems. No correlation can even be identified between the CFFs classified using the same system, as in the case of suppliers B and supplier C.

Table 6.
The corresponding CFF of 30, 50, and 60 PPI from supplier B and supplier C with the Grades 30, 50, 65, and 80 from supplier A.
4.4. Flow Regimes in CFF
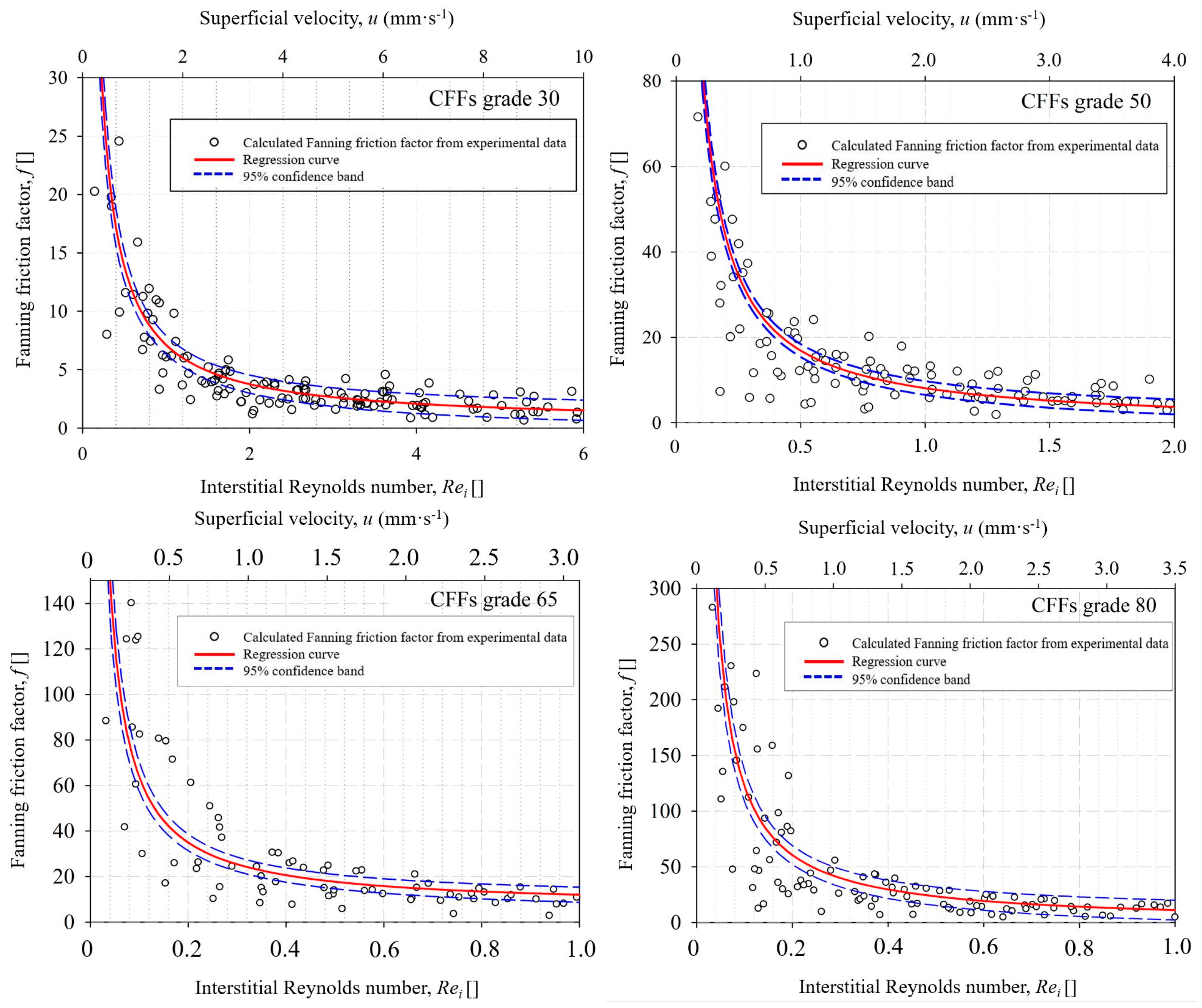
The velocity at which the laminar flow is transferred to transient flow and eventually turbulent flow can be identified using graphs correlating the dimensionless Fanning friction factor to Rei number, where the mean Window Feret diameter of CFF samples is used as the characteristic length scale for the estimation of Rei number. In Figure 9 the relation of the Fanning friction factor as a function of Rei number for CFF grade 30–80 from supplier A is presented. As can be seen from the Figure, the graph becomes almost horizontal at the onset of the turbulent flow regime, where the Fanning factor approaches zero.
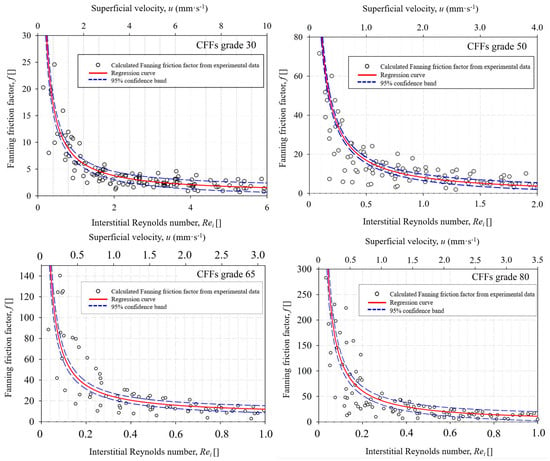
Figure 9.
The Fanning friction factor (dimensionless) as a function of the interstitial Reynolds numbers (Rei) and superficial velocity (u) for CFFs Grade 30–80 from supplier A.
The obtained laminar, transition, and turbulent flow regimes can be recognized by analogy with the three flow regions presented in Figure 2. The linear section of the diagram showing the laminar flow regime and the onset of the transitional flow regime can be defined by drawing a tangent line from the linear section of the graph to the interception with the “x” axis. In the laminar flow region, the friction factor of CFFs Grade 80 is one order of magnitude higher than the CFFs Grade 30, indicating that the wall shear stresses are higher for the CFFs with smaller pore sizes. As previously mentioned, the transitional flow region is reached a point where the drag forces are dominant, and the inertial forces are comparable to viscous forces. After that, the graph starts to decay until the velocity graph flattens horizontally.
The flow regimes in the CFFs from suppliers B and supplier C were also evaluated, and the results indicated that a laminar flow was achieved through CFFs of Grades/PPI numbers 30–80 at Rei ≤ 1, which corresponds to a superficial fluid velocity of ≤2 mm·s−1. This velocity is lower than the normally applied Al filtration velocities in the DC casting process, i.e., the velocity is in the superficial velocity range at which the flow in the channels is transient or turbulent. The presently obtained results are contrary to the assumption made by Bao et al. [8], where the laminar (creeping) flow was considered in a model of particle removal in CFFs during Al filtration. In view of this, a higher filtration efficiency was obtained in the derived model compared to the experimental work as the influence of the inertia as lifting forces on the collected particles partly resulted in particle re-entrainment.
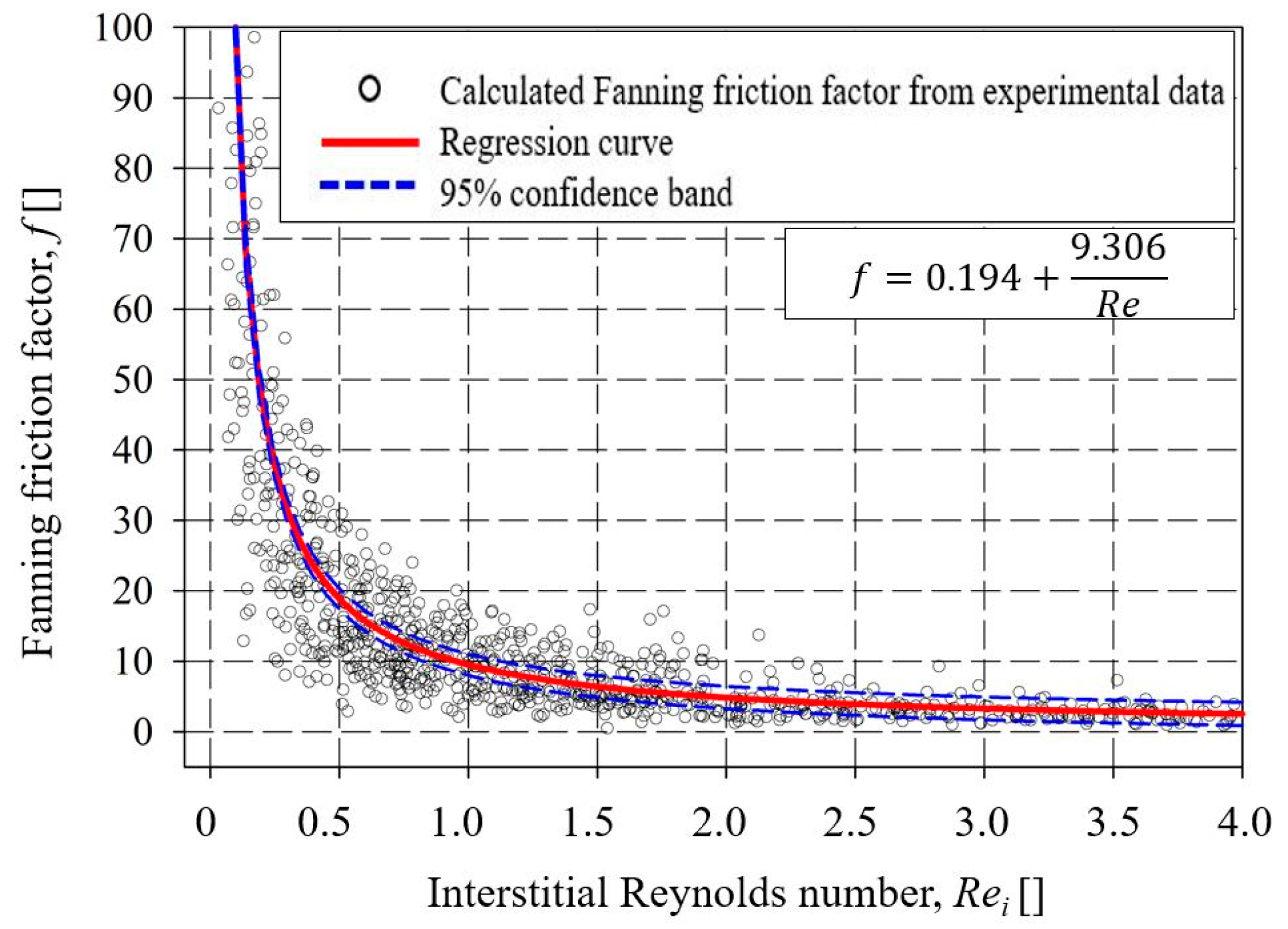
In the present study, the obtained pressure drop variations in the investigated CFFs can be analyzed through the model equations derived from graphs of Fanning friction factor (f) versus Rei number and their correlation to the Forchheimer equation (Equation (5)). In correlation to a characteristic length scale of CFFs, the model is identical to the Ergun equation (Equation (6)) that can derive the constants a and b in Equation (4) for CFFs of a specific Grade/PPI number. However, deriving global constants is, for straightforwardness, of more interest. Accordingly, the calculated Fanning friction factor (f) of all the investigated CFFs in the present study was plotted against the corresponding Rei number, and a model equation was derived using regression analysis, see Figure 10.
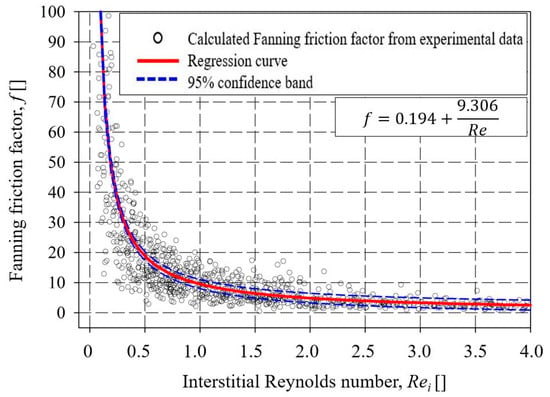
Figure 10.
The Fanning friction factor as a function of interstitial Reynolds numbers (Rei) of all the data points from supplier A, B, and C.
As can be seen from the figure, a nonlinear trend line at 95% confidence interval was fitted through the data points using regression analysis, and a polynomial inverse first-order equation was derived. The resulting function was later modified by substituting Equation (3) for the Fanning friction factor (f), and correlating the pressure drop of the CFFs to their characteristic length scale, i.e., to the Window Feret diameter (dw), see Equation (13):
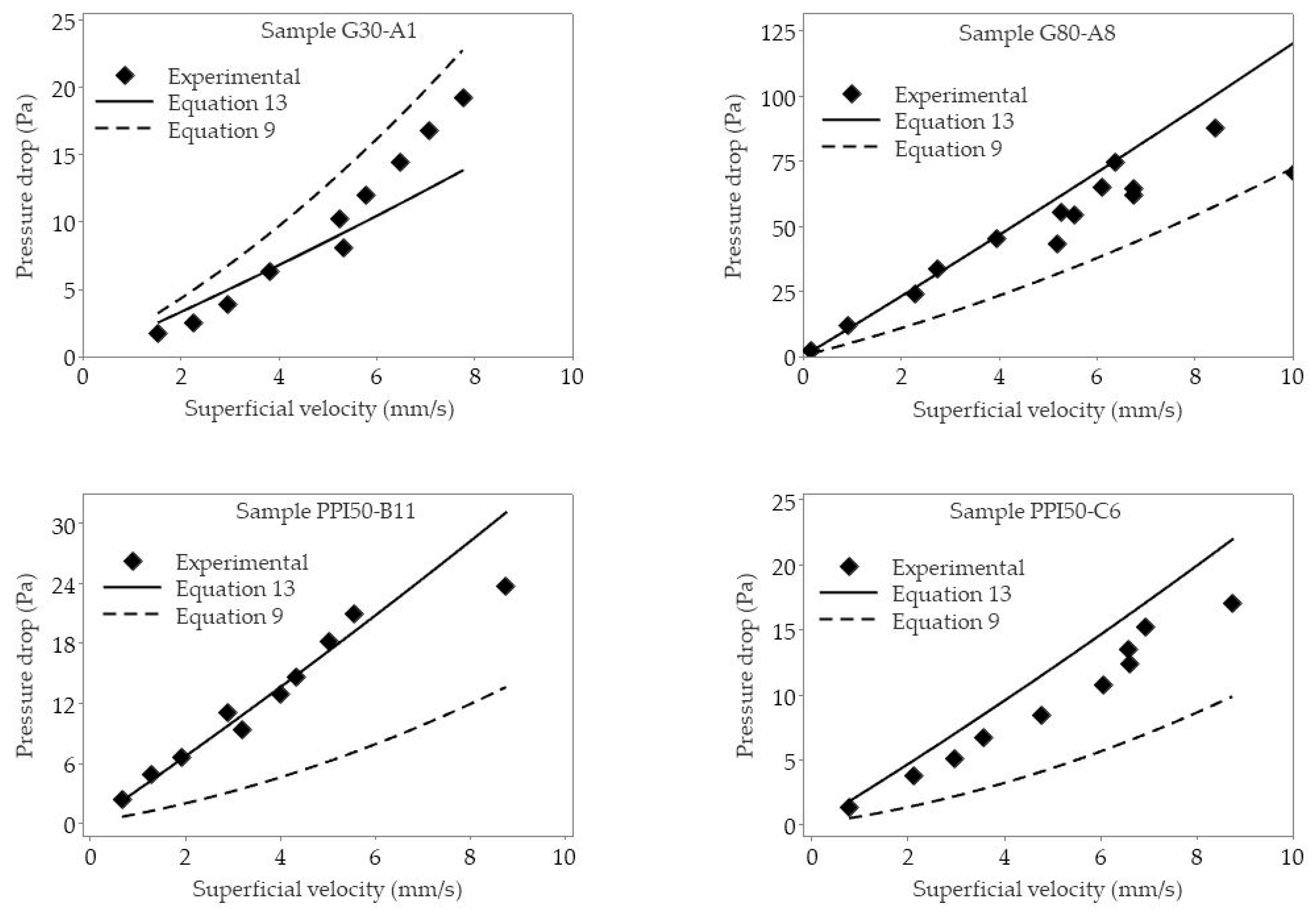
Equation (13), together with a previously published equation by Kennedy et al. [19] (Equation (9)), were then plotted against the experimental pressure drop values obtained for CFF samples from suppliers A, B, and C to find the model that could describes better the experimental work, see Figure 11. The Cell Feret diameter and Window Feret diameter of the samples were used, respectively, for dc and dw in Equations (9) and (13), see Table A1, Table A2, Table A5, and Table A6 for the measured data of dc, dw, and porosity of all the samples.
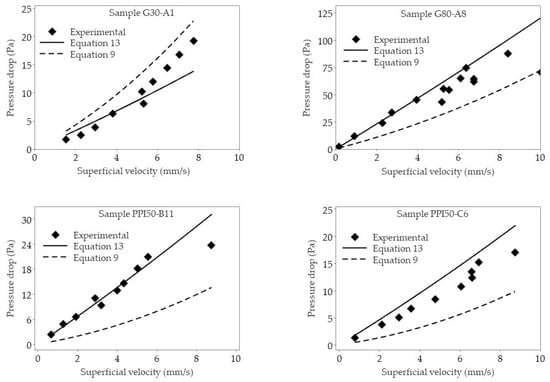
Figure 11.
The obtained pressure drops calculated using Equations (13) and (9) (published by Kennedy et al. [10]), as well as the experimentally measured pressure drop values as a function of the superficial velocity (u) for CFF samples.
In Equation (9), the Cell Feret diameter (dc) was substituted for the equivalent particle size (dp) in the Ergun equation (Equation (6)) using Equation (14) which allowed to obtain an equivalent particle size (dp) for CFFs based on their porosity (Ø) and mean Cell Feret diameter (dc) [19]:
In Figure 11, the presently measured experimental and calculated pressure drops values are shown by respective symbols and regression lines. As can be seen from the figure, there is an increased agreement between the obtained results based on the presently derived equation, i.e., Equation (13), and the experimental values when compared with the calculated pressure drop values based on the equation proposed by Kennedy et al. [10], i.e., Equation (9). It should, however, be noted that Kennedy et al. [10] used a similar experimental setup as in the present study but used a maximum velocity of 800 mm·s−1. In contrast, in the present case, the velocity used was set to simulate industrial casting conditions, i.e., ≤ 10 mm·s−1.
In the filtration of Al using CFFs, the filters are placed inside a filter box and preheated to a temperature of about 993 K (720 °C) to prevent solidification of the molten Al metal when it initially meets the filter at the start of the filtration step [29]. As a result, a metallostatic head is formed on the surface of the CFF, and the pressure from the metal head breaks the oxides layer that has formed on the interface between the CFF surface and the molten Al, thereby primes the filter, i.e., infiltrates the CFFs with molten Al [16]. From that point, the filtration process is initiated, and the molten Al flows through the CFF [16]. Equations (9) and (13) can both be used to evaluate the required metallostatic head needed to prime the CFF, and a metal head of 21.3 cm and 8.9 cm were presently obtained. In view of this result, it is clear that pressure drop experiments must be performed at velocities close to industrial casting conditions for Al to be able to accurately study and evaluate the hydraulic properties of CFF during the Al filtration.
5. Conclusions and Future Work
The present study investigates the morphological characteristics and permeability of commercial alumina (Al2O3) CFF. The main goals of the study have been to (i) define the different flow regimes inside CFFs at flow velocities in the range of industrial filtration of Al (10 mm·s−1) and (ii) derive a semi/empirical equation for calculation of pressure drop and the permeability of CFFs using their morphological characteristics. Based on the present investigation, the following conclusions have been made:
- Comparing the permeability and mean Window Feret diameter of different filters confirmed the need for a systemic method to categorize CFFs.
- Filtration of Al using CFF is performed at the superficial velocity at which the fluid flow in the channels is turbulent.
- The derived empirical model for the calculation of the pressure drop of CFFs correlates well with the experimental pressure drop data.
- Empirical expressions for calculating the pressure drop over CFF should be derived based on experimental measurements carried out at the velocity range of the application.
For the future work, the structural uniformity of CFFs and the effect of different flow regimes on the permeability of the filters will be investigated using pressure drop experiments at high and low fluid velocities.
Author Contributions
Conceptualization, M.H. and R.E.A.; Methodology, M.H. and R.E.A.; Validation, M.H., R.E.A., S.A. and T.B.; Investigation, M.H. and T.B.; Writing—original draft preparation, M.H.; Writing—review and editing, R.E.A. and S.A.; Supervision, R.E.A. and S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the SFI Metal Production (Center for Research-based Innovation) grant number 237738.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data created are presented in the Appendix A.
Acknowledgments
The authors gratefully acknowledge the financial support from the Research Council of Norway and the partners of the SFI Metal Production.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The porosity of CFF samples of Grade 30 and 50 from supplier A.
Table A1.
The porosity of CFF samples of Grade 30 and 50 from supplier A.
| Grade 30 | Grade 50 | |||
|---|---|---|---|---|
| Porosity | Uncertainty | Porosity | Uncertainty | |
| A1 | 8.72 × 10−1 | 3.92 × 10−4 | 8.39 × 10−1 | 8.19 × 10−4 |
| A2 | 8.79 × 10−1 | 7.30 × 10−4 | 8.50 × 10−1 | 1.09 × 10−3 |
| A3 | 8.98 × 10−1 | 8.09 × 10−4 | 8.68 × 10−1 | 1.22 × 10−3 |
| A4 | 8.77 × 10−1 | 1.02 × 10−4 | 8.41 × 10−1 | 1.16 × 10−3 |
| A5 | 8.84 × 10−1 | 9.95 × 10−4 | 8.50 × 10−1 | 7.68 × 10−4 |
| A6 | 8.69 × 10−1 | 6.36 × 10−4 | 8.49 × 10−1 | 8.47 × 10−4 |
| A7 | 8.80 × 10−1 | 8.87 × 10−4 | 8.56 × 10−1 | 2.43 × 10−3 |
| A8 | 8.94 × 10−1 | 8.37 × 10−4 | 8.42 × 10−1 | 8.42 × 10−4 |
| A9 | 8.74 × 10−1 | 1.32 × 10−4 | 8.33 × 10−1 | 1.05 × 10−3 |
| A10 | 8.83 × 10−1 | 7.53 × 10−4 | 8.45 × 10−1 | 9.21 × 10−4 |
| A11 | 8.98 × 10−1 | 1.64 × 10−4 | 8.41 × 10−1 | 7.33 × 10−4 |
| A12 | 8.95 × 10−1 | 4.98 × 10−4 | 8.43 × 10−1 | 1.19 × 10−3 |
| A13 | 8.95 × 10−1 | 1.54 × 10−4 | 8.60 × 10−1 | 1.14 × 10−3 |
| A14 | 8.98 × 10−1 | 1.01 × 10−4 | 8.48 × 10−1 | 1.14 × 10−3 |
| A15 | 8.75 × 10−1 | 6.79 × 10−4 | 8.47 × 10−1 | 1.37 × 10−3 |

Table A2.
The porosity of CFF samples of Grade 65 and Grade 80 from supplier A.
Table A2.
The porosity of CFF samples of Grade 65 and Grade 80 from supplier A.
| Grade 65 | Grade 80 | |||
|---|---|---|---|---|
| Porosity | Uncertainty | Porosity | Uncertainty | |
| A1 | 8.73 × 10−1 | 9.35 × 10−4 | 8.63 × 10−1 | 1.11 × 10−3 |
| A2 | 8.54 × 10−1 | 1.00 × 10−3 | 8.73 × 10−1 | 3.97 × 10−3 |
| A3 | 8.47 × 10−1 | 9.33 × 10−4 | 8.55 × 10−1 | 4.79 × 10−3 |
| A4 | 8.49 × 10−1 | 7.50 × 10−4 | 8.51 × 10−1 | 1.47 × 10−3 |
| A5 | 8.54 × 10−1 | 1.00 × 10−3 | 8.58 × 10−1 | 2.26 × 10−3 |
| A6 | 8.43 × 10−1 | 1.12 × 10−3 | - | - |
| A7 | 8.42 × 10−1 | 1.41 × 10−3 | 8.63 × 10−1 | 2.72 × 10−3 |
| A8 | 8.45 × 10−1 | 1.19 × 10−3 | 8.44 × 10−1 | 3.12 × 10−3 |
| A9 | 8.77 × 10−1 | 1.89 × 10−3 | 8.40 × 10−1 | 1.75 × 10−3 |
| A10 | 8.58 × 10−1 | 2.01 × 10−3 | 8.57 × 10−1 | 1.38 × 10−3 |
| A11 | 8.47 × 10−1 | 9.59 × 10−4 | 8.55 × 10−1 | 2.63 × 10−3 |
| A12 | 8.46 × 10−1 | 1.82 × 10−3 | 8.58 × 10−1 | 2.42 × 10−3 |
| A13 | 8.76 × 10−1 | 1.67 × 10−3 | 8.59 × 10−1 | 2.02 × 10−3 |
| A14 | 8.55 × 10−1 | 1.34 × 10−3 | 8.42 × 10−1 | 1.76 × 10−3 |
| A15 | 8.60 × 10−1 | 1.24 × 10−3 | 8.49 × 10−1 | 1.02 × 10−2 |

Table A3.
The porosity of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
Table A3.
The porosity of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
| 30 PPI | 50 PPI | 60 PPI | ||||
|---|---|---|---|---|---|---|
| Porosity | Uncertainty | Porosity | Uncertainty | Porosity | Uncertainty | |
| B1 | 8.83 × 10−1 | 2.89 × 10−4 | - | - | - | - |
| B2 | 8.72 × 10−1 | 3.16 × 10−4 | - | - | - | - |
| B3 | 8.84 × 10−1 | 2.88 × 10−4 | 8.76 × 10−1 | 3.06 × 10−4 | 8.79 × 10−1 | 2.98 × 10−4 |
| B4 | - | - | 8.69 × 10−1 | 3.24 × 10−4 | 8.82 × 10−1 | 2.91 × 10−4 |
| B5 | 8.82 × 10−1 | 2.91 × 10−4 | 8.67 × 10−1 | 3.28 × 10−4 | 8.70 × 10−1 | 3.20 × 10−4 |
| B6 | 8.87 × 10−1 | 2.80 × 10−4 | - | - | - | - |
| B7 | 8.89 × 10−1 | 2.75 × 10−4 | 8.71 × 10−1 | 3.19 × 10−4 | 8.74 × 10−1 | 3.12 × 10−4 |
| B8 | 8.77 × 10−1 | 3.04 × 10−4 | 8.80 × 10−1 | 2.96 × 10−4 | 8.79 × 10−1 | 2.98 × 10−4 |
| B9 | 8.77 × 10−1 | 3.04 × 10−4 | - | - | - | - |
| B10 | 8.77 × 10−1 | 3.04 × 10−4 | 8.73 × 10−1 | 1.78 × 10−3 | 8.67 × 10−1 | 3.28 × 10−4 |
| B11 | - | - | 8.69 × 10−1 | 3.23 × 10−4 | - | - |
| B12 | - | - | - | - | - | - |
| B13 | - | - | 8.79 × 10−1 | 3.00 × 10−4 | 8.67 × 10−1 | 3.29 × 10−4 |
| B14 | - | - | - | - | 8.73 × 10−1 | 3.14 × 10−4 |
| B15 | - | - | 8.70 × 10−1 | 3.22 × 10−4 | 8.70 × 10−1 | 3.22 × 10−4 |

Table A4.
The porosity of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
Table A4.
The porosity of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
| 30 PPI | 50 PPI | 60 PPI | ||||
|---|---|---|---|---|---|---|
| Porosity | Uncertainty | Porosity | Uncertainty | Porosity | Uncertainty | |
| C1 | 8.88 × 10−1 | 2.30 × 10−4 | - | - | 8.89 × 10−1 | 2.30 × 10−4 |
| C2 | 8.81 × 10−1 | 2.47 × 10−4 | 8.98 × 10−1 | 2.10 × 10−4 | 8.91 × 10−1 | 2.25 × 10−4 |
| C3 | 8.82 × 10−1 | 2.43 × 10−4 | 8.93 × 10−1 | 2.22 × 10−4 | - | - |
| C4 | 8.86 × 10−1 | 2.37 × 10−4 | - | - | - | - |
| C5 | - | - | 8.91 × 10−1 | 2.25 × 10−4 | 8.85 × 10−1 | 2.39 × 10−4 |
| C6 | 8.81 × 10−1 | 2.45 × 10−4 | 8.93 × 10−1 | 2.22 × 10−4 | 8.89 × 10−1 | 2.29 × 10−4 |
| C7 | 8.85 × 10−1 | 2.38 × 10−4 | - | - | - | - |
| C8 | - | - | - | - | - | - |
| C9 | 8.87 × 10−1 | 2.34 × 10−4 | 8.92 × 10−1 | 2.24 × 10−4 | 8.87 × 10−1 | 2.33 × 10−4 |
| C10 | 8.78 × 10−1 | 2.52 × 10−4 | 8.88 × 10−1 | 2.32 × 10−4 | 8.81 × 10−1 | 2.48 × 10−4 |
| C11 | - | - | 8.99 × 10−1 | 2.09 × 10−4 | - | - |
| C12 | - | - | 9.03 × 10−1 | 2.00 × 10−4 | - | - |
| C13 | - | - | - | - | 8.88 × 10−1 | 2.34 × 10−4 |
| C14 | - | - | - | - | 8.84 × 10−1 | 2.39 × 10−4 |
| C15 | - | - | 8.86 × 10−1 | 2.36 × 10−4 | 8.78 × 10−1 | 2.54 × 10−4 |

Table A5.
Mean Window’s Feret diameter (dw) of CFF samples of Grade 30 and Grade 50 from supplier A.
Table A5.
Mean Window’s Feret diameter (dw) of CFF samples of Grade 30 and Grade 50 from supplier A.
| G30 | G50 | |||||
|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| A1 | 97 | 252.3 | 853.3 | 240 | 201.1 | 444 |
| A2 | 543 | 257.9 | 685.4 | 183 | 163.1 | 579.7 |
| A3 | 485 | 256.1 | 654.5 | 485 | - | 386.2 |
| A4 | 209 | 226.6 | 960.4 | 191 | 206.9 | 604 |
| A5 | 105 | 270.4 | 768.9 | - | - | - |
| A6 | 212 | 284.2 | 948.6 | 219 | 214.9 | 433.3 |
| A7 | 117 | 254.4 | 759.8 | 158 | 151.3 | 537.1 |
| A8 | 135 | 206.1 | 564.5 | 135 | 130.7 | 471.2 |
| A9 | 83 | 268.2 | 626.5 | 766 | 173.9 | 464.5 |
| A10 | - | - | - | 136 | 109.7 | 430.8 |
| A11 | - | - | - | 146 | 124.4 | 521.7 |
| A12 | 108 | 296.8 | 725.6 | 178 | 121.4 | 539.7 |
| A13 | - | - | - | 129 | 147.4 | 573.4 |
| A14 | 172 | 252.2 | 759.1 | 189 | 184 | 529.1 |
| A15 | 446 | 292.3 | 705.8 | 174 | 133.8 | 534.2 |

Table A6.
Mean Window’s Feret diameter (dw) of CFF samples of Grade 65 and Grade 80 from supplier A.
Table A6.
Mean Window’s Feret diameter (dw) of CFF samples of Grade 65 and Grade 80 from supplier A.
| Grade 65 | Grade 80 | |||||
|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| A1 | 167 | 131.2 | 436.4 | 296 | 92.2 | 323.1 |
| A2 | 106 | 108 | 398.8 | 271 | 98.9 | 285.1 |
| A3 | 115 | 87.2 | 443.4 | - | - | - |
| A4 | 217 | 165.7 | 411.1 | 143 | 78.5 | 283.3 |
| A5 | - | - | - | 94 | 67.3 | 305.3 |
| A6 | 169 | 67.8 | 456 | 200 | 147.1 | 427.9 |
| A7 | 168 | 120.9 | 416.1 | 101 | 95 | 397.2 |
| A8 | 131 | 97 | 412.2 | 68 | 89.6 | 319.8 |
| A9 | 195 | 109.3 | 433.3 | 437 | 77.5 | 287.5 |
| A10 | - | - | - | - | - | - |
| A11 | 129 | 93.5 | 437 | 186 | 86.7 | 363.5 |
| A12 | 196 | 97.8 | 425.7 | 230 | 110.4 | 308.7 |
| A13 | - | - | - | 231 | 149.1 | 450.3 |
| A14 | 119 | 62.6 | 237.4 | 121 | 70.2 | 397.6 |
| A15 | 170 | 85.7 | 378.6 | - | - | - |

Table A7.
Mean Window’s Feret diameter (dw) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
Table A7.
Mean Window’s Feret diameter (dw) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
| 30 PPI | 50 PPI | 60 PPI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| B1 | 158 | 129 | 556.4 | 159 | 96.1 | 507.2 | 137 | 56.5 | 284.7 |
| B2 | 127 | 190.5 | 733.6 | 78 | 74 | 480 | 140 | 77.8 | 423.2 |
| B3 | 111 | 173.6 | 664.4 | 112 | 82.8 | 442.8 | - | - | - |
| B4 | 100 | 136.4 | 636.3 | - | 119.1 | 591.2 | 117 | 81.9 | 370.9 |
| B5 | 103 | 183 | 763.6 | 118 | 74.2 | 479.1 | 117 | 87 | 413.5 |
| B6 | 131 | 149.2 | 609.8 | 116 | 86.9 | 469 | 115 | 59.3 | 331.4 |
| B7 | 124 | 201.8 | 738.8 | 111 | 105.9 | 519.2 | 153 | 62.1 | 337.8 |
| B8 | 127 | 203.5 | 824.8 | 144 | 102.9 | 563.1 | 124 | 90.3 | 391.5 |
| B9 | 122 | 185 | 716.2 | 133 | 107.1 | 565 | 139 | 72.6 | 392.1 |
| B10 | 138 | 165 | 728.5 | 151 | 88.6 | 461.3 | 92 | 106.5 | 417 |
| B11 | - | - | - | 115 | 107.2 | 580.8 | 182 | 41.6 | 267.2 |
| B12 | - | - | - | 115 | 93.2 | 521.2 | - | 71.4 | 388.4 |
| B13 | - | - | - | 146 | 100.7 | 482.4 | 174 | 71.6 | 391.4 |
| B14 | - | - | - | 174 | 89 | 444.6 | 116 | 57.9 | 337.1 |
| B15 | - | - | - | 133 | 86 | 498.7 | 179 | 43.7 | 249.7 |

Table A8.
Mean Window’s Feret diameter (dw) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
Table A8.
Mean Window’s Feret diameter (dw) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
| 30 PPI | 50 PPI | 60 PPI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| C1 | 119 | 250.7 | 991 | 150 | 176.3 | 775.7 | 374 | 82.5 | 450.8 |
| C2 | - | - | - | 167 | 176.3 | 657.5 | - | - | - |
| C3 | 109 | 229 | 846.2 | 143 | 192.9 | 789.7 | 210 | 75.4 | 384.2 |
| C4 | 132 | 218.8 | 779.3 | 174 | 152.7 | 701.8 | 201 | 83.9 | 435.1 |
| C5 | 114 | 226.9 | 928.8 | 129 | 166.3 | 716.5 | - | 80.7 | 436.9 |
| C6 | 123 | 260.7 | 1026.8 | 216 | 163.5 | 703.7 | 232 | 84.8 | 449.2 |
| C7 | 110 | 293.3 | 1044.7 | 160 | 169.3 | 731.3 | 129 | 64.1 | 370 |
| C8 | 111 | 253.3 | 926 | 151 | 188.3 | 825.4 | 206 | 60.5 | 410.3 |
| C9 | 148 | 240.8 | 1083.2 | 165 | 130.7 | 640.2 | 231 | 79.6 | 365.7 |
| C10 | 148 | 218 | 870.5 | 176 | 162.4 | 712.4 | 201 | 60 | 332.7 |
| C11 | 157 | 267.2 | 1065.4 | 198 | 158.5 | 696.1 | 174 | 71.2 | 376.8 |
| C12 | 115 | 288.3 | 1040.6 | 133 | 169.4 | 895.8 | 192 | 79.1 | 410.8 |
| C13 | 131 | 269.4 | 999.9 | 107 | 176.9 | 720.6 | 183 | 63.9 | 359 |
| C14 | 142 | 259.8 | 995.9 | 150 | 146.2 | 644.2 | 238 | 59.2 | 334.6 |
| C15 | 160 | 210.2 | 845.9 | 127 | 190.8 | 667.3 | 173 | 68.1 | 382.1 |

Table A9.
Mean Cell’s Feret diameter (dC) of CFF samples of Grade 30 and Grade 50 from supplier A.
Table A9.
Mean Cell’s Feret diameter (dC) of CFF samples of Grade 30 and Grade 50 from supplier A.
| Grade 30 | Grade 50 | |||||
|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| A1 | 110 | 392.5 | 948.2 | 155 | 459.1 | 972.7 |
| A2 | 348 | 1237.7 | 1836.5 | 149 | 771.3 | 1186.3 |
| A3 | 561 | 755.7 | 1070.7 | 1203 | 336.2 | 565.3 |
| A4 | 94 | 290.6 | 740.1 | 143 | 797.5 | 1370.7 |
| A5 | 134 | 579.2 | 1179.4 | 109 | 722.6 | 1272 |
| A6 | 162 | 345.3 | 1083 | 164 | 469.5 | 879.1 |
| A7 | 143 | 630.6 | 1178.3 | 427 | 635.9 | 957.6 |
| A8 | 180 | 411.2 | 827.5 | 178 | 754.7 | 932.8 |
| A9 | 90 | 802.4 | 1661.8 | 948 | 686.9 | 993.4 |
| A10 | - | - | - | 69 | 599.3 | 1376.1 |
| A11 | - | - | - | 125 | 732.4 | 1571.5 |
| A12 | 107 | 1624 | 1871.9 | 160 | 537.8 | 1129.6 |
| A13 | - | - | - | 156 | 649.7 | 1006.9 |
| A14 | 148 | 360.5 | 983.1 | 225 | 537.5 | 796.9 |
| A15 | 421 | 1195.5 | 1676.2 | 97 | 277.4 | 706.4 |

Table A10.
Mean Cell’s Feret diameter (dC) of CFF samples of Grade 65 and Grade 80 from supplier A.
Table A10.
Mean Cell’s Feret diameter (dC) of CFF samples of Grade 65 and Grade 80 from supplier A.
| Grade 65 | Grade 80 | |||||
|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| A1 | 240 | 412.4 | 729.2 | - | - | - |
| A2 | 137 | 488.8 | 868.2 | 402 | 603.6 | 770 |
| A3 | 62 | 620.6 | 1154.6 | - | - | - |
| A4 | 219 | 612.2 | 1133.6 | 239 | 354.3 | 525.3 |
| A5 | - | - | - | 181 | 435.1 | 713.6 |
| A6 | 222 | 476.6 | 943.2 | 406 | 595.5 | 814.7 |
| A7 | 140 | 444 | 990.9 | 205 | 474.4 | 759.9 |
| A8 | 220 | 568.7 | 833.8 | 194 | 383.5 | 600.2 |
| A9 | 232 | 452.7 | 720.3 | 682 | 401.3 | 596.2 |
| A10 | - | - | - | - | - | - |
| A11 | 158 | 443.7 | 914.9 | 552 | 527.4 | 342.3 |
| A12 | 198 | 687.4 | 1020.8 | 329 | 282.9 | 594.9 |
| A13 | - | - | - | 226 | 343 | 767.9 |
| A14 | 186 | 548.9 | 812.4 | 195 | 310.5 | 739.3 |
| A15 | 509 | 552.7 | 513.3 | - | - | - |

Table A11.
Mean Cell´s Feret diameter (dC) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
Table A11.
Mean Cell´s Feret diameter (dC) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
| 30 PPI | 50 PPI | 60 PPI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| B1 | 196 | 980.1 | 1259.5 | 189 | 734.2 | 1252.2 | 257 | 807.9 | 1244.2 |
| B2 | 146 | 678.2 | 1491.6 | 135 | 440.2 | 1046 | 281 | 444.7 | 878.8 |
| B3 | 253 | 1157.4 | 1397.6 | 313 | 893.8 | 1208.9 | - | - | - |
| B4 | 277 | 1054.5 | 1520.6 | 205 | 505.7 | 1066.2 | 265 | 528.7 | 942.2 |
| B5 | 83 | 491.1 | 1280.1 | 216 | 468.5 | 1003.4 | 336 | 537.9 | 946.3 |
| B6 | 264 | 881 | 1105.2 | 167 | 744.9 | 1208.2 | 244 | 505.2 | 919 |
| B7 | 218 | 545.5 | 1140.6 | 151 | 462.5 | 1202.8 | 258 | 566.7 | 835.4 |
| B8 | 166 | 844.5 | 1382.5 | 409 | 567.9 | 919.3 | 252 | 629.2 | 1016.6 |
| B9 | 88 | 709.3 | 1484.6 | 146 | 595.7 | 1216.7 | 175 | 575.9 | 1139.6 |
| B10 | 182 | 613.4 | 1173.1 | 237 | 507.6 | 918.2 | 235 | 824.8 | 911.1 |
| B11 | - | - | - | 444 | 1162.7 | 1435.3 | 275 | 548.8 | 846.7 |
| B12 | - | - | - | 206 | 484.3 | 1012.3 | 247 | 414.1 | 631.7 |
| B13 | - | - | - | 141 | 684.9 | 1229.8 | 356 | 583 | 721.8 |
| B14 | - | - | - | 178 | 709.4 | 1156.8 | 392 | 346.5 | 559.7 |
| B15 | - | - | - | 205 | 669.8 | 1135.4 | 365 | 576.9 | 742 |

Table A12.
Mean Cell’s Feret diameter (dC) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
Table A12.
Mean Cell’s Feret diameter (dC) of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
| 30 PPI | 50 PPI | 60 PPI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | Counts | St. Dev. (µm) | Mean (µm) | |
| C1 | 125 | 1174.6 | 1778.9 | 164 | 991.1 | 1953.7 | 449 | 606.2 | 923.8 |
| C2 | - | - | - | 274 | 657 | 1167.2 | - | - | - |
| C3 | 136 | 1198.9 | 1955.1 | 153 | 1294.8 | 1908 | 236 | 567.4 | 1018.4 |
| C4 | 150 | 1428 | 2017.6 | 192 | 879.8 | 1499.9 | 298 | 509.9 | 960 |
| C5 | 82 | 1738.4 | 2530.5 | 173 | 876.9 | 1545 | 342 | 415.7 | 711.6 |
| C6 | 75 | 1251.1 | 2342.7 | 155 | 1003.1 | 1770.7 | 429 | 660.5 | 1012.6 |
| C7 | 101 | 1158.4 | 2292.3 | 269 | 515.5 | 1066.1 | 233 | 561 | 906.4 |
| C8 | 99 | 1066.9 | 2030.5 | 264 | 646.3 | 1098.3 | 295 | 563.4 | 933.9 |
| C9 | 109 | 1348.2 | 2211.3 | 354 | 582.2 | 1072.4 | 323 | 536.1 | 885.6 |
| C10 | 123 | 942.1 | 1866.3 | 263 | 821.4 | 1278.3 | 307 | 465.5 | 835 |
| C11 | 118 | 928.1 | 2011.2 | 195 | 755.3 | 1386.8 | 290 | 454.5 | 820.9 |
| C12 | 102 | 1054.4 | 2147.1 | 282 | 744.3 | 1229.6 | 308 | 650.1 | |
| C13 | 92 | 1518.3 | 2582.7 | 129 | 815.3 | 1453.6 | 407 | 480.7 | 846.7 |
| C14 | 112 | 709.8 | 1872 | 133 | 750.4 | 1396.7 | 301 | 460.1 | 838.1 |
| C15 | 110 | 1355.4 | 2239.4 | 111 | 842.4 | 1614.1 | 244 | 577.8 | 1012.3 |

Table A13.
Permeability of CFF samples of Grade 30 and Grade 50 from supplier A.
Table A13.
Permeability of CFF samples of Grade 30 and Grade 50 from supplier A.
| Grade 30 | Grade 50 | |||
|---|---|---|---|---|
| Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | |
| 1 | 8.80 × 10−8 | 6.70 × 10−10 | 1.00 × 10−8 | 8.60 × 10−11 |
| 2 | 4.40 × 10−8 | 6.40 × 10−9 | 2.30 × 10−8 | 3.60 × 10−10 |
| 3 | 2.80 × 10−8 | 3.30 × 10−9 | 2.40 × 10−8 | 3.80 × 10−10 |
| 4 | 4.90 × 10−8 | 1.10 × 10−8 | 4.50 × 10−8 | 1.20 × 10−9 |
| 5 | 4.10 × 10−8 | 5.00 × 10−10 | 2.50 × 10−8 | 1.20 × 10−9 |
| 6 | 7.20 × 10−8 | 7.60 × 10−10 | - | - |
| 7 | 7.40 × 10−8 | 5.10 × 10−9 | 2.50 × 10−8 | 8.60 × 10−10 |
| 8 | 3.90 × 10−8 | 1.10 × 10−9 | 1.30 × 10−8 | 5.50 × 10−10 |
| 9 | * 2.5 × 10−7 | 1.10 × 10−8 | 1.60 × 10−8 | 8.90 × 10−11 |
| 10 | 6.90 × 10−8 | 2.80 × 10−9 | 1.90 × 10−8 | 1.40 × 10−9 |
| 11 | 3.80 × 10−8 | 3.60 × 10−10 | 7.60 × 10−8 | 3.90 × 10−10 |
| 12 | 7.30 × 10−8 | 1.10 × 10−9 | 1.30 × 10−8 | 4.30 × 10−10 |
| 13 | 1.10 × 10−7 | 2.60 × 10−9 | 2.40 × 10−8 | 1.80 × 10−10 |
| 14 | 5.60 × 10−8 | 3.20 × 10−10 | 1.70 × 10−8 | 1.40 × 10−9 |
| 15 | 9.80 × 10−8 | 3.60 × 10−9 | 2.00 × 10−8 | 1.20 × 10−9 |
* The bold numbers are outliers and were disregarded in the calculations.

Table A14.
Permeability of CFF samples of Grade 65 and 80 from supplier A.
Table A14.
Permeability of CFF samples of Grade 65 and 80 from supplier A.
| Grade 65 | Grade 80 | |||
|---|---|---|---|---|
| Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | |
| 1 | - | - | 1.50 × 10−8 | 1.40 × 10−9 |
| 2 | 9.90 × 10−9 | 9.60 × 10−11 | 8.90 × 10−9 | 3.60 × 10−11 |
| 3 | 8.30 × 10−9 | 5.60 × 10−10 | 3.30 × 10−9 | 2.50 × 10−11 |
| 4 | 1.60 × 10−8 | 7.70 × 10−10 | 1.10 × 10−8 | 5.70 × 10−10 |
| 5 | 2.10 × 10−8 | 7.70 × 10−10 | 1.20 × 10−8 | 7.40 × 10−11 |
| 6 | - | - | - | - |
| 7 | 1.10 × 10−8 | 1.10 × 10−10 | 6.80 × 10−9 | 2.50 × 10−11 |
| 8 | 8.50 × 10−9 | 5.60 × 10−10 | 5.30 × 10−9 | 2.60 × 10−11 |
| 9 | 2.40 × 10−8 | 3.20 × 10−10 | 5.40 × 10−9 | 1.70 × 10−11 |
| 10 | 7.50 × 10−9 | 4.80 × 10−10 | 4.90 × 10−9 | 2.70 × 10−10 |
| 11 | - | - | 2.40 × 10−9 | 4.20 × 10−10 |
| 12 | 9.10 × 10−9 | 1.20 × 10−10 | 5.70 × 10−9 | 2.60 × 10−10 |
| 13 | 9.00 × 10−9 | 2.20 × 10−10 | 9.30 × 10−9 | 8.20 × 10−10 |
| 14 | 9.90 × 10−9 | 1.90 × 10−10 | 4.90 × 10−9 | 4.30 × 10−11 |
| 15 | 1.10 × 10−8 | 1.20 × 10−10 | 1.10 × 10−8 | 6.60 × 10−10 |

Table A15.
Permeability of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
Table A15.
Permeability of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier B.
| 30 PPI | 50 PPI | 60 PPI | ||||
|---|---|---|---|---|---|---|
| Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | |
| 1 | 4.1 × 10−8 | 1.1 × 10−9 | - | - | - | - |
| 2 | 3.5 × 10−8 | 8.2 × 10−10 | - | - | - | - |
| 3 | 1.7 × 10−7 | 2.9 × 10−9 | 1.0 × 10−8 | 8.7 × 10−11 | 1.1001 × 10−8 | 2 × 10−10 |
| 4 | - | - | 1.8 × 10−8 | 1.4 × 10−10 | 9.4303 × 10−9 | 1 × 10−10 |
| 5 | 9.1 × 10−8 | 8.9 × 10−10 | 2.2 × 10−8 | 2.2 × 10−10 | 5.8 × 10−9 | 8 × 10−11 |
| 6 | 4.5 × 10−8 | 3.7 × 10−10 | - | - | - | - |
| 7 | 1.1 × 10−7 | 9.7 × 10−10 | 1.6 × 10−8 | 2.4 × 10−10 | 1.09 × 10−8 | 1 × 10−10 |
| 8 | 5.9 × 10−8 | 8.3 × 10−10 | 1.3 × 10−8 | 1.3 × 10−10 | 9.5434 × 10−9 | 9 × 10−11 |
| 9 | 1.1 × 10−7 | 1.5 × 10−9 | - | - | - | - |
| 10 | 2.1 × 10−8 | 2.2 × 10−10 | 1.5 × 10−8 | 1.3 × 10−10 | 8.45 × 10−9 | 6 × 10−11 |
| 11 | - | - | 1.6 × 10−8 | 1.8 × 10−10 | - | - |
| 12 | - | - | - | - | - | - |
| 13 | - | - | * 5.5 × 10−8 | 3.1 × 10−10 | 6.16 × 10−9 | 4 × 10−11 |
| 14 | - | - | - | - | 6.06 × 10−9 | 2 × 10−11 |
| 15 | - | - | 1.3 × 10−8 | 1.0 × 10−10 | 6.66 × 10−9 | 4 × 10−11 |
* The bold numbers are outliers and were disregarded in the calculations.

Table A16.
Permeability of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
Table A16.
Permeability of CFF samples of 30 PPI, 50 PPI and 60 PPI from supplier C.
| 30 PPI | 50 PPI | 60 PPI | ||||
|---|---|---|---|---|---|---|
| Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | Permeability (m2) | St. Dev. (m2) | |
| 1 | 1.8 × 10−7 | 2.9 × 10−9 | - | - | 9.1 × 10−9 | 1.9 × 10−10 |
| 2 | 6.6 × 10−8 | 2.5 × 10−9 | 7.0 × 10−8 | 7.1 × 10−10 | 1.2 × 10−8 | 1.8 × 10−10 |
| 3 | 1.5 × 10−7 | 1.6 × 10−9 | 2.7 × 10−8 | 2.1 × 10−10 | - | - |
| 4 | 9.2 × 10−8 | 1.4 × 10−9 | - | - | - | - |
| 5 | - | - | * 9.8 × 10−8 | 2.2 × 10−9 | 1.2 × 10−8 | 1.7 × 10−10 |
| 6 | 8.8 × 10−8 | 8.6 × 10−10 | 3.8 × 10−8 | 5.4 × 10−10 | 9.2 × 10−9 | 1.1 × 10−10 |
| 7 | 2.2 × 10−7 | 2.4 × 10−9 | - | - | - | - |
| 8 | - | - | - | - | - | - |
| 9 | 7.0 × 10−8 | 1.1 × 10−9 | 3.8 × 10−8 | 5.5 × 10−10 | 1.1 × 10−8 | 1.1 × 10−10 |
| 10 | 9.9 × 10−8 | 6.5 × 10−10 | 4.3 × 10−8 | 7.4 × 10−10 | 1.2 × 10−8 | 4.1 × 10−10 |
| 11 | - | - | 3.9 × 10−8 | 3.3 × 10−10 | - | - |
| 12 | - | - | 4.8 × 10−8 | 1.4 × 10−9 | - | - |
| 13 | - | - | - | - | 1.7 × 10−8 | 4.5 × 10−10 |
| 14 | - | - | - | - | 1.0 × 10−8 | 6.8 × 10−11 |
| 15 | - | - | 3.2 × 10−8 | 5.0 × 10−10 | 1.2 × 10−8 | 8.7 × 10−11 |
* The bold numbers are outliers and were disregarded in the calculations.
References
- Scheffler, M. Cellular Ceramics: “Structure, Manufacturing, Properties and Applications”; Wiley-VCH; John Wiley Distributor: New York, NY, USA, 2005. [Google Scholar]
- Engh, T.A.; Sigworth, G.K.; Kvithyld, A. Principles of Metal Refining and Recycling; Oxford University Press: New York, NY, USA, 2021. [Google Scholar]
- Fritzsch, R.; Kennedy, M.W.; Akbarnejad, S.; Aune, R.E. Effect of Electromagnetic Fields on the Priming of High-Grade Ceramic Foam Filters (CFF) with Liquid Aluminium; Light Metals 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 929–935. [Google Scholar]
- Wu, J.; Djavanroodi, F.; Gode, C.; Attarilar, S.; Ebrahimi, M. Melt Refining and Purification Processes in Al alloys: A comprehensive study. Mater. Res. Express 2022, 9, 3. [Google Scholar] [CrossRef]
- Apelian, D.; Mutharasan, R. Filtration: A Melt Refining Method. JOM 1980, 32, 14–19. [Google Scholar] [CrossRef]
- Engh, T.A.; Rasch, B.; Bathen, E. Deep Bed Filtration Theory Compared with Experiments, in Essential Readings in Light Metals: Volume 3 Cast Shop for Aluminium Production; Grandfield, J.F., Eskin, D.G., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 263–270. [Google Scholar]
- Grandfield, J.F.; Eskin, D.G.; Bainbridge, I.F. Direct-Chill Casting of Light Alloys: Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bao, S.; Engh, T.A.; Syvertsen, M.; Kvithyld, A.; Tangstad, M. Inclusion (Particle) Removal by Interception and Gravity in Ceramic Foam Filters. J. Mater. Sci. 2012, 47, 7986–7998. [Google Scholar] [CrossRef]
- Kocaefe, D.; Murray-Chiasson, A.; Kocaefe, Y.; Waite, P. Modelling of Inclusion Re-entrainment During Filtration. Can. J. Chem. Eng. 2008, 82, 1191–1201. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Zhang, K.X.; Fritzsch, R.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Characterization of Ceramic Foam Filters Used for Liquid Metal Filtration. Met. Mater. Trans. B 2013, 44, 671–690. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Saffari Pour, M.; Jonsson, L.T.I.; Jönsson, P.G. Effect of Fluid Bypassing on the Experimentally Obtained Darcy and Non-Darcy Permeability Parameters of Ceramic Foam Filters. Met. Mater. Trans. B 2016, 48, 197–207. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Tilliander, A.; Sheng, D.-Y.; Jönsson, P.G. Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation. Metals 2022, 12, 1001. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Jonsson, L.T.I.; Kennedy, M.W.; Aune, R.E.; Jönsson, P.G. Analysis on experimental investigation and mathematical modeling of incompressible flow through ceramic foam filters. Met. Mater. Trans. B 2016, 47, 2229–2243. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Kennedy, M.W.; Fritzsch, R.; Aune, R.E. An Investigation on Permeability of Ceramic Foam Filters (CFF). Light Met. 2015, 949–954. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Saffari Pour, M.; Jonsson, L.; Jönsson, P. Significance of Fluid Bypassing Effect on Darcy and Non-Darcy Permeability Parameters of Ceramic Foam Filters. 2016. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-183073 (accessed on 22 March 2023).
- Milligan, B.; Ray, S.F. Recent Improvements in the Measurement and Control of Ceramic Foam Filter Quality. In Proceedings of the International Conference Advances in Production and Processing of Aluminium, (APPA 2001), Manama, Bahrain, 12–15 February 2001; Elsevier: Amsterdam, The Netherlands, 2001; p. 15. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications: New York, NY, USA, 1988; p. 764. [Google Scholar]
- Bağcı, Ö.; Dukhan, N.; Özdemir, M. Flow Regimes in Packed Beds of Spheres from Pre-Darcy to Turbulent. Transp. Porous Media 2014, 104, 501–520. [Google Scholar] [CrossRef]
- Innocentini, M.D.; Salvini, V.R.; Macedo, A.; Pandolfelli, V.C. Prediction of Ceramic Foams Permeability Using Ergun’s Equation. Mater. Res. 1999, 2, 283–289. [Google Scholar] [CrossRef]
- Dukhan, N.; Bagci, O.; Ozdemir, M. Experimental Flow in Various Porous Media and Reconciliation of Forchheimer and Ergun Relations. Exp. Therm. Fluid Sci. 2014, 57, 425–433. [Google Scholar] [CrossRef]
- Ingham, D.B.; Pop, I.I. Transport Phenomena in Porous Media; Kidlington: Oxford, UK, 1998. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wilson, L.; Narasimhan, A.; Venkateshan, S.P. Permeability and Form Coefficient Measurement of Porous Inserts with Non-Darcy Model Using Non-Plug Flow Experiments. J. Fluids Eng. 2005, 128, 638–642. [Google Scholar] [CrossRef]
- Ergun, S.; Orning, A.A. Fluid Flow Through Randomly Packed Columns and Fluidized Beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Dietrich, B.; Schabel, W.; Kind, M.; Martin, H. Pressure Drop Measurements of Ceramic Sponges-Determining the Hydraulic Diameter. Chem. Eng. Sci. 2009, 64, 3633–3640. [Google Scholar] [CrossRef]
- Fourie, J.G.; Plessis, J.P.D. Pressure Drop Modelling in Cellular Metallic Foams. Chem. Eng. Sci. 2002, 57, 2781–2789. [Google Scholar] [CrossRef]
- Viswanath, D.S. Viscosity of Liquids: Theory, Estimation, Experiment; Springer: Cham, The Netherlands, 2007. [Google Scholar]
- Ji, Z.G. Hydrodynamics and Water Quality: Modelling Rivers, Lakes, and Estuaries; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Tundal, U.; Steen, I.; Strmsvg, G.; Haugen, T.; Hkonsen, A. Drain Free Filtration (DFF)—A New CFF Technology; Springer International Publishing: Cham, The Netherlands, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).