Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames
Abstract
1. Introduction
2. Experimental Program
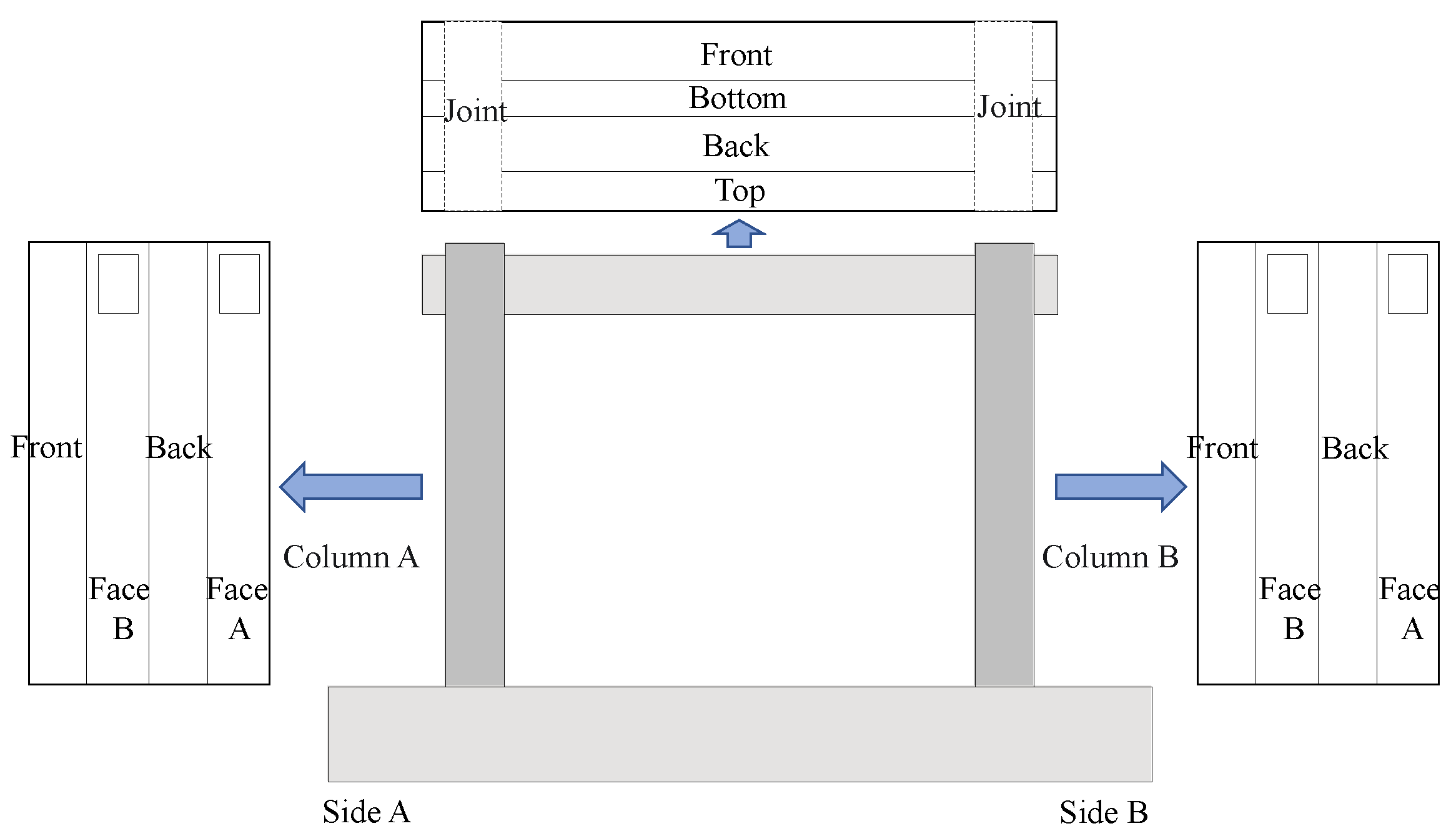
2.1. Specimen Information
2.2. Electrochemical Accelerated Corrosion
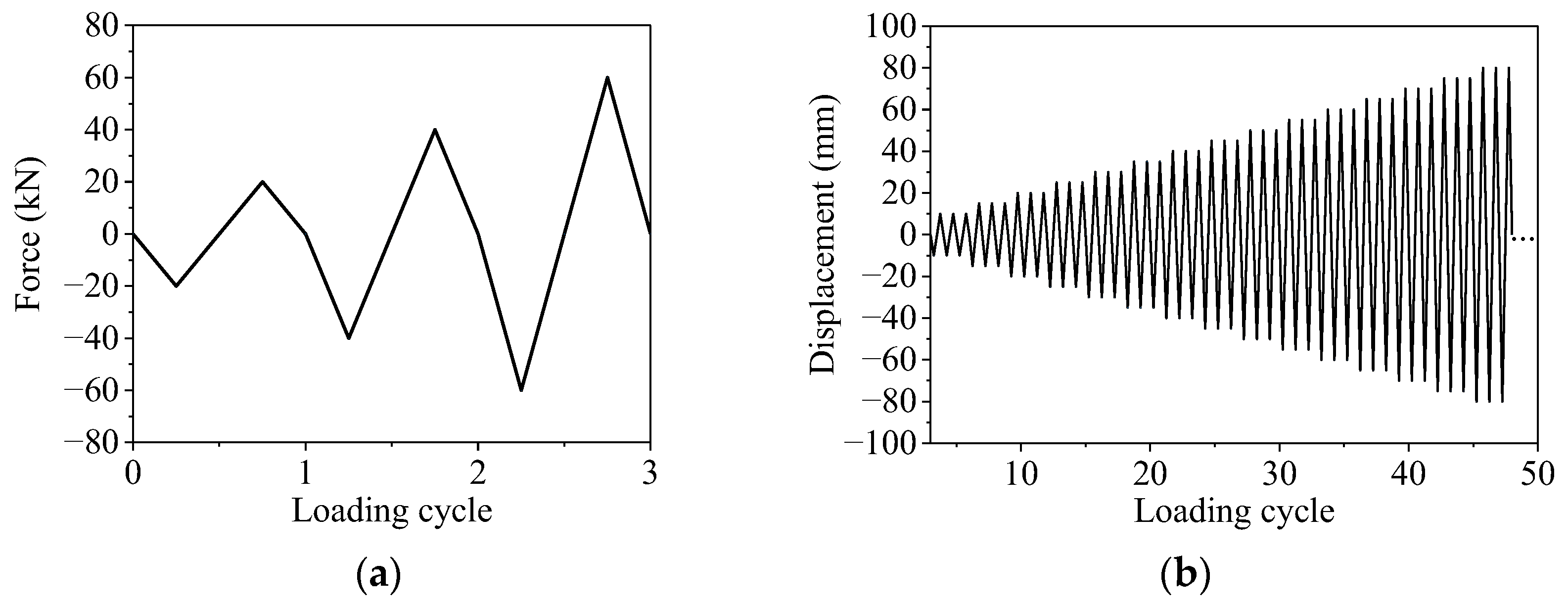
2.3. Test Setup, Instrumentation, and Loading Protocol
3. Experimental Results
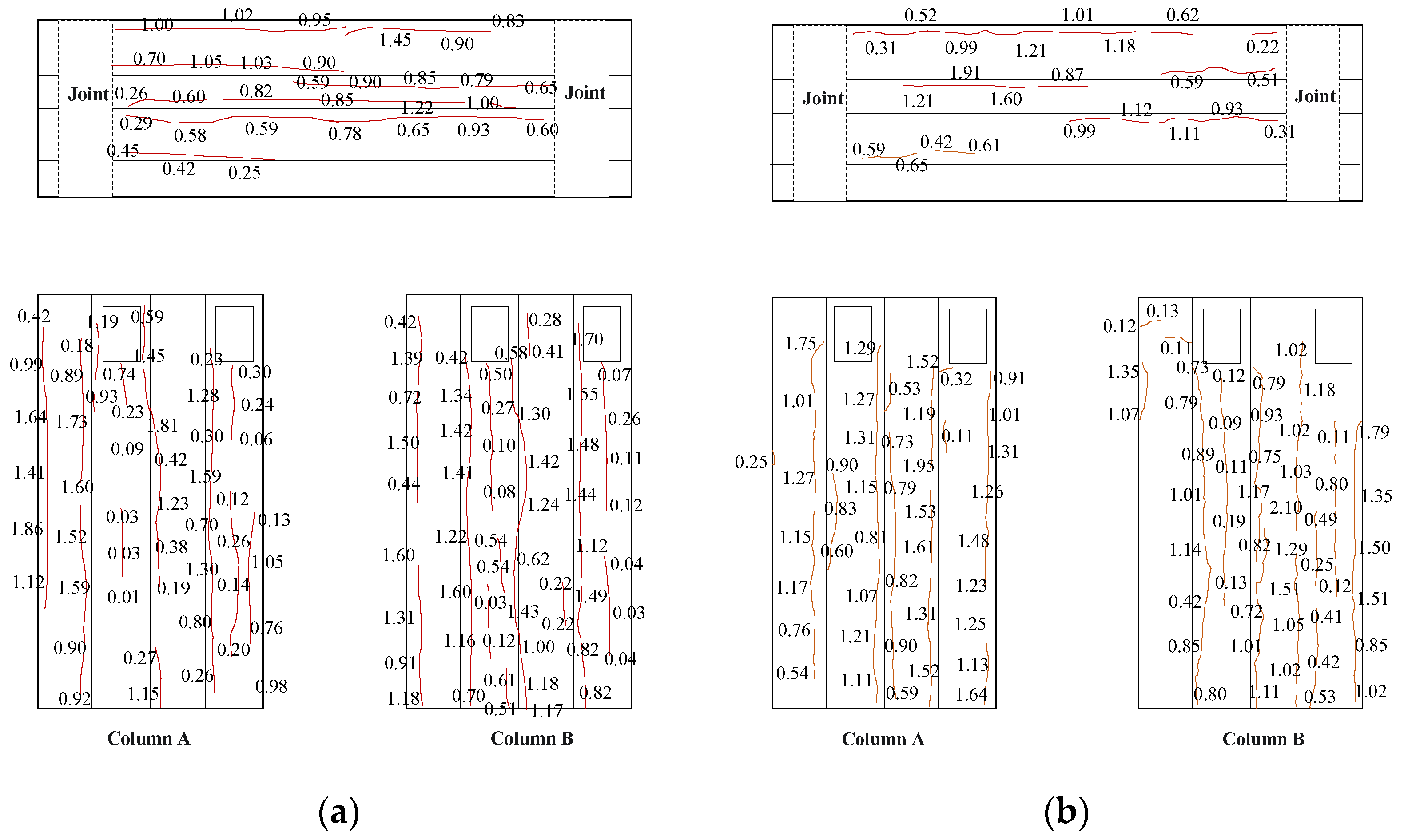
3.1. Damage Due to Corrosion
3.2. Damage Evolution
3.3. Hysteresis Behavior
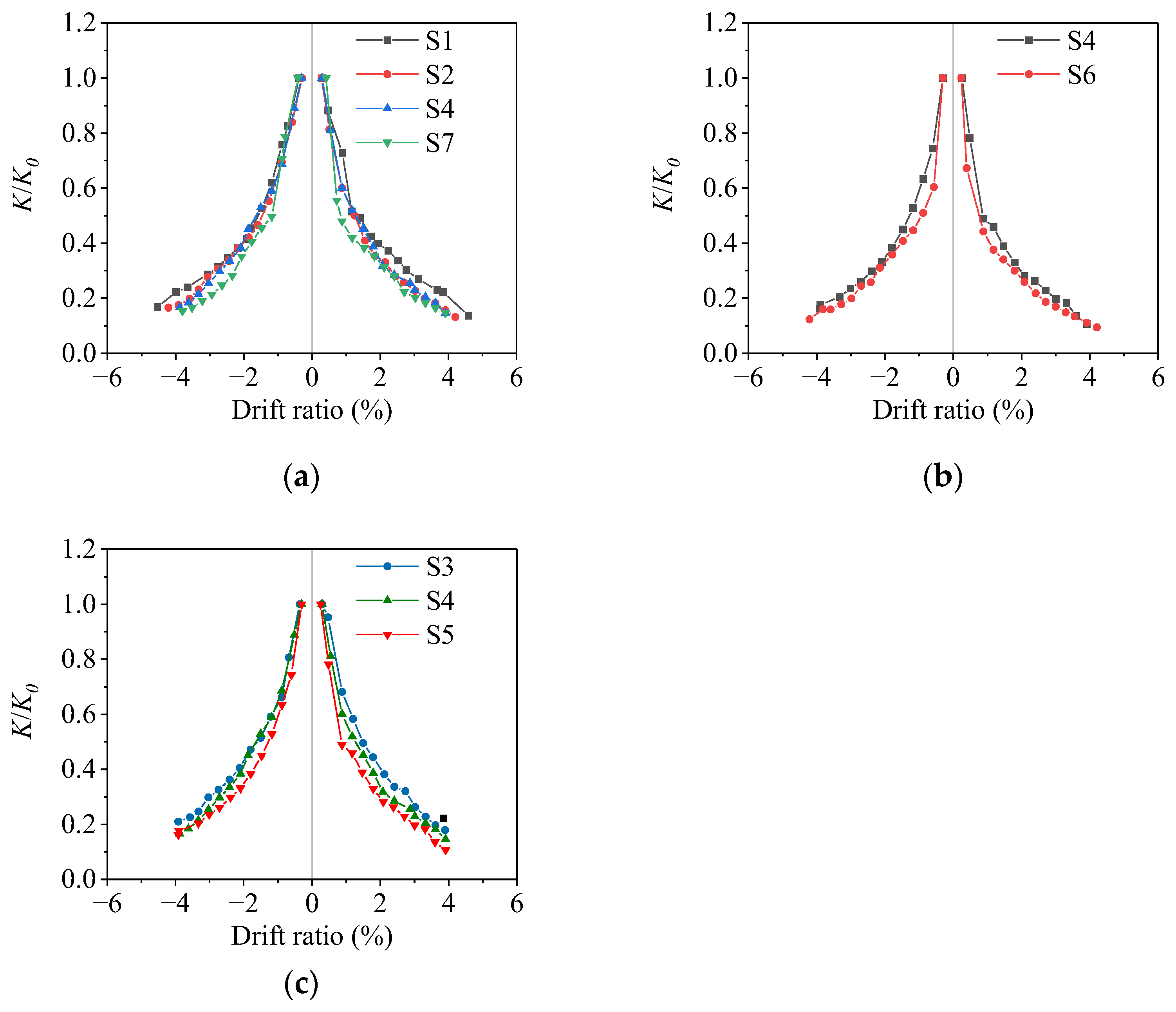
3.4. Stiffness Degradation
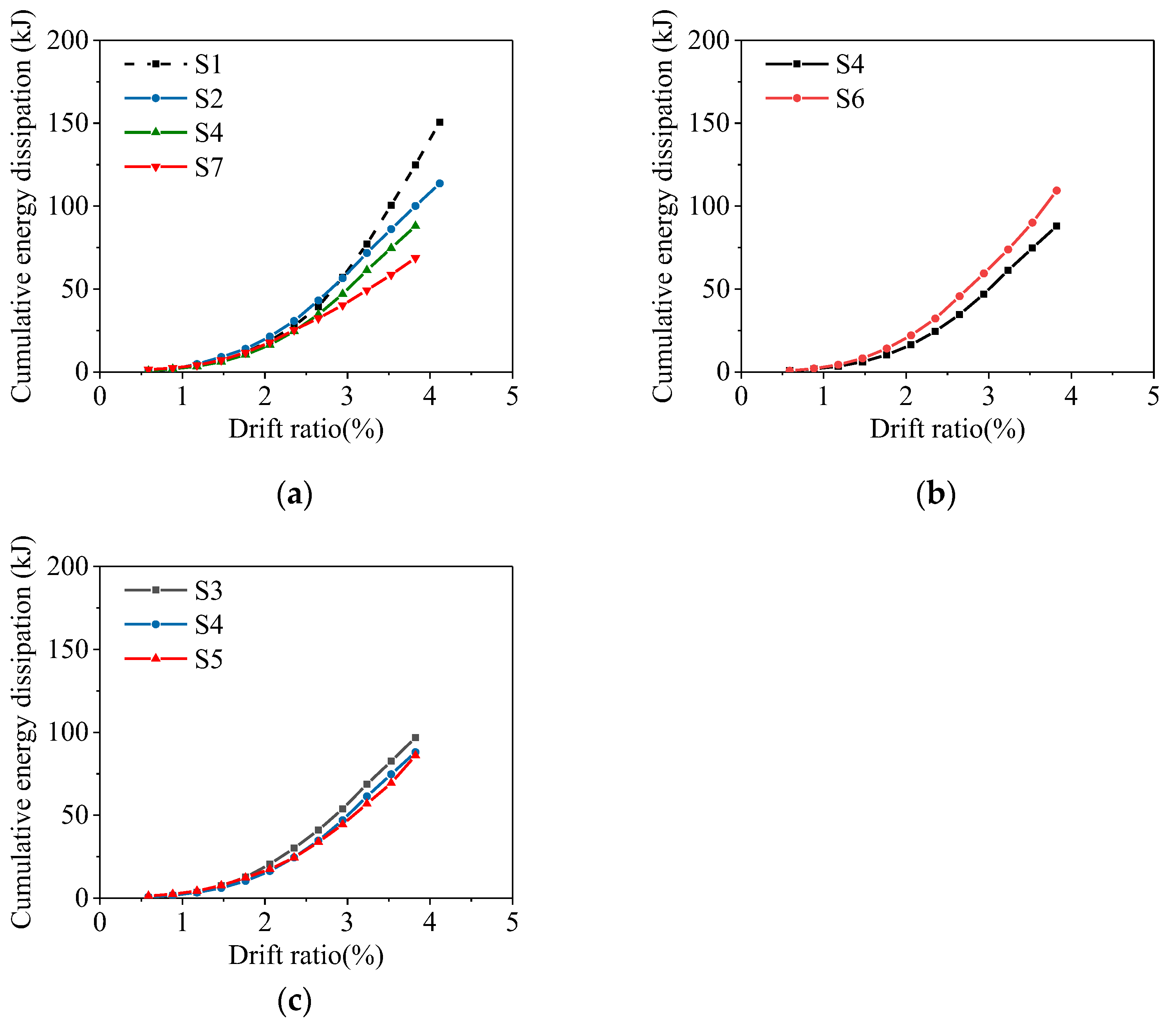
3.5. Energy Dissipation Capacity
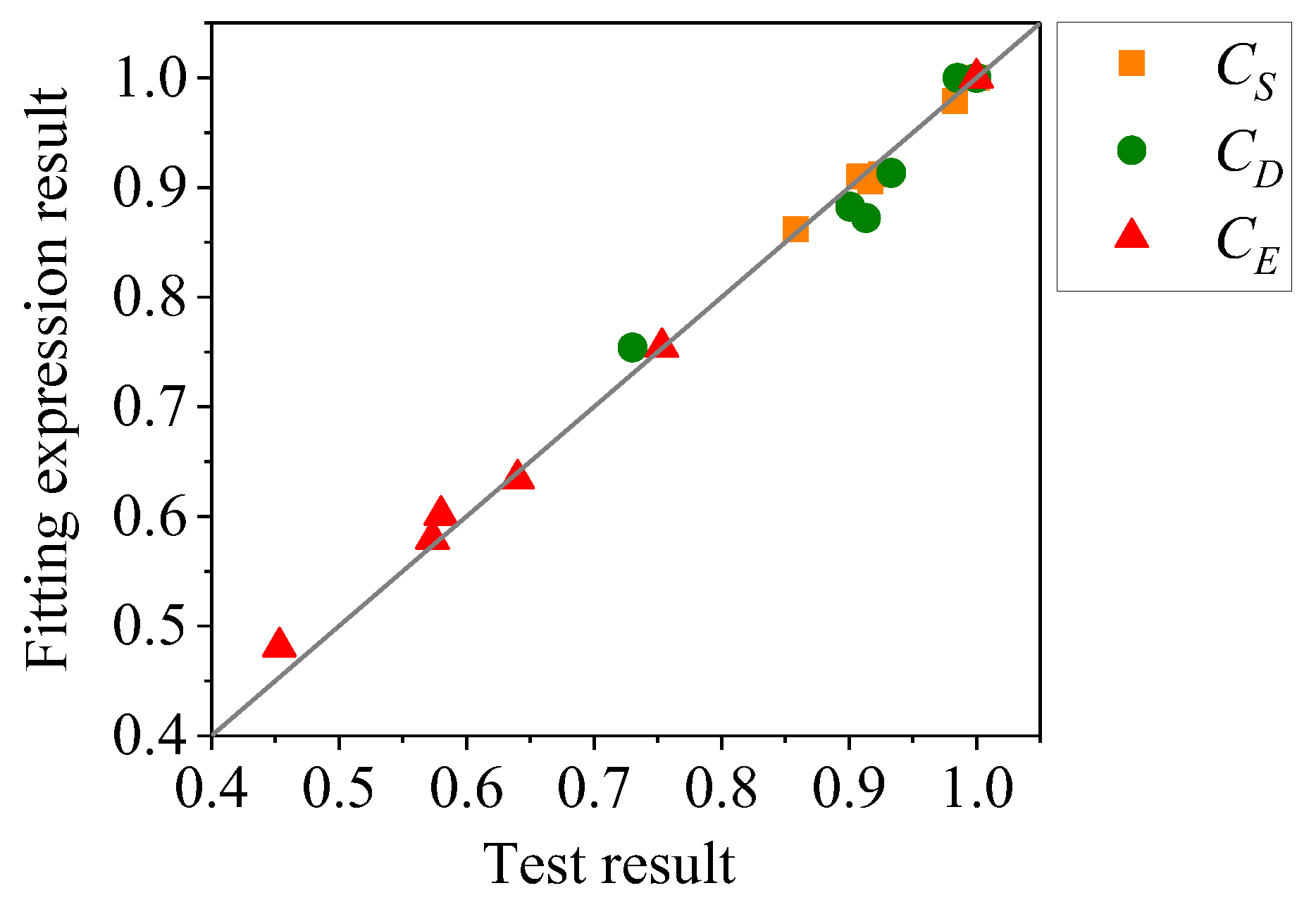
3.6. Quantitative Evaluation of Corrosion Effect
4. Conclusions
- (1)
- With the increase in the average corrosion ratio, the bearing capacity, energy dissipation capacity, and deformation capacity of the RC frame decrease, and the stiffness degradation becomes more significant. This adverse effect should be considered in the seismic design and assessment of RC structures.
- (2)
- With the increase in the non-uniform corrosion characteristic value, the unidirectional bearing capacity, energy dissipation capacity, and deformation capacity of the RC frame decrease, the stiffness degradation of the RC frame becomes more significant, the damage develops more rapidly, and the damage distribution is more concentrated.
- (3)
- In small axial compression ratio ranges, with the increase in the axial compression ratio, the bearing capacity and energy dissipation capacity of the RC frame increase, and the stiffness degradation is more significant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, C.; Fang, D.; Ye, H.; Huang, L.; Wang, J. Bond Degradation of Non-Uniformly Corroded Steel Rebars in Concrete. Eng. Struct. 2021, 226, 111392. [Google Scholar] [CrossRef]
- Chen, E.; Berrocal, C.G.; Fernandez, I.; Löfgren, I.; Lundgren, K. Assessment of the Mechanical Behaviour of Reinforcement Bars with Localised Pitting Corrosion by Digital Image Correlation. Eng. Struct. 2020, 219, 110936. [Google Scholar] [CrossRef]
- Chung, L.; Jay Kim, J.; Yi, S. Bond Strength Prediction for Reinforced Concrete Members with Highly Corroded Reinforcing Bars. Cem. Concr. Compos. 2008, 30, 603–611. [Google Scholar] [CrossRef]
- Ruggieri, S.; Porco, F.; Uva, G. A Practical Approach for Estimating the Floor Deformability in Existing Rc Buildings: Evaluation of the Effects in the Structural Response and Seismic Fragility. Bull. Earthq. Eng. 2020, 18, 2083–2113. [Google Scholar] [CrossRef]
- Ruggieri, S.; Calò, M.; Cardellicchio, A.; Uva, G. Analytical-Mechanical Based Framework for Seismic Overall Fragility Analysis of Existing Rc Buildings in Town Compartments. Bull. Earthq. Eng. 2022, 20, 8179–8216. [Google Scholar] [CrossRef]
- Yadav, D.; Kwatra, N.; Agarwal, P. Comparative Post-Yield Performance Evaluation of Flexure Member with Corroded Reinforcement. Struct. Infrastruct. Eng. 2021, 17, 103–123. [Google Scholar] [CrossRef]
- Huang, L.; Ye, H.; Jin, X.; Jin, N.; Xu, Z. Corrosion-Induced Shear Performance Degradation of Reinforced Concrete Beams. Constr. Build. Mater. 2020, 248, 118668. [Google Scholar] [CrossRef]
- Firouzi, A.; Taki, A.; Mohammadzadeh, S. Time-Dependent Reliability Analysis of RC Beams Shear and Flexural Strengthened with CFRP Subjected to Harsh Environmental Deteriorations. Eng. Struct. 2019, 196, 109326. [Google Scholar] [CrossRef]
- Ma, Y.; Che, Y.; Gong, J. Behavior of Corrosion Damaged Circular Reinforced Concrete Columns Under Cyclic Loading. Constr. Build. Mater. 2012, 29, 548–556. [Google Scholar] [CrossRef]
- Shang, Z.; Zheng, S.; Zheng, H.; Li, Y.; Dong, J. Seismic Behavior and Damage Evolution of Corroded RC Columns Designed for Bending Failure in an Artificial Climate. Structures 2022, 38, 184–201. [Google Scholar] [CrossRef]
- Dang, V.H.; François, R. Prediction of Ductility Factor of Corroded Reinforced Concrete Beams Exposed to Long Term Aging in Chloride Environment. Cem. Concr. Compos. 2014, 53, 136–147. [Google Scholar] [CrossRef]
- Okada, K.; KobayashiI, K.; Miyagawa, T. Influence of Longitudinal Cracking Due to Reinforcement Corrosion on Characteristics of Reinforced Concrete Members. ACI Struct. J. 1988, 85, 134–140. [Google Scholar]
- Torres-Acosta, A.A.; Fabela-Gallegos, M.J.; Muñoz-Noval, A.; Vázquez-Vega, D.; Hernandez-Jimenez, J.R.; Martínez-Madrid, M. Influence of Corrosion on the Structural Stiffness of Reinforced Concrete Beams. Corrosion 2004, 60, 862–872. [Google Scholar] [CrossRef]
- Meda, A.; Mostosi, S.; Rinaldi, Z.; Riva, P. Experimental Evaluation of the Corrosion Influence on the Cyclic Behaviour of RC Columns. Eng. Struct. 2014, 76, 112–123. [Google Scholar] [CrossRef]
- Goksu, C.; Ilki, A. Seismic Behavior of Reinforced Concrete Columns with Corroded Deformed Reinforcing Bars. ACI Struct. J. 2016, 113, 1053–1064. [Google Scholar] [CrossRef]
- Biswas, R.K.; Iwanami, M.; Chijiwa, N.; Uno, K. Effect of Non-Uniform Rebar Corrosion on Structural Performance of RC Structures: A Numerical and Experimental Investigation. Constr. Build. Mater. 2020, 230, 116908. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Gu, X. Modeling Time-Dependent Circumferential Non-Uniform Corrosion of Steel Bars in Concrete Considering Corrosion-Induced Cracking Effects. Eng. Struct. 2019, 201, 109766. [Google Scholar] [CrossRef]
- Su, R.K.L.; Zhang, Y. A Novel Elastic-Body-Rotation Model for Concrete Cover Spalling Caused by Non-Uniform Corrosion of Reinforcement. Constr. Build. Mater. 2019, 213, 549–560. [Google Scholar] [CrossRef]
- Zhao, Y.; Karimi, A.R.; Wong, H.S.; Hu, B.; Buenfeld, N.R.; Jin, W. Comparison of Uniform and Non-Uniform Corrosion Induced Damage in Reinforced Concrete Based on a Gaussian Description of the Corrosion Layer. Corros. Sci. 2011, 53, 2803–2814. [Google Scholar] [CrossRef]
- Zhang, M.; Song, H.; Lim, S.; Akiyama, M.; Frangopol, D.M. Reliability Estimation of Corroded RC Structures Based on Spatial Variability Using Experimental Evidence, Probabilistic Analysis and Finite Element Method. Eng. Struct. 2019, 192, 30–52. [Google Scholar] [CrossRef]
- Zhang, M.; Nishiya, N.; Akiyama, M.; Lim, S.; Masuda, K. Effect of the Correlation of Steel Corrosion in the Transverse Direction Between Tensile Rebars on the Structural Performance of RC Beams. Constr. Build. Mater. 2020, 264, 120678. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, W.; Gu, X. Deterioration of Shear Behavior of Corroded Reinforced Concrete Beams. Eng. Struct. 2018, 168, 708–720. [Google Scholar] [CrossRef]
- Yuan, W.; Guo, A.; Li, H. Experimental Investigation on the Cyclic Behaviors of Corroded Coastal Bridge Piers with Transfer of Plastic Hinge Due to Non-Uniform Corrosion. Soil Dyn. Earthq. Eng. 2017, 102, 112–123. [Google Scholar] [CrossRef]
- Li, D.; Wei, R.; Xing, F.; Sui, L.; Zhou, Y.; Wang, W. Influence of Non-Uniform Corrosion of Steel Bars on the Seismic Behavior of Reinforced Concrete Columns. Constr. Build. Mater. 2018, 167, 20–32. [Google Scholar] [CrossRef]
- GB50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- Lund University. Contecvet—A Validated Users Manual for Assessing the Residual Service Life of Concrete Structures; Report TVBM (Intern 7000-Rapport); Lund University: Lund, Sweden, 2001. [Google Scholar]
- Liu, X.; Jiang, H.; He, L. Experimental Investigation on Seismic Performance of Corroded Reinforced Concrete Moment-resisting Frames. Eng. Struct. 2017, 153, 639–652. [Google Scholar] [CrossRef]
- Park, R. Evaluation of Ductility of Structures and Structural Assemblages from Laboratory Testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
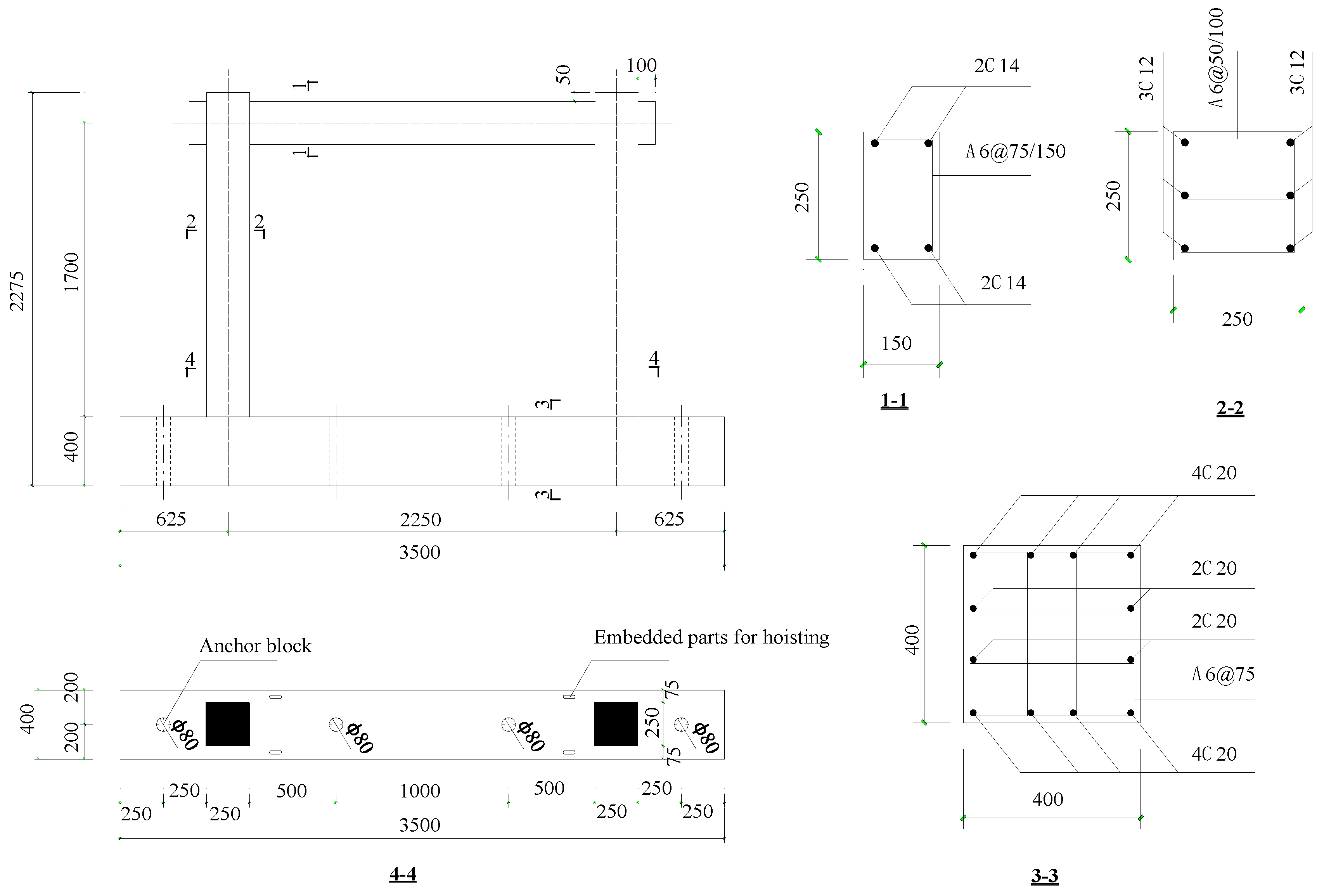
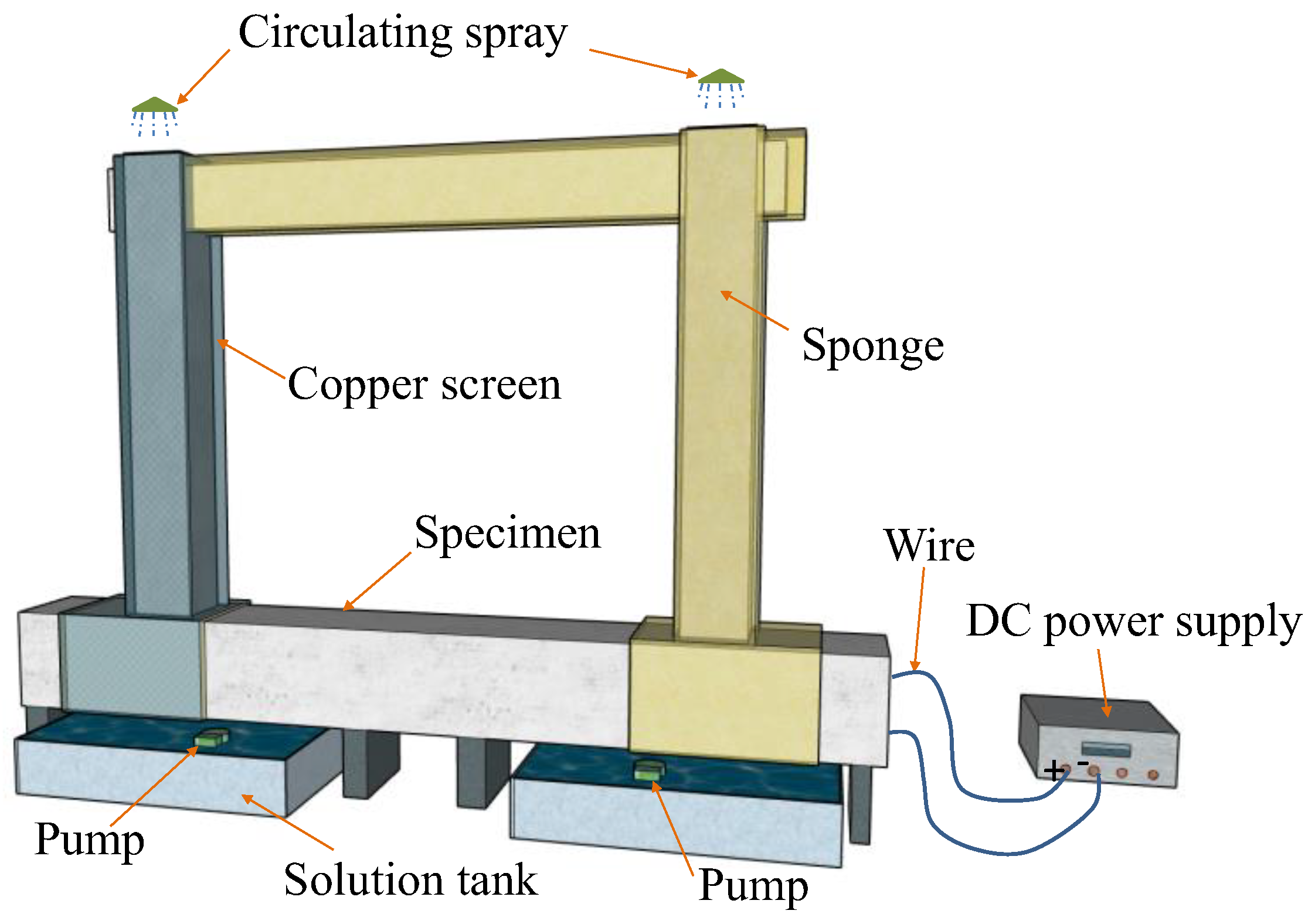
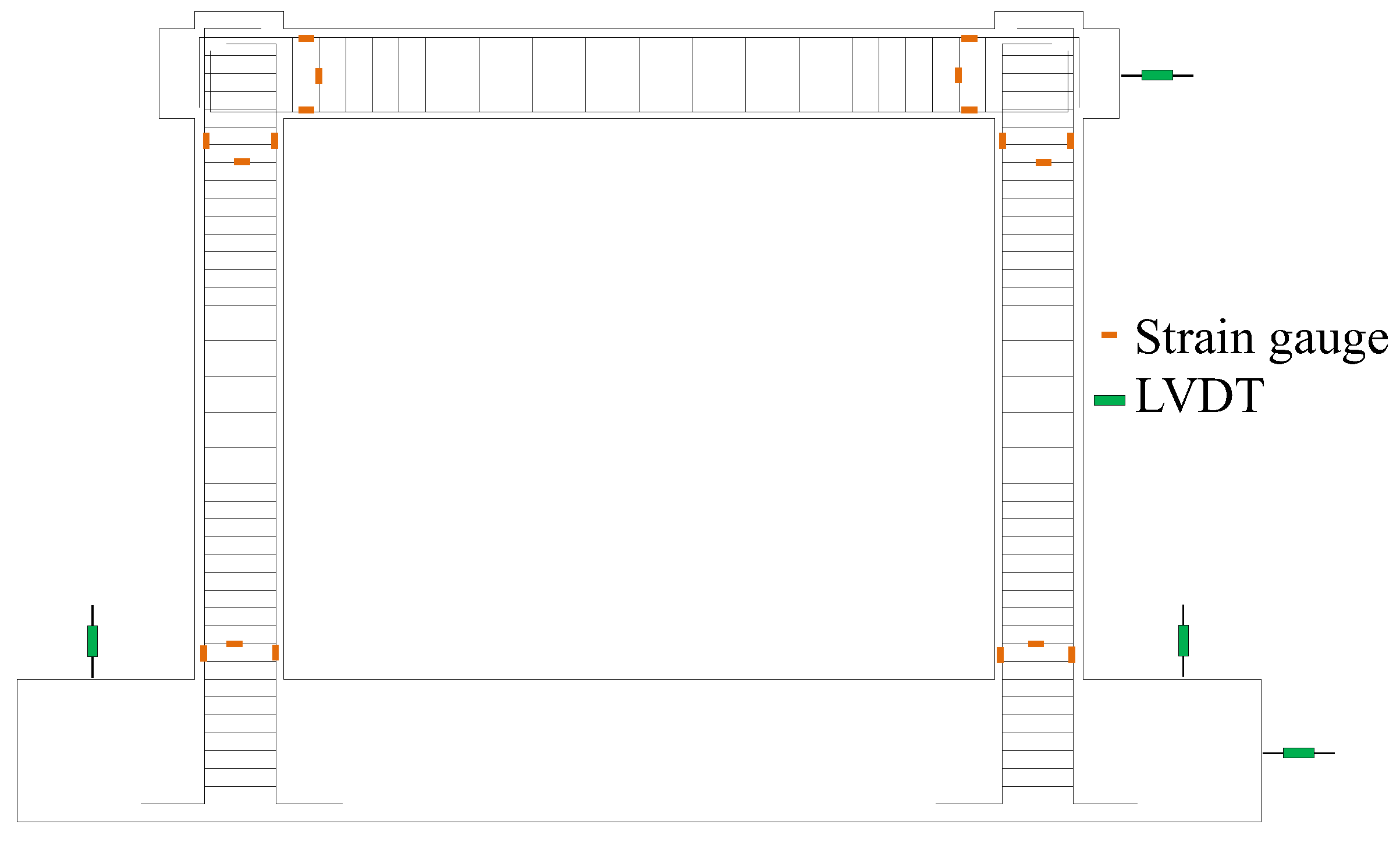
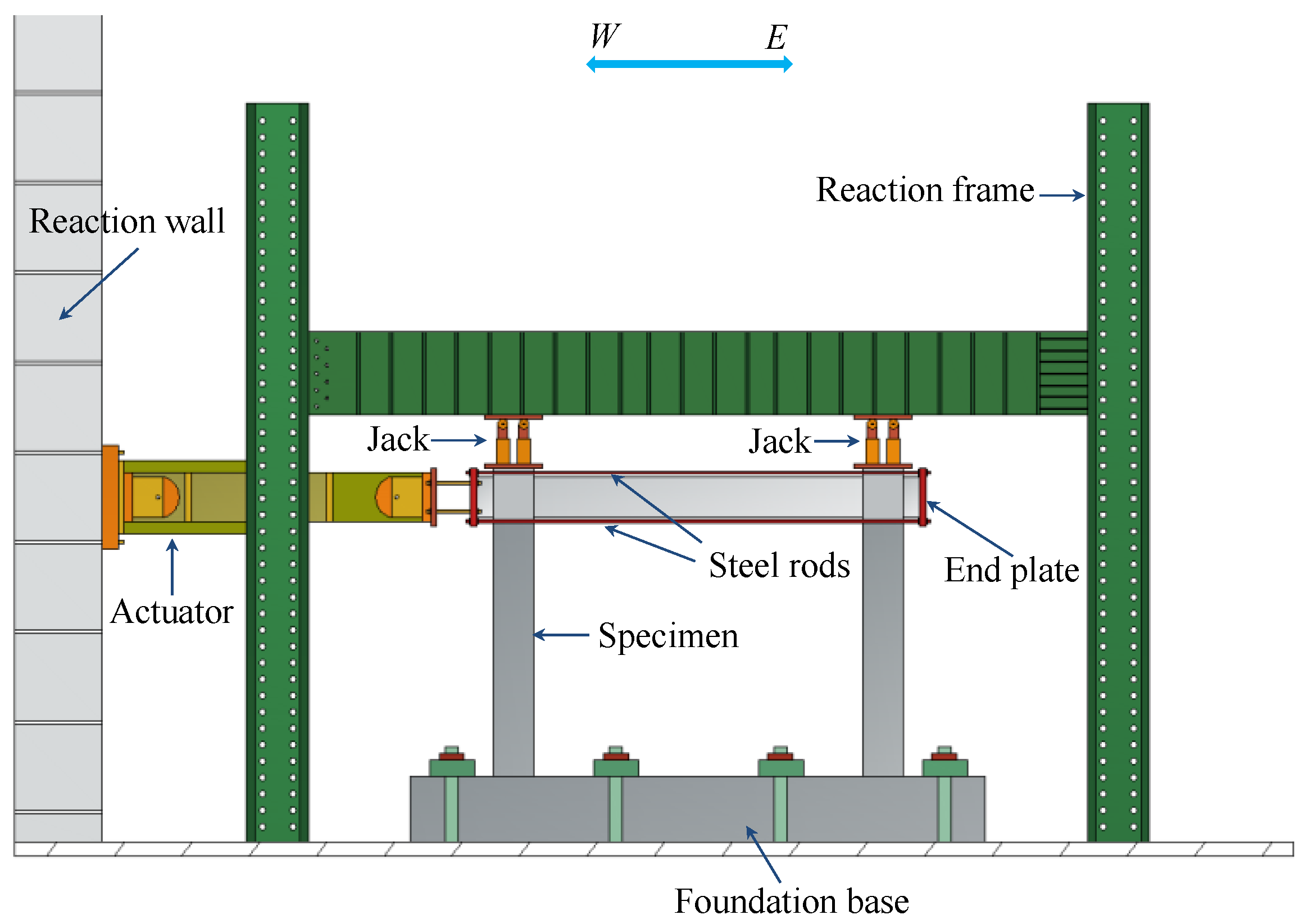


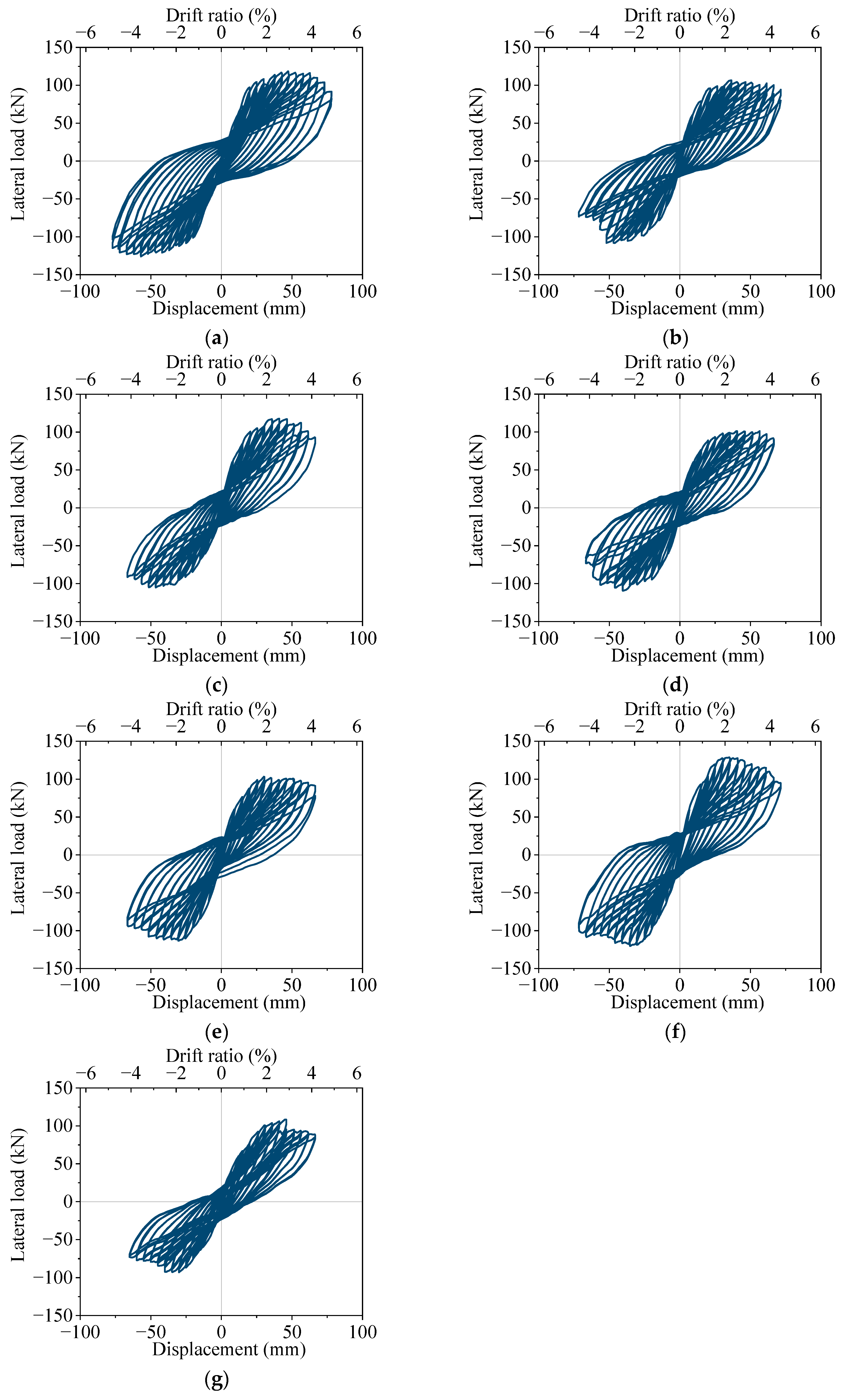

| Specimen No. | ηT (%) | ρT | n | ηactual (%) | ρactual |
|---|---|---|---|---|---|
| S1 | 0 | - | 0.1 | - | - |
| S2 | 5 | 0.6 | 0.1 | 4.8 | 0.56 |
| S3 | 10 | 0.2 | 0.1 | 6.7 | 0.18 |
| S4 | 10 | 0.6 | 0.1 | 9.2 | 0.59 |
| S5 | 10 | 0.8 | 0.1 | 9.4 | 0.72 |
| S6 | 10 | 0.6 | 0.2 | 9.3 | 0.56 |
| S7 | 15 | 0.6 | 0.1 | 12.7 | 0.61 |
| Specimen No. | Loading Direction | Fy (kN) | ∆y (mm) | Fm (kN) | ∆m (mm) | Fu (kN) | ∆u (mm) | μ |
|---|---|---|---|---|---|---|---|---|
| S1 | Positive | 105.3 | 23.8 | 119.6 | 42.9 | 101.6 | 73.0 | 4.04 |
| Negative | 95.6 | 13.2 | 121.9 | 57.1 | 103.6 | 76.4 | ||
| S2 | Positive | 92.8 | 19.2 | 109.9 | 36.5 | 92.5 | 69.1 | 3.98 |
| Negative | 64.7 | 12.4 | 108.8 | 47.0 | 93.4 | 56.5 | ||
| S3 | Positive | 102.2 | 22.0 | 118.4 | 41.0 | 100.6 | 62.0 | 3.77 |
| Negative | 68.2 | 13.0 | 105.5 | 46.6 | 89.6 | 70.1 | ||
| S4 | Positive | 95.2 | 21.2 | 110.1 | 40.5 | 93.6 | 57.2 | 3.69 |
| Negative | 56.9 | 12.4 | 102.2 | 40.6 | 86.9 | 65.5 | ||
| S5 | Positive | 86.6 | 20.4 | 103.9 | 30.6 | 88.5 | 63.7 | 3.64 |
| Negative | 61.5 | 12.1 | 104.2 | 30.5 | 96.8 | 62.7 | ||
| S6 | Positive | 107.9 | 21.2 | 129.1 | 35.4 | 109.8 | 62.1 | 3.95 |
| Negative | 67.9 | 11.4 | 120.6 | 35.6 | 102.5 | 66.8 | ||
| S7 | Positive | 91.8 | 25.8 | 109.5 | 46.0 | 93.0 | 62.1 | 2.95 |
| Negative | 57.7 | 12.5 | 93.3 | 35.1 | 79.3 | 51.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Jiang, H. Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames. Materials 2023, 16, 2649. https://doi.org/10.3390/ma16072649
Chen S, Jiang H. Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames. Materials. 2023; 16(7):2649. https://doi.org/10.3390/ma16072649
Chicago/Turabian StyleChen, Shang, and Huanjun Jiang. 2023. "Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames" Materials 16, no. 7: 2649. https://doi.org/10.3390/ma16072649
APA StyleChen, S., & Jiang, H. (2023). Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames. Materials, 16(7), 2649. https://doi.org/10.3390/ma16072649






