Role of Surface-Active Element Sulfur on Thermal Behavior, Driving Forces, Fluid Flow and Solute Dilution in Laser Linear Welding of Dissimilar Metals
Abstract
1. Introduction
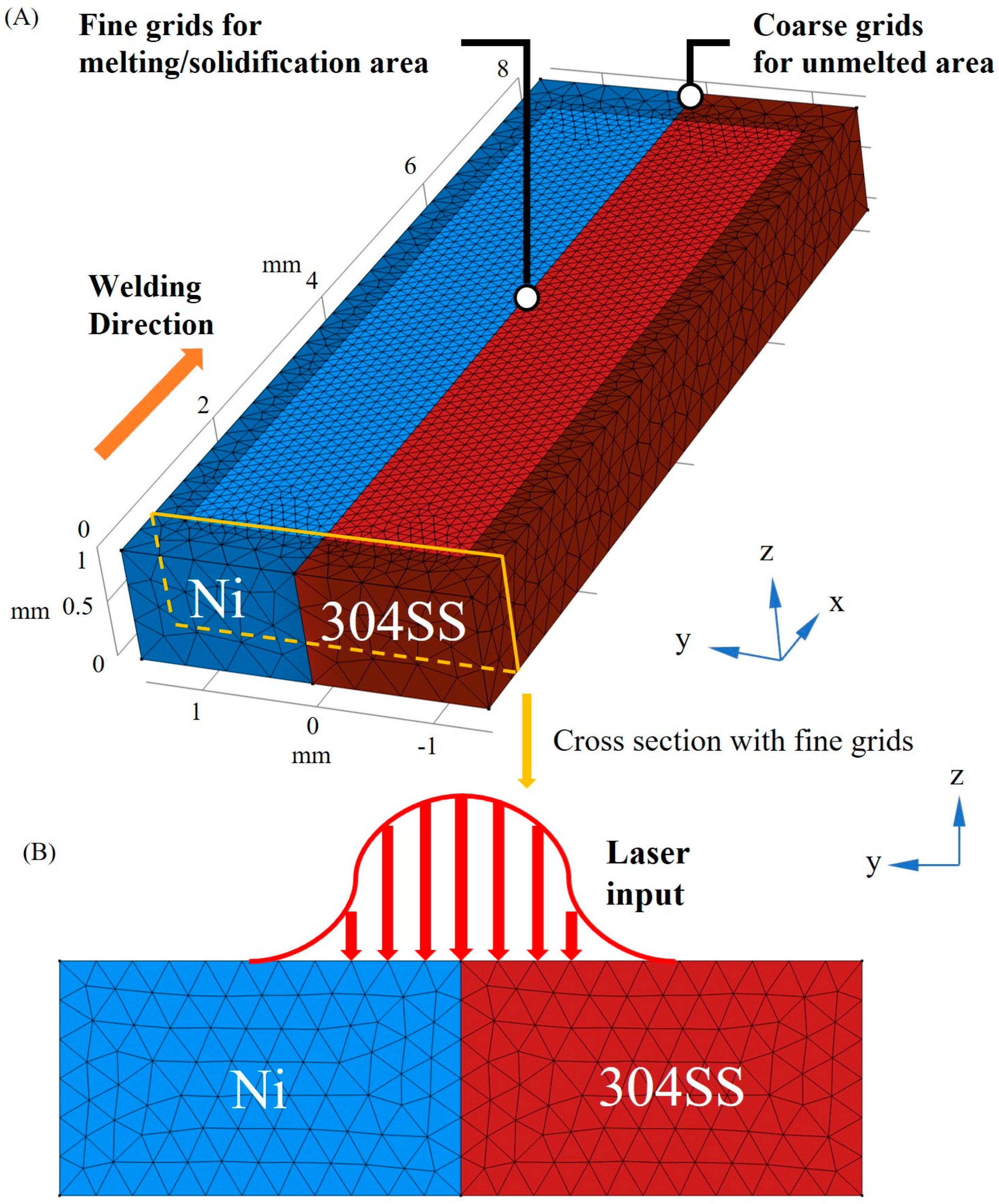
2. Numerical Model
- The liquid metal in the molten pool is an incompressible, Newtonian, and laminar flow.
- The laser power distribution is Gaussian.
- The free surface is set as a flat plane. The role of buoyancy is described by the Boussinesq approximation.
- Material properties are temperature-independent.
2.1. Governing Equations
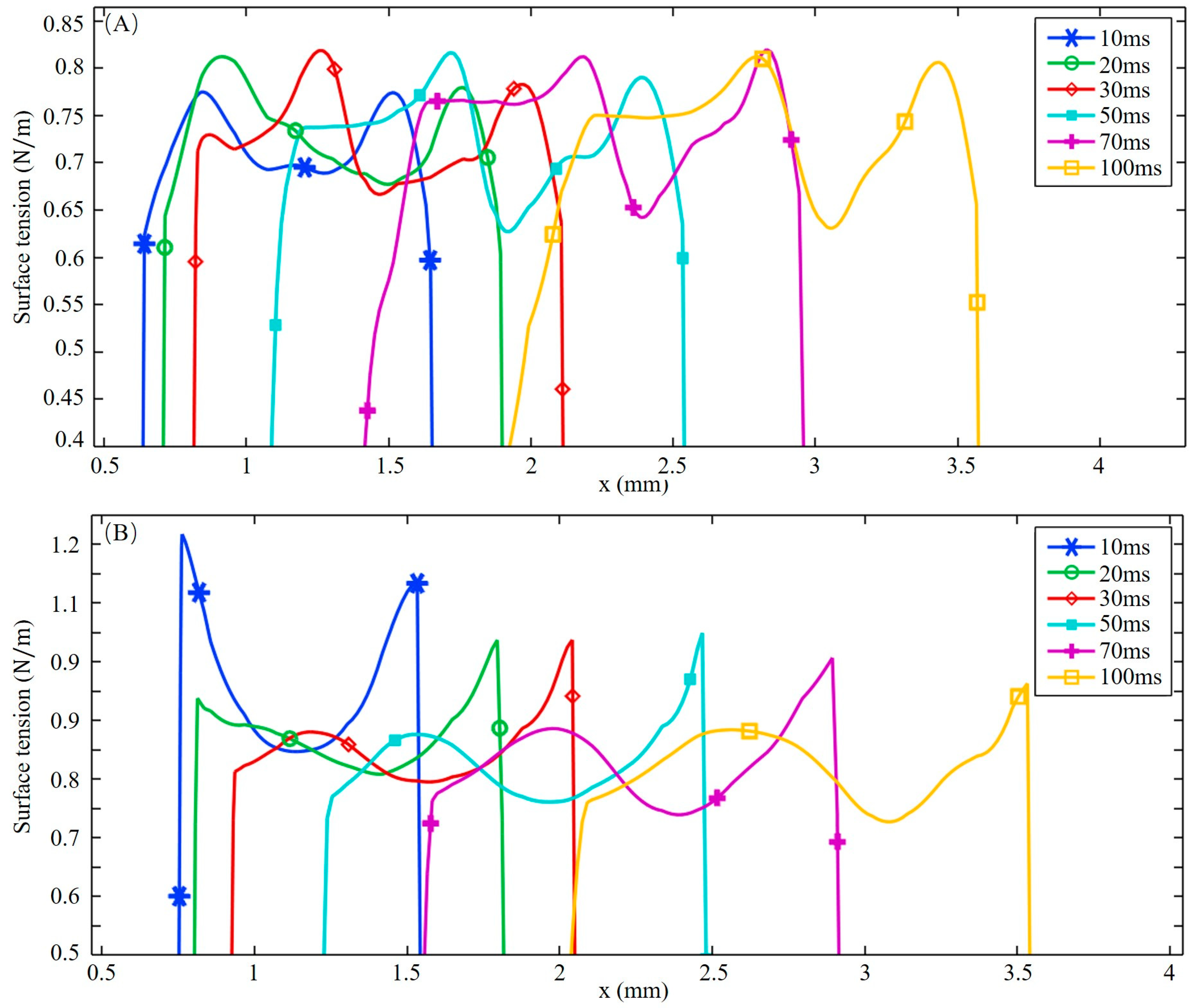
2.2. Sub-Model of Surface Tension
2.3. Boundary Conditions
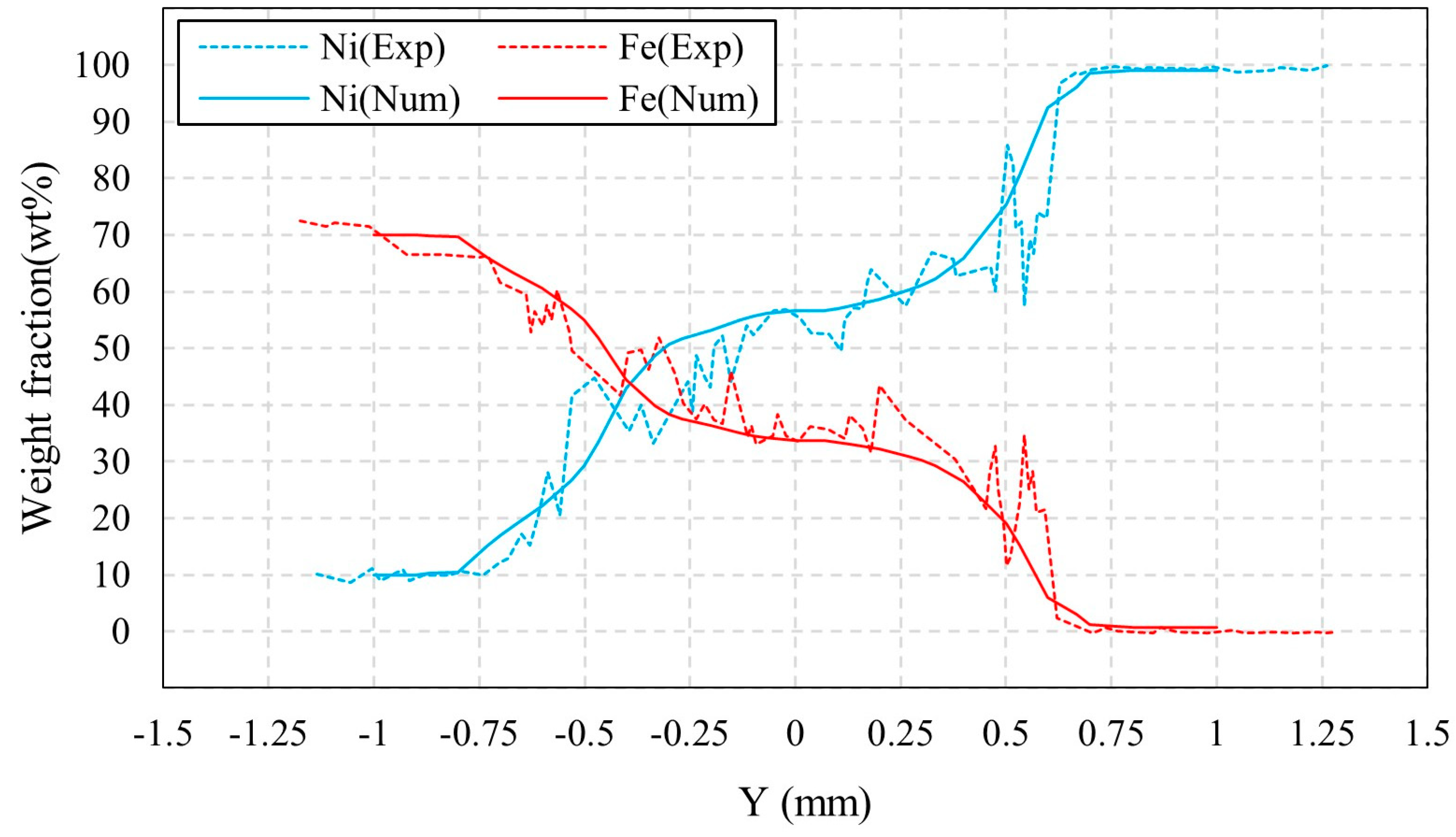
2.4. Model Verification
3. Results and Discussion
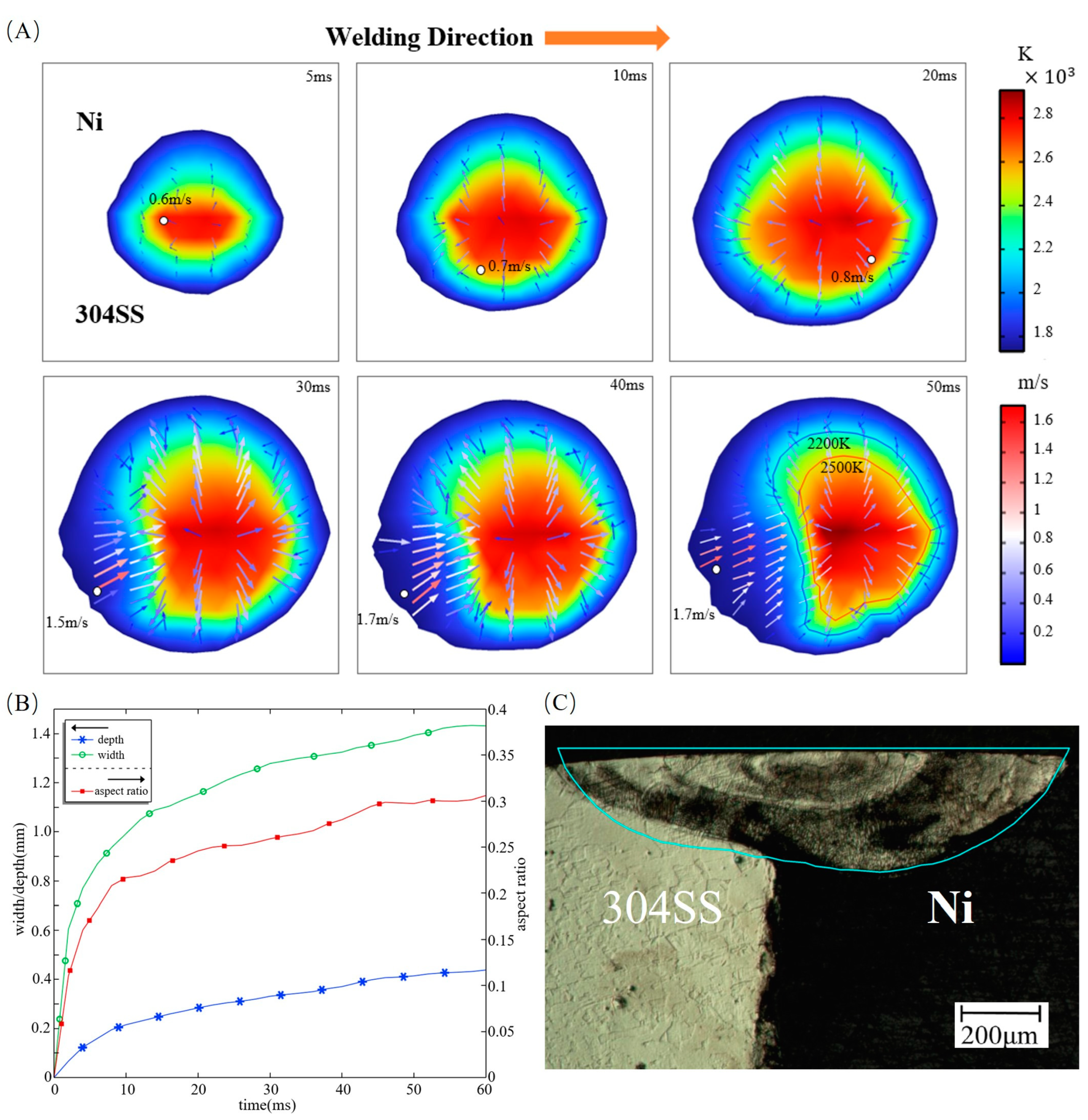
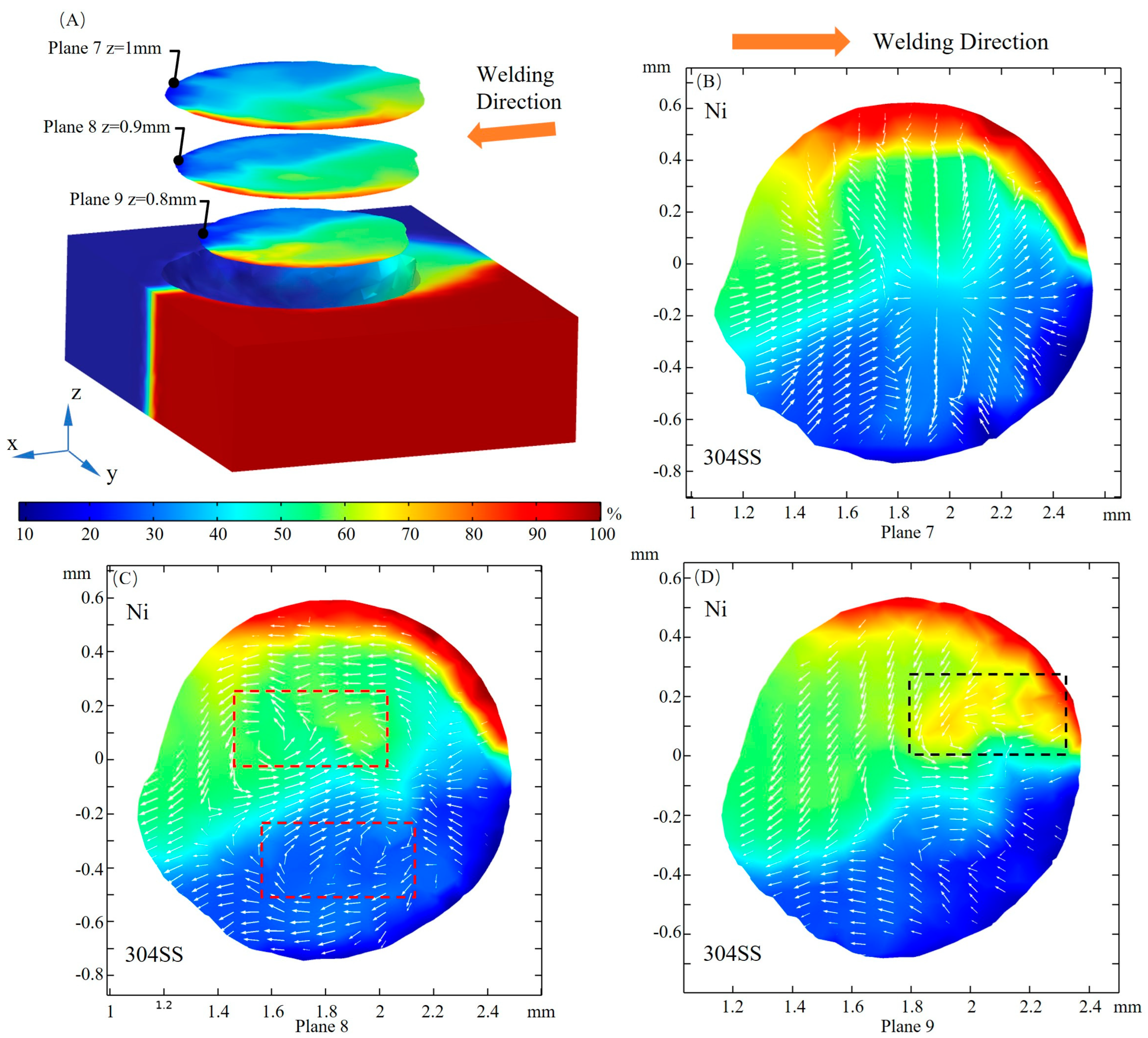
3.1. Thermal Behavior
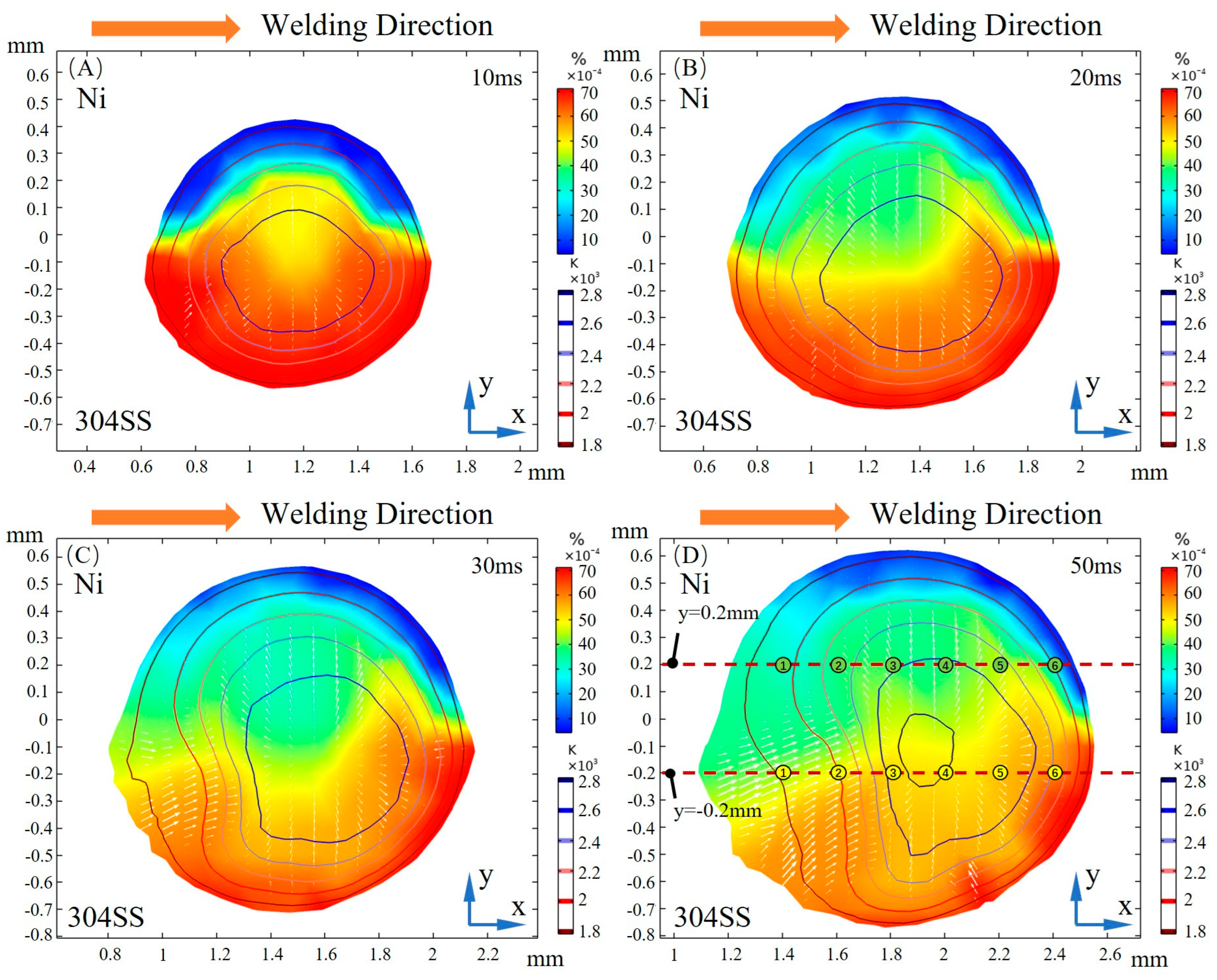
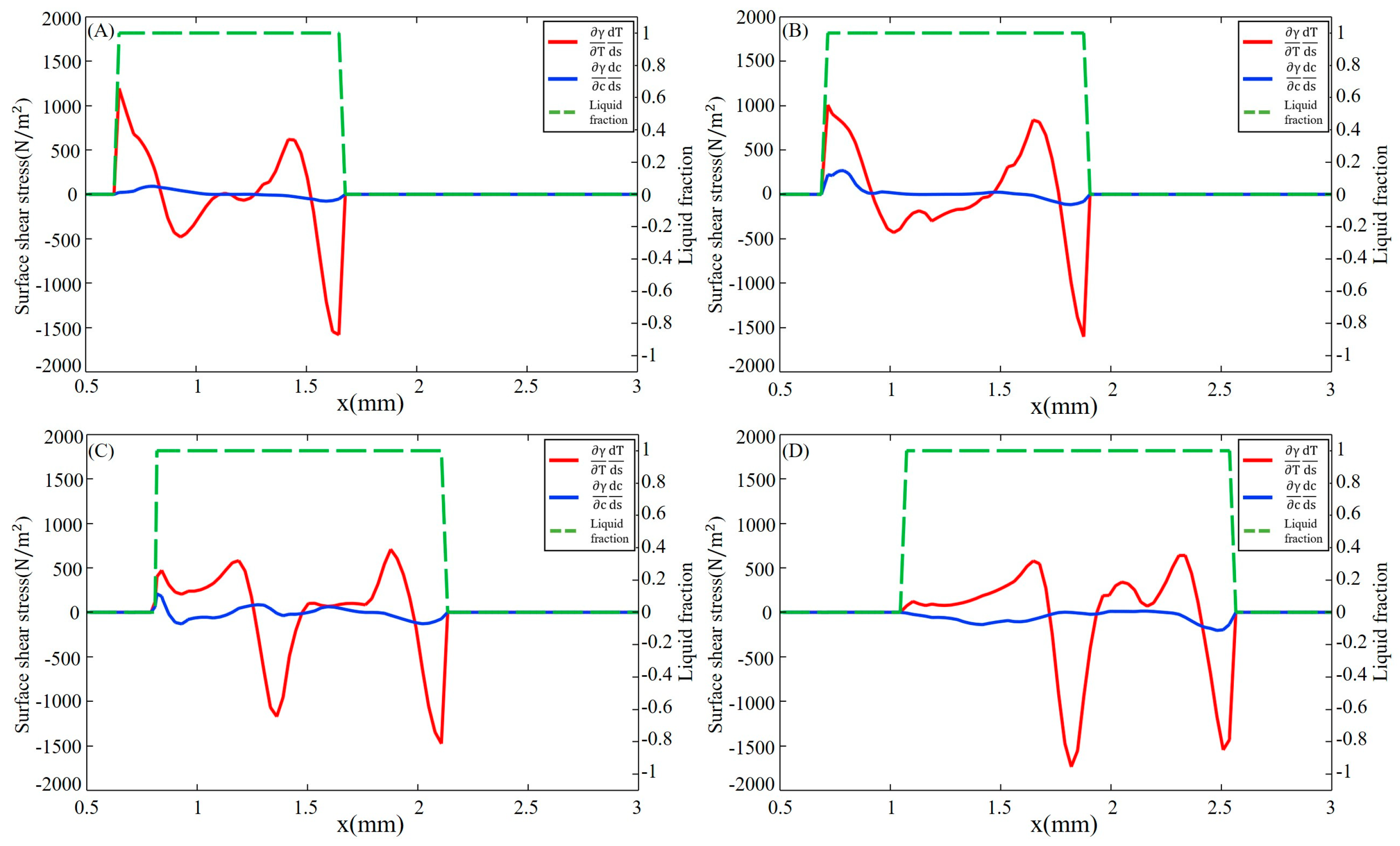
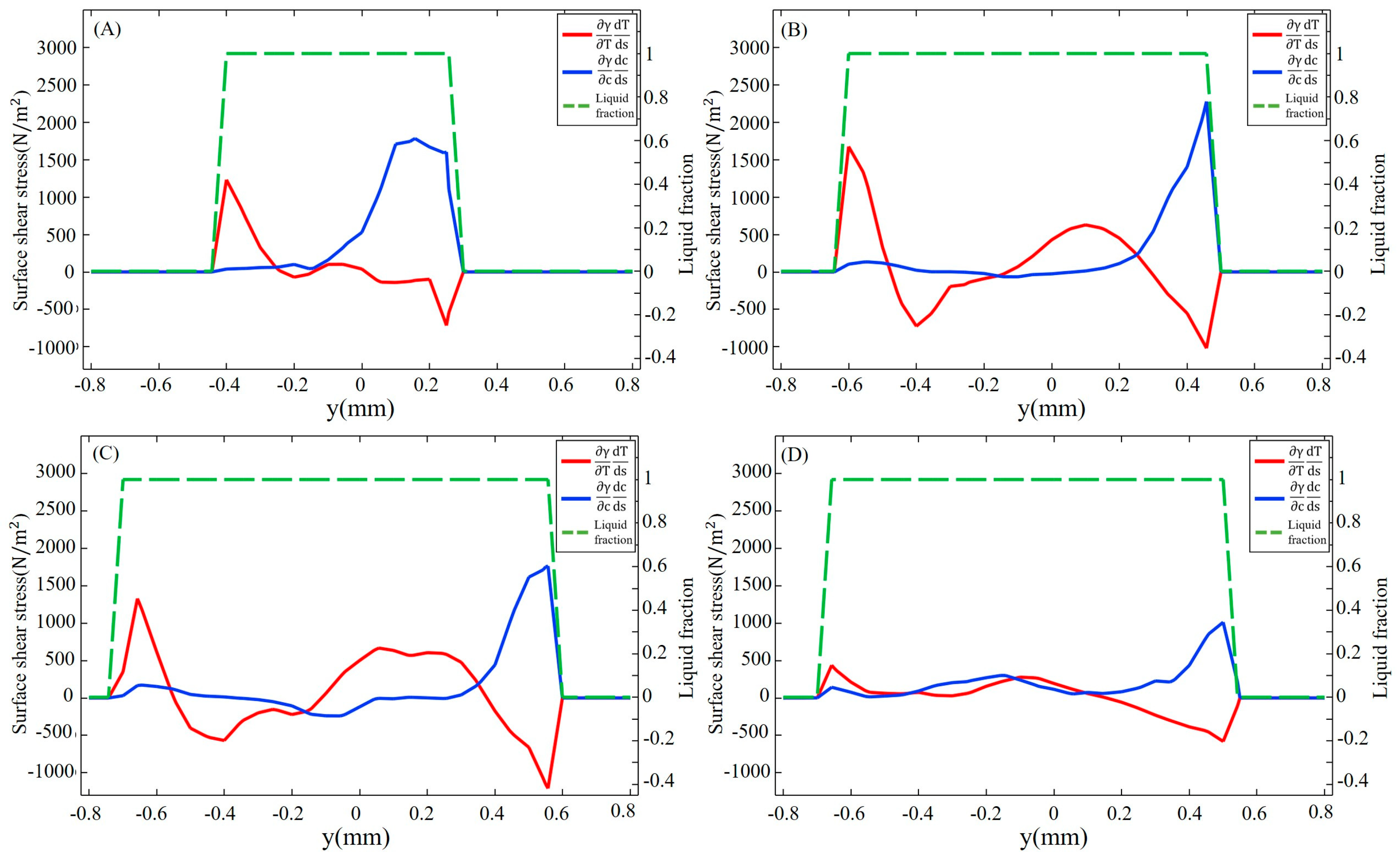
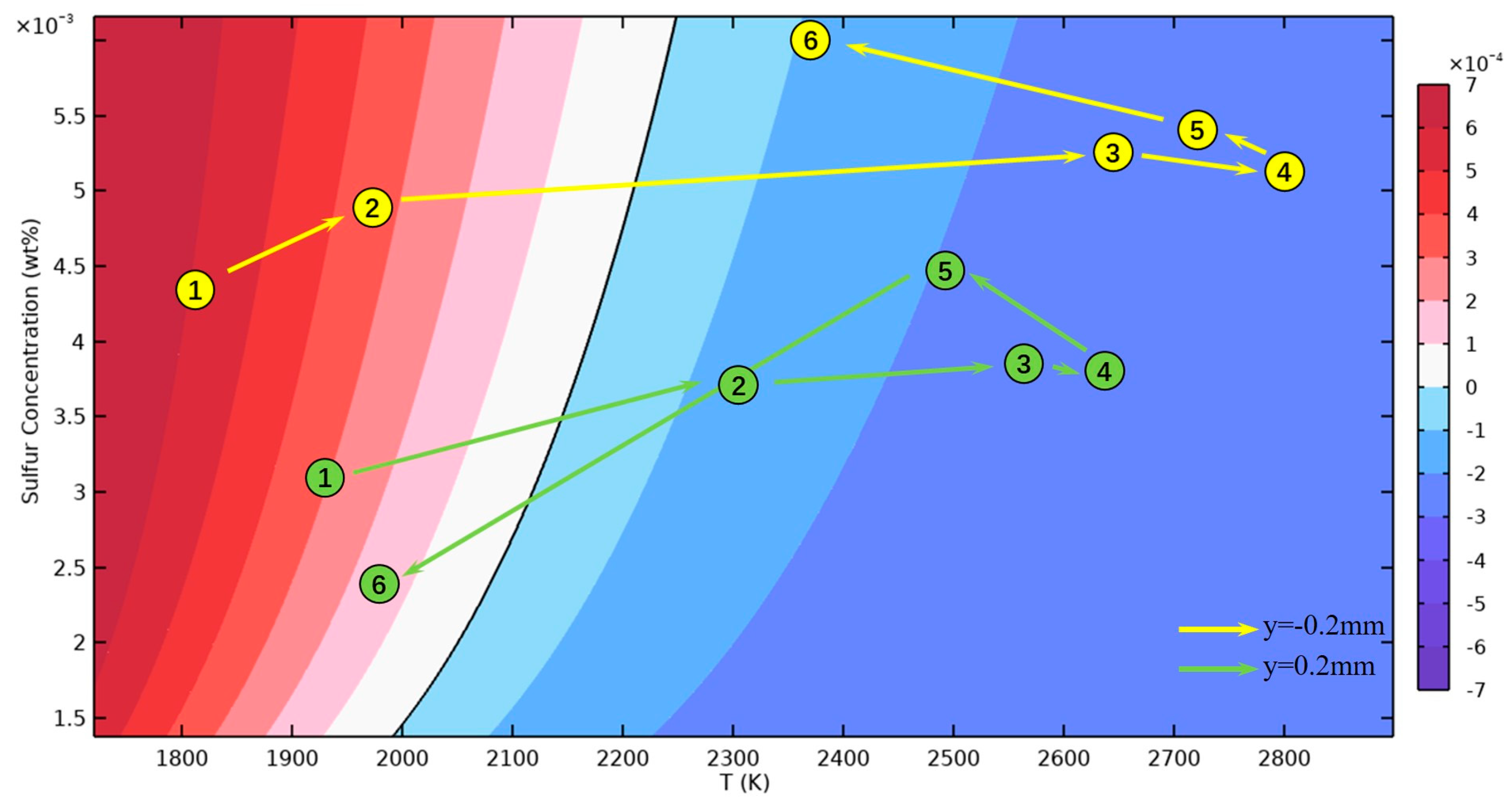
3.2. Dilution of Sulfur and Driving Forces
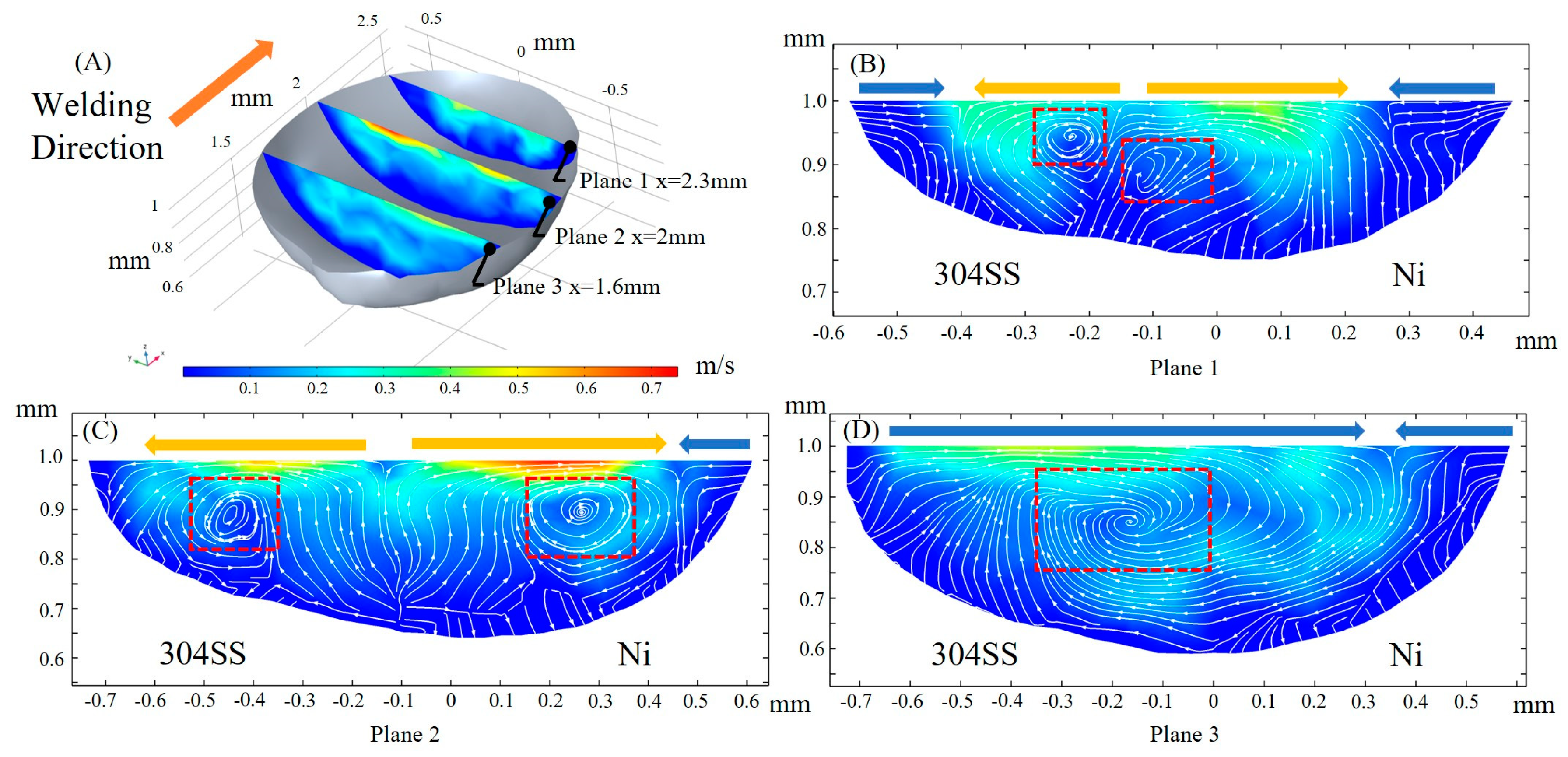
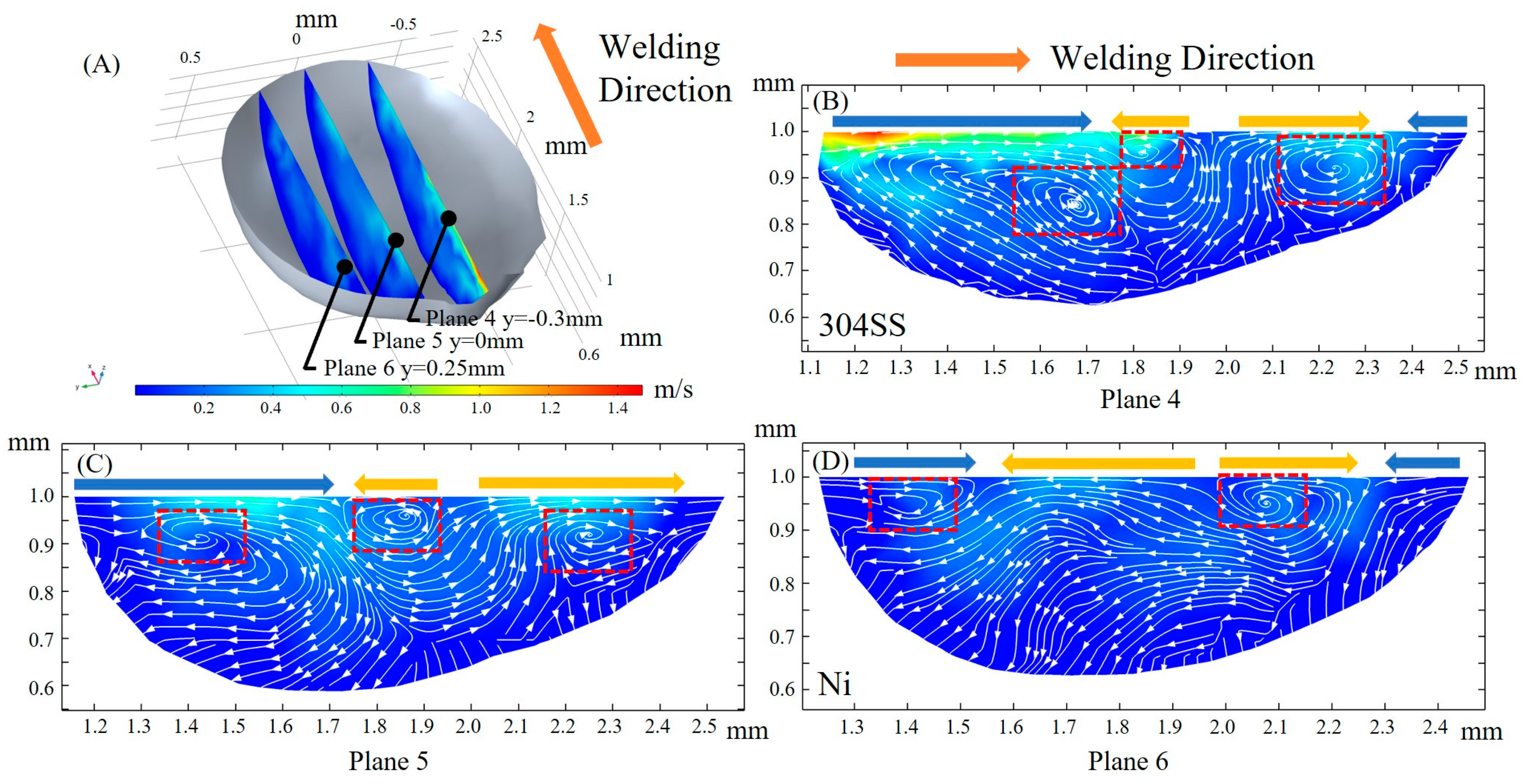
3.3. Fluid Flow
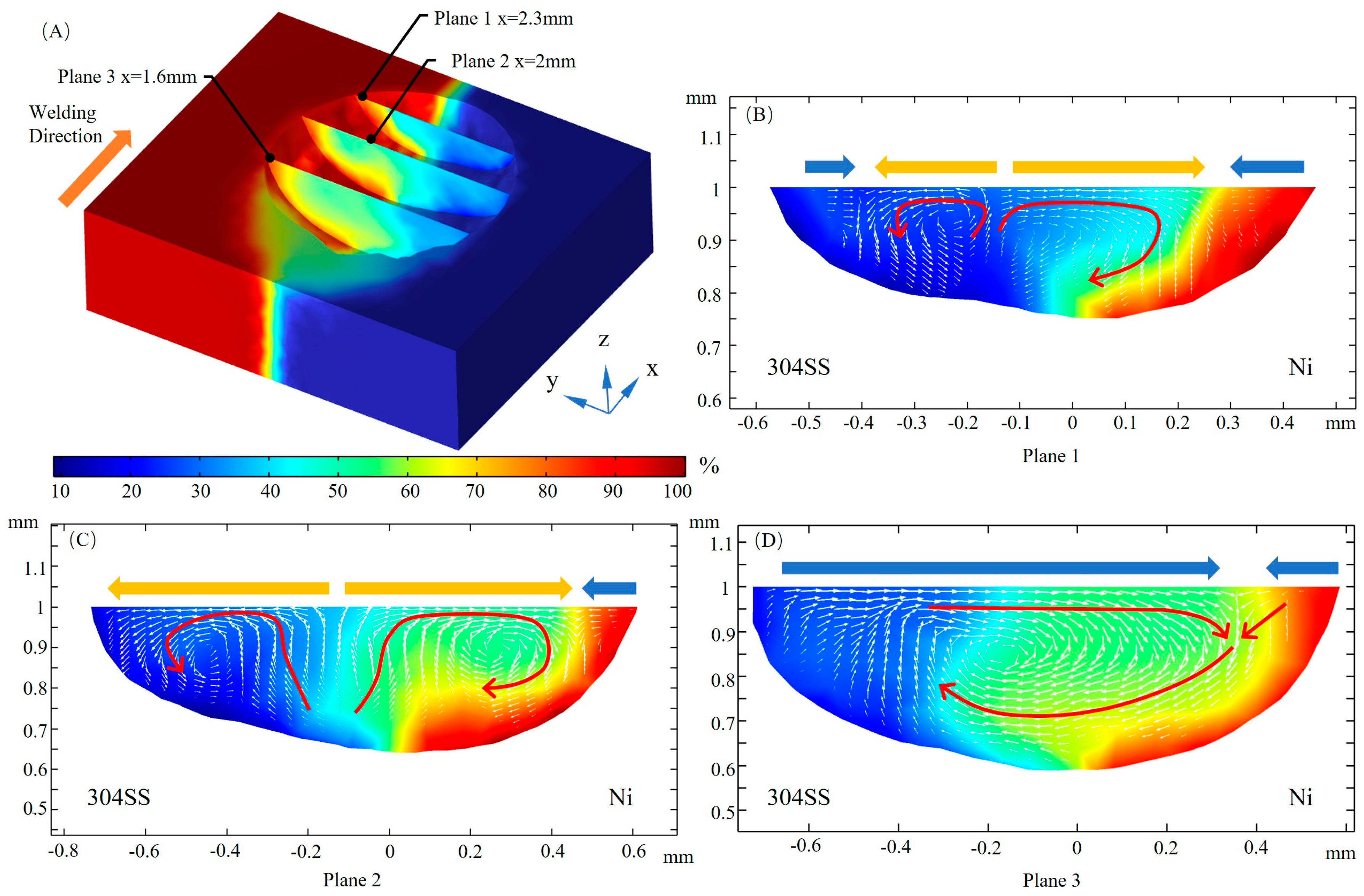
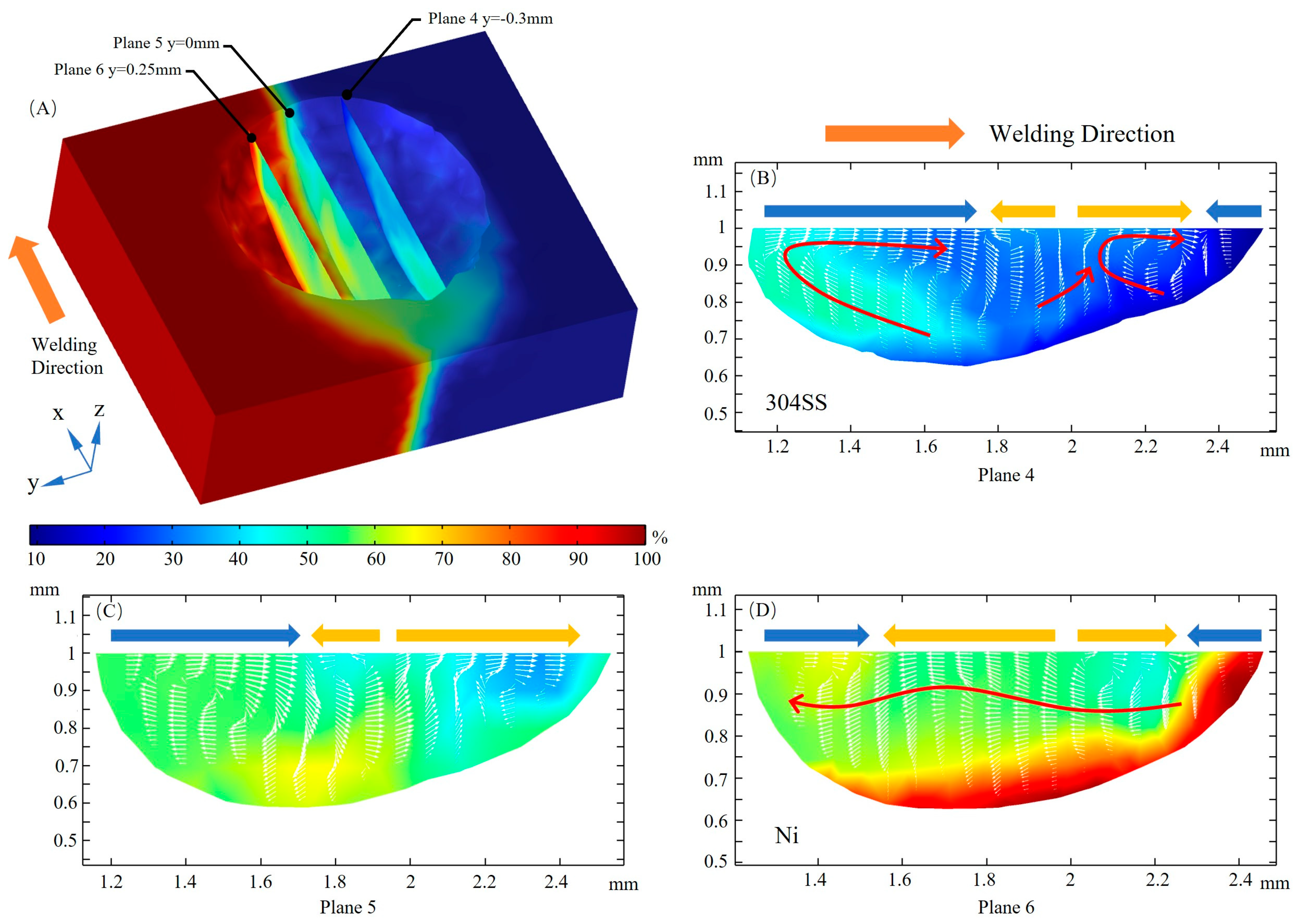
3.4. Mass Transfer
4. Conclusions
- The molten pool is fully developed after 45 ms under the influence of sulfur, and the aspect ratio is stabilized at about 0.3. The maximum flow velocity is 1.7 m/s, and the Peclet number reaches 400 on the 304SS side and 60 on the Ni side, indicating the predominance of convective heat transfer.
- After the molten pool reaches a quasi-steady state, sulfur is uniformly mixed in the front of the molten pool, and eventually there is a gradient distribution at the rear. The temperature-gradient term of surface shear stress plays a major role in welding direction. In the transverse direction, the temperature-gradient term of the surface shear stress is in the same order of magnitude as the concentration-gradient term, and they jointly determine the direction of inward convection. The spatial distribution of the surface-active element and temperature leads to differences in the TCST distribution. For the Ni side, the sign of the TCST shifts at 2100 K, and for the 304SS side, the sulfur element in the base metal is much higher than Ni, making the sign of the TCST shift at 2200 K. These differences further affect the fluid flow.
- When considering the role of elemental sulfur, the velocity of inward convection is significantly higher at the rear than the other positions of the molten pool. Inward convection collisions with outward convection inside the molten pool, along with the presence of complex vortices, are conducive to solute dilution. From the front part of the molten pool to the rear, the mixing of the solute gradually becomes homogeneous, and the rear of the molten pool is an important area for sufficient dilution of solute elements, e.g., Ni, Fe, and Cr.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Z.; Ion, J.C. Laser-welding of dissimilar metal combinations. J. Mater. Sci. 1995, 30, 4205–4214. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Ponder, K.; Brizes, E.; Abke, T.; Edwards, P.; Ramirez, A.J. Combining resistance spot welding and friction element welding for dissimilar joining of aluminum to high strength steels. J. Mater. Process. Technol. 2019, 273, 116192. [Google Scholar] [CrossRef]
- Hejripour, F.; Helenbrook, B.T.; Valentine, D.T.; Aidun, D.K. Mass transport and solidification phenomenon in dissimilar metals arc welding. Int. J. Heat Mass Transf. 2019, 144, 118703. [Google Scholar] [CrossRef]
- Bahrami, A.; Helenbrook, B.T.; Valentine, D.T.; Aidun, D.K. Fluid flow and mixing in linear GTA welding of dissimilar ferrous alloys. Int. J. Heat Mass Transf. 2016, 93, 729–741. [Google Scholar] [CrossRef]
- Zang, C.W.; Liu, J.G.; Tan, C.W.; Zhang, K.; Song, X.; Chen, B.; Li, L.; Feng, J. Laser conduction welding characteristics of dissimilar metals Mg/Ti with Al interlayer. J. Manuf. Process. 2018, 32, 595–605. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Zeng, Z.; Andrei, C.; Fernandes, F.B.; Miranda, R.M.; Ramirez, A.J.; Omoti, T.; Zhou, N. Dissimilar laser welding of superelastic NiTi and CuAlMn shape memory alloys. Mater. Des. 2017, 128, 166–175. [Google Scholar] [CrossRef]
- Li, Z.; Yu, G.; He, X.; Tian, C.; Li, S.; Li, H. Probing thermocapillary convection and multisolute dilution in laser welding of dissimilar miscible metals. Int. J. Therm. Sci. 2022, 172, 107242. [Google Scholar] [CrossRef]
- Hu, Y.; He, X.; Yu, G.; Ge, Z.; Zheng, C.; Ning, W. Heat and mass transfer in laser dissimilar welding of stainless steel and nickel. Appl. Surf. Sci. 2012, 258, 5914–5922. [Google Scholar] [CrossRef]
- Cao, X.; Jahazi, M.; Immarigeon, J.P.; Wallace, W. A review of laser welding techniques for magnesium alloys. J. Mater. Process. Technol. 2006, 171, 188–204. [Google Scholar] [CrossRef]
- Mai, T.A.; Spowage, A.C. Characterisation of dissimilar joints in laser welding of steel-kovar, copper-steel and copper-aluminium. Mater. Sci. Eng. A 2004, 374, 224–233. [Google Scholar] [CrossRef]
- Mukherjee, S.; Chakraborty, S.; Galun, R.; Estrin, Y.; Manna, I. Transport phenomena in conduction mode laser beam welding of Fe-Al dissimilar couple with Ta diffusion barrier. Int. J. Heat Mass Transf. 2010, 53, 5274–5282. [Google Scholar] [CrossRef]
- Schubert, E.; Klassen, M.; Zerner, I.; Walz, C.; Sepold, G. Light-weight structures produced by laser beam joining for future applications in automobile and aerospace industry. J. Mater. Process. Technol. 2001, 115, 2–8. [Google Scholar] [CrossRef]
- Meijer, J. Laser beam machining (LBM), state of the art and new opportunities. J. Mater. Process. Technol. 2004, 149, 2–17. [Google Scholar] [CrossRef]
- He, X.; Fuerschbach, P.W.; DebRoy, T. Heat transfer and fluid flow during laser spot welding of 304 stainless steel. J. Phys. D Appl. Phys. 2003, 36, 1388–1398. [Google Scholar] [CrossRef]
- Wang, R.; Lei, Y.; Shi, Y. Numerical simulation of transient temperature field during laser keyhole welding of 304 stainless steel sheet. Opt. Laser Technol. 2011, 43, 870–873. [Google Scholar] [CrossRef]
- Saldi, Z.S.; Kidess, A.; Kenjeres, S.; Zhao, C.; Richardson, I.M.; Kleijn, C.R. Effect of enhanced heat and mass transport and flow reversal during cool down on weld pool shapes in laser spot welding of steel. Int. J. Heat Mass Transf. 2013, 66, 879–888. [Google Scholar] [CrossRef]
- Li, Z.; Yu, G.; He, X.; Li, S.; Li, Z. Fluid flow and solute dilution in laser linear butt joining of 304SS and Ni. Int. J. Heat Mass Transf. 2020, 161, 120233. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, X.; Xu, L.; Lu, F.; Cui, H. Study of molten pool dynamics and porosity formation mechanism in full penetration fiber laser welding of Al-alloy. Int. J. Heat Mass Transf. 2020, 148, 119089. [Google Scholar] [CrossRef]
- Duggirala, A.; Kalvettukaran, P.; Acherjee, B.; Mitra, S. Numerical simulation of the temperature field, weld profile, and weld pool dynamics in laser welding of aluminium alloy. Optik 2021, 247, 167990. [Google Scholar] [CrossRef]
- Hu, Y.; He, X.; Yu, G.; Zhao, S. Capillary convection in pulsed-butt welding of miscible dissimilar couple. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2429–2440. [Google Scholar] [CrossRef]
- Shen, H.; Pan, Y.; Zhou, J.; Yao, Z. Forming Mechanism of Bump Shape in Pulsed Laser Melting of Stainless Steel. J. Heat Transf. 2017, 139, 062301. [Google Scholar] [CrossRef]
- Gan, Z.; Yu, G.; He, X.; Li, S. Surface-active element transport and its effect on liquid metal flow in laser-assisted additive manufacturing. Int. Commun. Heat Mass Transf. 2017, 86, 206–214. [Google Scholar] [CrossRef]
- Sahoo, P.; Debroy, T.; McNallan, M.J. Surface-tension of binary metal—Surface-active solute systems under conditions relevant to welding metallurgy. Metall. Trans. B 1988, 19, 483–491. [Google Scholar] [CrossRef]
- Zhao, C.X.; Kwakernaak, C.; Pan, Y.; Richardson, I.M.; Saldi, Z.; Kenjeres, S.; Kleijn, C.R. The effect of oxygen on transitional Marangoni flow in laser spot welding. Acta Mater. 2010, 58, 6345–6357. [Google Scholar] [CrossRef]
- Ribic, B.; Tsukamoto, S.; Rai, R.; DebRoy, T. Role of surface-active elements during keyhole-mode laser welding. J. Phys. D Appl. Phys. 2011, 44, 485203. [Google Scholar] [CrossRef]
- Lienert, T.J.; Burgardt, P.; Harada, K.L.; Forsyth, R.T.; DebRoy, T. Weld bead center line shift during laser welding of austenitic stainless steels with different sulfur content. Scr. Mater. 2014, 71, 37–40. [Google Scholar] [CrossRef]
- Wei, H.L.; Pal, S.; Manvatkar, V.; Lienert, T.J.; DebRoy, T. Asymmetry in steel welds with dissimilar amounts of sulfur. Scr. Mater. 2015, 108, 88–91. [Google Scholar] [CrossRef]
- Bahrami, A.; Valentine, D.T.; Helenbrook, B.T.; Aidun, D. Study of mass transport in autogenous GTA welding of dissimilar metals. Int. J. Heat Mass Transf. 2015, 85, 41–53. [Google Scholar] [CrossRef]

| Cr | Ni | Mn | Si | C | Fe |
|---|---|---|---|---|---|
| 20 | 10 | 1.32 | 0.83 | 0.08 | Bal. |
| Parameter | 304SS | Ni |
|---|---|---|
| Solidus temperature (K) | 1672 | 1730 |
| Density of solid metal (kg/m3) | 7450 | 8900 |
| Thermal conductivity of solid (W/m·K) | 19.2 | 60.7 |
| Specific heat of solid (J/kg·K) | 711.28 | 515 |
| Liquidus temperature (K) | 1727 | 1735 |
| Density of liquid metal (kg/m3) | 6910 | 8880 |
| Thermal conductivity of liquid (W/m·K) | 50 | 150 |
| Specific heat of liquid (J/kg·K) | 836.8 | 595 |
| Heat of fusion (kJ/kg) | 272 | 290 |
| Dynamic viscosity (kg/m·s) | 6.70 10−3 | 3.68 10−3 |
| Liquid volume thermal expansion (K−1) | 1.96 10−5 | 4.50 10−5 |
| Liquid volume concentration expansion (K−1) | 0.078 | 0.078 |
| Effective mass diffusivity (m2/s) | 7 10−7 | 7 10−7 |
| Parameter | Fe-S | Ni-S |
|---|---|---|
| γp (N/m) | 1.943 | 1.845 |
| A (N/m·K) | 4.3 | 4.3 |
| ΓS (mol/m2) | 1.3 | 1.5 |
| kl | 0.00318 | 0.00318 |
| ΔH0 (J/mol) | −1.88 | −1.47 |
| Parameter | Value |
|---|---|
| Welding speed (mm/s) | 20, 30 |
| Laser power (W) | 800 |
| Laser spot (mm) | 0.57 |
| Ambient temperature (K) | 300 |
| Laser absorption efficiency | 0.26 |
| Stefan-Boltzmann constant (W/) | 5.67 |
| Emissivity | 0.2 |
| Convective heat transfer coefficient at top surface (W/) | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, Z.; Yu, G.; Dong, B.; He, X.; Li, Z.; Li, S. Role of Surface-Active Element Sulfur on Thermal Behavior, Driving Forces, Fluid Flow and Solute Dilution in Laser Linear Welding of Dissimilar Metals. Materials 2023, 16, 2609. https://doi.org/10.3390/ma16072609
Shu Z, Yu G, Dong B, He X, Li Z, Li S. Role of Surface-Active Element Sulfur on Thermal Behavior, Driving Forces, Fluid Flow and Solute Dilution in Laser Linear Welding of Dissimilar Metals. Materials. 2023; 16(7):2609. https://doi.org/10.3390/ma16072609
Chicago/Turabian StyleShu, Zhuang, Gang Yu, Binxin Dong, Xiuli He, Zhiyong Li, and Shaoxia Li. 2023. "Role of Surface-Active Element Sulfur on Thermal Behavior, Driving Forces, Fluid Flow and Solute Dilution in Laser Linear Welding of Dissimilar Metals" Materials 16, no. 7: 2609. https://doi.org/10.3390/ma16072609
APA StyleShu, Z., Yu, G., Dong, B., He, X., Li, Z., & Li, S. (2023). Role of Surface-Active Element Sulfur on Thermal Behavior, Driving Forces, Fluid Flow and Solute Dilution in Laser Linear Welding of Dissimilar Metals. Materials, 16(7), 2609. https://doi.org/10.3390/ma16072609








