A Methodology for Predicting the Phase Fraction and Microhardness of Welded Joints Using Integrated Models
Abstract
1. Introduction
2. Modeling Methodology
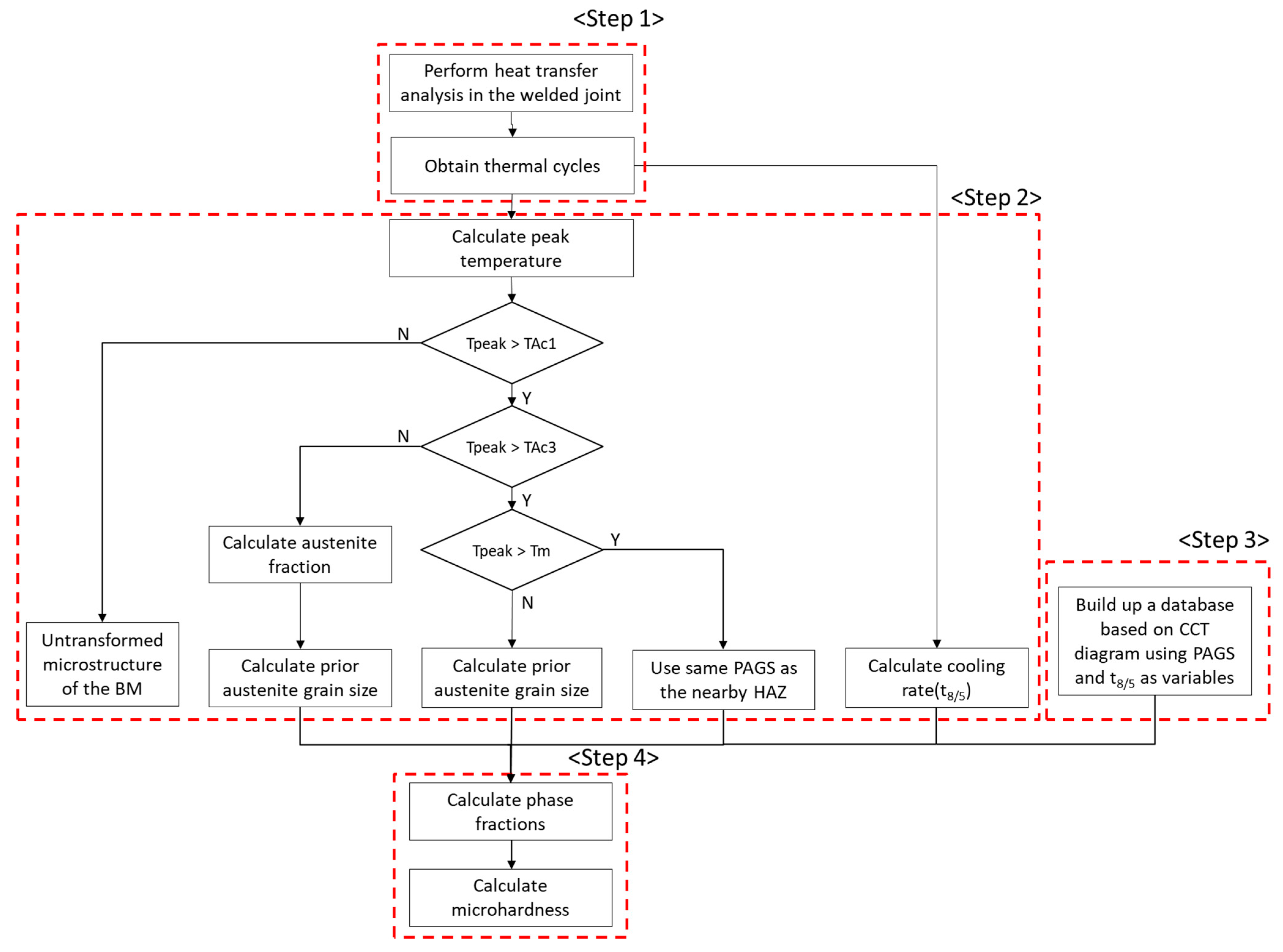
2.1. Integrated Model for Predicting the Phase Fraction and Microhardness of Welded Joints
2.2. Heat Transfer Analysis
2.3. Prediction of Austenite Fraction and Prior Austenite Grain Size
2.4. Prediction of Microhardness
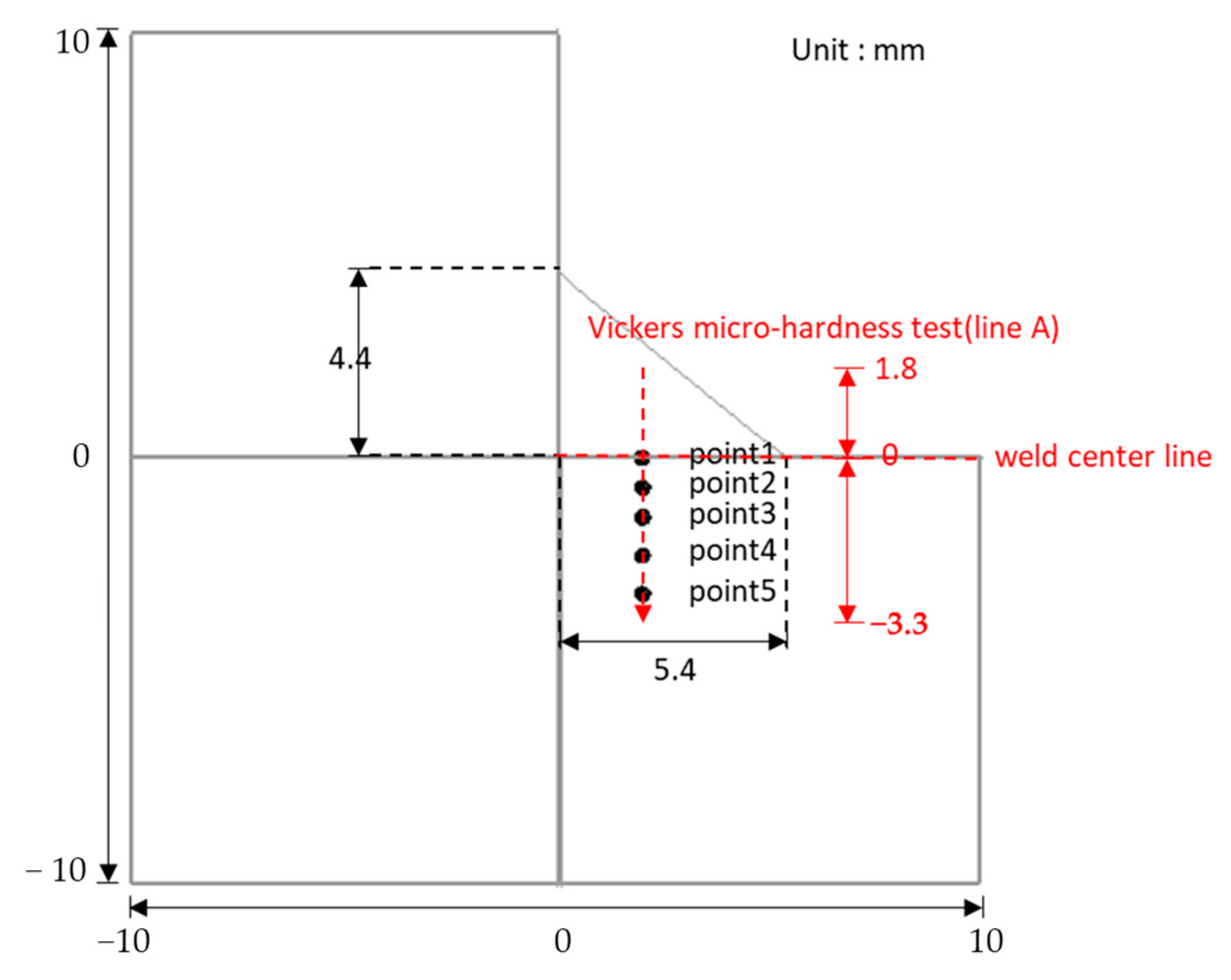
3. Experiment
4. Results and Discussion
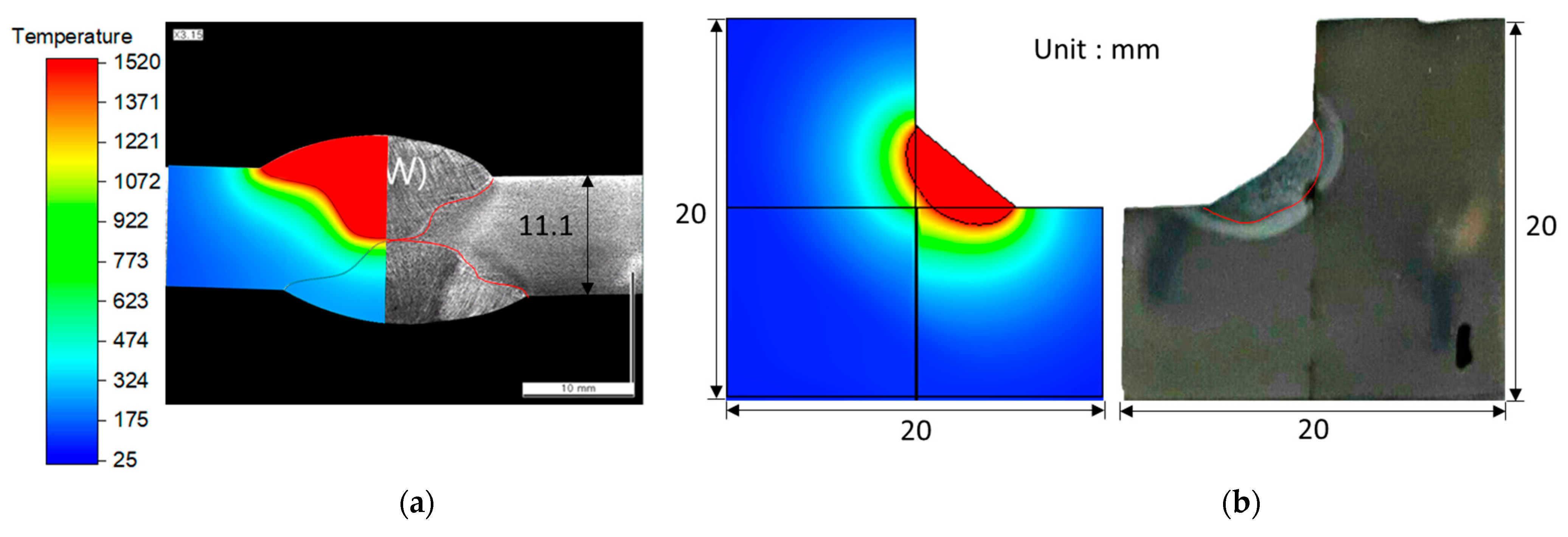
4.1. Heat Transfer Model Validation for SAW and GTAW
4.2. Thermal Behavior during GTAW
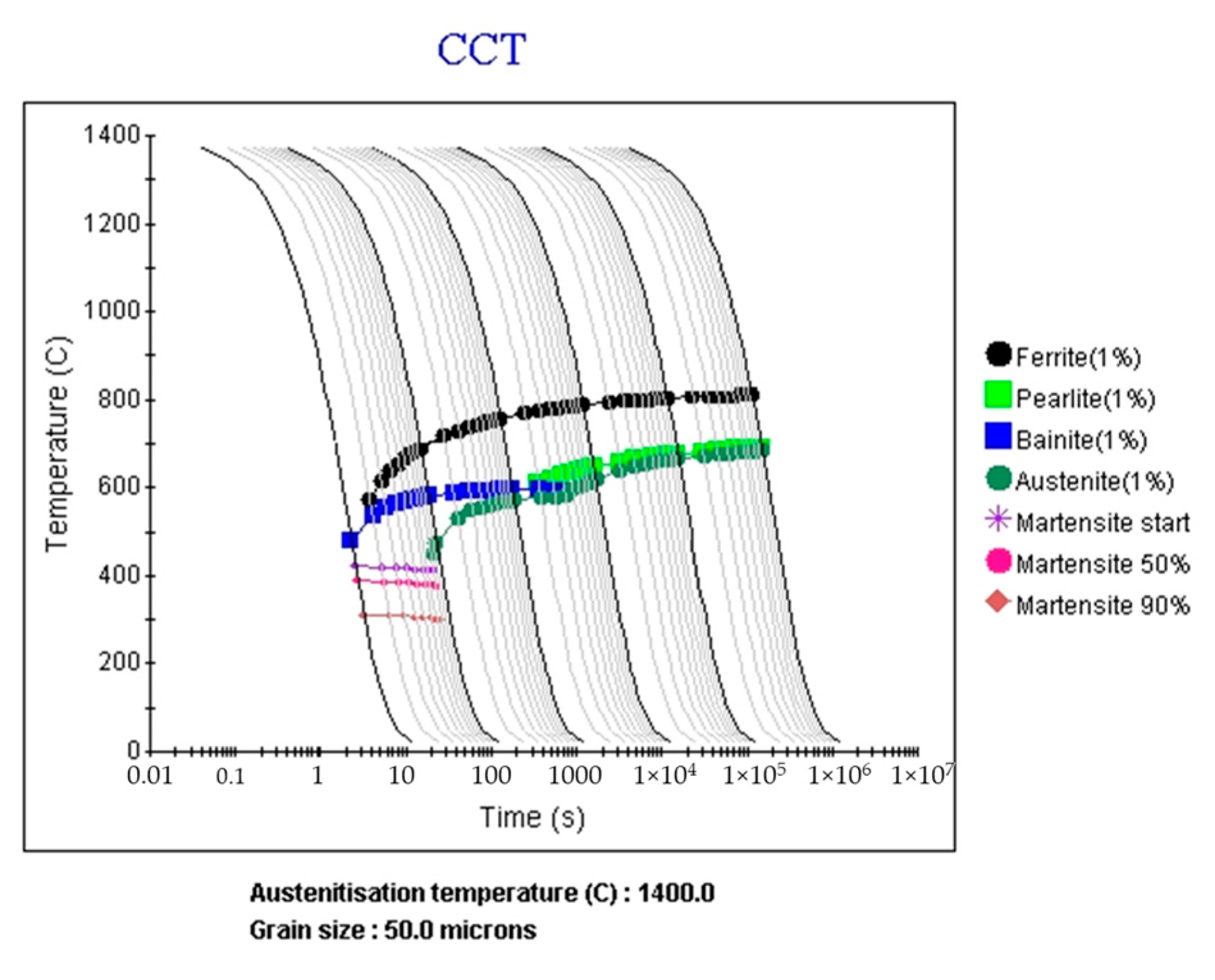
4.3. Prediction of PAGS and CCT Diagram
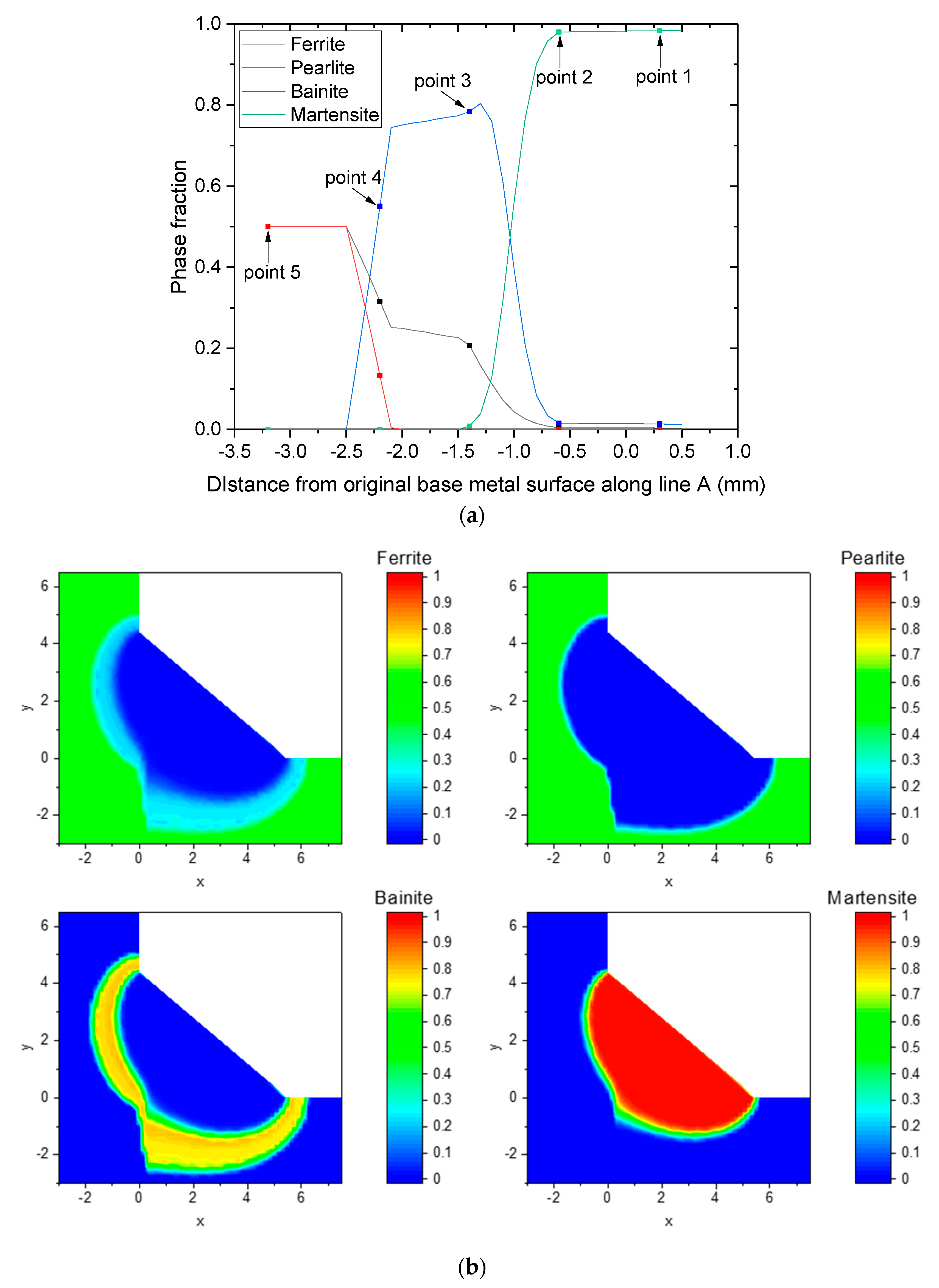
4.4. Prediction of Phase Transformation and Fraction
4.5. Microstructure and Grain Morphology of Experiments
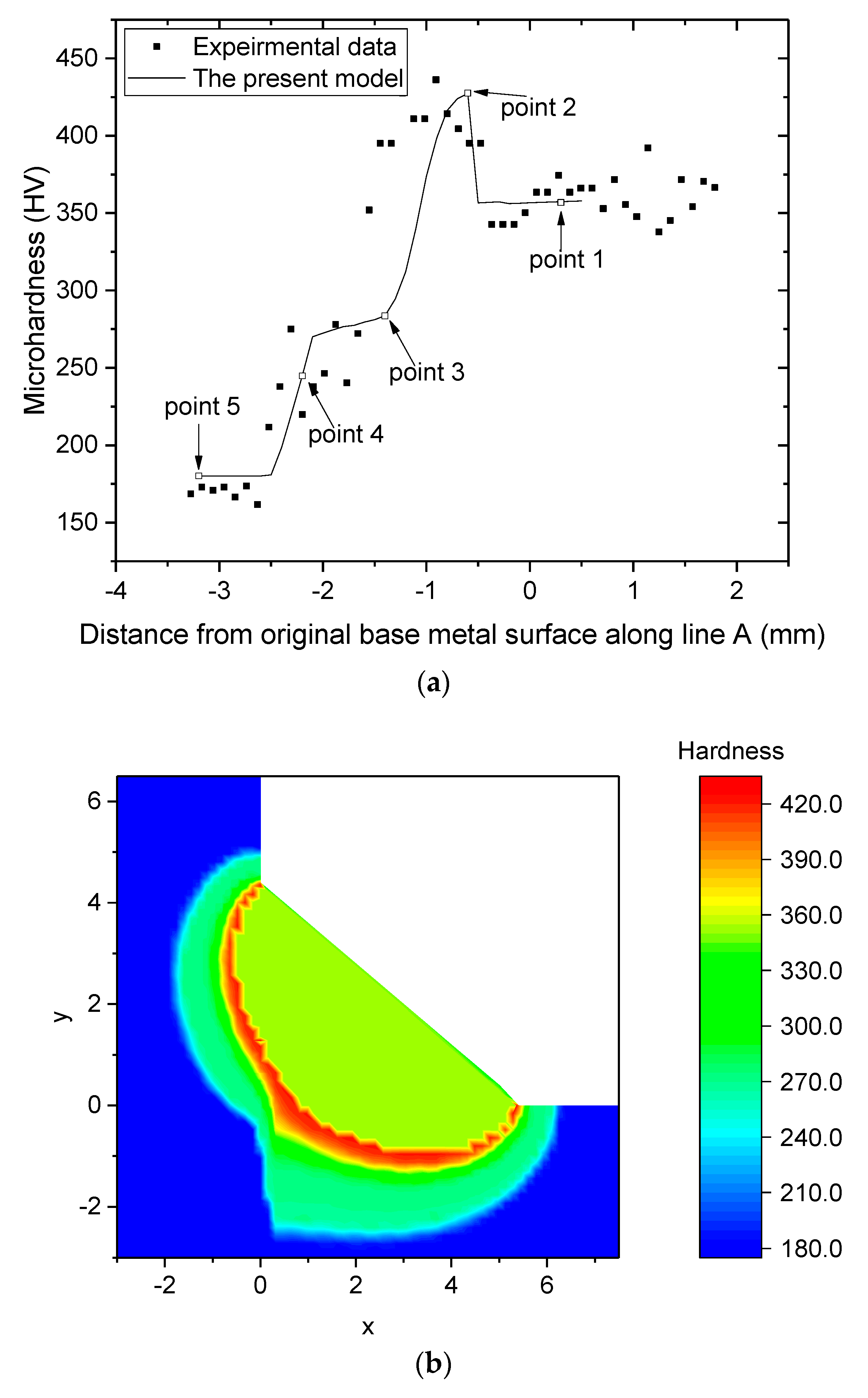
4.6. Prediction of the Microhardness of Welded Joint and Comparison with Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac1 | austenite start temperature |
| Ac3 | austenite complete temperature |
| specific heat capacity | |
| D | final grain size |
| D0 | initial grain size |
| surface tension | |
| gravitational acceleration | |
| h | sensible enthalpy |
| H | enthalpy |
| k | thermal conductivity |
| K | kinetic constant |
| L | latent heat |
| n | time exponent |
| P | pressure |
| Qapp | activation energy for the grain boundary movement |
| t | time |
| t1, t2 | grain growth start, end times |
| T | temperature |
| T(t) | the time-dependent thermal cycle |
| Tm | melting temperature |
| liquidus and solidus temperature | |
| t8/5 | the cooling time between 800 and 500 °C |
| fluid velocity | |
| V | cooling rate at 700 °C |
| Greek symbols | |
| liquid fraction | |
| density | |
| viscosity |
References
- Wang, H.T.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Fracture Mechanism of a Dissimilar Metal Welded Joint in Nuclear Power Plant. Eng. Fail. Anal. 2013, 28, 134–148. [Google Scholar] [CrossRef]
- Ming, H.; Zhang, Z.; Wang, J.; Han, E.-H.; Wang, P.; Sun, Z. Microstructure of a Safe-End Dissimilar Metal Weld Joint (SA508-52-316L) Prepared by Narrow-Gap GTAW. Mater. Charact. 2017, 123, 233–243. [Google Scholar] [CrossRef]
- Li, Y.; Yang, S.; Peng, Z.; Wang, Z.; Gao, Z. Microstructure, Fatigue Properties and Stress Concentration Analysis of 6005 Aluminum Alloy MIG Welded Lap Joint. Materials 2022, 15, 7729. [Google Scholar] [CrossRef] [PubMed]
- Vuherer, T.; Smaili, F.; Bjelajac, E.; Manjgo, M.; Lojen, G. Simulation and Mechanical Properties of Fine-Grained Heat-Affected Zone Microstructure in 18CrNiMo7-6 Steel. Materials 2022, 15, 6782. [Google Scholar] [CrossRef] [PubMed]
- Lambert, A.; Lambert, A.; Drillet, J.; Gourgues, A.F.; Sturel, T.; Pineau, A. Microstructure of Martensite–Austenite Constituents in Heat Affected Zones of High Strength Low Alloy Steel Welds in Relation to Toughness Properties. Sci. Technol. Weld. Join. 2000, 5, 168–173. [Google Scholar] [CrossRef]
- Kim, J.-O.M.S.-H.; Lee, Y.-K.; Jeong, H.-C.; Lee, C.-H. Prediction Model for the Microstructure and Properties in Weld Heat Affected Zone: Ⅴ. Prediction Model for the Phase Transformation Considering the Influence of Prior Austenite Grain Size and Cooling Rate in Weld HAZ of Low Alloyed Steel. J. Korean Weld. Join. Soc. 2010, 28, 104–113. [Google Scholar]
- Carbos, T.R.; Jorge, J.C.F.; Souza, L.F.G.d.; Bott, I.d.S.; Mendes, M.C. Investigation Into the Impact Toughness of API 5L X80 Steel Weldments and Its Relationship With Safe Welding Procedures. Mater. Res. 2020, 23. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, K.; Cui, S.; Zeng, M.; Yi, J.; Shen, X.; Yi, Y. Microstructure Evolution and Mechanical Properties of Underwater Dry and Local Dry Cavity Welded Joints of 690 MPa Grade High Strength Steel. Materials 2018, 11, 167. [Google Scholar] [CrossRef]
- Wang, X.-N.; Chen, C.-J.; Wang, H.-S.; Zhang, S.-H.; Zhang, M.; Luo, X. Microstructure Formation and Precipitation in Laser Welding of Microalloyed C–Mn Steel. J. Mater. Process. Technol. 2015, 226, 106–114. [Google Scholar] [CrossRef]
- Wu, X.; Lin, H.; Luo, W.; Jiang, H. Microstructure and Microhardness Evolution of Thermal Simulated HAZ of Q&P980 Steel. J. Mater. Res. Technol. 2021, 15, 6067–6078. [Google Scholar] [CrossRef]
- Di, X.; Tong, M.; Li, C.; Zhao, C.; Wang, D.J. Microstructural Evolution and Its Influence on Toughness in Simulated Inter-critical Heat Affected Zone of Large Thickness Bainitic Steel. Mater. Sci. Eng. A 2019, 743, 67–76. [Google Scholar] [CrossRef]
- Yang, K.; Wang, F.; Duan, D.; Xia, B.; Luo, C.; Yu, Z.; Li, W.; Yang, L.; Li, H. Prediction of HAZ Microstructure and Hardness for Q960E Joints Welded by Triple-Wire GMAW Based on Thermal and Numerical Simulation. Materials 2021, 14, 4898. [Google Scholar] [CrossRef]
- Zong, Y.; Liu, C.-M. Continuous Cooling Transformation Diagram, Microstructures, and Properties of the Simulated Coarse-Grain Heat-Affected Zone in a Low-Carbon Bainite E550 Steel. Metals 2019, 9, 939. [Google Scholar] [CrossRef]
- Deng, D. FEM Prediction of Welding Residual Stress and Distortion in Carbon Steel Considering Phase Transformation Effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, L.; Shi, Q. Correlation Between Weld Metal Microstructure Evolution and Welding Process Parameters of Low Alloy Ferritic Steel Weldments. Steel Res. Int. 2023, 3, 2200797. [Google Scholar] [CrossRef]
- Furuhara, T.; Kikumoto, K.; Saito, H.; Sekine, T.; Ogawa, T.; Morito, S.; Maki, T. Phase Transformation From Fine-Grained Austenite. ISIJ Int. 2008, 48, 1038–1045. [Google Scholar] [CrossRef]
- Morito, S.; Saito, H.; Ogawa, T.; Furuhara, T.; Maki, T. Effect of Austenite Grain Size on the Morphology and Crystallography of Lath Martensite in Low Carbon Steels. ISIJ Int. 2005, 45, 91–94. [Google Scholar] [CrossRef]
- Kauffmann, F.; Klein, T.; Klenk, A.; Maile, K. Creep Behavior and In-Depth Microstructural Characterization of Dissimilar Joints. Sci. Technol. Adv. Mater. 2013, 14, 014203. [Google Scholar] [CrossRef] [PubMed]
- Schönmaier, H.; Loder, B.; Fischer, T.; Grimm, F.; Krein, R.; Schmitz-Niederau, M.; Schnitzer, R. Continuous Cooling Transformation Diagrams of 2.25 Cr-1Mo-0.25 V Submerged-Arc Weld Metal and Base Metal. Metals 2020, 10, 1055. [Google Scholar] [CrossRef]
- Perulli, P.; Dassisti, M.; Casalino, G. Thermo-mechanical Simulation of Hybrid Welding of DP/AISI 316 and TWIP/AISI 316 Dissimilar Weld. Materials 2020, 13, 2088. [Google Scholar] [CrossRef]
- Dornelas, P.H.G.; Payão Filho, J.; Farias, F.W.C.; Moraes e Oliveira, V.H.P.M.; Moraes, D.; Zumpano Júnior, P.Z. FEM-Thermodynamic Simulation Methodology to Predict the Influence of t8/5 on the Coarse Grain Heat-Affected Zone of a Cr-Mo Low-Alloy Steel Pipe. J. Manuf. Processes. 2020, 60, 520–529. [Google Scholar] [CrossRef]
- Cheon, J.; Kiran, D.V.; Na, S.-J. Thermal Metallurgical Analysis of GMA Welded AH36 Steel Using CFD–FEM Framework. Mater. Des. 2016, 91, 230–241. [Google Scholar] [CrossRef]
- Morawiec, M.; Kik, T.; Stano, S.; Różański, M.; Grajcar, A. Numerical Simulation and Experimental Analysis of Thermal Cycles and Phase Transformation Behavior of Laser-Welded Advanced Multiphase Steel. Symmetry 2022, 14, 477. [Google Scholar] [CrossRef]
- Cho, W.-I.; Na, S.-J.; Thomy, C.; Vollertsen, F. Numerical Simulation of Molten Pool Dynamics in High Power Disk Laser Welding. J. Mater. Process. Technol. 2012, 212, 262–275. [Google Scholar] [CrossRef]
- Bhatti, A.A.; Barsoum, Z.; Murakawa, H.; Barsoum, I. Influence of Thermo-mechanical Material Properties of Different Steel Grades on Welding Residual Stresses and Angular Distortion. Mater. Des. 2015, 65, 878–889. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhuo, Z.; Zhou, H.; Wang, J. Microstructure Analysis and Hardness Prediction Based on Microstructure Evolution Theory in Multi-pass Welded Joint. Proc. Inst. Mech. Eng. C 2022, 236, 7246–7258. [Google Scholar] [CrossRef]
- Anderson, T.D.; DuPont, J.N.; DebRoy, T. Origin of Stray Grain Formation in Single-Crystal Superalloy Weld Pools From Heat Transfer and Fluid Flow Modeling. Acta Mater. 2010, 58, 1441–1454. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Y.-H.; Zhang, X.-X.; Wu, C.-S. An Improved Simulation of Heat Transfer and Fluid Flow in Plasma Arc Welding With Modified Heat Source Model. Int. J. Therm. Sci. 2013, 64, 93–104. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C. Effect of Fluid Flow in the Weld Pool on the Numerical Simulation Accuracy of the Thermal Field in Hybrid Welding. J. Manuf. Processes. 2015, 20, 215–223. [Google Scholar] [CrossRef]
- Traidia, A.; Roger, F.; Guyot, E. Optimal Parameters for Pulsed Gas Tungsten Arc Welding in Partially and Fully Penetrated Weld Pools. Int. J. Therm. Sci. 2010, 49, 1197–1208. [Google Scholar] [CrossRef]
- Uhm, S.; Moon, J.; Lee, C.; Yoon, J.; Lee, B. Prediction Model for the Austenite Grain Size in the Coarse Grained Heat Affected Zone of Fe-C-Mn Steels: Considering the Effect of Initial Grain Size on Isothermal Growth Behavior. ISIJ Int. 2004, 44, 1230–1237. [Google Scholar] [CrossRef]
- Moon, J.; Lee, J.; Lee, C. Prediction for the Austenite Grain Size in the Presence of Growing Particles in the Weld HAZ of Ti-Microalloyed Steel. Mater. Sci. Eng. A 2007, 459, 40–46. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, Y.; Wang, J.; Zhang, L.J.I.I. Microstructural Characteristics and Prediction of Austenite Grain Size in Heat Affected Zone of High Strength Low Alloy Steel. ISIJ Int. 2011, 51, 269–273. [Google Scholar] [CrossRef]
- Maynier, P.; Dollet, J.; Bastien, P. Hardenability Concepts With Applications to Steels; AIME: New York, NY, USA, 1978; p. NY518. [Google Scholar]
- Ali, M.; Porter, D.; Kömi, J.; Eissa, M.; El Faramawy, H.; Mattar, T. Effect of Cooling Rate and Composition on Microstructure and Mechanical Properties of Ultrahigh-Strength Steels. J. Iron Steel Res. Int. 2019, 26, 1350–1365. [Google Scholar] [CrossRef]
- Wang, R.; Lei, Y.; Shi, Y. Numerical Simulation of Transient Temperature Field During Laser Keyhole Welding of 304 Stainless Steel Sheet. Opt. Laser Technol. 2011, 43, 870–873. [Google Scholar] [CrossRef]
- Joshi, S.; Hildebrand, J.; Aloraier, A.S.; Rabczuk, T. Characterization of Material Properties and Heat Source Parameters in Welding Simulation of Two Overlapping Beads on a Substrate Plate. Comput. Mater. Sci. 2013, 69, 559–565. [Google Scholar] [CrossRef]
- Celada-Casero, C.; Sietsma, J.; Santofimia, M.J. The Role of the Austenite Grain Size in the Martensitic Transformation in Low Carbon Steels. Mater. Des. 2019, 167, 107625. [Google Scholar] [CrossRef]
- García-Junceda, A.; Capdevila, C.; Caballero, F.G.; De Andrés, C.G. Dependence of Martensite Start Temperature on Fine Austenite Grain Size. Scr. Mater. 2008, 58, 134–137. [Google Scholar] [CrossRef]
- Wang, X.-N.; Sun, Q.; Zheng, Z.; Di, H.-S. Microstructure and Fracture Behavior of Laser Welded Joints of DP Steels With Different Heat Inputs. Mater. Sci. Eng. A 2017, 699, 18–25. [Google Scholar] [CrossRef]
- Santillan Esquivel, A.S.; Nayak, S.S.; Xia, M.S.; Zhou, Y. Microstructure, Hardness and Tensile Properties of Fusion Zone in Laser Welding of Advanced High Strength Steels. Can. Metall. Q. 2012, 51, 328–335. [Google Scholar] [CrossRef]
- Grange, R.A.; Hribal, C.R.; Porter, L.F. Hardness of Tempered Martensite in Carbon and Low-Alloy Steels. Metall. Trans. A 1977, 8, 1775–1785. [Google Scholar] [CrossRef]
- Hutchinson, B.; Hagström, J.; Karlsson, O.; Lindell, D.; Tornberg, M.; Lindberg, F.; Thuvander, M. Microstructures and Hardness of as-Quenched Martensites (0.1–0.5% C). Acta Mater. 2011, 59, 5845–5858. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, J.; Yang, S.; Tao, W.; Wu, F.; Xia, W. Experiment-Based Regional Characterization of HAZ Mechanical Properties for Laser Welding. Int. J. Adv. Manuf. Technol. 2015, 78, 1629–1640. [Google Scholar] [CrossRef]










| Property | Case 1: SAW | Case 2: GTAW | |
|---|---|---|---|
| Internal Pass | External Pass | Single Pass | |
| Density (kg/m3) | 7500 | Temperature-dependent function | |
| Specific heat [J/(kg·K)] | Temperature-dependent function | 726 (solid), 732 (liquid) | |
| Thermal conductivity [W/m·K)] | Temperature-dependent function | Temperature-dependent function | |
| Viscosity [kg/(m·s)] | Temperature-dependent function | Temperature-dependent function | |
| Pure solvent melting heat (J/kg) | 270,000 | 270,000 | |
| External emissivity | 0.4 | 0.4 | |
| Flux thickness (mm) | 20 | - | |
| Process | Material | C | Si | Mn | Ni | Cr | Mo | Fe |
|---|---|---|---|---|---|---|---|---|
| Case 1: SAW | ASTM A516-60 (Base metal) | 0.158 | 0.227 | 0.95 | 0.012 | 0.341 | 0.0018 | Bal. |
| API 2H-50 (Filler metal) | 0.124 | 0.202 | 1.512 | 0.305 | 0.024 | 0.068 | Bal | |
| Case 2: GTAW | SS400 (Base metal) | 0.17 | 0.21 | 1.06 | 0.005 | 0.02 | 0.02 | Bal. |
| Er70s-6 (Filler metal) | 0.071 | 0.84 | 1.50 | 0.01 | 0.03 | 0.001 | Bal. |
| Process | Voltage (V)/Current (A) | Weld Velocity (mm/s) | Heat Input (kJ/mm) | |
|---|---|---|---|---|
| Case 1: SAW | Internal | DC: 31/620 AC1: 33/560, 34/520 | 21.6 | 2.56 |
| External | DC: 32/830 AC1: 35/520, 35/500 | 2.87 | ||
| Case 2: GTAW | 18.5/160 | 1.92 | 1.54 | |
| Distance from Weld Center Line (mm) | Peak Temperature (°C) | T8/5 (s) | PAGS (μm) | |
|---|---|---|---|---|
| Point 1 | 0 | 1872 | 1.45 | - |
| Point 2 | −0.6 | 1485 | 1.57 | 103 |
| Point 3 | −1.4 | 1090 | 1.78 | 6.4 |
| Point 4 | −2.2 | 785 | 2.62 | 5 |
| Point 5 | −3.2 | 551 | - | - |
| PAGS (μm) | Ferrite | Pearlite | Bainite | Martensite |
|---|---|---|---|---|
| 5 | 0.24 | 0.00 | 0.76 | 0.00 |
| 10 | 0.16 | 0.00 | 0.84 | 0.00 |
| 20 | 0.08 | 0.00 | 0.73 | 0.19 |
| 30 | 0.05 | 0.00 | 0.50 | 0.45 |
| 40 | 0.03 | 0.00 | 0.29 | 0.68 |
| 50 | 0.02 | 0.00 | 0.16 | 0.82 |
| 60 | 0.02 | 0.00 | 0.10 | 0.88 |
| 70 | 0.02 | 0.00 | 0.06 | 0.92 |
| 80 | 0.01 | 0.00 | 0.05 | 0.94 |
| 90 | 0.01 | 0.00 | 0.03 | 0.96 |
| 100 | 0.01 | 0.00 | 0.02 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.-H.; Yi, K.-W. A Methodology for Predicting the Phase Fraction and Microhardness of Welded Joints Using Integrated Models. Materials 2023, 16, 2599. https://doi.org/10.3390/ma16072599
Song J-H, Yi K-W. A Methodology for Predicting the Phase Fraction and Microhardness of Welded Joints Using Integrated Models. Materials. 2023; 16(7):2599. https://doi.org/10.3390/ma16072599
Chicago/Turabian StyleSong, Ji-Hyo, and Kyung-Woo Yi. 2023. "A Methodology for Predicting the Phase Fraction and Microhardness of Welded Joints Using Integrated Models" Materials 16, no. 7: 2599. https://doi.org/10.3390/ma16072599
APA StyleSong, J.-H., & Yi, K.-W. (2023). A Methodology for Predicting the Phase Fraction and Microhardness of Welded Joints Using Integrated Models. Materials, 16(7), 2599. https://doi.org/10.3390/ma16072599




