Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit
Abstract
1. Introduction
2. Materials and Methods
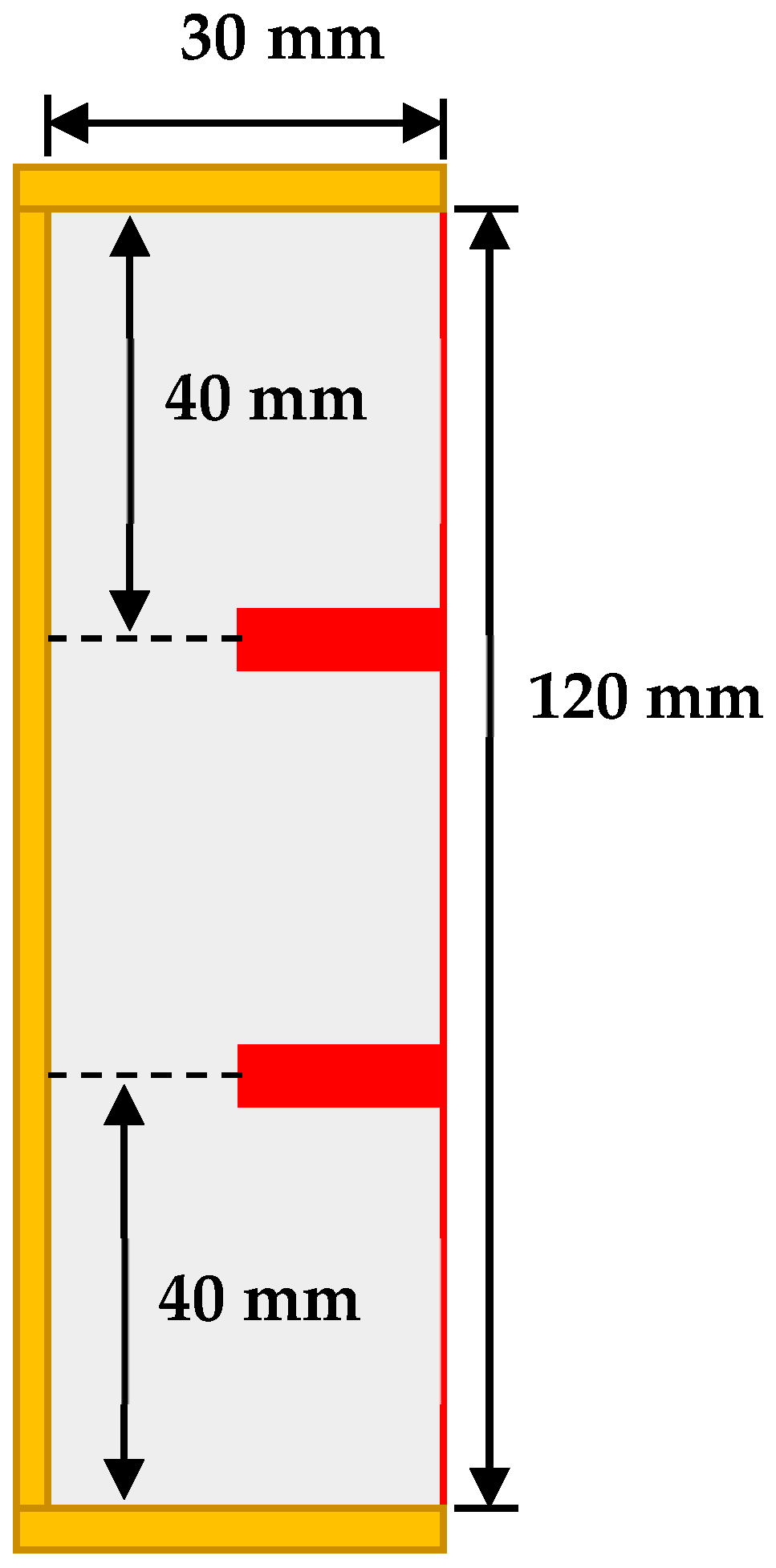
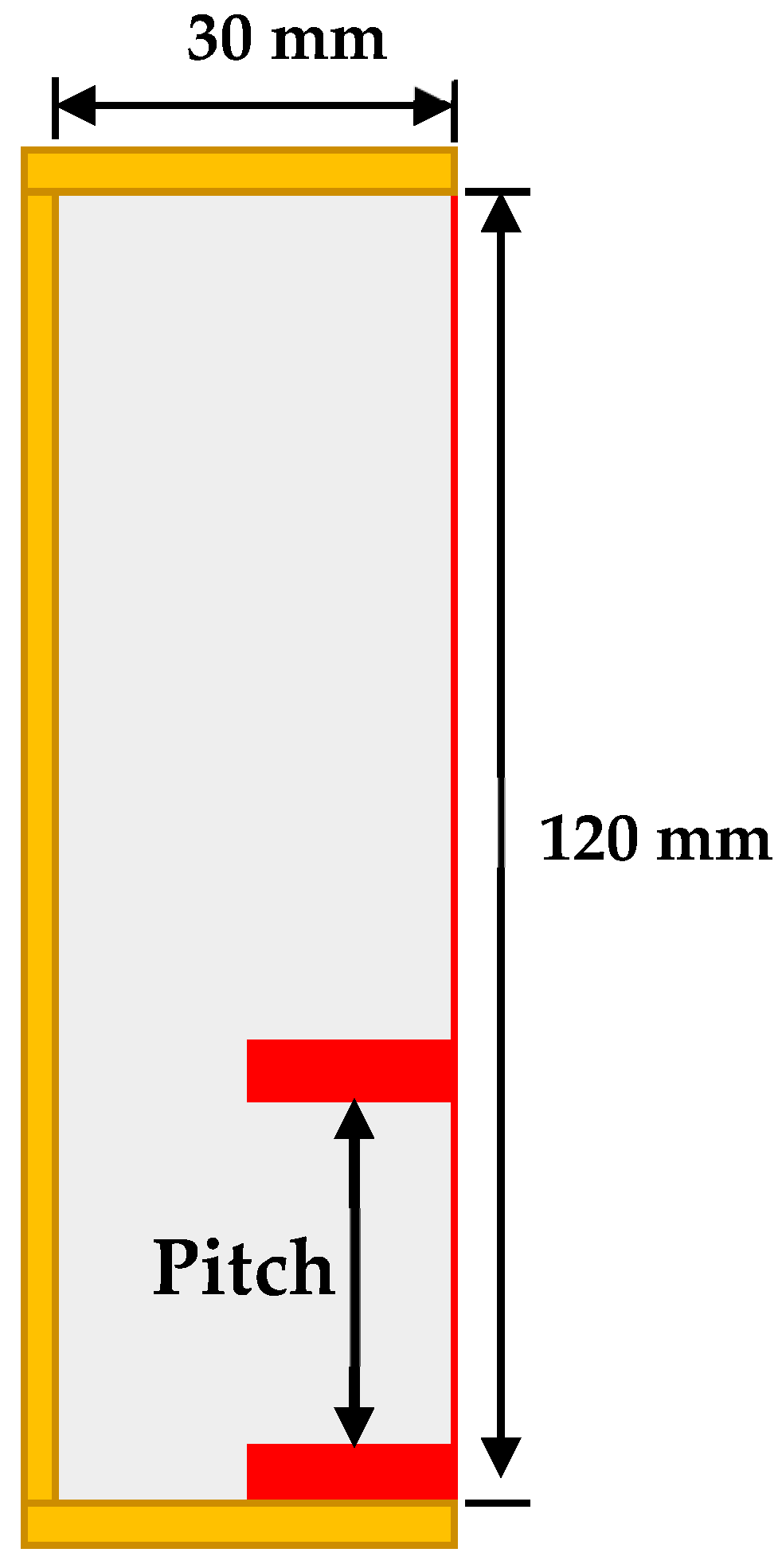
2.1. Physical Domain and Boundary Conditions
2.2. Numerical Model
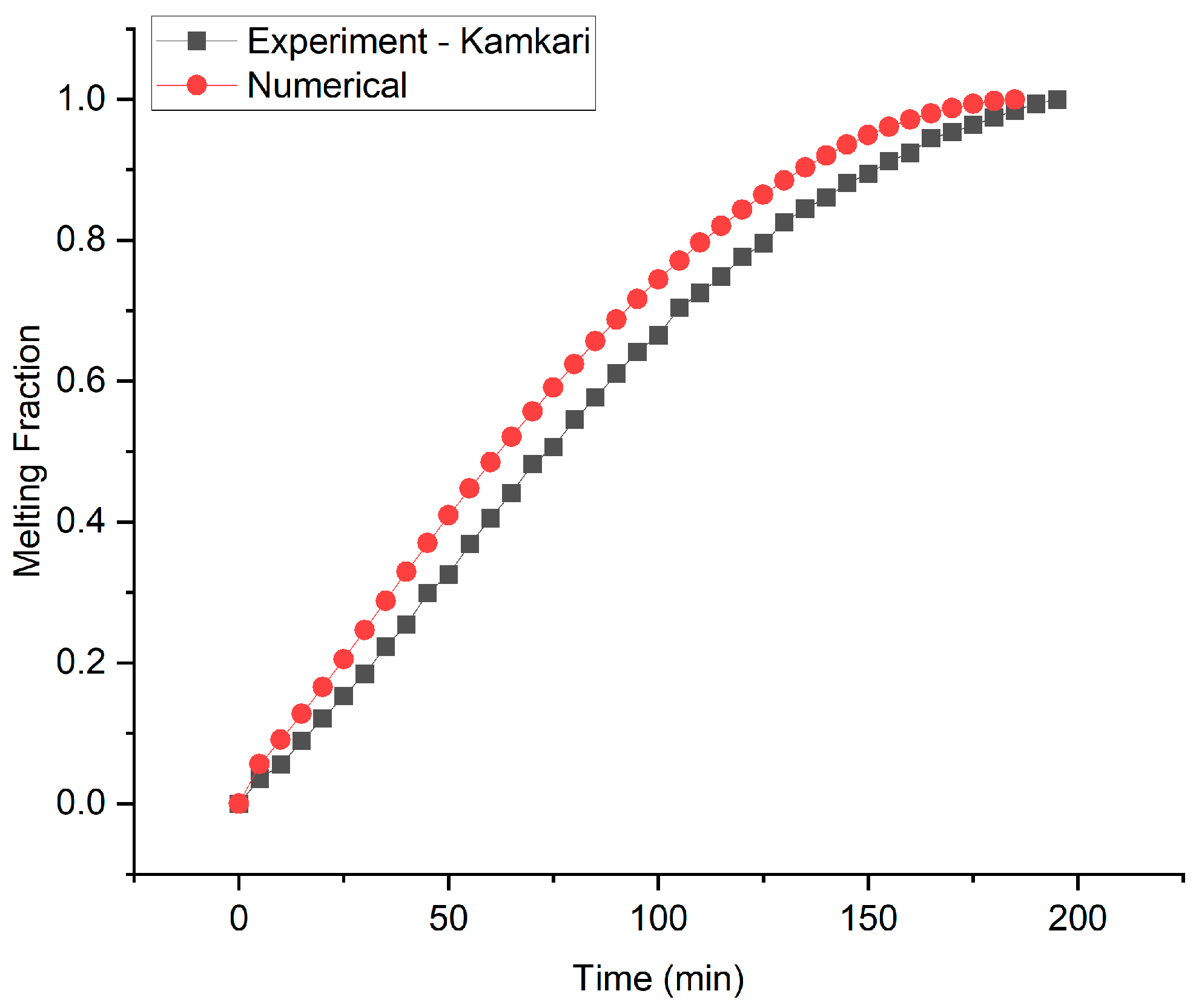
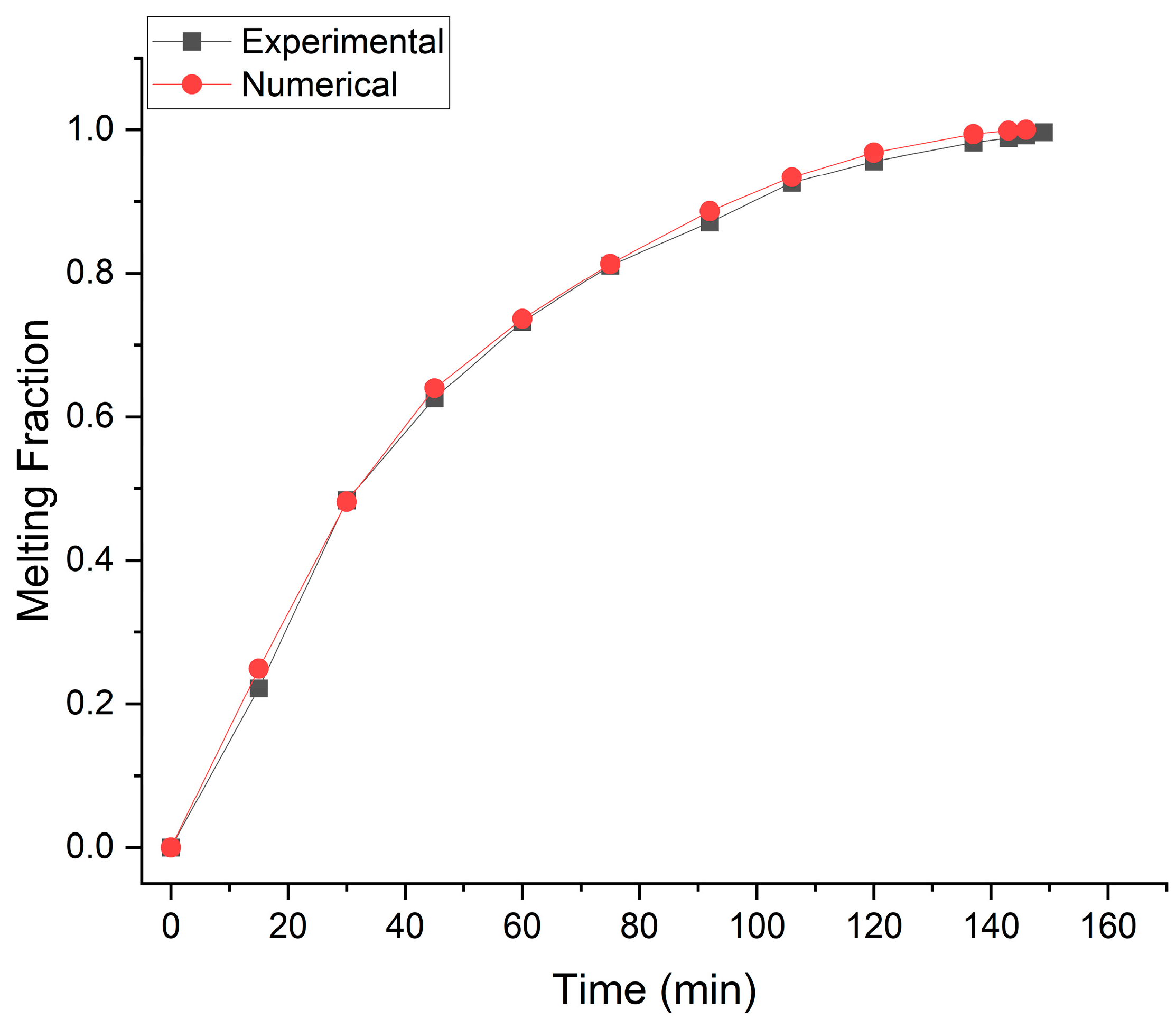
2.3. Numerical Model Validation
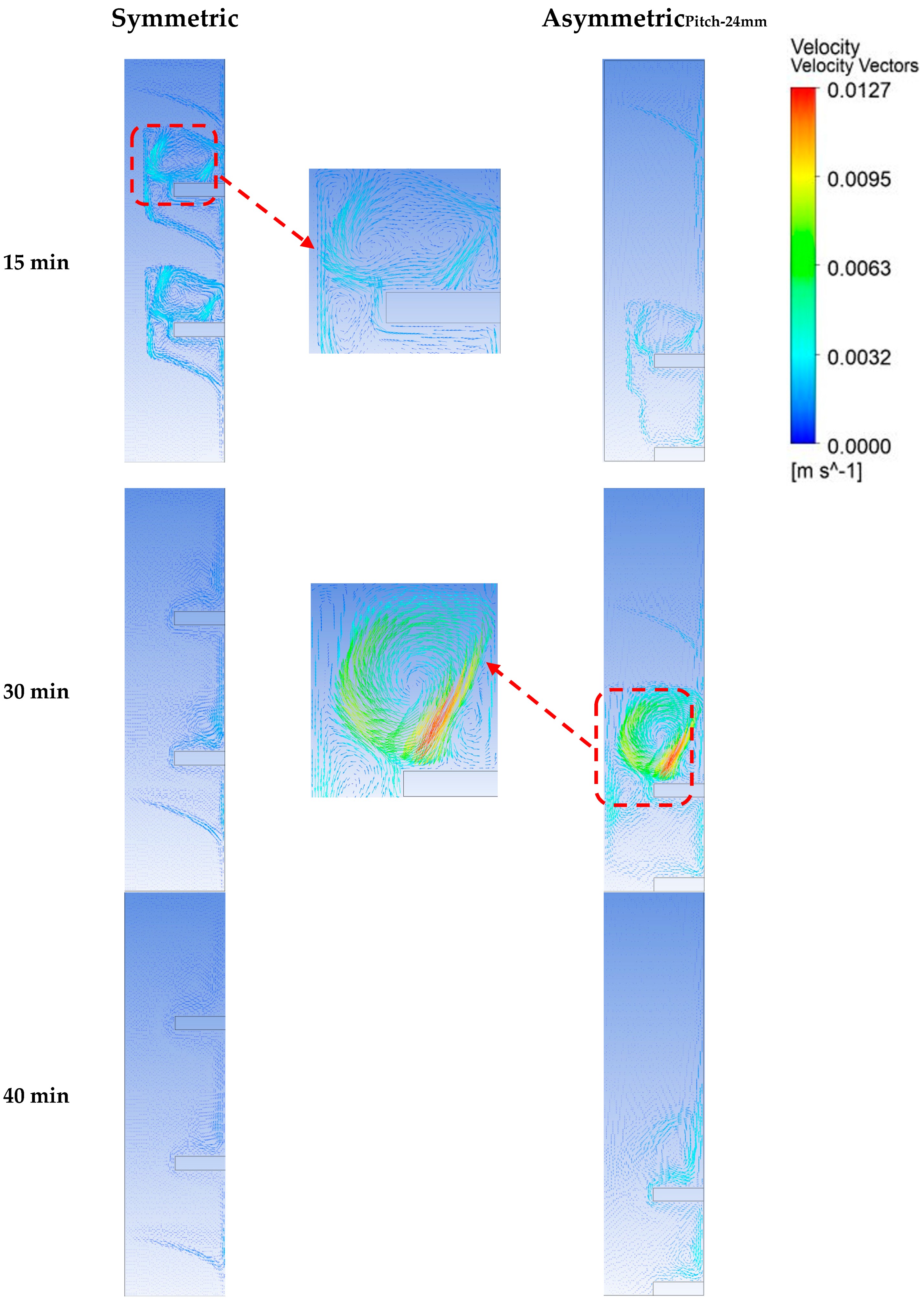
3. Results and Discussion
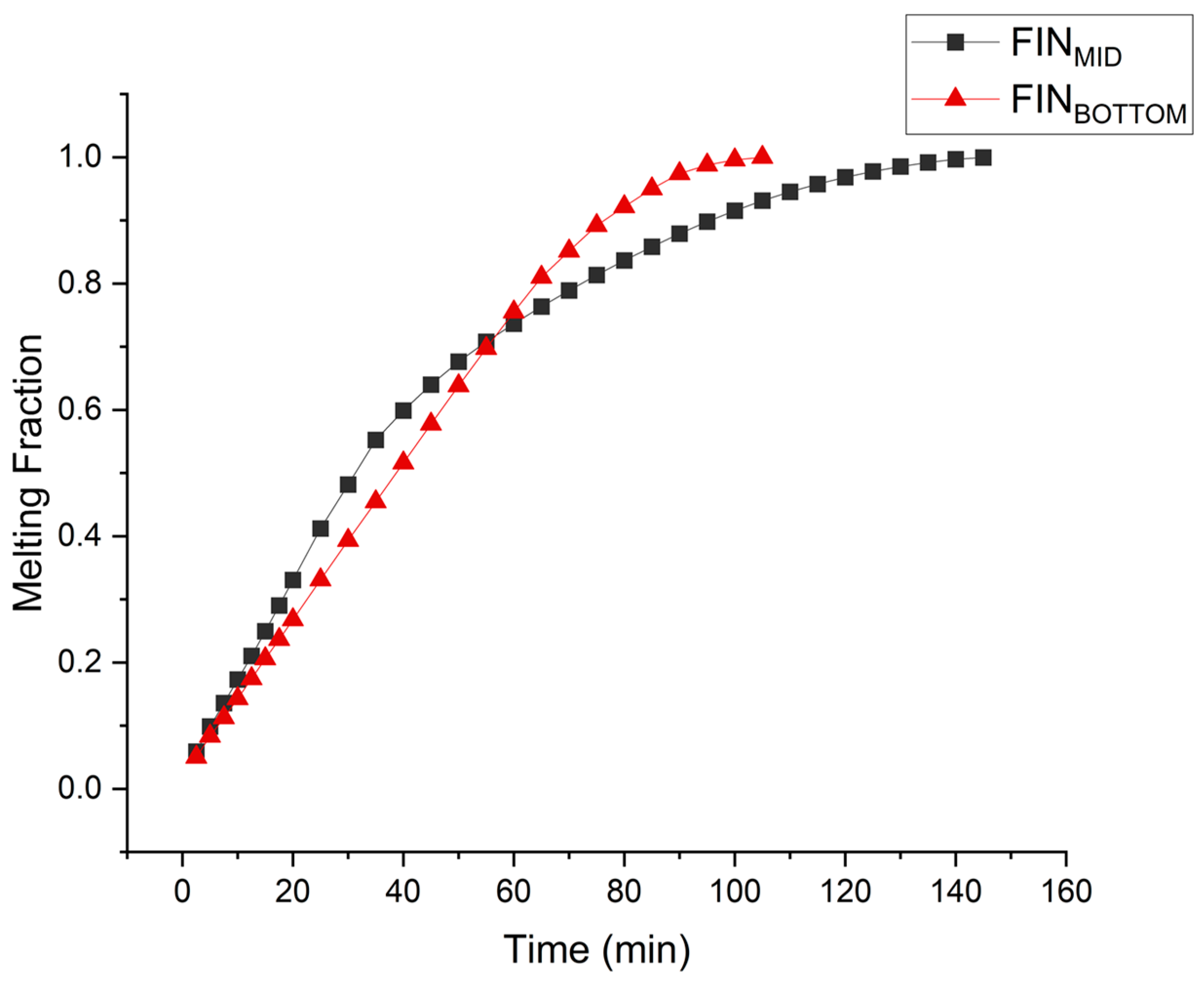
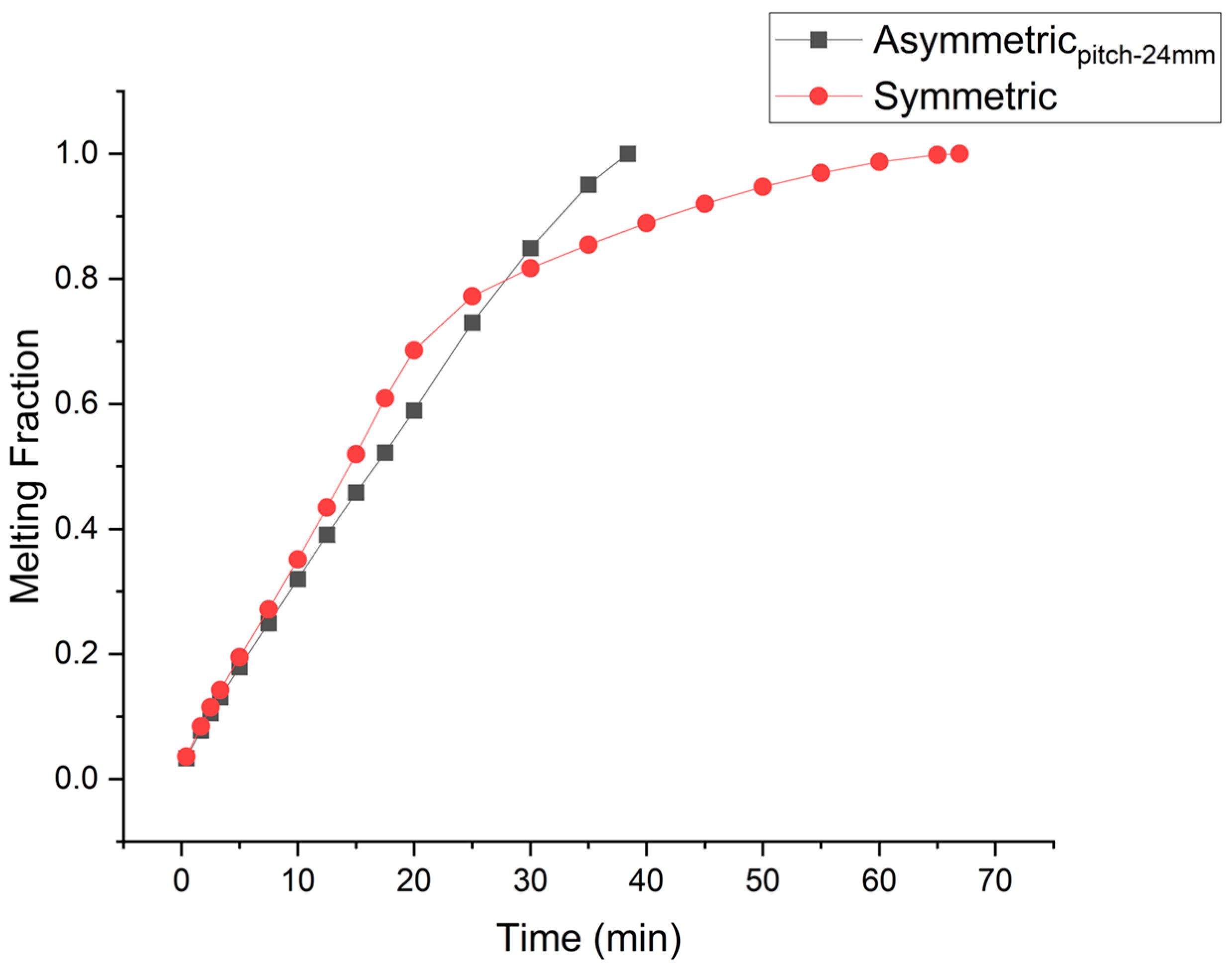
3.1. Melting Rate
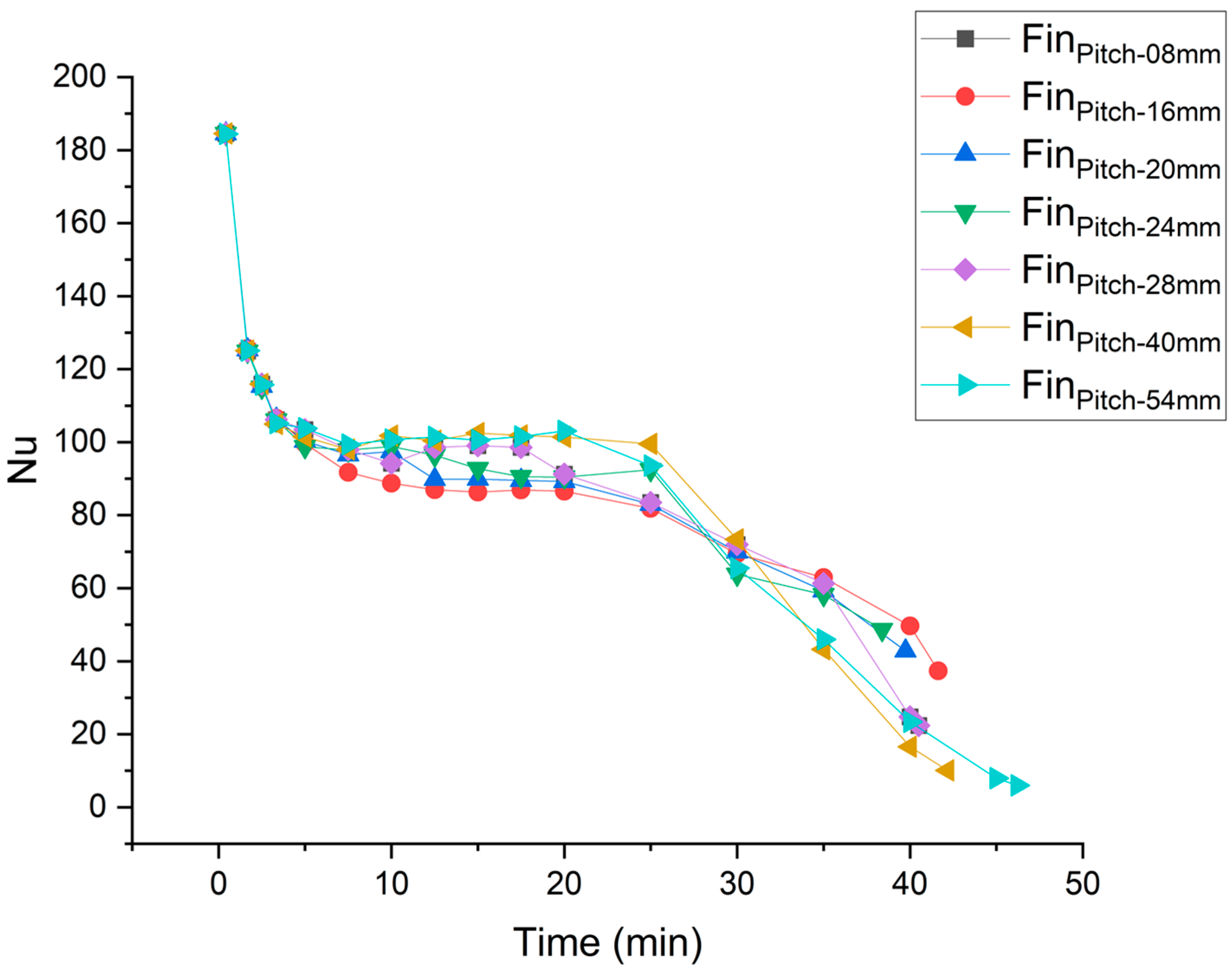
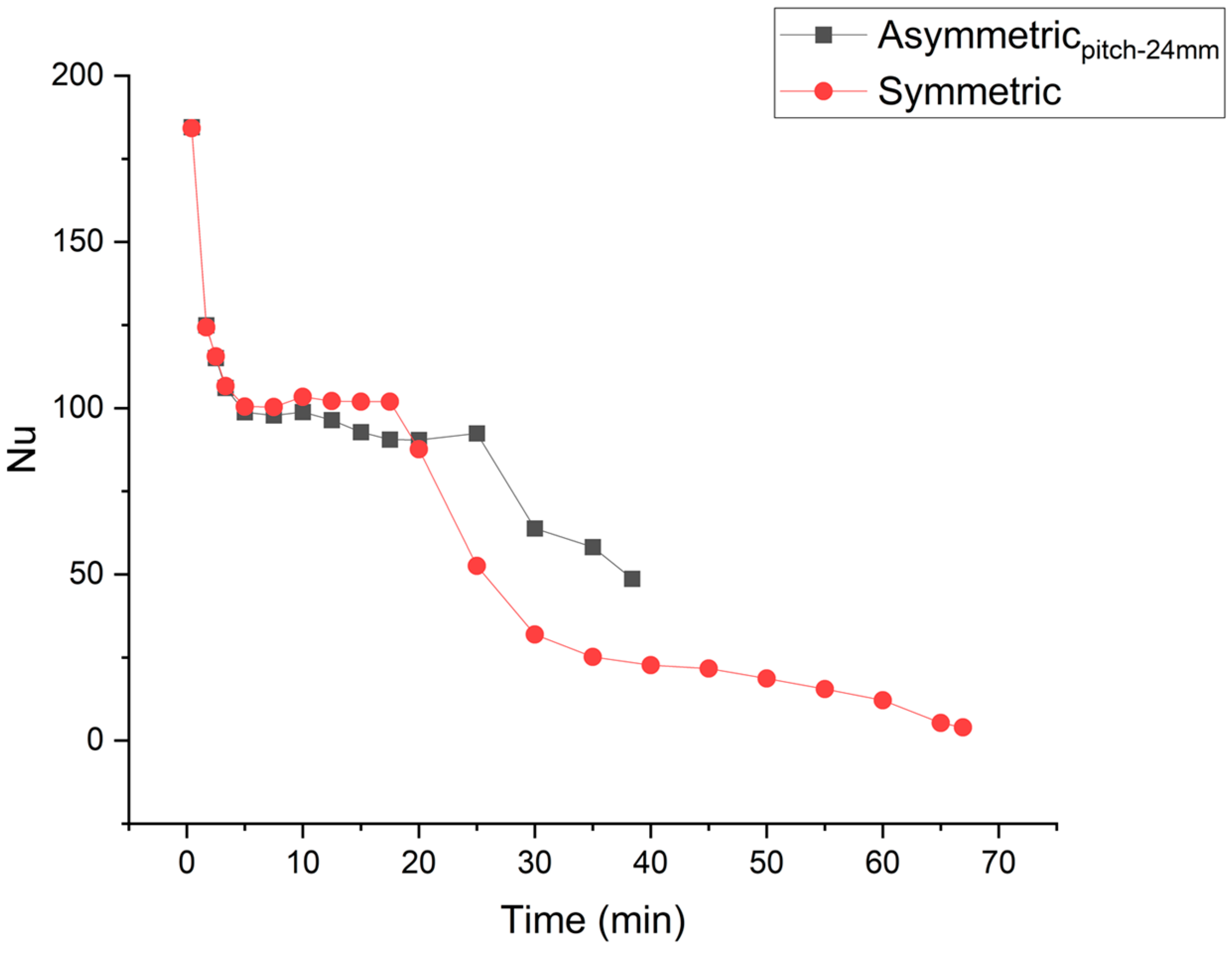
3.2. Nusselt Number
3.3. Thermal Energy Stored
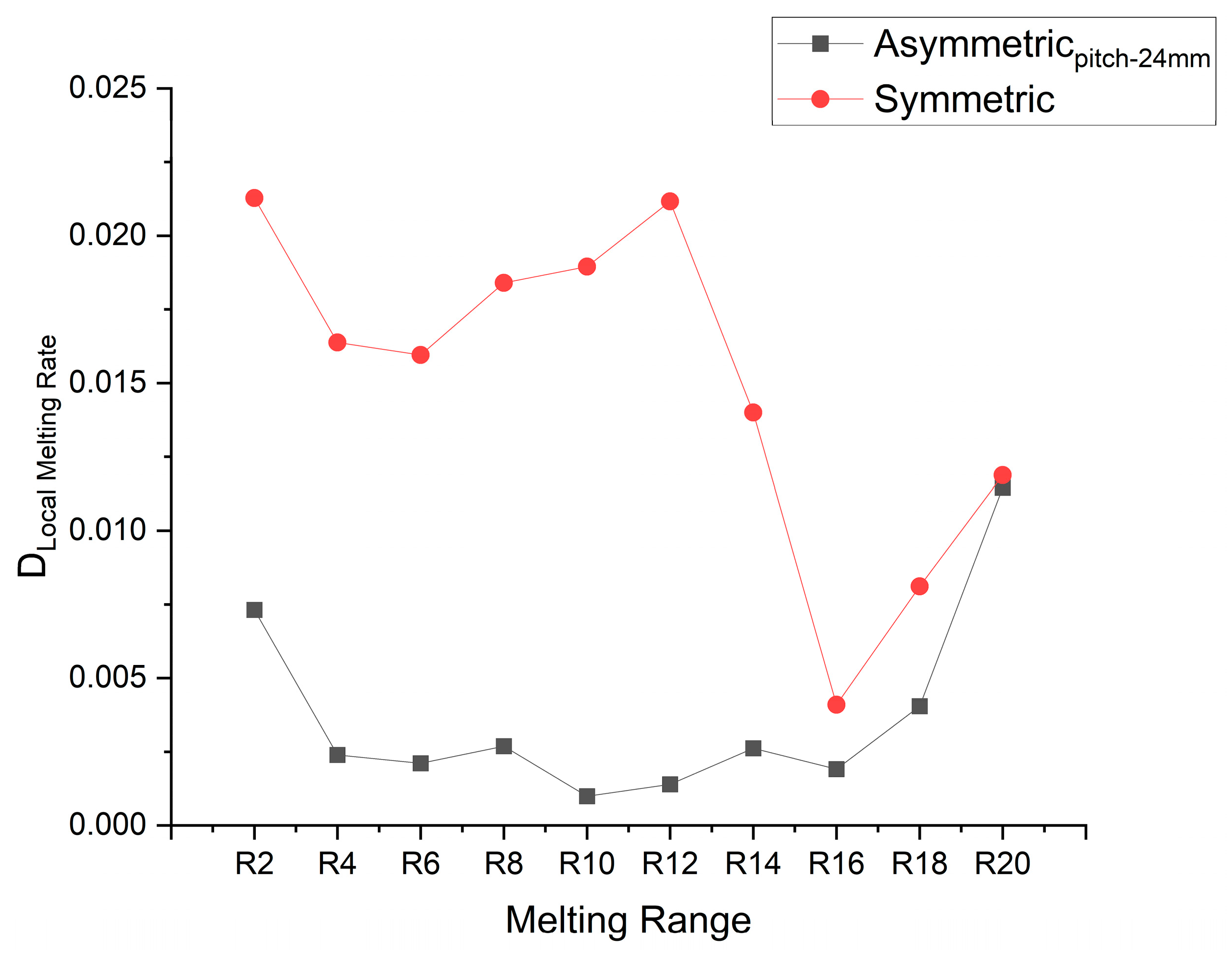
3.4. Melting Rate Uniformity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| TM | Melting temperature (K) |
| ρS | Density of solid (kg/m3) |
| ρL | Density of liquid (kg/m3) |
| CP,S | Specific heat capacity of solid PCM (J/kg·K) |
| CP,L | Specific heat capacity of liquid PCM (J/kg·K) |
| kS | Thermal conductivity of solid (W/m·K) |
| kL | Thermal conductivity of liquid (W/m·K) |
| β | Thermal Expansion Coefficient (K−1) |
| H | Total Enthalpy (J/kg) |
| HL | Latent Enthalpy (J/kg) |
| HS | Sensible Enthalpy (J/kg) |
| Nu | Nusselt Number |
| f | Melting Fraction |
References
- Zhang, S.; Zhu, Y.; Zhang, H.; Xu, F.; Sun, L.; Xia, Y.; Lin, X.; Peng, H.; Ma, L.; Li, B.; et al. Cadmium Sulfide—Reinforced Double-Shell Microencapsulated Phase Change Materials for Advanced Thermal Energy Storage. Polymers 2023, 15, 106. [Google Scholar] [CrossRef]
- Kalaiselvam, S.; Parameshwaran, R.; Harikrishnan, S. Analytical and experimental investigations of nanoparticles embedded phase change materials for cooling application in modern buildings. Renew. Energy 2012, 39, 375–387. [Google Scholar] [CrossRef]
- Motahar, S.; Nikkam, N.; Alemrajabi, A.A.; Khodabandeh, R.; Toprak, M.S.; Muhammed, M. A novel phase change material containing mesoporous silica nanoparticles for thermal storage: A study on thermal conductivity and viscosity. Int. Commun. Heat Mass Transf. 2014, 56, 114–120. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.F.; Darzi, A.A.R.; Tan, F.L. Numerical investigations of unconstrained melting of nano-enhanced phase change material (NEPCM) inside a spherical container. Int. J. Therm. Sci. 2012, 51, 77–83. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Sol. Energy 2010, 84, 1402–1412. [Google Scholar] [CrossRef]
- Baby, R.; Balaji, C. Experimental investigations on thermal performance enhancement and effect of orientation on porous matrix filled PCM based heat sink. Int. Commun. Heat Mass Transf. 2013, 46, 27–30. [Google Scholar] [CrossRef]
- Zhao, C.; Wu, Z. Heat transfer enhancement of high temperature thermal energy storage using metal foams and expanded graphite. Sol. Energy Mater. Sol. Cells 2011, 95, 636–643. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, D.; Shi, J. Experimental and numerical study on melting of phase change materials in metal foams at pore scale. Int. J. Heat Mass Transf. 2014, 72, 646–655. [Google Scholar] [CrossRef]
- Gama, N.V.; Amaral, C.; Silva, T.; Vicente, R.; Coutinho, J.A.P.; Barros-Timmons, A.; Ferreira, A. Thermal Energy Storage and Mechanical Performance of Crude Glycerol Polyurethane Composite Foams Containing Phase Change Materials and Expandable Graphite. Materials 2018, 11, 1896. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Jia, S.; Lv, G.; Yu, D. A Unique Strategy for Polyethylene Glycol/Hybrid Carbon Foam Phase Change Materials: Morphologies, Thermal Properties, and Energy Storage Behavior. Materials 2018, 11, 2011. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Shi, Z.; Zhang, B.; Huang, J. Silver Attached Graphene-Based Aerogel Composite Phase Change Material and the Enhancement of Thermal Conductivity. Materials 2020, 13, 3271. [Google Scholar] [CrossRef]
- AlOtaibi, M.; Alsuhybani, M.; Khayyat, M.; AlOtaibi, B. Performance of Nanocomposites of a Phase Change Material Formed by the Dispersion of MWCNT/TiO2 for Thermal Energy Storage Applications. Materials 2022, 15, 3063. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Zhang, D.; An, M.; Li, Z. Enhanced Thermal Performance of Composite Phase Change Materials Based on Hybrid Graphene Aerogels for Thermal Energy Storage. Materials 2022, 15, 5380. [Google Scholar] [CrossRef] [PubMed]
- Prieto, C.; Lopez-Roman, A.; Martínez, N.; Morera, J.; Cabeza, L. Improvement of Phase Change Materials (PCM) Used for Solar Process Heat Applications. Molecules 2021, 26, 1260. [Google Scholar] [CrossRef]
- Shatikian, V.; Ziskind, G.; Letan, R. Numerical investigation of a PCM-based heat sink with internal fins. Int. J. Heat Mass Transf. 2005, 48, 3689–3706. [Google Scholar] [CrossRef]
- Baby, R.; Balaji, C. Experimental investigations on phase change material based finned heat sinks for electronic equipment cooling. Int. J. Heat Mass Transf. 2012, 55, 1642–1649. [Google Scholar] [CrossRef]
- Sharifi, N.; Bergman, T.L.; Faghri, A. Enhancement of PCM melting in enclosures with horizontally-finned internal surfaces. Int. J. Heat Mass Transf. 2011, 54, 4182–4192. [Google Scholar] [CrossRef]
- Ismail, K.; Lino, F. Fins and turbulence promoters for heat transfer enhancement in latent heat storage systems. Exp. Therm. Fluid Sci. 2011, 35, 1010–1018. [Google Scholar] [CrossRef]
- Baby, R.; Balaji, C. Thermal optimization of PCM based pin fin heat sinks: An experimental study. Appl. Therm. Eng. 2013, 54, 65–77. [Google Scholar] [CrossRef]
- Akhilesh, R.; Narasimhan, A.; Balaji, C. Method to improve geometry for heat transfer enhancement in PCM composite heat sinks. Int. J. Heat Mass Transf. 2005, 48, 2759–2770. [Google Scholar] [CrossRef]
- Qin, Z.; Ji, C.; Low, Z.H.; Tong, W.; Wu, C.; Duan, F. Geometry effect of phase change material container on waste heat recovery enhancement. Appl. Energy 2022, 327, 120108. [Google Scholar] [CrossRef]
- Huang, B.; Yang, S.; Wang, J.; Lund, P.D. Optimizing the shape of PCM container to enhance the melting process. Oxf. Open Energy 2022, 1, oiab006. [Google Scholar] [CrossRef]
- Kamkari, B.; Shokouhmand, H.; Bruno, F. Experimental investigation of the effect of inclination angle on convection-driven melting of phase change material in a rectangular enclosure. Int. J. Heat Mass Transf. 2014, 72, 186–200. [Google Scholar] [CrossRef]
- Zhao, J.; Zhai, J.; Lu, Y.; Liu, N. Theory and experiment of contact melting of phase change materials in a rectangular cavity at different tilt angles. Int. J. Heat Mass Transf. 2018, 120, 241–249. [Google Scholar] [CrossRef]
- Al Siyabi, I.; Khanna, S.; Mallick, T.; Sundaram, S. An experimental and numerical study on the effect of inclination angle of phase change materials thermal energy storage system. J. Energy Storage 2019, 23, 57–68. [Google Scholar] [CrossRef]
- Deng, Y.; Xu, J.; Li, Y.; Zhang, Y.; Kuang, C. Study of the Phase-Change Thermal-Storage Characteristics of a Solar Collector. Materials 2022, 15, 7497. [Google Scholar] [CrossRef]
- Gharebaghi, M.; Sezai, I. Enhancement of Heat Transfer in Latent Heat Storage Modules with Internal Fins. Int. J. Comput. Methodol. Numer. Heat Transfer Part A Appl. 2007, 53, 749–765. [Google Scholar] [CrossRef]
- Huang, M.; Eames, P.; Norton, B.; Hewitt, N. Natural convection in an internally finned phase change material heat sink for the thermal management of photovoltaics. Energy 2011, 95, 1598–1603. [Google Scholar] [CrossRef]
- Mahdi, M.S.; Mahood, H.B.; Campbell, A.N.; Khadom, A.A. Natural convection improvement of PCM melting in partition latent heat energy storage: Numerical study with experimental validation. Int. Commun. Heat Mass Transf. 2021, 126, 105463. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.; Tan, F.; Moosania, S. Experimental and numerical studies on performance of PCM-based heat sink with different configurations of internal fins. Appl. Therm. Eng. 2011, 31, 3827–3838. [Google Scholar] [CrossRef]
- Dmitruk, A.; Naplocha, K.; Grzęda, J.; Kaczmar, J.W. Aluminum Inserts for Enhancing Heat Transfer in PCM Accumulator. Materials 2020, 13, 415. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Mohammed, H.I.; Naghizadeh, A.; Islam, M.S.; Younis, O.; Mahdi, J.M.; Chatroudi, I.S.; Talebizadehsardari, P. Optimum Placement of Heating Tubes in a Multi-Tube Latent Heat Thermal Energy Storage. Materials 2021, 14, 1232. [Google Scholar] [CrossRef] [PubMed]
- Kamkari, B.; Shokouhmand, H. Experimental investigation of phase change material melting in rectangular enclosures with horizontal partial fins. Int. J. Heat Mass Transf. 2014, 78, 839–851. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Low, Z.; Dubeya, S.; Chooa, F.H.; Duan, F. Non-uniform heat transfer suppression to enhance PCM melting by angled. Appl. Therm. Eng. 2017, 129, 269–279. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Kamkari, B. Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 2013, 50, 201–212. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Groulx, D. The effect of the mushy-zone constant on simulated phase change heat transfer. In Proceedings of the CHT-15. 6th International Symposium on Advances in Computational Heat Transfer, New Brunswick, NJ, USA, 25–29 May 2015. [Google Scholar] [CrossRef]





| 316 K | |
| 940 kg/m3 | |
| 885 kg/m3 | |
| 2,180 J/kg K | |
| 2,390 J/kg K | |
| 0.16 W/m K | |
| 0.14 W/m K | |
| 0.0008 K−1 | |
| 187,200 J/kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaban, M.; Khan, T.I.; Anwar, M.; Alzaid, M.; Alanazi, R. Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit. Materials 2023, 16, 2567. https://doi.org/10.3390/ma16072567
Shaban M, Khan TI, Anwar M, Alzaid M, Alanazi R. Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit. Materials. 2023; 16(7):2567. https://doi.org/10.3390/ma16072567
Chicago/Turabian StyleShaban, Muhammad, Talha Irfan Khan, Muhammad Anwar, Meshal Alzaid, and Rakan Alanazi. 2023. "Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit" Materials 16, no. 7: 2567. https://doi.org/10.3390/ma16072567
APA StyleShaban, M., Khan, T. I., Anwar, M., Alzaid, M., & Alanazi, R. (2023). Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit. Materials, 16(7), 2567. https://doi.org/10.3390/ma16072567






