A New Theoretical Method for Studying Effects of Microstructure on Effective Thermal Conductivity of Vermicular Graphite Cast Iron
Abstract
1. Introduction
2. Methods
2.1. Computational Methods
2.2. Experimental Methods
3. Results and Discussion
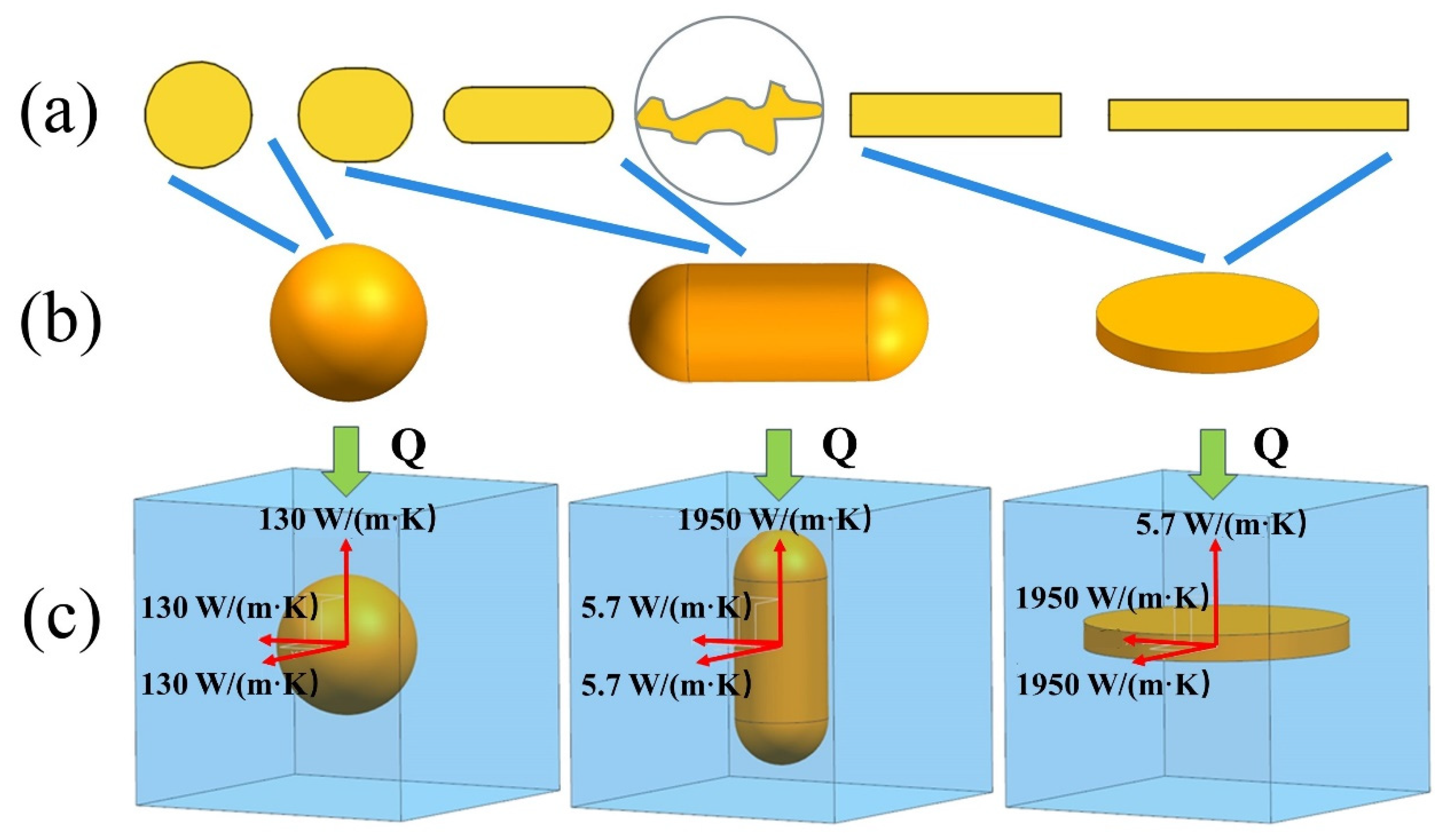
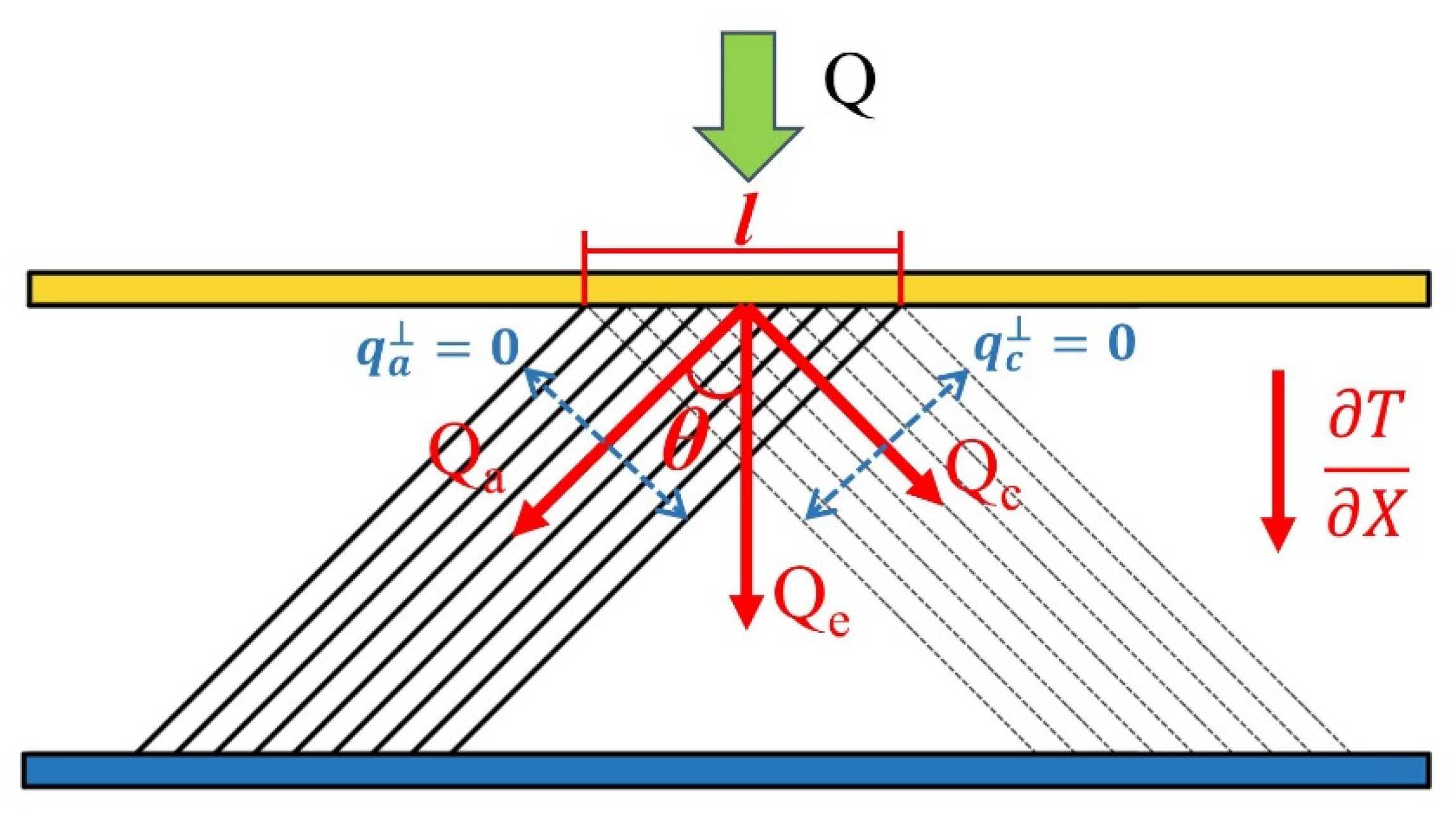
3.1. Basis of Theoretical Model
3.2. Effects of Microstructure on Effective Thermal Conductivity
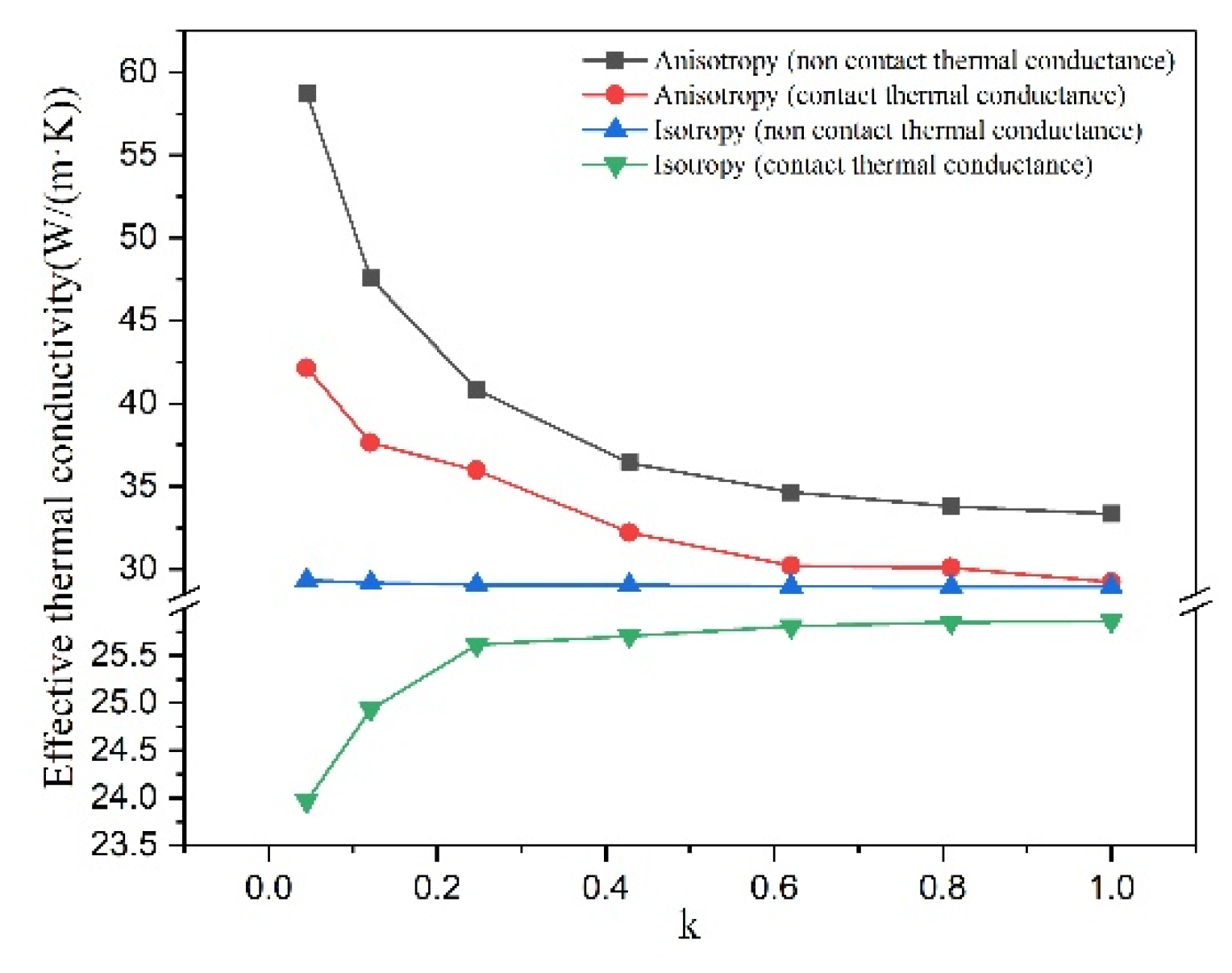
3.2.1. Anisotropy of Graphite and Interface between Graphite and Matrix
3.2.2. Graphite Shape Parameter
3.2.3. Graphite Volume Fraction
3.2.4. Thermal Conductivity of Matrix
3.3. Establishment of Quantitative Model and Verification
4. Conclusions
- (1)
- The effective thermal conductivity of VGI increases in power function with the decrease in graphite shape parameter, and increases linearly with the increase in graphite volume fraction and thermal conductivity of matrix.
- (2)
- The change in graphite shape affects both graphite anisotropy and area of interface. The more the graphite shape deviates from the sphere, the greater the enhancement effect of graphite anisotropy on thermal conductivity than the hindrance effect of interface. These two effects are close when the graphite is spherical type.
- (3)
- A quantitative model was built to predict the effective thermal conductivity of VGI, which was suitable for the vermicularity of 0–100%.
- (4)
- The experimental results are in good agreement with the model calculations, and the error is about 3%. This proves the rationality of the models and assumptions adopted in the theoretical method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.X.; Zhang, G.W.; Xu, H. Homogeneity Research on Microstructure and Properties of Vermicular Graphite Cast Iron. Hot Work. Technol. 2014, 43, 27–30. [Google Scholar]
- Wang, X.X.; Zhou, J.R.; Su, W. Casting of Cylinder Block and Cylinder Head of Engine. J. Netshape Form. Eng. 2010, 2, 79–86. [Google Scholar]
- Zhang, M.X.; Pang, J.C.; Qiu, Y.; Li, S.X.; Wang, M.; Zhang, Z.F. Thermo-mechanical fatigue property and life prediction of vermicular graphite iron. Mater. Sci. Eng. A 2017, 698, 63–72. [Google Scholar] [CrossRef]
- Soeudy, R.I.E. The effect of graphite aspect ratio on the mechanical and microstructural properties of cast iron. Mater. Und Werkst. 2002, 33, 73–79. [Google Scholar] [CrossRef]
- Riposan, L.; Chisamera, M.; Stan, S. New developments in high quality grey cast Irons. China Foundry 2014, 11, 351–364. [Google Scholar]
- Zhang, M.X.; Pang, J.C.; Meng, L.J.; Li, S.X.; Liu, Q.; Jiang, A.L.; Zhang, Z.F. Study on thermal fatigue behaviors of two kinds of vermicular graphite cast irons. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2021, 814, 141212. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, Z.; Guo, Y.; Tao, D.; Li, J.; Wang, S. 3d morphology characterization of graphite and its effect on the thermal conductivity of vermicular graphite iron. Int. J. Mater. Res. 2019, 110, 591–599. [Google Scholar] [CrossRef]
- Mroz, M.; Orlowicz, A.W.; Tupaj, M.; Jacek-Burek, M.; Radon, M.; Kawinski, M. The effect of structure on thermal power of cast-iron heat exchangers. Arch. Foundry Eng. 2020, 20, 27–30. [Google Scholar]
- Selin, M.; Holmgren, D.; Svensson, I.L. Influence of alloying additions on microstructure and thermal properties in compact graphite irons. Int. J. Cast Met. Res. 2009, 22, 283–285. [Google Scholar] [CrossRef]
- Lopez-Covaleda, E.A.; Ghodrat, S.; Kestens, L.A.; Sacre, C.H.; Pardoen, T. Proposal of characterization procedure of metal-graphite interfac strength in compacted graphite iron. Materials 2018, 11, 1159. [Google Scholar] [CrossRef] [PubMed]
- Ming, P.; Tan, W. Numerical simulation of stress field of laser phase transformation hardening vermicular graphite cast iron based on beam discretization. Laser Optoelectron. Prog. 2019, 56, 231403. [Google Scholar] [CrossRef]
- Wang, G.-Q.; Liu, Z.-L.; Li, Y.-X.; Chen, X. Different thermal fatigue behaviors between gray cast iron and vermicular graphite cast iron. China Foundry 2022, 19, 245–252. [Google Scholar] [CrossRef]
- Holmgren, D. Review of thermal conductivity of cast iron. Int. J. Cast. Met. Res. 2005, 18, 331–345. [Google Scholar] [CrossRef]
- Witik, R.A.; Payet, J.; Michaud, V.; Ludwig, C.; Månson, J.A. Assessing the life cycle costs and environmental performance of lightweight materials in automobile applications. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1694–1709. [Google Scholar] [CrossRef]
- Helsing, J.; Grimvall, G. Thermal conductivity of cast iron: Models and analysis of experiments. J. Appl. Phys. 1991, 70, 1198–1206. [Google Scholar] [CrossRef]
- Wang, G.H.; Li, Y.X. Calculating the effective thermal conductivity of gray cast iron by using an interconnected graphite model. China Foundry 2020, 17, 5–11. [Google Scholar] [CrossRef]
- Selin, M.; Konig, M. Regression analysis of thermal conductivity based on measurements of compacted graphite irons. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2009, 40, 3235–3244. [Google Scholar] [CrossRef]
- Ma, Z.; Tao, D.; Yang, Z.; Guo, Y.; Li, J.; Liang, M.; Yeung, L.T.L. The effect of vermicularity on the thermal conductivity of vermicular graphite cast iron. Mater. Des. 2016, 93, 418–422. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J.; Yang, Z.; Ma, Z.; Guo, Y.; Tao, D.; Yang, T.; Liang, M. Computational Assessment of Thermal Conductivity of Compacted Graphite Cast Iron. Adv. Mater. Sci. Eng. 2019, 2019, 1–7. [Google Scholar] [CrossRef]
- Ma, Z.J.; Wen, Q.; Gao, P.H.; Yang, Z.; Guo, Y.C.; Li, J.P.; Liang, M.X. Experimental assessment of interfacial contact thermal conductance between graphite and matrix in cast iron. Int. J. Cast Met. Res. 2017, 31, 1–7. [Google Scholar] [CrossRef]
- Velichko, A.; Wiegmann, A.; Mücklich, F. Estimation of the effective conductivities of complex cast iron microstructures using FIB tomographic analysis. Acta Mater. 2009, 57, 5023–5035. [Google Scholar] [CrossRef]
- Velichko, A.; Holzapfel, C.; Muecklich, F. 3D characterization of graphite morphologies in cast iron. Adv. Eng. Mater. 2007, 9, 39–45. [Google Scholar] [CrossRef]
- Gao, B.Z.; Xu, J.Z.; Peng, J.J.; Kang, F.Y.; Du, H.D.; Li, J.; Chiang, S.W.; Xu, C.J.; Hu, N.; Ning, X.S. Experimental and theoretical studies of effective thermal conductivity of composites made of silicone rubber and Al2O3 particles. Thermochim. Acta 2015, 614, 1–8. [Google Scholar] [CrossRef]
- Kidalov, S.V.; Shakhov, F.M. Thermal Conductivity of Diamond Composites. Materials 2009, 2, 2467–2495. [Google Scholar] [CrossRef]
- Matsushita, T.; Saro, A.G.; Elmquist, L.; Jarfors, A.E.W. On the thermal conductivity of CGI and SGI cast irons. Int. J. Cast Met. Res. 2018, 31, 135–143. [Google Scholar] [CrossRef]
- Hasselman, D.; Johnson, L.F. Effective Thermal Conductivity of Composites with Interfacial Thermal Barrier Resistance. J. Compos. Mater. 1987, 21, 508–515. [Google Scholar] [CrossRef]
- Hatta, H.; Taya, M.; Kulacki, F.; Harder, J. Thermal diffusivities of composites with various types of filler. J. Compos. Mater. 1992, 26, 612–625. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Xu, J.Z.; Gao, B.Z.; Kang, F.Y. A reconstruction of Maxwell model for effective thermal conductivity of composite materials. Appl. Therm. Eng. 2016, 102, 972–979. [Google Scholar] [CrossRef]
- Tewary, U.; Paul, D.; Mehtani, H.K.; Bhagavath, S.; Alankar, A.; Mohapatra, G.; Sahay, S.S.; Panwar, A.S.; Karagadde, S.; Samajdar, I. The Origin of Graphite Morphology in Cast Iron. Acta Mater. 2022, 226, 117660. [Google Scholar] [CrossRef]
- Armstrong, M.A. Basic Topology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Deissler, R.G.; Boegli, J.S. An investigation of effective thermal conductivities of powders in various gases. ASME Trans. 1958, 80, 1417–1425. [Google Scholar] [CrossRef]
- Qian, L.; Pang, X.; Zhou, J.; Yang, J.; Lin, S.; Hui, D. Theoretical model and finite element simulation on the effective thermal conductivity of particulate composite materials. Compos. Part B Eng. 2017, 116, 291–297. [Google Scholar] [CrossRef]
- Ljustina, G.; Larsson, R.; Fagerström, M. A FE based maching simulation methodology accounting for cast iron microstructure. Finite Elem. Anal. Des. 2014, 80, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; An, C.G.; He, Y.Z.; Li, H. Structure and properties of graphite microspheres containing ferromagnetic metal prepared by acid corrosion of cast iron. J. Mater. Eng. Perform. 2014, 23, 4446–4452. [Google Scholar] [CrossRef]
- Liu, Y.; Xing, J.; Li, Y.; Sun, L.; Wang, Y. A first principles study of adhesion and electronic structure at Fe (110)/graphite (0001) interface. Appl. Surf. Sci. 2017, 405, 497–502. [Google Scholar] [CrossRef]
- Xu, D.M.; Wang, G.Q.; Chen, X.; Li, Y.X.; Liu, Y.; Zhang, H.W. Effects of alloy elements on ductility and thermal conductivity of compacted graphite iron. China Foundry 2018, 15, 189–195. [Google Scholar] [CrossRef]
- Stefanescu, D.M.; Alonso, G.; Larranaga, P.; De la Fuente, E.; Suarez, R. On the crystallization of graphite from liquid iron–carbon–silicon melts. Acta Mater. 2016, 107, 102–126. [Google Scholar] [CrossRef]
- Lin, X.; Hua, M.; Tian, X.; Jiang, A.; Li, S.; Zhang, X.; Song, L.; Shao, A.; Wang, L. Growth mechanisms of vermicular graphite in cast iron. Mater. Today Commun. 2021, 29, 102993. [Google Scholar] [CrossRef]
- Amini, S.; Abbaschian, R. Nucleation and growth kinetics of graphene layers from a molten phase. Carbon 2013, 51, 110–123. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, F.; Bi, K.; Yang, J.; Chen, Y. Tuning the interfacial thermal conductance via the anisotropic elastic properties of graphite. Carbon 2019, 144, 109–115. [Google Scholar] [CrossRef]
- Wang, G.H.; Li, Y.X. Thermal conductivity of cast iron—A review. China Foundry 2020, 17, 29–39. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Zhang, X.F.; Sun, Y.C.; Jiang, A.L.; Li, J.C.; Zheng, H.L.; Tian, X.L. Quantitative models for microstructure and thermal conductivity of vermicular graphite cast iron cylinder block based on cooling rate. China Foundry 2021, 18, 52–59. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Xing, J.; Wang, S.; Zheng, B.; Tao, D.; Li, W. Effect of graphite morphology on the tensile strength and thermal conductivity of cast iron. Mater. Charact. 2018, 144, 155–165. [Google Scholar] [CrossRef]




| v = = 130 | 28.60 | 25.86 | 13.20 |
| v = = 130 | 45.87 | 36.17 | 11.61 |
| Parameters | Valuation |
|---|---|
| Size of unit cell model | 80 × 80 × 80 |
| Number of calculation angles | 1061 |
| Steps of mesh generation | 100 × 100 × 100 |
| Graphite volume fraction | v = 4–10% |
| Thermal conductivity of isotropic graphite (spherical type) | = 130 W/(m·K) |
| Thermal conductivity of anisotropic graphite (capsule-based type and disc type) | = 5.7 W/(m·K) |
| Thermal conductivity of matrix | = 25–40 W/(m·K) |
| Thermal conductivity of interface | = 10−6 W/(m·K) |
| Thickness of interface | T = 10−9 m |
| 553 × 553 × 707 μm3 | v | k | W/(m·K) | Experimental Value [43] W/(m·K) | Predicted Value W/(m·K) | Error % |
|---|---|---|---|---|---|---|
| specimen 1 | 0.060 | 0.145 | 25 | 38.904 | 39.689 | 2.017 |
| specimen 2 | 0.042 | 0.150 | 25 | 34.951 | 35.737 | 2.248 |
| specimen 3 | 0.043 | 0.145 | 25 | 36.095 | 36.144 | 0.135 |
| 599 × 599 × 839 μm3 | v | k | W/(m·K) | Experimental Value W/(m·K) | Predicted Value W/(m·K) | Error % |
|---|---|---|---|---|---|---|
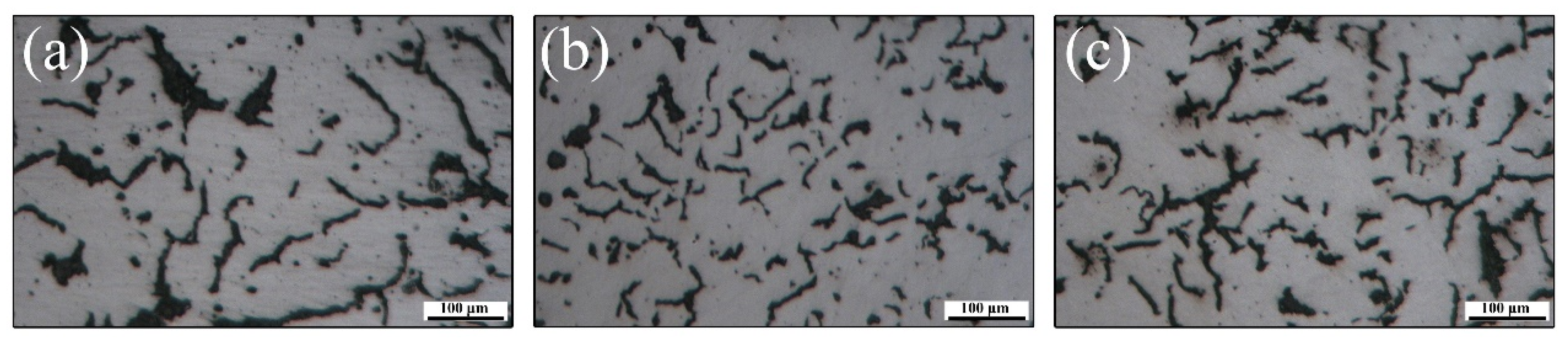
| (a) | 0.0998 | 0.428 | 7.02 | 23.65 | 23.75 | 0.42 |
| (b) | 0.0999 | 0.407 | 7.02 | 24.47 | 24.20 | 1.10 |
| (c) | 0.1029 | 0.250 | 7.02 | 28.16 | 29.04 | 3.13 |
| (d) | 0.1032 | 0.246 | 7.02 | 29.95 | 29.24 | 2.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, A.; Shao, A.; Song, L.; Hua, M.; Zheng, H.; Zhang, X.; Tian, X.; Lin, X. A New Theoretical Method for Studying Effects of Microstructure on Effective Thermal Conductivity of Vermicular Graphite Cast Iron. Materials 2023, 16, 2158. https://doi.org/10.3390/ma16062158
Jiang A, Shao A, Song L, Hua M, Zheng H, Zhang X, Tian X, Lin X. A New Theoretical Method for Studying Effects of Microstructure on Effective Thermal Conductivity of Vermicular Graphite Cast Iron. Materials. 2023; 16(6):2158. https://doi.org/10.3390/ma16062158
Chicago/Turabian StyleJiang, Ailong, Anchen Shao, Lin Song, Minghao Hua, Hongliang Zheng, Xiaofu Zhang, Xuelei Tian, and Xiaohang Lin. 2023. "A New Theoretical Method for Studying Effects of Microstructure on Effective Thermal Conductivity of Vermicular Graphite Cast Iron" Materials 16, no. 6: 2158. https://doi.org/10.3390/ma16062158
APA StyleJiang, A., Shao, A., Song, L., Hua, M., Zheng, H., Zhang, X., Tian, X., & Lin, X. (2023). A New Theoretical Method for Studying Effects of Microstructure on Effective Thermal Conductivity of Vermicular Graphite Cast Iron. Materials, 16(6), 2158. https://doi.org/10.3390/ma16062158








