Thermodynamic Relationships for Perfectly Elastic Solids Undergoing Steady-State Heat Flow
Abstract
:1. Introduction
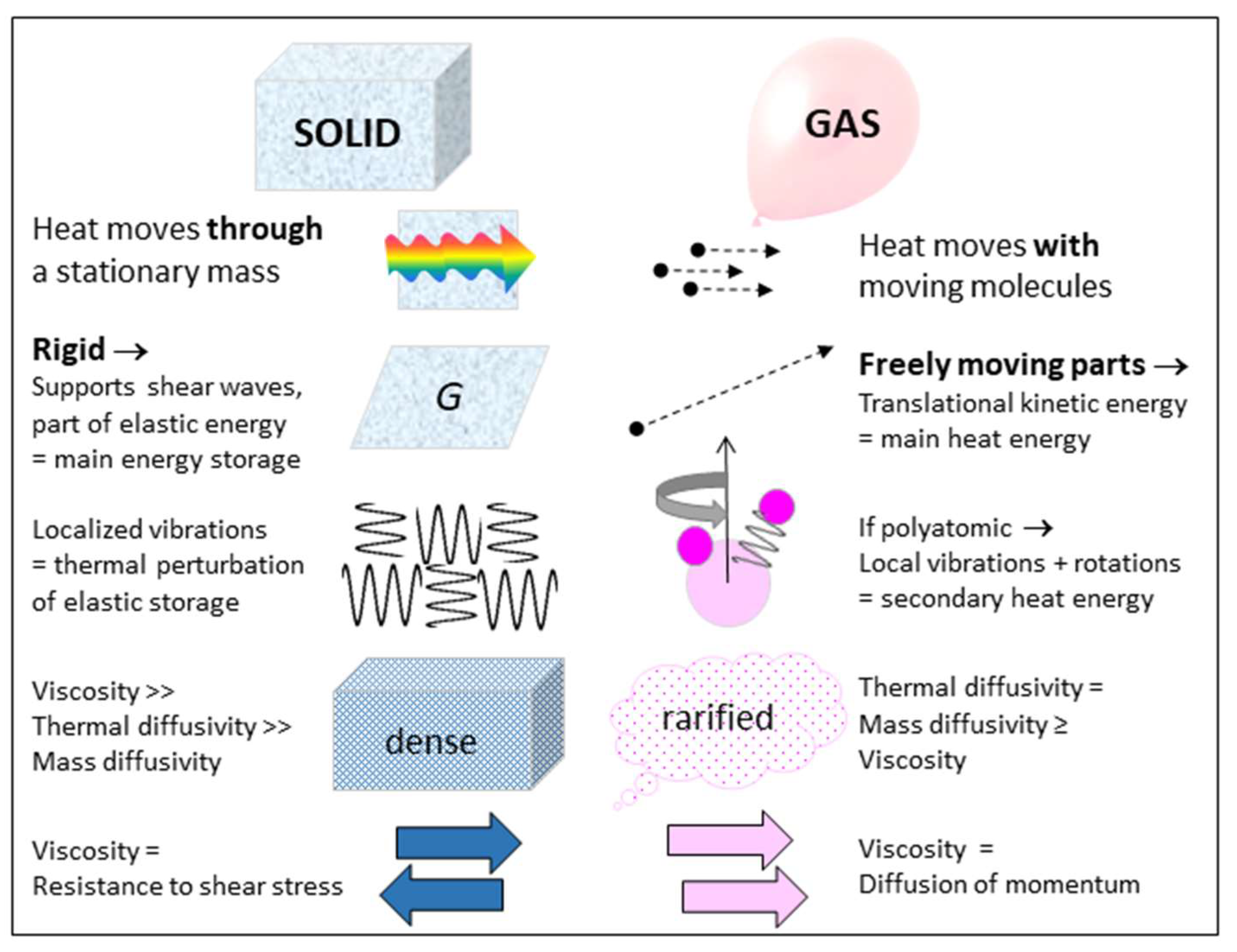
1.1. Different Behaviors of Solids and Gases May Affect Thermostatic Equations
1.2. Purpose and Limitations of the Paper
1.3. Organization of the Paper and Key Results
2. Theoretical Description of Solids Conducting Heat in Steady State
2.1. Link of Temperature to Heat Flux
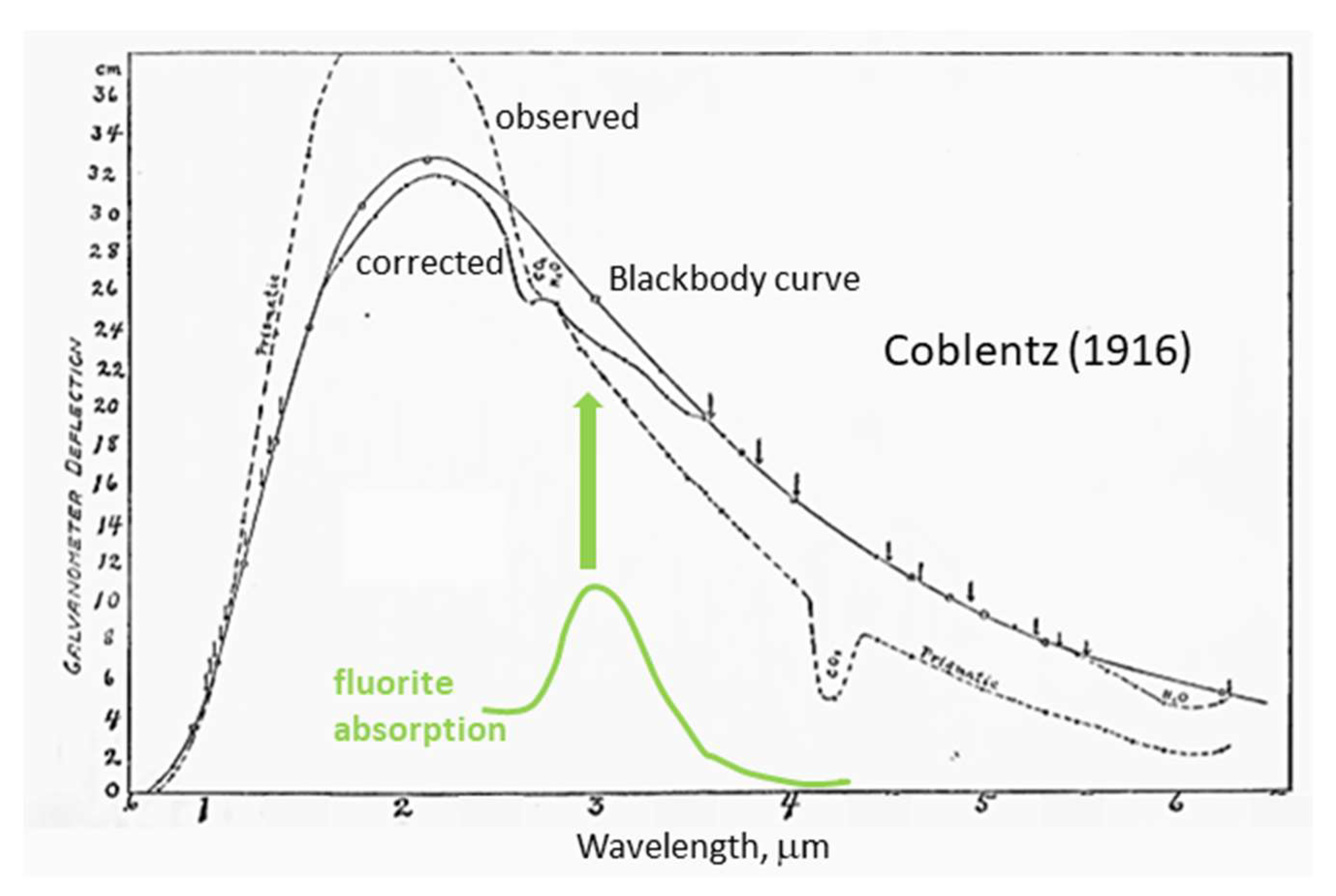
2.1.1. Wien’s Law
2.1.2. Repercussions of Temperature Depending on Emitted Flux and Spectral Properties
- The hallmark of a hot dense body is that it emits heat over a wide spectral range (Figure 2). This unavoidable loss signifies that its state is dynamic, not static.
- Temperature governs the total flux emitted, with the following caveat:
- Because thermal emissions depend on the spectral properties of the material, Q may also depend on characteristics beyond the static physical properties considered in the historical model.
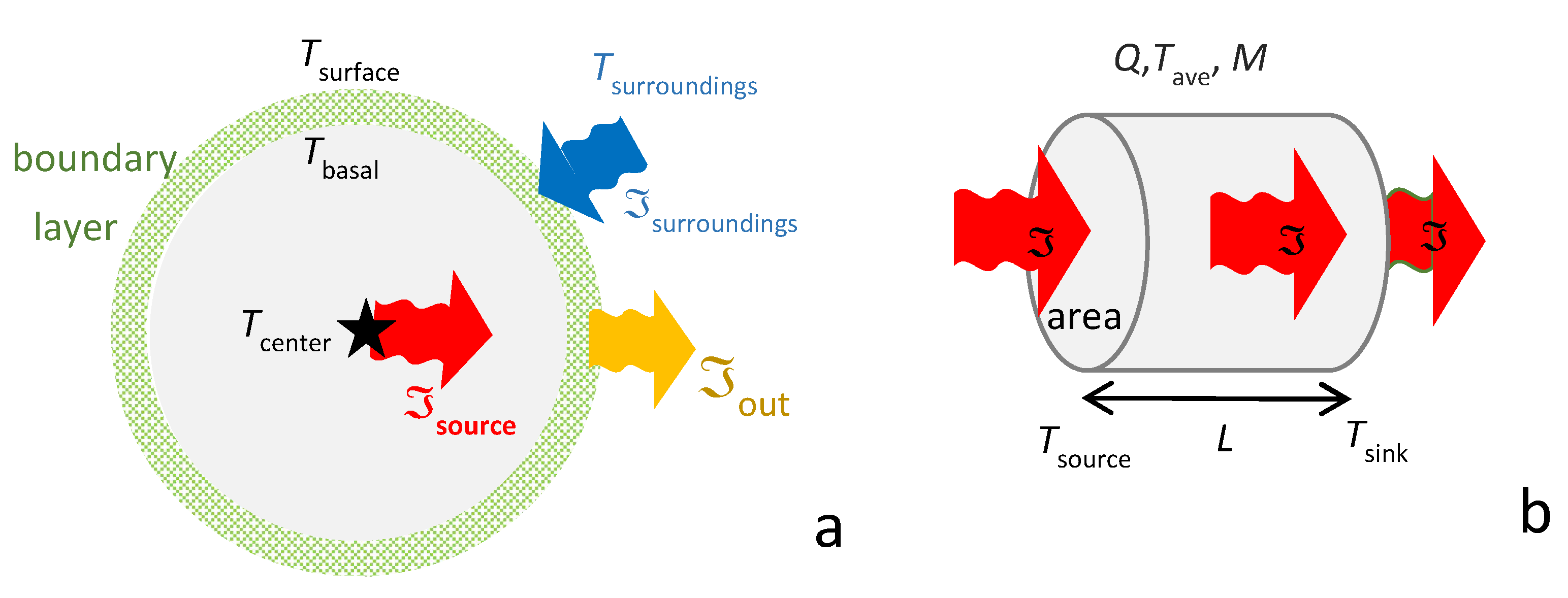
2.2. Connection of Steady-State Behavior with Coincident Adiabatic and Isothermal Conditions
2.2.1. Spherical Coordinates
2.2.2. Longitudinal Flow in Cylindrical Geometry and in Cartesian Systems
2.3. Equations of State, Elastic Behavior, and Work
2.3.1. Classical Definitions and Their Link to Mathematical Constraints
2.3.2. Rigidity and Its Relationship to EOS Formulations for Solids
2.3.3. Irrelevance of Friction to a Static Model and Implications for Work-Heat Relations
2.3.4. Connection of the EOS with Perfectly Frictionless Elastic Behavior
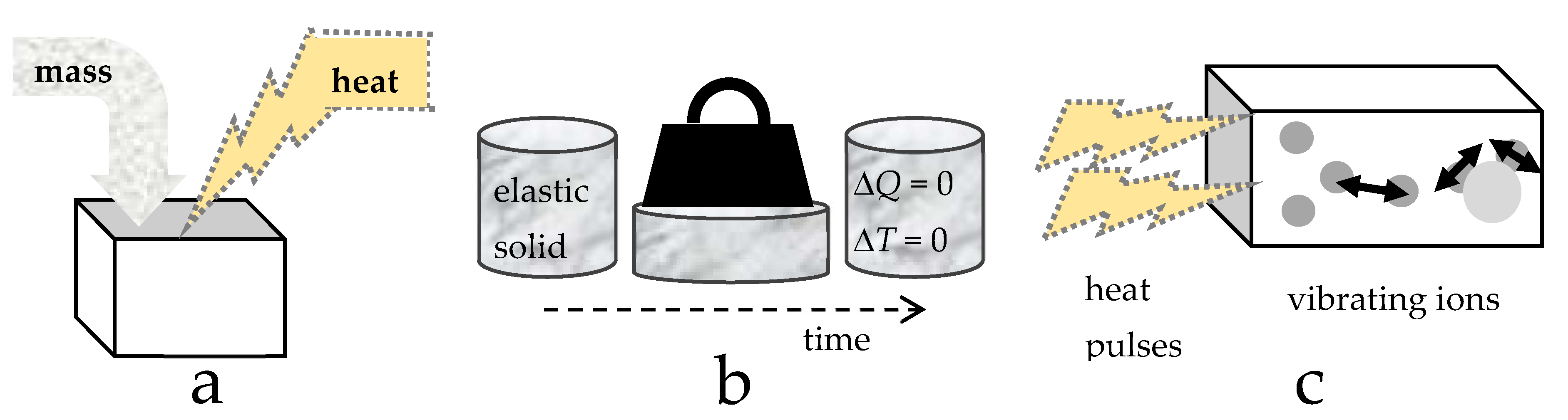
- The perfectly frictionless elastic approximation is static: time is not involved and systems are fully restorable. That is, the ideal system is reversible (Figure 4b), although in a real system changes are made via manipulating and changing the surroundings.
- Because reversibility of the system and an instantaneous response to changing conditions are central to the PFES approximation, adding heat to the system has no effect other than raising temperature, after which P and/or V respond, in accord with imposed experimental constraints and the EOS. The time-dependent nature of heat uptake (Section 2.3.5) explains why this is the driver of change.
- Independence of mass and heat (Figure 4) and conservative behavior require separate treatment of variables related to mass occupying space (i.e., the EOS and shear modulus, G, which governs shape) and to heat occupying space (i.e., the heat content Q, storativity C, or a specific heat). Yet, the latter three parameters may depend on the size of the box (V), and thus on P (or T) conditions, as well as on B (or α) which describe volumetric changes.
2.3.5. Uptake of Heat during Frictionless Elastic Behavior

2.3.6. Why Rigid Solids under Steady State Have One Bulk Modulus
2.3.7. Young’s Modulus and Work in a PFES
2.4. Behavior of Heat in Perfectly Frictionless Elastic Solids during Steady-State Conduction
2.4.1. Specific Heat Definitions
2.4.2. Incremental Responses for a PFES
2.4.3. Pressure Derivatives of Specific Heat during Steady State
2.4.4. Pressure Derivatives of Storativity during Steady State
2.4.5. Temperature Derivative of Specific Heat during Steady State from Stefan’s Law
2.4.6. Heat Uptake Provides Non-Dissipative Work
2.4.7. Ratio of Specific Heats
3. Evaluation of New and Old Formulations via Comparison with Experimental Data
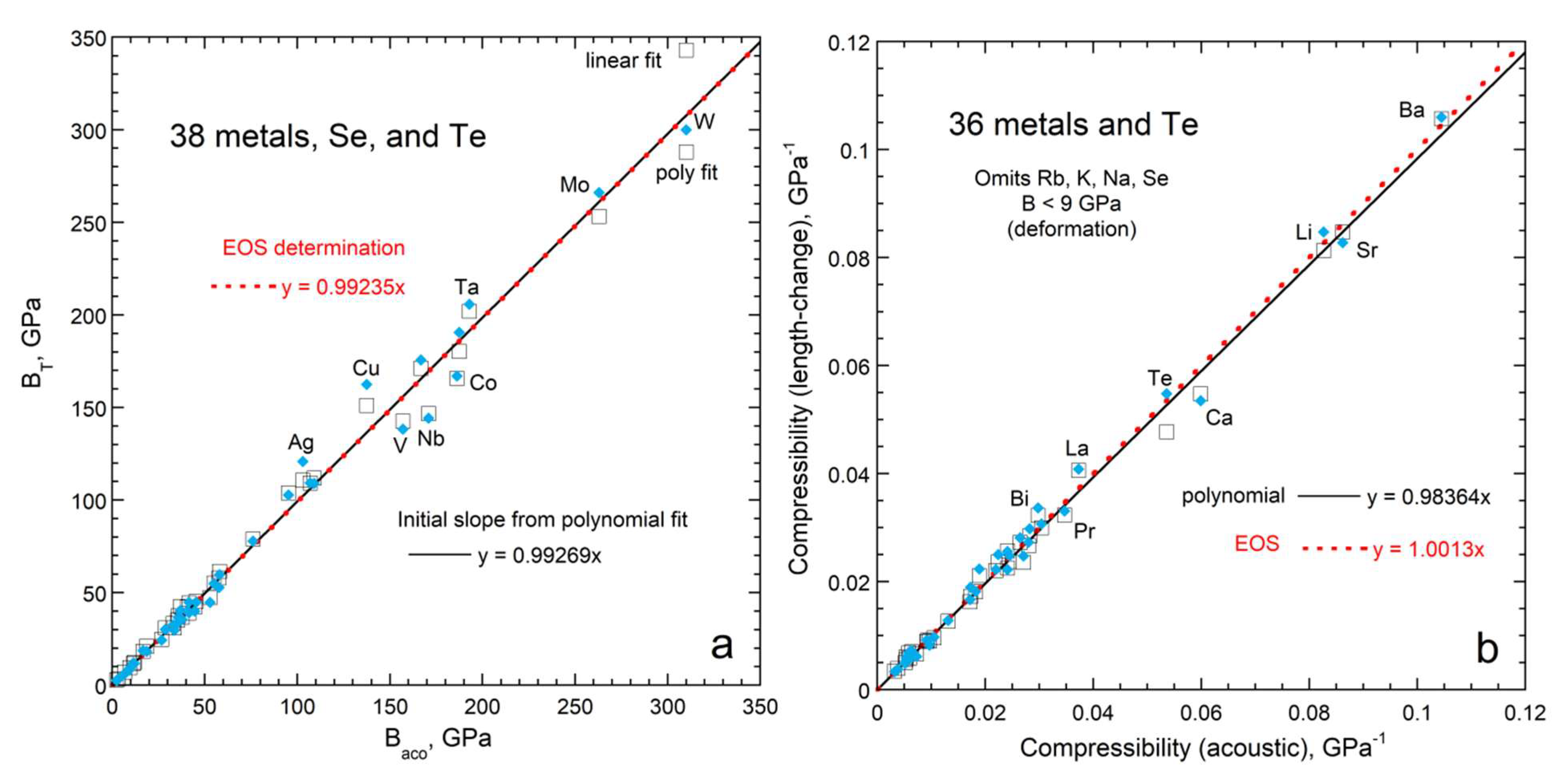
3.1. Comparison of Bulk Moduli from Acoustic and Volumetric Studies
3.1.1. Techniques
3.1.2. Bulk Moduli for Solids at NTP

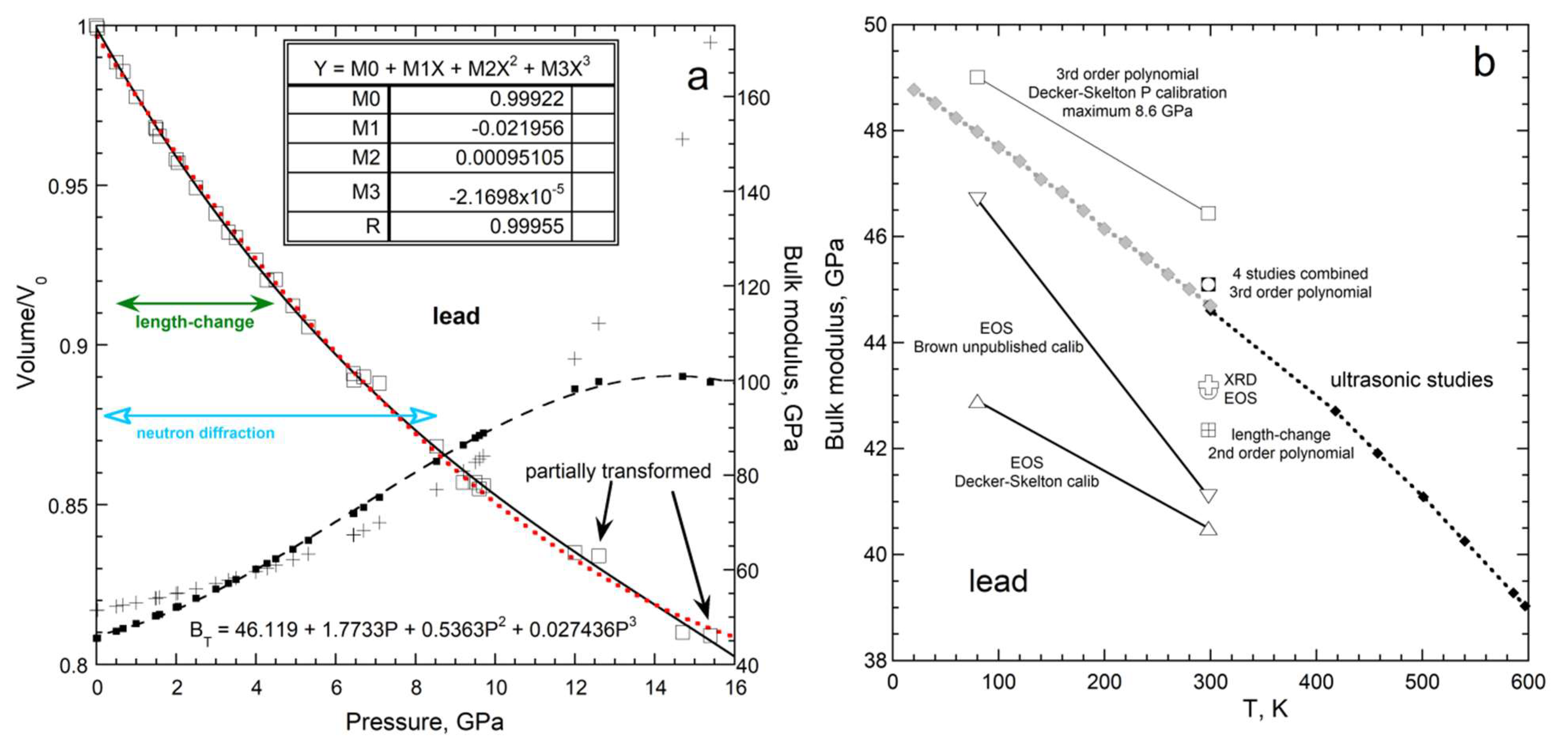
3.1.3. Uncertainty in Bulk Moduli Arising from Fitting Volume vs. Pressure
3.1.4. Comparison of Acoustic to XRD Determinations of ∂B/∂T for Solids
3.2. Response of Heat Capacity at NTP to Compression
3.2.1. Static Compression Techniques
3.2.2. Dynamic Compression Techniques
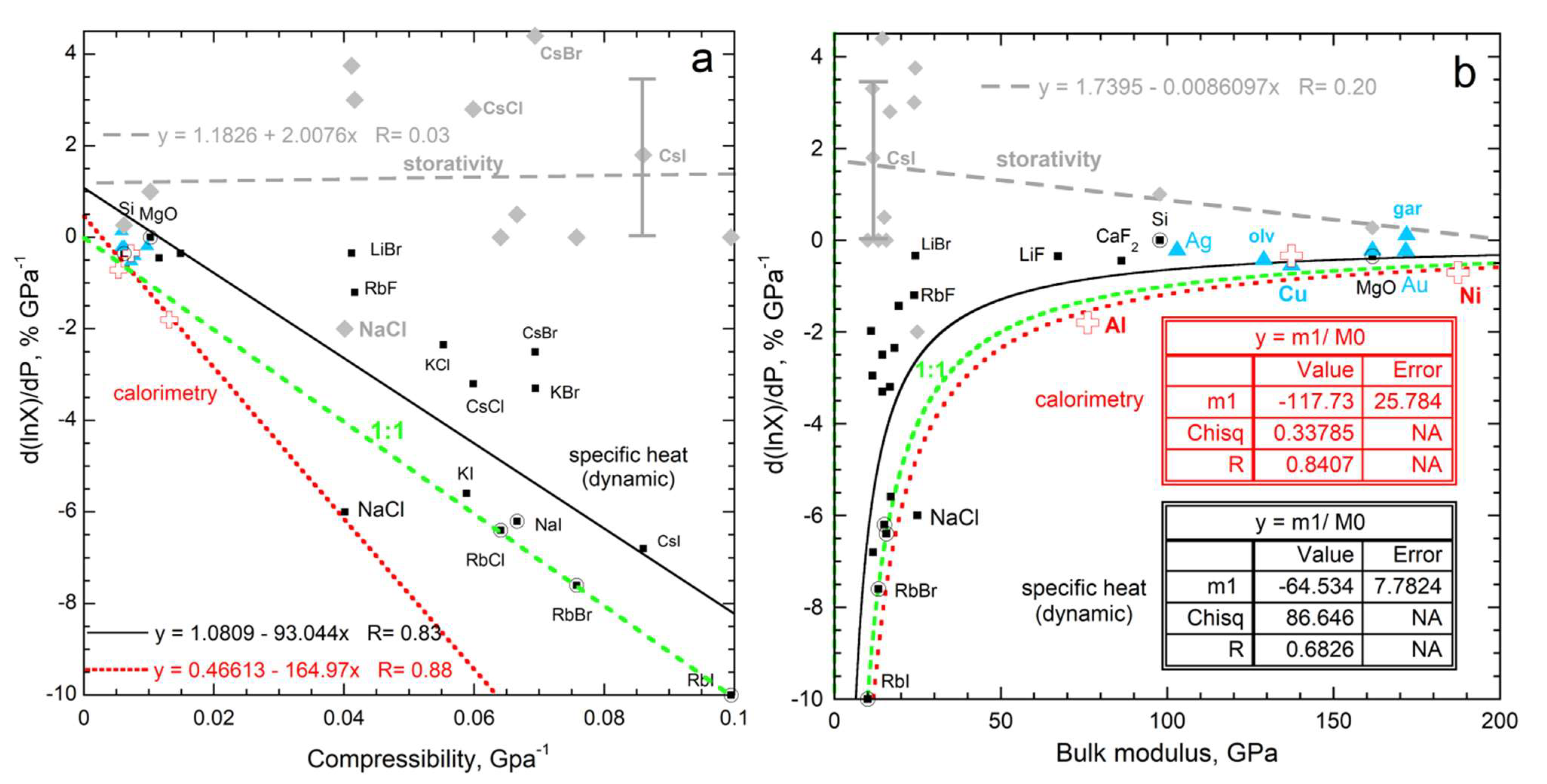
3.2.3. Relationship of the Pressure Response of Specific Heat and Storativity to Bulk Moduli
3.2.4. Evaluation of the Historic Relationship of the Pressure Response of Specific Heat to Thermal Expansivity
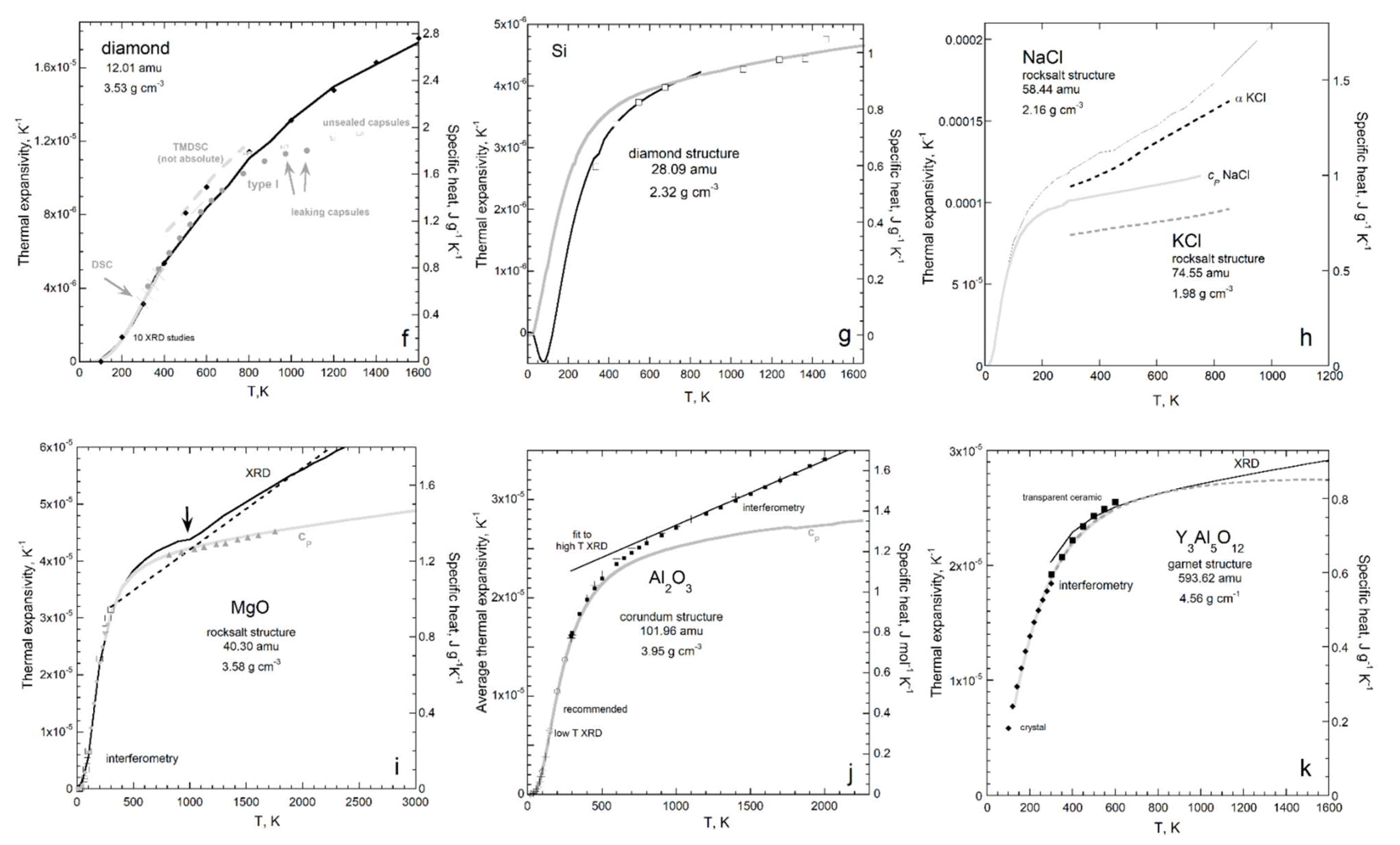
3.3. Connection of Thermal Expansion to Heat Uptake and Internal Strength
3.3.1. Ambient Temperature
3.3.2. Temperature from a Few Kelvins to Nearly Melting
4. Discussion and Implications
- Only one bulk modulus exists, so the historically alleged difference between acoustic and volumetric moduli is unsupported. Likewise, the isothermal and adiabatic values for the 2nd Grüneisen parameter (Equation (14)) must be identical.
- Changes in heat content with pressure are controlled by the compressibility, which dominates changes in specific heat at moderate laboratory temperatures.
- Changes in heat content with temperature are described by specific heat by definition. Specific heat and thermal expansivity are linked, as the process of increasing V involves overcoming the elastic, tensile forces within the solid. Deformation solely occurs as shape changes arising from shear stresses uptake energy without expansion, confirmed by comparison of results from Equation (46) to Poisson’s ratio for cubic solids. If heat stimulates other processes, expansion is reduced as in Fe, or even reversed, as in Si.
4.1. Heat Storage Reservoirs and Permissible Exchanges of Energy
4.2. Key Variables
4.3. Reservoirs vs. Historic State Functions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Nordstrom, D.K.; Munoz, J.L. Geochemical Thermodynamics; Blackwell Scientific: Palo Alto, CA, USA, 1986. [Google Scholar]
- Norton, J.D. The impossible process: Thermodynamic reversibility. Stud. Hist. Philos. Mod. Phys. 2016, 55, 43–61. [Google Scholar] [CrossRef] [Green Version]
- Hofmeister, A.M. Measurements, Mechanisms, and Models of Heat Transport; Elsevier: Amsterdam, The Netherlands, 2019; Chapters 1 and 7. [Google Scholar]
- Purrington, R.D. Physics in the Nineteenth Century; Rutgers University Press: New Brunswick, NJ, USA, 1997. [Google Scholar]
- Truesdell, C. The Tragicomical History of Thermodynamics; Springer: New York, NY, USA, 1980. [Google Scholar]
- Pippard, A.B. The Elements of Classical Thermodynamics; Cambridge University Press: London, UK, 1974. [Google Scholar]
- Hofmeister, A.M. Dependence of Heat Transport in Solids on Length-scale, Pressure, and Temperature: Implications for Mechanisms and Thermodynamics. Materials 2021, 14, 449. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D.C. Thermodynamics of Crystals; John-Wiley and Sons Inc.: New York, NY, USA, 1972. [Google Scholar]
- Hofmeister, A.M.; Criss, E.M. How properties that distinguish solids from fluids and constraints of spherical geometry suppress lower mantle convection. J. Earth Sci. 2018, 29, 1–20. [Google Scholar] [CrossRef]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics, 6th ed.; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Bates, J.B. Infrared emission spectroscopy. Fourier Transform IR Spect. 1978, 1, 99–142. [Google Scholar]
- Coblentz, W.W. Constants of spectral radiation of a uniformly heated enclosure or so-called blackbody. II. Bull. Bur. Stand. 1916, 13, 459–477. [Google Scholar] [CrossRef]
- Williams, B.W. A specific mathematical form for Wien’s displacement law as νmax/T = constant. J. Chem. Educ. 2014, 91, 623. [Google Scholar] [CrossRef]
- Valluri, S.R.; Corless, R.M.; Jeffrey, D.J. Some applications of the Lambert W function to physics. Can. J. Phys. 2000, 78, 823–831. [Google Scholar]
- Henderson, J.B.; Giblin, F.; Blumm, J.; Hagemann, L. SRM 1460 series as a thermal diffusivity standard for laser flash instruments. Int. J. Thermophys. 1998, 19, 1647–1656. [Google Scholar] [CrossRef]
- Hearmon, R.F.S. The elastic constants of anisotropic materials. Revs. Mod. Phys. 1946, 18, 409–440. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Mao, H.K. Redefinition of the mode Gruneisen parameter for polyatomic substances and thermodynamic implications. Proc. Natl. Acad. Sci. USA 2002, 99, 559–564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-86675-0. [Google Scholar]
- Zener, C. Internal friction in solids II. General theory of thermoelastic internal friction. Phys. Rev. 1938, 53, 90–99. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic Press, Inc.: San Diego, CA, USA, 1972. [Google Scholar]
- Criss, E.M.; Hofmeister, A.M. Isolating lattice from electronic contributions in thermal transport measurements of metals and alloys and a new model. Int. J. Mod. Phys. B 2017, 31, 1750205. [Google Scholar] [CrossRef] [Green Version]
- Mitra, S.S. Infrared and Raman Spectra due to lattice vibrations. In Optical Properties of Solids; Nudelman, S., Mitra, S.S., Eds.; Plenum Press: New York, NY, USA, 1969; pp. 333–451. [Google Scholar]
- Harris, D.C.; Bertolucci, M.D. Symmetry and Spectroscopy; Oxford University Press: New York, NY, USA, 1978. [Google Scholar]
- Burns, G. Solid State Physics; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Hofmeister, A.M.; Dong, J.J.; Branlund, J.M. Thermal diffusivity of electrical insulators at high temperatures: Evidence for diffusion of phonon-polaritons at infrared frequencies augmenting phonon heat conduction. J. Appl. Phys. 2014, 115, 163517. [Google Scholar] [CrossRef]
- Marr, J.M.; Wilkin, F.P. A better presentation of Planck’s radiation law. Am. J. Phys. 2012, 80, 339–405. [Google Scholar] [CrossRef] [Green Version]
- Bodryakov, V.Y. Correlation of Temperature Dependences of Thermal Expansion and Heat Capacity of Refractory Metal up to the Melting Point: Tungsten. High Temp. 2015, 53, 643–648. [Google Scholar] [CrossRef]
- Bodryakov, V.Y.; Bykov, A.A. Correlation characteristics of the volumetric thermal expansion coefficient and specific heat of corundum. Glass Ceram. 2015, 72, 67–70. [Google Scholar] [CrossRef]
- Bodryakov, V.Y. Correlation of temperature dependencies of thermal expansion and heat capacity of refractory metal up to the melting point: Molybdenum. High Temp. 2014, 52, 840–845. [Google Scholar] [CrossRef]
- Bodryakov, V.Y. Correlation between temperature dependences of thermal expansivity and heat capacity up to the melting point of tantalum. High Temp. 2016, 54, 316–321. [Google Scholar] [CrossRef]
- Vaidya, S.N.; Kennedy, G.C. Compressibility of 18 metals to 45 kbar. J. Phys. Chem. Solids 1970, 31, 2329–2345. [Google Scholar]
- Knittle, E. Static compression measurements of equations of state. In Mineral Physics and Crystallography. A Handbook of Physical Constants; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; Volume 2, pp. 98–142. [Google Scholar]
- Beyer, R.T.; Letcher, S.V. Physical Ultrasonics; Academic Press: London, UK, 1969; Chapter 8. [Google Scholar]
- Vacher, R.; Boyer, L. Brillouin scattering: A tool for the measurement of elastic and photoelastic constants. Phys. Rev. B 1972, 6, 639–673. [Google Scholar] [CrossRef]
- Ledbetter, H.M. Elastic properties of zinc: A compilation and a review. J. Phys. Chem. Ref. Data 1997, 6, 1181–1203. [Google Scholar] [CrossRef] [Green Version]
- Guinan, M.W.; Steinberg, D.J. Pressure and temperature derivatives of the isotropic polycrystalline shear modulus for 65 elements. J. Phys. Chem. Solids 1974, 35, 1501–1512. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Kirby, R.K.; Taylor, R.E.; Desai, P.D. Thermal Expansion: Metallic Elements and Alloys; IFI/Plenum: New York, NY, USA, 1975. [Google Scholar]
- Vold, C.L.; Glicksman, M.E.; Kammer, E.W.; Cardinal, L.C. The elastic constants for single-crystal lead and indium from room temperature to the melting point. Phys. Chem. Solids 1977, 38, 157–170. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Buyco, E.H. Specific Heat: Metallic Elements and Alloys; IFI/Plenum: New York, NY, USA, 1970. [Google Scholar]
- McSkimin, H.J. Measurement of elastic constants at low temperatures by means of ultrasonic waves–data for silicon and germanium single crystals, and for fused silica. J. Appl. Phys. 1953, 24, 988–997. [Google Scholar] [CrossRef]
- Bass, J.D. Elasticity of minerals, glasses, and melts. In Mineral Physics and Crystallography. A Handbook of Physical Constants; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; Volume 2, pp. 29–44. [Google Scholar]
- Leger, J.M.; Haines, J.; Atouf, A.; Schulte, O. High-pressure X-ray- and neutron-diffraction studies of BaF2: An example of a coordination number of 11 in AX2 compounds. Phys. Rev. B 1995, 52, 13247–13256. [Google Scholar] [CrossRef] [PubMed]
- Fiquet, G.; Guyot, F.; Itie, J.-P. High-pressure X-ray diffraction study of carbonates: MgCO3, CaMg(CO3)2, and CaCO3. Am. Mineral. 1994, 79, 15–23. [Google Scholar]
- Zhang, L. Single crystal hydrostatic compression of (Mg,Mn,Fe,Co)2SiO4 olivines. Phys Chem. Miner. 1998, 25, 308–312. [Google Scholar] [CrossRef]
- Sumino, Y.; Anderson, O.L. Elastic constants of minerals. In CRC Handbook of Physical Properties of Rocks; Carmichael, R.S., Ed.; CRC Press, Inc.: Boca Raton, FL, USA, 1984; Volume 3, pp. 39–139. [Google Scholar]
- Vaidya, S.N.; Getting, I.C.; Kennedy, G.C. The compression of the alkali metals to 45 kbar. J. Phys. Chem. Solids 1971, 32, 2545–2556. [Google Scholar] [CrossRef]
- Vaidya, S.N.; Kennedy, G.C. Compressibility of 22 elemental solids to 45 kbar. J. Phys. Chem. Solids 1972, 33, 1377–1389. [Google Scholar] [CrossRef]
- Schulte, O.; Holzapfel, W. Equation-of-state behavior for different phases of lead under strong compression. Phys. Rev. B 1995, 53, 12636–12639. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.K.; Bell, P.M. Study of lead at high pressure: Compressibility and fixed-point transition between the FCC and HCP po1ymorphs under various degrees of non-hydrostatic stress. Year Book 1978, 77, 842–848. [Google Scholar]
- Vohra, Y.K.; Ruoff, A.L. Static compression of metals Mo, Pb, and Pt to 272 GPa: Comparison with shock data. Phys. Rev. B 1990, 42, 8651–8654. [Google Scholar] [CrossRef]
- Strässle, T.; Klotz, S.; Kunc, K.; Pomjakushin, V.; White, J.S. Equation of state of lead from high-pressure neutron diffraction up to 8.9 GPa and its implication for the NaCl pressure scale. Phys. Rev. B 2014, 90, 014101. [Google Scholar] [CrossRef] [Green Version]
- Waldorf, D.L.; Alers, G.A. Low-Temperature Elastic Moduli of Lead. J. Appl. Phys. 1962, 33, 3266–3269. [Google Scholar] [CrossRef]
- Muller, R.A.; Schuele, D.E. The pressure derivatives of the elastic constants of lead. J. Phys. Chem. Solids 1969, 30, 589–600. [Google Scholar] [CrossRef]
- Anderson, O.L.; Isaak, D. Elastic constants of mantle minerals at high temperatures. In Mineral Physics and Crystallography. A Handbook of Physical Constants; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; Volume 2, pp. 64–97. [Google Scholar]
- Yagi, T. Experimental determination of thermal expansivity of several alkali halides at high pressures. J. Phys. Chem. Solids 1978, 39, 563–571. [Google Scholar] [CrossRef]
- Decker, D.L. High pressure equation of state for NaCl, KCl, and CsCl. J. Appl. Phys. 1971, 42, 3239–3244. [Google Scholar] [CrossRef] [Green Version]
- Vaidya, S.N.; Kennedy, G.C. Compressibility of 27 halides to 45 kbar. J. Phys. Chem. Solids 1971, 32, 951–964. [Google Scholar] [CrossRef]
- Hart, S. The high-temperature elastic moduli of alkali halides. J. Phys. D Appl. Phys. 1977, 10, L261–L263. [Google Scholar] [CrossRef]
- Jones, L.E. A High-temperature behaviour of the elastic moduli of LiF and NaF: Comparison with MgO and CaO. Phys. Earth Planet. Inter. 1976, 13, 105–118. [Google Scholar] [CrossRef]
- Skelton, E.F.; Webb, A.W.; Qadri, S.B.; Wolf, S.A.; Lacoe, R.C.; Feldman, J.L.; Elam, W.T.; Elam, E.R.; Carpenter, E.R., Jr.; Huang, C.Y. Energy-dispersive x-ray diffraction with synchrotron radiation at cryogenic temperatures. Rev. Sci. Instrum. 1984, 55, 849–855. [Google Scholar] [CrossRef]
- Martinson, R.H. Variation of the elastic constants of sodium with temperature and pressure. Phys. Rev. 1969, 178, 902–913. [Google Scholar] [CrossRef]
- Marquardt, H.K.; Trivisonno, J. Low temperature elastic constants of potassium. J. Phys. Chem. Solids 1965, 26, 273–278. [Google Scholar] [CrossRef]
- Gutman, E.J.; Trivisonno, J. Temperature dependence of the elastic constants of rubidium. J. Phys. Chem. Solids 1967, 28, 805–809. [Google Scholar] [CrossRef]
- Anderson, M.S.; Swenson, C.A. Experimental compressions for sodium, potassium, and rubidium metals to 20 kbar from 4.2 to 300 K. Phys. Rev. B 1983, 28, 5395–5418. [Google Scholar] [CrossRef]
- Loriers-Suisse, C.; Bastide, J.-P.; Bäckström, G. Specific heat measured at high pressures by a pulse method. Rev. Sci. Instrum. 1973, 44, 1344–1349. [Google Scholar] [CrossRef]
- Bastide, J.-P.; Loriers-Suisse, C. Specific heats of copper, nickel and aluminum to 100 Kbar at 293 K. High Temp.-High Press. 1975, 7, 153–163. [Google Scholar]
- Bridgmann, P.W. The effect of pressure on the thermal conductivity of metals. Proc. Am. Acad. Arts Sci. 1922, 57, 77–127. [Google Scholar] [CrossRef]
- Andersson, P. Thermal conductivity under pressure and through phase transitions in solid alkali halides. I. Experimental results for KCl, KBr, KI, RbCl, RbBr and RbI. J. Phys. C Solid State Phys. 1985, 18, 3943–3955. [Google Scholar] [CrossRef]
- Andersson, S.; Bäckström, G. Techniques for determining thermal conductivity and heat capacity under hydrostatic pressure. Rev. Sci. Instrum. 1986, 57, 1633–1639. [Google Scholar] [CrossRef]
- Gerlich, D.; Andersson, P. Temperature and pressure effects on the thermal conductivity and heat capacity of CsCl, CsBr and CsI. J. Phys. C Solid State Phys. 1982, 15, 5211–5222. [Google Scholar] [CrossRef]
- Andersson, S.; Bäckström, G. Thermal conductivity and heat capacity of single-crystal LiF and CaF2 under hydrostatic pressure. J. Phys. C Solid State Phys. 1987, 20, 5951–5962. [Google Scholar] [CrossRef]
- Håkansson, B.; Andersson, P. Thermal conductivity and heat capacity of solid NaCl and NaI under pressure. J. Phys. Chem. Solids 1986, 47, 355–362. [Google Scholar] [CrossRef]
- Håkansson, B.; Ross, R.G. Thermal conductivity and heat capacity of solid LiBr and RbF under pressure. J. Phys. Condens. Matter 1989, 1, 3977–3985. [Google Scholar] [CrossRef]
- Osako, M.; Ito, E.; Yoneda, A. Simultaneous measurements of thermal conductivity and thermal diffusivity for garnet and olivine under high pressure. Phys. Earth Planet. Inter. 2004, 143–144, 311–320. [Google Scholar] [CrossRef]
- Katsura, T. Thermal diffusivity of periclase at high temperatures and pressures. Phys. Earth Planet. Inter. 1997, 101, 73–77. [Google Scholar] [CrossRef]
- Starr, C. The pressure coefficient of thermal conductivity of metals. Phys. Rev. 1938, 54, 210–216. [Google Scholar] [CrossRef]
- Sundqvist, B.; Bäckström, G. Pressure dependence of the thermal conductivity of aluminum. Solid State Commun. 1977, 23, 773–775. [Google Scholar] [CrossRef]
- Sundqvist, B.; Bäckström, G. Thermal conductivity of gold and silver at high pressures. J. Phys. Chem. Solids 1978, 39, 1133–1137. [Google Scholar] [CrossRef]
- Rapp, J.E.; Merchant, H.D. Thermal expansion of alkali halides from 70 to 570 K. J. Appl. Phys. 1956, 44, 3919–3923. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Kirky, R.K.; Taylor, R.E.; Lee, T.Y.R. Thermal Expansion of Non-Metallic Solids; Plenum Press: New York, NY, USA, 1977. [Google Scholar]
- Touloukian, Y.S.; Buyco, E.H. Specific Heat of Non-Metallic Solids; Plenum Press: New York, NY, USA, 1970. [Google Scholar]
- Elastic Properties of the Elements (Data Page). Available online: https://en.wikipedia.org/wiki/Elastic_properties_of_the_elements_(data_page) (accessed on 26 December 2021).
- De Jong, M.; Chen, W.; Angsten, T.; Jain, A.; Notestine, R.; Gamst, A.; Sluiter, M.; Ande, C.K.; van der Zwaag, S.; Plata, J.J.; et al. Charting the complete elastic properties of inorganic crystalline compounds. Sci. Data 2015, 2, 150009. [Google Scholar] [CrossRef] [Green Version]
- Kieffer, S.W. Thermodynamics and lattice vibrations of minerals: 3. Lattice dynamics and an approximation for minerals with application to simple substances and framework silicates. Rev. Geophys. Space Phys. 1979, 17, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Ferrarro, R.J.; McLellan, R.B. High temperature elastic properties of polycrystalline niobium, tantalum, and vanadium. Metall. Trans. A 1979, 10A, 1699–1702. [Google Scholar] [CrossRef]
- McLellan, R.B.; Ishikawa, T. The elastic properties of aluminum at high temperatures. J. Phys. Chem. Solids 1987, 48, 603–606. [Google Scholar] [CrossRef]
- Ferrarro, R.J.; McLellan, R.B. Temperature dependence of the Young’s modulus and shear modulus of pure nickel, platinum, and molybdenum. Metall. Trans. A 1977, 10A, 1563–1565. [Google Scholar] [CrossRef]
- Ono, N.; Kitamura, K.; Nakajima, K.; Shimanuki, Y. Measurement of Young’s modulus of silicon single crystal at high temperature and its dependency on boron concentration using the flexural vibration method. Jpn. J. Appl. Phys. 2000, 39, 368–371. [Google Scholar] [CrossRef]
- Yagi, H.; Yanagitani, T.; Numazawa, T.; Ueda, K. The physical properties of transparent Y3Al5O12: Elastic modulus at high temperature and thermal conductivity at low temperature. Ceram. Int. 2007, 33, 711–714. [Google Scholar] [CrossRef]
- Wachtman, J.B., Jr.; Tempt, W.E.; Lam, D.G., Jr.; Apstkin, C.S. Exponential temperature dependence of Young’s modulus for several oxides. Phys. Rev. B 1961, 122, 1754–1759. [Google Scholar] [CrossRef]
- Shen, X.; Wu, K.; Sun, H.; Sang, L.; Huang, Z.; Imura, M.; Koide, Y.; Koizumi, S.; Liao, M. Temperature dependence of Young’s modulus of single-crystal diamond determined by dynamic resonance. Diam. Relat. Mater. 2021, 116, S108403. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Spatial and symmetry constraints as the basis of the virial theorem and astrophysical implications. Can. J. Phys. 2016, 94, 380–388. [Google Scholar] [CrossRef]
- Fiquet, G.; Richet, P.; Montagnac, G. High-temperature thermal expansion of lime, periclase, corundum and spinel. Phys. Chem. Miner. 1999, 27, 103–111. [Google Scholar] [CrossRef]
- Lu, X.-G.; Selleby, M.; Sundman, B. Assessments of molar volume and thermal expansion for selected bcc, fcc and hcp metallic elements. Comp. Coupling Phase Diag. Thermochem. 2005, 29, 68–89. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Li, D. Assessment of thermal expansion coefficient for pure metals. Calphad 2013, 43, 7–17. [Google Scholar] [CrossRef]
- Gray, D.E. American Institute of Physics Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Kroeger, F.R.; Swenson, C.A. Absolute linear thermal-expansion measurements on copper and aluminum from 5 to 320 K. J. Appl. Phys. 1977, 48, 853–864. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of aluminum. Int. J. Thermophys. 1987, 8, 621–638. [Google Scholar] [CrossRef]
- Takahashi, Y.; Azumi, T.; Sekine, Y. Heat capacity of aluminum from 80 to 880 K. Thermochim. Acta 1989, 139, 133–137. [Google Scholar] [CrossRef]
- White, G.K. Thermal expansion of magnetic metals at low temperatures. Proc. Phys. Soc. 1965, 86, 159–169. [Google Scholar] [CrossRef]
- Kozlovskii, Y.M.; Stankus, S.V. The linear thermal expansion coefficient of iron in the temperature range of 130–1180 K. J. Phys. Conf. Ser. 2019, 1382, S012181. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of iron and silicon. J. Phys. Chem. Ref. Data 1986, 15, 967–983. [Google Scholar] [CrossRef]
- Wang, K.; Reeber, R.R. The role of defects on thermophysical properties: Thermal expansion of V, Nb, Ta, Mo and W. Mater. Sci. Eng. 1998, R23, 101–137. [Google Scholar] [CrossRef]
- Miiller, A.P.; Cezairliyan, A. Thermal expansion of molybdenum in the range 1500–2800 K by a transient interferometric technique. Int. J. Thermophys. 1985, 6, 695–704. [Google Scholar] [CrossRef]
- Suh, I.-K.; Ohta, H.; Waseda, Y. High-temperature thermal expansion of six metallic elements measured by dilatation method and X-ray diffraction. J. Mater. Sci. 1988, 23, 757–760. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of manganese and molybdenum. J. Phys. Chem. Ref. Data 1987, 16, 91–108. [Google Scholar] [CrossRef]
- White, G.K. Thermal expansion at low temperatures—V. Dilute alloys of manganese in copper. J. Phys. Chem. Solids 1962, 23, 169–171. [Google Scholar] [CrossRef]
- Miiller, A.P.; Cezairliyan, A. Transient interferometric technique for measuring thermal expansion at high temperatures: Thermal expansion of tantalum in the range 1500–3200 K. Int. J. Thermophys. 1982, 3, 259–288. [Google Scholar] [CrossRef]
- Sterrett, K.F.; Wallace, W.E. Heat capacities, entropies and enthalpies of tantalum between 12 and 550 °K. J. Am. Chem. Soc. 1958, 80, 3176–3177. [Google Scholar] [CrossRef]
- Takahashi, Y.; Nakamura, J. The heat capacity of tantalum from 80 to 1000 K. Thermochim. Acta 1996, 282–283, 317–322. [Google Scholar] [CrossRef]
- Milosevic, N.D.; Vukovic, G.S.; Pavicic, D.Z.; Maglic, K.D. Thermal properties of tantalum between 300 and 2300 K. Int. J. Thermophys. 1999, 20, 1129–1136. [Google Scholar] [CrossRef]
- Cezairliyan, A.; McClure, J.L.; Beckett, C.W. Beckett, 1971 High-speed (subsecond) measurement of heat capacity, electrical resistivity, and thermal radiation properties of tantalum in the range 1900 to 3200 K. J. Res. Natl. Bur. Stand. 1971, 75A, 41–54. [Google Scholar] [CrossRef]
- White, G.K.; Collins, J.G. Thermal expansion of copper, silver, and gold at low temperatures. J. Low Temp. Phys. 1972, 7, 43–75. [Google Scholar] [CrossRef]
- Pamato, M.G.; Wood, I.G.; Dobson, D.P.; Hunt, S.A.; Vočadlo, L. The thermal expansion of gold: Point defect concentrations and pre-melting in an fcc metal. J. Appl. Cryst. 2018, 51, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Geballe, T.H.; Giauque, W.F. The heat capacity and entropy of gold from 15 to 300 °K. J. Am. Chem. Soc. 1952, 74, 2368–2369. [Google Scholar] [CrossRef]
- Cordoba, G.; Brooks, C.R. Heat capacity of gold from 300 to 1000 °K: Experimental data and analysis of contributions. Phys. Status Solidi A 1972, 6, 581–595. [Google Scholar] [CrossRef]
- Slack, G.A.; Bartram, S.F. Thermal expansion of some diamond like crystals. J. Appl. Phys. 1975, 46, 89–98. [Google Scholar] [CrossRef]
- Desnoyehs, J.E.; Morrison, J.A. The heat capacity of diamond between 12 and 277 °K. Philos. Mag. 1958, 3, 43–48. [Google Scholar] [CrossRef]
- O’Neill, M.J. Measurement of specific heat functions by differential scanning calorimetry. Anal. Chem. 1966, 38, 1331–1336. [Google Scholar] [CrossRef]
- Victor, A.C. Heat capacity of diamond at high temperatures. J. Chem. Phys. 1962, 36, 1903–1911. [Google Scholar] [CrossRef]
- Weber, H.F. XXI. The specific heat of the elements carbon, boron, and silicon.—Part I. The relation between the specific heat of these elements in the free state and the temperature. Philos. Mag. 1875, 49, 161–183. [Google Scholar] [CrossRef]
- Manikandan, G.; Murugan, G.; Raghukanda, K. Effect of grain size upon the thermal behavior of copper and diamond powders using differential scanning calorimetry (DSC). Indian J. Sci. Tech. 2016, 9. [Google Scholar] [CrossRef]
- Swenson, C.A. Recommended values for the thermal expansivity of silicon from 0 to 1000 K. J. Phys. Chem. Ref. Data 1983, 12, 179–182. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y.; Tokumura, Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 1984, 56, 314–320. [Google Scholar] [CrossRef]
- Reeber, R.R.; Goessel, K.; Wang, K. Thermal expansion and molar volume of MgO, periclase, from 5 to 2900 K. Eur. J. Mineral. 1995, 7, 1039–1047. [Google Scholar] [CrossRef]
- White, G.K.; Anderson, O.L. Gruneisen parameter of magnesium oxide. J. Appl. Phys. 1991, 37, 430–432. [Google Scholar] [CrossRef]
- Ganesan, S. Temperature variation of the Grüneisen parameter in magnesium oxide. Philos. Mag. 1962, 7, 197–205. [Google Scholar] [CrossRef]
- Barron, T.H.K.; Berg, W.T.; Morrison, J.A. On the heat capacity of crystalline magnesium oxide. Proc. R. Soc. A 1959, 250, 70–83. [Google Scholar]
- Richet, P.; Fiquet, G. High temperature heat capacity and premelting of minerals in the system MgO-CaO-Al2O3-SiO2. J. Geophys. Res. 1991, 96, 445–456. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. NIST-JANAF Thermochemical Tables, Fourth Edition. J. Phys. Chem. Ref. Data 1998, 25, 551–603. [Google Scholar] [CrossRef]
- Reeber, R.R.; Wang, K. Lattice parameters and thermal expansion of important semiconductors and their substrates. MRS Proc. 2000, 622, 1–6. [Google Scholar] [CrossRef]
- White, G.K.; Roberts, R.B. Thermal expansion of reference materials: Tungsten and α-Al2O3. High Temp.-High Press. 1983, 15, 321–328. [Google Scholar]
- Hahn, T.A. Thermal expansion of single crystal sapphire from 293 to 2000 K Standard reference material 732. In Thermal Expansion 6; Springer: Boston, MA, USA, 1978; p. 191. [Google Scholar]
- Ditmars, D.A.; Ishihara, S.; Chang, S.S.; Bernstein, G.; West, E.D. Enthalpy and heat capacity standard reference material: Synthetic sapphire (α-Al2O3) from 10 to 2250 K. J. Res. Natl. Bur. Stand. 1982, 87, 159–163. [Google Scholar] [CrossRef]
- Aggarwal, R.L.; Ripin, D.J.; Ochoa, J.R.; Fan, T.Y. Measurement of thermo-optic properties of Y3Al5O12, Lu3Al5O12, YAlO3, LiYF4, LiLuF4, BaY2F8, KGd(WO4)2, and KY(WO4)2 laser crystals in the 80–300 K temperature range. J. Appl. Phys. 2005, 98, 103514. [Google Scholar] [CrossRef]
- Furuse, H.; Yasuhara, R.; Hiraga, K. Thermo-optic properties of ceramic YAG at high temperatures. Opt. Mater. Express 2014, 4, 1794–1799. [Google Scholar] [CrossRef]
- Geller, S.; Espinosa, G.P.; Crandall, P.B. Thermal expansion of yttrium and gadolinium iron, gallium and aluminum garnets. J. Appl. Cryst. 1969, 2, 86–88. [Google Scholar] [CrossRef]
- Sato, Y.; Taira, T. Study on the specific heat of Y3Al5O12 between 129 K and 573 K. Opt. Mater. Express 2021, 11, 551–558. [Google Scholar] [CrossRef]
- Sagi, S.; Hayun, S. High-temperature heat capacity of SPS-processed Y3Al5O12 (YAG) and Nd:YAG. J. Chem. Thermodyn. 2016, 93, 123–126. [Google Scholar] [CrossRef]

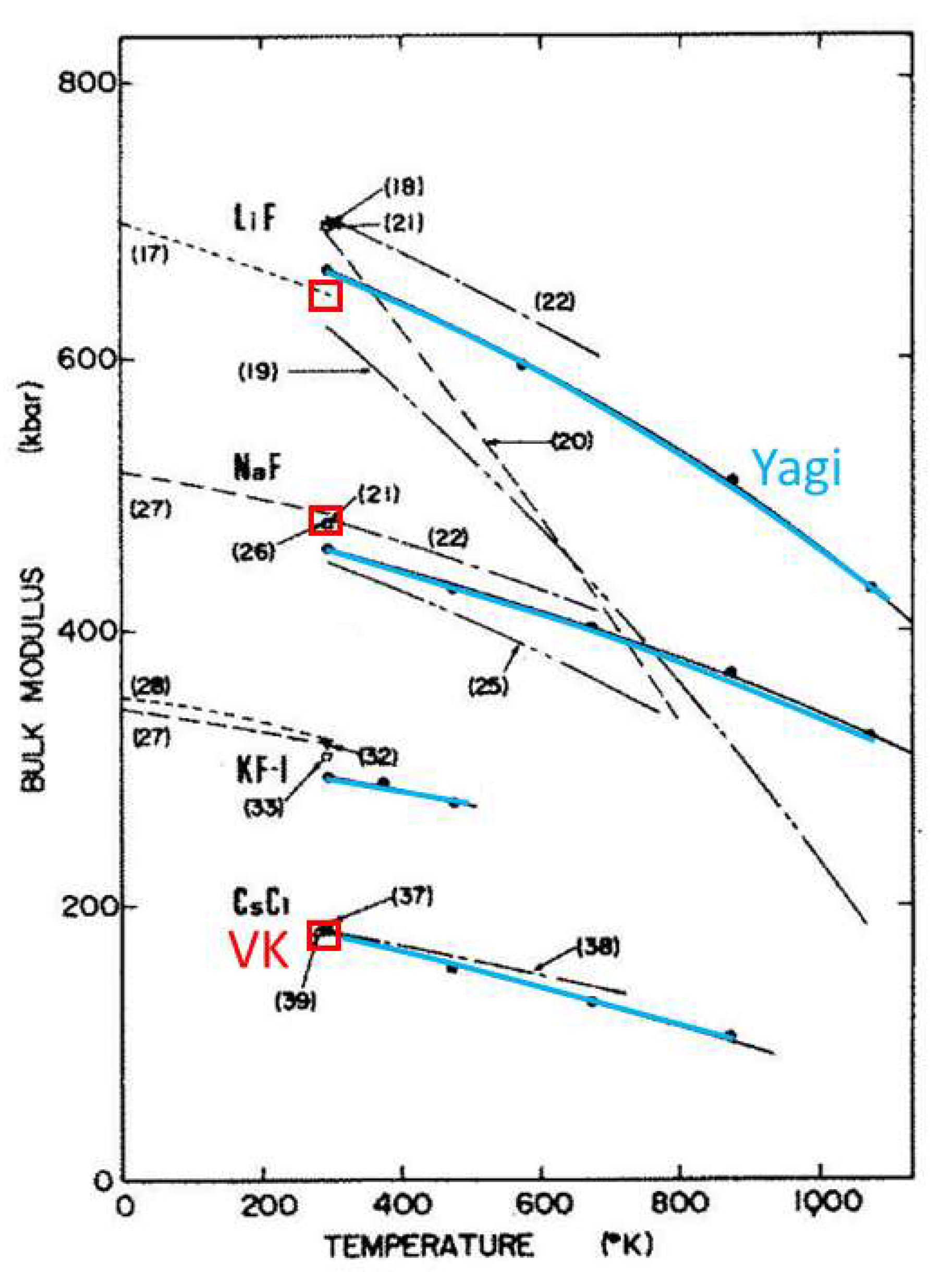

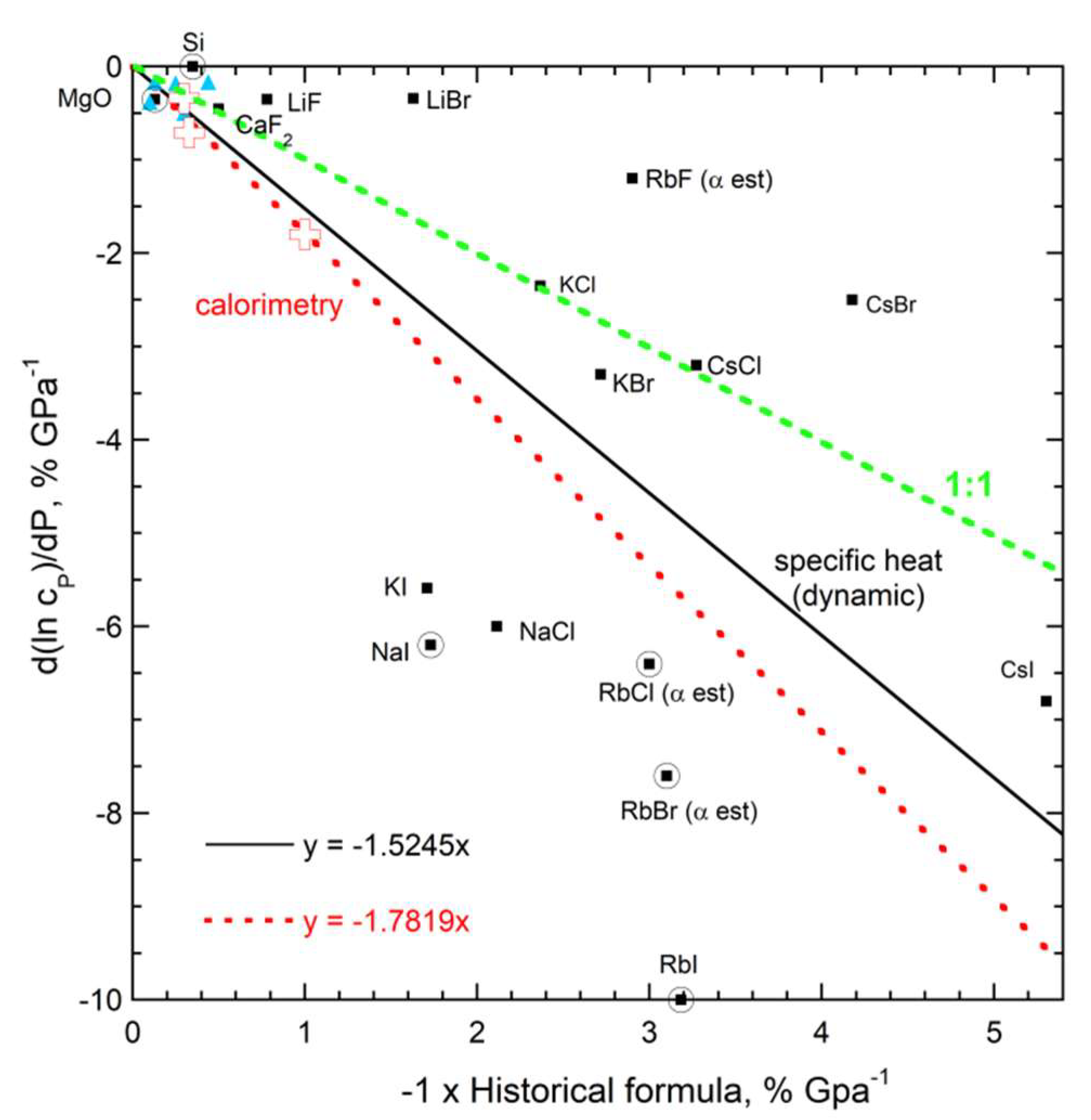
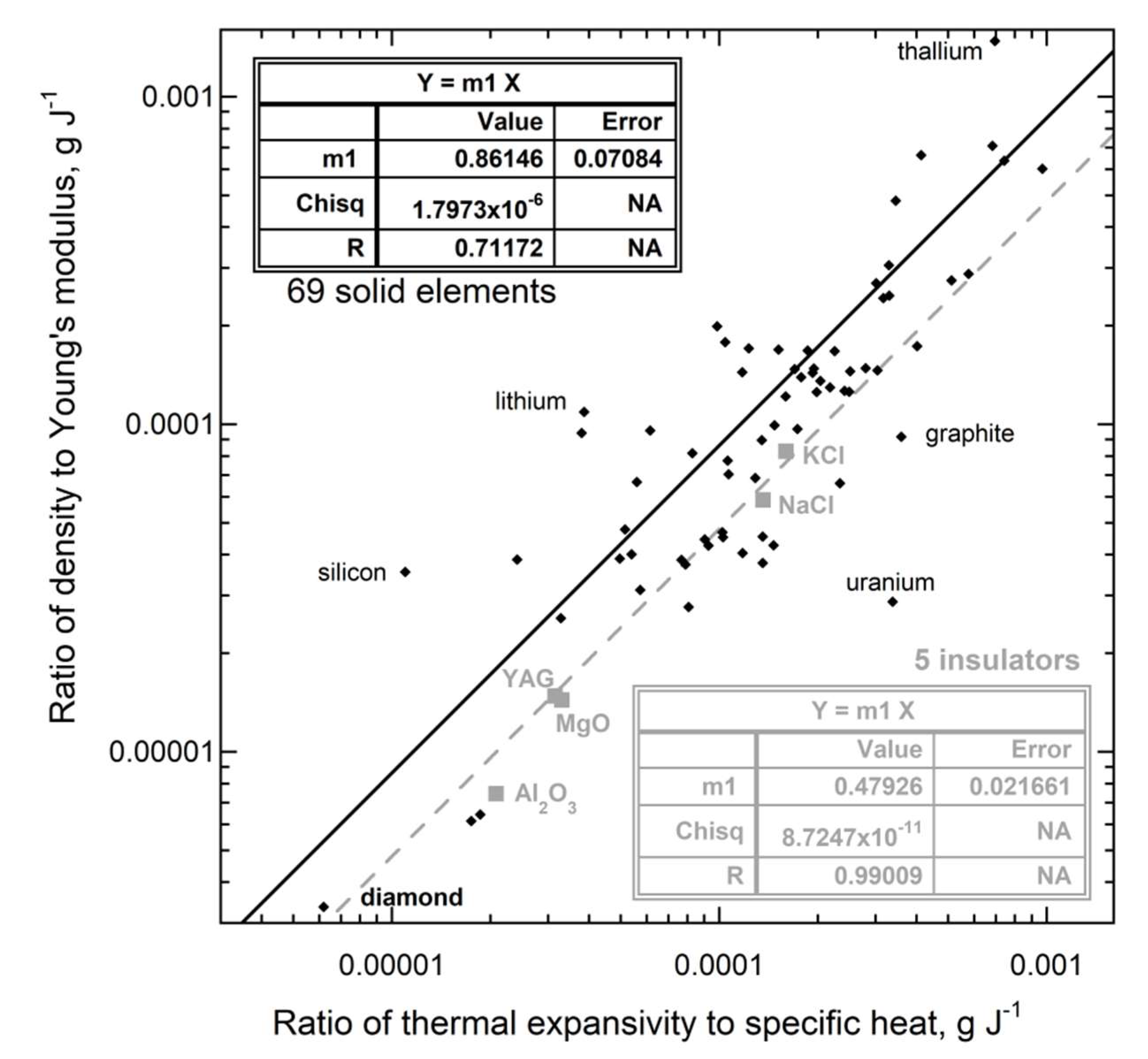
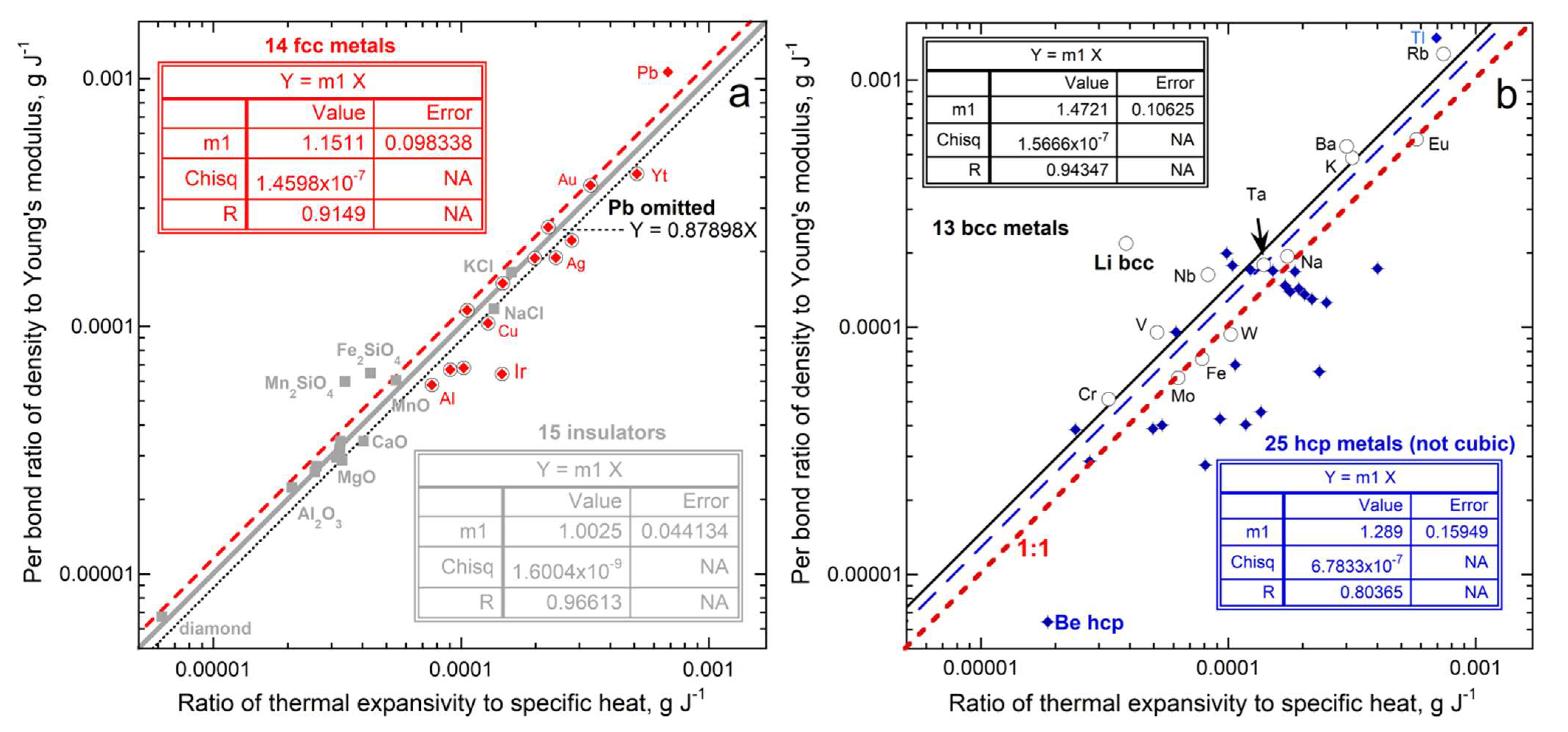
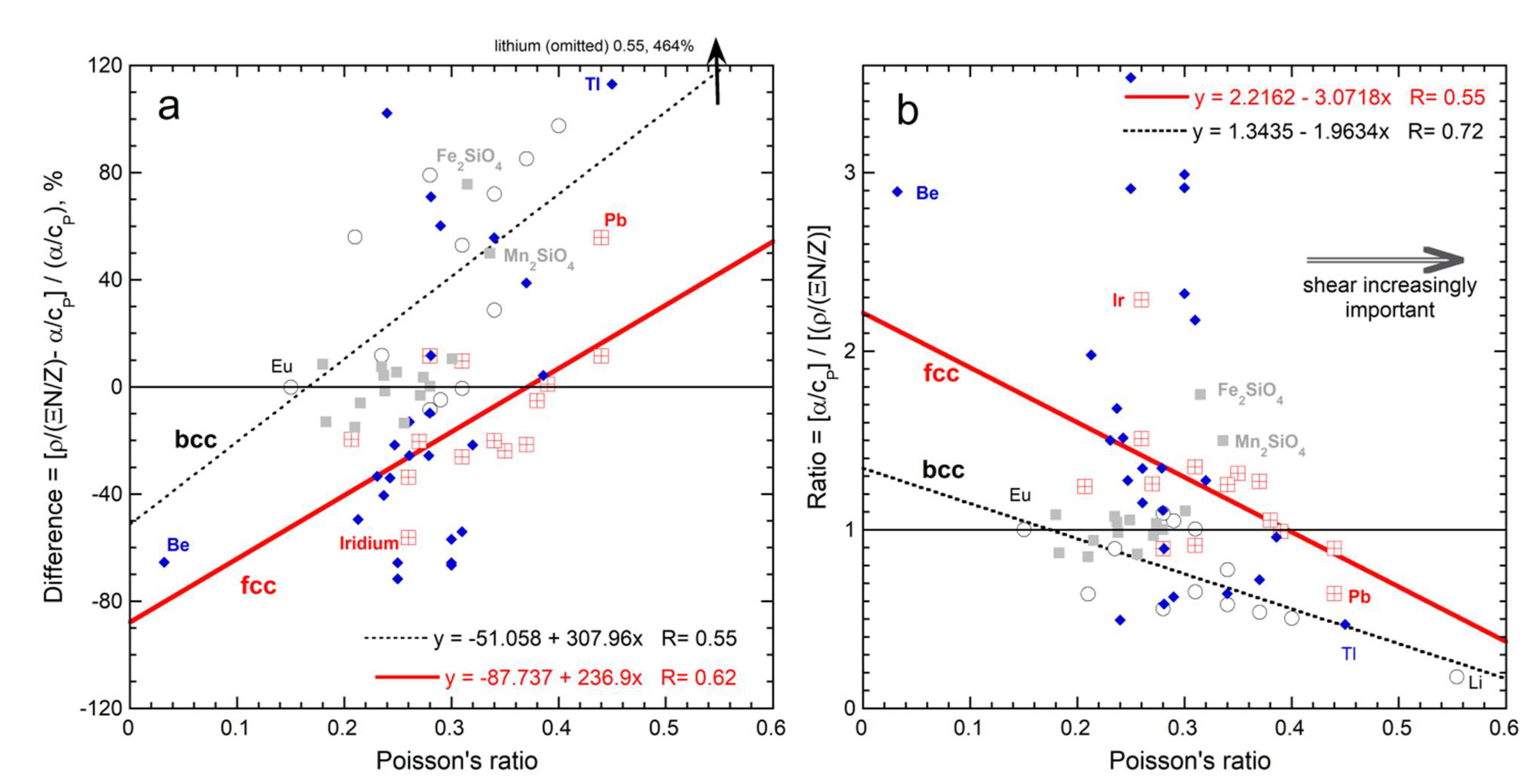
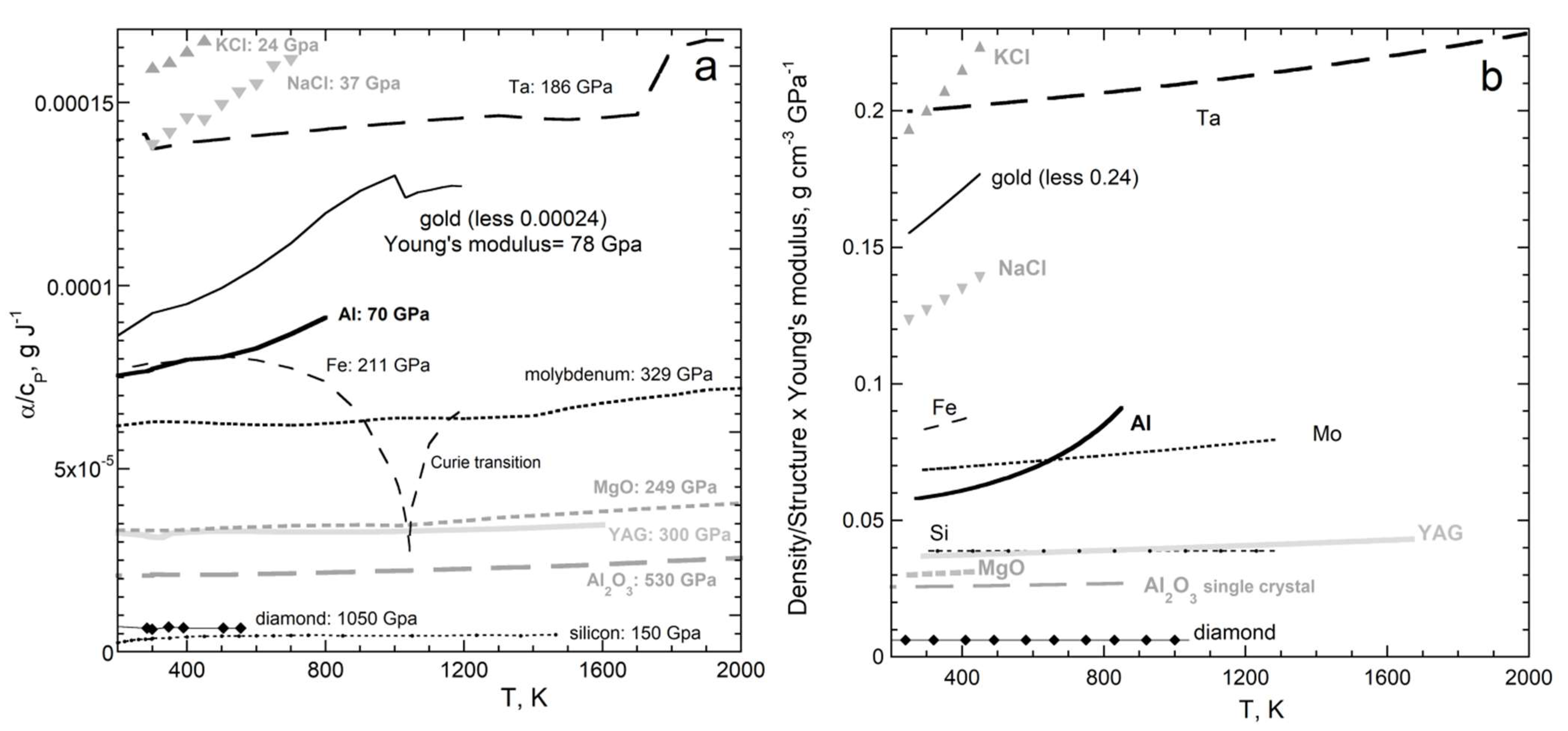
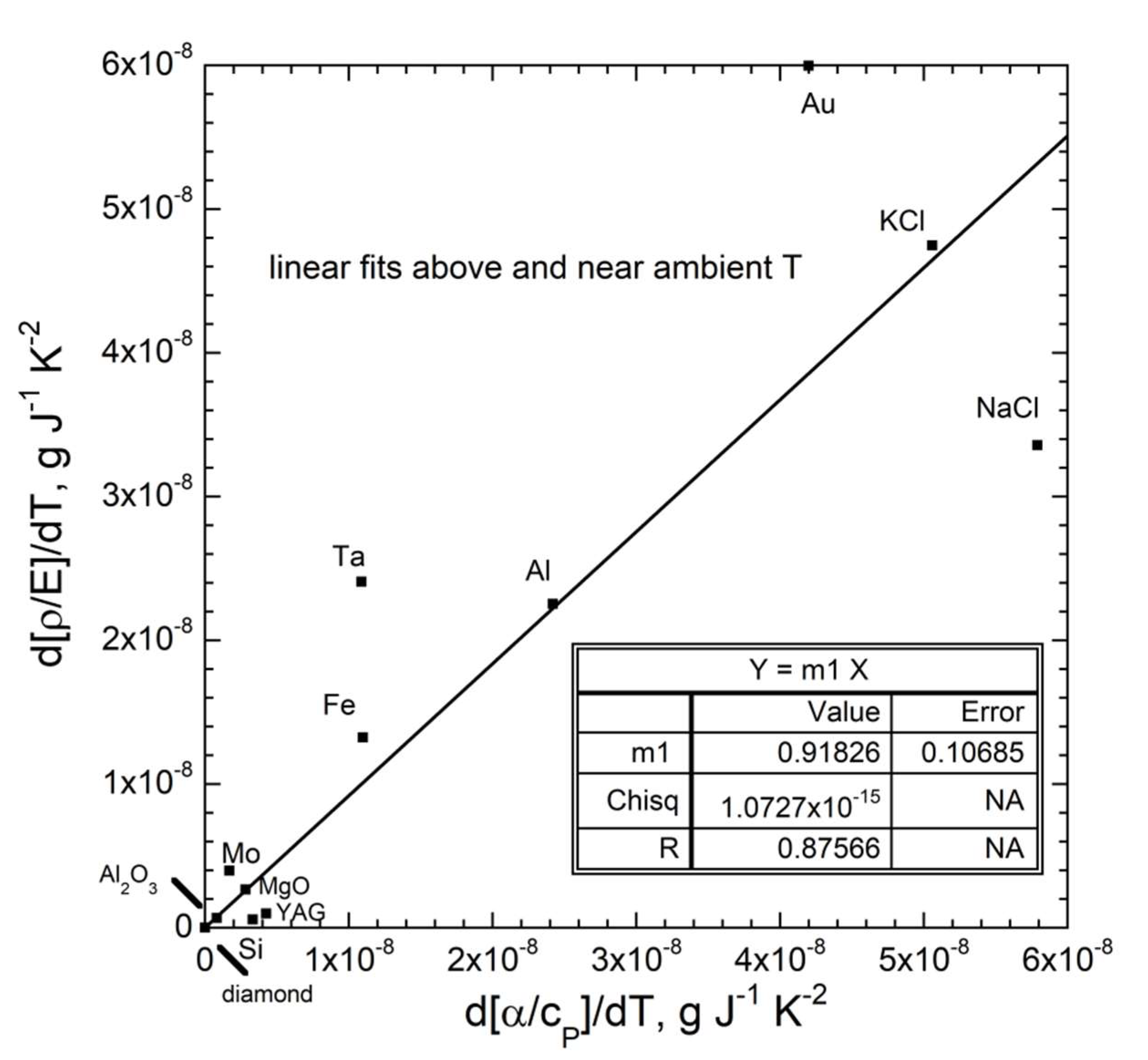
| New Formula | Theory | Experimental Confirmation |
|---|---|---|
| BT = B from elasticity measurements | Section 2.3.2 and Section 2.3.6 | Section 3.1 (ambient and elevated T) |
| Section 2.4.2 | Section 3.2 (ambient T) | |
| Section 2.4.6 | Section 3.3 (ambient and elevated T) |
| Type | Motion | Solids | Gases | ||
|---|---|---|---|---|---|
| Manifestation | Energy Storage | Manifestation | Storage | ||
| monatomic | Displacements parallel to path | Longitudinal acoustic mode | Longitudinal stress/strain 1 | Translational K.E. | Heat |
| Displacements perpendicular to path | Transverse acoustic modes | Transverse stress/strain 1 | n/a | n/a | |
| Electron-cation dipoles | Optical continuum | Heat | Collisions | n/a 3 | |
| polyatomic | Longitudinal | Longitudinal acoustic mode | Longitudinal stress/strain 1 | Translational KE | Heat |
| Transverse | Transverse acoustic modes | Transverse stress/strain 1 | n/a | n/a | |
| Electron-cation dipoles | Optical continuum | Heat | Collisions | n/a 3 | |
| Cyclical, tiny 2 | Optical modes | Additional heat | Internal modes | Heat | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmeister, A.M.; Criss, E.M.; Criss, R.E. Thermodynamic Relationships for Perfectly Elastic Solids Undergoing Steady-State Heat Flow. Materials 2022, 15, 2638. https://doi.org/10.3390/ma15072638
Hofmeister AM, Criss EM, Criss RE. Thermodynamic Relationships for Perfectly Elastic Solids Undergoing Steady-State Heat Flow. Materials. 2022; 15(7):2638. https://doi.org/10.3390/ma15072638
Chicago/Turabian StyleHofmeister, Anne M., Everett M. Criss, and Robert E. Criss. 2022. "Thermodynamic Relationships for Perfectly Elastic Solids Undergoing Steady-State Heat Flow" Materials 15, no. 7: 2638. https://doi.org/10.3390/ma15072638
APA StyleHofmeister, A. M., Criss, E. M., & Criss, R. E. (2022). Thermodynamic Relationships for Perfectly Elastic Solids Undergoing Steady-State Heat Flow. Materials, 15(7), 2638. https://doi.org/10.3390/ma15072638






