Spatio-Temporal Dynamics of Diffusion-Associated Deformations of Biological Tissues and Polyacrylamide Gels Observed with Optical Coherence Elastography
Abstract
1. Introduction
2. Materials and Methods
2.1. Polyacryalmide Hydrogels (Tissue Phantoms)
2.2. Cartilaginous Tissue
2.3. Spectrophotometry
2.4. Diffusion Kinetics
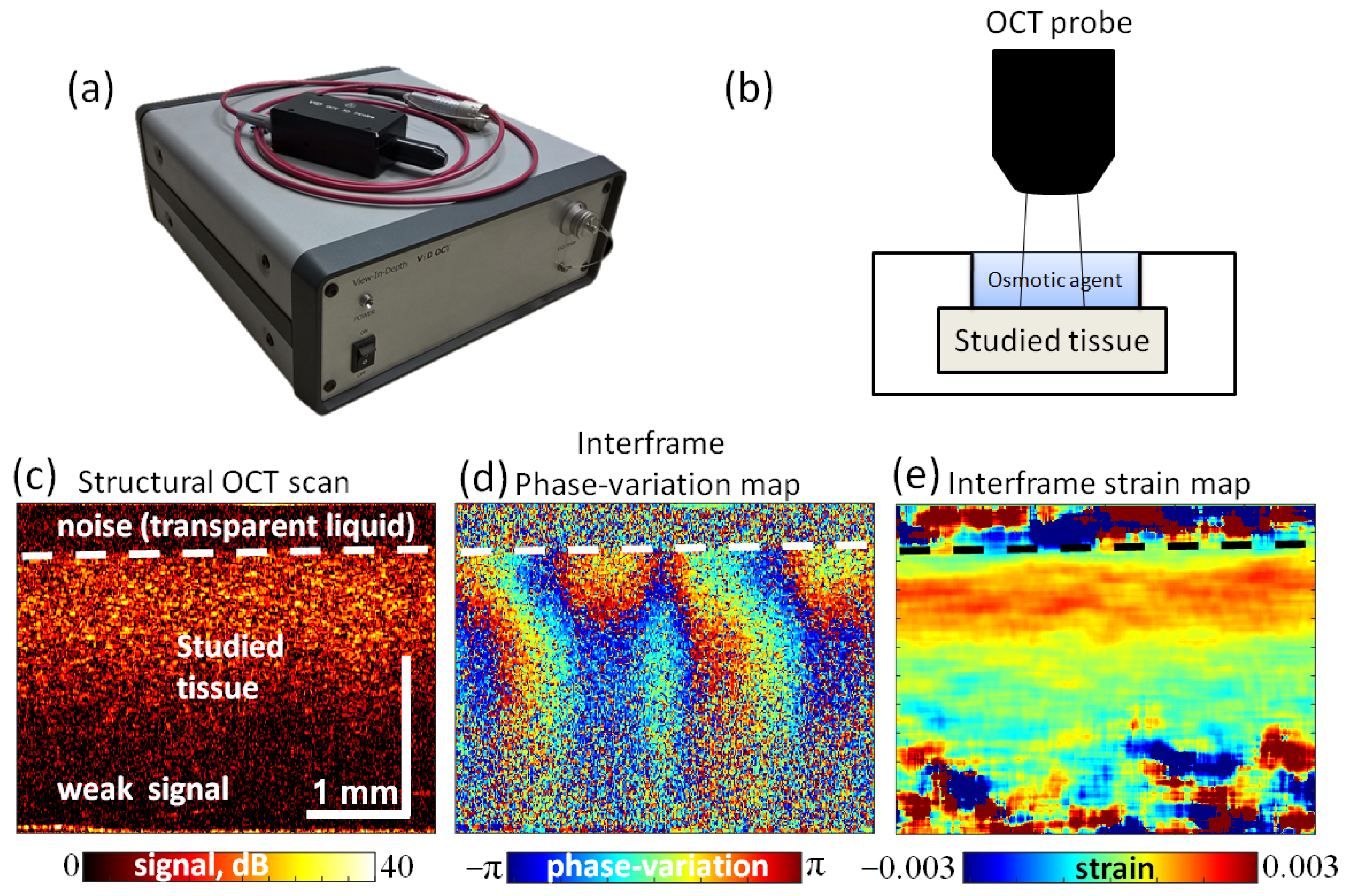
2.5. OCE Observation
3. Results
3.1. Kinetics of Optical Clearing of Cartilaginous Samples
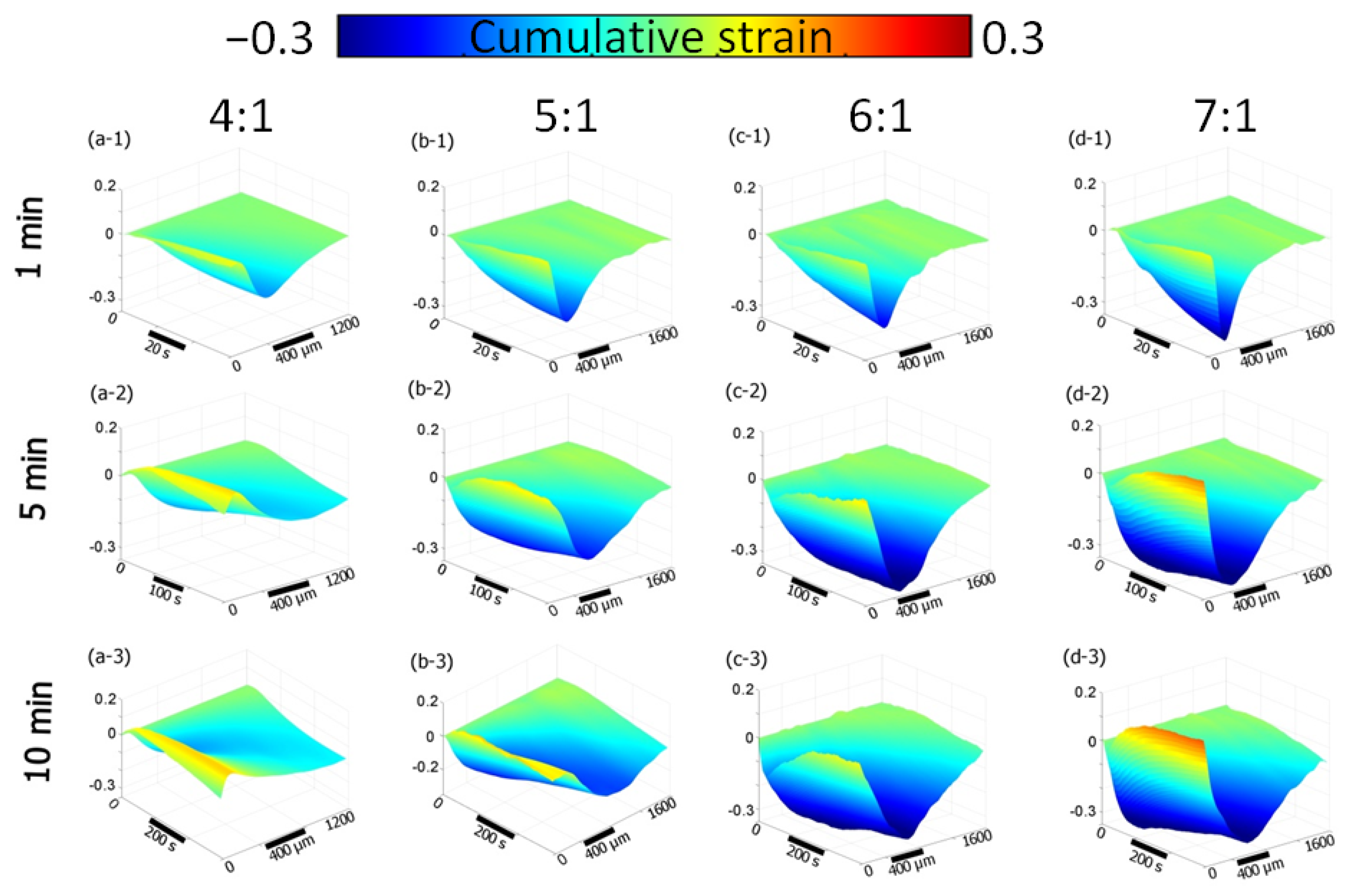
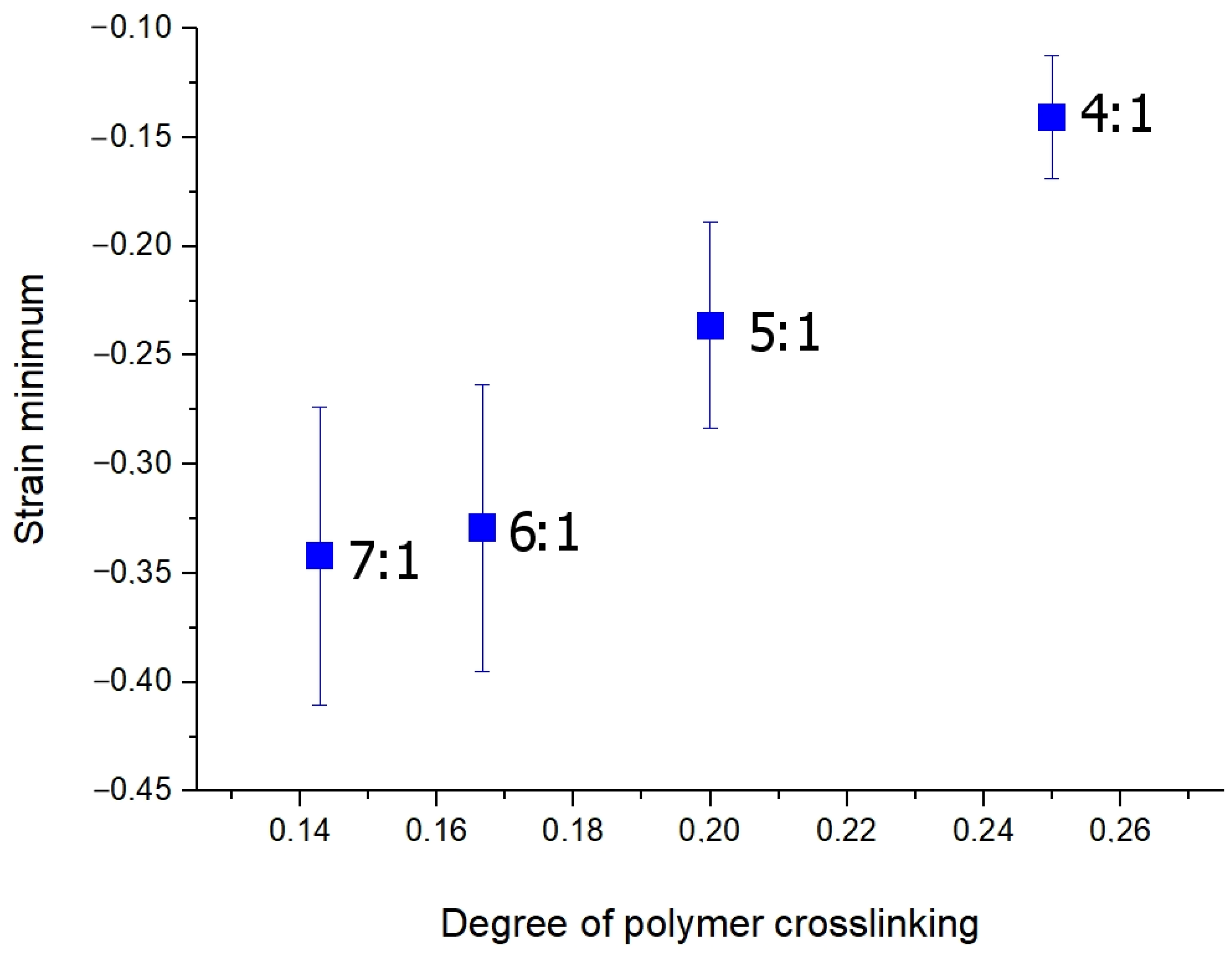
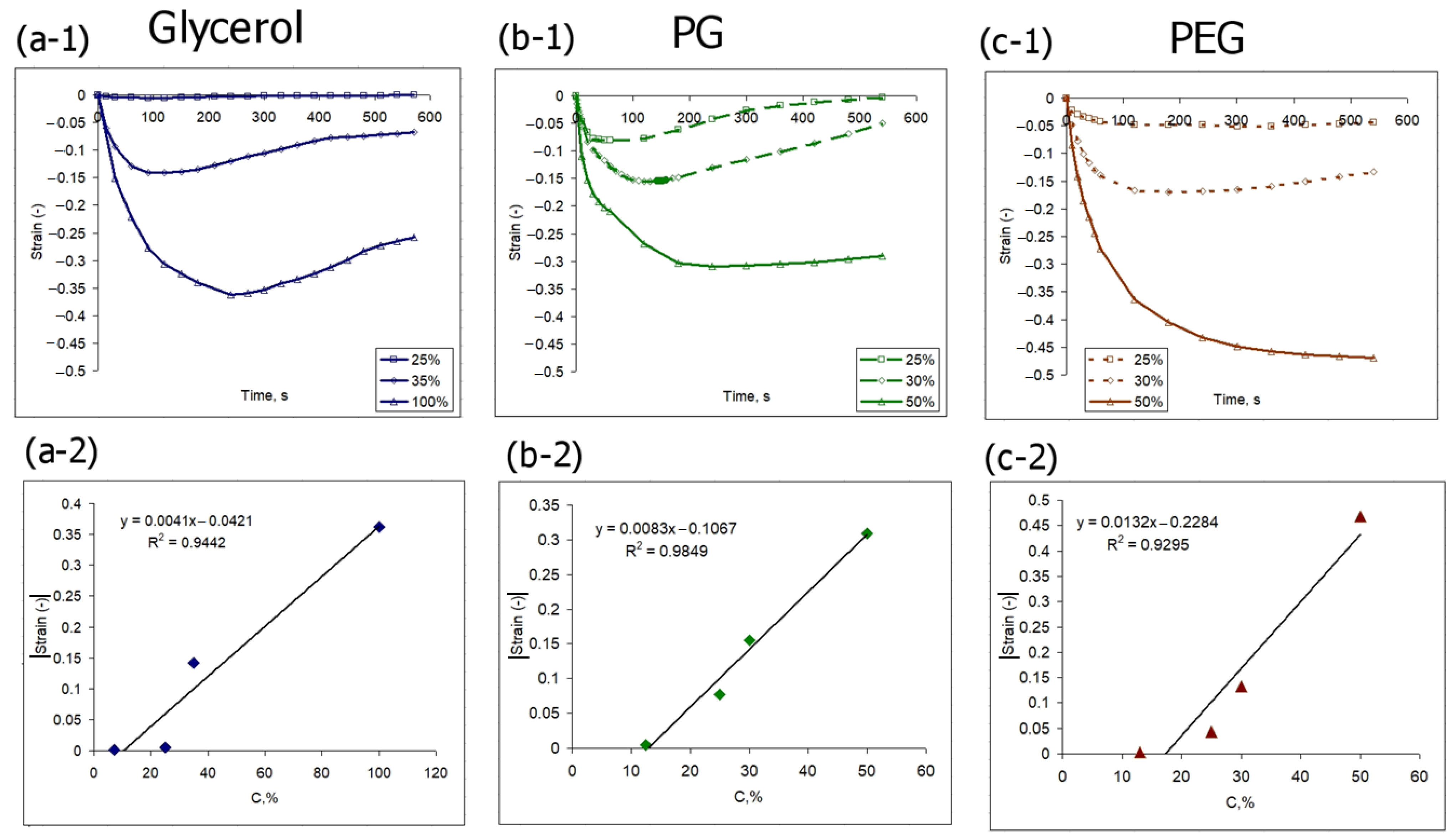
3.2. Osmotic-Induced Strain Dynamics in Polymeric Tissue Phantoms
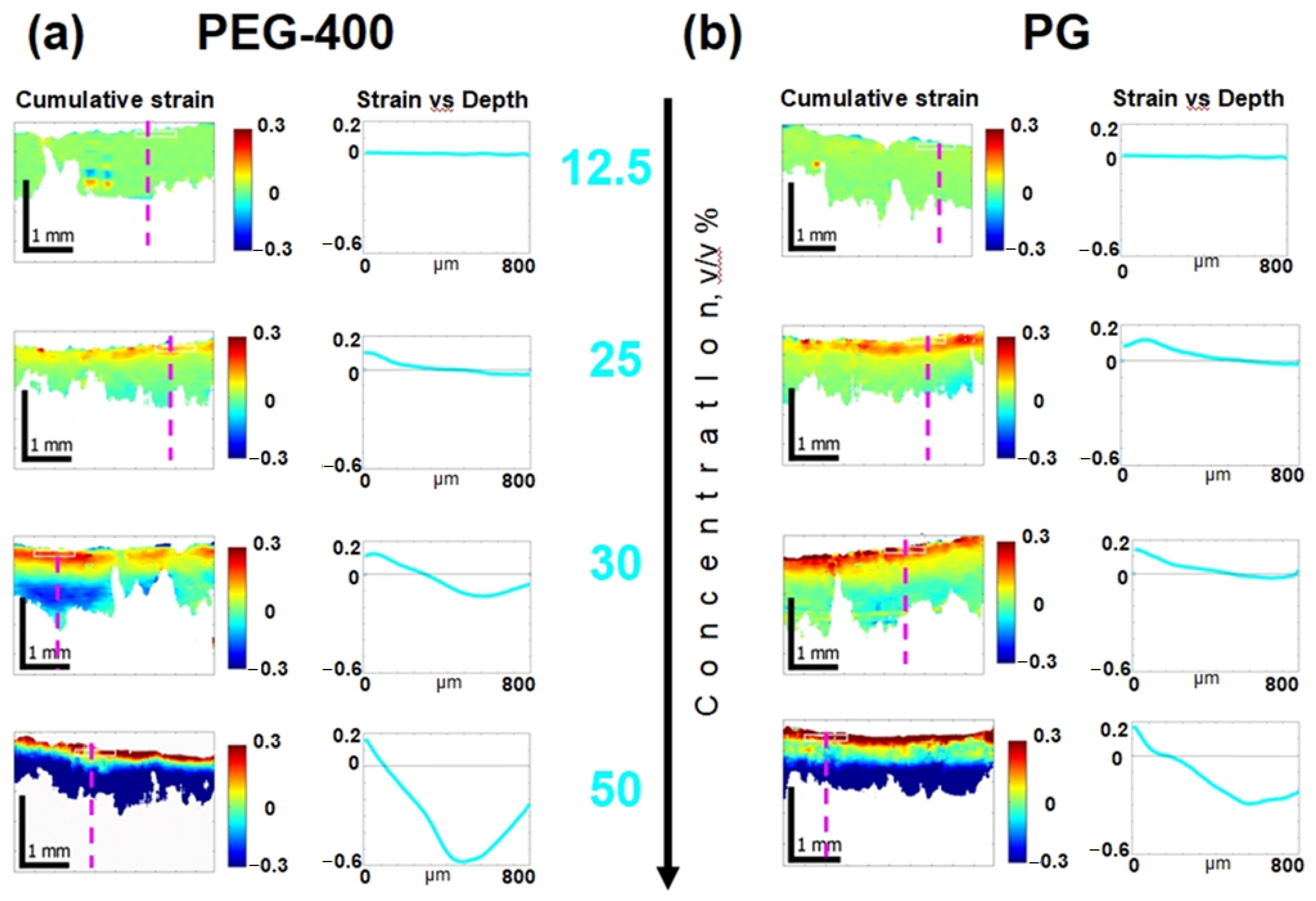
3.3. Osmotic-Induced Strain Dynamics in Cartilaginous Tissue
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tuchin, V.V.; Dan, Z.; Genina, E.A. (Eds.) Handbook of Tissue Optical Clearing: New Prospects in Optical Imaging, 1st ed.; CRC Press: Boca Raton, FL, USA, 2022; ISBN 9781003025252. [Google Scholar]
- Genina, E.A.; Bashkatov, A.N.; Sinichkin, Y.P.; Yanina, I.Y.; Tuchin, V.V. Optical Clearing of Biological Tissues: Prospects of Application in Medical Diagnostics and Phototherapy. J. Biomed. Photonics Eng. 2015, 1, 22–58. [Google Scholar] [CrossRef]
- Neu, C.P.; Novak, T.; Gilliland, K.F.; Marshall, P.; Calve, S. Optical Clearing in Collagen- and Proteoglycan-Rich Osteochondral Tissues. Osteoarthr. Cartil. 2015, 23, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Costantini, I.; Cicchi, R.; Silvestri, L.; Vanzi, F.; Pavone, F.S. In-Vivo and Ex-Vivo Optical Clearing Methods for Biological Tissues: Review. Biomed. Opt. Express 2019, 10, 5251. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Berezin, K.V.; Dvoretskiy, K.N.; Chernavina, M.L.; Genina, E.A.; Genin, V.D.; Kochubey, V.I. Measurement of Tissue Optical Properties in the Context of Tissue Optical Clearing. J. Biomed. Opt. 2018, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Finan, J.D.; Guilak, F. The Effects of Osmotic Stress on the Structure and Function of the Cell Nucleus. J. Cell. Biochem. 2010, 109, 460–467. [Google Scholar] [CrossRef] [PubMed]
- Van den Abbeel, E.; Schneider, U.; Liu, J.; Agca, Y.; Critser, J.K.; Van Steirteghem, A. Osmotic Responses and Tolerance Limits to Changes in External Osmolalities, and Oolemma Permeability Characteristics, of Human in Vitro Matured MII Oocytes. Hum. Reprod. 2007, 22, 1959–1972. [Google Scholar] [CrossRef]
- Giraldo, G.; Talens, P.; Fito, P.; Chiralt, A. Influence of Sucrose Solution Concentration on Kinetics and Yield during Osmotic Dehydration of Mango. J. Food Eng. 2003, 58, 33–43. [Google Scholar] [CrossRef]
- Aboltins, A.; Rubina, T.; Palabinskis, J. Shrinkage Effect on Diffusion Coefficient during Carrot Drying. Agron. Res. 2018, 16, 1301–1311. [Google Scholar] [CrossRef]
- Lazarides, H.N.; Mavroudis, N.E. Kinetics of Osmotic Dehydration of a Highly Shrinking Vegetable Tissue in a Salt-Free Medium. J. Food Eng. 1996, 30, 61–74. [Google Scholar] [CrossRef]
- Fajrial, A.K.; Liu, K.; Gao, Y.; Gu, J.; Lakerveld, R.; Ding, X. Characterization of Single-Cell Osmotic Swelling Dynamics for New Physical Biomarkers. Anal. Chem. 2021, 93, 1317–1325. [Google Scholar] [CrossRef] [PubMed]
- Natonik-Białoń, S.; Borowska-Wykręt, D.; Mosca, G.; Grelowski, M.; Wrzalik, R.; Smith, R.S.; Kwiatkowska, D. Deformation of a Cell Monolayer Due to Osmotic Treatment: A Case Study of Onion Scale Epidermis. Botany 2020, 98, 21–36. [Google Scholar] [CrossRef]
- Song, Z.; Song, W.; Cheng, Y.; Yang, T.; Wang, T.; Wang, K. Investigation on Strain Characteristics and Fatigue Constitutive Model of Limestone under Osmotic Pressure and Cyclic Disturbance Coupling. KSCE J. Civ. Eng. 2022, 26, 1740–1753. [Google Scholar] [CrossRef]
- Acosta Santamaría, V.A.; García, M.F.; Molimard, J.; Avril, S. Characterization of Chemoelastic Effects in Arteries Using Digital Volume Correlation and Optical Coherence Tomography. Acta Biomater. 2020, 102, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Tuchina, D.; Bashkatov, A.; Bucharskaya, A.; Genina, E.; Tuchin, V. Study of Glycerol Diffusion in Skin and Myocardium Ex Vivo under the Conditions of Developing Alloxan-Induced Diabetes. JBPE 2017, 3, 020302. [Google Scholar] [CrossRef]
- Smolyanskaya, O.A.; Schelkanova, I.J.; Kulya, M.S.; Odlyanitskiy, E.L.; Goryachev, I.S.; Tcypkin, A.N.; Grachev, Y.V.; Toropova, Y.G.; Tuchin, V.V. Glycerol Dehydration of Native and Diabetic Animal Tissues Studied by THz-TDS and NMR Methods. Biomed. Opt. Express 2018, 9, 1198. [Google Scholar] [CrossRef] [PubMed]
- Sdobnov, A.; Darvin, M.E.; Lademann, J.; Tuchin, V. A Comparative Study of Ex Vivo Skin Optical Clearing Using Two-Photon Microscopy. J. Biophoton. 2017, 10, 1115–1123. [Google Scholar] [CrossRef]
- Kim, K.; Na, M.; Oh, K.; Cho, E.; Han, S.S.; Chang, S. Optimized Single-Step Optical Clearing Solution for 3D Volume Imaging of Biological Structures. Commun. Biol. 2022, 5, 431. [Google Scholar] [CrossRef]
- Varaka, M.; Vardaki, M.Z.; Gaitanis, G.; Bassukas, I.D.; Kourkoumelis, N. The Effect of Different Optical Clearing Agents on the Attenuation Coefficient and Epidermal Thickness of Human Skin Assessed by Optical Coherence Tomography. Appl. Sci. 2022, 12, 8277. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Hepburn, M.S.; Mowla, A.; Kennedy, B.F. Strain and Elasticity Imaging in Compression Optical Coherence Elastography: The Two-decade Perspective and Recent Advances. J. Biophotonics 2021, 14, e202000257. [Google Scholar] [CrossRef]
- Lawman, S.; Madden, P.W.; Romano, V.; Dong, Y.; Mason, S.; Williams, B.M.; Kaye, S.B.; Willoughby, C.E.; Harding, S.P.; Shen, Y.-C.; et al. Deformation Velocity Imaging Using Optical Coherence Tomography and Its Applications to the Cornea. Biomed. Opt. Express 2017, 8, 5579. [Google Scholar] [CrossRef]
- Liu, C.-H.; Singh, M.; Li, J.; Han, Z.; Wu, C.; Wang, S.; Idugboe, R.; Raghunathan, R.; Sobol, E.N.; Tuchin, V.V.; et al. Quantitative Assessment of Hyaline Cartilage Elasticity During Optical Clearing Using Optical Coherence Elastography. Sovrem Teh. Med. 2015, 7, 44–51. [Google Scholar] [CrossRef]
- Alexandrovskaya, Y.; Baum, O.; Sovetsky, A.; Matveyev, A.; Matveev, L.; Sobol, E.; Zaitsev, V. Optical Coherence Elastography as a Tool for Studying Deformations in Biomaterials: Spatially-Resolved Osmotic Strain Dynamics in Cartilaginous Samples. Materials 2022, 15, 904. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, L.; Lage, A.; Clemente, M.P.; Tuchin, V.V. Optical Clearing of Muscle with Propylene Glycol. Proc. SPIE 2009, 7547, 75470E. [Google Scholar] [CrossRef]
- Tuchina, D.K.; Genin, V.D.; Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical Clearing of Skin Tissue Ex Vivo with Polyethylene Glycol. Opt. Spectrosc. 2016, 120, 28–37. [Google Scholar] [CrossRef]
- Jaafar, A.; Darvin, M.E.; Tuchin, V.V.; Veres, M. Confocal Raman Micro-Spectroscopy for Discrimination of Glycerol Diffusivity in Ex Vivo Porcine Dura Mater. Life 2022, 12, 1534. [Google Scholar] [CrossRef]
- Silva, H.F.; Martins, I.S.; Bogdanov, A.A.; Tuchin, V.V.; Oliveira, L.M. Characterization of Optical Clearing Mechanisms in Muscle during Treatment with Glycerol and Gadobutrol Solutions. J. Biophotonics 2022. [Google Scholar] [CrossRef]
- Lai, J.-H.; Liao, E.-Y.; Liao, Y.-H.; Sun, C.-K. Investigating the Optical Clearing Effects of 50% Glycerol in Ex Vivo Human Skin by Harmonic Generation Microscopy. Sci. Rep. 2021, 11, 329. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Mao, Z.; Han, Z.; Tuchin, V.V.; Zhu, D. In Vivo Skin Optical Clearing by Glycerol Solutions: Mechanism. J. Biophoton. 2009, 3, 44–52. [Google Scholar] [CrossRef]
- Yu, T.; Zhu, J.; Li, D.; Zhu, D. Physical and Chemical Mechanisms of Tissue Optical Clearing. iScience 2021, 24, 102178. [Google Scholar] [CrossRef]
- Mao, Z.; Zhu, D.; Hu, Y.; Wen, X.; Han, Z. Influence of Alcohols on the Optical Clearing Effect of Skin in Vitro. J. Biomed. Opt. 2008, 13, 021104. [Google Scholar] [CrossRef]
- Alexandrovskaya, Y.; Sadovnikov, K.; Sharov, A.; Sherstneva, A.; Evtushenko, E.; Omelchenko, A.; Obrezkova, M.; Tuchin, V.; Lunin, V.; Sobol, E. Controlling the Near-Infrared Transparency of Costal Cartilage by Impregnation with Clearing Agents and Magnetite Nanoparticles. J. Biophotonics 2018, 11, e201700105. [Google Scholar] [CrossRef]
- Alexandrovskaya, Y.M.; Evtushenko, E.G.; Obrezkova, M.V.; Tuchin, V.V.; Sobol, E.N. Control of Optical Transparency and Infrared Laser Heating of Costal Cartilage via Injection of Iohexol. J. Biophotonics 2018, 11, e201800195. [Google Scholar] [CrossRef] [PubMed]
- Bykov, A.; Hautala, T.; Kinnunen, M.; Popov, A.; Karhula, S.; Saarakkala, S.; Nieminen, M.T.; Tuchin, V.; Meglinski, I. Imaging of Subchondral Bone by Optical Coherence Tomography upon Optical Clearing of Articular Cartilage. J. Biophotonics 2016, 9, 270–275. [Google Scholar] [CrossRef] [PubMed]
- Fedulova, V.; Yuzhakov, A.; Baum, O. Study of Laser Radiation Effect on the Cornea of the Eye by Speckle Interferometry. J. Biomed. Photonics Eng. 2020, 6, 010302. [Google Scholar] [CrossRef]
- Holmes, D.L.; Stellwagen, N.C. Estimation of Polyacrylamide Gel Pore Size from Ferguson Plots of Linear DNA Fragments. II. Comparison of Gels with Different Crosslinker Concentrations, Added Agarose and Added Linear Polyacrylamide. Electrophoresis 1991, 12, 612–619. [Google Scholar] [CrossRef]
- Carvalho, B.M.A.; Da Silva, S.L.; Da Silva, L.H.M.; Minim, V.P.R.; Da Silva, M.C.H.; Carvalho, L.M.; Minim, L.A. Cryogel Poly(Acrylamide): Synthesis, Structure and Applications. Sep. Purif. Rev. 2014, 43, 241–262. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; ISBN 9780198533443. [Google Scholar]
- Bagratashvili, V.N.; Sobol, E.N.; Sviridov, A.P.; Popov, V.K.; Omel’chenko, A.I.; Howdle, S.M. Thermal and Diffusion Processes in Laser-Induced Stress Relaxation and Reshaping of Cartilage. J. Biomech. 1997, 30, 813–817. [Google Scholar] [CrossRef]
- Ophir, J.; Cespedes, I.; Ponnekanti, H.; Yazdi, Y.; Li, X. Elastography: A Quantitative Method for Imaging the Elasticity of Biological Tissues. Ultrason. Imaging 1991, 13, 111–134. [Google Scholar] [CrossRef]
- Schmitt, J.M. OCT Elastography: Imaging Microscopic Deformation and Strain of Tissue. Opt. Express 1998, 3, 199. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveev, L.A.; Gelikonov, G.V.; Matveyev, A.L.; Gelikonov, V.M. A Correlation-Stability Approach to Elasticity Mapping in Optical Coherence Tomography. Laser Phys. Lett. 2013, 10, 065601. [Google Scholar] [CrossRef]
- Fu, J.; Haghighi-Abayneh, M.; Pierron, F.; Ruiz, P.D. Depth-Resolved Full-Field Measurement of Corneal Deformation by Optical Coherence Tomography and Digital Volume Correlation. Exp. Mech. 2016, 56, 1203–1217. [Google Scholar] [CrossRef]
- Kennedy, B.F.; Koh, S.H.; McLaughlin, R.A.; Kennedy, K.M.; Munro, P.R.T.; Sampson, D.D. Strain Estimation in Phase-Sensitive Optical Coherence Elastography. Biomed. Opt. Express 2012, 3, 1865. [Google Scholar] [CrossRef]
- Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Gelikonov, G.V.; Moiseev, A.A.; Zaitsev, V.Y. Vector Method for Strain Estimation in Phase-Sensitive Optical Coherence Elastography. Laser Phys. Lett. 2018, 15, 065603. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Ksenofontov, S.Y.; Sovetsky, A.A.; Matveyev, A.L.; Matveev, L.A.; Zykov, A.A.; Gelikonov, G.V. Real-Time Strain and Elasticity Imaging in Phase-Sensitive Optical Coherence Elastography Using a Computationally Efficient Realization of the Vector Method. Photonics 2021, 8, 527. [Google Scholar] [CrossRef]
- Sovetsky, A.A.; Matveyev, A.L.; Matveev, L.A.; Shabanov, D.V.; Zaitsev, V.Y. Manually-Operated Compressional Optical Coherence Elastography with Effective Aperiodic Averaging: Demonstrations for Corneal and Cartilaginous Tissues. Laser Phys. Lett. 2018, 15, 085602. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveev, L.A.; Matveyev, A.L.; Sovetsky, A.A.; Shabanov, D.V.; Ksenofontov, S.Y.; Gelikonov, G.V.; Baum, O.I.; Omelchenko, A.I.; Yuzhakov, A.V.; et al. Optimization of Phase-Resolved Optical Coherence Elastography for Highly-Sensitive Monitoring of Slow-Rate Strains. Laser Phys. Lett. 2019, 16, 065601. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Gelikonov, G.V.; Baum, O.I.; Omelchenko, A.I.; Shabanov, D.V.; Sovetsky, A.A.; Yuzhakov, A.V.; Fedorov, A.A.; et al. Revealing Structural Modifications in Thermomechanical Reshaping of Collagenous Tissues Using Optical Coherence Elastography. J. Biophotonics 2019, 12, e201800250. [Google Scholar] [CrossRef]
- Alexandrovskaya, Y.M.; Baum, O.I.; Sovetsky, A.A.; Matveyev, A.L.; Matveev, L.A.; Sobol, E.N.; Zaitsev, V.Y. Observation of Internal Stress Relaxation in Laser-Reshaped Cartilaginous Implants Using OCT-Based Strain Mapping. Laser Phys. Lett. 2020, 17, 085603. [Google Scholar] [CrossRef]
- Genina, E.A. Tissue Optical Clearing: State of the Art and Prospects. Diagnostics 2022, 12, 1534. [Google Scholar] [CrossRef]
- Reddi, B.A. Why Is Saline So Acidic (and Does It Really Matter?). Int. J. Med. Sci. 2013, 10, 747–750. [Google Scholar] [CrossRef]
- Berezin, K.V.; Dvoretsky, K.N.; Chernavina, M.L.; Nechaev, V.V.; Likhter, A.M.; Shagautdinova, I.T.; Antonova, E.M.; Tuchin, V.V. In Vivo Optical Clearing of Human Skin under the Effect of Aqueous Solutions of Some Monosaccharides. J. Phys. Conf. Ser. 2019, 1400, 033018. [Google Scholar] [CrossRef]
- Wan, L.Q.; Miller, C.; Guo, X.E.; Mow, V.C. Fixed Electrical Charges and Mobile Ions Affect the Measurable Mechano-Electrochemical Properties of Charged-Hydrated Biological Tissues: The Articular Cartilage Paradigm. Mech. Chem. Biosyst. 2004, 1, 81–99. [Google Scholar] [PubMed]
- Maroudas, A. Biophysical Chemistry of Cartilaginous Tissues with Special Reference to Solute and Fluid Transport. BIR 1975, 12, 233–248. [Google Scholar] [CrossRef] [PubMed]
- Maroudas, A. Balance between Swelling Pressure and Collagen Tension in Normal and Degenerate Cartilage. Nature 1976, 260, 808–809. [Google Scholar] [CrossRef] [PubMed]
- Lanir, Y. Mechanisms of Residual Stress in Soft Tissues. J. Biomech. Eng. 2009, 131, 044506. [Google Scholar] [CrossRef]
- Allen, W.M.; Chin, L.; Wijesinghe, P.; Kirk, R.W.; Latham, B.; Sampson, D.D.; Saunders, C.M.; Kennedy, B.F. Wide-Field Optical Coherence Micro-Elastography for Intraoperative Assessment of Human Breast Cancer Margins. Biomed. Opt. Express 2016, 7, 4139. [Google Scholar] [CrossRef] [PubMed]
- Gubarkova, E.V.; Sovetsky, A.A.; Zaitsev, V.Y.; Matveyev, A.L.; Vorontsov, D.A.; Sirotkina, M.A.; Matveev, L.A.; Plekhanov, A.A.; Pavlova, N.P.; Kuznetsov, S.S.; et al. OCT-Elastography-Based Optical Biopsy for Breast Cancer Delineation and Express Assessment of Morphological/Molecular Subtypes. Biomed. Opt. Express 2019, 10, 2244. [Google Scholar] [CrossRef]
- Sirotkina, M.A.; Gubarkova, E.V.; Plekhanov, A.A.; Sovetsky, A.A.; Elagin, V.V.; Matveyev, A.L.; Matveev, L.A.; Kuznetsov, S.S.; Zagaynova, E.V.; Gladkova, N.D.; et al. In Vivo Assessment of Functional and Morphological Alterations in Tumors under Treatment Using OCT-Angiography Combined with OCT-Elastography. Biomed. Opt. Express 2020, 11, 1365. [Google Scholar] [CrossRef]
- Plekhanov, A.A.; Sirotkina, M.A.; Sovetsky, A.A.; Gubarkova, E.V.; Kuznetsov, S.S.; Matveyev, A.L.; Matveev, L.A.; Zagaynova, E.V.; Gladkova, N.D.; Zaitsev, V.Y. Histological Validation of in Vivo Assessment of Cancer Tissue Inhomogeneity and Automated Morphological Segmentation Enabled by Optical Coherence Elastography. Sci. Rep. 2020, 10, 11781. [Google Scholar] [CrossRef]
- Qiu, Y.; Zaki, F.R.; Chandra, N.; Chester, S.A.; Liu, X. Nonlinear Characterization of Elasticity Using Quantitative Optical Coherence Elastography. Biomed. Opt. Express 2016, 7, 4702. [Google Scholar] [CrossRef]
- Gubarkova, E.V.; Sovetsky, A.A.; Matveev, L.A.; Matveyev, A.L.; Vorontsov, D.A.; Plekhanov, A.A.; Kuznetsov, S.S.; Gamayunov, S.V.; Vorontsov, A.Y.; Sirotkina, M.A.; et al. Nonlinear Elasticity Assessment with Optical Coherence Elastography for High-Selectivity Differentiation of Breast Cancer Tissues. Materials 2022, 15, 3308. [Google Scholar] [CrossRef] [PubMed]
- Baum, O.I.; Zaitsev, V.Y.; Yuzhakov, A.V.; Sviridov, A.P.; Novikova, M.L.; Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Sobol, E.N. Interplay of Temperature, Thermal-stresses and Strains in Laser-assisted Modification of Collagenous Tissues: Speckle-contrast and OCT-based Studies. J. Biophotonics 2020, 13. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Lazareva, E.N.; Kochubey, V.I.; Duan, Y.; Tuchin, V.V. Kinetics of Optical Clearing of Human Skin Studied in Vivo Using Portable Raman Spectroscopy. Laser Phys. Lett. 2020, 17, 105601. [Google Scholar] [CrossRef]




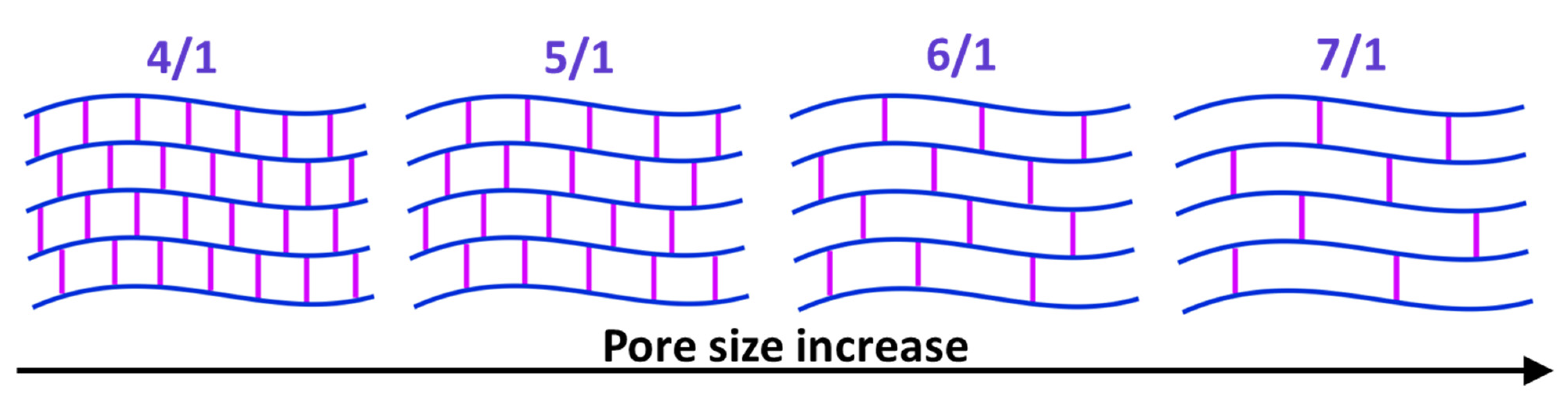
| Acrylamide, g | Bis-Acrylamide, g | Total Mass, g | Crosslinking Degree, Acrylamide/Bis-acrylamide |
|---|---|---|---|
| 0.400 | 0.1 | 2.500 | 4/1 |
| 0.417 | 0.083 | 2.500 | 5/1 |
| 0.428 | 0.071 | 2.499 | 6/1 |
| 0.438 | 0.0625 | 2.5005 | 7/1 |
| Agent | Glycerol | PG | PEG-400 | Omnipaque |
|---|---|---|---|---|
| D, cm2/s·10−6 | 7.4 ± 1.8 | 5.0 ± 0.8 | 4.4 ± 0.8 | 4.6 ± 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandrovskaya, Y.M.; Kasianenko, E.M.; Sovetsky, A.A.; Matveyev, A.L.; Zaitsev, V.Y. Spatio-Temporal Dynamics of Diffusion-Associated Deformations of Biological Tissues and Polyacrylamide Gels Observed with Optical Coherence Elastography. Materials 2023, 16, 2036. https://doi.org/10.3390/ma16052036
Alexandrovskaya YM, Kasianenko EM, Sovetsky AA, Matveyev AL, Zaitsev VY. Spatio-Temporal Dynamics of Diffusion-Associated Deformations of Biological Tissues and Polyacrylamide Gels Observed with Optical Coherence Elastography. Materials. 2023; 16(5):2036. https://doi.org/10.3390/ma16052036
Chicago/Turabian StyleAlexandrovskaya, Yulia M., Ekaterina M. Kasianenko, Alexander A. Sovetsky, Alexander L. Matveyev, and Vladimir Y. Zaitsev. 2023. "Spatio-Temporal Dynamics of Diffusion-Associated Deformations of Biological Tissues and Polyacrylamide Gels Observed with Optical Coherence Elastography" Materials 16, no. 5: 2036. https://doi.org/10.3390/ma16052036
APA StyleAlexandrovskaya, Y. M., Kasianenko, E. M., Sovetsky, A. A., Matveyev, A. L., & Zaitsev, V. Y. (2023). Spatio-Temporal Dynamics of Diffusion-Associated Deformations of Biological Tissues and Polyacrylamide Gels Observed with Optical Coherence Elastography. Materials, 16(5), 2036. https://doi.org/10.3390/ma16052036








