Perspective on the Application of Machine Learning Algorithms for Flow Parameter Estimation in Recycled Concrete Aggregate
Abstract
:1. Introduction
2. Materials and Methods
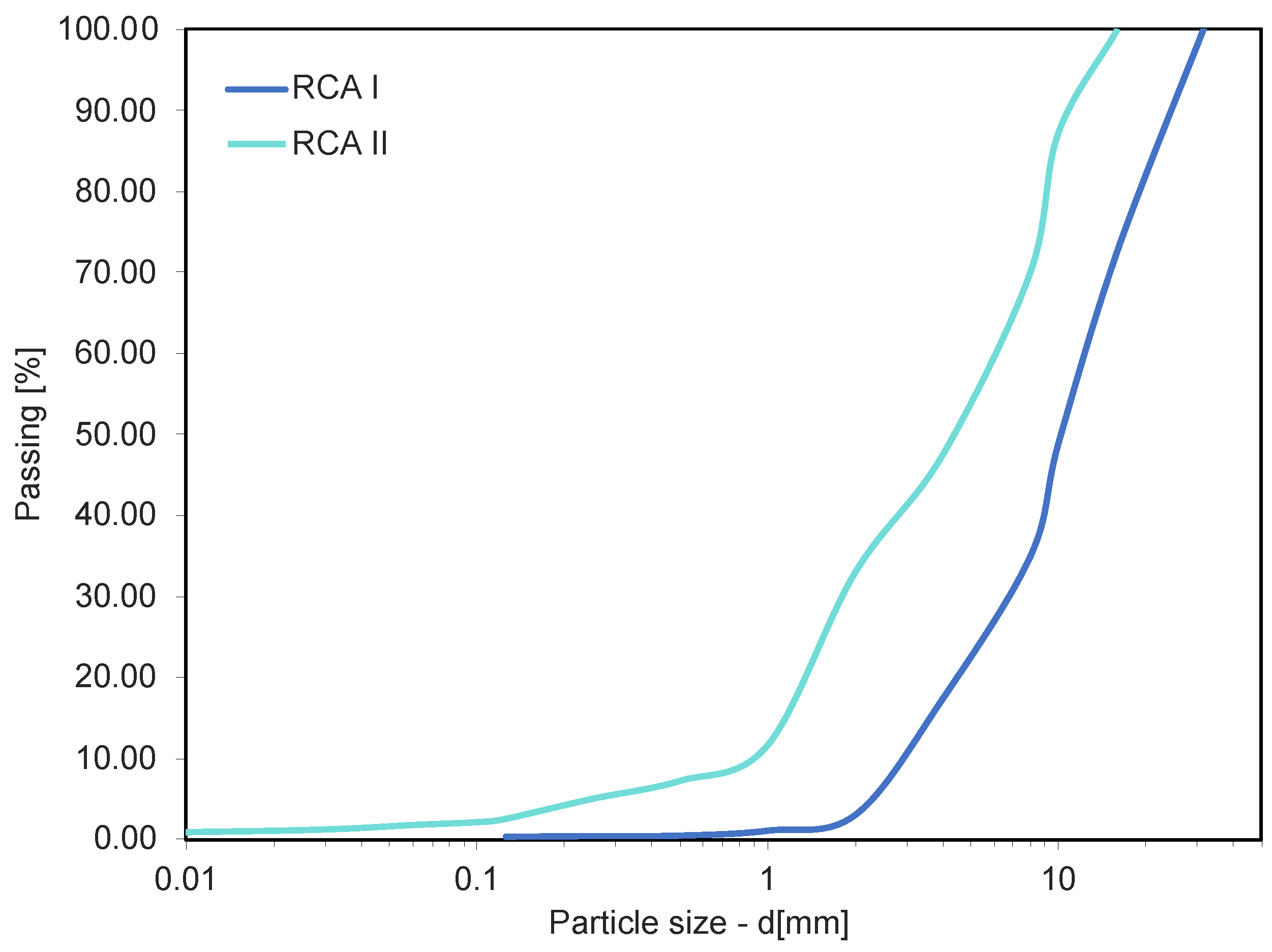
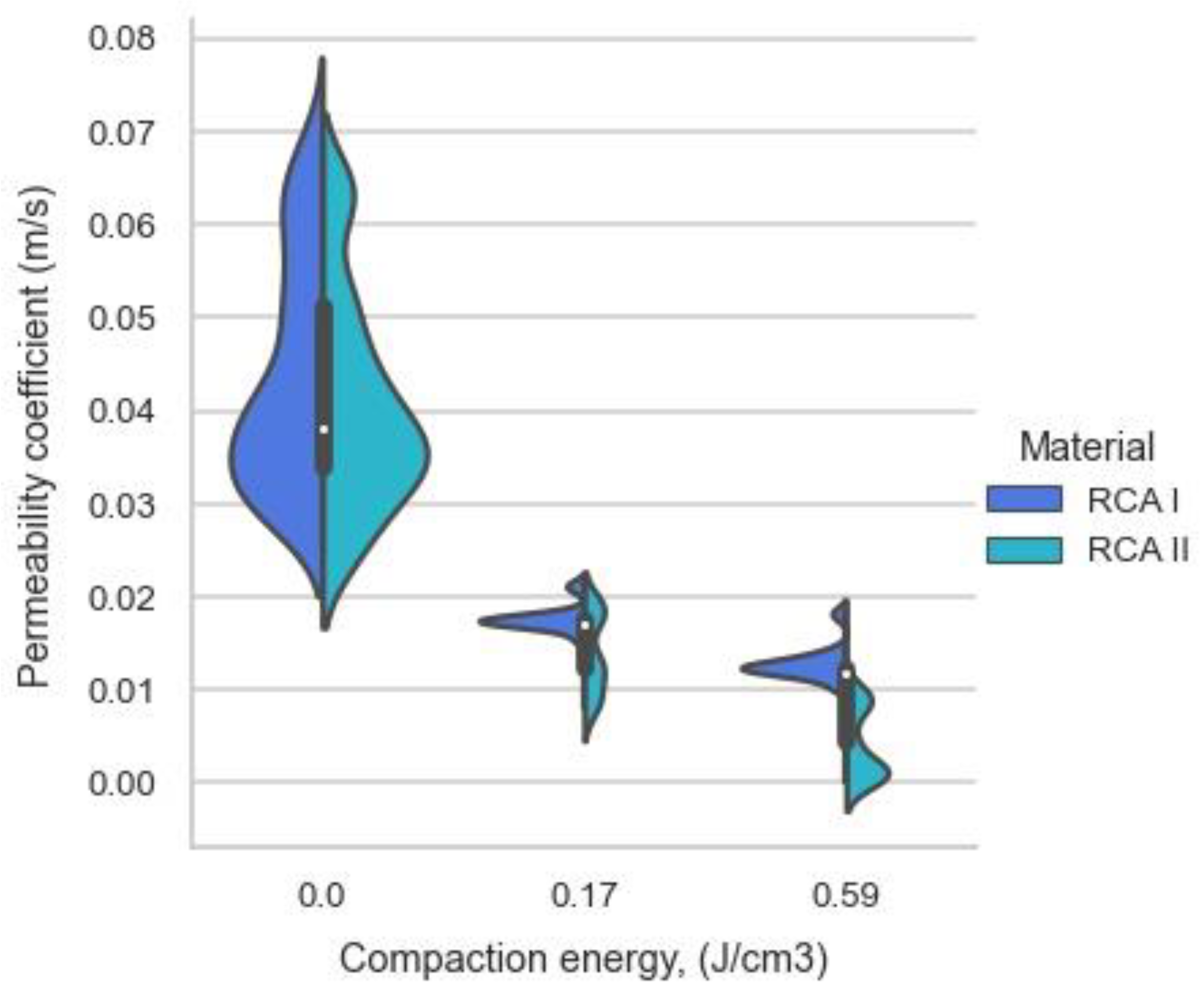
2.1. Materials and Filtration Study Method
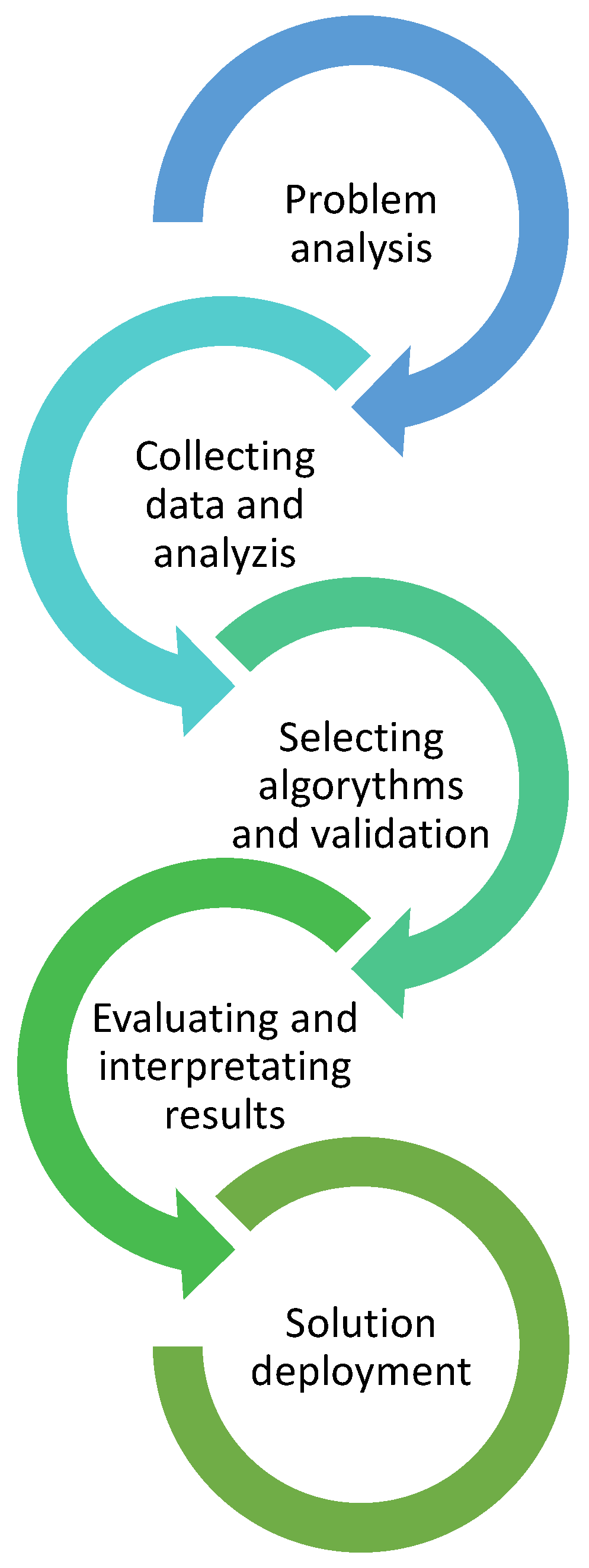
2.2. Data Preparation and Overall Methodology for the Applied Machine Learning Algorithms
2.3. Artificial Neural Networks
2.4. k-Nearest Neighbors
2.5. Error Analysis
- Mean square error (MSE) represents the mean squared difference between the raw and predicted values in a data set. It measures the variance of the residuals.
- Root mean square error (RMSE) is the square root of the mean squared error. It measures the standard deviation of the residuals.
- Mean absolute error (MAE) represents the average absolute difference between the observed and predicted values in a data set. It measures the average of the residuals in a data set.
- Coefficient of determination (R2) represents the portion of the variance of the dependent variable that is explained by the linear regression model. This is a scale-free result, i.e., whether the values are small or large, the R2 value will be less than one.
3. Results and Discussion
4. Conclusions
- The results of the study suggest that the methods of machine learning algorithms may be applicable for the prediction of the coefficient of permeability and, more broadly, geotechnical parameters.
- To ensure the quality and reliability of the estimated model, a sufficiently large database should be provided and continuously developed. Also important is the proper preparation of the database for analysis, which is the basis for the determination of reliable models.
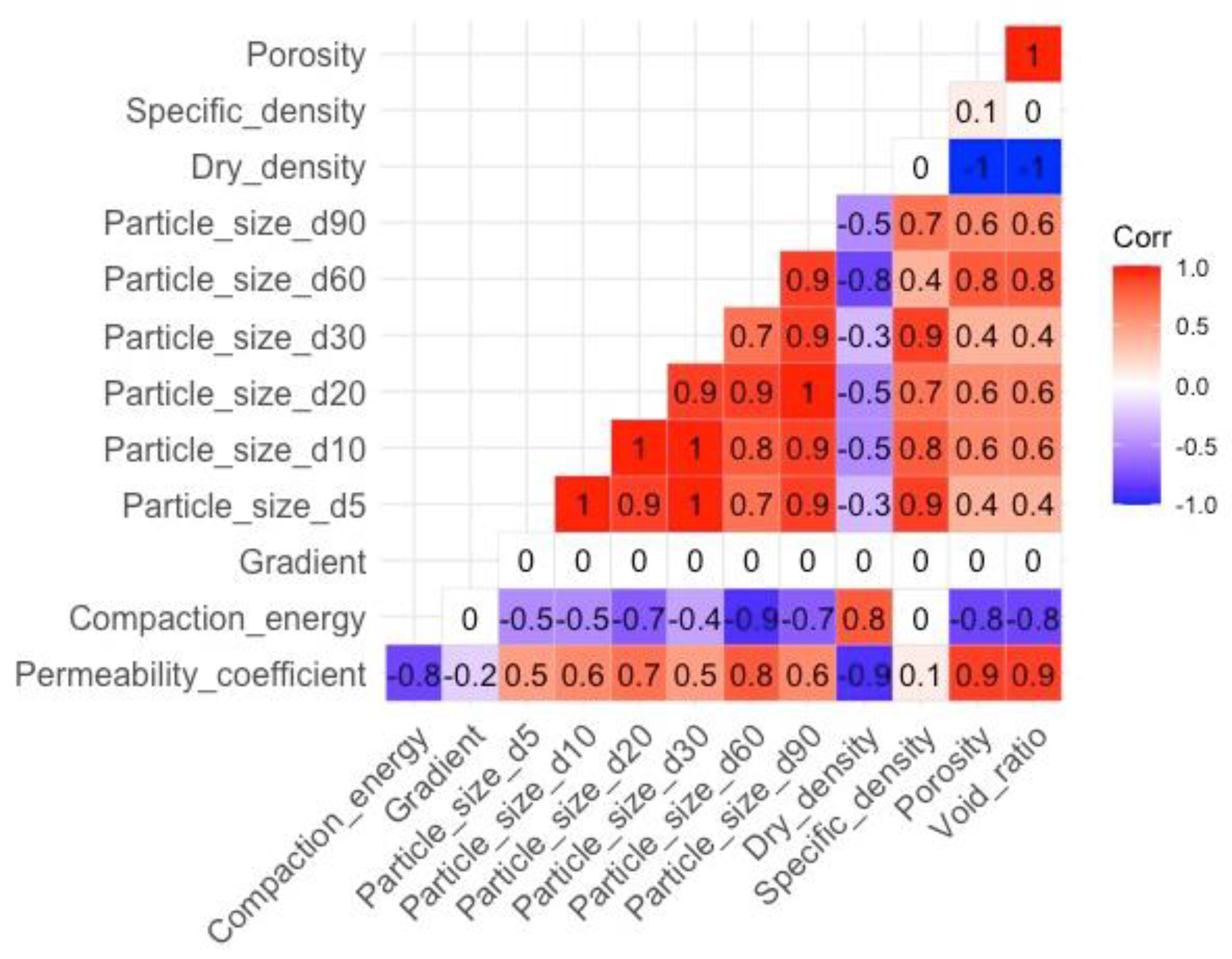
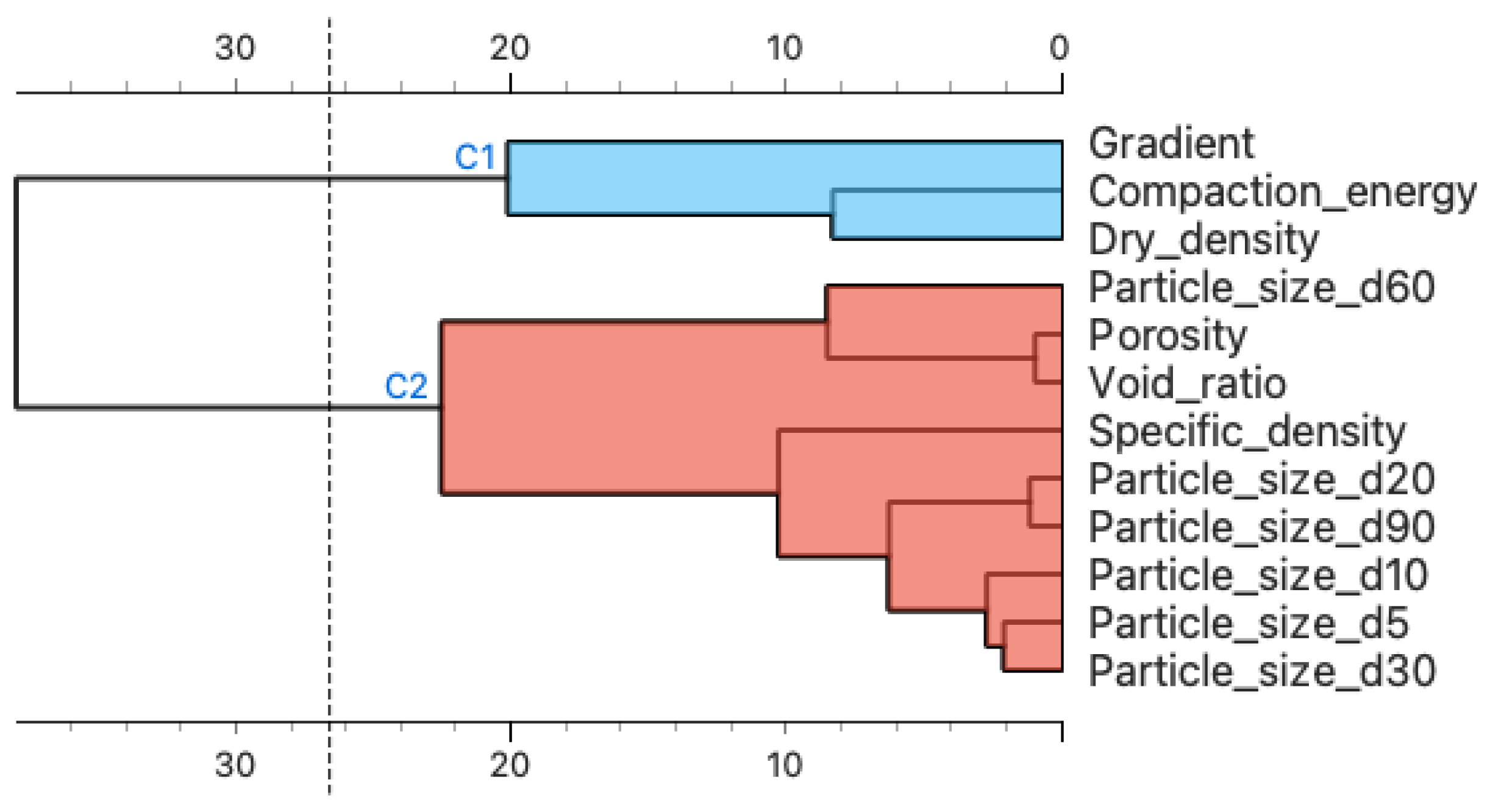
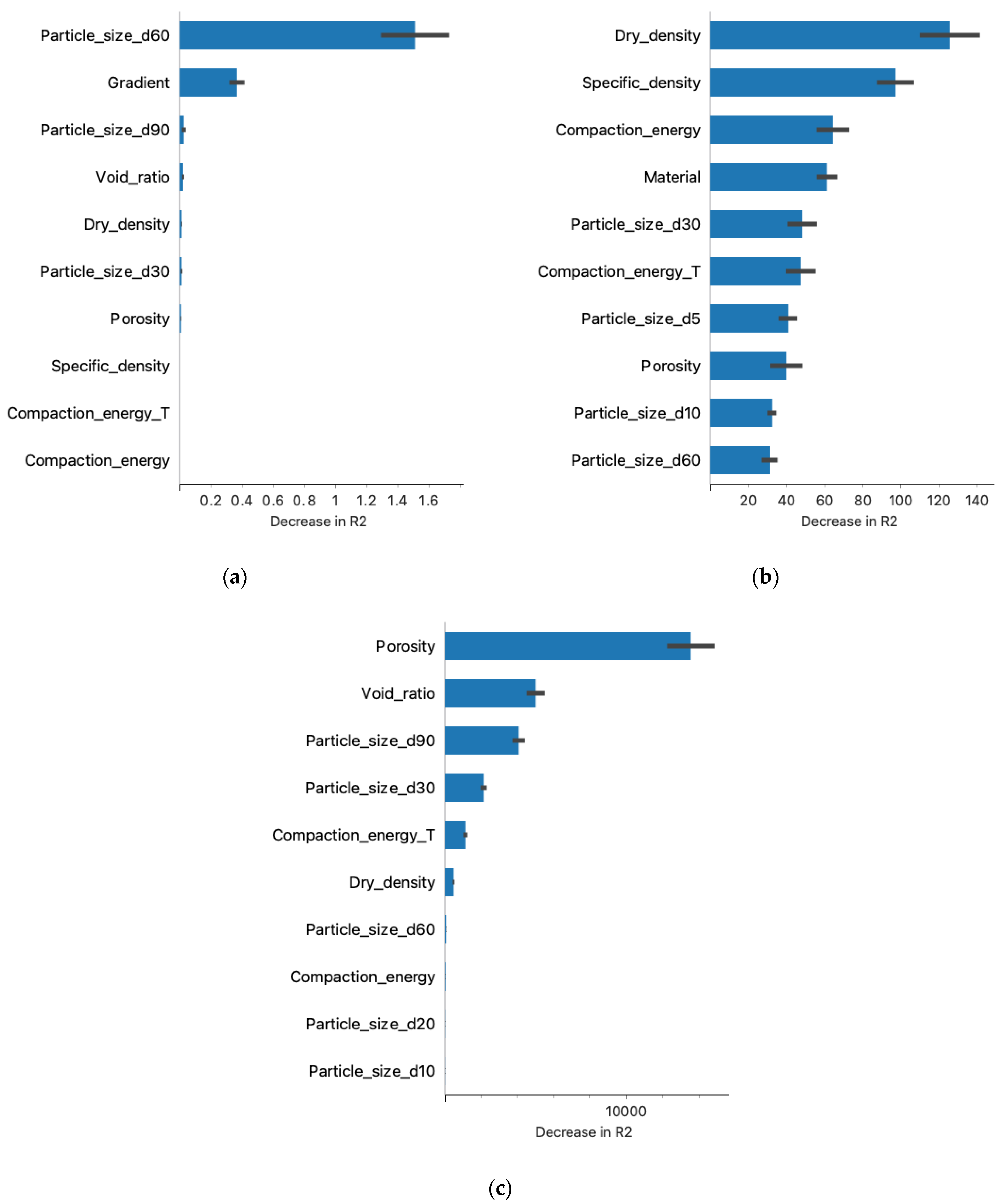
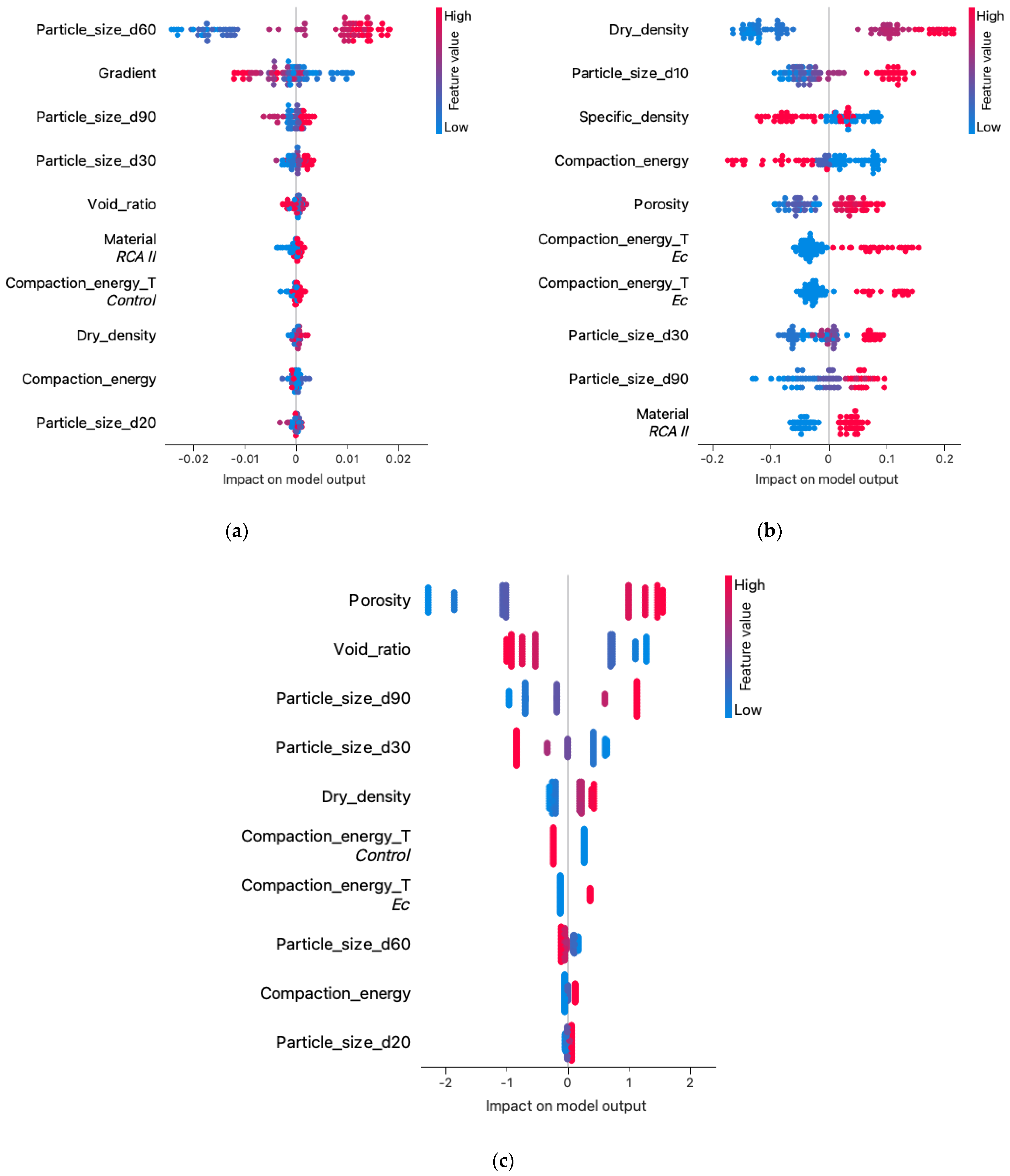
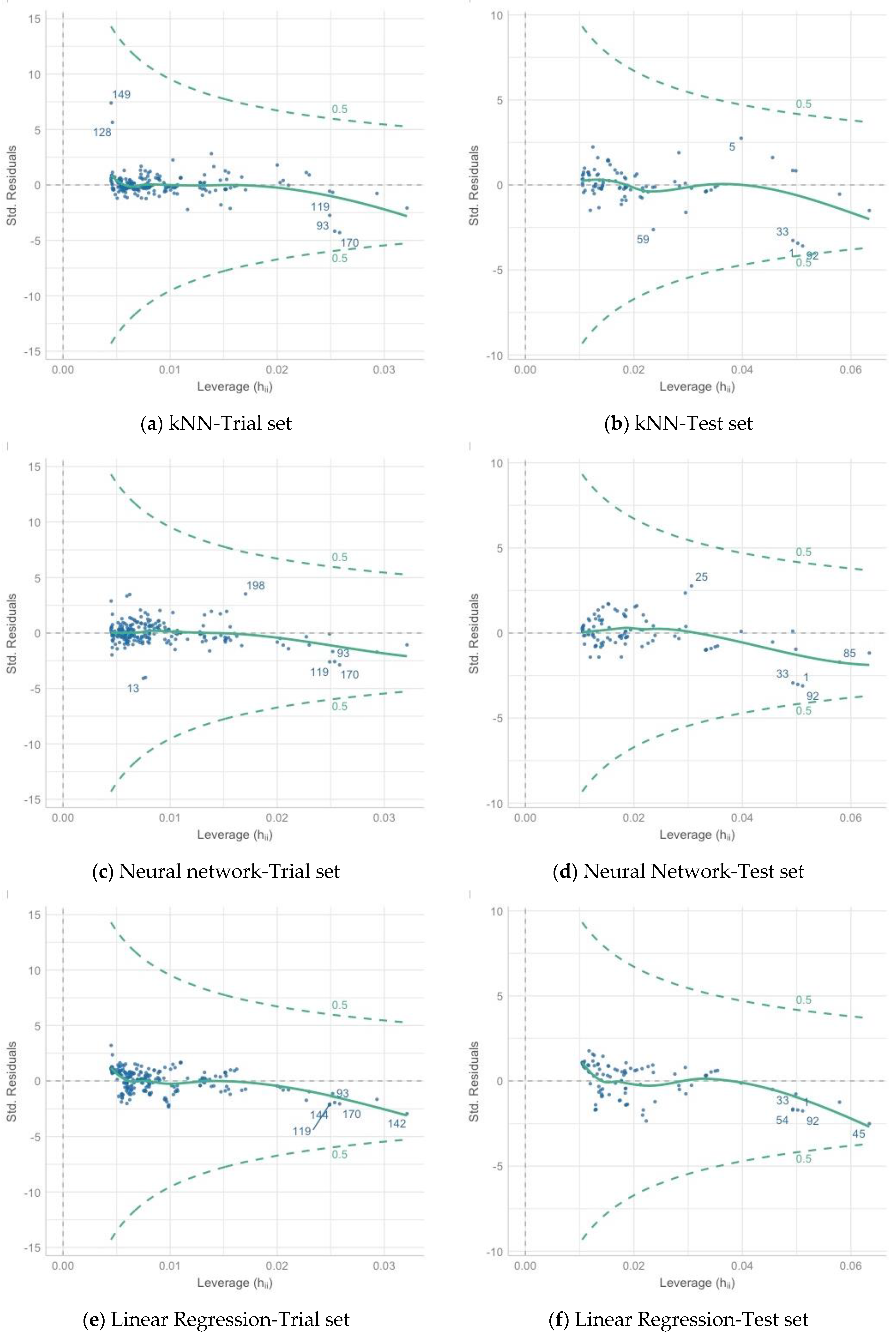
- The results of the post-prediction error analysis obtained for the k-NN algorithm may indicate the correct choice of the model for estimating the coefficient of permeability for recycled anthropogenic aggregates. Error analysis for the training sample showed an RMSE error of 0.004, while the MAE was 0.002. The coefficients of determination for both the training and test sets were accordingly 0.947 and 0.980. However, taking into consideration the analysis of significant characteristics impacting the explanation of the model (Figure 8 and Figure 9), one should take into account the lower resistance of the model to changes in the characteristics of materials.
- Given the above conclusions, the neural network model should also be considered. Admittedly, the model performs worse when analyzing errors (RMSE: 0.005–0.006 and MAE: 0.003–0.004) and R2 (0.877 for the trial set and 0.936 for the test set) than the model based on the k-NN algorithm, but it takes into account more features that affect the prediction of the model. As a result, it can affect lower errors when estimating the coefficient of permeability for other materials.
- According to Darcy’s law, the dependence of gradient and filtration velocity is linear, and most of the empirical equations formed based on this relation are linear regression. The research presented in this article proves that this model is not suitable for generalizing predictions based on the features and parameters of anthropogenic materials and allowing at the same time the consideration that machine learning algorithms are better suited to these prediction tasks.
- The analysis should be repeated for other anthropogenic and post-industrial materials used in civil engineering to validate the usefulness of the analyzed algorithms.
- The use of interpretive methods such as SHAP allows for better insight into the performance of the model and provides valuable information about parameters that have an important impact on the final model and are a significant part of the study. We suggest using interpretive machine learning methods to support decision criteria in civil engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benachio, G.L.F.; do Freitas, M.C.D.; Tavares, S.F. Circular Economy in the Construction Industry: A Systematic Literature Review. J. Clean. Prod. 2020, 260, 121046. [Google Scholar] [CrossRef]
- Silva, R.V.; de Brito, J.; Dhir, R.K. Availability and Processing of Recycled Aggregates within the Construction and Demolition Supply Chain: A Review. J. Clean. Prod. 2017, 143, 598–614. [Google Scholar] [CrossRef]
- Sharma, H.; Sharma, S.K.; Ashish, D.K.; Adhikary, S.K.; Singh, G. Effect of Various Bio-Deposition Treatment Techniques on Recycled Aggregate and Recycled Aggregate Concrete. J. Build. Eng. 2023, 66, 105868. [Google Scholar] [CrossRef]
- Basu, D.; Misra, A.; Puppala, A.J. Sustainability, and Geotechnical Engineering: Perspectives and Review. Can. Geotech. J. 2014, 52, 96–113. [Google Scholar] [CrossRef]
- MacAskill, K.; Guthrie, P. Risk-Based Approaches to Sustainability in Civil Engineering. Proc. Inst. Civ. Eng. Eng. Sustain. 2013, 166, 181–190. [Google Scholar] [CrossRef]
- Ghisellini, P.; Ripa, M.; Ulgiati, S. Exploring Environmental and Economic Costs and Benefits of a Circular Economy Approach to the Construction and Demolition Sector. A Literature Review. J. Clean. Prod. 2018, 178, 618–643. [Google Scholar] [CrossRef]
- Vieira, D.R.; Calmon, J.L.; Coelho, F.Z. Life Cycle Assessment (LCA) Applied to the Manufacturing of Common and Ecological Concrete: A Review. Constr. Build. Mater. 2016, 124, 656–666. [Google Scholar] [CrossRef]
- Dzięcioł, J.; Radziemska, M. Blast Furnace Slag, Post-Industrial Waste or Valuable Building Materials with Remediation Potential? Minerals 2022, 12, 478. [Google Scholar] [CrossRef]
- Pomponi, F.; Moncaster, A. Circular Economy for the Built Environment: A Research Framework. J. Clean. Prod. 2017, 143, 710–718. [Google Scholar] [CrossRef]
- Tuladhar, R.; Marshall, A.; Sivakugan, N. Use of Recycled Concrete Aggregate for Pavement Construction. Adv. Constr. Demolition Waste Recycl. 2020, 10, 181–197. [Google Scholar] [CrossRef]
- Cassiani, J.; Martinez-Arguelles, G.; Peñabaena-Niebles, R.; Keßler, S.; Dugarte, M. Sustainable Concrete Formulations to Mitigate Alkali-Silica Reaction in Recycled Concrete Aggregates (RCA) for Concrete Infrastructure. Constr. Build. Mater. 2021, 307, 124919. [Google Scholar] [CrossRef]
- Francioso, V.; Moro, C.; Velay-Lizancos, M. Effect of Recycled Concrete Aggregate (RCA) on Mortar’s Thermal Conductivity Susceptibility to Variations of Moisture Content and Ambient Temperature. J. Build. Eng. 2021, 43, 103208. [Google Scholar] [CrossRef]
- Sas, W.; Dziȩcioł, J.; Głuchowski, A. Estimation of Recycled Concrete Aggregate’swater Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method. Materials 2019, 12, 2920. [Google Scholar] [CrossRef]
- Głuchowski, A.; Sas, W.; Dziecioł, J.; Soból, E.; Szymaňski, A. Permeability and Leaching Properties of Recycled Concrete Aggregate as an Emerging Material in Civil Engineering. Appl. Sci. 2018, 9, 81. [Google Scholar] [CrossRef]
- Sas, W.; Dziȩcioł, J. Determination of the Filtration Rate for Anthropogenic Soil from the Recycled Concrete Aggregate by Analytical Methods. Sci. Rev. Eng. Environ. Sci. 2018, 27, 236–248. [Google Scholar] [CrossRef]
- Khambra, G.; Shukla, P. Novel Machine Learning Applications on Fly Ash Based Concrete: An Overview. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A Novel Hybrid Intelligent Model of Support Vector Machines and the MultiBoost Ensemble for Landslide Susceptibility Modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Shirzadi, A.; Shahabi, H.; Chapi, K.; Bui, D.T.; Pham, B.T.; Shahedi, K.; Ahmad, B.B. A Comparative Study between Popular Statistical and Machine Learning Methods for Simulating Volume of Landslides. Catena 2017, 157, 213–226. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Fu, J. Review on Application of Artificial Intelligence in Civil Engineering. CMES Comput. Model. Eng. Sci. 2019, 121, 845–875. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H. Artificial Intelligence for Civil Engineering. Tumu Gongcheng Xuebao China Civ. Eng. J. 2019, 52, 1–11. [Google Scholar]
- Pham, B.T.; Prakash, I.; Jaafari, A.; Bui, D.T. Spatial Prediction of Rainfall-Induced Landslides Using Aggregating One-Dependence Estimators Classifier. J. Indian Soc. Remote Sens. 2018, 46, 1457–1470. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Recent Advances and Future Challenges for Artificial Neural Systems in Geotechnical Engineering Applications. Adv. Artif. Neural Syst. 2009, 2009, 308239. [Google Scholar] [CrossRef]
- Mishra, P.; Samui, P.; Mahmoudi, E. Probabilistic Design of Retaining Wall Using Machine Learning Methods. Appl. Sci. 2021, 11, 5411. [Google Scholar] [CrossRef]
- Amin, M.N.; Iqtidar, A.; Khan, K.; Javed, M.F.; Shalabi, F.I.; Qadir, M.G. Comparison of Machine Learning Approaches with Traditional Methods for Predicting the Compressive Strength of Rice Husk Ash Concrete. Crystals 2021, 11, 779. [Google Scholar] [CrossRef]
- Lechowicz, Z.; Sulewska, M.J. Assessment of the Undrained Shear Strength and Settlement of Organic Soils under Embankment Loading Using Artificial Neural Networks. Materials 2022, 16, 125. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pratama Putra Thedja, J. Metaheuristic Optimization within Machine Learning-Based Classification System for Early Warnings Related to Geotechnical Problems. Autom. Constr. 2016, 68, 65–80. [Google Scholar] [CrossRef]
- Legendre, A.M. Nouvelles Méthodes Pour La Détermination Des Orbites Des Comètes; F. Didot: Paris, France, 1806. [Google Scholar]
- McCarthy, J.; Minsky, M.L.; Shannon, C.E. A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence–31 August 1955. AI Mag. 1955, 27, 12–14. [Google Scholar]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- da Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial Neural Networks: A Practical Course; Springer International Publishing: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Krogh, A. What Are Artificial Neural Networks? In Nature Biotechnology; Nature Publishing Group: London, UK, 2008; pp. 195–197. [Google Scholar] [CrossRef]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary Artificial Neural Networks: A Review. In Artificial Intelligence Review; Springer: Berlin/Heidelberg, Germany, 2013; pp. 251–260. [Google Scholar] [CrossRef]
- Yang, X. Artificial Neural Networks. In Handbook of Research on Geoinformatics; IGI Global: Hershey, PA, USA, 2009; pp. 122–128. [Google Scholar] [CrossRef]
- White, H. Learning in Artificial Neural Networks: A Statistical Perspective. Neural Comput. 1989, 1, 425–464. [Google Scholar] [CrossRef]
- Trach, R.; Trach, Y.; Lendo-Siwicka, M. Using ANN to Predict the Impact of Communication Factors on the Rework Cost in Construction Projects. Energies 2021, 14, 4376. [Google Scholar] [CrossRef]
- Yu, K.; Ji, L.; Zhang, X. Kernel Nearest-Neighbor Algorithm. Neural Process. Lett. 2002, 15, 147–156. [Google Scholar] [CrossRef]
- Chernoff, K.; Nielsen, M. Weighting of the K-Nearest-Neighbors. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 666–669. [Google Scholar] [CrossRef]
- Kramer, O. Dimensionality Reduction by Unsupervised k-Nearest Neighbor Regression. In Proceedings of the 10th International Conference on Machine Learning and Applications and Applications and Workshops, Honolulu, HI, USA, 18–21 December 2011; Volume 1, pp. 275–278. [Google Scholar] [CrossRef]
- KNN: K-Nearest Neighbors. In The Top Ten Algorithms in Data Mining; Chapman and Hall/CRC: New York, NY, USA, 2020; pp. 165–176. [CrossRef]
- Ghatak, A. Machine Learning with R; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Carbonell, J.G.; Michalski, R.S.; Mitchell, T.M. An overview of machine learning. Mach. Learn. 1983, 1, 3–23. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA; London, UK, 2004. [Google Scholar]
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.X.; Chen, J.; Wei, Z.; Lei, M. Machine Learning in Materials Science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
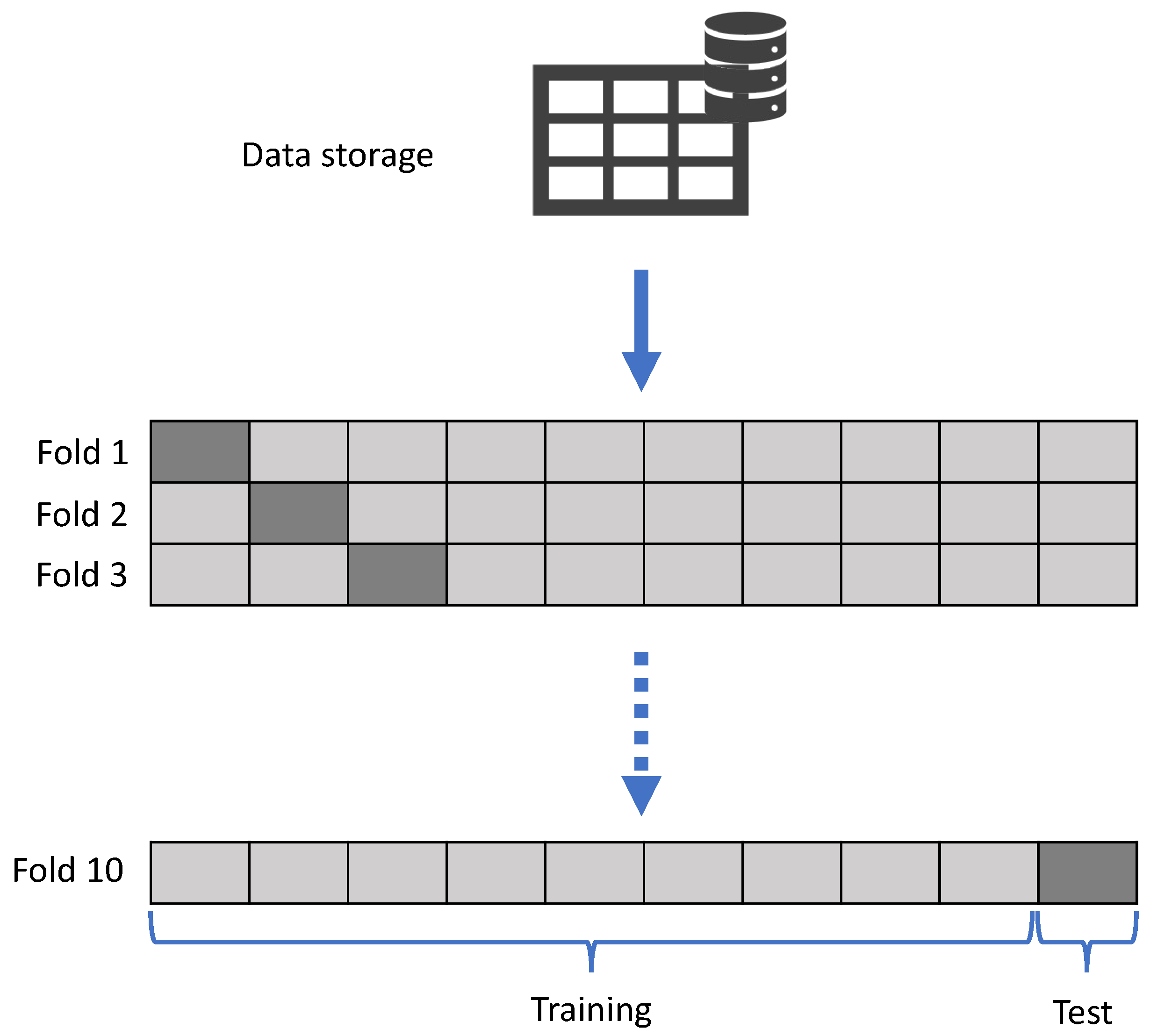
- Fushiki, T. Estimation of Prediction Error by Using K-Fold Cross-Validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Browne, M.W. Cross-Validation Methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef] [PubMed]
- Revilla-Cuesta, V.; Skaf, M.; Faleschini, F.; Manso, J.M.; Ortega-López, V. Self-Compacting Concrete Manufactured with Recycled Concrete Aggregate: An Overview. J. Clean. Prod. 2020, 262, 121362. [Google Scholar] [CrossRef]
- Bai, G.; Zhu, C.; Liu, C.; Liu, B. An Evaluation of the Recycled Aggregate Characteristics and the Recycled Aggregate Concrete Mechanical Properties. Constr. Build. Mater. 2020, 240, 117978. [Google Scholar] [CrossRef]
- Silva, S.; Evangelista, L.; de Brito, J. Durability and Shrinkage Performance of Concrete Made with Coarse Multi-Recycled Concrete Aggregates. Constr. Build. Mater. 2021, 272, 121645. [Google Scholar] [CrossRef]
- Zhang, Z. Introduction to Machine Learning: K-Nearest Neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef]
- Hart, S. Shapley Value. In Game Theory; Palgrave Macmillan: London, UK, 1989; pp. 210–216. [Google Scholar] [CrossRef]
- Winter, E. Chapter 53: The Shapley Value. Handb. Game Theory Econ. Appl. 2002, 3, 2025–2054. [Google Scholar] [CrossRef]
- Merrick, L.; Taly, A. The Explanation Game: Explaining Machine Learning Models Using Shapley Values. Lect. Notes Comput. Sci. 2020, 12279 LNCS, 17–38. [Google Scholar] [CrossRef]
- Quan Tran, V.; Quoc Dang, V.; Si Ho, L. Evaluating Compressive Strength of Concrete Made with Recycled Concrete Aggregates Using Machine Learning Approach. Constr. Build. Mater. 2022, 323, 126578. [Google Scholar] [CrossRef]

| Description | Mean Value |
|---|---|
| Particle size d5 [mm] | 0.27 |
| Particle size d10 [mm] | 0.60 |
| Particle size d20 [mm] | 1.78 |
| Particle size d30 [mm] | 3.38 |
| Particle size d60 [mm] | 11.06 |
| Particle size d90 [mm] | 23.38 |
| Dry density [g/cm3] | 1.35 |
| Porosity [-] | 0.465 |
| Void ratio [-] | 0.902 |
| Trial Set | ||||
|---|---|---|---|---|
| Model | MSE | RMSE | MAE | R2 |
| kNN | 0.000 | 0.004 | 0.002 | 0.947 |
| Neural network | 0.000 | 0.006 | 0.004 | 0.877 |
| Linear regresion | 0.000 | 0.007 | 0.005 | 0.829 |
| Test Set | ||||
|---|---|---|---|---|
| Model | MSE | RMSE | MAE | R2 |
| kNN | 0.000 | 0.003 | 0.002 | 0.980 |
| Neural network | 0.000 | 0.005 | 0.003 | 0.936 |
| Linear regresion | 0.000 | 0.007 | 0.006 | 0.844 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzięcioł, J.; Sas, W. Perspective on the Application of Machine Learning Algorithms for Flow Parameter Estimation in Recycled Concrete Aggregate. Materials 2023, 16, 1500. https://doi.org/10.3390/ma16041500
Dzięcioł J, Sas W. Perspective on the Application of Machine Learning Algorithms for Flow Parameter Estimation in Recycled Concrete Aggregate. Materials. 2023; 16(4):1500. https://doi.org/10.3390/ma16041500
Chicago/Turabian StyleDzięcioł, Justyna, and Wojciech Sas. 2023. "Perspective on the Application of Machine Learning Algorithms for Flow Parameter Estimation in Recycled Concrete Aggregate" Materials 16, no. 4: 1500. https://doi.org/10.3390/ma16041500
APA StyleDzięcioł, J., & Sas, W. (2023). Perspective on the Application of Machine Learning Algorithms for Flow Parameter Estimation in Recycled Concrete Aggregate. Materials, 16(4), 1500. https://doi.org/10.3390/ma16041500







