Load-Oriented Nonplanar Additive Manufacturing Method for Optimized Continuous Carbon Fiber Parts
Abstract
1. Introduction
1.1. Prior Work
1.2. Developed Method
- 1.
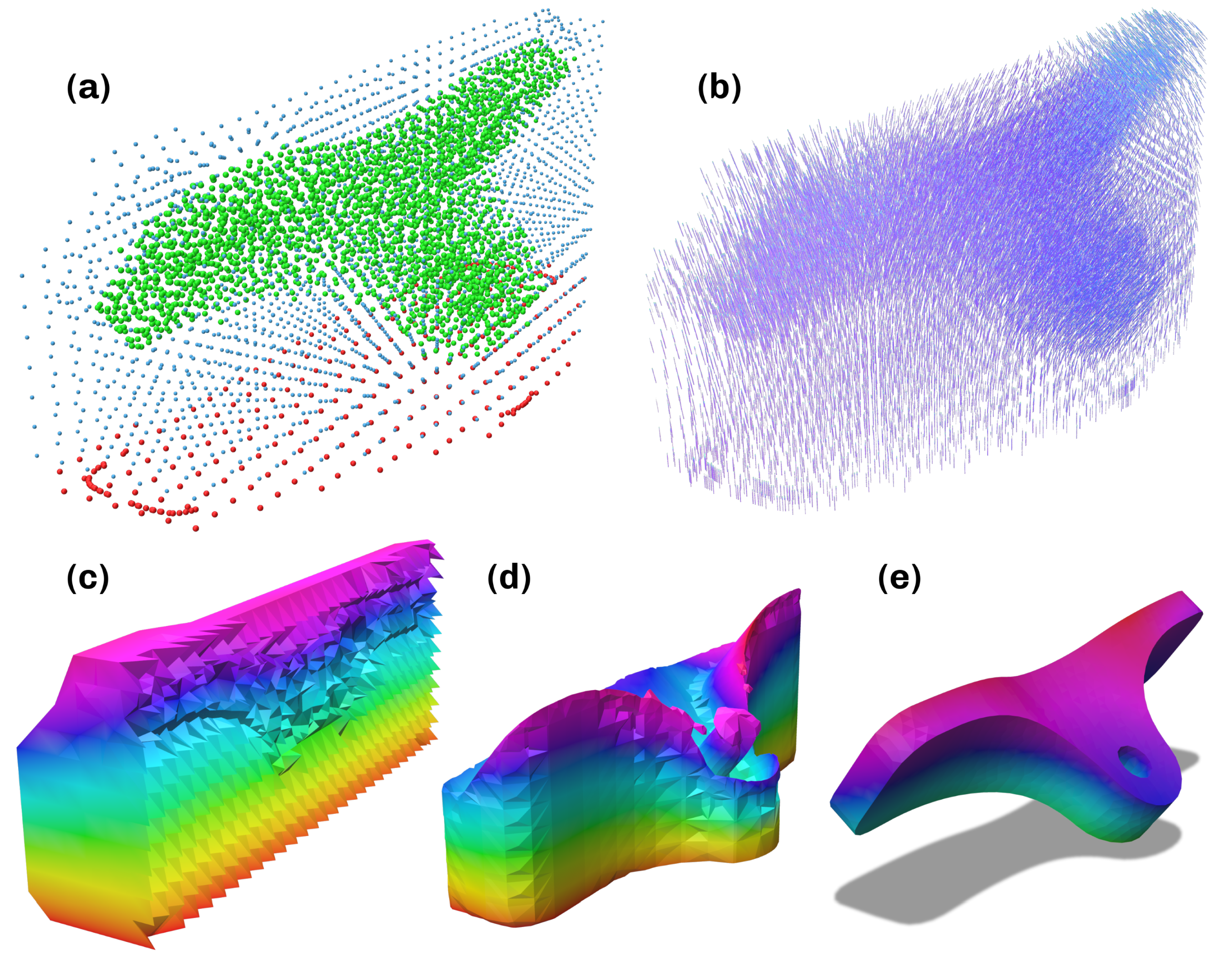
- The procedure starts by conducting an FEA in an external software to extract the major principal stresses and direction vectors. Boundary conditions are defined and the geometry is established, possibly through topology optimization. The output of this process is a tetrahedral mesh with information on the stress tensor stored for every element.
- 2.
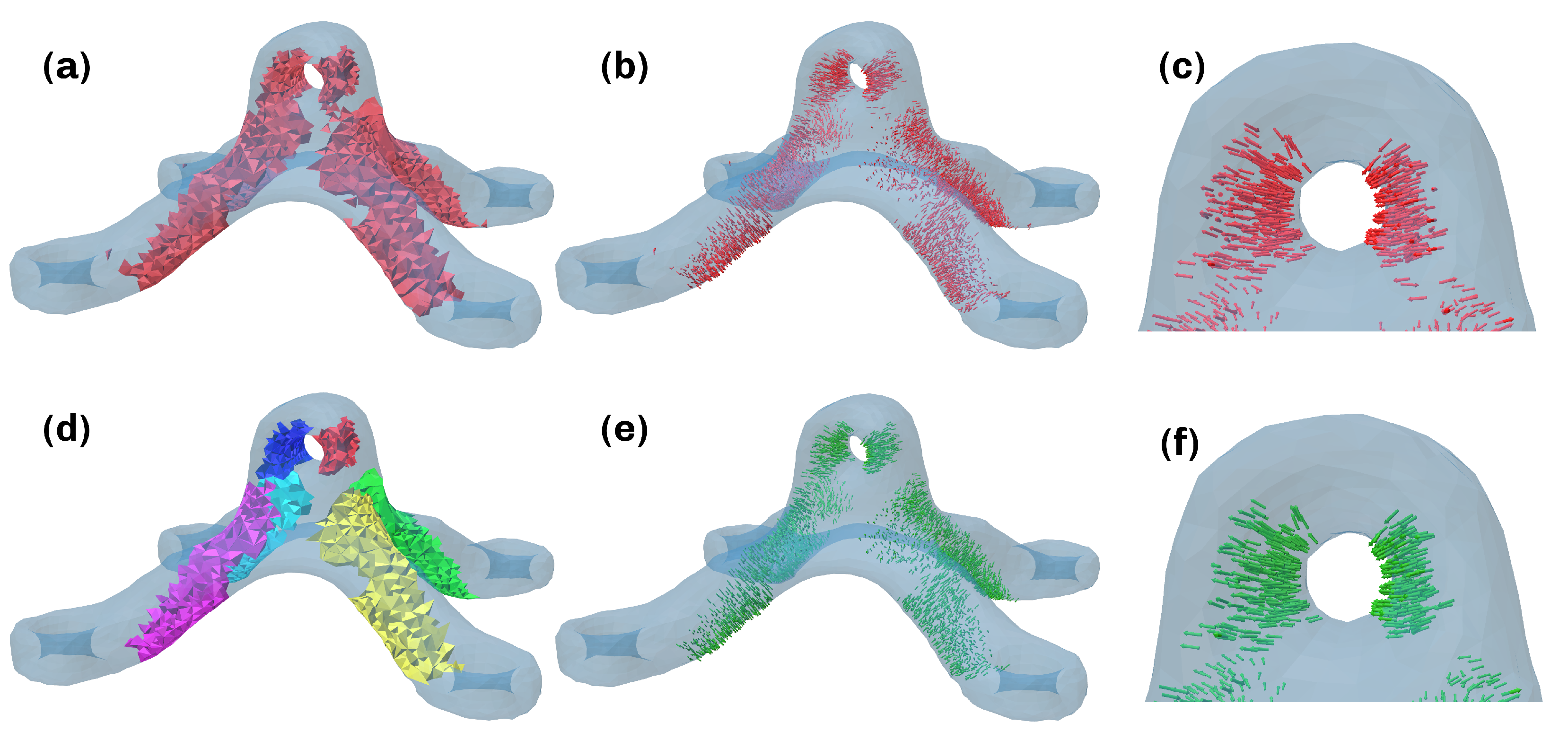
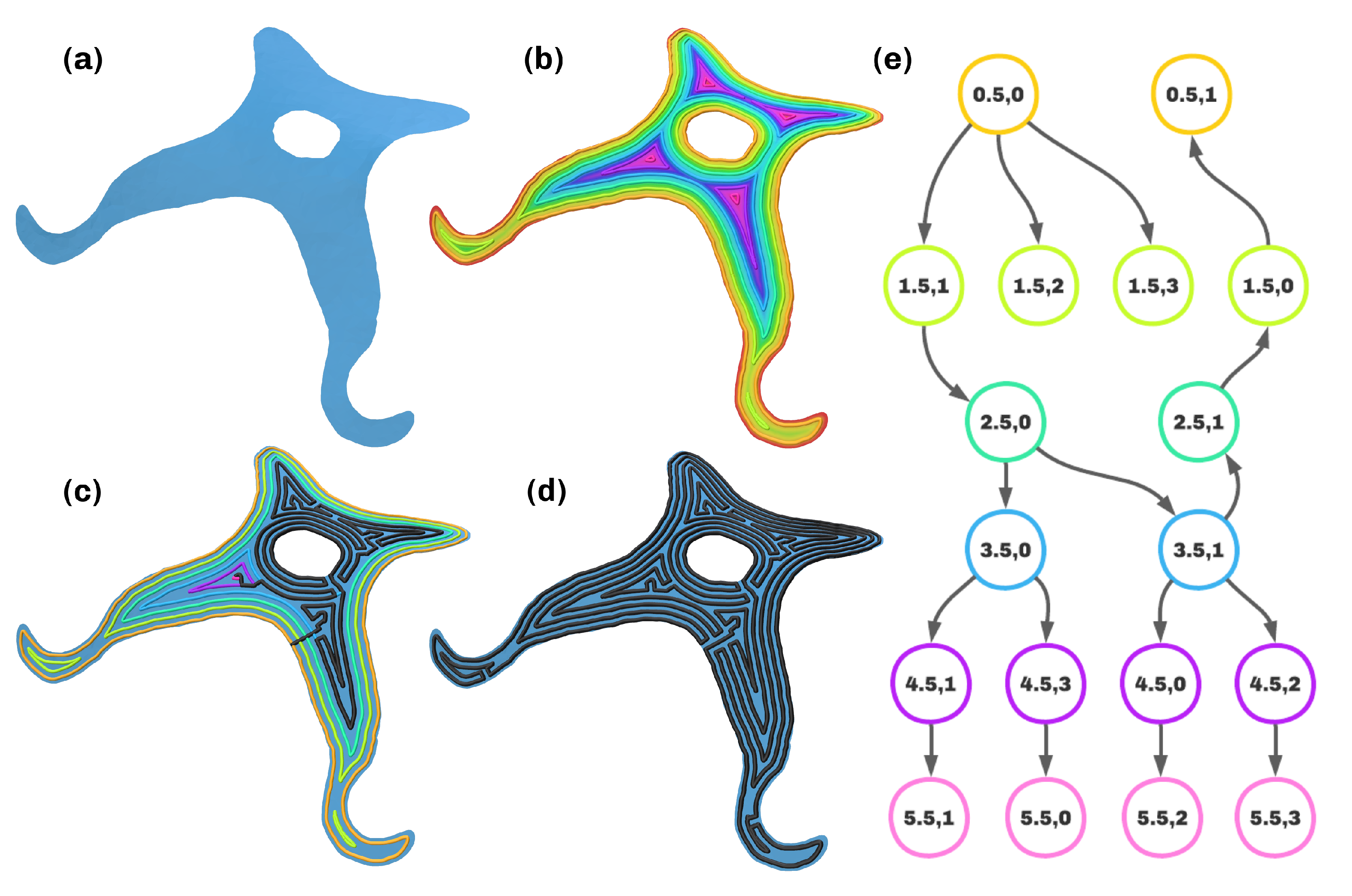
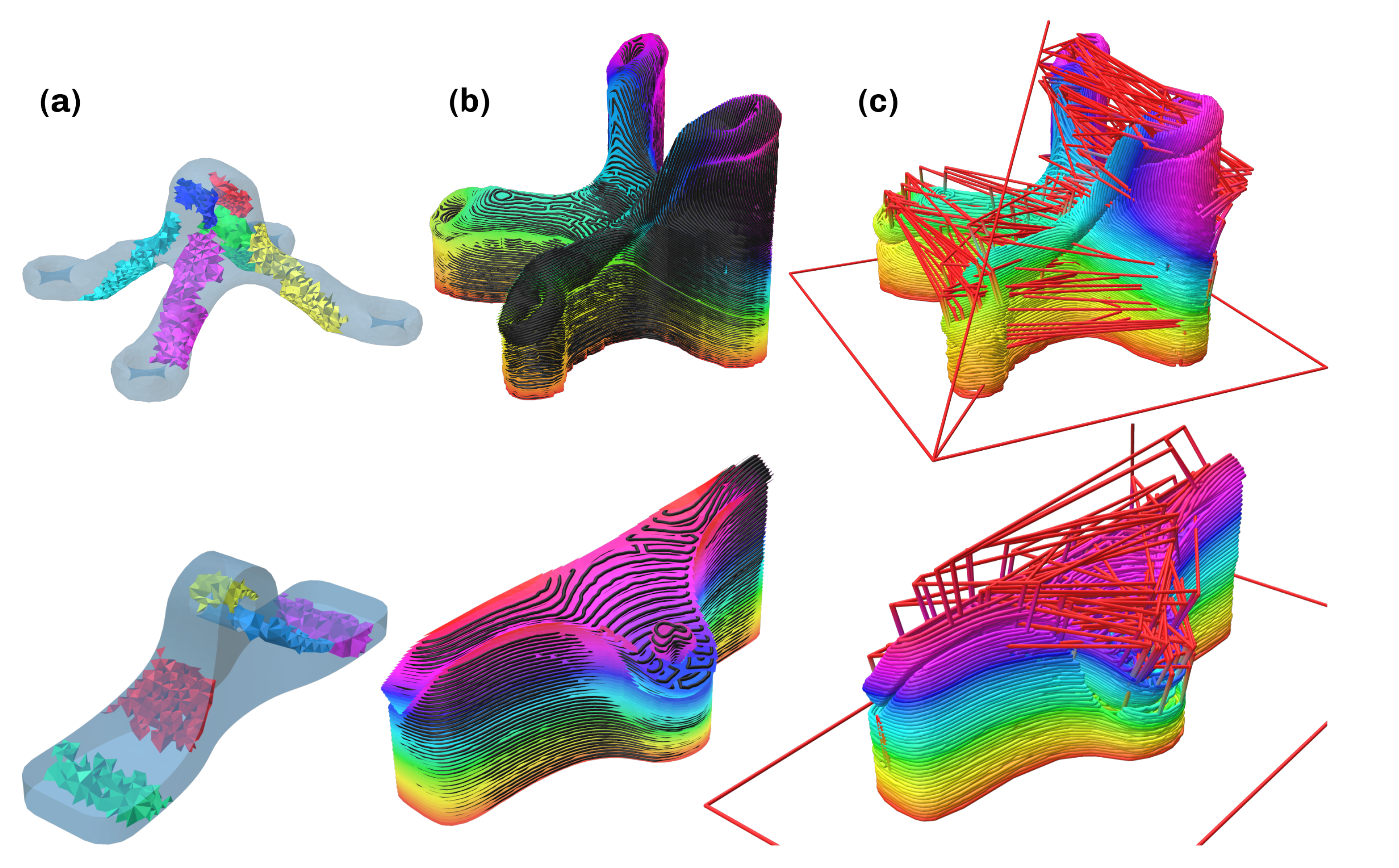
- To circumvent the sometimes highly turbulent and divergent properties of the field of minimal principal directions, critical regions in the part are identified. These are determined as the set of elements that surpass a user-defined threshold and then are labeled corresponding to the region’s connectivity and compatibility.
- 3.
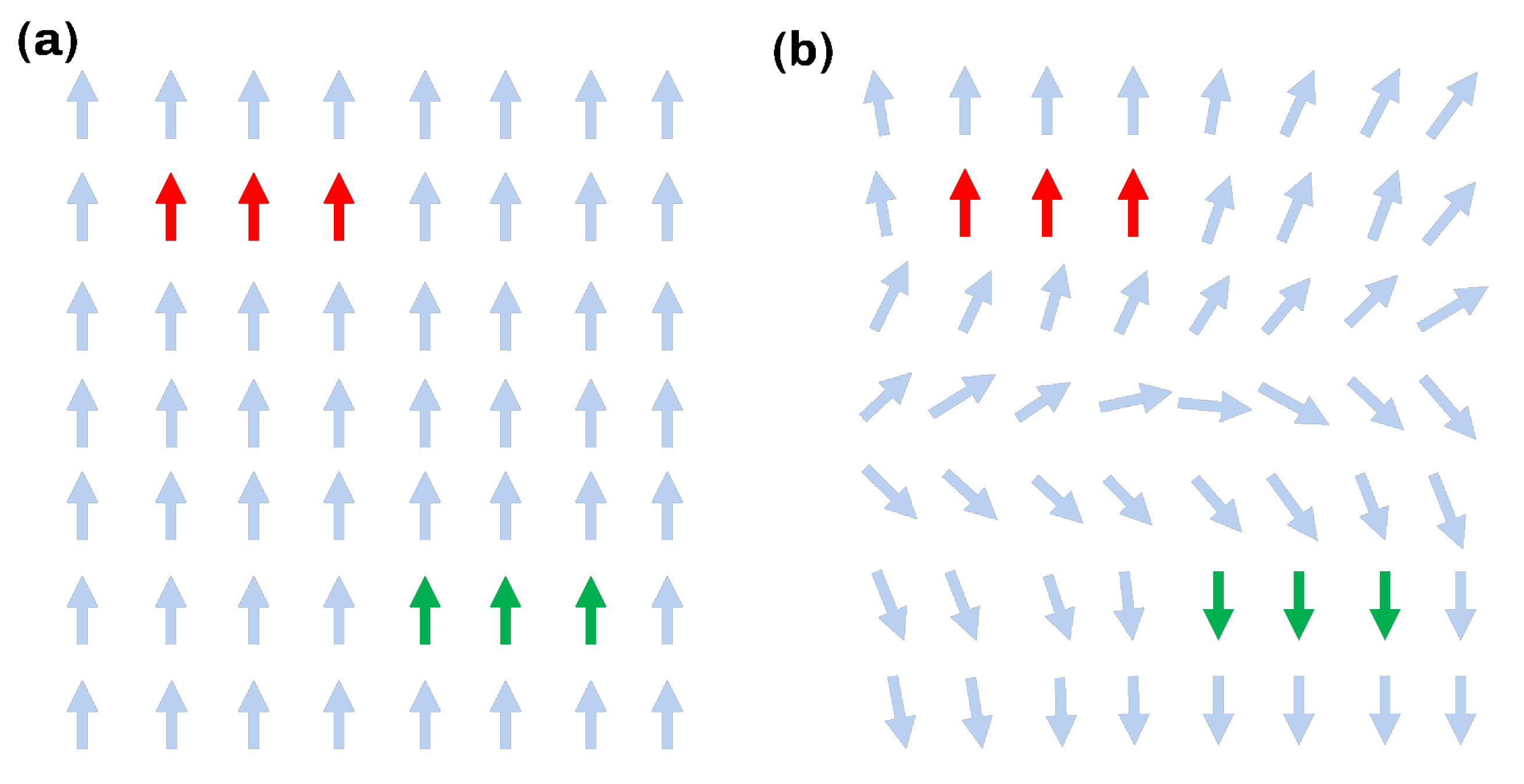
- The minimum principal directions in these regions are used as the source for a construction of an optimized vector field. This is performed by minimizing the Dirichlet energy, resulting in smooth transitions between the regions. Special attention has to be paid to the ambiguity of orientation, as the coordinate frames resulting from the principal axis transform are independent of sign.
- 4.
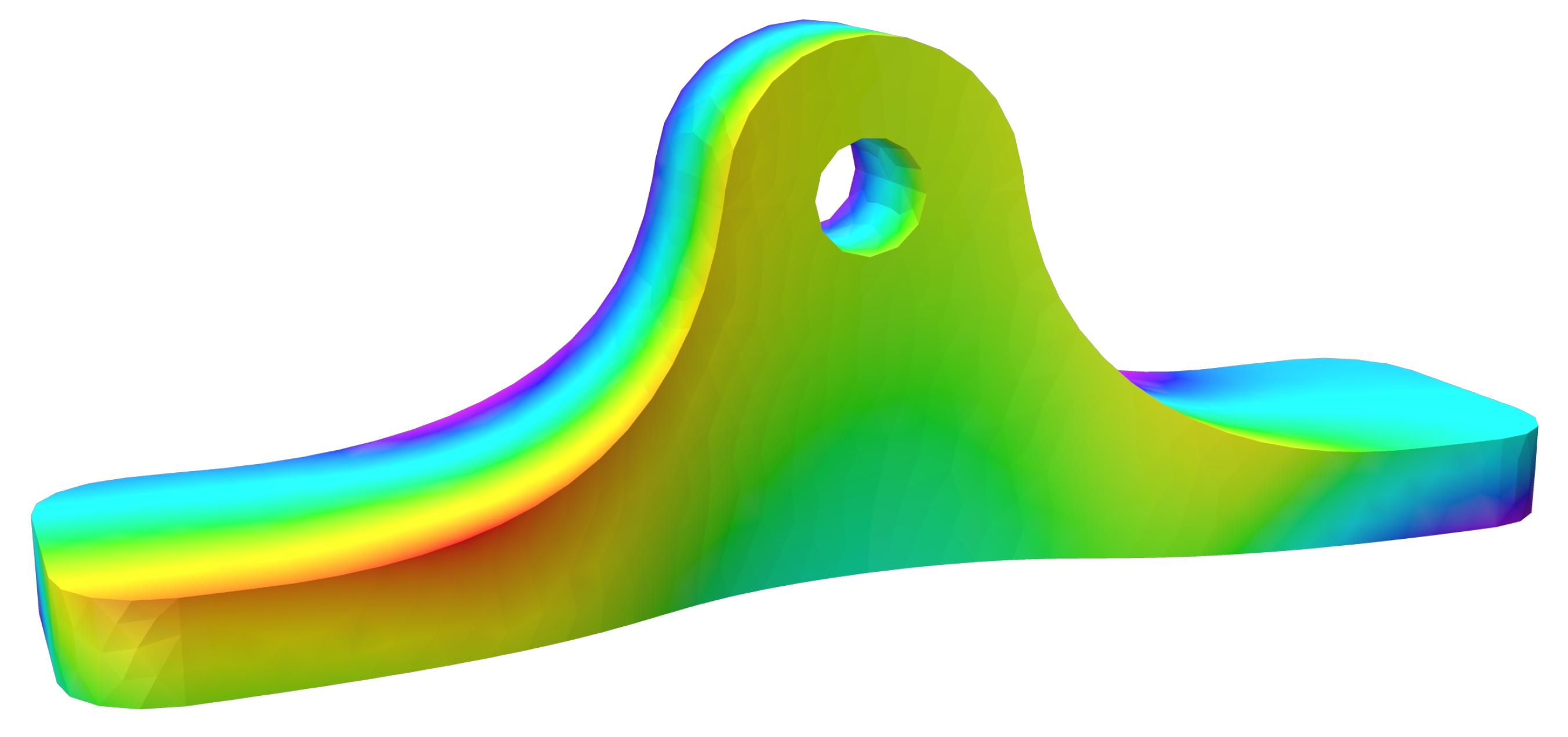
- The optimized scalar field is then computed by minimizing the difference of its gradient to the determined vector field.
- 5.
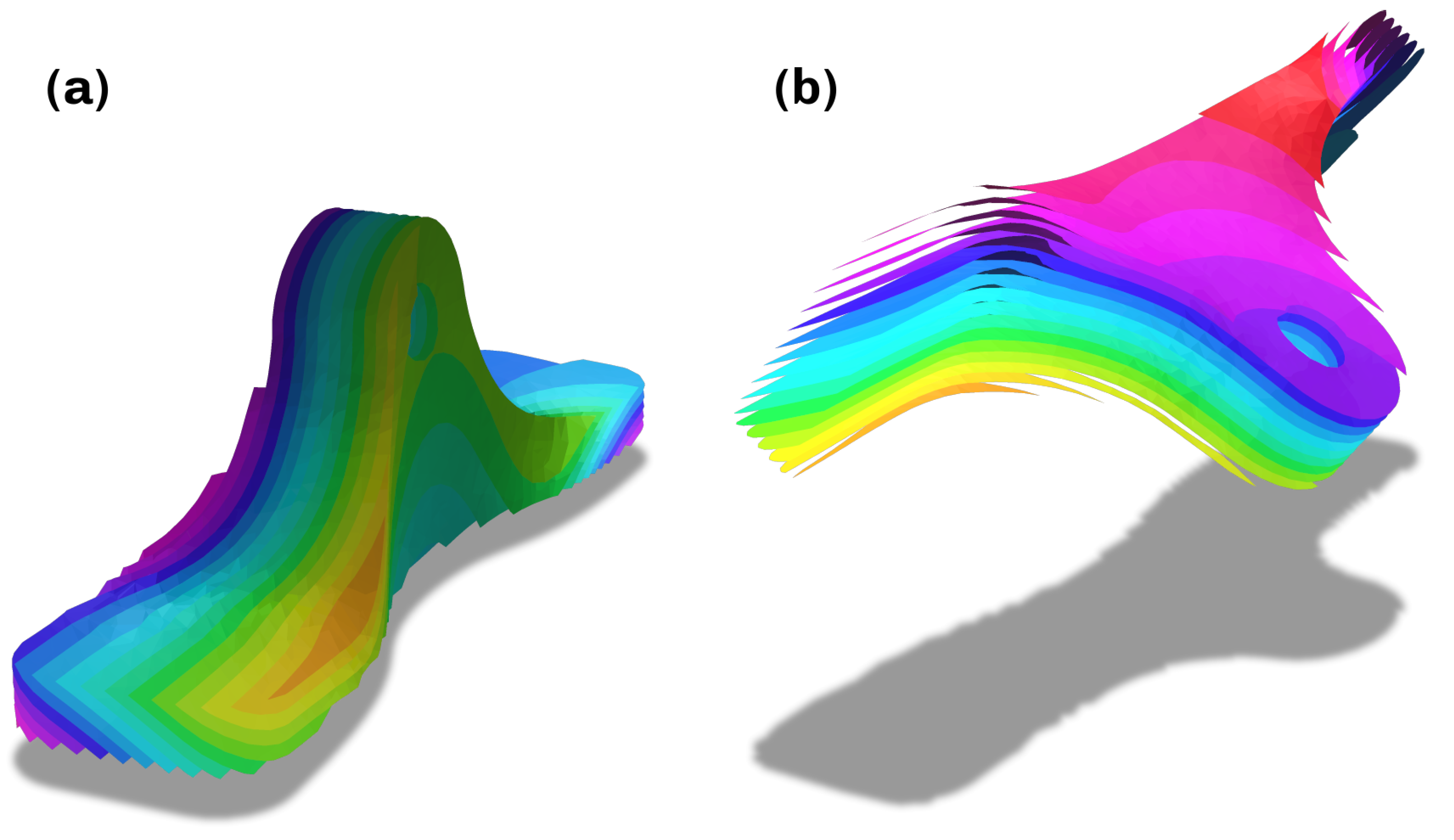
- After computing the supporting structures geometry, the process above is repeated with a critical region being added at the printing bed to ensure the first layer being planar. Slicing the scalar field at fixed values corresponding to the user-defined layer height yields the constituting surfaces for both the support and part. This ensures the compatibility of the layers along the parts outer surface.
- 6.
- Pathplanning with the continuous FISO algorithm is executed, and the subpaths are connected with travel motions.
- 7.
- Finally, post-processing of the path results in machine instructions to be executed on a multi-axis printer.
2. Methods and Derivation
3. Algorithm
3.1. Critical Regions
3.2. Vector Field
3.3. Optimized Scalar Field
3.4. Slicing and Support
3.4.1. Slicing
3.4.2. Orientation and Preprocessing
3.4.3. Support
3.5. Pathplanning
3.6. Post-Processing
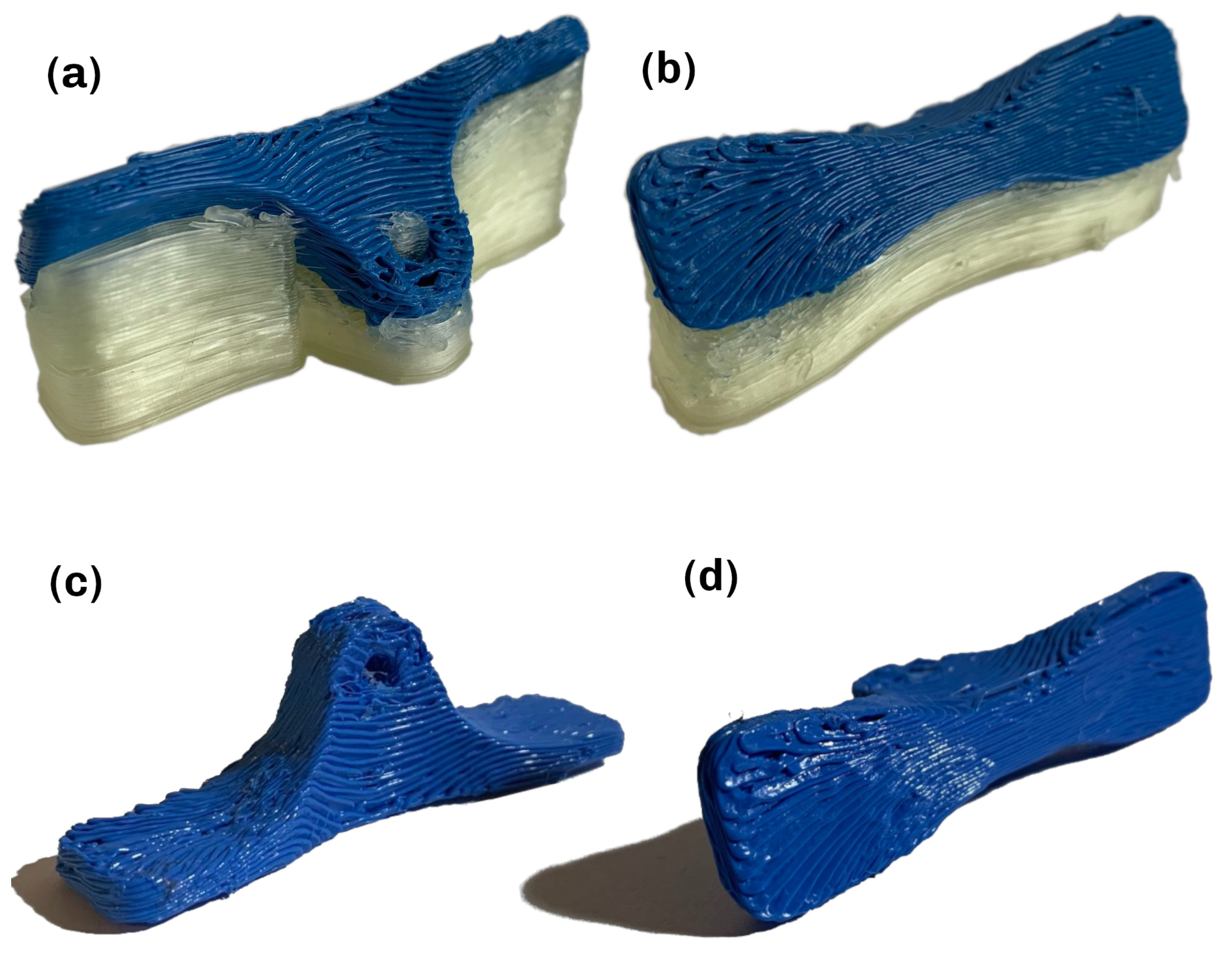
4. Results
5. Conclusions and Prospects
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| CAD | Computer-aided design |
| CFRP | Carbon-fiber-reinforced polymers |
| FDM | Fused deposition modeling |
| FEA | Finite-element-analysis |
| FEM | Finite-element-methods |
| FISO | First in spiral out |
| PLA | Polylactic acid |
| PVA | Polyvinyl alcohol |
| SIMP | Solid isotropic material with penalization |
| SOMP | Solid orthotropic material with penalization |
References
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, W.; Zhou, K. Recent Progress on Polymer Materials for Additive Manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Sanei, S.H.R.; Popescu, D. 3D-Printed Carbon Fiber Reinforced Polymer Composites: A Systematic Review. J. Compos. Sci. 2020, 4, 98. [Google Scholar] [CrossRef]
- Pandelidi, C.; Bateman, S.; Piegert, S.; Hoehner, R.; Kelbassa, I.; Brandt, M. The technology of continuous fibre-reinforced polymers: A review on extrusion additive manufacturing methods. Int. J. Adv. Manuf. Technol. 2021, 113, 3057–3077. [Google Scholar] [CrossRef]
- Dickson, A.N.; Abourayana, H.M.; Dowling, D.P. 3D Printing of Fibre-Reinforced Thermoplastic Composites Using Fused Filament Fabrication-A Review. Polymers 2020, 12, 2188. [Google Scholar] [CrossRef]
- Zhuo, P.; Li, S.; Ashcroft, I.A.; Jones, A.I. Material extrusion additive manufacturing of continuous fibre reinforced polymer matrix composites: A review and outlook. Compos. Part B Eng. 2021, 224, 109143. [Google Scholar] [CrossRef]
- de vivo, L. Design and Manufacture of Optimized Continuous Composite Fiber Filament Using Additive Manufacturing Systems. J. Mater. Sci. Eng. 2017, 6, 363. [Google Scholar] [CrossRef]
- Nayyeri, P.; Zareinia, K.; Bougherara, H. Planar and nonplanar slicing algorithms for fused deposition modeling technology: A critical review. Int. J. Adv. Manuf. Technol. 2022, 119, 2785–2810. [Google Scholar] [CrossRef]
- Marchal, V.; Zhang, Y.; Labed, N.; Peyraut, F. Experimental investigation of the impacts of fibre routing strategy on the properties of composite printing. Procedia CIRP 2022, 109, 311–315. [Google Scholar] [CrossRef]
- Chen, X.; Fang, G.; Liao, W.H.; Wang, C.C. Field-Based Toolpath Generation for 3D Printing Continuous Fibre Reinforced Thermoplastic Composites. Addit. Manuf. 2022, 49, 102470. [Google Scholar] [CrossRef]
- Hou, Z.; Tian, X.; Zhang, J.; Zheng, Z.; Zhe, L.; Li, D.; Malakhov, A.V.; Polilov, A.N. Optimization design and 3D printing of curvilinear fiber reinforced variable stiffness composites. Compos. Sci. Technol. 2021, 201, 108502. [Google Scholar] [CrossRef]
- Plocher, J.; Wioland, J.B.; Panesar, A.S. Additive manufacturing with fibre-reinforcement—Design guidelines and investigation into the influence of infill patterns. Rapid Prototyp. J. 2022, 28, 1241–1259. [Google Scholar] [CrossRef]
- Fang, G.; Zhang, T.; Zhong, S.; Chen, X.; Zhong, Z.; Wang, C.C.L. Reinforced FDM: Multi-Axis Filament Alignment with Controlled Anisotropic Strength. ACM Trans. Graph. 2020, 39, 204. [Google Scholar] [CrossRef]
- Yamanaka, Y.; Todoroki, A.; Ueda, M.; Hirano, Y.; Matsuzaki, R. Fiber Line Optimization in Single Ply for 3D Printed Composites. Open J. Compos. Mater. 2016, 6, 11. [Google Scholar] [CrossRef]
- Sugiyama, K.; Matsuzaki, R.; Malakhov, A.V.; Polilov, A.N.; Ueda, M.; Todoroki, A.; Hirano, Y. 3D printing of optimized composites with variable fiber volume fraction and stiffness using continuous fiber. Compos. Sci. Technol. 2020, 186, 107905. [Google Scholar] [CrossRef]
- Wang, T.; Li, N.; Link, G.; Jelonnek, J.; Fleischer, J.; Dittus, J.; Kupzik, D. Load-dependent path planning method for 3D printing of continuous fiber reinforced plastics. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106181. [Google Scholar] [CrossRef]
- Li, N.; Link, G.; Wang, T.; Ramopoulos, V.; Neumaier, D.; Hofele, J.; Walter, M.; Jelonnek, J. Path-designed 3D printing for topological optimized continuous carbon fibre reinforced composite structures. Compos. Part B Eng. 2020, 182, 107612. [Google Scholar] [CrossRef]
- Qiu, Z.; Li, Q.; Luo, Y.; Liu, S. Concurrent topology and fiber orientation optimization method for fiber-reinforced composites based on composite additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 395, 114962. [Google Scholar] [CrossRef]
- Safonov, A.A. 3D topology optimization of continuous fiber-reinforced structures via natural evolution method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
- Avanzini, A.; Battini, D.; Giorleo, L. Finite element modelling of 3D printed continuous carbon fiber composites: Embedded elements technique and experimental validation. Compos. Struct. 2022, 292, 115631. [Google Scholar] [CrossRef]
- Schmidt, M.P.; Couret, L.; Gout, C.; Pedersen, C.B.W. Structural topology optimization with smoothly varying fiber orientations. Struct. Multidiscip. Optim. 2020, 62, 3105–3126. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, X.; Zheng, Z.; Li, D.; Malakhov, A.V.; Polilov, A.N. Multiscale concurrent design and 3D printing of continuous fiber reinforced thermoplastic composites with optimized fiber trajectory and topological structure. Compos. Struct. 2022, 285, 115241. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, W.; Ding, X. Multi-axis additive manufacturing process for continuous fibre reinforced composite parts. Procedia CIRP 2019, 85, 114–120. [Google Scholar] [CrossRef]
- Kwon, H.; Eichenhofer, M.; Kyttas, T.; Dillenburger, B. Digital Composites: Robotic 3D Printing of Continuous Carbon Fiber-Reinforced Plastics for Functionally-Graded Building Components. In Robotic Fabrication in Architecture, Art and Design 2018. ROBARCH 2018; Willmann, J., Block, P., Hutter, M., Byrne, K., Schork, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 363–376. [Google Scholar]
- Yao, Y.; Zhang, Y.; Aburaia, M.; Lackner, M. 3D Printing of Objects with Continuous Spatial Paths by a Multi-Axis Robotic FFF Platform. Appl. Sci. 2021, 11, 4825. [Google Scholar] [CrossRef]
- Kipping, J.; Kállai, Z.; Schüppstuhl, T. A Set of Novel Procedures for Carbon Fiber Reinforcement on Complex Curved Surfaces Using Multi Axis Additive Manufacturing. Appl. Sci. 2022, 12, 5819. [Google Scholar] [CrossRef]
- Li, Y.; He, D.; Wang, X.; Tang, K. Geodesic Distance Field-based Curved Layer Volume Decomposition for Multi-Axis Support-free Printing. arXiv 2020, arXiv:2003.05938. [Google Scholar]
- Wulle, F.; Coupek, D.; Schäffner, F.; Verl, A.; Oberhofer, F.; Maier, T. Workpiece and Machine Design in Additive Manufacturing for Multi-Axis Fused Deposition Modeling. Procedia CIRP 2017, 60, 229–234. [Google Scholar] [CrossRef]
- Wulle, F.; Wolf, M.; Riedel, O.; Verl, A. Method for load-capable path planning in multi-axis fused deposition modeling. Procedia CIRP 2019, 84, 335–340. [Google Scholar] [CrossRef]
- Harnisch, M.; Kipping, J.; Schueppstuhl, T. Evaluation of path planning strategies in automated honeycomb potting. In Proceedings of the ISR 2020 52th International Symposium on Robotics, Online, 9–10 December 2020; pp. 1–7. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Schroeder, W.; Martin, K.; Lorensen, B. The Visualization Toolkit—An Object-Oriented Approach to 3D Graphics, 4th ed.; Kitware, Inc.: Clifton Park, NY, USA, 2006. [Google Scholar]
- Sullivan, C.B.; Kaszynski, A. PyVista: 3D plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). J. Open Source Softw. 2019, 4, 1450. [Google Scholar] [CrossRef]
- Sharp, N. potpourri3d. 2022. Available online: https://github.com/nmwsharp/potpourri3d (accessed on 2 May 2022).
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2009. [Google Scholar]
- FreeCAD. 2022. Available online: https://github.com/FreeCAD/FreeCAD (accessed on 3 December 2022).
- Kallai, Z.; Dammann, M.; Schueppstuhl, T. Operation and experimental evaluation of a 12-axis robot-based setup used for 3D-printing. In Proceedings of the ISR 2020 52th International Symposium on Robotics, Online, 9–10 December 2020; pp. 1–9. [Google Scholar]


| Part | Dim. [mm] | # Tets | k | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | 52 × 52 × 27 | 32,666 | 0.16 | 0.75 | 200 | 0.35 | 15 | 0.9 | 5 | |
| B | 80 × 20 × 28 | 8514 | 0.46 | 0.75 | 200 | 0.35 | 10 | 0.9 | 5 |
| Part | Slices | Ori. | Paths | Path | Post | ||||
|---|---|---|---|---|---|---|---|---|---|
| A | 12.86 | 71.53 | 18.12 | 15.66 | 0.97 | 126.52 | 892.88 | 254.55 | 38 |
| B | 4.82 | 8.71 | 3.52 | 2.74 | 0.07 | 34.11 | 204.58 | 62.55 | 8.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kipping, J.; Schüppstuhl, T. Load-Oriented Nonplanar Additive Manufacturing Method for Optimized Continuous Carbon Fiber Parts. Materials 2023, 16, 998. https://doi.org/10.3390/ma16030998
Kipping J, Schüppstuhl T. Load-Oriented Nonplanar Additive Manufacturing Method for Optimized Continuous Carbon Fiber Parts. Materials. 2023; 16(3):998. https://doi.org/10.3390/ma16030998
Chicago/Turabian StyleKipping, Johann, and Thorsten Schüppstuhl. 2023. "Load-Oriented Nonplanar Additive Manufacturing Method for Optimized Continuous Carbon Fiber Parts" Materials 16, no. 3: 998. https://doi.org/10.3390/ma16030998
APA StyleKipping, J., & Schüppstuhl, T. (2023). Load-Oriented Nonplanar Additive Manufacturing Method for Optimized Continuous Carbon Fiber Parts. Materials, 16(3), 998. https://doi.org/10.3390/ma16030998





