A Parametric Study of Optimum Road Modular Hinged Frames by Hybrid Metaheuristics
Abstract
1. Introduction
2. Optimization Problem
2.1. Variables
2.2. Parameters
2.3. Constrains
3. Proposed Hybrid Metaheuristic Strategies
3.1. Hybrid Simulated Annealing
3.2. Hybrid Threshold Accepting
3.3. Hybrid Old Bachelor’s Acceptance
3.4. Design of Experiments
4. Results of the Parametric Study and Regression Analysis
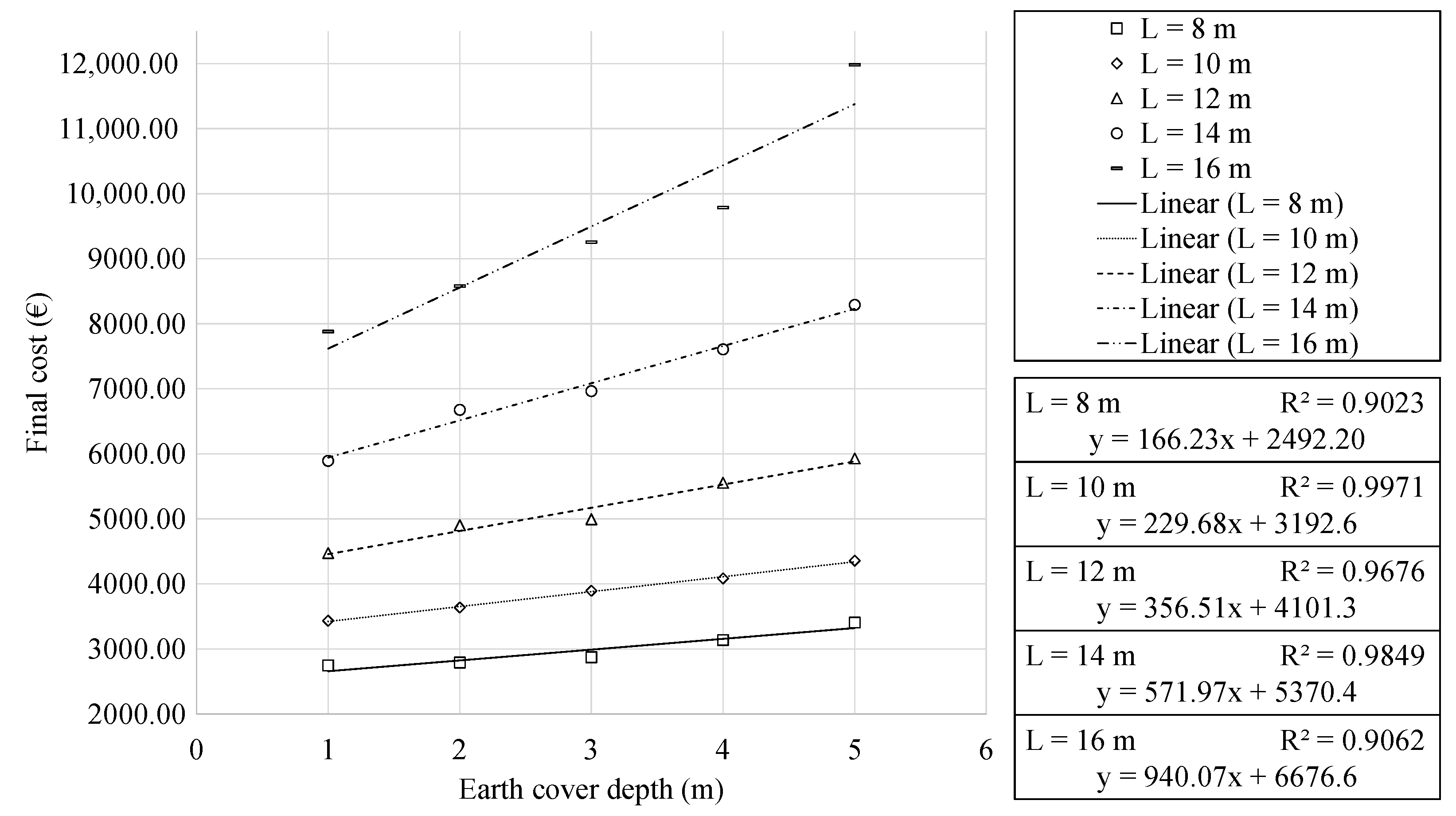
4.1. Final Cost Analysis
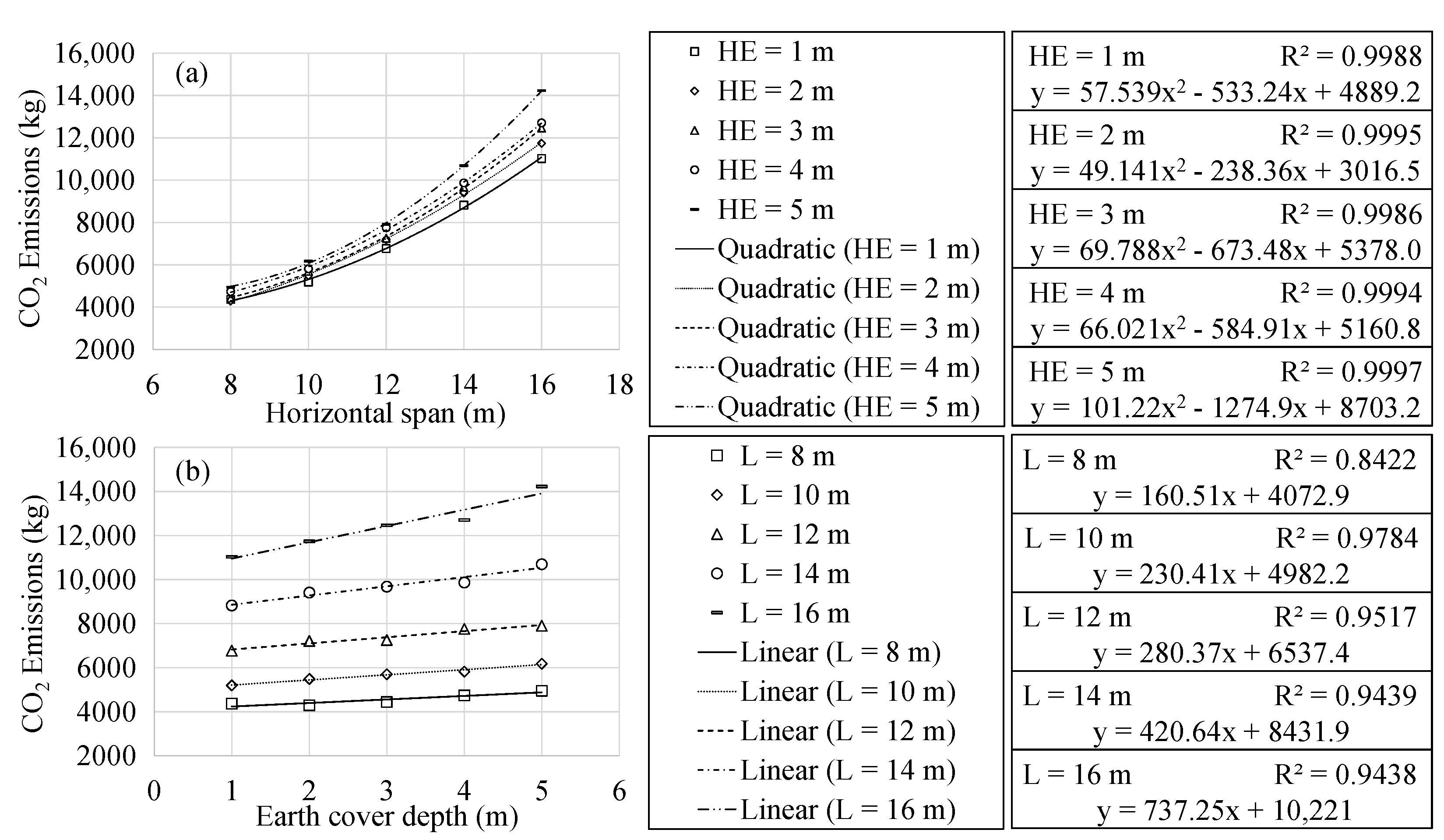
4.2. Sustainability Analysis
4.3. Geometrical Characteristics Analysis
4.4. Materials Analysis
5. Conclusions
- The hybridization of local search-based algorithms with GA mutation operators gives rise to hybrid metaheuristics. These techniques are applicable in automating the optimal design of precast structures. The SAMO presents the best performance in solving the problem posed. The calibrated method has Markov chain lengths of 10,000 iterations, a cooling coefficient of 0.8 and a stopping criterion of 5 chains without improvement. In addition, the mutation operator affects one variable with a standard deviation of 0.1.
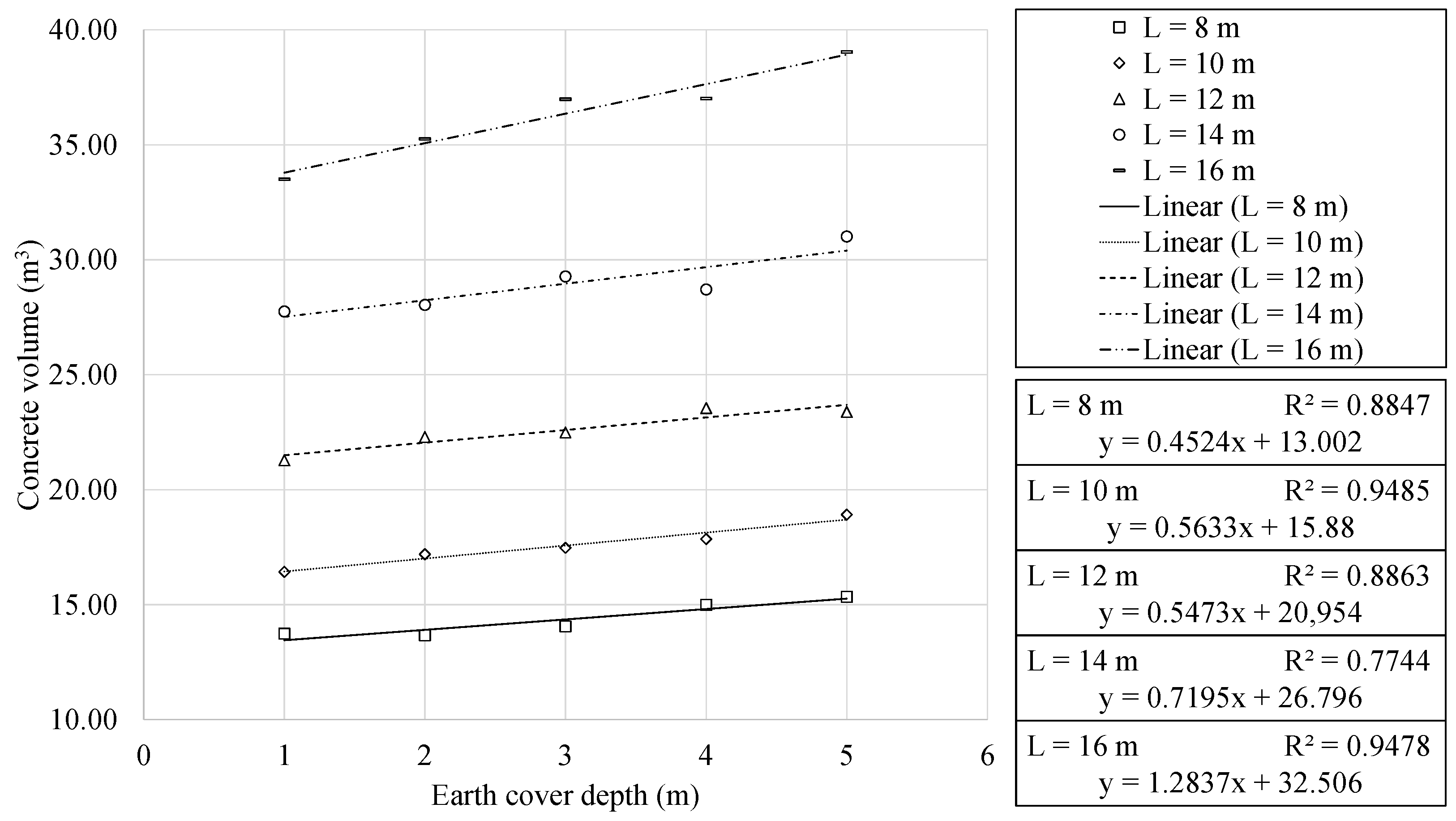
- The cost and environmental impact meters present an excellent fitting quadratic relationship when studied as a function of the horizontal span. This relationship is linear when considered a function of the earth cover depth. The expressions obtained are representative and form a valuable tool for the approximate calculation of the final cost, the associated CO2 emissions and the embodied energy of RMHFs.
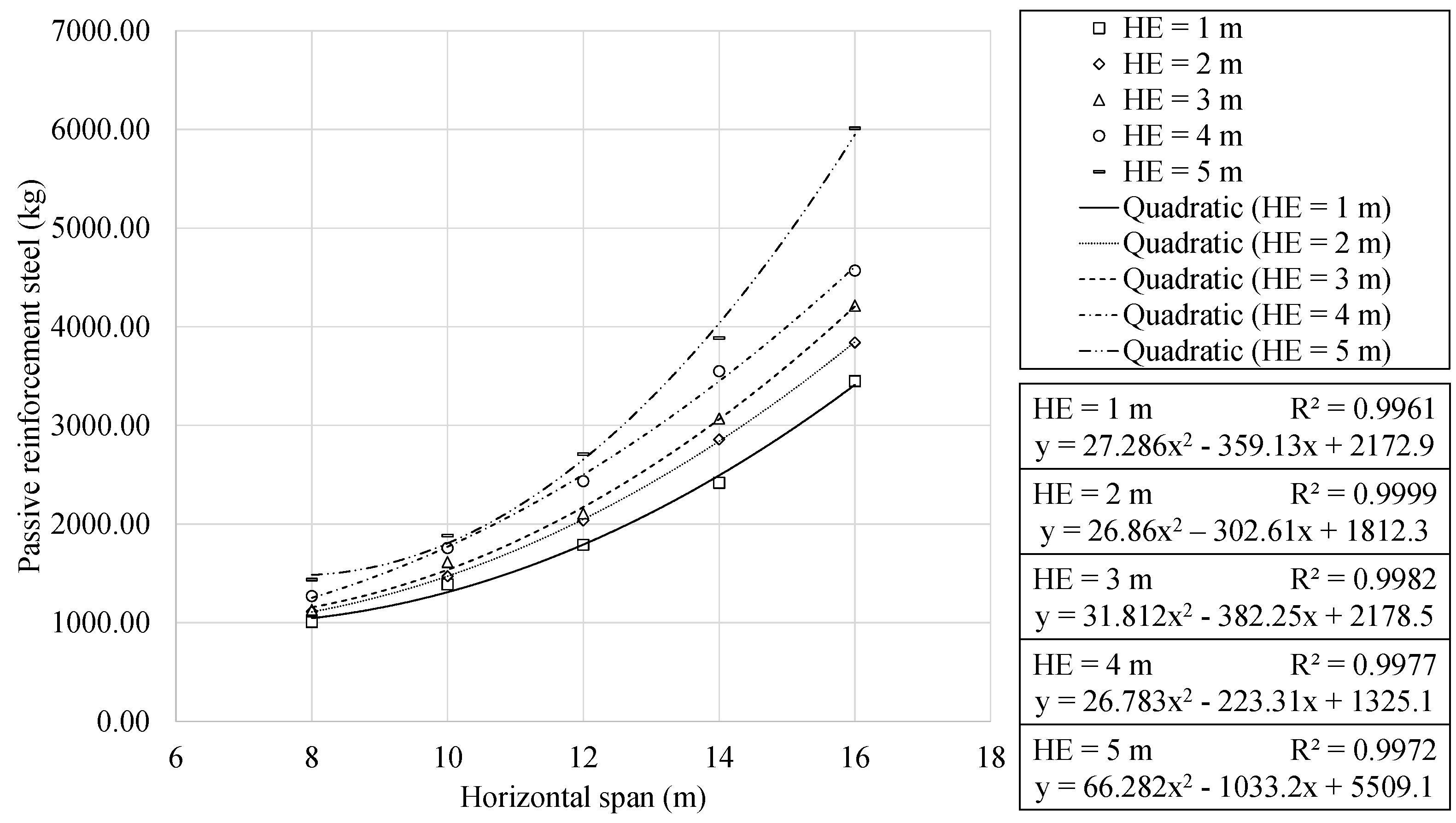
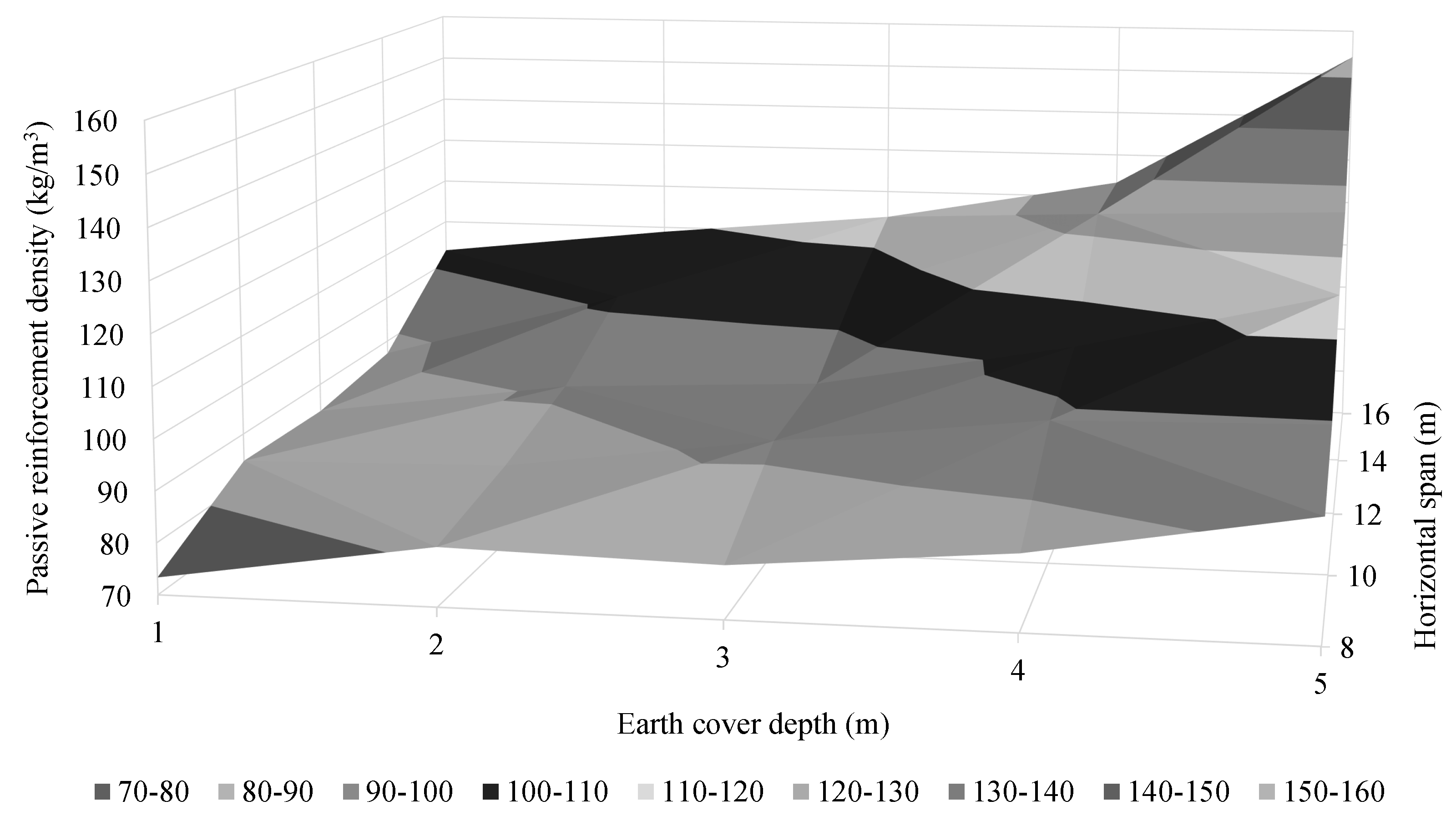
- The RMHF design depends on a large number of variables. The study of each particular variable lands out of the scope of the present work. However, optimal structures present reduced depths with dense reinforcement designs. This density increases with both span and earth cover depth. In addition, the mid-span upper slab reinforcement area shows quadratic and linear relationships with the span and burial depth, respectively.
- Previous designs do not condition the structures conceived using the proposed methodology. Thus, any configuration that verifies the requirements is considered a feasible solution. In this context, the 8 and 10 m span RMHF buried one meter deep presented specific characteristics that differ from the general. With considerable reductions in shear reinforcement, these structures have upper slabs with greater depth and mid-span reinforcement areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SA | Simulated Annealing |
| TA | Threshold Accepting |
| OBA | Old Bachelor’s Acceptance |
| MO | Mutation Operator |
| GA | Genetic Algorithm |
| RMHF | Road Modular Hinged Frame |
| CPRF | Cast in Place Road Frame |
| DoE | Design of Experiments |
| SAMO | Simulated Annealing with Mutation Operator |
| TAMO | Threshold Accepting with Mutation Operator |
| OBMO | Old Bachelor’s Acceptance with Mutation Operator |
| ULS | Ultimate Limit State |
| SLS | Service Limit State |
| MCL | Markov Chain Length |
| CC | Cooling Coefficient |
| SC | Stopping Criterion |
| VN | Variable Number |
| SD | Standard Deviation |
| CL | Chain Length |
| RC | Reduction Coefficient |
| TC | Termination Criterion |
| IC | Increase Coefficient |
| DC | Decrease Coefficient |
References
- Khan, K.; Ishfaq, M.; Amin, M.N.; Shahzada, K.; Wahab, N.; Faraz, M.I. Evaluation of Mechanical and Microstructural Properties and Global Warming Potential of Green Concrete with Wheat Straw Ash and Silica Fume. Materials 2022, 15, 3177. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Kaewunruen, S. Environment-friendly recycled steel fibre reinforced concrete. Constr. Build. Mater. 2022, 327, 126967. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhan, Y.; Zhu, M.; Wang, S.; Liu, J.; Ning, N. A Review of the Effects of Raw Material Compositions and Steam Curing Regimes on the Performance and Microstructure of Precast Concrete. Materials 2022, 15, 2859. [Google Scholar] [CrossRef] [PubMed]
- Gan, V.J.; Wong, C.; Tse, K.; Cheng, J.C.; Lo, I.M.; Chan, C. Parametric modelling and evolutionary optimization for cost-optimal and low-carbon design of high-rise reinforced concrete buildings. Adv. Eng. Informatics 2019, 42, 100962. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. CO2-Optimization of Post-Tensioned Concrete Slab-Bridge Decks Using Surrogate Modeling. Materials 2022, 15, 4776. [Google Scholar] [CrossRef] [PubMed]
- Garcia, J.; Villavicencio, G.; Altimiras, F.; Crawford, B.; Soto, R.; Minatogawa, V.; Franco, M.; Martínez-Muñoz, D.; Yepes, V. Machine learning techniques applied to construction: A hybrid bibliometric analysis of advances and future directions. Autom. Constr. 2022, 142, 104532. [Google Scholar] [CrossRef]
- Azam, R.; Riaz, M.R.; Farooq, M.U.; Ali, F.; Mohsan, M.; Deifalla, A.F.; Mohamed, A.M. Optimization-Based Economical Flexural Design of Singly Reinforced Concrete Beams: A Parametric Study. Materials 2022, 15, 3223. [Google Scholar] [CrossRef]
- Torres-Machi, C.; Chamorro, A.; Videla, C.; Pellicer, E.; Yepes, V. An Iterative Approach for the Optimization of Pavement Maintenance Management at the Network Level. Sci. World J. 2014, 2014, 524329. [Google Scholar] [CrossRef]
- Yepes, V.; Alcalá, J.; Perea, C.; González-Vidosa, F. A parametric study of optimum earth-retaining walls by simulated annealing. Eng. Struct. 2008, 30, 821–830. [Google Scholar] [CrossRef]
- Carbonell, A.; González-Vidosa, F.; Yepes, V. Design of reinforced concrete road vaults by heuristic optimization. Adv. Eng. Softw. 2011, 42, 151–159. [Google Scholar] [CrossRef]
- Sarma, K.C.; Adeli, H. Cost Optimization of Concrete Structures. J. Struct. Eng. 1998, 124, 570–578. [Google Scholar] [CrossRef]
- Hare, W.; Nutini, J.; Tesfamariam, S. A survey of non-gradient optimization methods in structural engineering. Adv. Eng. Softw. 2013, 59, 19–28. [Google Scholar] [CrossRef]
- Afzal, M.; Liu, Y.; Cheng, J.C.; Gan, V.J. Reinforced concrete structural design optimization: A critical review. J. Clean. Prod. 2020, 260, 120623. [Google Scholar] [CrossRef]
- Arandian, B.; Iraji, A.; Alaei, H.; Keawsawasvong, S.; Nehdi, M.L. White-Tailed Eagle Algorithm for Global Optimization and Low-Cost and Low-CO2 Emission Design of Retaining Structures. Sustainability 2022, 14, 10673. [Google Scholar] [CrossRef]
- Fei, K.; Junjie, L.; Qing, X. Structural inverse analysis by hybrid simplex artificial bee colony algorithms. Comput. Struct. 2009, 87, 861–870. [Google Scholar] [CrossRef]
- Dong, W.; Qie, Z.; Zhou, Z.; Wu, X.; Liu, M.; Zheng, W. The optimization of mixture ratio of model sand based on Simplex Particle Swarm Optimization Algorithm. In Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 3868–3872. [Google Scholar] [CrossRef]
- Bekdaş, G.; Cakiroglu, C.; Kim, S.; Geem, Z.W. Optimization and Predictive Modeling of Reinforced Concrete Circular Columns. Materials 2022, 15, 624. [Google Scholar] [CrossRef] [PubMed]
- Sarir, P.; Armaghani, D.J.; Jiang, H.; Sabri, M.M.S.; He, B.; Ulrikh, D.V. Prediction of Bearing Capacity of the Square Concrete-Filled Steel Tube Columns: An Application of Metaheuristic-Based Neural Network Models. Materials 2022, 15, 309. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. An Optimization-LCA of a Prestressed Concrete Precast Bridge. Sustainability 2018, 10, 685. [Google Scholar] [CrossRef]
- Hussein, H.H.; Sargand, S.M.; Steinberg, E.P. Shape Optimization of UHPC Shear Keys for Precast, Prestressed, Adjacent Box-Girder Bridges. J. Bridge Eng. 2018, 23, 04018009. [Google Scholar] [CrossRef]
- Pons, J.J.; Penadés-Plà, V.; Yepes, V.; Martí, J.V. Life cycle assessment of earth-retaining walls: An environmental comparison. J. Clean. Prod. 2018, 192, 411–420. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Shakeel, M.; Azam, R.; Riaz, M.R.; Shihata, A. Design optimization of reinforced concrete cantilever retaining walls: A state-of-the-art review. Adv. Civil Eng. 2022, 2022, 4760175. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Perea, C.; Yepes, V.; Alcalá, J.; Hospitaler, A.; González-Vidosa, F. A parametric study of optimum road frame bridges by threshold acceptance. Indian J. Eng. Mater. Sci. 2010, 17, 427–437. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Yepes, V.; Medina, J. Economic heuristic optimization for heterogeneous fleet VRPHESTW. J. Transp. Eng. 2006, 132. [Google Scholar] [CrossRef]
- BEDEC. Catalonia Institute of Construction Technology. BEDEC ITEC Materials Database. 2022. Available online: https://metabase.itec.cat/vide/es/bedec (accessed on 8 September 2022).
- CEN. Eurocode 2: Design of Concrete Structures; European Comittee for Standarization: Brussels, Belgium, 2013. [Google Scholar]
- CEN. Eurocode 1: Actions on Structures; European Comittee for Standarization: Brussels, Belgium, 2009. [Google Scholar]
- MFOM. IAP-11: Code on the Actions for the Design of Road Bridges; Ministerio de Fomento: Madrid, Spain, 2011.
- MFOM. Guía de Cimentaciones en Obra de Carretera; Ministerio de Fomento: Madrid, Spain, 2009.
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Medina, J. Estimation of Incident and Reflected Waves Using Simulated Annealing. J. Waterw. Port Coast. Ocean.-Eng. 2001, 127, 213–221. [Google Scholar] [CrossRef]
- Partskhaladze, G.; Alcala, J.; Medzmariashvili, E.; Chavleshvili, G.; Surguladze, B.; Yepes, V. Heuristic Optimization of a New Type of Prestressed Arched Truss. Materials 2022, 15, 8144. [Google Scholar] [CrossRef]
- Dueck, G.; Scheuer, T. Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Hu, T.C.; Kahng, A.B.; Tsao, C.W.A. Old Bachelor Acceptance: A New Class of Non-Monotone Threshold Accepting Methods. ORSA J. Comput. 1995, 7, 417–425. [Google Scholar] [CrossRef]
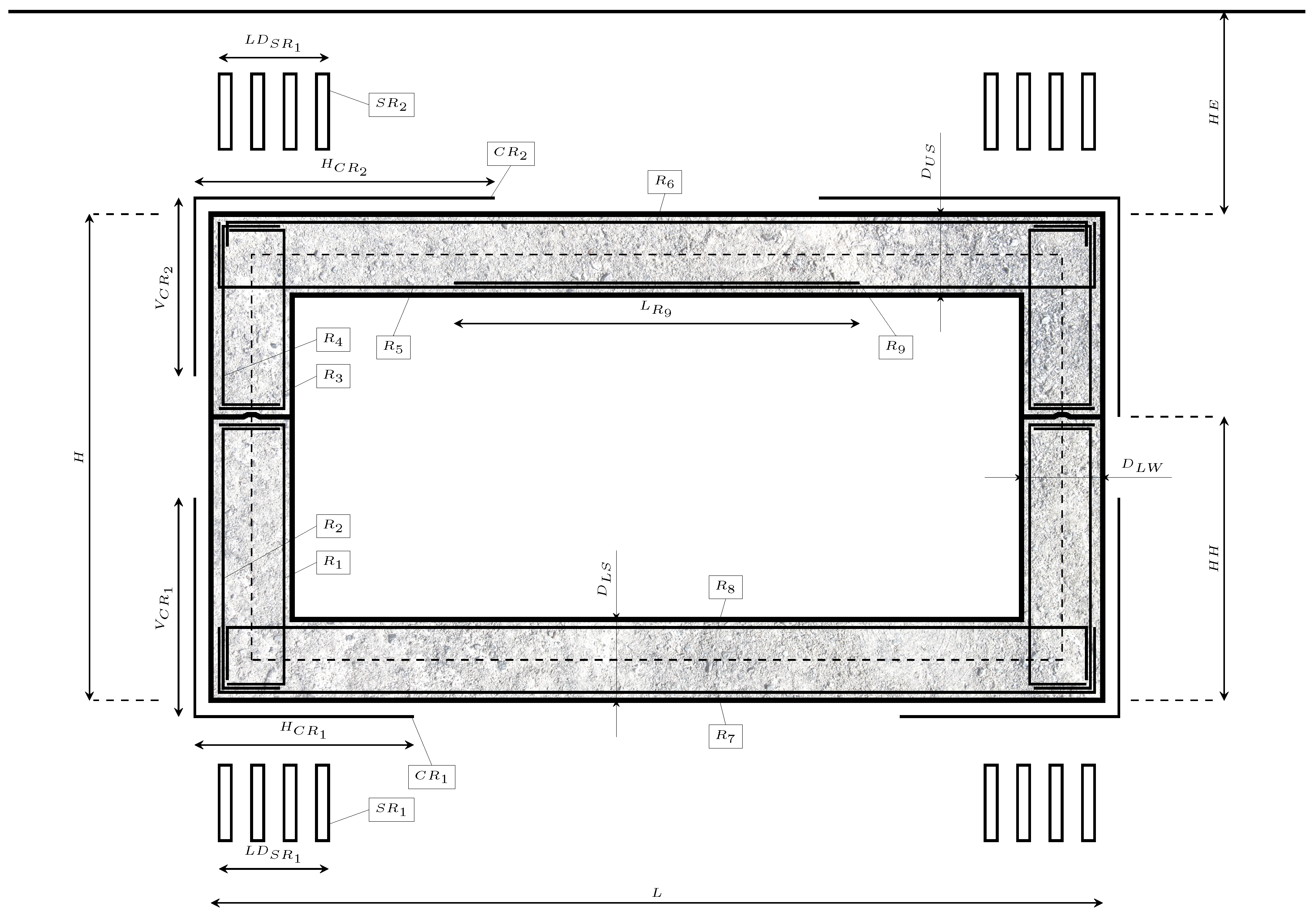

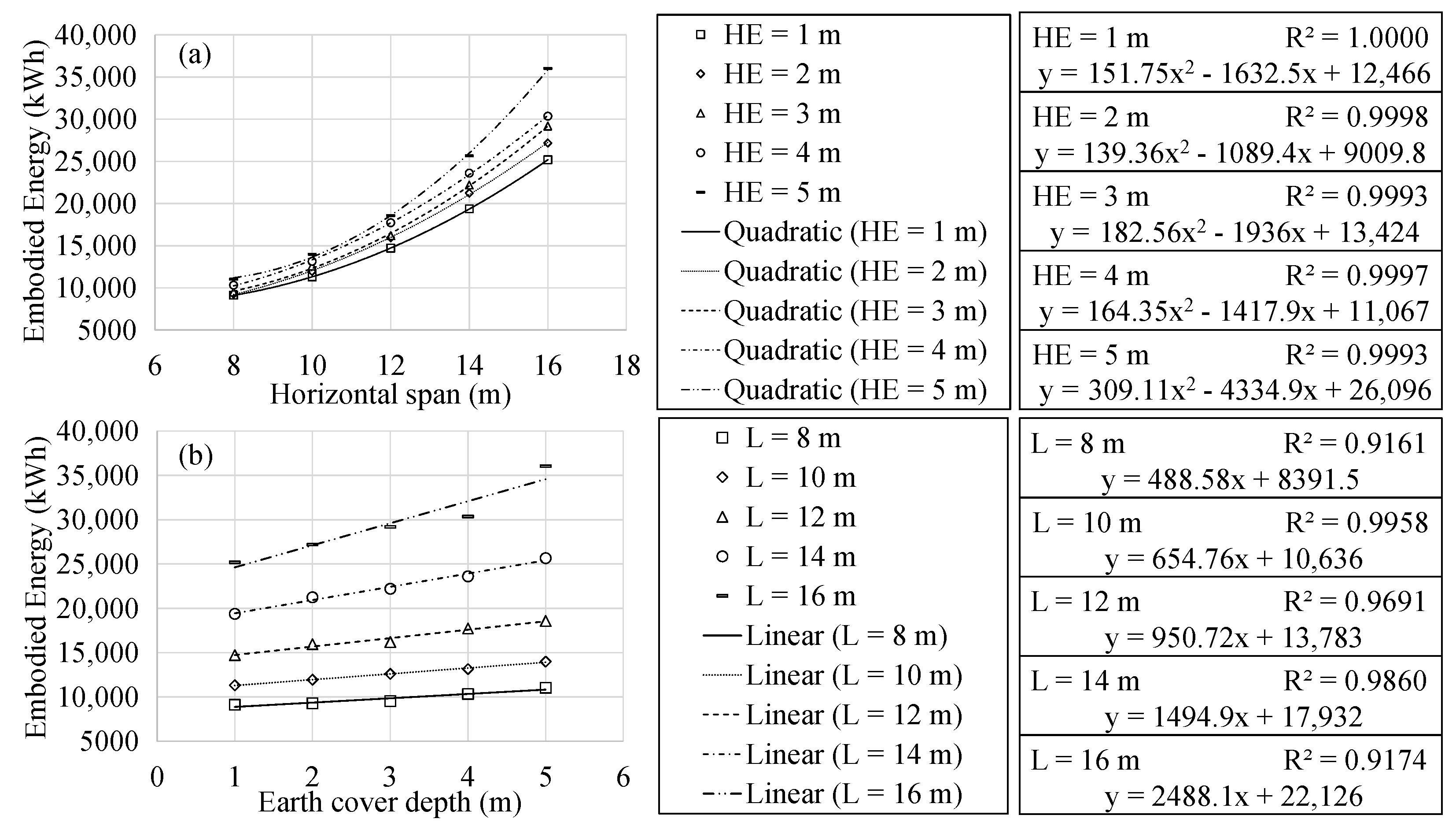
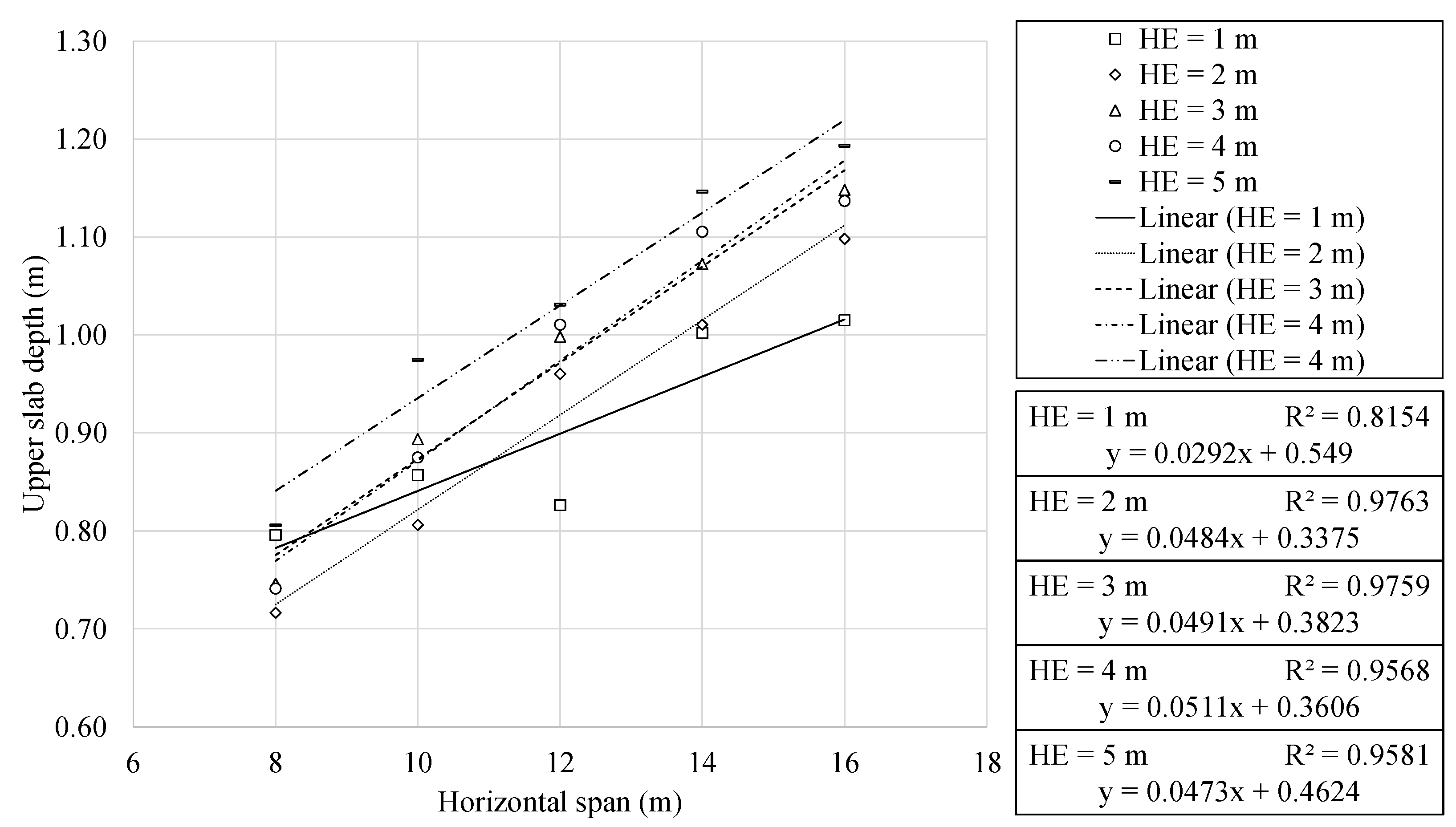
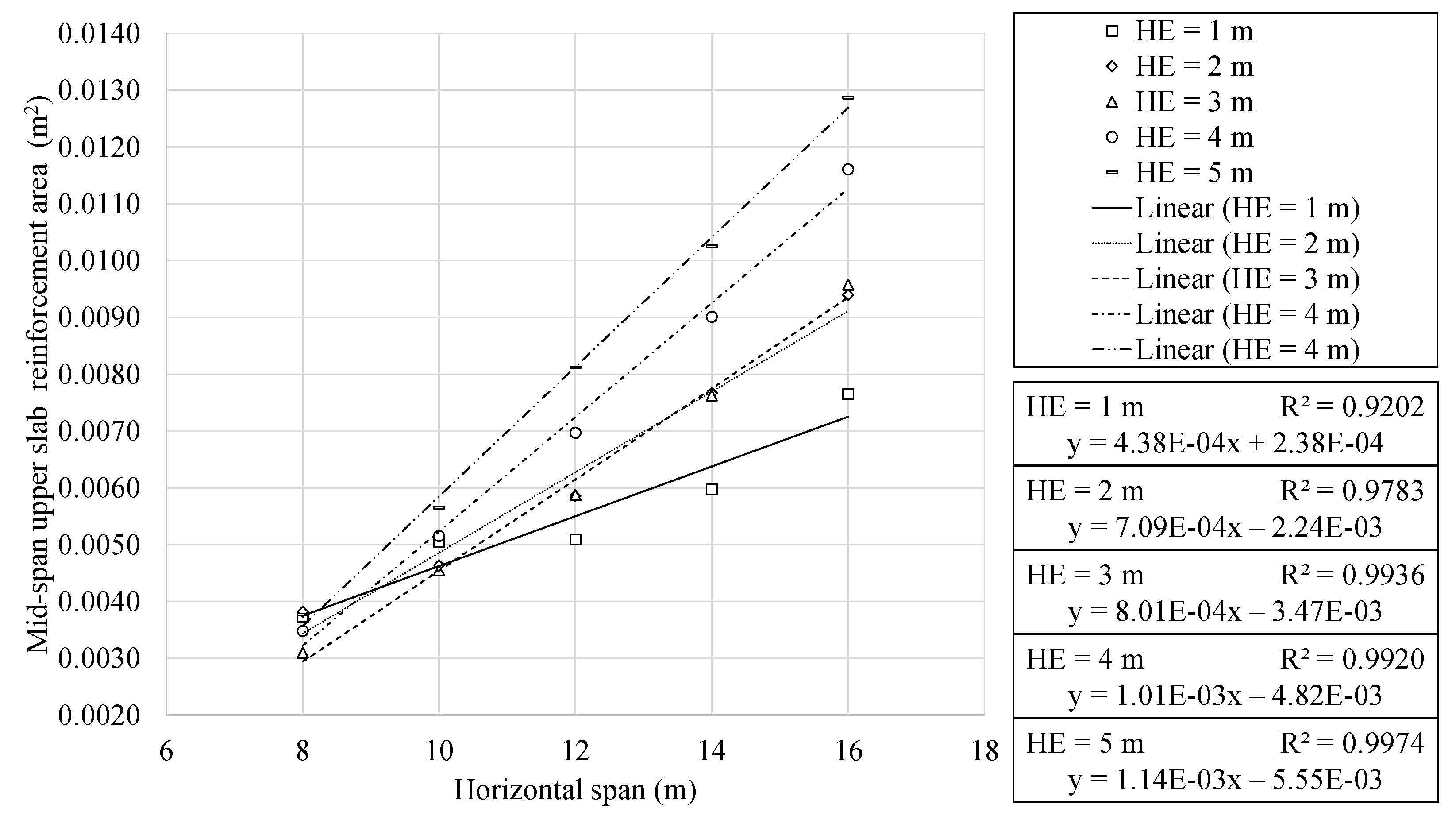
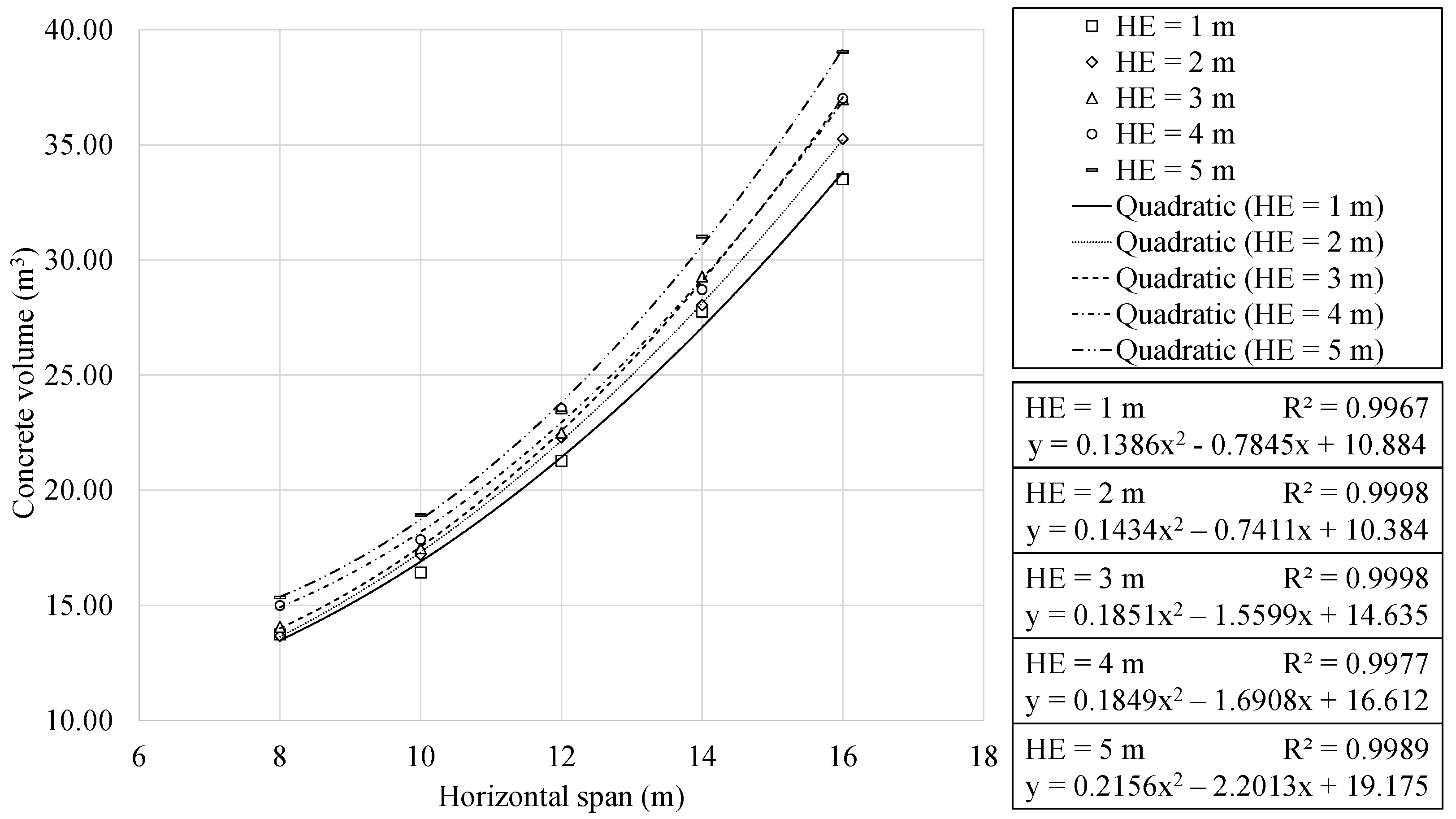

| Unit | Material | Unit Cost (EUR) | CO2 Emissions (kg) | Energy (kWh) |
|---|---|---|---|---|
| m | C25/30 Concrete | 88.86 | 256.66 | 402.44 |
| m | C30/37 Concrete | 97.80 | 277.72 | 428.29 |
| m | C35/45 Concrete | 101.83 | 278.04 | 429.95 |
| m | C40/50 Concrete | 104.83 | 278.04 | 429.95 |
| kg | B 400 S | 1.40 | 0.70 | 3.38 |
| kg | B 500 S | 1.42 | 0.70 | 3.38 |
| Geometrical Variables | Num. Values | Range Values | ||
|---|---|---|---|---|
| Upper slab depth | (m) | 46 | 0.30 to 1.20 | |
| Lower slab depth | (m) | 41 | 0.40 to 1.20 | |
| Lateral walls depth | (m) | 46 | 0.30 to 1.20 | |
| Materials variables | ||||
| Concrete grade | (MPa) | C | 4 | 25, 30, 35 or 40 |
| Steel grade | (MPa) | S | 2 | 400 or 500 |
| Passive reinforcement variables | ||||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 10 | 3 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| Flexural reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 9 | 4 to 12 | ||
| (m) | 151 to 451 | 3 to 0.75 | ||
| Corner reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 10 | 3 to 12 | ||
| (m) | 76 to 226 | 1.5 to 0.375 | ||
| (m) | 76 | 1 to 2.5 | ||
| Corner reinforcement | (mm) | 6 | 10 to 32 | |
| (bars) | 10 | 3 to 12 | ||
| (m) | 101 to 251 | 1 to 0.375 | ||
| (m) | 26 | 1 to 1.5 | ||
| Shear reinforcement | (mm) | 7 | 8 to 32 | |
| (m) | 7 | 0.10 to 0.40 | ||
| (m) | 76 to 226 | 1.5 to 0.375 | ||
| Shear reinforcement | (mm) | 7 | 8 to 32 | |
| (m) | 7 | 0.10 to 0.40 | ||
| (m) | 101 to 251 | 1 to 0.375 |
| Geometrical Parameters | ||
|---|---|---|
| Free height (m) | H | 5 |
| Horizontal span (m) | L | 8 to 16 |
| Hinge height (m) | (3/5) · H | |
| Earth cover (m) | 1 to 5 | |
| Loading parameters | ||
| Earth specific weight (kN/m) | 20 | |
| Reinforced concrete specific weight (kN/m) | 25 | |
| Earth internal friction angle () | 30 | |
| Active earth pressure coefficient | 0.33 | |
| Resting earth pressure coefficient | 0.50 | |
| Heavy traffic vehicle load (kN/m) | 150 | |
| Heavy traffic vehicle load lenght (m) | 1.20 | |
| Uniform overload (kN/m) | 10 | |
| Ballast coefficient (MN/m) | 10 | |
| Economic and sustainability parameters | ||
| Unit costs (EUR) | Table 1 | |
| Unit CO2 emissions (CO2 kg) | Table 1 | |
| Unit embodied energy (kWh) | Table 1 | |
| Exposure related parameters | ||
| Exposure class | XC2 | |
| Legislative related parameters | ||
| Standard regulations | CEN [30,31]/MFOM [32] | |
| Code considerations | MFOM [33] | |
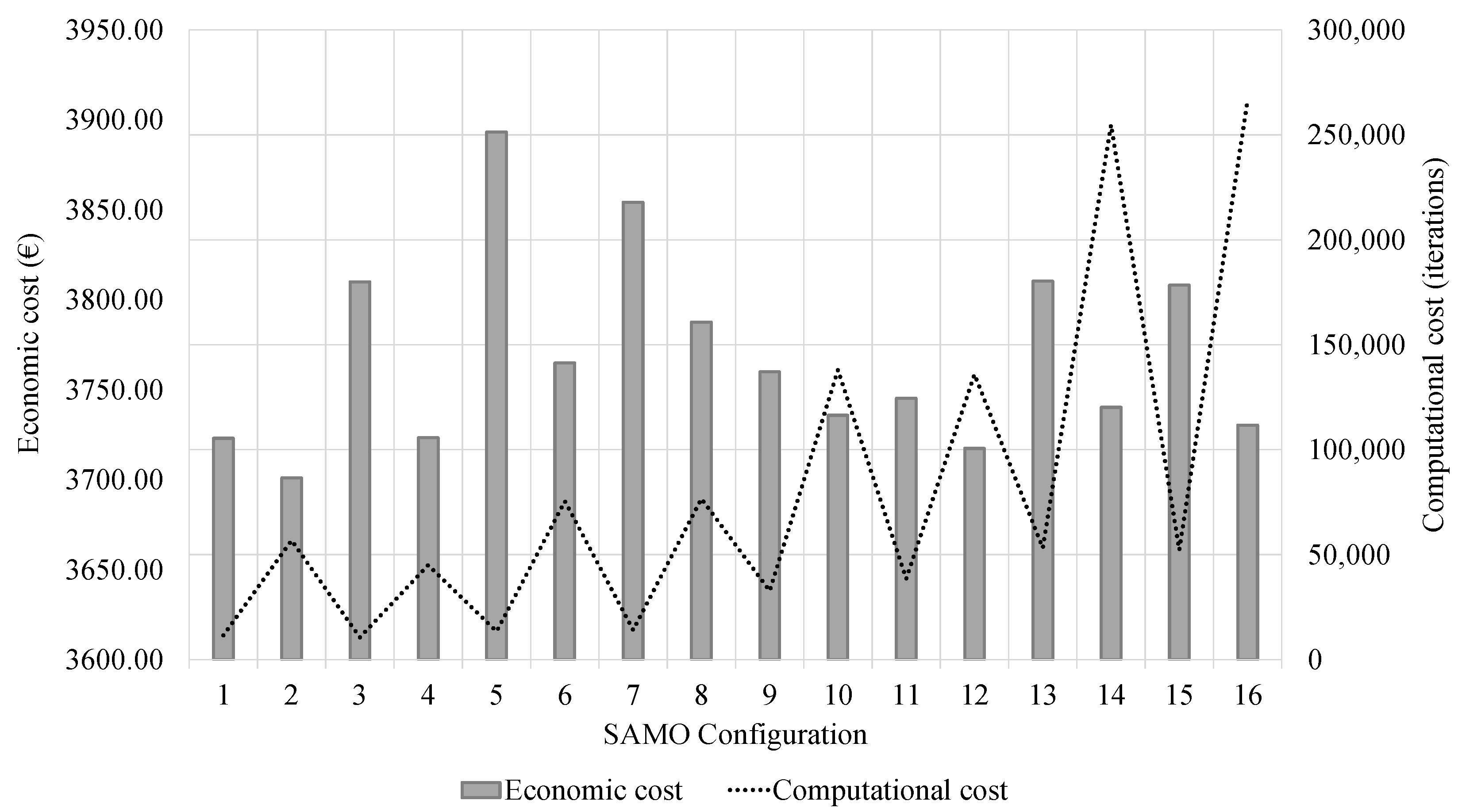
| SAMO | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|
| Parameter | MCL | SD | VN | CC | SC |
| Lower bound (−) | 1000 | 0.1 | 1 | 0.8 | 1 |
| Upper bound (+) | 5000 | 0.3 | 5 | 0.9 | 5 |
| TAMO | P1 | P2 | P3 | P4 | P5 |
| Parameter | CL | SD | VN | RC | SC |
| Lower bound (−) | 1000 | 0.1 | 1 | 0.8 | 1 |
| Upper bound (+) | 5000 | 0.3 | 5 | 0.9 | 5 |
| OBAMO | P1 | P2 | P3 | P4 | P5 |
| Parameter | TC | SD | VN | IC | DC |
| Lower bound (−) | 10,000 | 0.1 | 1 | 1 | 1 |
| Upper bound (+) | 50,000 | 0.3 | 5 | 5 | 5 |
| SAMO | TAMO | OBAMO | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | Cost (EUR) | Iter. | % Min. | Cost (EUR) | Iter. | % Min. | Cost (EUR) | Iter. | % Min. |
| − | − | − | − | + | 3722.99 | 11,472 | 0.0067 | 4484.78 | 7790 | 0.2127 | 4266.87 | 5621 | 0.1538 |
| + | − | − | − | − | 3700.97 | 56,759 | 0.0008 | 4206.81 | 28,405 | 0.1376 | 3935.18 | 15,901 | 0.0641 |
| − | + | − | − | − | 3809.90 | 10,551 | 0.0302 | 4005.26 | 6823 | 0.0831 | 3939.44 | 6688 | 0.0653 |
| + | + | − | − | + | 3723.28 | 44,999 | 0.0068 | 3933.48 | 19,124 | 0.0636 | 4108.21 | 30,886 | 0.1109 |
| − | − | + | − | − | 3893.24 | 13,428 | 0.0528 | 3844.05 | 14,008 | 0.0395 | 4131.20 | 6607 | 0.1171 |
| + | − | + | − | + | 3764.81 | 75,442 | 0.0180 | 3764.61 | 64,237 | 0.0180 | 4420.60 | 31,150 | 0.1954 |
| − | + | + | − | + | 3854.21 | 14,101 | 0.0422 | 3917.74 | 12,470 | 0.0594 | 4470.99 | 3043 | 0.2090 |
| + | + | + | − | − | 3787.60 | 76,644 | 0.0242 | 3764.19 | 62,072 | 0.0179 | 3978.78 | 23,037 | 0.0759 |
| − | − | − | + | − | 3759.89 | 32,726 | 0.0167 | 3900.58 | 20,817 | 0.0548 | 4233.84 | 5175 | 0.1449 |
| + | − | − | + | + | 3735.80 | 137,994 | 0.0102 | 3990.50 | 61,719 | 0.0791 | 3808.35 | 30,193 | 0.0298 |
| − | + | − | + | + | 3745.25 | 38,517 | 0.0127 | 3953.74 | 22,026 | 0.0691 | 3878.68 | 7326 | 0.0488 |
| + | + | − | + | − | 3717.33 | 135,874 | 0.0052 | 4376.86 | 41,030 | 0.1835 | 4103.01 | 28,609 | 0.1095 |
| − | − | + | + | + | 3810.35 | 53,194 | 0.0304 | 3759.25 | 53,703 | 0.0165 | 4135.06 | 8395 | 0.1182 |
| + | − | + | + | − | 3740.23 | 254,796 | 0.0114 | 3711.42 | 227,138 | 0.0036 | 3788.71 | 30,451 | 0.0245 |
| − | + | + | + | − | 3808.14 | 52,211 | 0.0298 | 3755.12 | 52,050 | 0.0154 | 4188.70 | 4486 | 0.1327 |
| + | + | + | + | + | 3730.33 | 266,381 | 0.0087 | 3698.10 | 258,351 | 0.0000 | 3838.12 | 43,960 | 0.0379 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Vélez, A.; Alcalá, J.; Yepes, V. A Parametric Study of Optimum Road Modular Hinged Frames by Hybrid Metaheuristics. Materials 2023, 16, 931. https://doi.org/10.3390/ma16030931
Ruiz-Vélez A, Alcalá J, Yepes V. A Parametric Study of Optimum Road Modular Hinged Frames by Hybrid Metaheuristics. Materials. 2023; 16(3):931. https://doi.org/10.3390/ma16030931
Chicago/Turabian StyleRuiz-Vélez, Andrés, Julián Alcalá, and Víctor Yepes. 2023. "A Parametric Study of Optimum Road Modular Hinged Frames by Hybrid Metaheuristics" Materials 16, no. 3: 931. https://doi.org/10.3390/ma16030931
APA StyleRuiz-Vélez, A., Alcalá, J., & Yepes, V. (2023). A Parametric Study of Optimum Road Modular Hinged Frames by Hybrid Metaheuristics. Materials, 16(3), 931. https://doi.org/10.3390/ma16030931








