Investigation on Performance of Hydraulically Expanded Joint of Titanium–Steel Clad Tubesheet
Abstract
1. Introduction
2. Finite Element Model Analysis
2.1. Material Performance
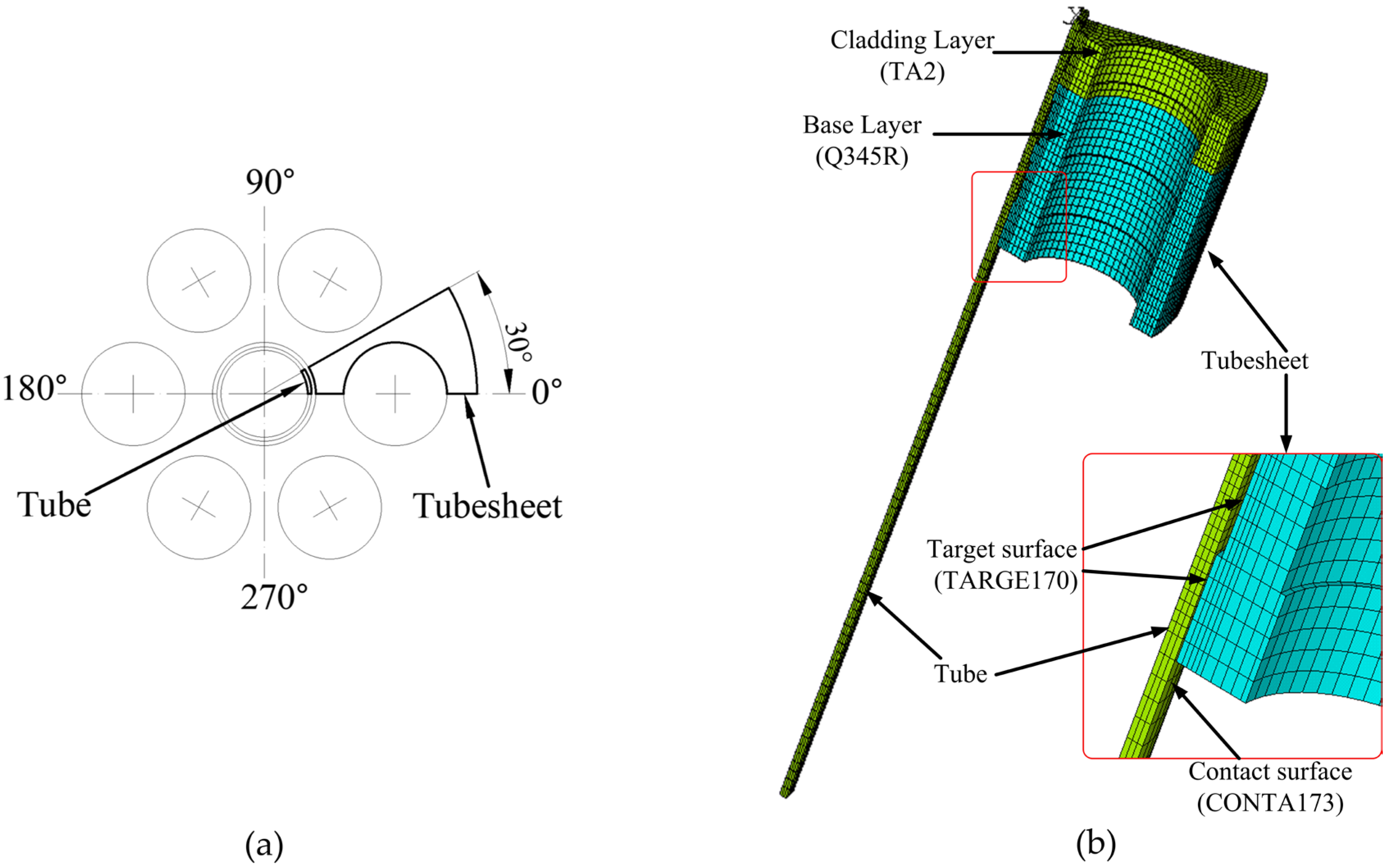
2.2. Finite Element Model
3. Tight Expansion Analysis
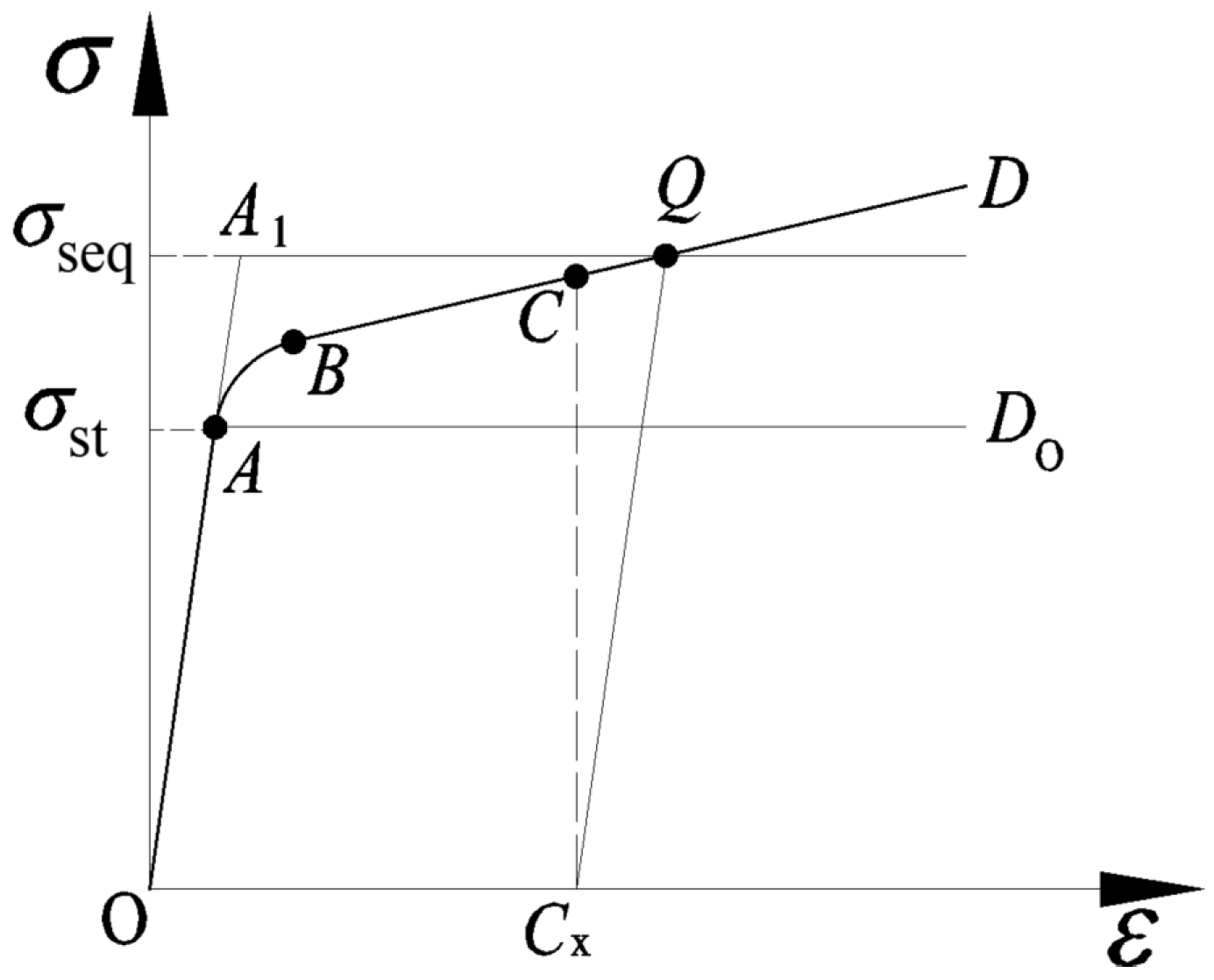
3.1. Theoretical Calculation Method
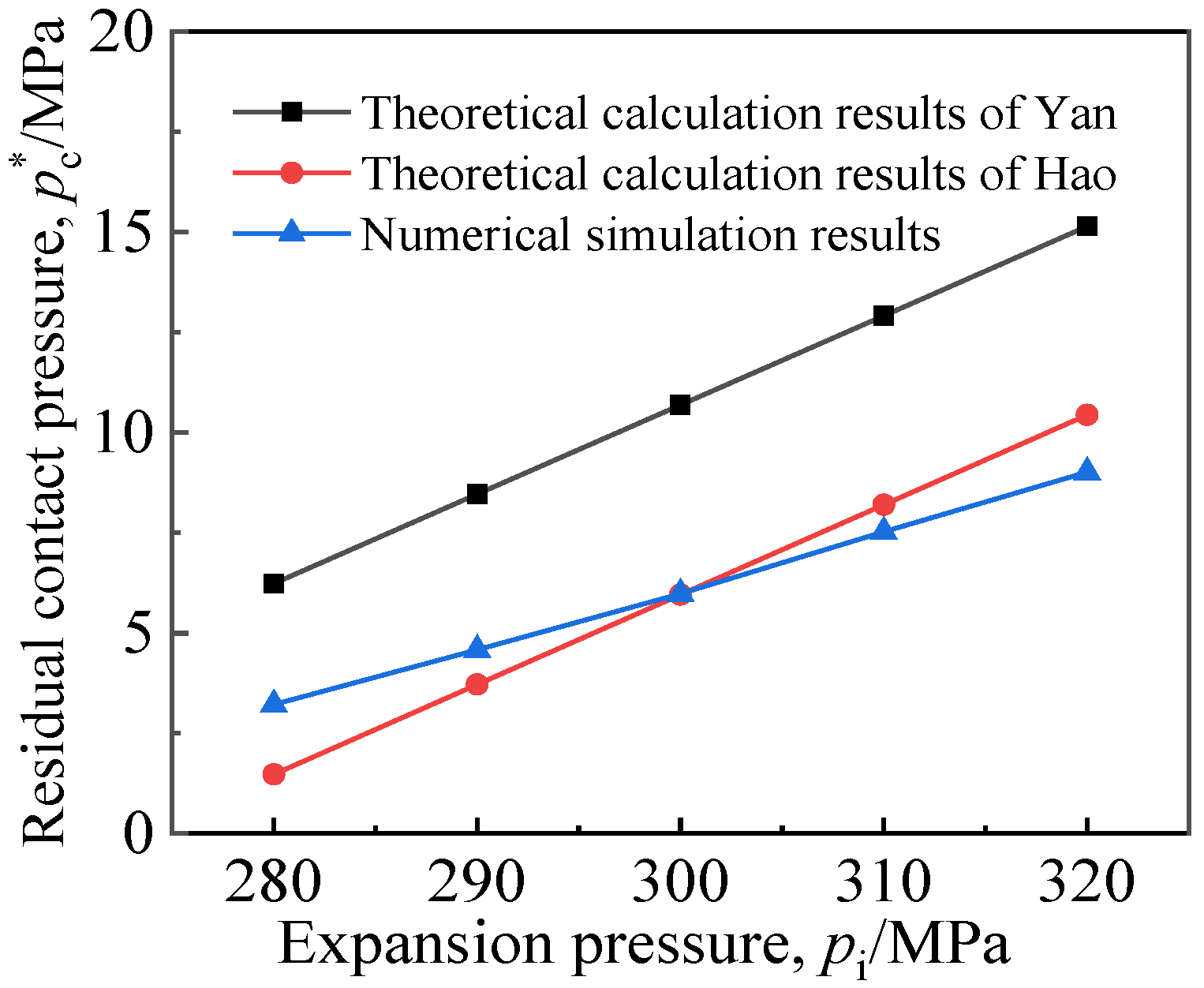
3.2. Comparison of Simulation Results and Theoretical Calculation Results
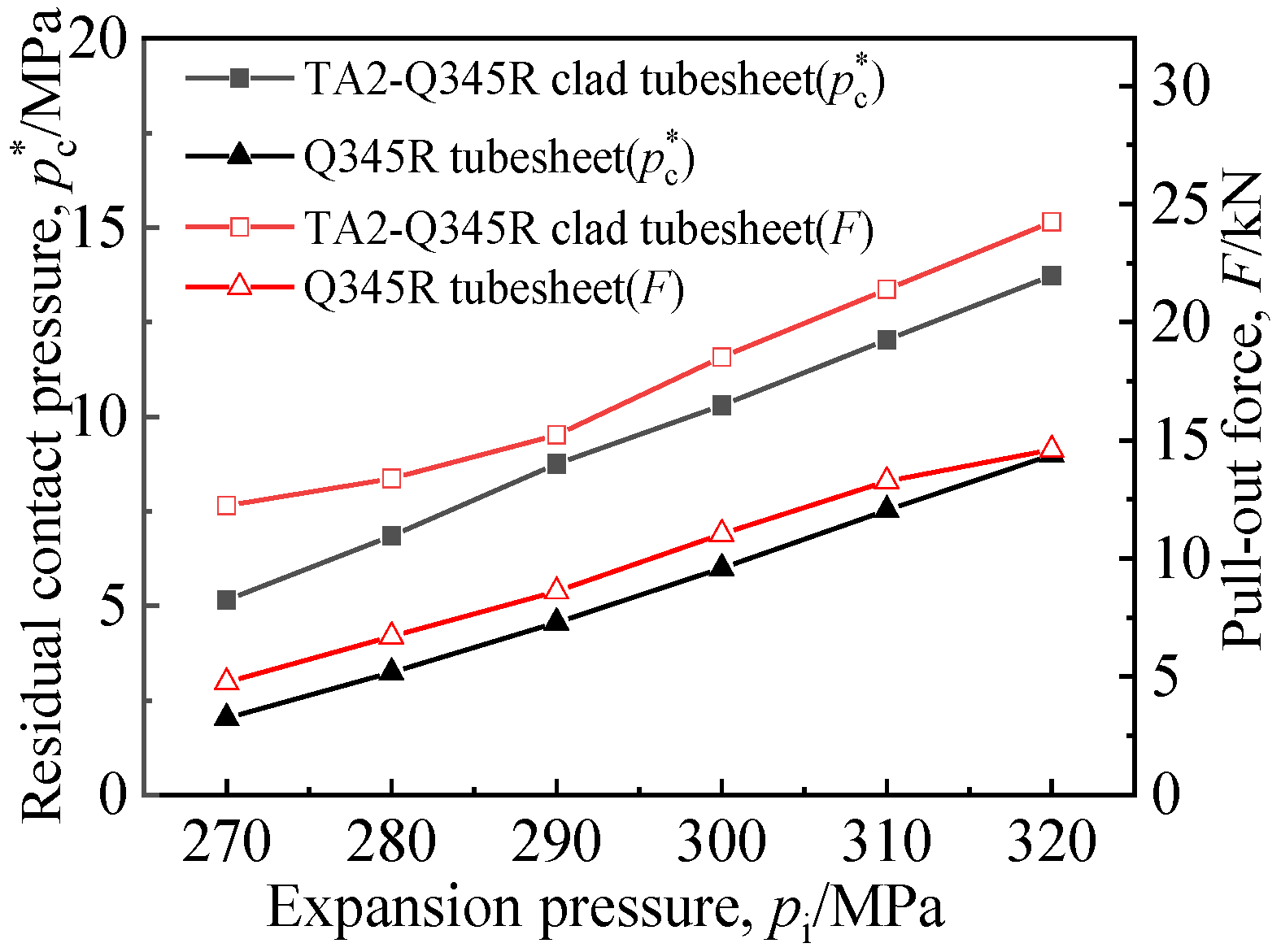
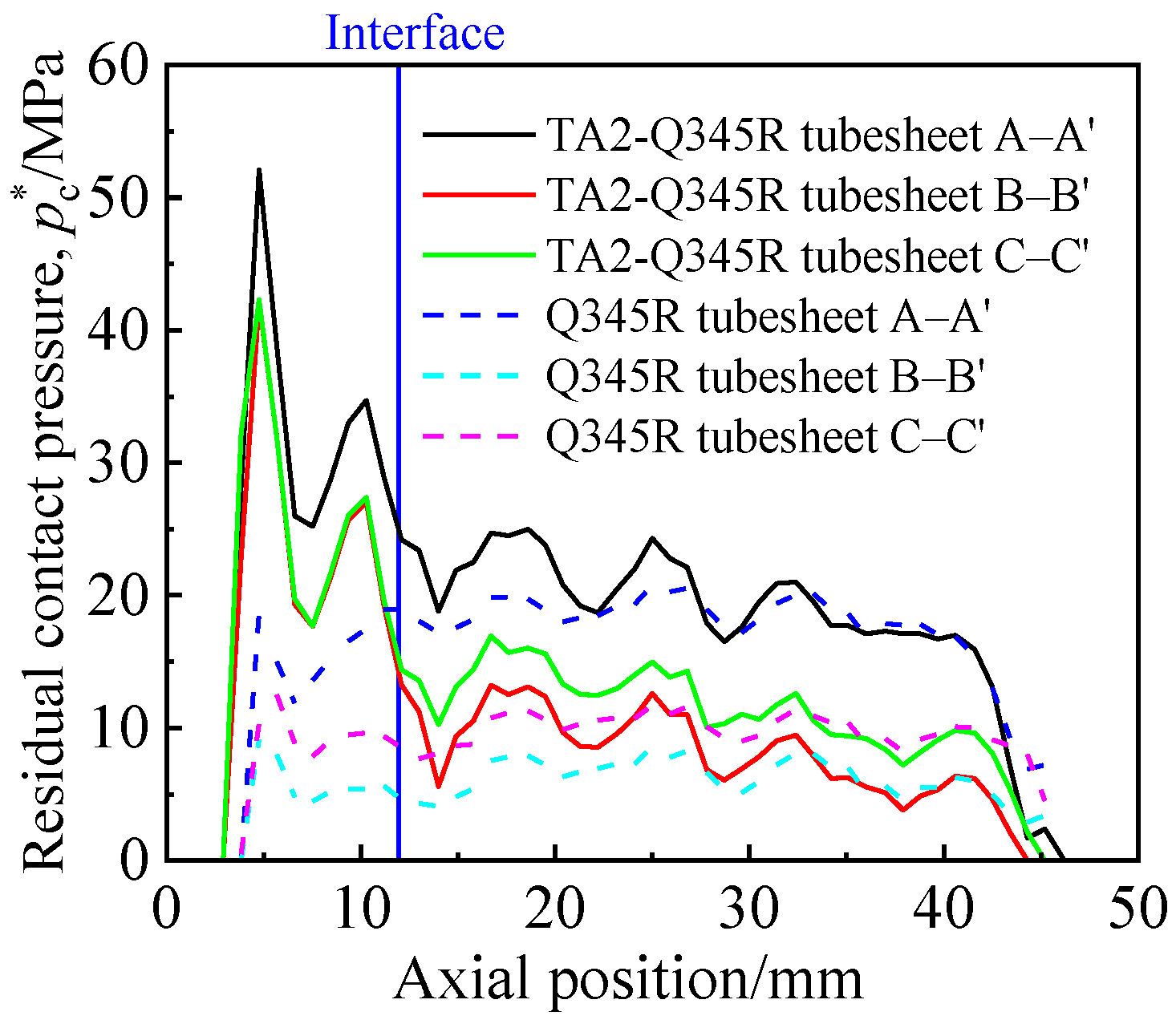
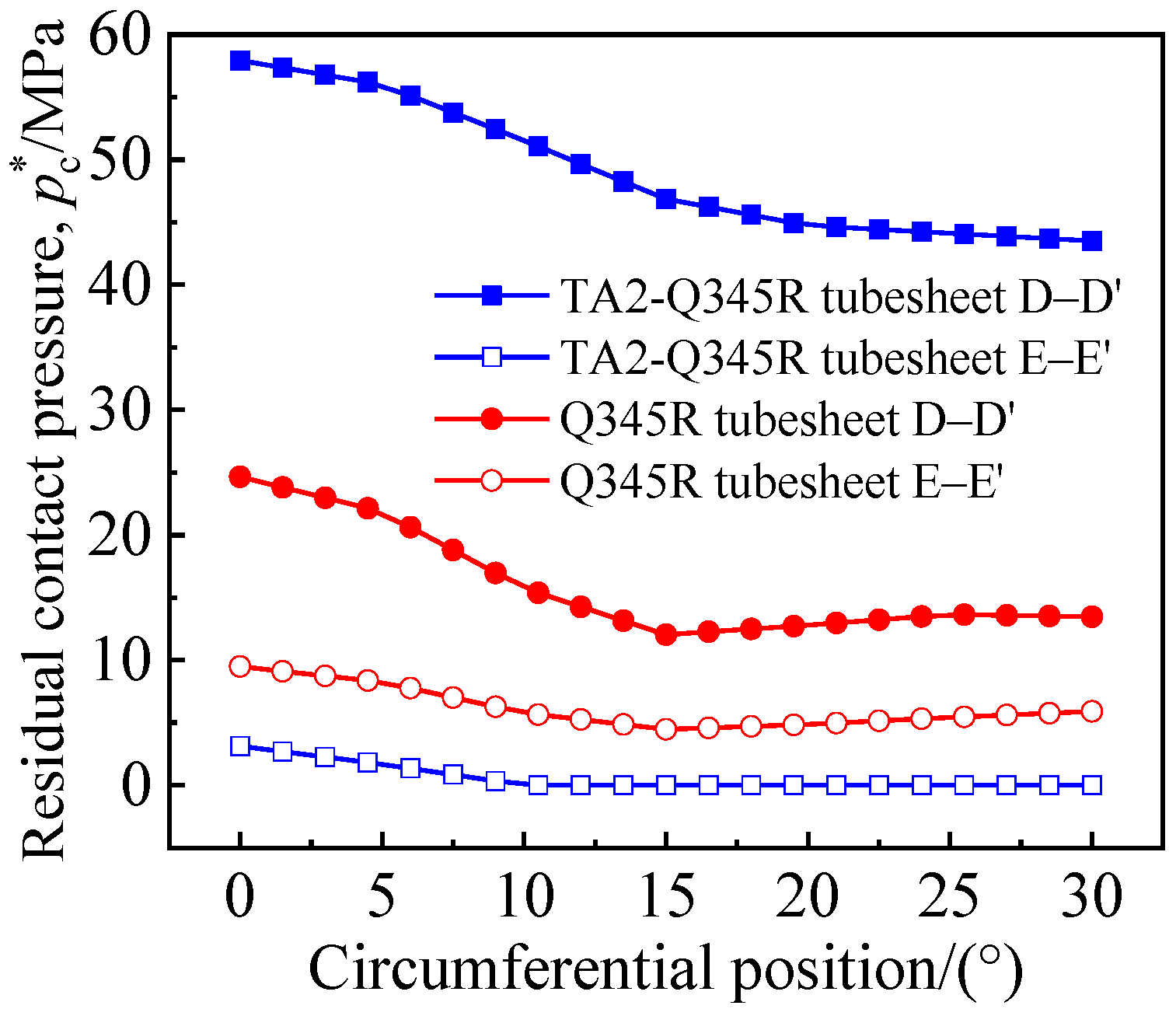
3.3. Performance Analysis of Tight Expansion Joint
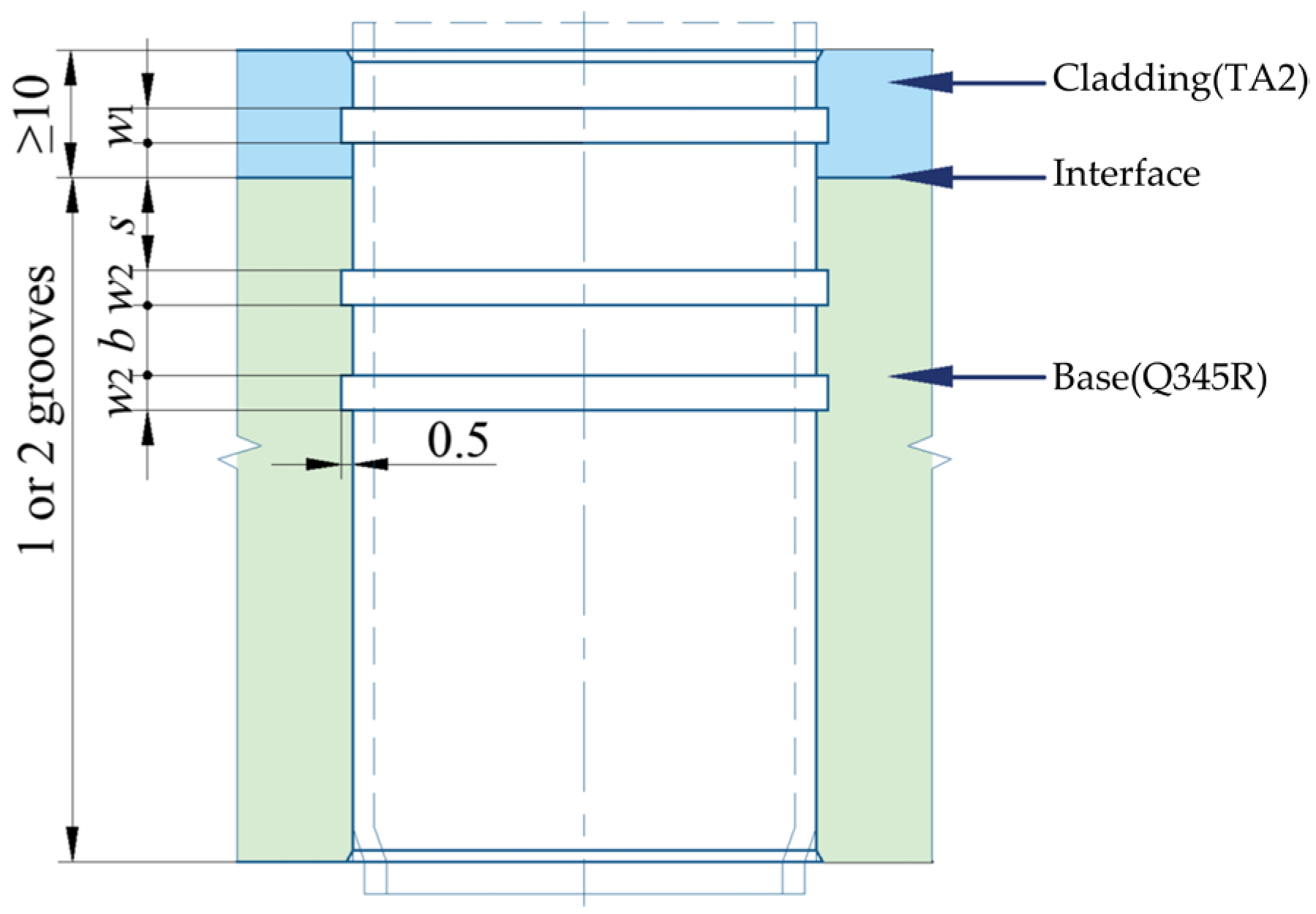
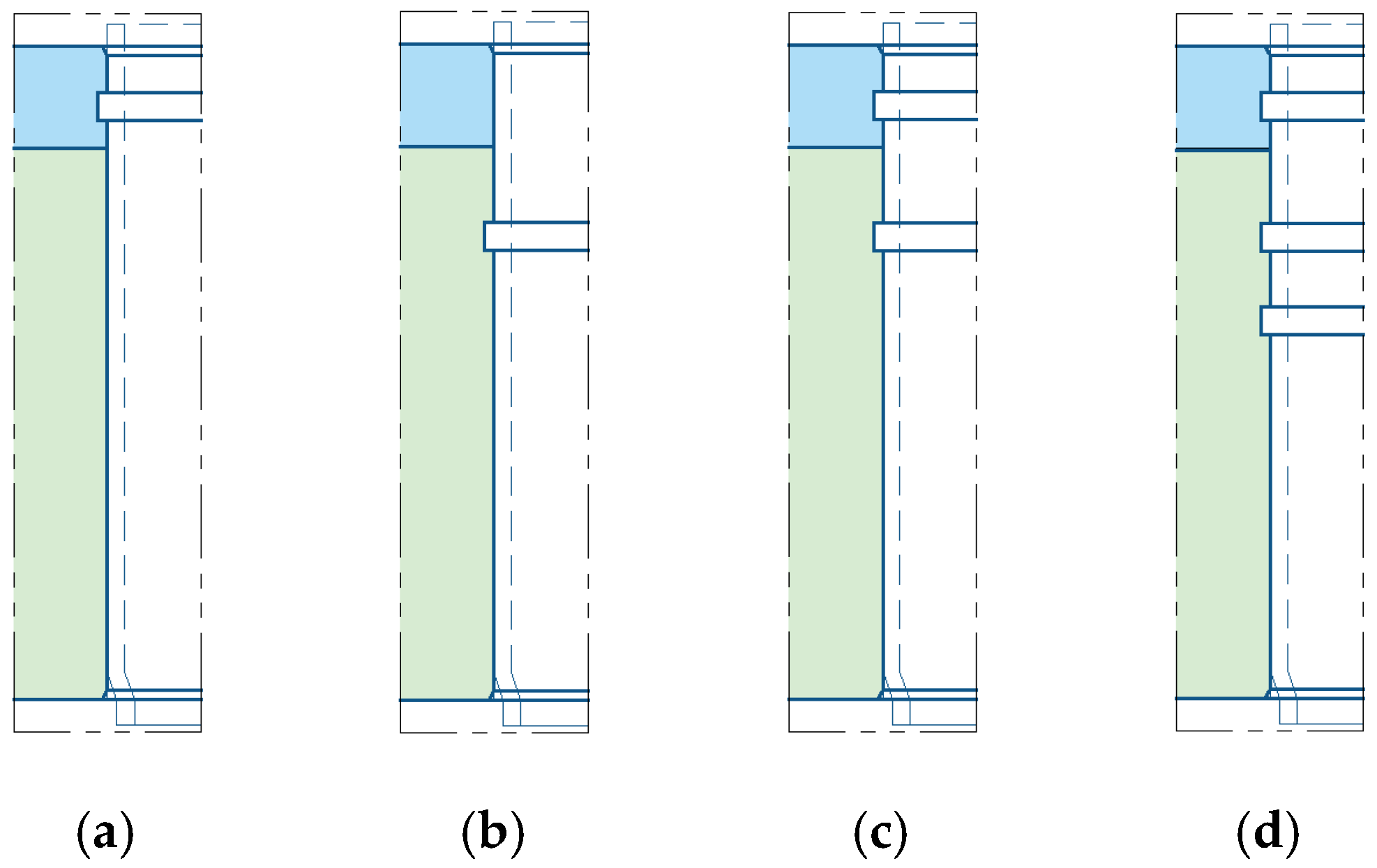
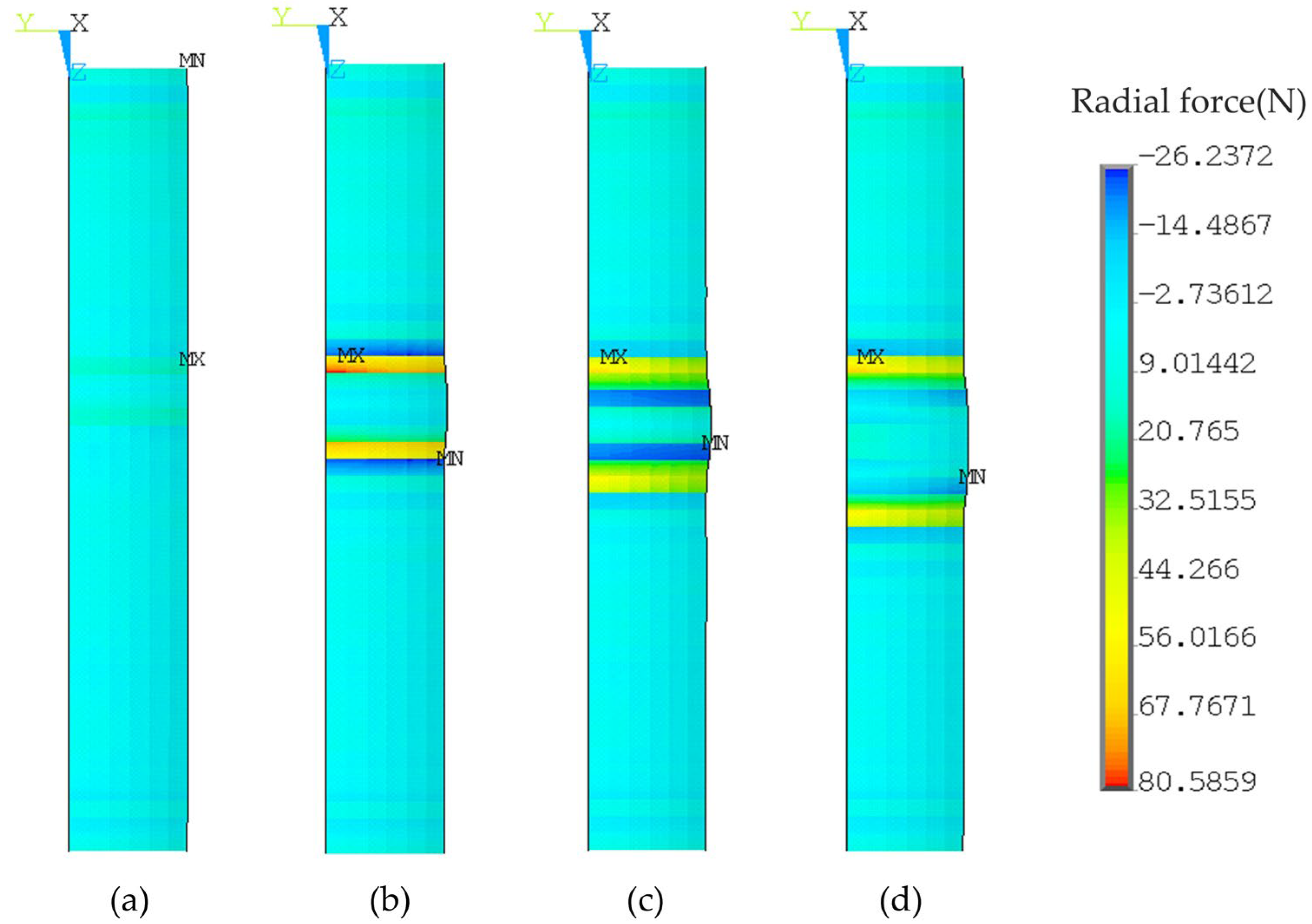
4. Expanded Joint with Grooved Clad Tubesheet Holes
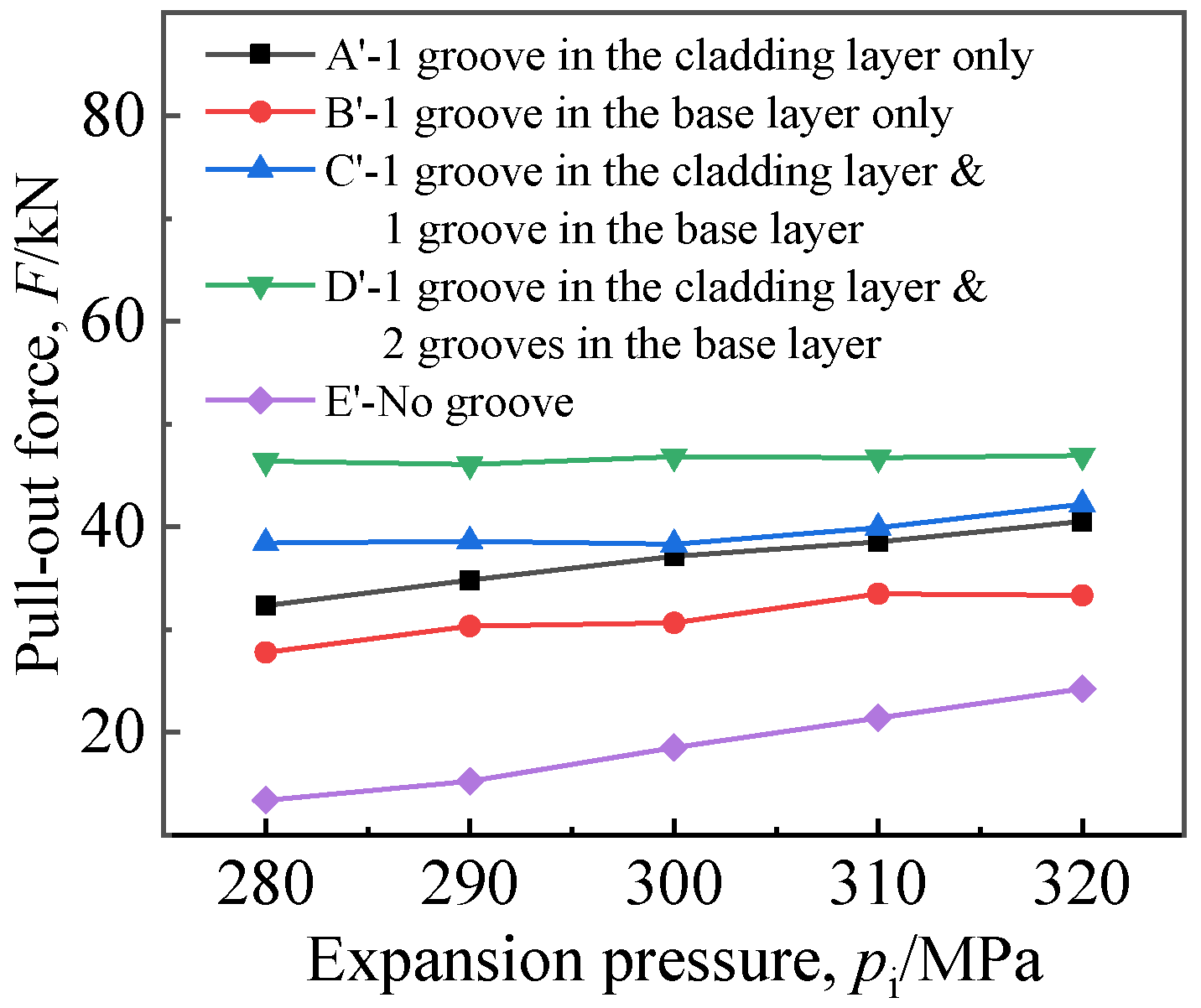
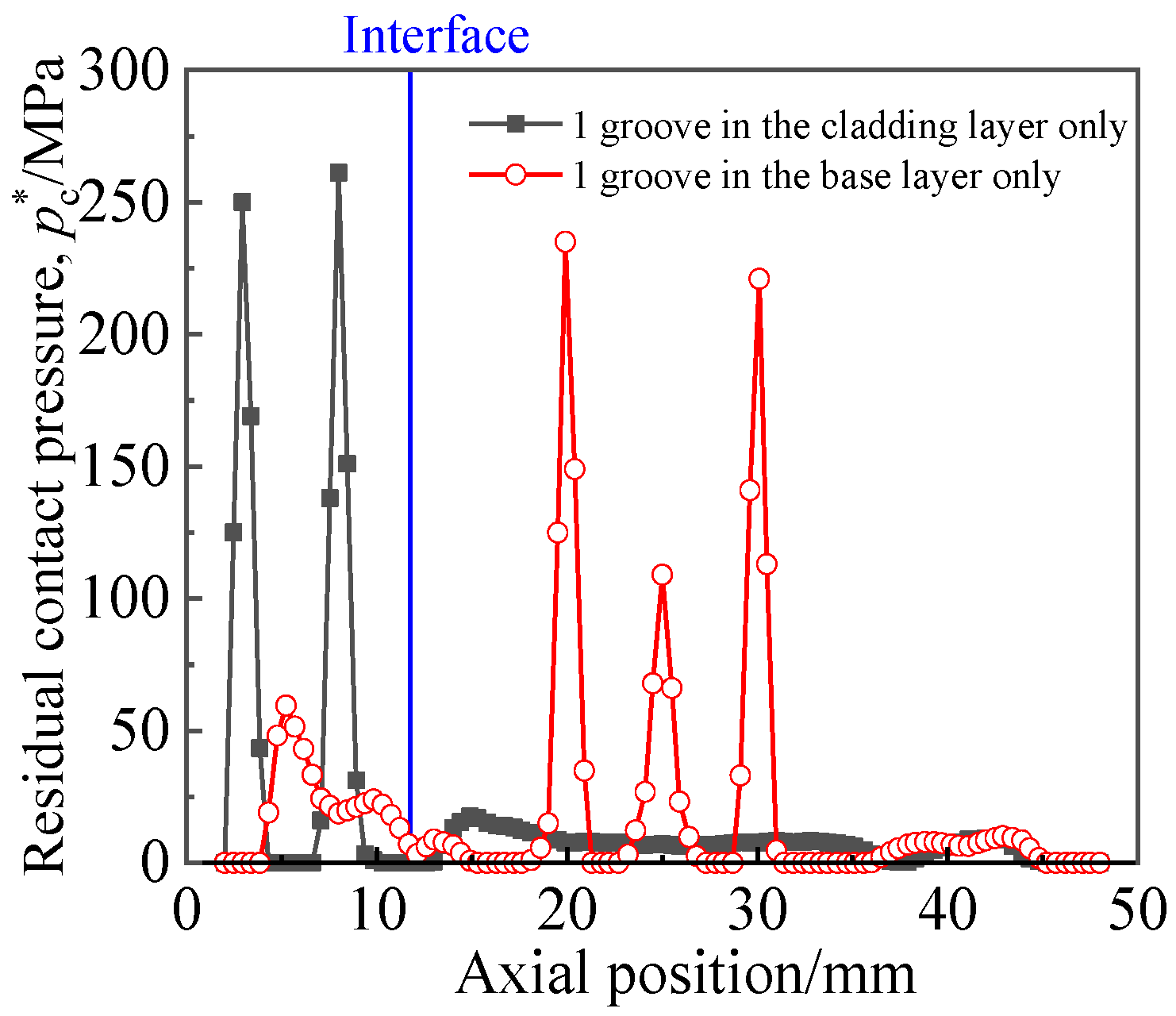
4.1. Effect of Groove Form
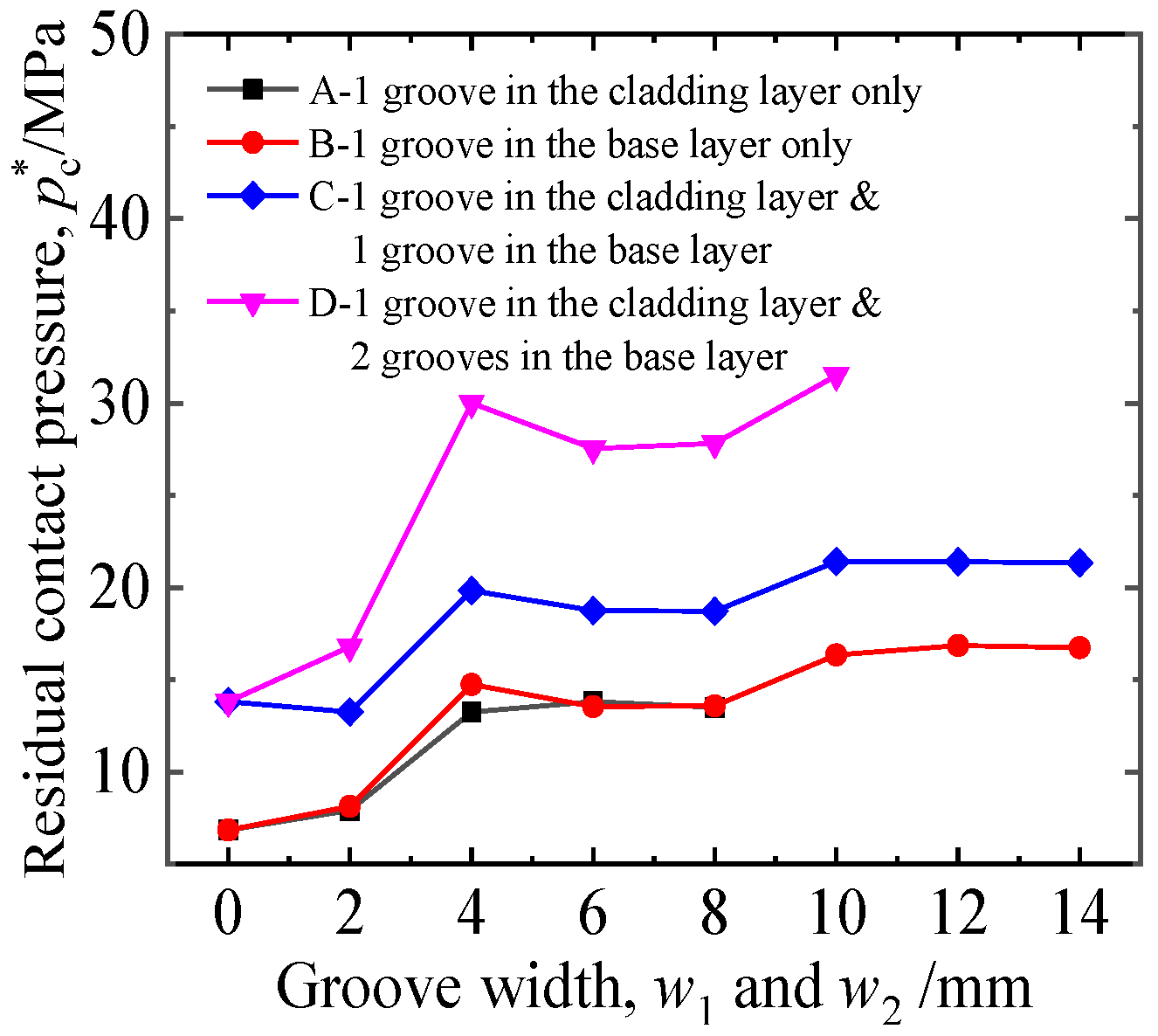
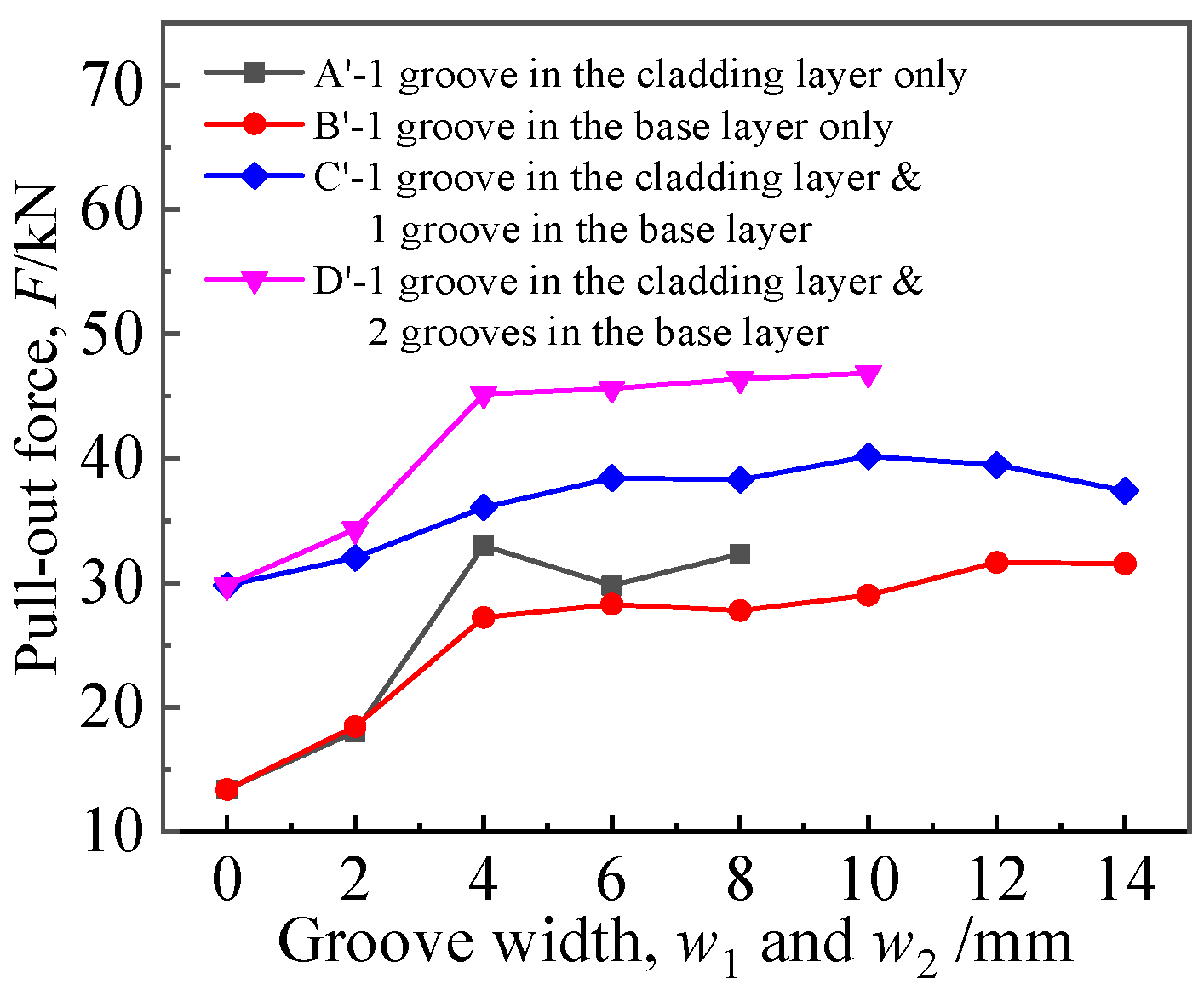
4.2. Effect of Groove Width
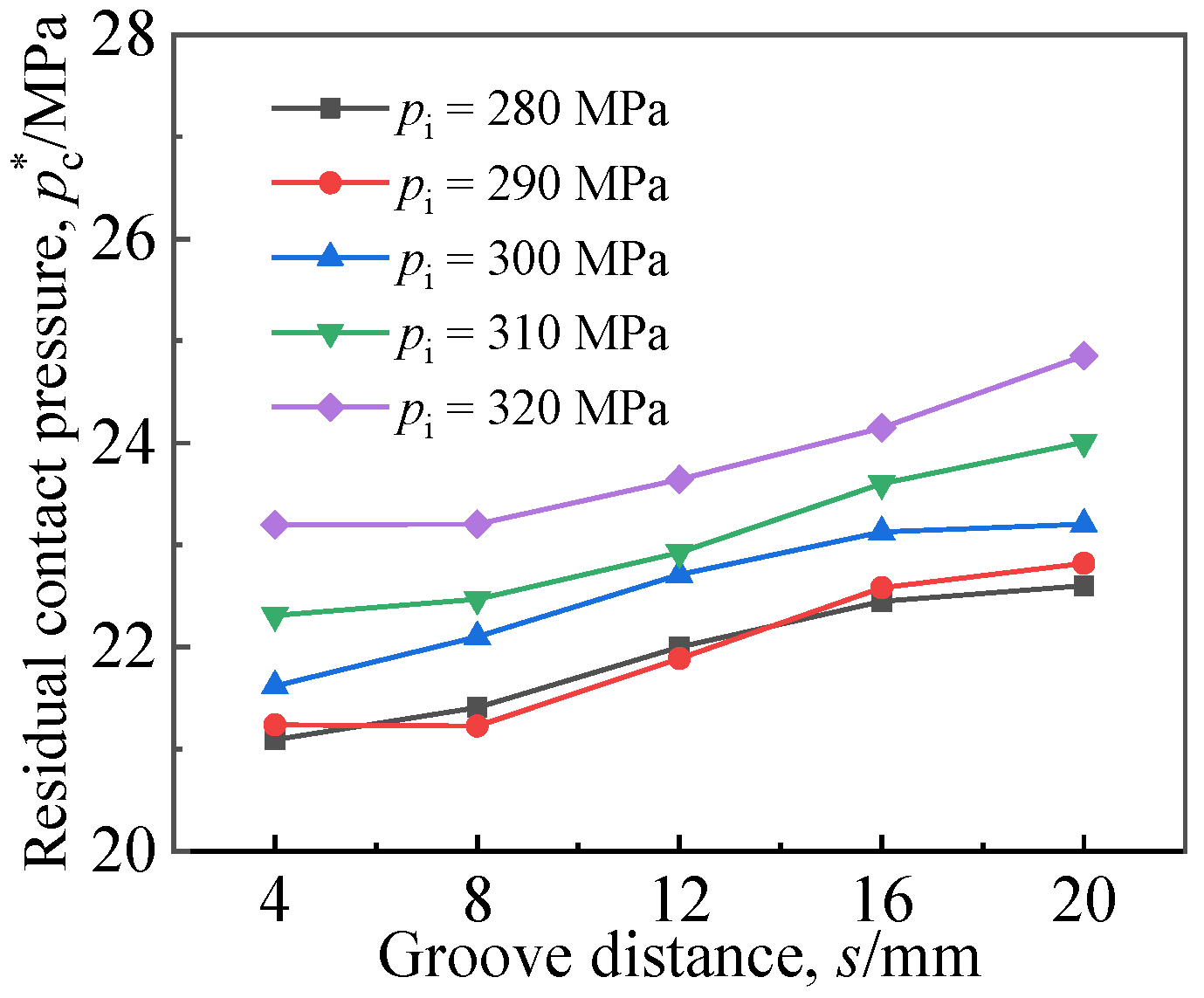
4.3. Effects of Groove Location in the Base
5. Conclusions
- (1)
- During tight expansion, the clad tubesheet and the tube were both made of titanium, the rebound after the expansion was consistent; thus, pc* and F in the cladding layer were higher than in the base layer. The connection strength of the TA2-Q345R clad tubesheet joint was better than that of the Q345R tubesheet joint.
- (2)
- In the case of single groove, the residual contact pressure of grooving in the cladding layer was equivalent to that in the base layer, while the pullout force of grooving in the cladding layer was higher than that in the base layer. When the number of grooves in the base layer was two, the optimal pc* and F could be obtained.
- (3)
- The expansion performance of the joint was gradually enhanced with the increase in groove width within the range of 2–14 mm. When the groove width was 4 mm, the residual contact pressure increased significantly due to the higher radial force of the groove edge. The position of the groove had no obvious effect on the joint performance in the base layer or in the cladding layer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiu, G.Z.; Guo, Y.F. Current situation and development trend of titanium metal industry in China. Int. J. Miner. Metall. Mater. 2022, 29, 599–610. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, S.; Zhou, F. Electrochemical and tribological properties of TiSiCN coatings in coolant. Mater. Sci. Medzg. 2019, 25, 159–165. [Google Scholar] [CrossRef]
- Huang, X.P.; Xie, T. Modeling hydraulically expanded tube-to-tubesheet joint based on general stress-strain curves of tube and tubesheet materials. J. Press. Vessel Technol. 2011, 133, 031205. [Google Scholar] [CrossRef]
- Ge, T.Z.; Li, J.; Zhou, C.Y.; He, X.H. Performance of hydraulic expanding-joint of titanium tube heat exchanger. Rare Met. Mater. Eng. 2018, 47, 3800–3805. [Google Scholar]
- Sui, R.J.; Wang, W.Q.; Liu, Y.; Qu, Y.P. Effects of austenitic stainless steel tube and tubesheet hole dimensional deviations on the hydraulic expansion pressure. Int. J. Press. Vessels Pip. 2016, 138, 1–7. [Google Scholar] [CrossRef]
- Yoganathan, R.; Shanmugam, N.S.; Ramanathan, A. Effects of thickness offset on the tube-to-tube sheet expansion joint strength: An experimental evaluation. J. Mater. Eng. Perform. 2022, 31, 2770–2782. [Google Scholar] [CrossRef]
- Jawad, M.H.; Clarkin, E.J.; Schuessler, R.E. Evaluation of tube-to-tubesheet junctions. J. Press. Vessel Technol. 1987, 109, 19–26. [Google Scholar] [CrossRef]
- Thekkuden, D.T.; Mourad, A.-H.I.; Bouzid, A.-H. Impact of Grooves in Hydraulically Expanded Tube-to-Tubesheet Joints. In Proceedings of the ASME 2020 Pressure Vessels & Piping Conference, Virtual, 3 August 2020. [Google Scholar]
- Alaboodi, A.S. Finite element study of the hybrid expansion of tube-to-tubesheet joints. Thin Wall Struct. 2019, 137, 347–352. [Google Scholar] [CrossRef]
- Bouzid, A.-H.; Zhu, L. A study of neighbouring tube expansion effect on the residual contact pressure of tube-to-tubesheet joints. Int. J. Press. Vessels Pip. 2018, 165, 185–192. [Google Scholar] [CrossRef]
- Updike, D.P.; Kalnins, A.; Caldwell, S.M. Residual stresses in tube-tubesheet joints with grooves. J. Press. Vessel Technol. 1992, 114, 249–251. [Google Scholar] [CrossRef]
- Wang, H.F.; Sang, Z.F. Effect of geometry of grooves on connection strength of hydraulically expanded tube-to-tubesheet joints. J. Press. Vessel Technol. 2005, 127, 430–435. [Google Scholar] [CrossRef]
- Hao, J.W. Mechanical Analysis of Uniform-pressure Tube-expanding and Investigation of Rubber Tube-expanding Key Technology. Ph.D. Thesis, East China University of Science and Technology, Shanghai, China, 2006. [Google Scholar]
- Allam, M.; Bazergui, A.; Chaaban, A. The Effect of Tube Strain Hardening Level on the Residual Contact Pressure and Residual Stresses of Hydraulically Expanded Tube-to-tubesheet Joint. In Proceedings of the ASME 1998 Pressure Vessels & Piping Conference, San Diago, CA, USA, 27–30 July 1998. [Google Scholar]
- Laghzale, N.E.; Bouzid, A.-H. Theoretical analysis of hydraulically expanded tube-to-tubesheet joints with linear strain hardening material behavior. J. Press. Vessel Technol. 2009, 131, 061202. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Z.C.; Xu, W.F.; Tan, G.F.; Wang, Y.Q.; Ma, L. Stress Analysis and Optimization Research of Cladding Titanium-Steel Tube Sheets in Different Tube Patterns. In Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Wang, K.; Xu, W.F.; Liu, Z.C.; Liu, M.S. Stress Analysis and Optimization Research for Ti Clad Steel Tube Sheet. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015. [Google Scholar]
- Yao, X.A.; Wang, H.F. Effect of creep on residual contact stress of hydraulically expanded tube-to-tubesheet joints. Titanium Ind. Prog. 2016, 33, 41–45. [Google Scholar]
- Yao, X.A. Study on Connection Property of Titanium Expanded-and-Welded Tube-to-Tubesheet Joint. Master’s Thesis, Nanjing Tech University, Nanjing, China, 2017. [Google Scholar]
- MA, Q.L. Research on Time-Dependent Mechanical Behaviors of Commercially Pure Titanium and Its Tube-to-Tubesheet Joints. Ph.D. Thesis, East China University of Science and Technology, Shanghai, China, 2006. [Google Scholar]
- Lin, J.F. Research on the Expanding-Joint of the Titanium Tube and the Tubesheet. Master’s Thesis, East China University of Science and Technology, Shanghai, China, 2011. [Google Scholar]
- YS/T 749-2011; Titanium-Steel Clad Tubesheet for Condenser and Heat Exchanger Used in Electric Power Station. National Technical Committee for Standardization of Non-ferrous Metals: Beijing, China, 2012.
- Ni, X.Y.; Zhang, Y.H.; Zhao, H.X.; Pan, C.W. Numerical research on the biomechanical behaviour of braided stents with different end shapes and stent-oesophagus interaction. Int. J. Numer. Meth. Biomed. Eng. 2018, 34, e2971. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Ni, X.Y.; Pan, C.W. Finite element simulation and optimization of mechanical performance of the magnesium-alloy biliary stent. Int. J. Numer. Meth. Biomed. Eng. 2022, 38, e3592. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.G.; Zhang, B.S.; GE, L.T.; Li, P.N. Research on hydraulically expanding of heat exchangers(1)—Determination of the expanding pressure. China Press. Vessel Technol. 1996, 36–40, 3. [Google Scholar]
- GB/T 151-2014; Heat Exchangers. National Boiler and Pressure Vessel Standardization Technical Committee: Beijing, China, 2015.
- Wang, H.F.; Sang, Z.F.; Widera, G.E.O. Connection strength and tightness of hydraulically expanded tube-to-tubesheet joints. J. Mater. Process. Technol. 2007, 194, 93–99. [Google Scholar] [CrossRef]
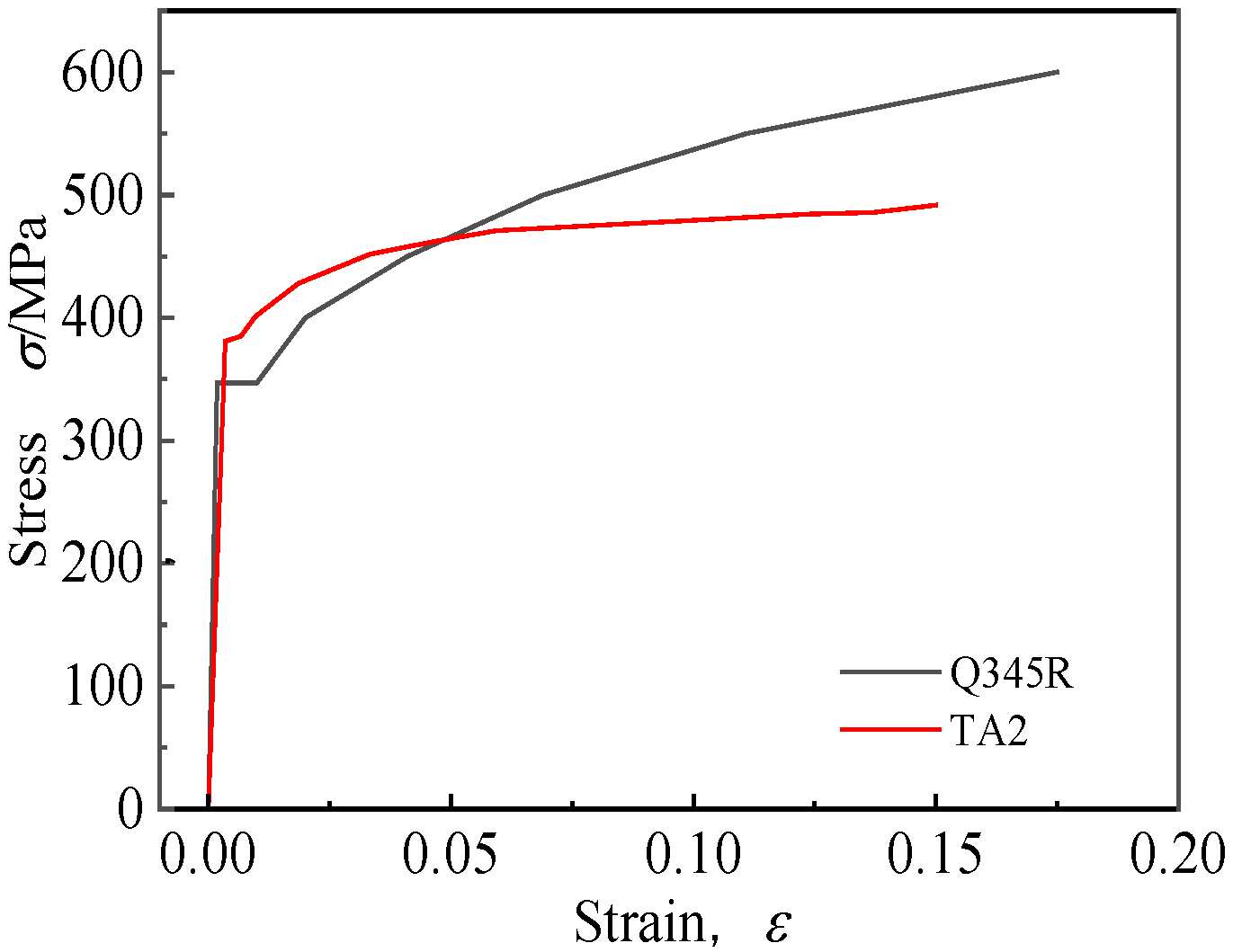



| Material | Yield Strength, σs (MPa) | Elasticity Modulus, E (× 105 MPa) | Poisson’s Ratio, μ |
|---|---|---|---|
| TA2 | 380 | 1.1 | 0.41 |
| Q345R | 347 | 1.95 | 0.3 |
| Parameter Level | Groove Width w1 (mm) | Groove Width w2 (mm) | Groove Distance S (mm) | Groove Spacing B (mm) |
|---|---|---|---|---|
| 1 | 2 | 2 | 4 | 2 |
| 2 | 4 | 4 | 8 | 4 |
| 3 | 6 | 6 | 12 | 6 |
| 4 | 8 | 8 | 16 | 8 |
| 5 | 10 | 20 | 10 | |
| 6 | 12 | |||
| 7 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, J.; Zhang, Y.; Zhou, C. Investigation on Performance of Hydraulically Expanded Joint of Titanium–Steel Clad Tubesheet. Materials 2023, 16, 1106. https://doi.org/10.3390/ma16031106
Li J, Li J, Zhang Y, Zhou C. Investigation on Performance of Hydraulically Expanded Joint of Titanium–Steel Clad Tubesheet. Materials. 2023; 16(3):1106. https://doi.org/10.3390/ma16031106
Chicago/Turabian StyleLi, Jia, Juan Li, Yuyan Zhang, and Changyu Zhou. 2023. "Investigation on Performance of Hydraulically Expanded Joint of Titanium–Steel Clad Tubesheet" Materials 16, no. 3: 1106. https://doi.org/10.3390/ma16031106
APA StyleLi, J., Li, J., Zhang, Y., & Zhou, C. (2023). Investigation on Performance of Hydraulically Expanded Joint of Titanium–Steel Clad Tubesheet. Materials, 16(3), 1106. https://doi.org/10.3390/ma16031106