Room-Temperature Single-Photon Sources Based on Colloidal Quantum Dots: A Review
Abstract
:1. Introduction
2. Optical Properties of Colloidal Quantum Dots
2.1. Emission Spectrum Engineering in Colloidal Quantum Dots
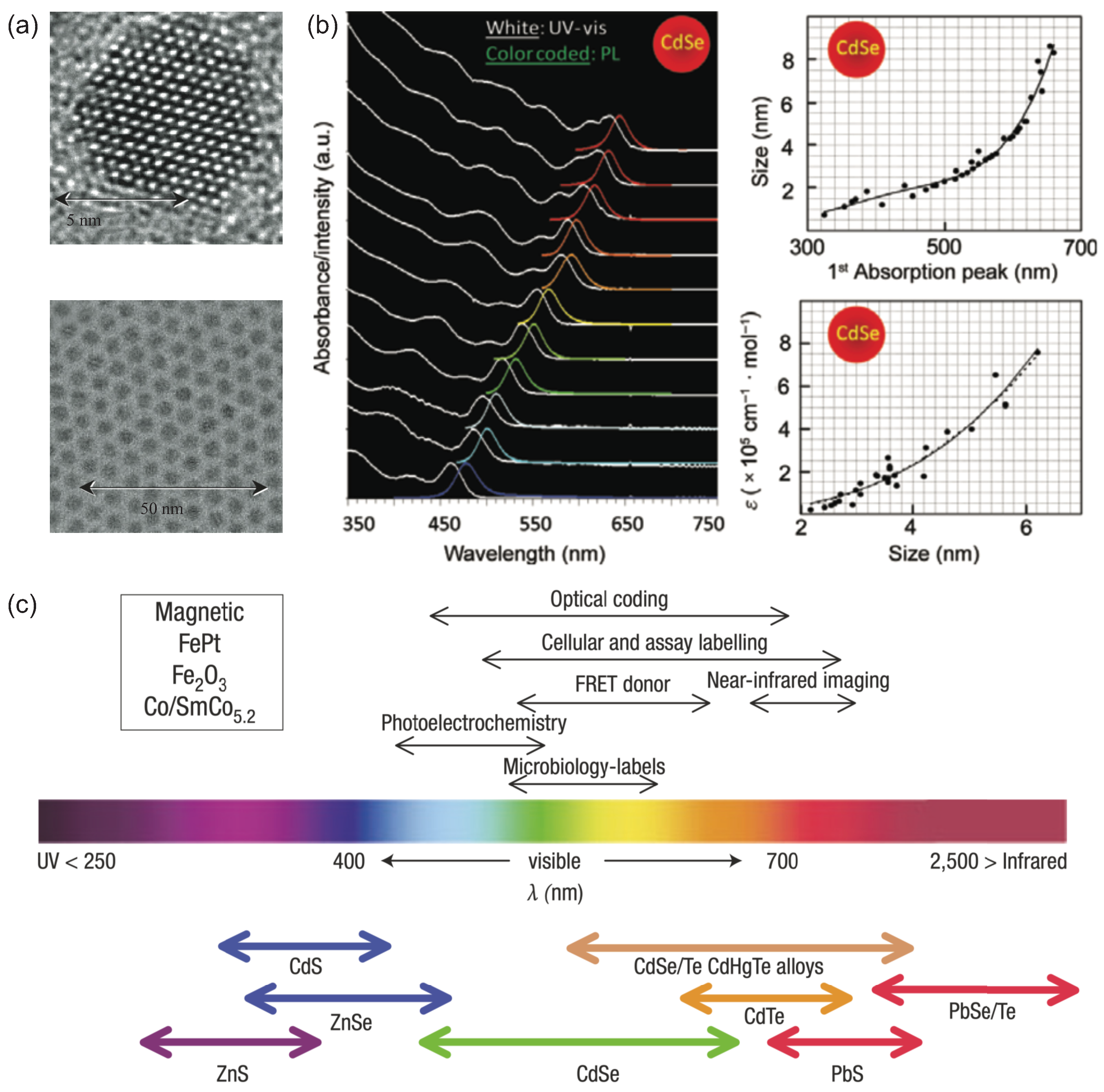
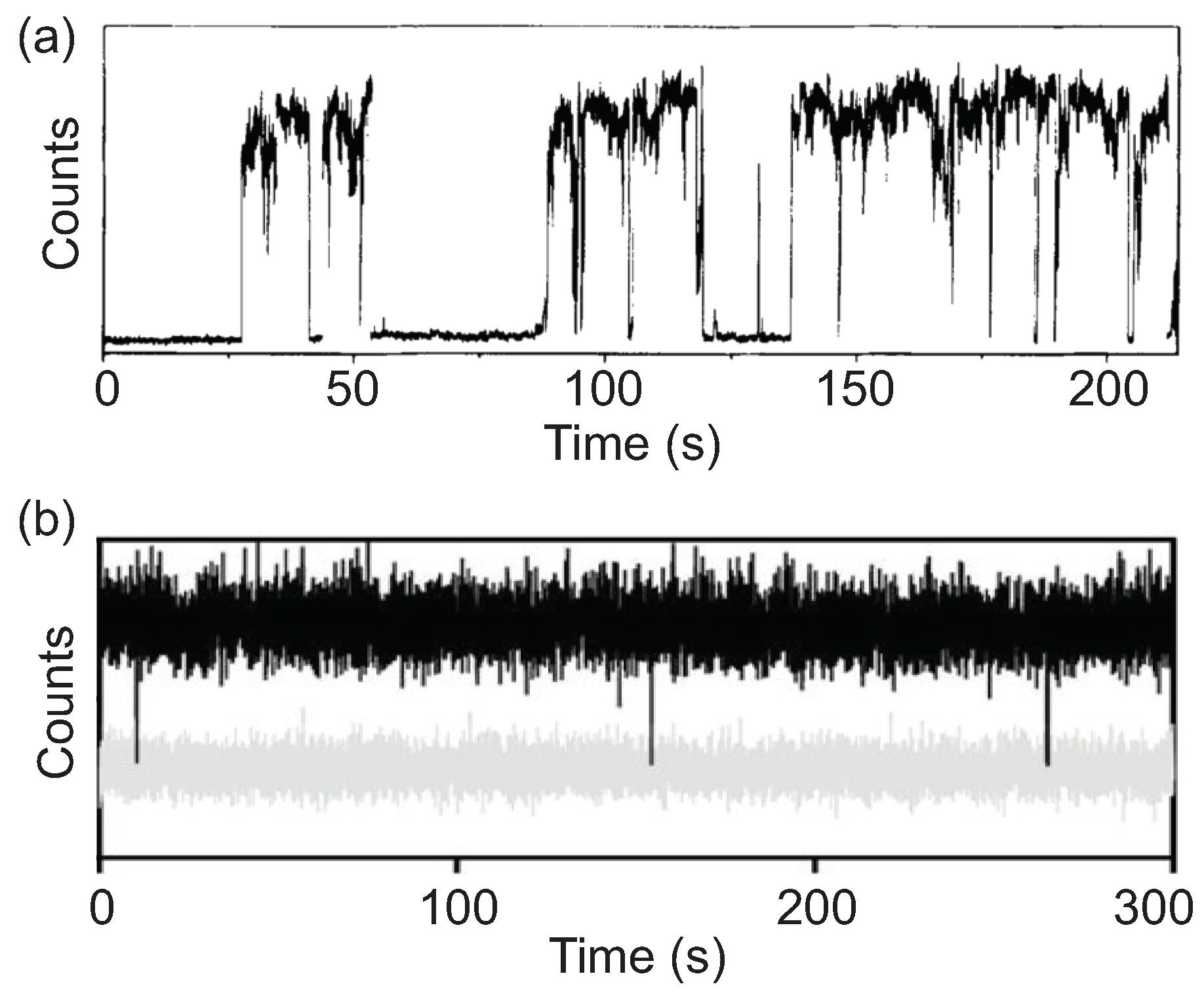
2.2. Photoluminescence Intermittency of Single Colloidal Quantum Dots
3. Single-Photon Generation from Colloidal Quantum Dots
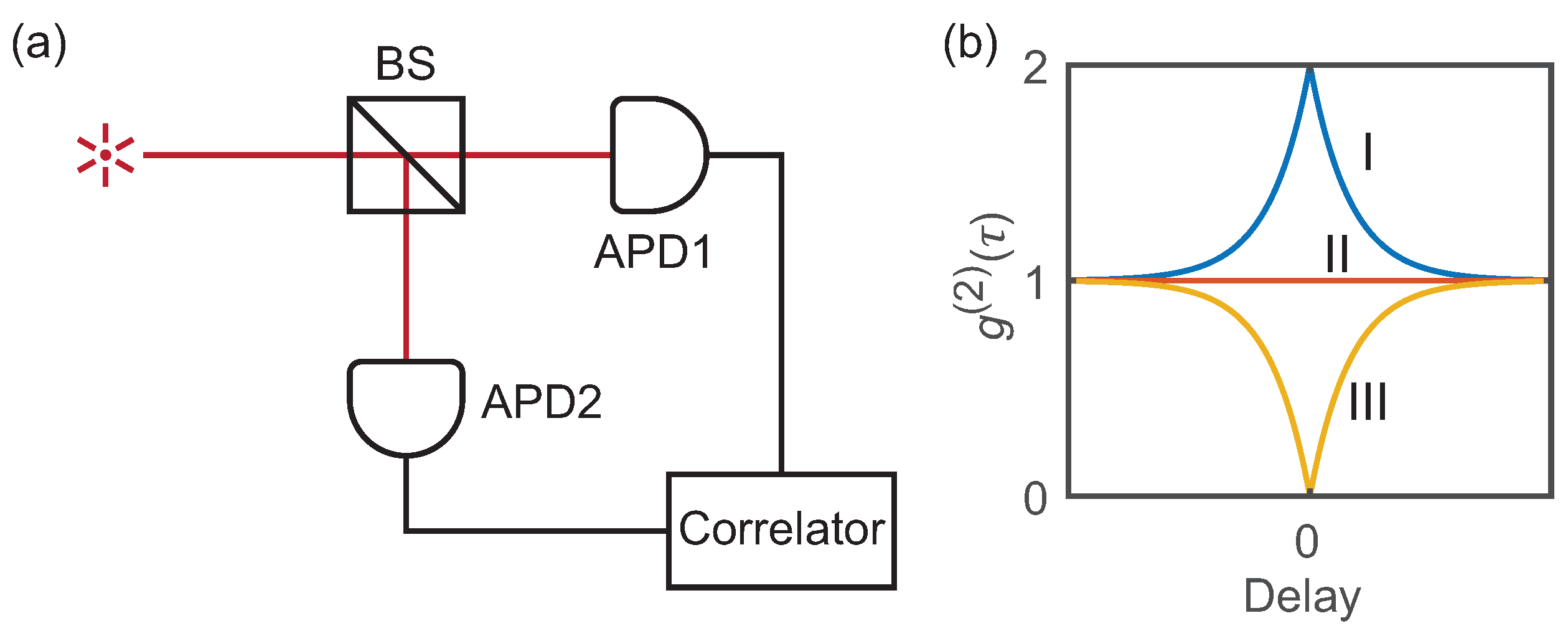
3.1. Photon Statistics Measurement of a Light Source
3.2. Colloidal Quantum Dots as Single-Photon Emitters
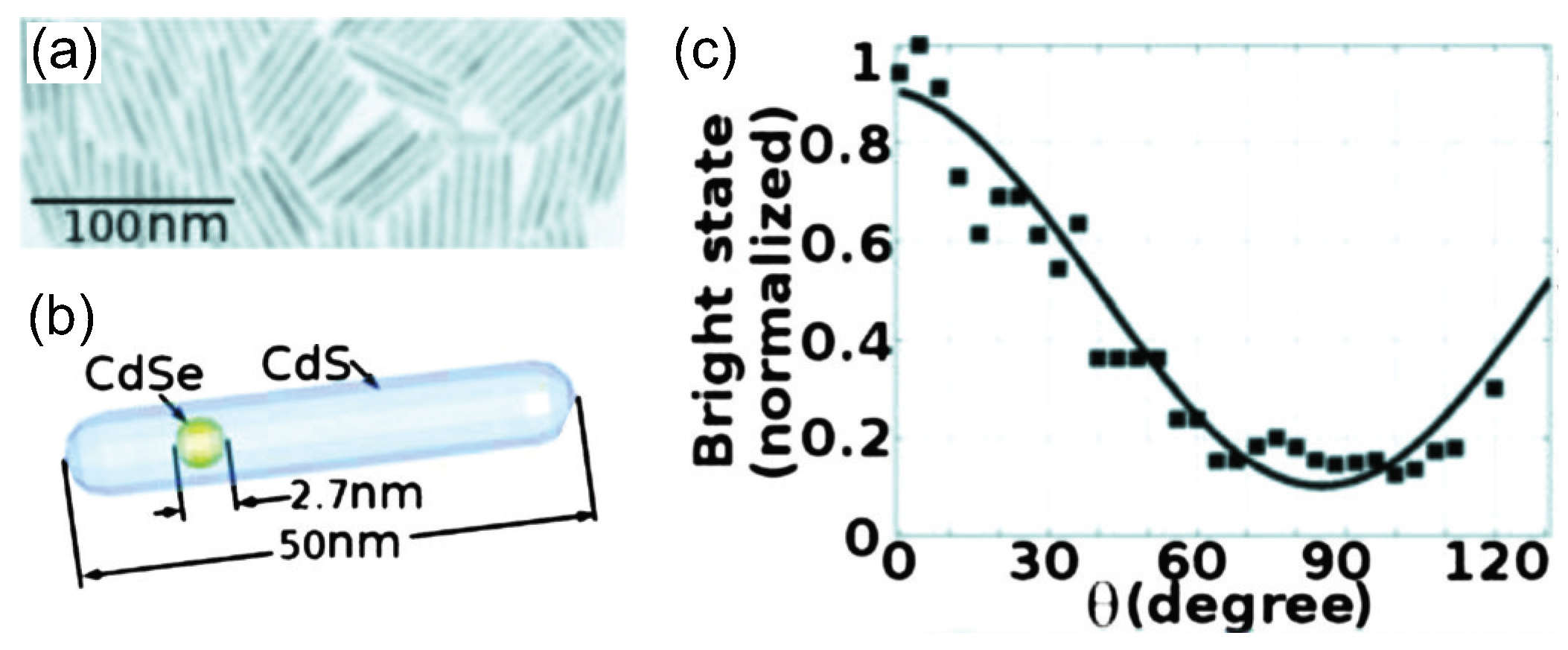
3.3. Polarized Single-Photon Generation from Collodial Quantum Dots
4. Single-Photon Devices Based on Colloidal Quantum Dots
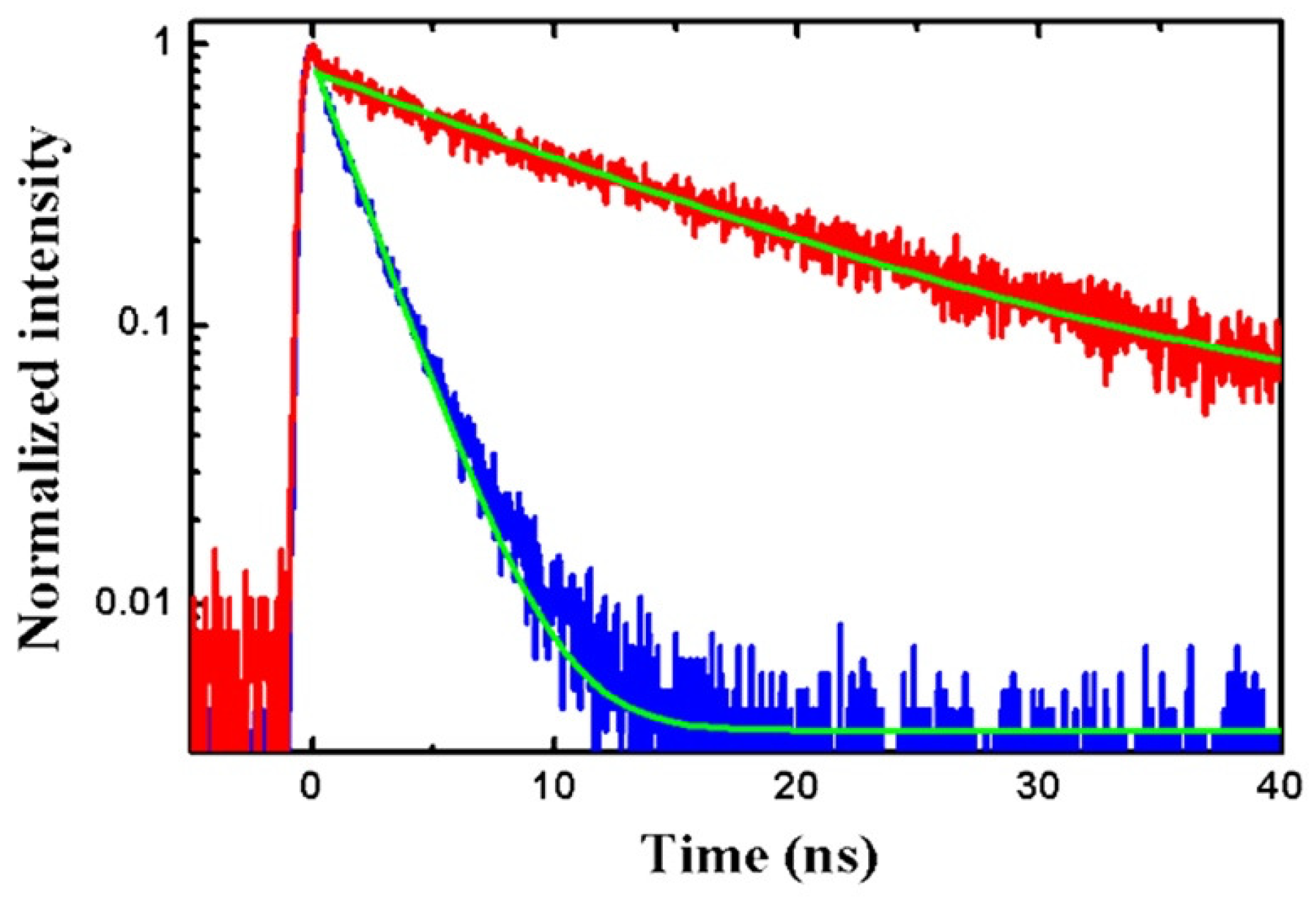
4.1. Cavity Quantum Electrodynamics Effects
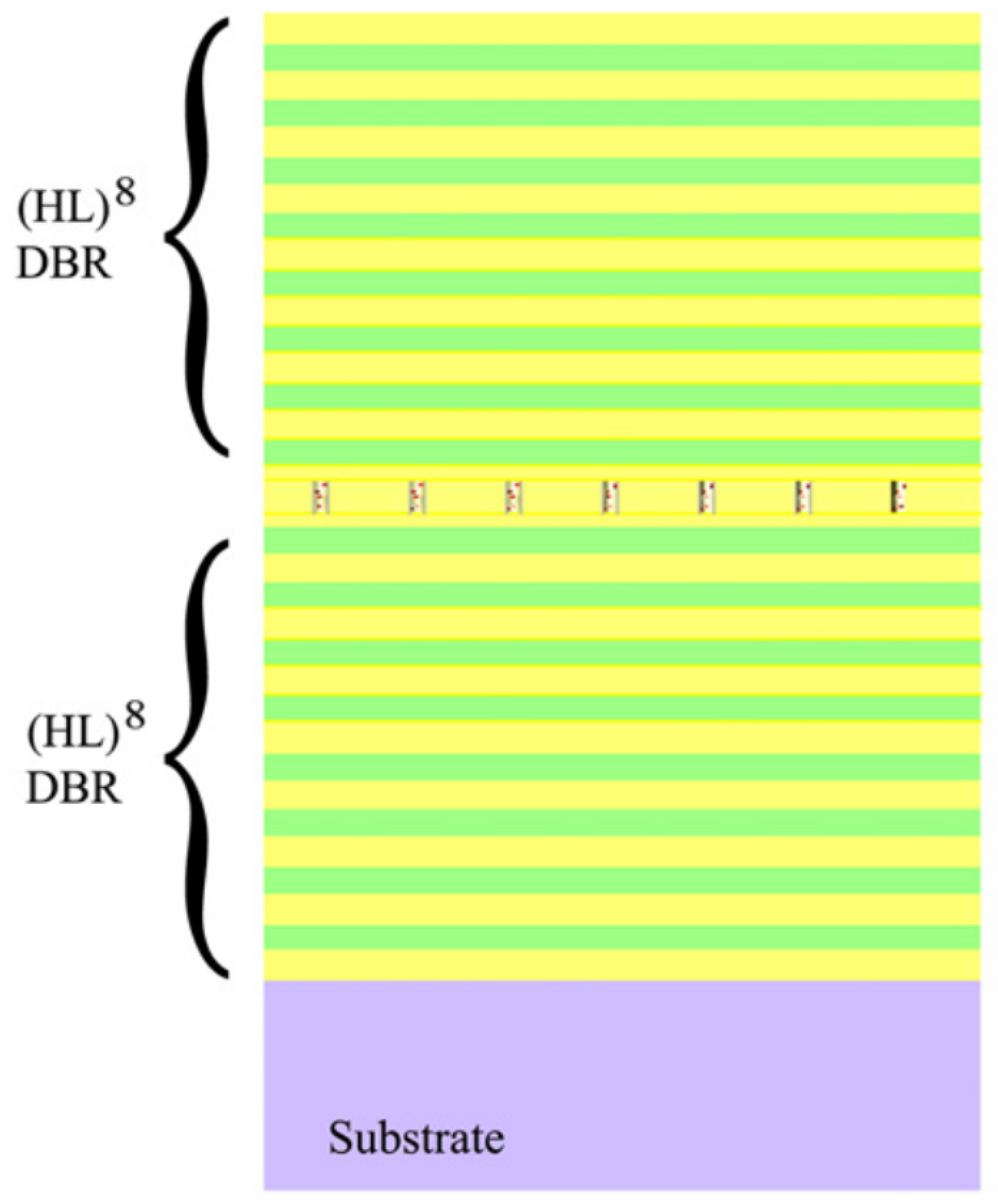
4.2. Fabry–Pérot Microcavity
4.3. Whispering-Gallery Mode Microcavity
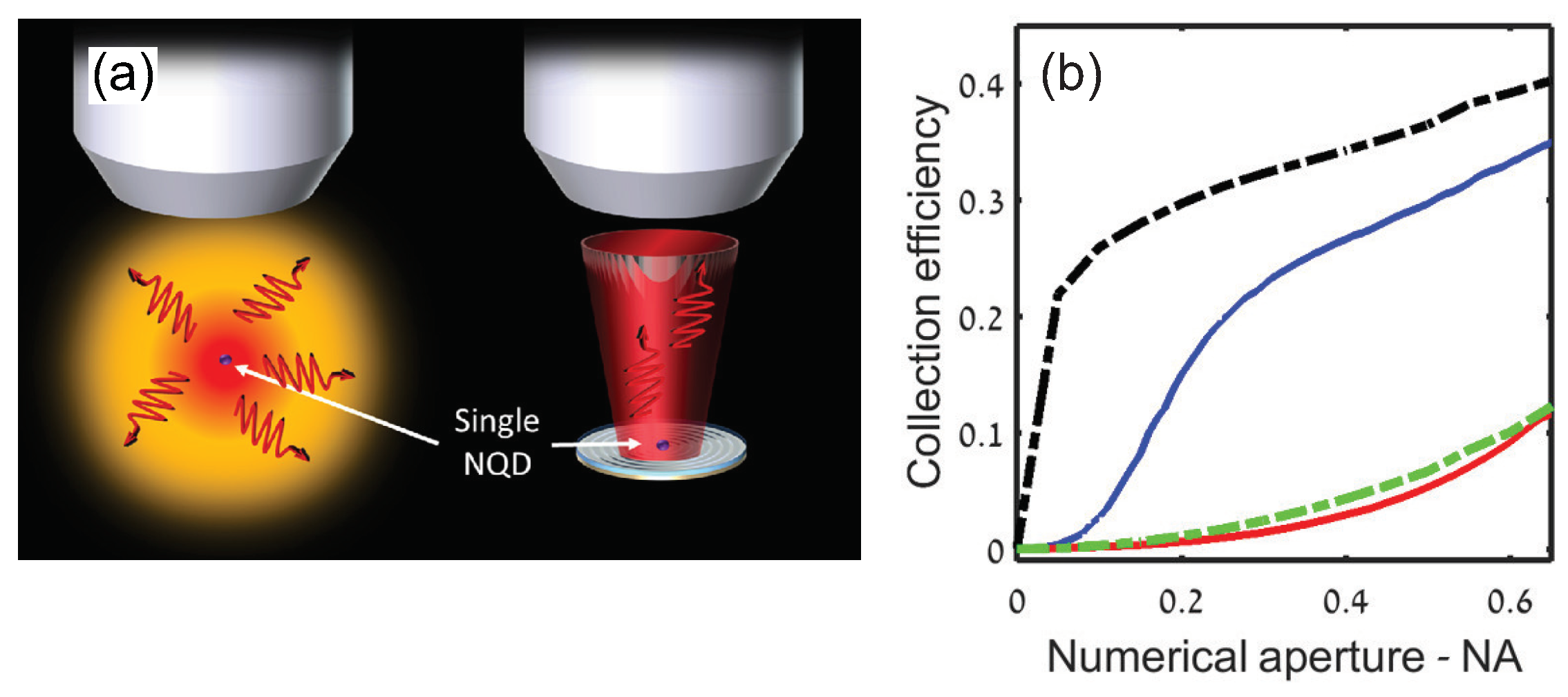
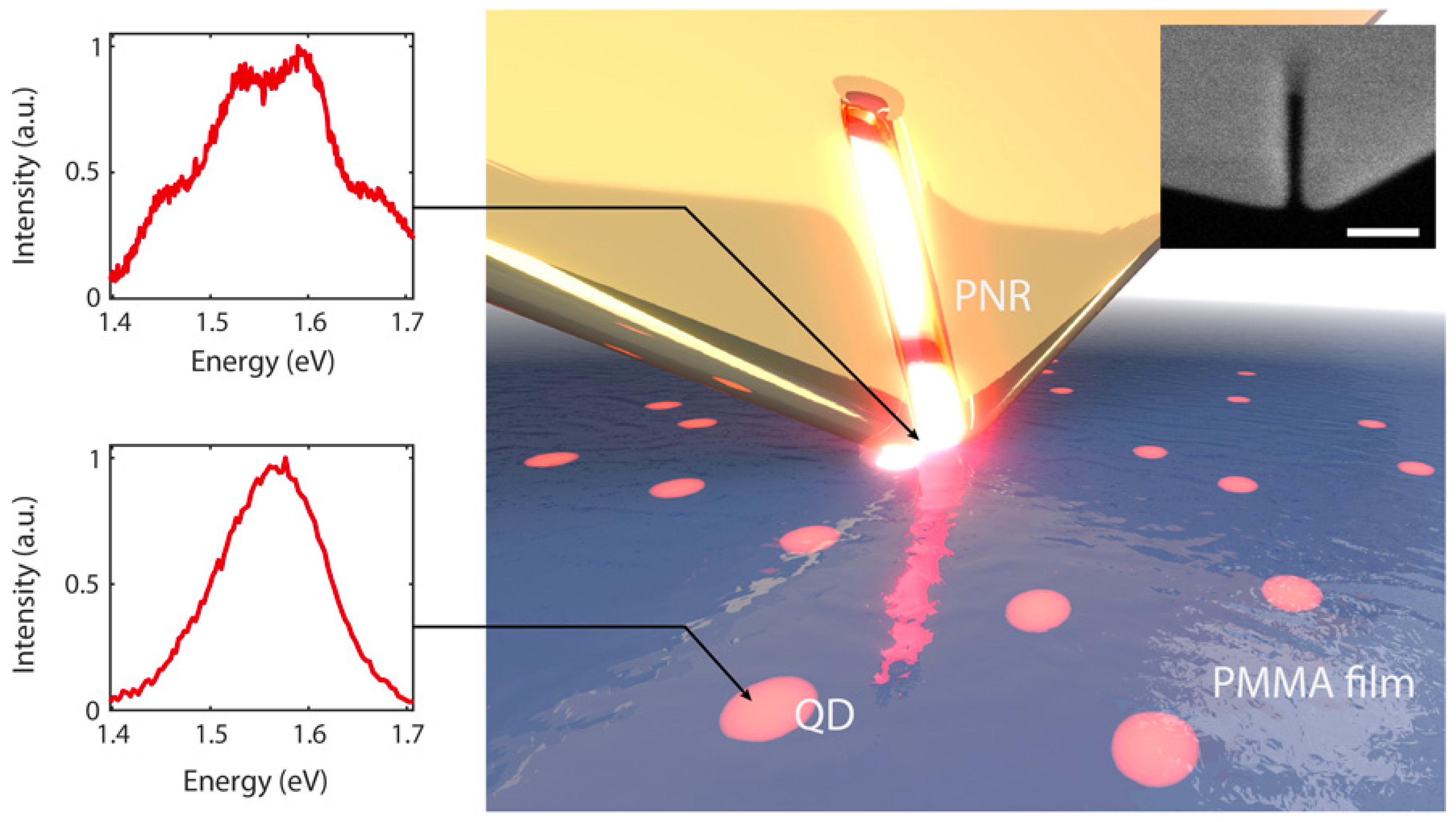
4.4. Plasmonic Nanoresonator
4.5. Photonic Nanowire
4.6. Electrical Driven Single-Photon Source
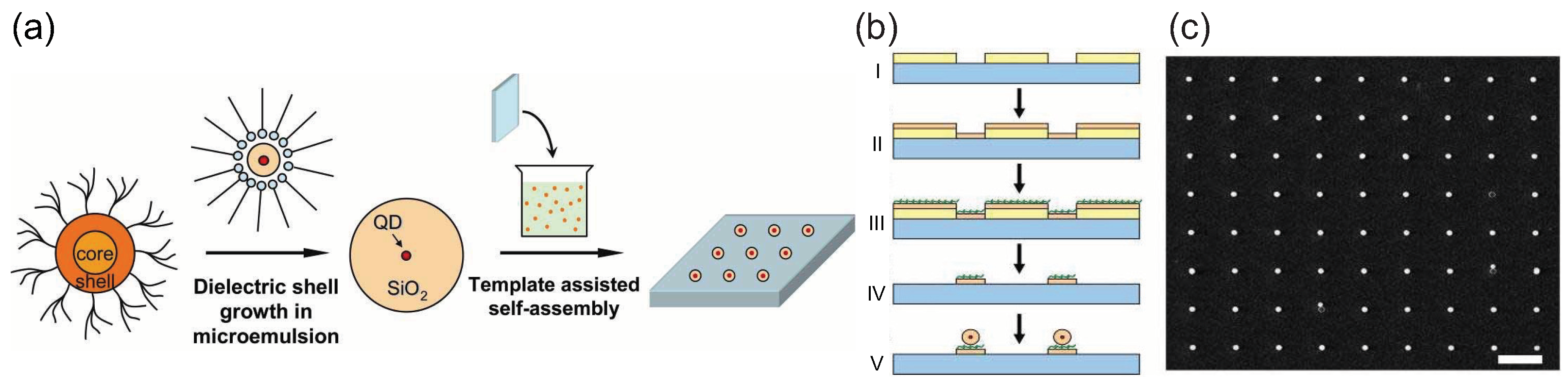
5. Precise Positioning of Single Quantum Dots
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CLC | Cholesteric liquid crystal |
| cQED | Cavity quantum electrodynamics |
| CQD | Colloidal quantum dot |
| EOFC | Electroosmotic flow control |
| EQD | Epitaxial quantum dot |
| ETL | Electron-transport layer |
| FWHM | Full width at half maximum |
| HBT setup | Hanbury Brown and Twiss setup |
| HTL | Hole-transport layer |
| IRF | Instrument response function |
| NV | Nitrogen-vacancy |
| PL | Photoluminescence |
| PNR | Plasmonic nanoresonator |
| QD | Quantum dot |
| QY | Quantum yield |
| SEM | Scanning electron microscope |
| SPD | Single-photon detectors |
| SPS | Single-photon source |
| TEM | Transmission electron microscopy |
References
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Bennett Ch, H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Senellart, P.; Solomon, G.; White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039. [Google Scholar] [CrossRef]
- Burnham, D.C.; Weinberg, D.L. Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett. 1970, 25, 84. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Chiao, R.Y. Observation of a nonclassical Berry’s phase for the photon. Phys. Rev. Lett. 1991, 66, 588. [Google Scholar] [CrossRef]
- Fasel, S.; Alibart, O.; Tanzilli, S.; Baldi, P.; Beveratos, A.; Gisin, N.; Zbinden, H. High-quality asynchronous heralded single-photon source at telecom wavelength. New J. Phys. 2004, 6, 163. [Google Scholar] [CrossRef]
- Azzini, S.; Grassani, D.; Strain, M.J.; Sorel, M.; Helt, L.G.; Sipe, J.; Liscidini, M.; Galli, M.; Bajoni, D. Ultra-low power generation of twin photons in a compact silicon ring resonator. Opt. Express 2012, 20, 23100–23107. [Google Scholar] [CrossRef]
- Li, Q.; Davanço, M.; Srinivasan, K. Efficient and low-noise single-photon-level frequency conversion interfaces using silicon nanophotonics. Nat. Photonics 2016, 10, 406–414. [Google Scholar] [CrossRef]
- Signorini, S.; Pavesi, L. On-chip heralded single photon sources. AVS Quantum Sci. 2020, 2, 041701. [Google Scholar] [CrossRef]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Diedrich, F.; Walther, H. Nonclassical radiation of a single stored ion. Phys. Rev. Lett. 1987, 58, 203. [Google Scholar] [CrossRef] [PubMed]
- Basché, T.; Moerner, W.; Orrit, M.; Talon, H. Photon antibunching in the fluorescence of a single dye molecule trapped in a solid. Phys. Rev. Lett. 1992, 69, 1516. [Google Scholar] [CrossRef] [PubMed]
- Beveratos, A.; Brouri, R.; Gacoin, T.; Poizat, J.P.; Grangier, P. Nonclassical radiation from diamond nanocrystals. Phys. Rev. A 2001, 64, 061802. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Gammon, D.; Snow, E.; Shanabrook, B.; Katzer, D.; Park, D. Homogeneous linewidths in the optical spectrum of a single gallium arsenide quantum dot. Science 1996, 273, 87–90. [Google Scholar] [CrossRef]
- Michler, P.; Imamoğlu, A.; Mason, M.; Carson, P.; Strouse, G.; Buratto, S. Quantum correlation among photons from a single quantum dot at room temperature. Nature 2000, 406, 968. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Duan, Z.C.; Gregersen, N.; Chen, M.C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Höfling, S.; et al. On-demand single photons with high extraction efficiency and near-unity indistinguishability from a resonantly driven quantum dot in a micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef]
- Murray, C.; Norris, D.J.; Bawendi, M.G. Synthesis and characterization of nearly monodisperse CdE (E = sulfur, selenium, tellurium) semiconductor nanocrystallites. J. Am. Chem. Soc. 1993, 115, 8706–8715. [Google Scholar] [CrossRef]
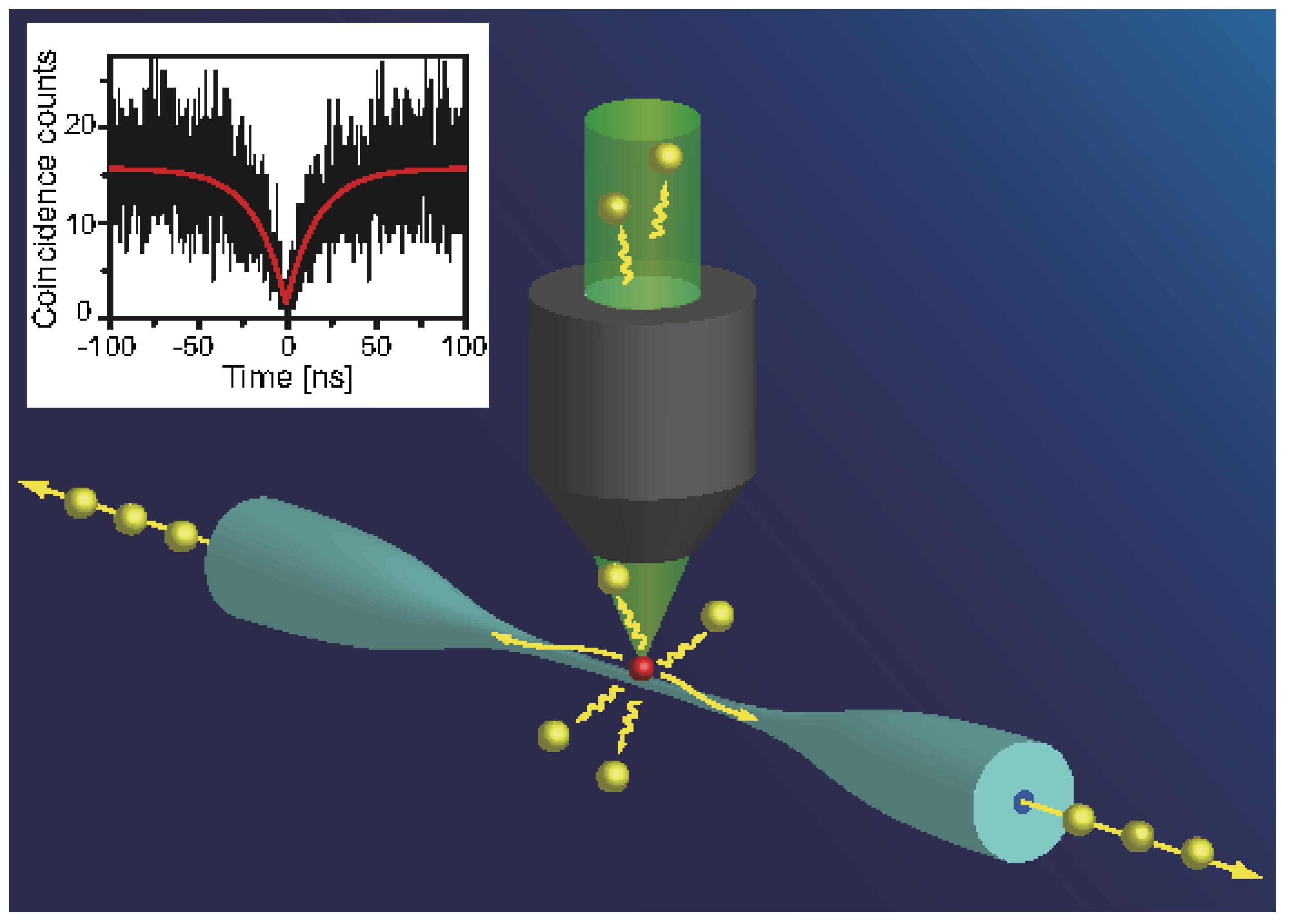
- Livneh, N.; Harats, M.G.; Istrati, D.; Eisenberg, H.S.; Rapaport, R. Highly directional room-temperature single photon device. Nano Lett. 2016, 16, 2527–2532. [Google Scholar] [CrossRef] [PubMed]
- Medintz, I.L.; Uyeda, H.T.; Goldman, E.R.; Mattoussi, H. Quantum dot bioconjugates for imaging, labelling and sensing. Nat. Mater. 2005, 4, 435–446. [Google Scholar] [CrossRef] [PubMed]
- Greytak, A.B.; Allen, P.M.; Liu, W.; Zhao, J.; Young, E.R.; Popović, Z.; Walker, B.J.; Nocera, D.G.; Bawendi, M.G. Alternating layer addition approach to CdSe/CdS core/shell quantum dots with near-unity quantum yield and high on-time fractions. Chem. Sci. 2012, 3, 2028–2034. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Niu, Y.; Meng, R.; Lin, X.; Lai, R.; Fang, W.; Peng, X. Single-dot spectroscopy of zinc-blende CdSe/CdS core/shell nanocrystals: Nonblinking and correlation with ensemble measurements. J. Am. Chem. Soc. 2014, 136, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Meng, R.; Qin, H.; Niu, Y.; Fang, W.; Yang, S.; Lin, X.; Cao, H.; Ma, J.; Lin, W.; Tong, L.; et al. Charging and discharging channels in photoluminescence intermittency of single colloidal CdSe/CdS core/shell quantum dot. J. Phys. Chem. Lett. 2016, 7, 5176–5182. [Google Scholar] [CrossRef] [PubMed]
- de Vittorio, M.; Pisanello, F.; Martiradonna, L.; Qualtieri, A.; Stomeo, T.; Bramati, A.; Cingolani, R. Recent advances on single photon sources based on single colloidal nanocrystals. Opto-Electron. Rev. 2009, 18, 1–9. [Google Scholar] [CrossRef]
- Pisanello, F.; Qualtieri, A.; Leménager, G.; Martiradonna, L.; Stomeo, T.; Cingolani, R.; Bramati, A.; De Vittorio, M. Single colloidal quantum dots as sources of single photons for quantum cryptography. In Quantum Dots and Nanostructures: Synthesis, Characterization, and Modeling VIII; SPIE: Bellingham, WA, USA, 2011; Volume 7947, p. 794709. [Google Scholar]
- Lukishova, S.G.; Winkler, J.M.; Bissell, L.J.; Mihaylova, D.; Liapis, A.C.; Shi, Z.; Goldberg, D.; Menon, V.M.; Boyd, R.W.; Chen, G.; et al. Room-temperature single-photon sources based on nanocrystal fluorescence in photonic/plasmonic nanostructures. In Emerging Technologies in Security and Defence II; and Quantum-Physics-based Information Security III; SPIE: Bellingham, WA, USA, 2014; Volume 9254, p. 925405. [Google Scholar]
- Brus, L.E. Electron–electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state. J. Chem. Phys. 1984, 80, 4403–4409. [Google Scholar] [CrossRef]
- Efros, A.; Efros, A.L. Interband light absorption in semiconductor spheres. Sov. Phys. Semicond. 1982, 16, 772–775. [Google Scholar]
- Henglein, A. Photochemistry of colloidal cadmium sulfide. 2. Effects of adsorbed methyl viologen and of colloidal platinum. J. Phys. Chem. 1982, 86, 2291–2293. [Google Scholar] [CrossRef]
- Steigerwald, M.L.; Brus, L.E. Semiconductor crystallites: A class of large molecules. Accounts Chem. Res. 1990, 23, 183–188. [Google Scholar] [CrossRef]
- Peng, X.; Wickham, J.; Alivisatos, A.P. Kinetics of II-VI and III-V colloidal semiconductor nanocrystal growth: “Focusing” of size distributions. J. Am. Chem. Soc. 1998, 120, 5343–5344. [Google Scholar] [CrossRef]
- Cao, H.; Ma, J.; Huang, L.; Qin, H.; Meng, R.; Li, Y.; Peng, X. Design and synthesis of antiblinking and antibleaching quantum dots in multiple colors via wave function confinement. J. Am. Chem. Soc. 2016, 138, 15727–15735. [Google Scholar] [CrossRef] [PubMed]
- Schaller, R.; Petruska, M.; Klimov, V. Tunable near-infrared optical gain and amplified spontaneous emission using PbSe nanocrystals. J. Phys. Chem. B 2003, 107, 13765–13768. [Google Scholar] [CrossRef]
- Weller, H. Synthesis and self—Assembly of colloidal nanoparticles. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 361, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Peng, X. An essay on synthetic chemistry of colloidal nanocrystals. Nano Res. 2009, 2, 425–447. [Google Scholar] [CrossRef]
- Pietryga, J.M.; Park, Y.S.; Lim, J.; Fidler, A.F.; Bae, W.K.; Brovelli, S.; Klimov, V.I. Spectroscopic and device aspects of nanocrystal quantum dots. Chem. Rev. 2016, 116, 10513–10622. [Google Scholar] [CrossRef]
- Efros, A.L.; Brus, L.E. Nanocrystal Quantum Dots: From Discovery to Modern Development. ACS Nano 2021, 15, 6192–6210. [Google Scholar] [CrossRef]
- Efros, A.L.; Rosen, M. Random telegraph signal in the photoluminescence intensity of a single quantum dot. Phys. Rev. Lett. 1997, 78, 1110–1113. [Google Scholar] [CrossRef]
- Kuno, M.; Fromm, D.P.; Hamann, H.F.; Gallagher, A.; Nesbitt, D.J. Nonexponential “blinking” kinetics of single CdSe quantum dots: A universal power law behavior. J. Chem. Phys. 2000, 112, 3117–3120. [Google Scholar] [CrossRef]
- Chepic, D.I.; Efros, A.L.; Ekimov, A.I.; Ivanov, M.G.; Kharchenko, V.A.; Kudriavtsev, I.A.; Yazeva, T.V. Auger ionization of semiconductor quantum drops in a glass matrix. J. Lumin. 1990, 47, 113–127. [Google Scholar] [CrossRef]
- Galland, C.; Ghosh, Y.; Steinbrück, A.; Sykora, M.; Hollingsworth, J.A.; Klimov, V.I.; Htoon, H. Two types of luminescence blinking revealed by spectroelectrochemistry of single quantum dots. Nature 2011, 479, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Efros, A.L.; Nesbitt, D.J. Origin and control of blinking in quantum dots. Nat. Nanotechnol. 2016, 11, 661–671. [Google Scholar] [CrossRef] [PubMed]
- Nirmal, M.; Dabbousi, B.O.; Bawendi, M.G.; Macklin, J.; Trautman, J.; Harris, T.; Brus, L.E. Fluorescence intermittency in single cadmium selenide nanocrystals. Nature 1996, 383, 802. [Google Scholar] [CrossRef]
- Pu, C.; Qin, H.; Gao, Y.; Zhou, J.; Wang, P.; Peng, X. Synthetic control of exciton behavior in colloidal quantum dots. J. Am. Chem. Soc. 2017, 139, 3302–3311. [Google Scholar] [CrossRef] [PubMed]
- Dabbousi, B.O.; Rodriguez-Viejo, J.; Mikulec, F.V.; Heine, J.R.; Mattoussi, H.; Ober, R.; Jensen, K.F.; Bawendi, M.G. (CdSe) ZnS core-shell quantum dots: Synthesis and characterization of a size series of highly luminescent nanocrystallites. J. Phys. Chem. B 1997, 101, 9463–9475. [Google Scholar] [CrossRef]
- Peng, X.; Schlamp, M.C.; Kadavanich, A.V.; Alivisatos, A.P. Epitaxial growth of highly luminescent CdSe/CdS core/shell nanocrystals with photostability and electronic accessibility. J. Am. Chem. Soc. 1997, 119, 7019–7029. [Google Scholar] [CrossRef]
- Talapin, D.V.; Rogach, A.L.; Kornowski, A.; Haase, M.; Weller, H. Highly luminescent monodisperse CdSe and CdSe/ZnS nanocrystals synthesized in a hexadecylamine-trioctylphosphine oxide-trioctylphospine mixture. Nano Lett. 2001, 1, 207–211. [Google Scholar] [CrossRef]
- Talapin, D.V.; Mekis, I.; Götzinger, S.; Kornowski, A.; Benson, O.; Weller, H. CdSe/CdS/ZnS and CdSe/ZnSe/ZnS core-shell-shell nanocrystals. J. Phys. Chem. B 2004, 108, 18826–18831. [Google Scholar] [CrossRef]
- Tian, Y.; Newton, T.; Kotov, N.A.; Guldi, D.M.; Fendler, J.H. Coupled composite CdS-CdSe and core-shell types of (CdS) CdSe and (CdSe) CdS nanoparticles. J. Phys. Chem. 1996, 100, 8927–8939. [Google Scholar] [CrossRef]
- Reiss, P.; Bleuse, J.; Pron, A. Highly luminescent CdSe/ZnSe core/shell nanocrystals of low size dispersion. Nano Lett. 2002, 2, 781–784. [Google Scholar] [CrossRef]
- Li, J.J.; Wang, Y.A.; Guo, W.; Keay, J.C.; Mishima, T.D.; Johnson, M.B.; Peng, X. Large-scale synthesis of nearly monodisperse CdSe/CdS core/shell nanocrystals using air-stable reagents via successive ion layer adsorption and reaction. J. Am. Chem. Soc. 2003, 125, 12567–12575. [Google Scholar] [CrossRef] [PubMed]
- Xie, R.; Kolb, U.; Li, J.; Basché, T.; Mews, A. Synthesis and characterization of highly luminescent CdSe-core CdS/Zn0.5Cd0.5S/ZnS multishell nanocrystals. J. Am. Chem. Soc. 2005, 127, 7480–7488. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.; Treadway, J.; Feldman, L.C.; Pennycook, S.J.; Rosenthal, S.J. Structural basis for near unity quantum yield core/shell nanostructures. Nano Lett. 2006, 6, 1496–1501. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Vela, J.; Htoon, H.; Casson, J.L.; Werder, D.J.; Bussian, D.A.; Klimov, V.I.; Hollingsworth, J.A. “Giant” multishell CdSe nanocrystal quantum dots with suppressed blinking. J. Am. Chem. Soc. 2008, 130, 5026–5027. [Google Scholar] [CrossRef] [PubMed]
- Mahler, B.; Spinicelli, P.; Buil, S.; Quelin, X.; Hermier, J.P.; Dubertret, B. Towards non-blinking colloidal quantum dots. Nat. Mater. 2008, 7, 659. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Waclawik, E.R. Colloidal semiconductor nanocrystals: Controlled synthesis and surface chemistry in organic media. RSC Adv. 2014, 4, 23505–23527. [Google Scholar] [CrossRef]
- Chou, H.L.; Tseng, C.H.; Pillai, K.C.; Hwang, B.J.; Chen, L.Y. Surface related emission in CdS quantum dots. DFT simulation studies. J. Phys. Chem. C 2011, 115, 20856–20863. [Google Scholar] [CrossRef]
- Dannhauser, T.; O’neil, M.; Johansson, K.; Whitten, D.; McLendon, G. Photophysics of quantized colloidal semiconductors. Dramatic luminescence enhancement by binding of simple amines. J. Phys. Chem. 1986, 90, 6074–6076. [Google Scholar] [CrossRef]
- Thangadurai, P.; Balaji, S.; Manoharan, P. Surface modification of CdS quantum dots using thiols—Structural and photophysical studies. Nanotechnology 2008, 19, 435708. [Google Scholar] [CrossRef]
- Chen, O.; Zhao, J.; Chauhan, V.P.; Cui, J.; Wong, C.; Harris, D.K.; Wei, H.; Han, H.S.; Fukumura, D.; Jain, R.K.; et al. Compact high-quality CdSe–CdS core–shell nanocrystals with narrow emission linewidths and suppressed blinking. Nat. Mater. 2013, 12, 445. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q. Interferometry of the intensity fluctuations in light-i. basic theory: The correlation between photons in coherent beams of radiation. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1957, 242, 300–324. [Google Scholar]
- Dalibard, J.; Reynaud, S. Correlation signals in resonance fluorescence: Interpretation via photon scattering amplitudes. J. Phys. 1983, 44, 1337–1343. [Google Scholar] [CrossRef]
- Lounis, B.; Bechtel, H.A.; Gerion, D.; Alivisatos, P.; Moerner, W.E. Photon antibunching in single CdSe/ZnS quantum dot fluorescence. Chem. Phys. Lett. 2000, 329, 399–404. [Google Scholar] [CrossRef]
- Gschrey, M.; Gericke, F.; Schüßler, A.; Schmidt, R.; Schulze, J.H.; Heindel, T.; Rodt, S.; Strittmatter, A.; Reitzenstein, S. In situ electron-beam lithography of deterministic single-quantum-dot mesa-structures using low-temperature cathodoluminescence spectroscopy. Appl. Phys. Lett. 2013, 102, 251113. [Google Scholar] [CrossRef]
- Nair, G.; Zhao, J.; Bawendi, M.G. Biexciton quantum yield of single semiconductor nanocrystals from photon statistics. Nano Lett. 2011, 11, 1136–1140. [Google Scholar] [CrossRef]
- Hu, J.; Li, L.S.; Yang, W.; Manna, L.; Wang, L.W.; Alivisatos, A.P. Linearly polarized emission from colloidal semiconductor quantum rods. Science 2001, 292, 2060–2063. [Google Scholar] [CrossRef]
- Talapin, D.V.; Koeppe, R.; Götzinger, S.; Kornowski, A.; Lupton, J.M.; Rogach, A.L.; Benson, O.; Feldmann, J.; Weller, H. Highly emissive colloidal CdSe/CdS heterostructures of mixed dimensionality. Nano Lett. 2003, 3, 1677–1681. [Google Scholar] [CrossRef]
- Sitt, A.; Salant, A.; Menagen, G.; Banin, U. Highly emissive nano rod-in-rod heterostructures with strong linear polarization. Nano Lett. 2011, 11, 2054–2060. [Google Scholar] [CrossRef]
- Pisanello, F.; Martiradonna, L.; Spinicelli, P.; Fiore, A.; Hermier, J.; Manna, L.; Cingolani, R.; Giacobino, E.; De Vittorio, M.; Bramati, A. Dots in rods as polarized single photon sources. Superlattices Microstruct. 2010, 47, 165–169. [Google Scholar] [CrossRef]
- Pisanello, F.; Martiradonna, L.; Leménager, G.; Spinicelli, P.; Fiore, A.; Manna, L.; Hermier, J.P.; Cingolani, R.; Giacobino, E.; De Vittorio, M.; et al. Room temperature-dipolelike single photon source with a colloidal dot-in-rod. Appl. Phys. Lett. 2010, 96, 033101. [Google Scholar] [CrossRef]
- Belyakov, V. Diffraction Optics of Complex-Structured Periodic Media: Localized Optical Modes of Spiral Media; Springer: Berlin/Heidelberg, Germany, 2019; p. 42. [Google Scholar]
- Lukishova, S.G.; Bissell, L.J.; Winkler, J.; Stroud, C. Resonance in quantum dot fluorescence in a photonic bandgap liquid crystal host. Opt. Lett. 2012, 37, 1259–1261. [Google Scholar] [CrossRef] [PubMed]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. In Confined Electrons and Photons; Springer: Berlin/Heidelberg, Germany, 1995; p. 839. [Google Scholar]
- Kuhn, A.; Ljunggren, D. Cavity-based single-photon sources. Contemp. Phys. 2010, 51, 289–313. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Qualtieri, A.; Morello, G.; Spinicelli, P.; Todaro, M.T.; Stomeo, T.; Martiradonna, L.; De Giorni, M.; Quélin, X.; Buil, S.; Bramati, A.; et al. Room temperature single-photon sources based on single colloidal nanocrystals in microcavities. Superlattices Microstruct. 2010, 47, 187–191. [Google Scholar] [CrossRef]
- Artemyev, M.V.; Woggon, U.; Wannemacher, R.; Jaschinski, H.; Langbein, W. Light trapped in a photonic dot: Microspheres act as a cavity for quantum dot emission. Nano Lett. 2001, 1, 309–314. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, Y.; Yang, Y.; Wu, M.; Tang, J.; Shih, M. Modification of spontaneous emission rates in single colloidal CdSe/ZnS quantum dots by a submicron-sized dielectric disk. Appl. Phys. Lett. 2011, 99, 053116. [Google Scholar] [CrossRef]
- Berini, P.; De Leon, I. Surface plasmon–polariton amplifiers and lasers. Nat. Photonics 2012, 6, 16. [Google Scholar] [CrossRef]
- Hoang, T.B.; Akselrod, G.M.; Mikkelsen, M.H. Ultrafast room-temperature single photon emission from quantum dots coupled to plasmonic nanocavities. Nano Lett. 2015, 16, 270–275. [Google Scholar] [CrossRef]
- Groß, H.; Hamm, J.M.; Tufarelli, T.; Hess, O.; Hecht, B. Near-field strong coupling of single quantum dots. Sci. Adv. 2018, 4, eaar4906. [Google Scholar] [CrossRef]
- Santhosh, K.; Bitton, O.; Chuntonov, L.; Haran, G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 2016, 7, ncomms11823. [Google Scholar] [CrossRef]
- Reiserer, A.; Kalb, N.; Rempe, G.; Ritter, S. A quantum gate between a flying optical photon and a single trapped atom. Nature 2014, 508, 237. [Google Scholar] [CrossRef]
- Faraon, A.; Fushman, I.; Englund, D.; Stoltz, N.; Petroff, P.; Vučković, J. Coherent generation of non-classical light on a chip via photon-induced tunnelling and blockade. Nat. Phys. 2008, 4, 859. [Google Scholar] [CrossRef]
- Majumdar, A.; Bajcsy, M.; Rundquist, A.; Vučković, J. Loss-enabled sub-Poissonian light generation in a bimodal nanocavity. Phys. Rev. Lett. 2012, 108, 183601. [Google Scholar] [CrossRef] [PubMed]
- Shore, B.W. Picturing stimulated Raman adiabatic passage: A STIRAP tutorial. Adv. Opt. Photonics 2017, 9, 563–719. [Google Scholar] [CrossRef]
- Tong, L.; Sumetsky, M. Subwavelength and Nanometer Diameter Optical Fibers; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Fujiwara, M.; Toubaru, K.; Noda, T.; Zhao, H.Q.; Takeuchi, S. Highly efficient coupling of photons from nanoemitters into single-mode optical fibers. Nano Lett. 2011, 11, 4362–4365. [Google Scholar] [CrossRef] [PubMed]
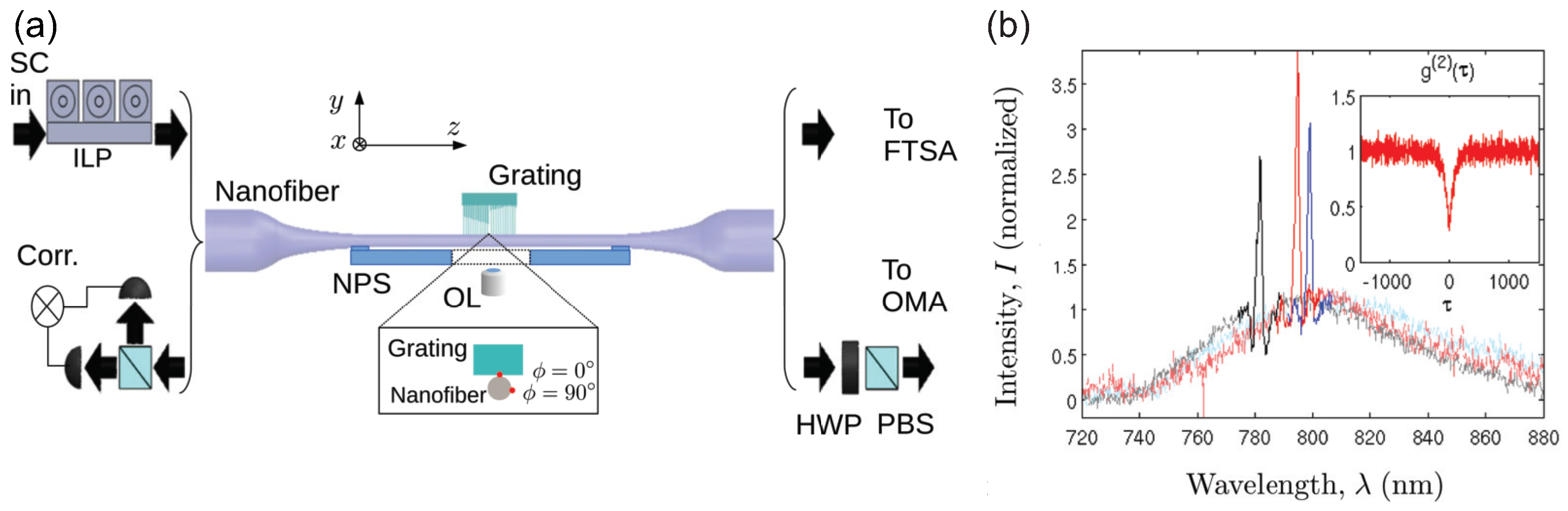
- Yalla, R.; Le Kien, F.; Morinaga, M.; Hakuta, K. Efficient channeling of fluorescence photons from single quantum dots into guided modes of optical nanofiber. Phys. Rev. Lett. 2012, 109, 063602. [Google Scholar] [CrossRef] [PubMed]
- Yalla, R.; Nayak, K.; Hakuta, K. Fluorescence photon measurements from single quantum dots on an optical nanofiber. Opt. Express 2012, 20, 2932–2941. [Google Scholar] [CrossRef]
- Le Kien, F.; Gupta, S.D.; Nayak, K.P.; Hakuta, K. Nanofiber-mediated radiative transfer between two distant atoms. Phys. Rev. A 2005, 72, 063815. [Google Scholar] [CrossRef]
- Yalla, R.; Sadgrove, M.; Nayak, K.P.; Hakuta, K. Cavity quantum electrodynamics on a nanofiber using a composite photonic crystal cavity. Phys. Rev. Lett. 2014, 113, 143601. [Google Scholar] [CrossRef]
- Kolchin, P.; Pholchai, N.; Mikkelsen, M.H.; Oh, J.; Ota, S.; Islam, M.S.; Yin, X.; Zhang, X. High purcell factor due to coupling of a single emitter to a dielectric slot waveguide. Nano Lett. 2015, 15, 464–468. [Google Scholar] [CrossRef]
- Boretti, A.; Rosa, L.; Mackie, A.; Castelletto, S. Electrically driven quantum light sources. Adv. Opt. Mater. 2015, 3, 1012–1033. [Google Scholar] [CrossRef]
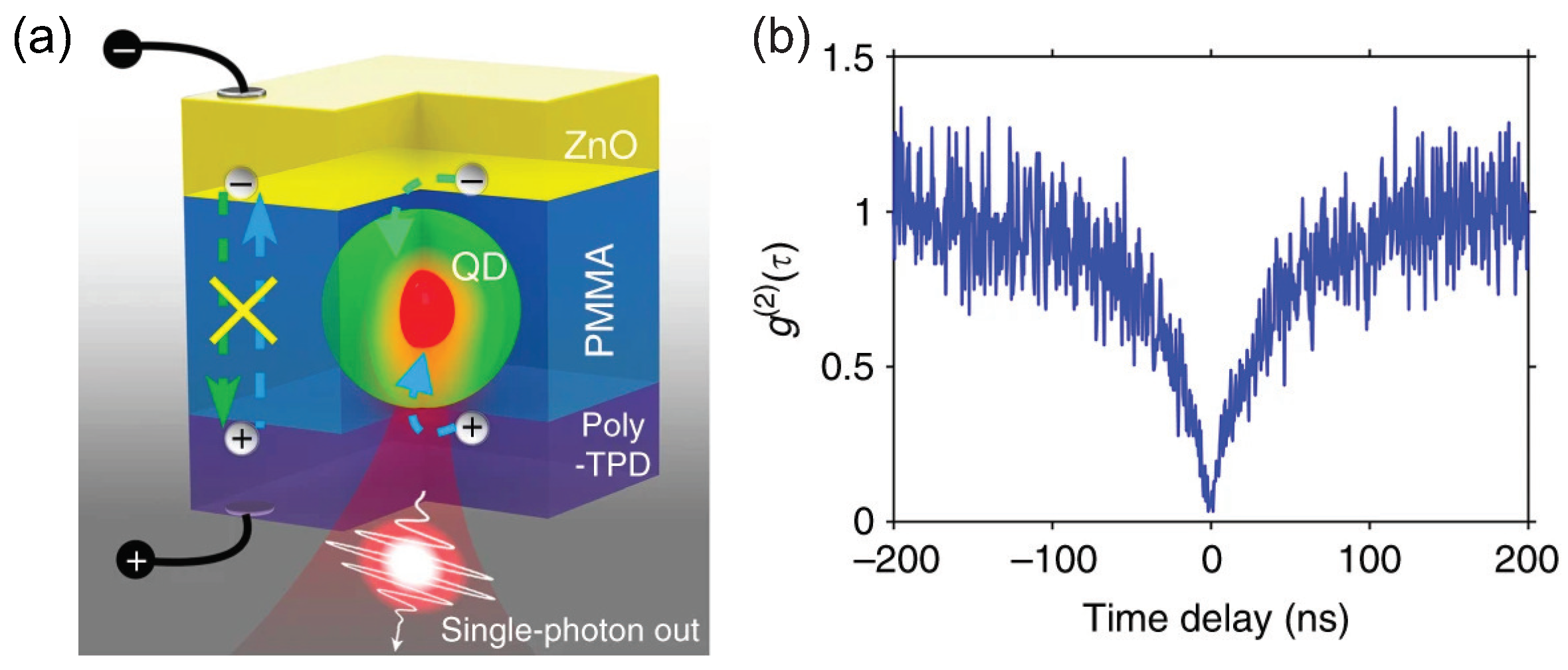
- Lin, X.; Dai, X.; Pu, C.; Deng, Y.; Niu, Y.; Tong, L.; Fang, W.; Jin, Y.; Peng, X. Electrically-driven single-photon sources based on colloidal quantum dots with near-optimal antibunching at room temperature. Nat. Commun. 2017, 8, 1132. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.B.; Bennett, A.J.; Cooper, K.; Atkinson, P.; Nicoll, C.A.; Ritchie, D.A.; Shields, A.J. Quantum interference of electrically generated single photons from a quantum dot. Nanotechnology 2010, 21, 274011. [Google Scholar] [CrossRef] [PubMed]
- Mizuochi, N.; Makino, T.; Kato, H.; Takeuchi, D.; Ogura, M.; Okushi, H.; Nothaft, M.; Neumann, P.; Gali, A.; Jelezko, F.; et al. Electrically driven single-photon source at room temperature in diamond. Nat. Photonics 2012, 6, 299. [Google Scholar] [CrossRef]
- Nothaft, M.; Höhla, S.; Jelezko, F.; Frühauf, N.; Pflaum, J.; Wrachtrup, J. Electrically driven photon antibunching from a single molecule at room temperature. Nat. Commun. 2012, 3, 628. [Google Scholar] [CrossRef] [PubMed]
- Eich, A.; Spiekermann, T.C.; Gehring, H.; Sommer, L.; Bankwitz, J.R.; Schrinner, P.P.; Preuß, J.A.; Michaelis de Vasconcellos, S.; Bratschitsch, R.; Pernice, W.H.; et al. Single-photon emission from individual nanophotonic-integrated colloidal quantum dots. ACS Photonics 2022, 9, 551–558. [Google Scholar] [CrossRef]
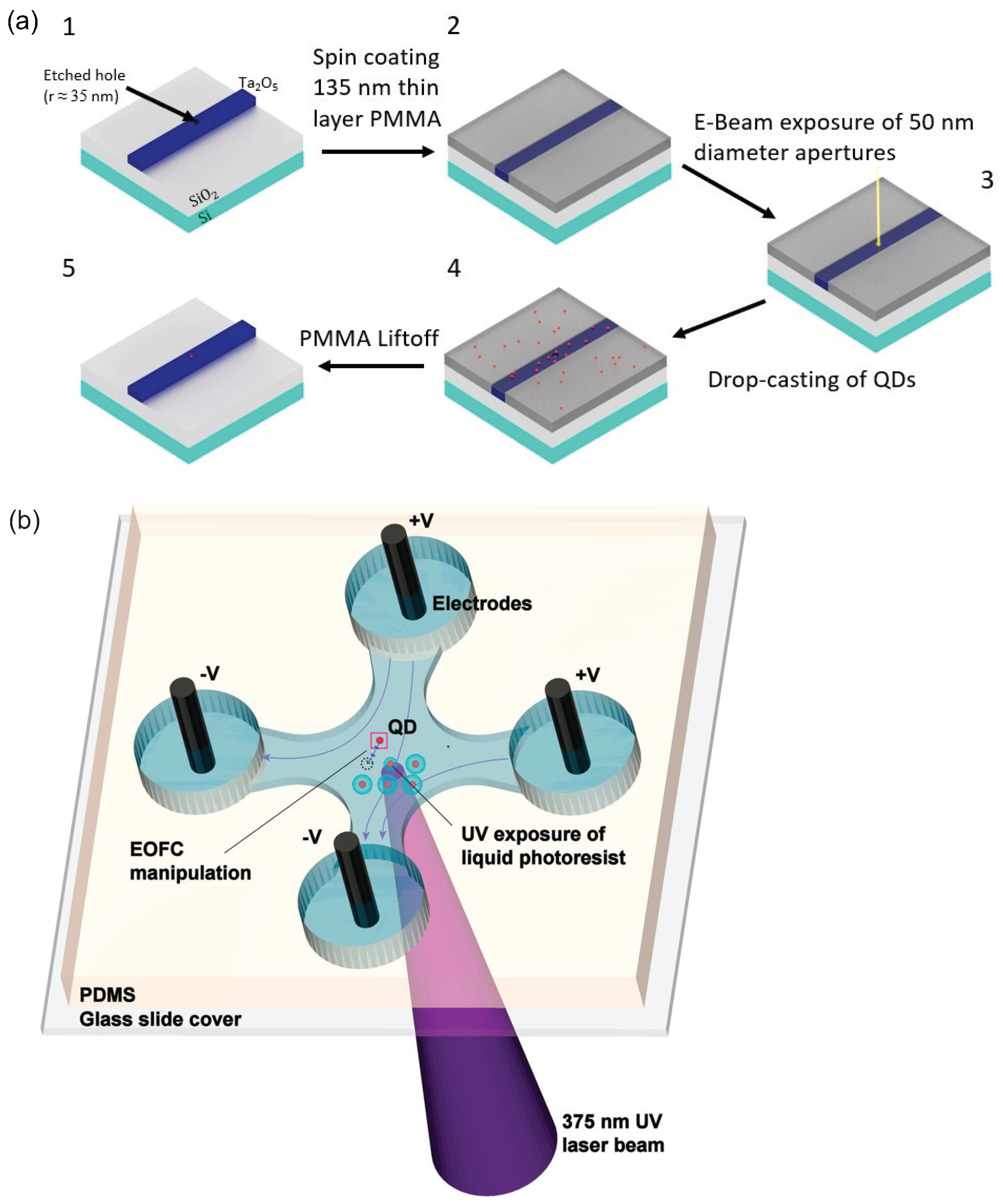
- Ropp, C.; Cummins, Z.; Probst, R.; Qin, S.; Fourkas, J.T.; Shapiro, B.; Waks, E. Positioning and immobilization of individual quantum dots with nanoscale precision. Nano Lett. 2010, 10, 4673–4679. [Google Scholar] [CrossRef] [PubMed]
- LaFratta, C.N.; Fourkas, J.T.; Baldacchini, T.; Farrer, R.A. Multiphoton fabrication. Angew. Chem. Int. Ed. 2007, 46, 6238–6258. [Google Scholar] [CrossRef]
- Maruo, S.; Fourkas, J.T. Recent progress in multiphoton microfabrication. Laser Photonics Rev. 2008, 2, 100–111. [Google Scholar] [CrossRef]
- Zhang, Q.; Dang, C.; Urabe, H.; Wang, J.; Sun, S.; Nurmikko, A. Large ordered arrays of single photon sources based on II–VI semiconductor colloidal quantum dot. Opt. Express 2008, 16, 19592–19599. [Google Scholar] [CrossRef]
- Aizenberg, J.; Braun, P.V.; Wiltzius, P. Patterned colloidal deposition controlled by electrostatic and capillary forces. Phys. Rev. Lett. 2000, 84, 2997. [Google Scholar] [CrossRef]
- Cui, Y.; Björk, M.T.; Liddle, J.A.; Sönnichsen, C.; Boussert, B.; Alivisatos, A.P. Integration of colloidal nanocrystals into lithographically patterned devices. Nano Lett. 2004, 4, 1093–1098. [Google Scholar] [CrossRef]
- Kraus, T.; Malaquin, L.; Schmid, H.; Riess, W.; Spencer, N.D.; Wolf, H. Nanoparticle printing with single-particle resolution. Nat. Nanotechnol. 2007, 2, 570. [Google Scholar] [CrossRef] [PubMed]
- Kagan, C.R.; Bassett, L.C.; Murray, C.B.; Thompson, S.M. Colloidal Quantum Dots as Platforms for Quantum Information Science. Chem. Rev. 2021, 121, 3186–3233. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, A.E.; Krajewska, C.J.; Proppe, A.H.; Sun, W.; Sverko, T.; Berkinsky, D.B.; Utzat, H.; Bawendi, M.G. Hong-Ou-Mandel interference in colloidal CsPbBr3 perovskite nanocrystals. Nat. Photonics 2023, 17, 775–780. [Google Scholar] [CrossRef]
- Empedocles, S.A.; Norris, D.J.; Bawendi, M.G. Photoluminescence spectroscopy of single CdSe nanocrystallite quantum dots. Phys. Rev. Lett. 1996, 77, 3873–3876. [Google Scholar] [CrossRef]
- Empedocles, S.A.; Bawendi, M.G. Influence of spectral diffusion on the line shapes of single CdSe nanocrystallite quantum dots. J. Phys. Chem. B 1999, 103, 1826–1830. [Google Scholar] [CrossRef]
- Beyler, A.P.; Marshall, L.F.; Cui, J.; Brokmann, X.; Bawendi, M.G. Direct observation of rapid discrete spectral dynamics in single colloidal CdSe-CdS core-shell quantum dots. Phys. Rev. Lett. 2013, 111, 177401. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Lin, X.; Fang, W. Room-Temperature Single-Photon Sources Based on Colloidal Quantum Dots: A Review. Materials 2023, 16, 7684. https://doi.org/10.3390/ma16247684
Ye Y, Lin X, Fang W. Room-Temperature Single-Photon Sources Based on Colloidal Quantum Dots: A Review. Materials. 2023; 16(24):7684. https://doi.org/10.3390/ma16247684
Chicago/Turabian StyleYe, Yongzheng, Xing Lin, and Wei Fang. 2023. "Room-Temperature Single-Photon Sources Based on Colloidal Quantum Dots: A Review" Materials 16, no. 24: 7684. https://doi.org/10.3390/ma16247684
APA StyleYe, Y., Lin, X., & Fang, W. (2023). Room-Temperature Single-Photon Sources Based on Colloidal Quantum Dots: A Review. Materials, 16(24), 7684. https://doi.org/10.3390/ma16247684






