Critical Insight into Pretransitional Behavior and Dielectric Tunability of Relaxor Ceramics
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Model Discussion
3.1.1. “Critical” View on Dielectric-Constant-Related Behavior in Relaxor Systems
3.1.2. “Critical” View on Dynamics in Relaxor Systems
3.1.3. “Critical” View on Clausius–Mossotti Local Field in Ferroelectric Systems
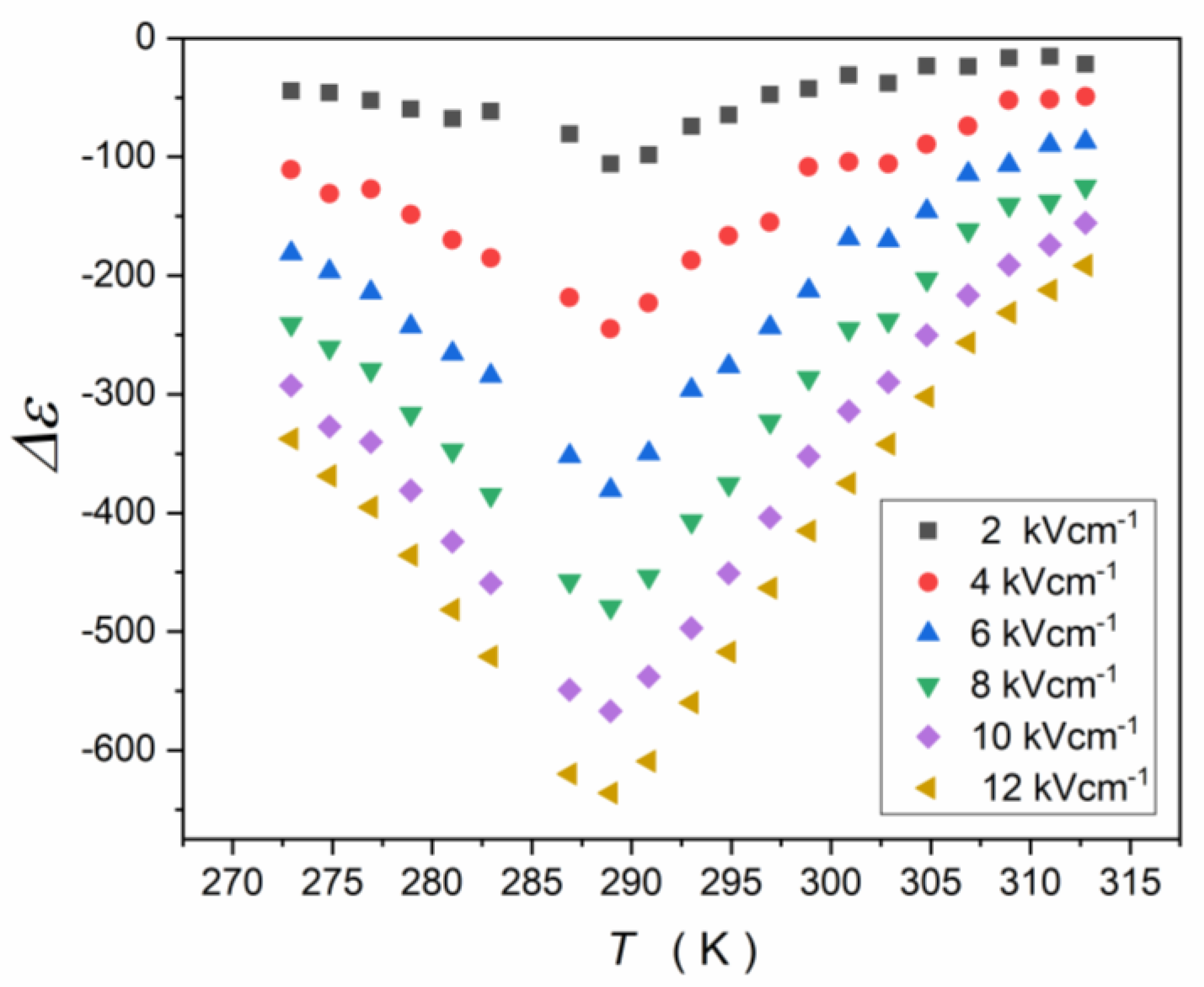
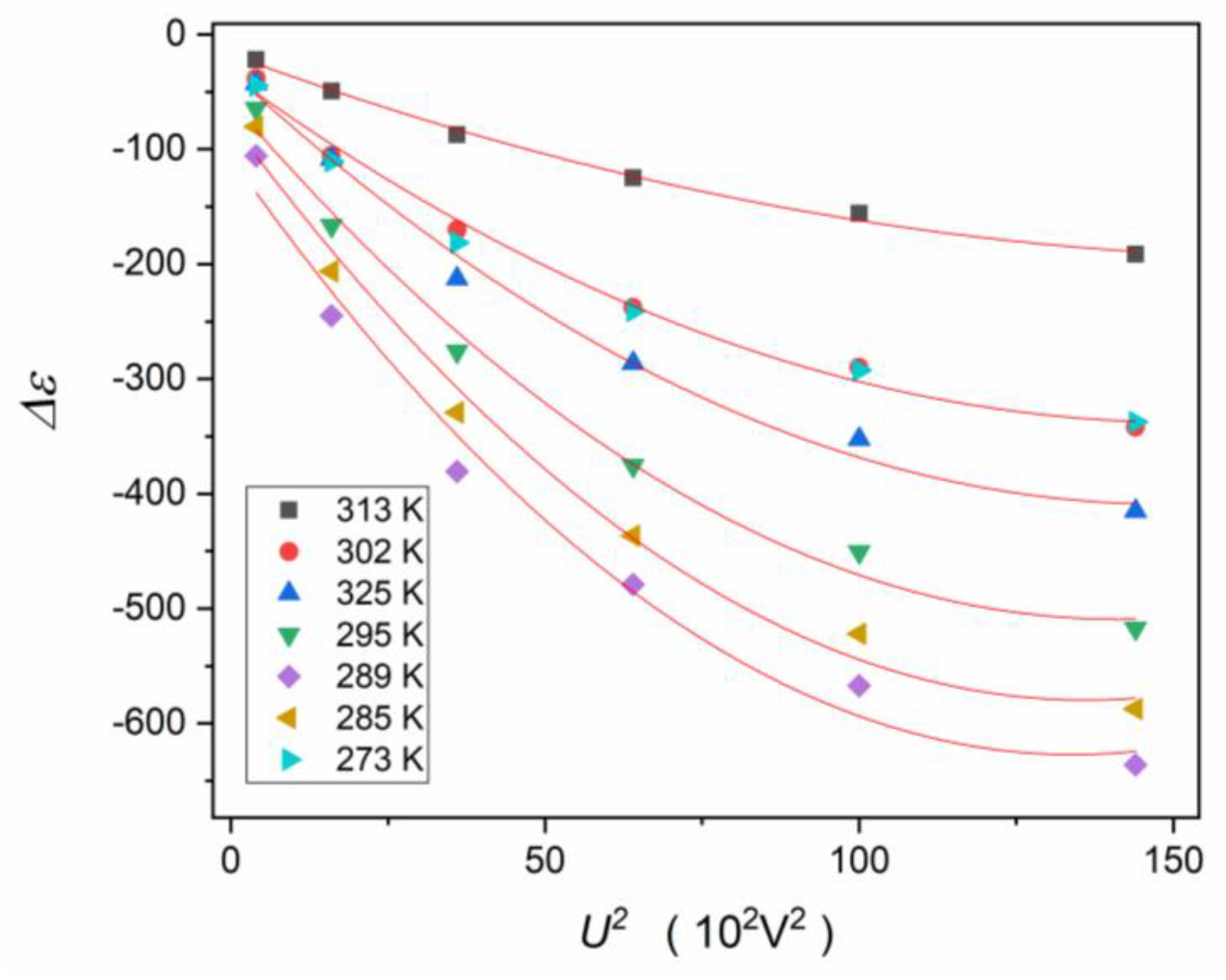
3.2. Experimental Results and Discussion
3.3. Summary of Results
- First, a new model for understanding and explaining the physics of relaxor ceramics is presented. It is based on references to the fundamentals of Critical Phenomena Physics and Glass Transition Physics. A particularly notable feature is the focus on the role of local symmetry, in this case uniaxial, which is particularly focused. The proposed model combines the unique properties of ceramic relaxors with the formation of random local electric fields resulting from pretransitional ferroelectric fluctuations inside ceramic “grains”, i.e., confined by grain boundaries. Local electric fields create a specific feedback mechanism that couples the grain-constrained ferroelectric domains and also affect the interior of the grain-constrained ferroelectric domains, causing a bias towards the discontinuous transition. This gives rise to a singular pseudospinodal behavior [89], similar to the critical one, but is associated with an inherent non-zero order parameter (polarization in this case). Another notable feature of the model is the inherent link to basic experimental features. These are characteristic temperature changes in the “dielectric constant”, electric-field-related stability, and glassy dynamics. The latter relates to the natural introduction of non-Arrhenius temperature variations and extreme non-Debye broadening of the primary loss curves.
- 2.
- The second part of the report presents the experimental results. They are based on relaxor ceramics specially prepared for this work. The innovative differential analysis for the temperature evolution of “dielectric constant” was used. An important result is an explicit demonstration that the “dielectric constant” in the paraelectric phase prefers not the Curie–Weiss portrayal but the exponential description. The results also challenge the “omnipotence” of the VFT relation as the “proof” for the glassy dynamics.
- 3.
- Based on the results discussed in points (1) and (2), it was possible to describe in a new way the full range of temperature changes of the “dielectric constant” in the para- and ferroelectric phases, for the “diffused” top-domain, and in the ferroelectric phase, virtually without gaps between domains. Equations describing the temperature dependences of the electric-field-related tunability have also been proposed.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
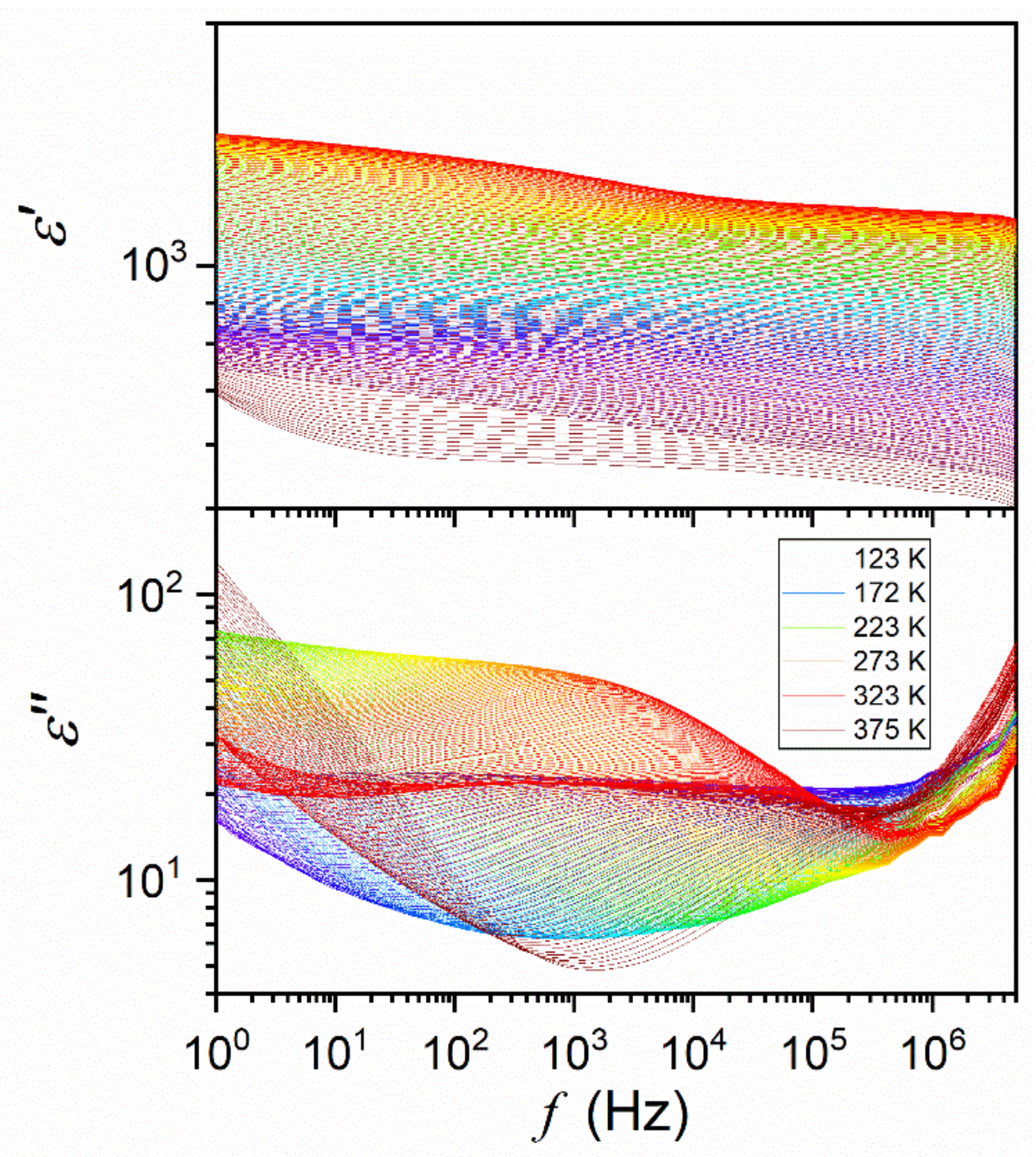
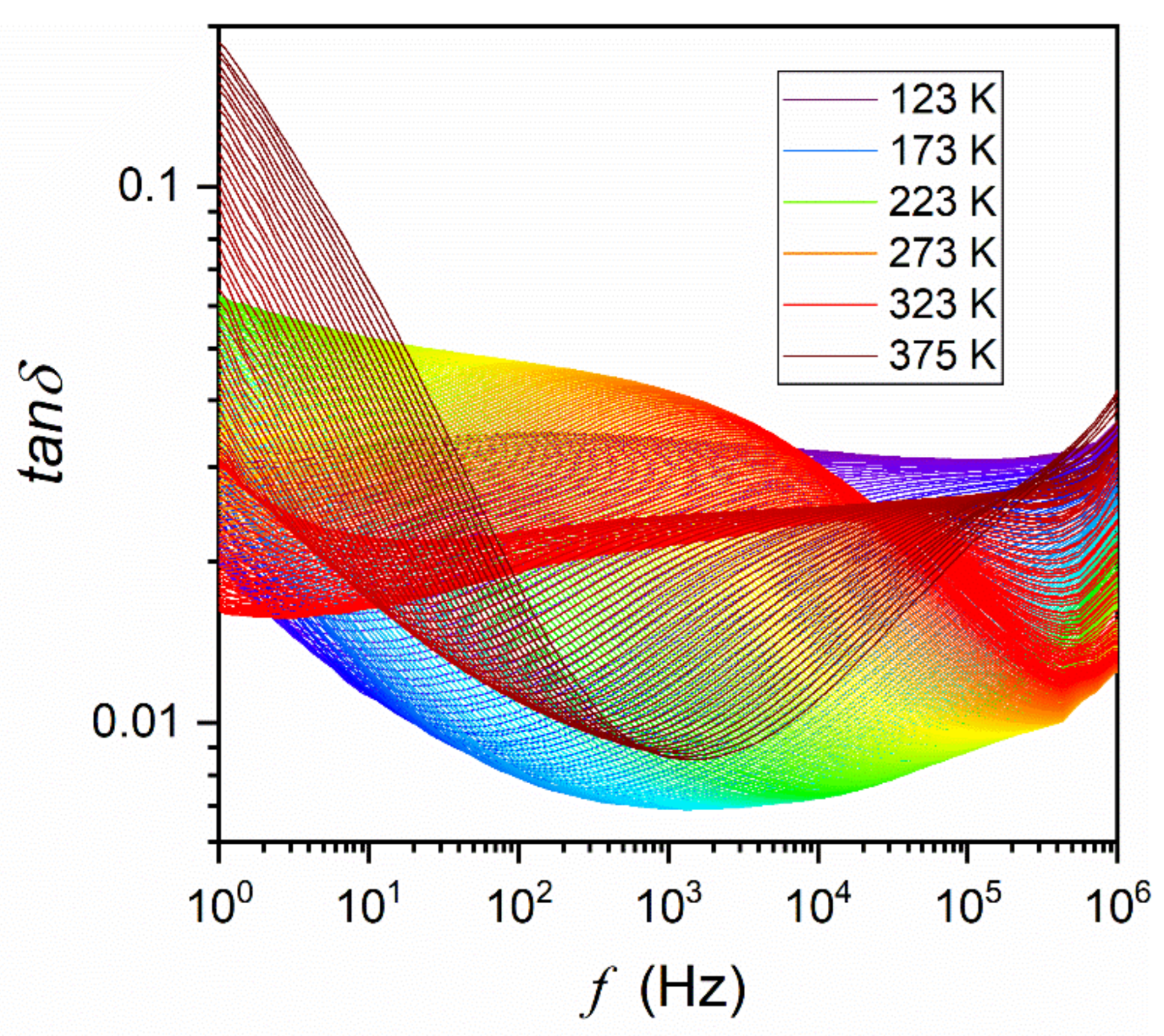
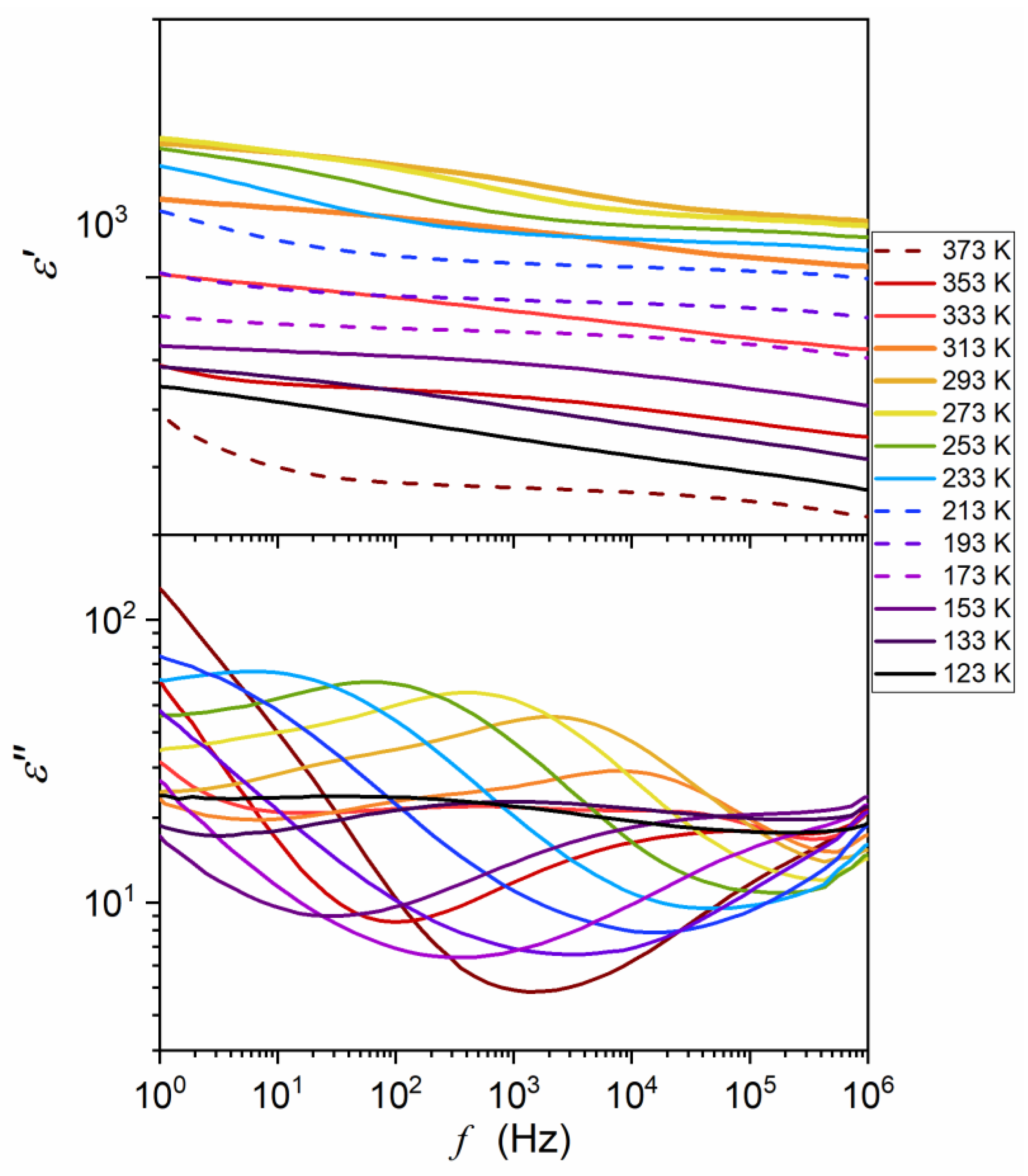
References and Note
- Smolenskii, G.A.; Rozgachev, K.I. Segnetoelektricheskie svoistva tverdykh rastvorov v sisteme titanat bariya titanat strontsiya (in English: Ferroelectric properties of solid solutions in barium strontium titanate system). Z. Tekhn. Fiz. 1954, 24, 1751–1760. [Google Scholar]
- Uchino, K.; Nomura, S. Critical exponents of the dielectric constants in diffused-phase-transition- crystals. Ferroelectrics 1982, 44, 55–61. [Google Scholar] [CrossRef]
- Burns, G.; Dacol, F.H. Crystalline ferroelectrics with glassy polarization behavior. Phys. Rev. B 1983, 28, 2527–2529. [Google Scholar] [CrossRef]
- Burns, G.; Dacol, F.H. Ferroelectrics with a glassy polarization phase. Ferroelectrics 1990, 104, 25–35. [Google Scholar] [CrossRef]
- Westphal, V.; Kleemann, W.; Glinchuk, M.D. Diffuse phase-transitions and random-field-induced domain states of the relaxor ferroelectric PbMg1/3Nb2/3O3. Phys. Rev. Lett. 1992, 68, 847–850. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Vogel-Fulcher relationship for the dielectric permittivity of relaxor ferroelectrics. Phys. Rev. Lett. 1994, 72, 1100–1103. [Google Scholar] [CrossRef]
- Cheng, Z.-Y.; Katiyar, R.S.; Yao, X.; Bhalla, A.S. Temperature dependence of the dielectric constant of relaxor ferroelectrics. Phys. Rev. B 1998, 57, 8166. [Google Scholar] [CrossRef]
- Pirc, R.; Blinc, R. Spherical random-bond-random-field model of relaxor ferroelectrics. Phys. Rev. B 1999, 60, 13470–13478. [Google Scholar] [CrossRef]
- Tang, X.G.; Chew, K.-H.; Chan, H.L.W. Diffuse phase transition and dielectric tunability of Ba(ZryTi1−y)O3 relaxor ferroelectric ceramics. Acta Mater. 2004, 52, 5177–5183. [Google Scholar] [CrossRef]
- Poplavko, Y.M. The nature of high dielectric constant in relaxor ferroelectric. Ferroelectrics 2004, 298, 253–259. [Google Scholar] [CrossRef]
- Du, H.; Zhou, W.; Luo, F.; Zhu, D.; Qu, S.; Pei, Z. Phase structure, dielectric properties, and relaxor behavior of (K0.5Na0.5)NbO3–(Ba0.5 Sr0.5)TiO3 lead-free solid solution for high temperature applications. J. Appl. Phys. 2009, 105, 124104. [Google Scholar] [CrossRef]
- Cowley, R.A.; Gvasaliya, S.N.; Lushnikov, S.G.; Roessli, B.; Rotaru, G.M. Relaxing with relaxors: A review of relaxor ferroelectrics. Adv. Phys. 2011, 60, 229–327. [Google Scholar] [CrossRef]
- Bokov, A.A.; Ye, Z.-G. Dielectric relaxation in relaxor ferroelectrics. J. Adv. Dielectr. 2012, 2, 1241010. [Google Scholar] [CrossRef]
- Peláiz-Barranco, A.; Calderón-Piñar, F. Relaxor Behaviour in Ferroelectric Ceramics, Advances in Ferroelectrics; IntechOpen: Rijeka, Croatia, 2012; pp. 85–107. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhai, J.; Kong, L.B. Relaxor ferroelectric materials for microwave tunable applications. J. Adv. Diel. 2012, 2, 1230002. [Google Scholar] [CrossRef]
- Blinc, R. Relaxor ferroelectrics. In Advanced Ferroelectricity; International Series of Monographs on Physics; Oxford Academic: Oxford, UK, 2011; pp. 144–186. [Google Scholar] [CrossRef]
- Sherrington, D. BZT: A soft pseudospin glass. Phys. Rev. Lett. 2013, 111, 227601. [Google Scholar] [CrossRef] [PubMed]
- Phelan, D.; Stock, C.; Rodriguez-Rivera, J.A.; Chi, S.; Leão, J.; Long, X.; Xie, Y.; Bokov, A.; Ye, Z.-G.; Ganesh, P.; et al. Role of random electric fields in relaxors. Proc. Natl. Acad. Sci. USA 2014, 111, 1754–1759. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin glasses: Redux: An updated experimental/materials survey. Rep. Prog. Phys. 2015, 78, 52501. [Google Scholar] [CrossRef]
- Guo, H.; Liu, X.; Xue, F.; Chen, L.Q.; Hong, W.; Tan, X. Disrupting long-range polar order with an electric field. Phys. Rev. B 2016, 93, 174114. [Google Scholar] [CrossRef]
- Garten, L.; Burch, M.M.; Gupta, A.S.; Haislmaier, R.; Gopalan, V.; Dickey, E.C.; Trolier-McKinstry, S. Relaxor Ferroelectric behavior in barium strontium titanate. J. Am. Ceram. Soc. 2016, 99, 1645–1650. [Google Scholar] [CrossRef]
- Arce-Gamboa, J.R.; Guzmán-Verrí, G.G. Random electric field instabilities of relaxor ferroelectrics. NPJ Quantum Mater. 2017, 2, 28. [Google Scholar] [CrossRef]
- Martín, J.; Iturrospe, A.; Cavallaro, A.; Arbe, A.; Stingelin, N.; Ezquerra, T.A.C.; Mijangos, A. Nogales Relaxations and relaxor-ferroelectric-like response of nanotubularly confined poly(vinylidene fluoride). Chem. Mater. 2017, 29, 3515–3525. [Google Scholar] [CrossRef]
- Uchino, K. (Ed.) Relaxor based ferroelectrics. In Advanced Piezoelectric Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2017; pp. 127–153. [Google Scholar] [CrossRef]
- Hagiwara, M.; Ehara, Y.; Novak, N.; Khansur, N.H.; Ayrikyan, A.; Webber, K.G.; Fujihara, S. Relaxor-ferroelectric crossover in (Bi1/2K1/2)TiO3: Origin of the spontaneous phase transition and the effect of an applied external field. Phys. Rev. B 2017, 96, 014103. [Google Scholar] [CrossRef]
- Krogstad, M.J.; Gehring, P.M.; Rosenkranz, S.; Osborn, R.; Ye, F.; Liu, Y.; Ruff, J.P.C.; Chen, W.; Wozniak, J.M.; Luo, H.; et al. The relation of local order to material properties in relaxor ferroelectrics. Nat. Mater. 2018, 17, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Palneedi, H.; Peddigari, M.; Hwang, G.T.; Jeong, D.Y.; Ryu, J. High-performance dielectric ceramic films for energy storage capacitors: Progress and outlook. Adv. Funct. Mater. 2018, 28, 1803665. [Google Scholar] [CrossRef]
- Bobic, J.D.; Vijatovic Petrovic, M.M.; Stojanovic, B.D. Review of the most common relaxor ferroelectrics and their applications. In Magnetic, Ferroelectric, and Multiferroic Metal Oxides; Elsevier: Amsterdam, The Netherlands, 2018; pp. 233–249. [Google Scholar] [CrossRef]
- Raddauoi, Z.; El-Kossi, S.; Dhari, J.; Abdelmoula, N.; Taibi, K. Study of diffuse phase transition and relaxor ferroelectric behavior of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic. RSC Adv. 2019, 18, 2412–2425. [Google Scholar] [CrossRef] [PubMed]
- Adamchuk, D.; Grigalaitis, R.; Svirskas, S.; Macutkevic, J.; Palaimiene, E.; Banys, J.; Mitoseriu, L.; Canu, G.; Buscaglia, M.T.; Buscaglia, V. Distributions of relaxation times in relaxor ferroelectric Ba(Ti0.8 Ce0.2)O3. Ferroelectrics 2019, 553, 103–110. [Google Scholar] [CrossRef]
- Zhang, L.L.; Huang, Y.N. Theory of relaxor-ferroelectricity. Sci. Rep. 2020, 10, 5060. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Zhang, K.; Guo, Y.; Xu, J.; Szafran, M. (Ba, Sr)TiO3/polymer dielectric composites–progress and perspective. Prog. Mater. Sci. 2021, 121, 100813. [Google Scholar] [CrossRef]
- Henaish, A.M.; Mostafa, M.; Weinstein, I.; Hemeda, O.; Salem, B. Ferroelectric and dielectric properties of strontium titanate doped with barium. Magnetism 2021, 1, 22–36. [Google Scholar] [CrossRef]
- Wang, G.; Lu, Z.L.; Li, Y.; Li, L.H.; Ji, H.F.; Feteira, A.; Zhou, D.; Wang, D.W.; Zhang, S.J.; Reaney, I.M. Electroceramics for high-energy density capacitors: Current status and future perspectives. Chem. Rev. 2021, 121, 6124–6172. [Google Scholar] [CrossRef]
- Kumar Pradhan, L.; Kar, M. Relaxor Ferroelectric Oxides: Concept to Applications; IntechOpen: Rijeka, Croatia, 2021; p. 212021. [Google Scholar] [CrossRef]
- Xie, A.; Fu, J.; Zuo, R.; Jiang, X.; Li, T.; Fu, Z.; Yin, Y.; Li, X.; Zhang, S. Supercritical relaxor nanograined ferroelectrics for ultrahigh-energy-storage capacitors. Adv. Mater. 2022, 34, 2204356. [Google Scholar] [CrossRef]
- Shi, X.; Wang, J.; Xu, J.; Cheng, X.; Huang, H. Quantitative investigation of polar nanoregion size effects in relaxor ferroelectrics. Acta Mater. 2022, 237, 118147. [Google Scholar] [CrossRef]
- Vendrell, X.; Ramírez-González, J.; Ye, Z.-G.; West, A.R. Revealing the role of the constant phase element in relaxor ferroelectrics. Commun. Phys. 2022, 5, 9. [Google Scholar] [CrossRef]
- Macutkevič, J.; Banys, J.; Kania, A. Electrical Conductivity and Dielectric Relaxation in Ag1−xLixNbO3. Crystals 2022, 12, 158. [Google Scholar] [CrossRef]
- Jayakrishnan, A.R.; Silva, J.P.B.; Kamakshi, K.; Dastan, D.; Annapureddy, V.; Pereira, M.; Sekhar, K.C. Are lead-free relaxor ferroelectric materials the most promising candidates for energy storage capacitors? Prog. Mater. Sci. 2022, 132, 101046. [Google Scholar] [CrossRef]
- Dwivedi, A.; Singh, K.N.; Hait, M.; Bajpai, P.K. Ferroelectric relaxor behavior and dielectric relaxation in strontium barium niobate—A lead-free relaxor ceramic material. Eng. Sci. 2022, 20, 117–124. [Google Scholar] [CrossRef]
- Hong, Z.; Ke, X.; Wang, D.; Yang, S.; Ren, X.; Wang, Y. Role of point defects in the formation of relaxor ferroelectrics. Acta Mater. 2022, 225, 117558. [Google Scholar] [CrossRef]
- Badole, M.; Dwivedi, S.; Vasavan, H.N.; Saxena, S.; Srihari, V.; Kumar, S. Improved dielectric and relaxor behavior in LaScO3-doped K0.5Bi0.5TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2022, 33, 25661–25673. [Google Scholar] [CrossRef]
- Zhang, L.; Pu, Y.; Chen, M. Complex impedance spectroscopy for capacitive energy-storage ceramics: A review and prospects. Mater. Today Chem. 2023, 28, 101353. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Q.; Huang, H.; Pan, H.; Zhu, W.; Meng, F.; Lan, S.; Liu, Y.; Wei, B.; Liu, Y.; et al. Engineering relaxors by entropy for high energy storage performance. Nat. Energy 2023, 8, 956–964. [Google Scholar] [CrossRef]
- Li, Y.; Lin, W.; Yang, B.; Zhang, S.; Zhao, S. Domain dynamics engineering in ergodic relaxor ferroelectrics for dielectric energy storage. Acta Mater. 2023, 255, 119071. [Google Scholar] [CrossRef]
- Filipič, C.; Canu, G.; Pirc, R.; Kutnjak, Z. Glassy properties of the lead-free isovalent relaxor BaZr0.4Ti0.6O3. Crystals 2023, 13, 1303. [Google Scholar] [CrossRef]
- Li, Y.; Rao, R.; Wang, Y.; Du, H.; Shi, J.; Liu, X. Effect of chemical inhomogeneity on the dielectric and impedance behaviors of bismuth sodium titanate based relaxors. ECS J. Solid State Sci. Technol. 2023, 12, 013005. [Google Scholar] [CrossRef]
- Su, X.; Li, J.; Hou, Y.; Yin, R.; Li, J.; Qin, S.; Su, Y.; Qiao, L.; Liu, C.; Bai, Y. Large electrocaloric effect over a wide temperature span in lead-free bismuth sodium titanate-based relaxor ferroelectrics. J. Mater. 2023, 9, 289–298. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, G.; Zhang, Y.; Li, A.; Sun, Y.; Tu, R.; Shen, Q. Wide temperature range of stable dielectric properties in relaxor BaTiO3-based ceramics by co-doping synergistic engineering. Mat. Chem. Phys. 2023, 302, 127629. [Google Scholar] [CrossRef]
- Chen, X.; Qin, H.; Zhu, W.; Zhang, B.; Lu, W.; Bernholc, J.; Zhang, Q.M. Giant electrostriction enabled by defect-induced critical phenomena in relaxor ferroelectric polymers. Macromolecules 2023, 56, 690–696. [Google Scholar] [CrossRef]
- Sojecka, A.A. The Search and Analysis Carried out for This Report, Using Google Scholar Database. (accessed on 15 October 2023).
- Market Research Report: Relaxor Ferroelectric Ceramics Sales Market Research Report (DataIntelo, 2022.id 2863). Available online: https://dataintelo.com/report/global-relaxor-ferroelectric-ceramics-sales-market/ (accessed on 15 October 2023).
- Donth, E. Glass Transition: Relaxation Dynamics in Liquids and Disordered Solids; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-3540418016. [Google Scholar]
- Kremer, F.; Schoenhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3642628092. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New scaling paradigm for dynamics in glass-forming systems. Prog. Mat. Sci. 2023, 134, 101074. [Google Scholar] [CrossRef]
- Jonsher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectric Press: London, UK, 1983; ISBN 9780950871103. [Google Scholar]
- Łoś, J.; Drozd-Rzoska, A.; Rzoska, S.J. Critical-like behavior of low-frequency dielectric properties in compressed liquid crystalline octyloxycyanobiphenyl (8OCB) and its nanocolloid with paraelectric BaTiO3. J. Mol. Liq. 2023, 377, 121555. [Google Scholar] [CrossRef]
- Stanley, H.E. Introduction to Phase Transition and Critical Phenomena; Oxford University Press: New York, NY, USA, 1992; ISBN 978-0195053166. [Google Scholar]
- Domb, C.; Lebovitz, J. Phase Transitions and Critical Phenomena; Academic Press: New York, NY, USA, 1984; Volume 9, ISBN 0122203097. [Google Scholar]
- Anisimov, M.A. Critical in Liquids and Liquid Crystals; Gordon and Breach: Reading, UK, 1992. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Kalabiński, J. The impact of pressure on low molecular weight near-critical mixtures of limited miscibility. ACS Omega 2020, 5, 20141–20152. [Google Scholar] [CrossRef]
- Murray, C. Ferroelectric Materials: Science and Technology; States Academic Press: Cambridge, UK, 2022; ISBN 978-1639891986. [Google Scholar]
- Rabe, K.M.; Ahn, C.H. Physics of Ferroelectrics: A Modern Perspective; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3540345909. [Google Scholar]
- Editorial: A century of ferroelectricity. Nat. Mater. 2020, 19, 129. [CrossRef]
- Editorial. Ferroelectricity: 100 Years on. Physics World. Issue 10 November 2021. Available online: https://physicsworld.com/a/ferroelectricity-100-years-on/ (accessed on 15 October 2023).
- Blinc, R.; Musevic, I.; Zeks, B. The Physics of Ferroelectric and Antiferroelectric Liquid; World Scientific: Singapore, 2000. [Google Scholar]
- Guo, Q.; Yan, K.; Chigrinov, V.; Zhao, H.; Tribelsky, M. Ferroelectric Liquid Crystals: Physics and Applications. Crystals 2019, 9, 470. [Google Scholar] [CrossRef]
- Mugiraneza, S.; Hallas, A.M. Tutorial: A beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law. Commun. Phys. 2022, 5, 95. [Google Scholar] [CrossRef]
- Jonker, G.H. On dielectric Curie-Weiss law and diffuse phase transition in ferroelectrics. Mat. Res. Bull. 1983, 18, 301–308. [Google Scholar] [CrossRef]
- Trainer, M. Ferroelectrics and the Curie–Weiss law. Eur. J. Phys. 2000, 21, 459–464. [Google Scholar] [CrossRef]
- Devonshire, A.F. Theory of ferroelectrics. Adv. Phys. 1954, 3, 85–130. [Google Scholar] [CrossRef]
- Levanlyuk, A.; Misirlioglu, I.B.; Okatan, M.B. Landau, Ginzburg, Devonshire and others. Ferroelectrics 2020, 569, 310–323. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statisticheskaya Fizika (Statistical Physics); GTTI: Moscow, Russia, 1938. [Google Scholar]
- Honig, J.M.; Spalek, J. A Primer to the Theory of Critical Phenomena; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 978-0128046852. [Google Scholar]
- Kumar, A.; Krishnamurthy, H.R.; Gopal, E.S.R. Equilibrium critical phenomena in binary liquid mixtures. Phys. Rep. 1983, 98, 57–143. [Google Scholar] [CrossRef]
- Bausch, R. Ginzburg criterion for tricritical points. Z. Phys. 1972, 254, 81–88. [Google Scholar] [CrossRef]
- Als-Nielsen, J.; Birgeneau, R.J. Mean field theory, the Ginzburg criterion, and marginal dimensionality of phase transitions. Am. J. Phys. 1977, 45, 54–56. [Google Scholar] [CrossRef]
- Beysens, D.; Gbadamassi, M.; Boyer, L. Light-scattering study of a critical mixture with shear flow. Phys. Rev. Lett. 1979, 43, 1253. [Google Scholar] [CrossRef]
- Beysens, D.; Gbadamassi, M. Shear-induced transition to mean-field critical behavior. J. Phys. Lett. 1979, 40, 565–567. [Google Scholar] [CrossRef]
- Chan, C.K.; Lin, L. Effects of shear on the phase transition of binary mixtures. EPL 1990, 11, 13–18. [Google Scholar] [CrossRef]
- Baumberger, T.; Perrot, F.; Beysens, D. Shear flow effects on a critical binary mixture during phase separation. Phys. A 1991, 174, 31–46. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Shear viscosity studies above and below the critical consolute. point in a nitrobenzene-decane mixture. Phys. Rev. E 2000, 62, 8071–8074. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J. Kerr effect and nonlinear dielectric effect on approaching the critical consolute point. Phys. Rev. E 1993, 48, 1136–1143. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Martinez-Garcia, J.C. Nonlinear dielectric effect in supercritical diethyl ether. J. Chem. Phys. 2014, 141, 094907. [Google Scholar] [CrossRef] [PubMed]
- Chrapeć, J.; Rzoska, S.J.; Zioło, J. Pseudospinodal curve for binary solutions determined from the nonlinear dielectric effect. Chem. Phys. 1987, 111, 155–160. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New paradigm for configurational entropy in glass forming liquids. Sci. Rep. 2022, 12, 3058. [Google Scholar] [CrossRef]
- Starzonek, S.; Zhang, K.; Drozd-Rzoska, A.; Rzoska, S.J.; Pawlikowska, E.; Szafran, M.; Gao, F. Polyvinylidene difluoride-based composite: Glassy dynamics and pretransitional behaviour. Eur. Phys. J. 2020, 93, 55. [Google Scholar] [CrossRef]
- Levit, R.; Martinez-Garcia, J.C.; Ochoa, D.A.; García, J.E. The generalized Vogel-Fulcher-Tamman equation for describing the dynamics of relaxor ferroelectrics. Sci. Rep. 2019, 9, 12390. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Universal behavior of the apparent fragility in ultraslow glass forming systems. Sci. Rep. 2019, 9, 6816. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Paluch, M. Universal critical-like scaling of dynamic properties in symmetry-selected glass formers. J. Chem. Phys. 2008, 129, 184509. [Google Scholar] [CrossRef] [PubMed]
- Colby, R.H. Dynamic scaling approach to glass formation. Phys. Rev. E 2000, 61, 1783–1791. [Google Scholar] [CrossRef]
- Hirshfeld, A. The Electric Life of Michael Faraday; Raincoast Books: New York, NY, USA, 2006; ISBN 978-1551929453. [Google Scholar]
- Arelli, S.G. Dielectric Materials: Types of Dielectrics, Various Polarizations, Clausius Mossotti Relation, Classical Theory of Electronic Polarizability; Independently Publisher: Traverse City, MI, USA, 2021; ISBN 979-8598251652. [Google Scholar]
- Von Hippel, R. Dielectrics and Waves; Chapman & Hall: New York, NY, USA, 1954. [Google Scholar]
- Chełkowski, A. Dielectric Physics; PWN-Elsevier: Warsaw, Poland, 1990; ISBN 978-044499766. [Google Scholar]
- Starzonek, S.; Rzoska, S.J.; Drozd-Rzoska, A.; Pawlus, S.; Biała, E.; Cesar Martinez-Garcia, J.; Kistersky, L. Fractional Debye-Stokes-Einstein behaviour in an ultraviscous nanocolloid: Glycerol and silver nanoparticles. Soft Matter 2015, 11, 5554–5562. [Google Scholar] [CrossRef]
- Fugiel, B.; Ćwikiel, K.; Zioło, J. Gap exponents determined from the pressure measurements of the nonlinear electric permittivity for triglycine sulfate in the paraelectric region. Phys. Rev. B 1987, 36, 3963–3964. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.B. Nonanalytic behavior above the critical point in a random Ising ferromagnet. Phys. Rev. Lett. 1969, 23, 17. [Google Scholar] [CrossRef]
- Voyta, T. Phases and phase transitions in disordered quantum systems. AIP Conf. Proc. 2013, 1550, 188–247. [Google Scholar] [CrossRef]
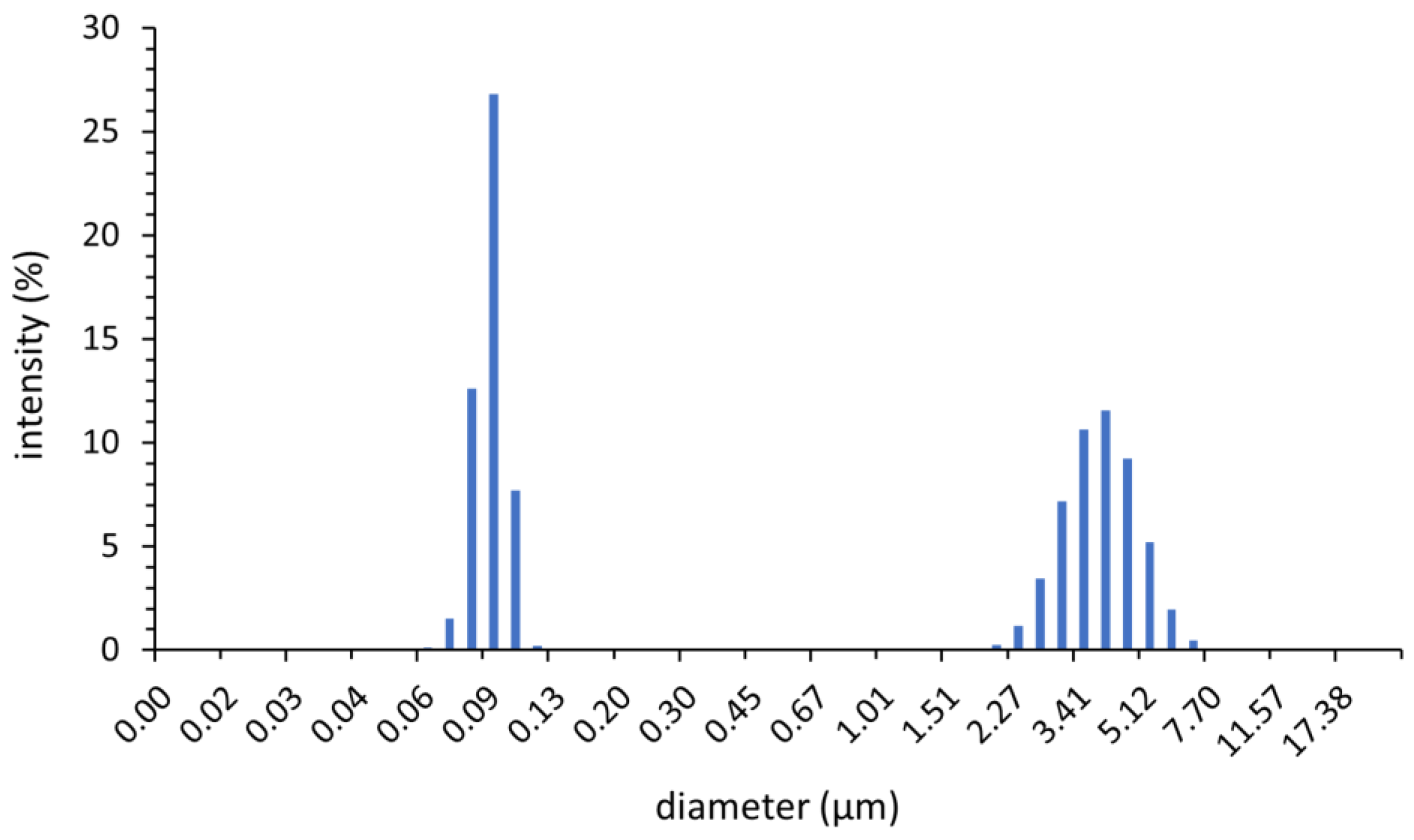

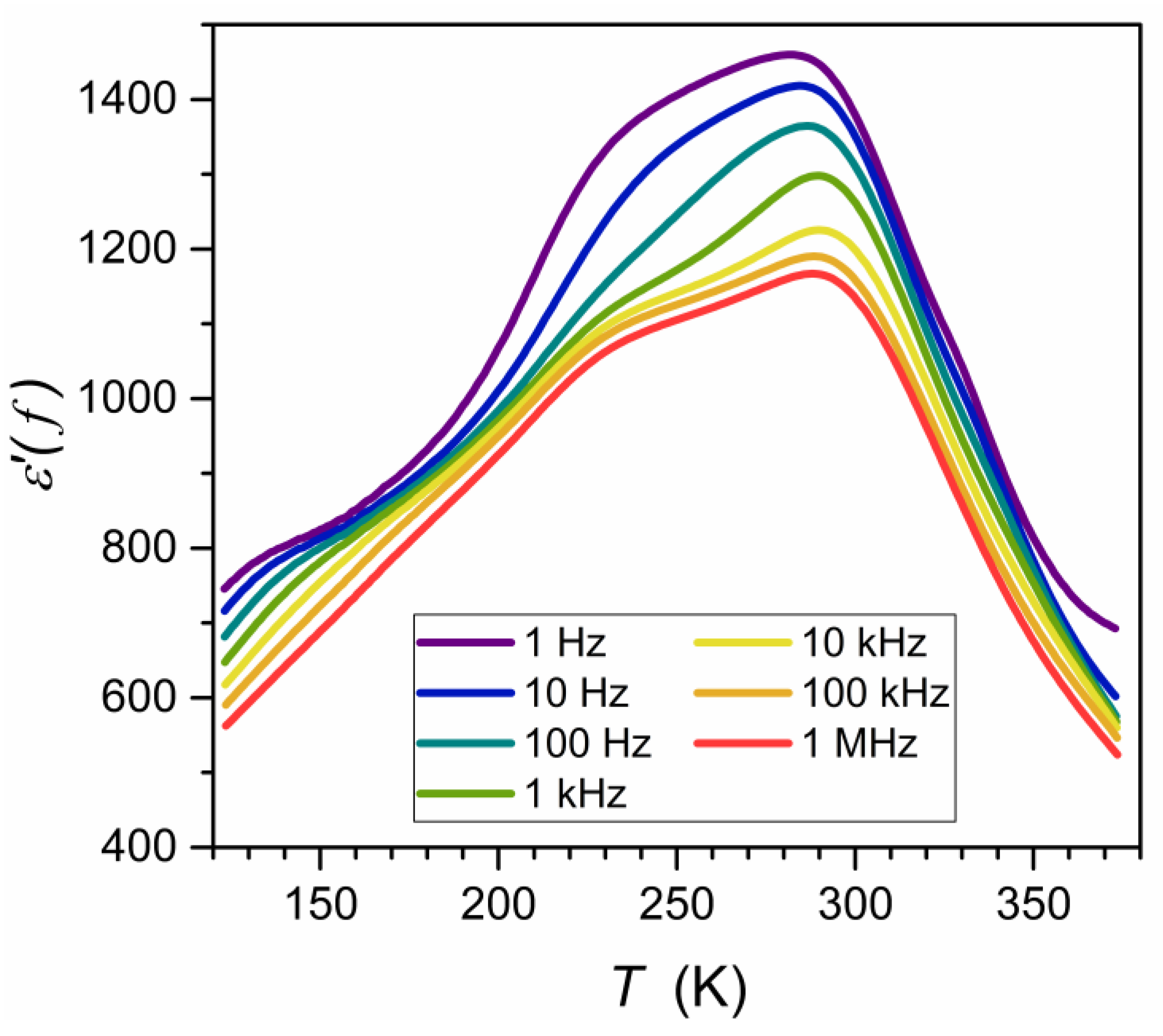
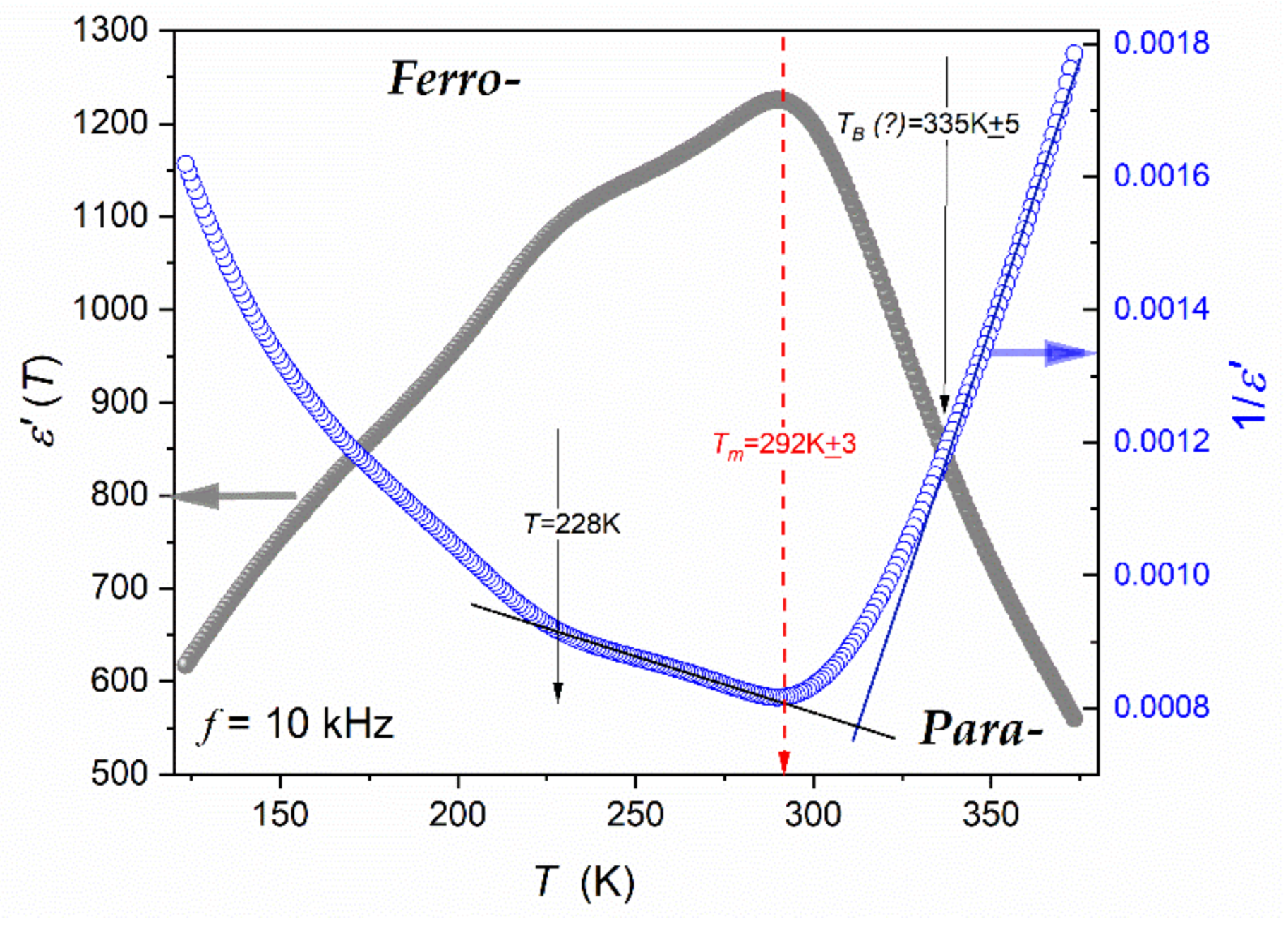
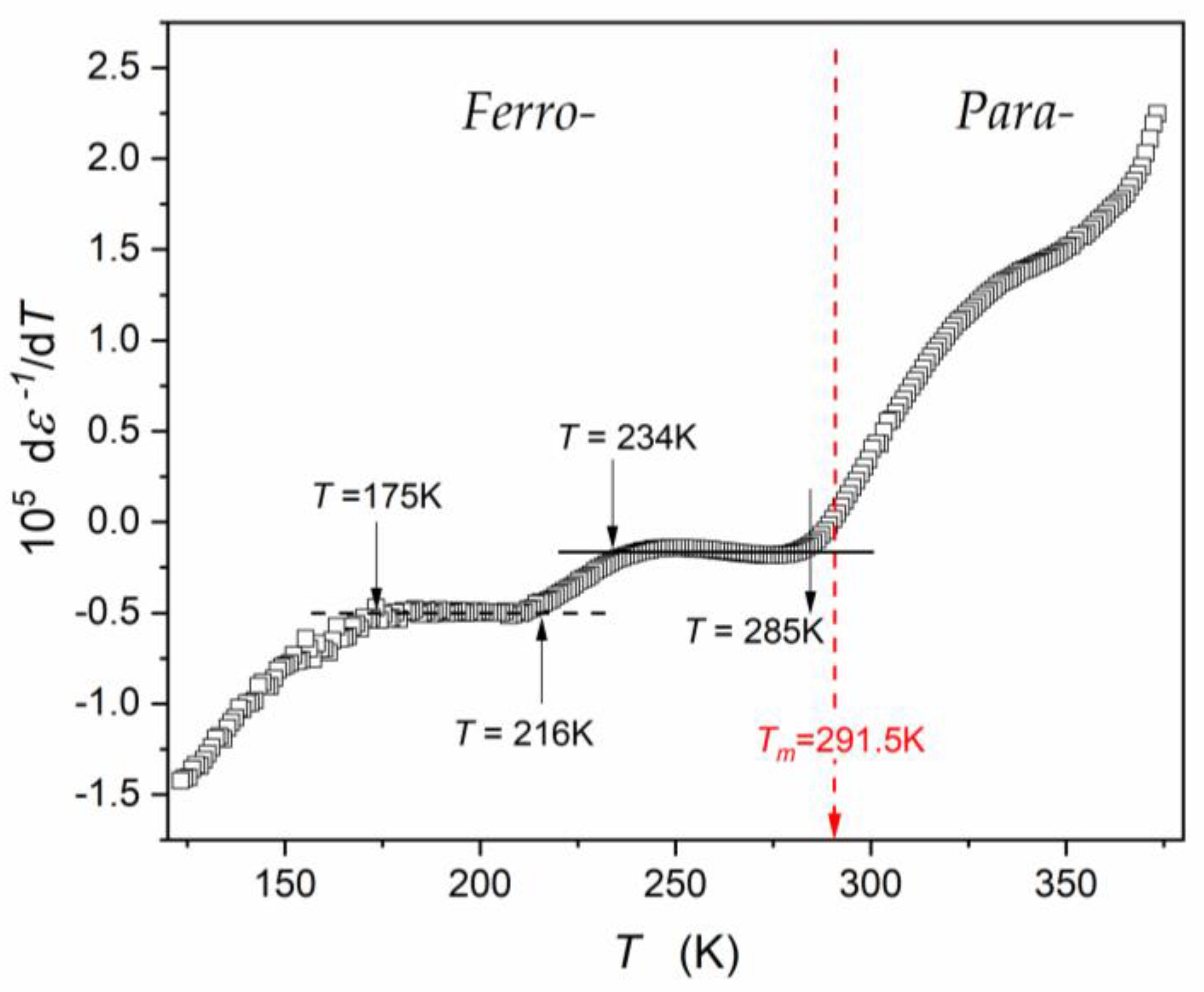
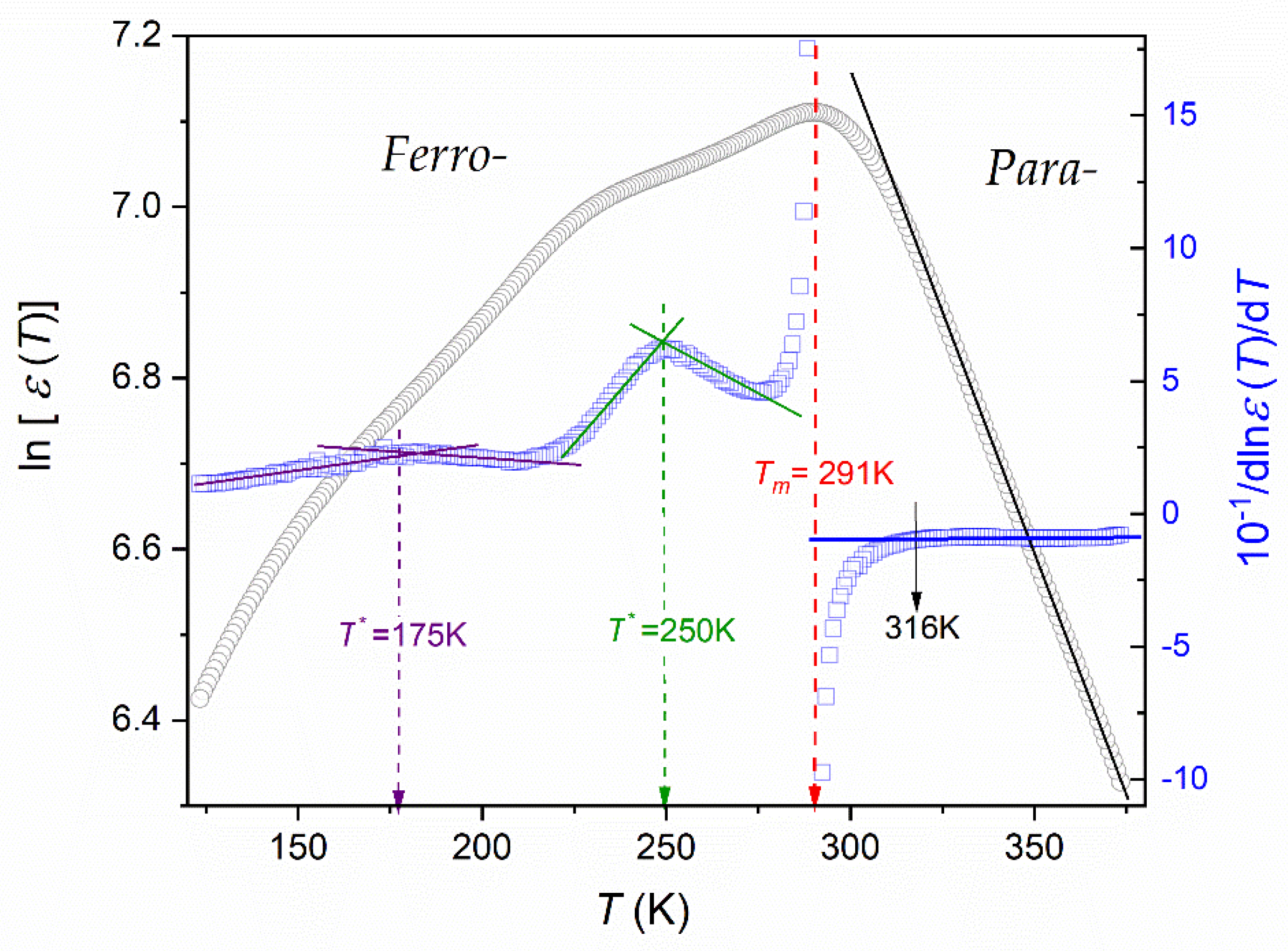

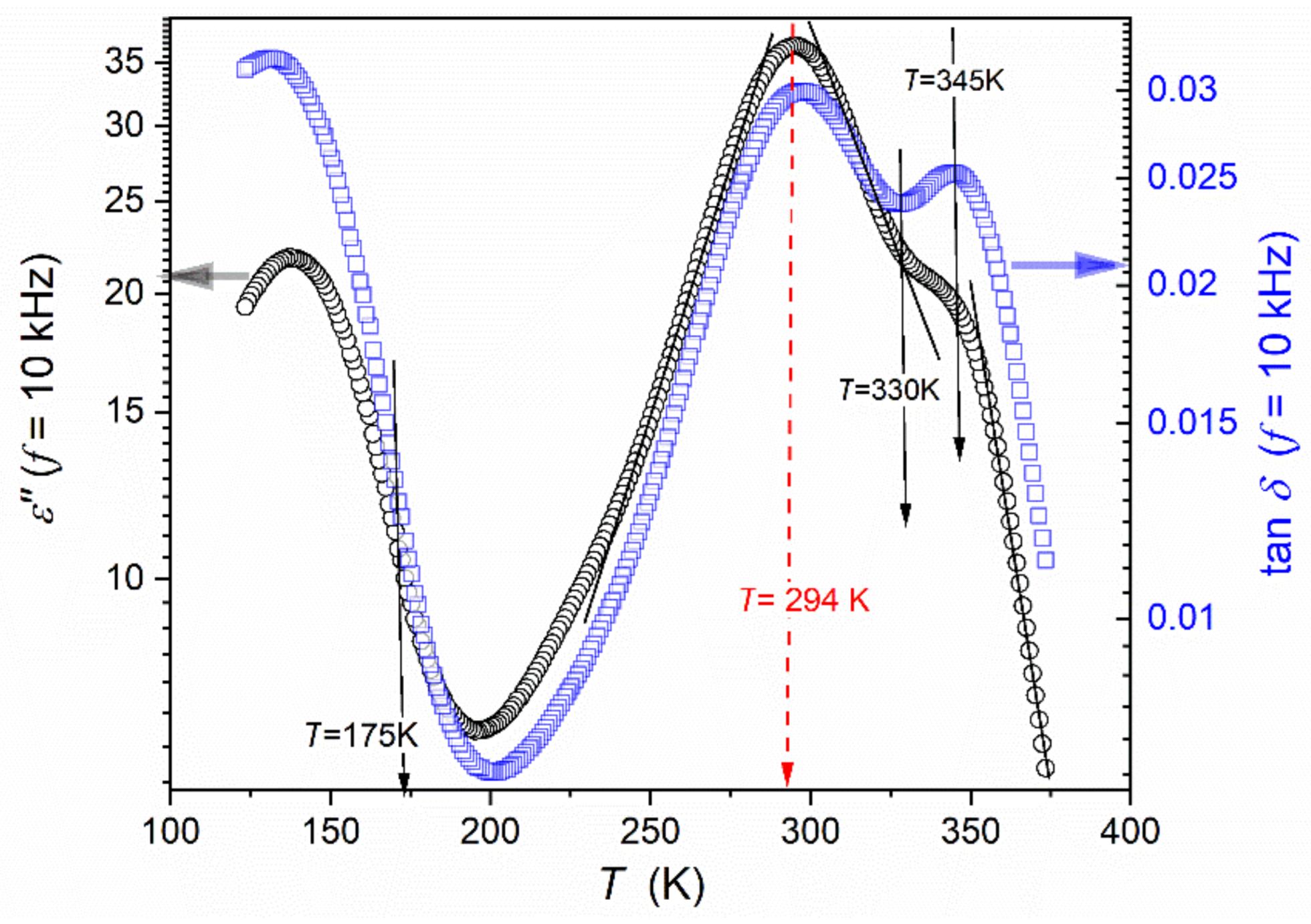
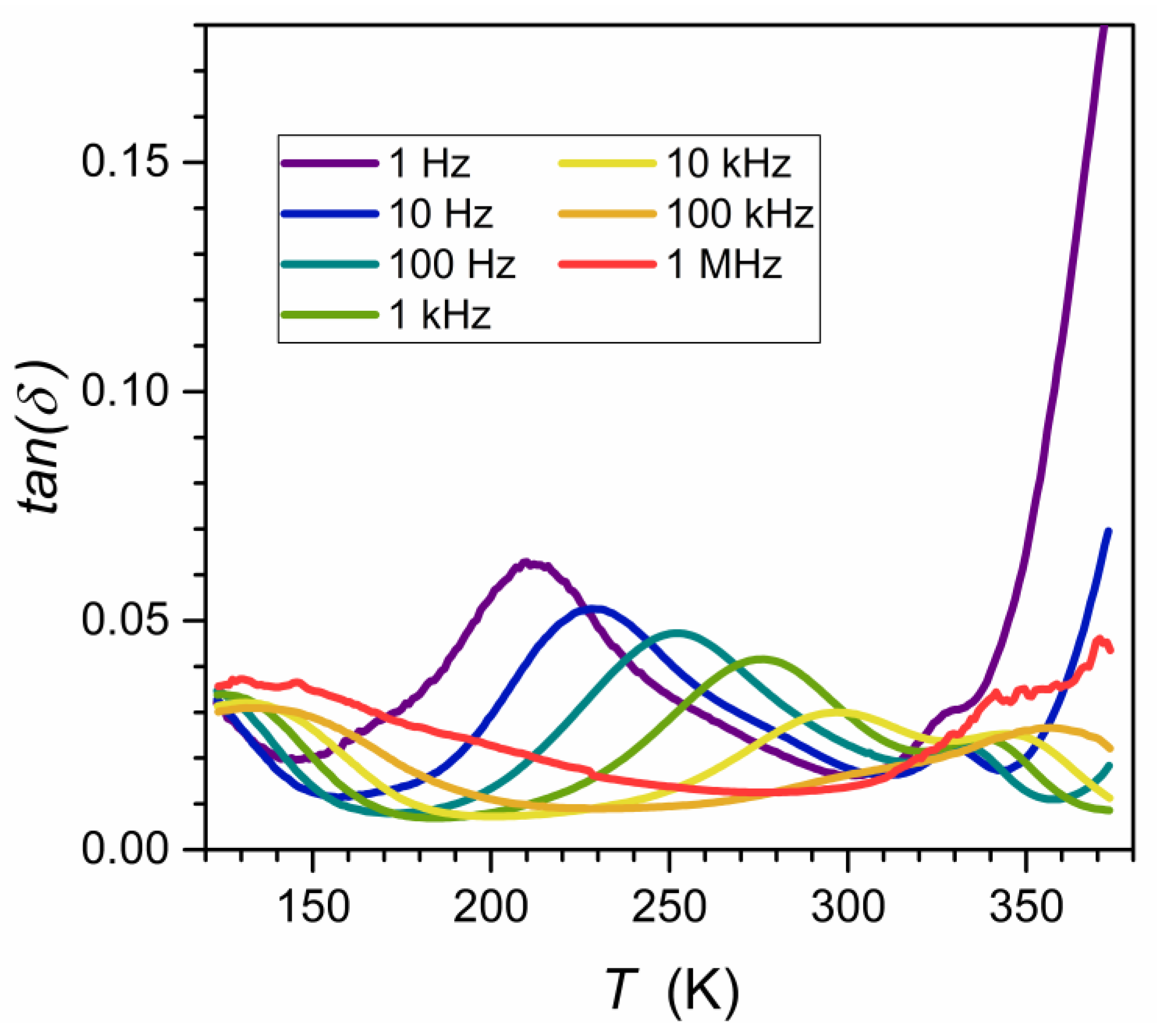
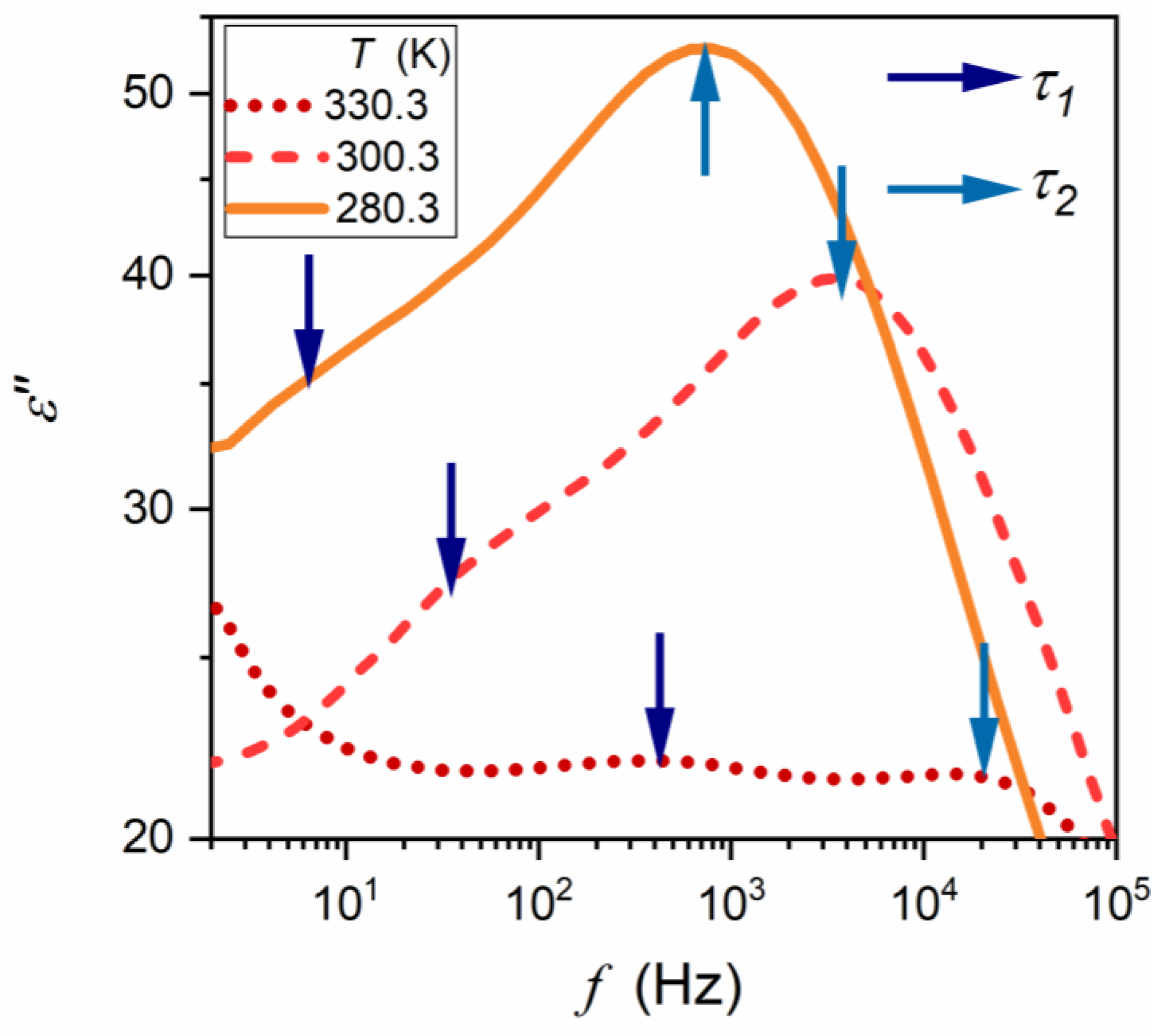
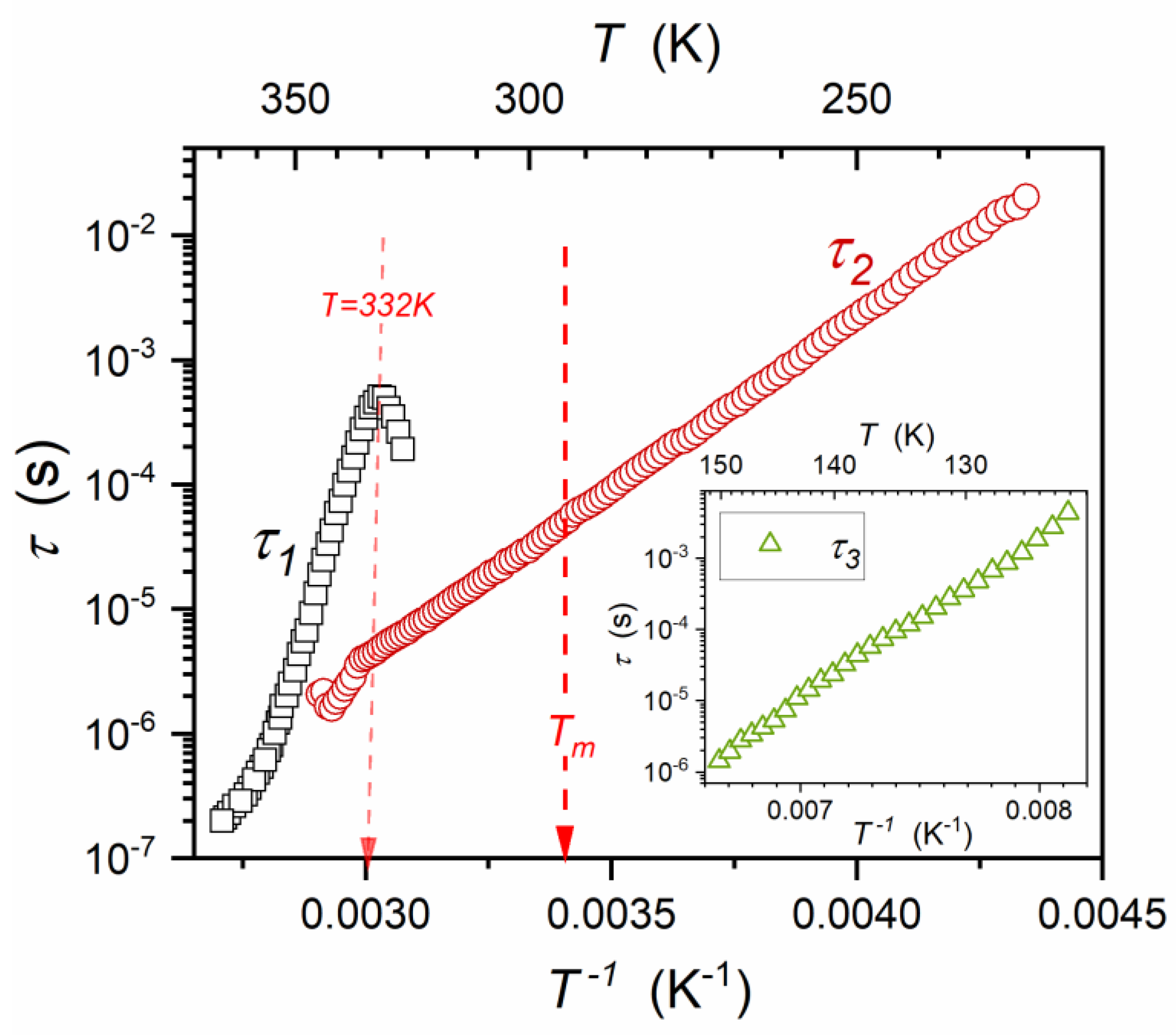
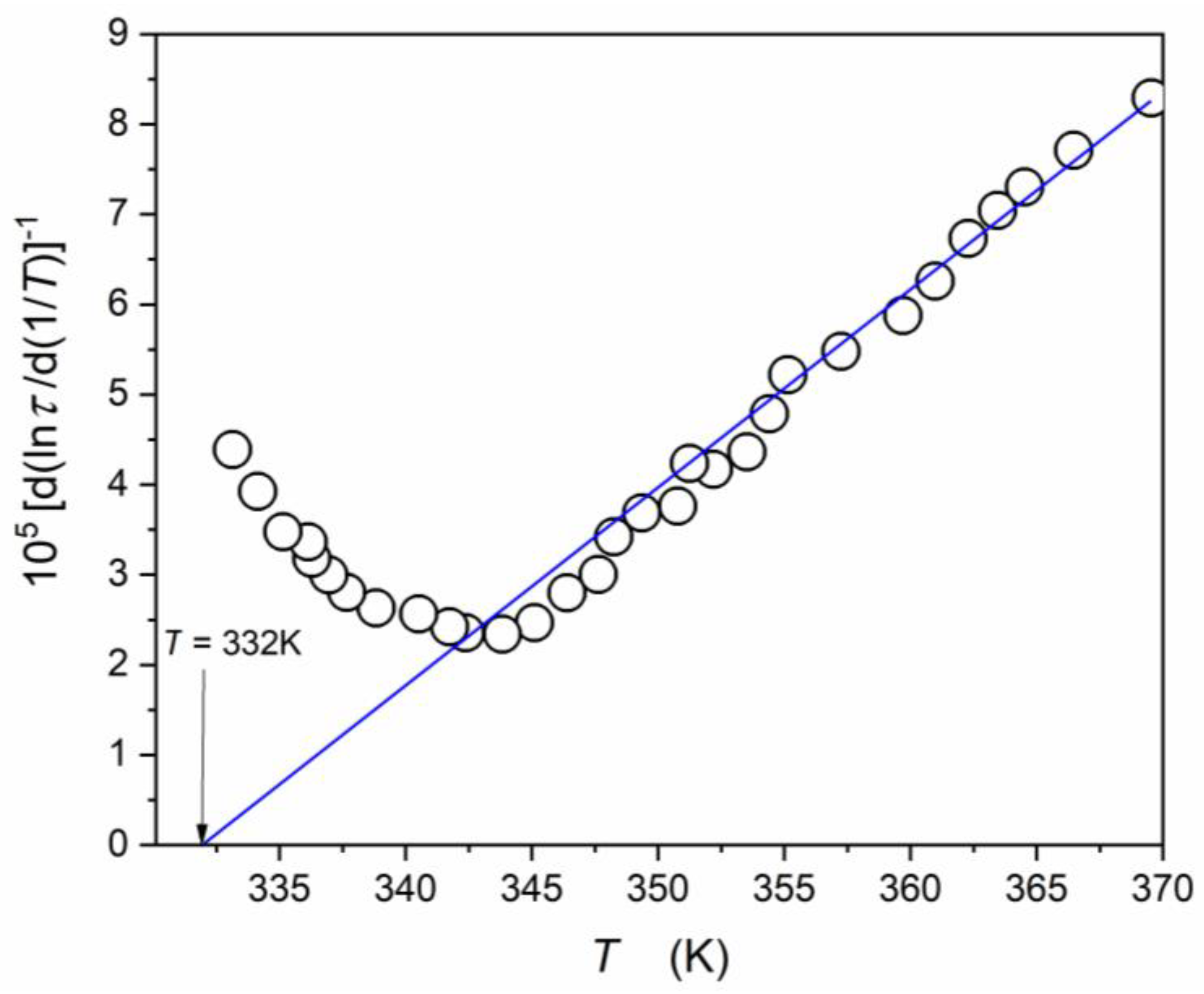
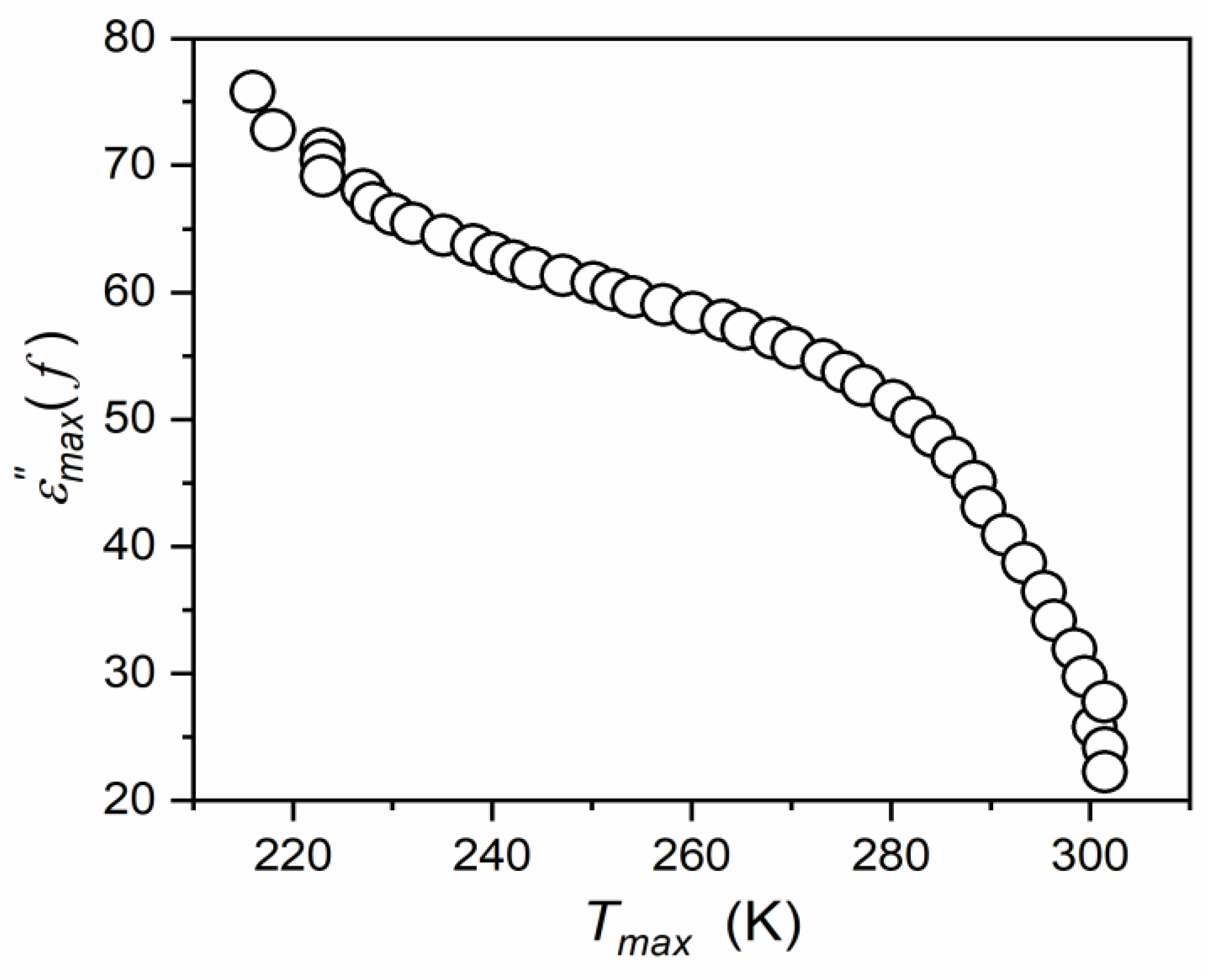
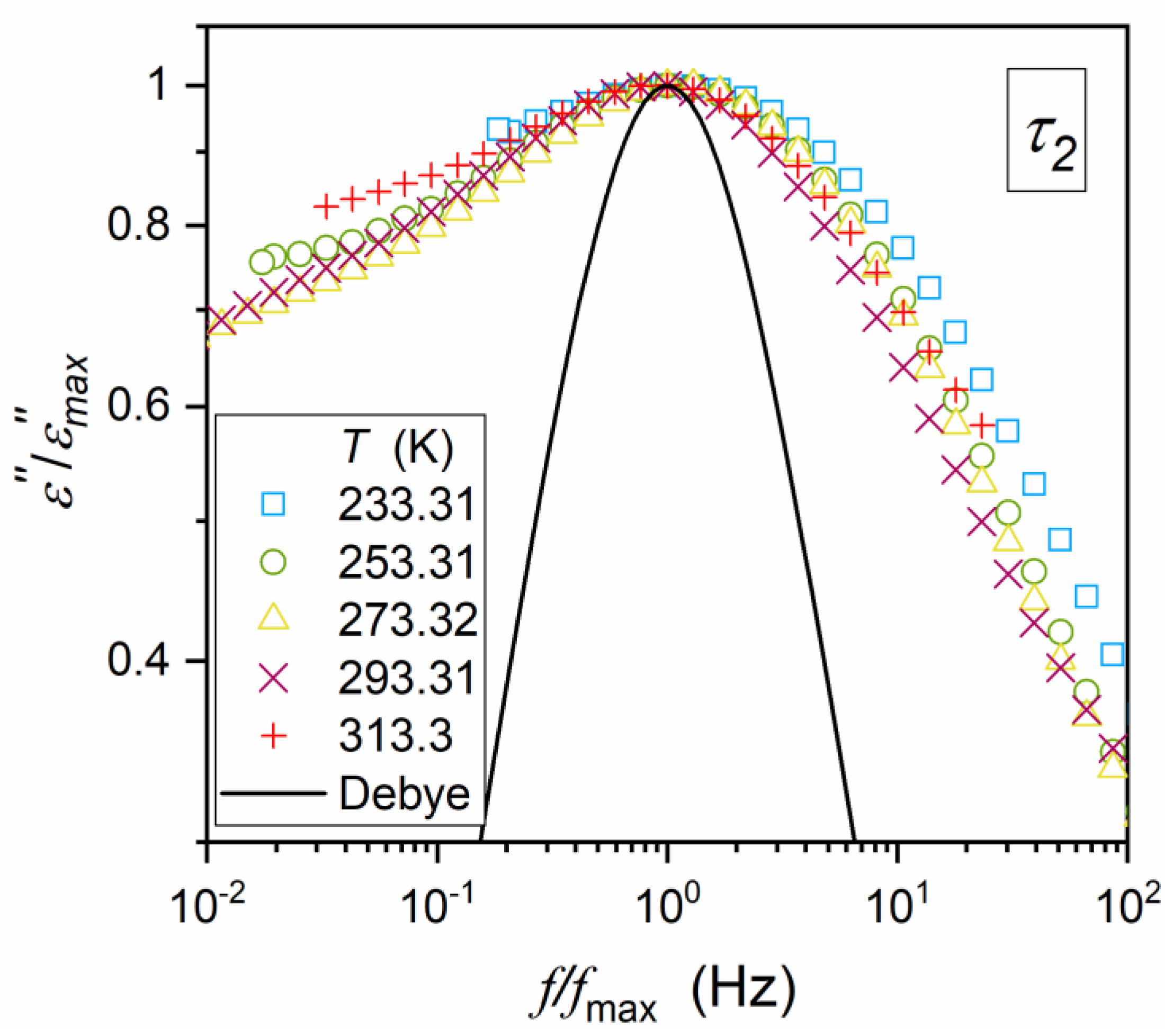
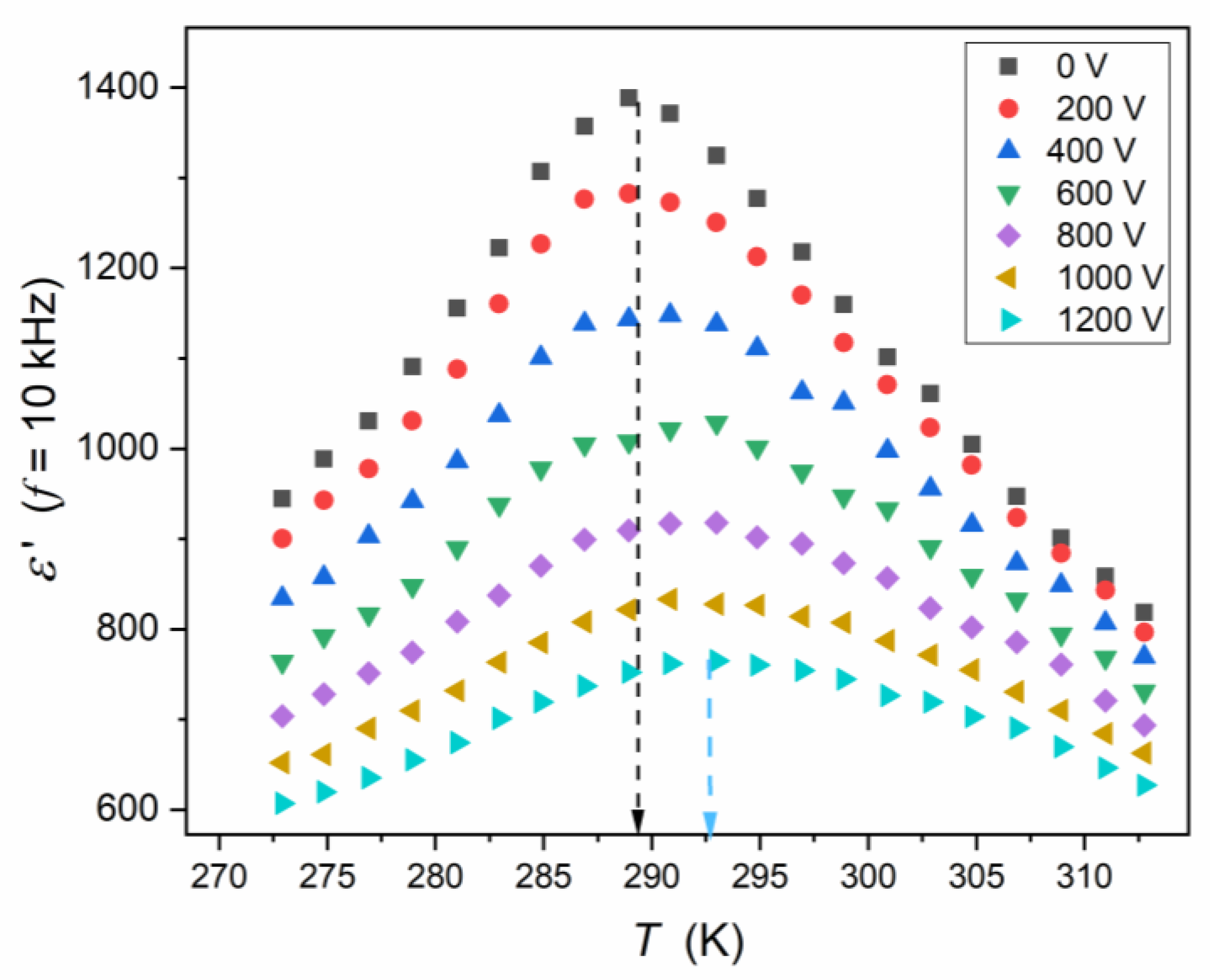
| Composition | Share (%) | Crystalline Structure Type | The Share of the Given CS Type % |
|---|---|---|---|
| Ba0.65Sr0.35TiO3 | 99.3 | Cubic | 77.1 |
| Tetragonal | 22.9 | ||
| BaTiO3 | 0.7 | Cubic | 100 |
| Temperature Range | (ferro-) | (para-ferro) | (para-) |
|---|---|---|---|
| Scaling equation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzoska, S.J.; Drozd-Rzoska, A.; Bulejak, W.; Łoś, J.; Starzonek, S.; Szafran, M.; Gao, F. Critical Insight into Pretransitional Behavior and Dielectric Tunability of Relaxor Ceramics. Materials 2023, 16, 7634. https://doi.org/10.3390/ma16247634
Rzoska SJ, Drozd-Rzoska A, Bulejak W, Łoś J, Starzonek S, Szafran M, Gao F. Critical Insight into Pretransitional Behavior and Dielectric Tunability of Relaxor Ceramics. Materials. 2023; 16(24):7634. https://doi.org/10.3390/ma16247634
Chicago/Turabian StyleRzoska, Sylwester J., Aleksandra Drozd-Rzoska, Weronika Bulejak, Joanna Łoś, Szymon Starzonek, Mikołaj Szafran, and Feng Gao. 2023. "Critical Insight into Pretransitional Behavior and Dielectric Tunability of Relaxor Ceramics" Materials 16, no. 24: 7634. https://doi.org/10.3390/ma16247634
APA StyleRzoska, S. J., Drozd-Rzoska, A., Bulejak, W., Łoś, J., Starzonek, S., Szafran, M., & Gao, F. (2023). Critical Insight into Pretransitional Behavior and Dielectric Tunability of Relaxor Ceramics. Materials, 16(24), 7634. https://doi.org/10.3390/ma16247634









