High-Mobility Topological Semimetals as Novel Materials for Huge Magnetoresistance Effect and New Type of Quantum Hall Effect
Abstract
:1. Introduction
2. Band Structure and Electrical Transport Properties in High-Mobility Semimetals
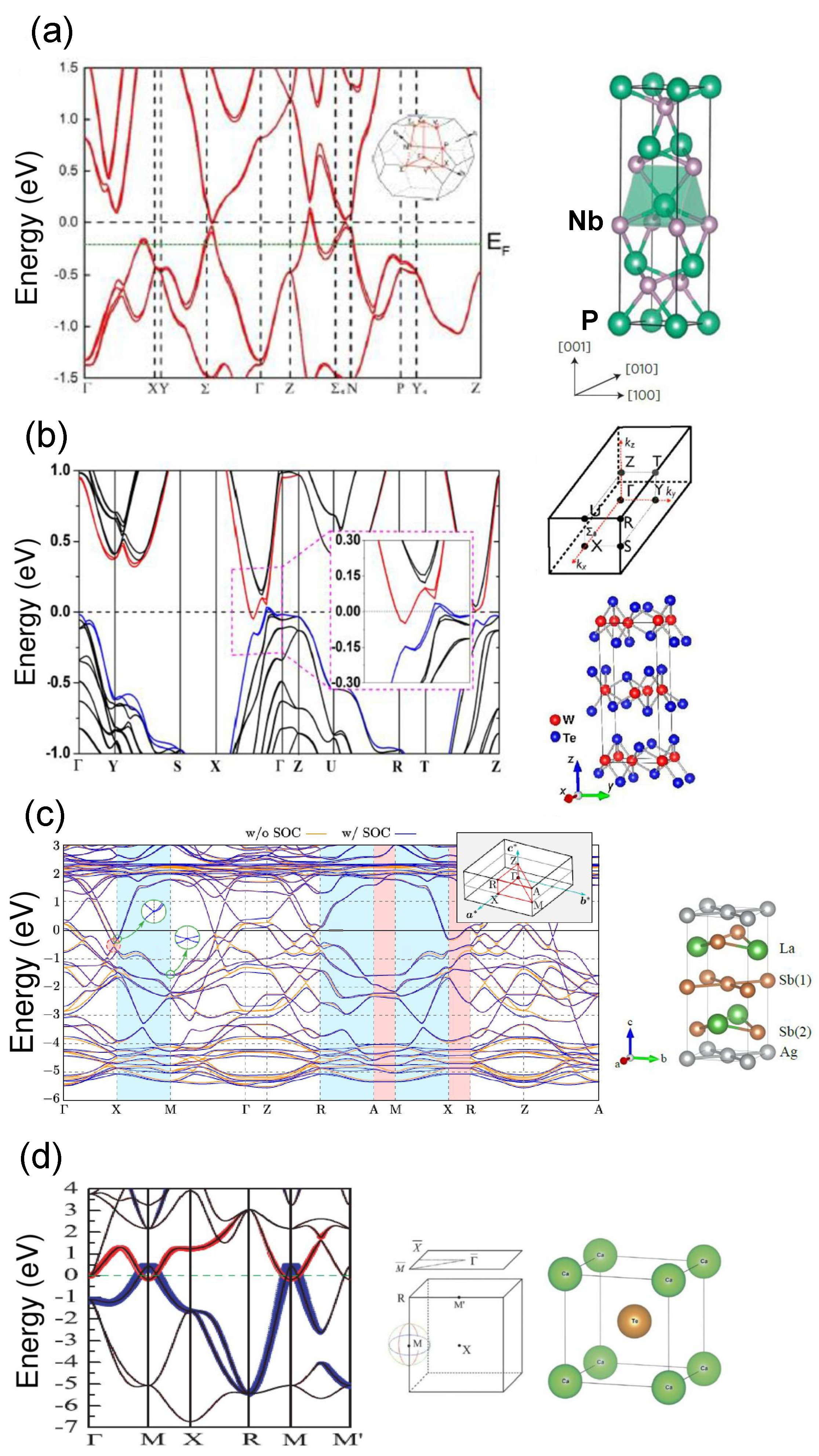
2.1. Relation between Topology and Physics
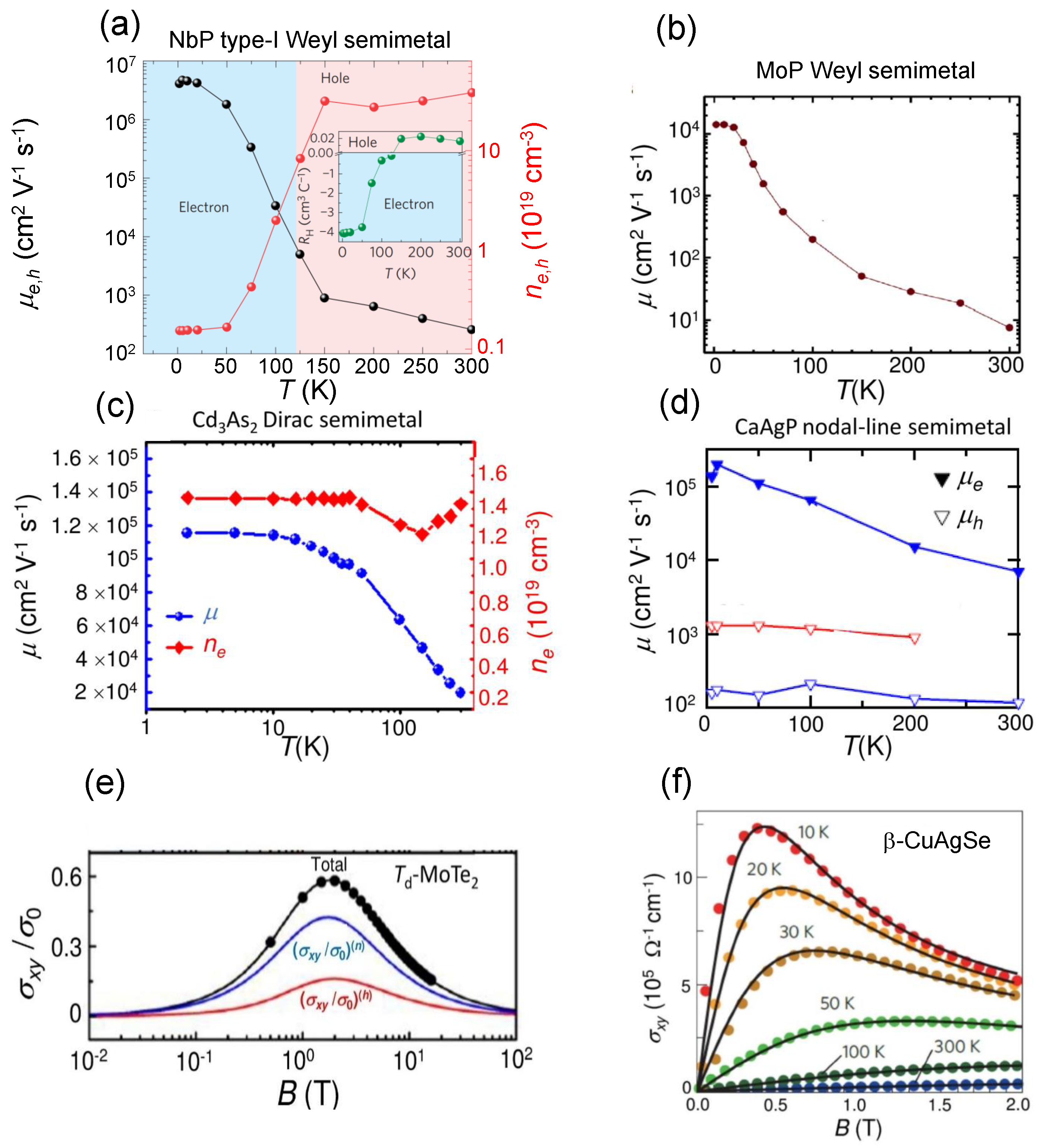
2.2. Electrical Transport Properties: Carrier Mobility and Electrical Conductivity
3. High-Mobility Semimetals and Magnetotransport Properties
3.1. Magnetoresistance Effect: Theoretical Framework and Applications
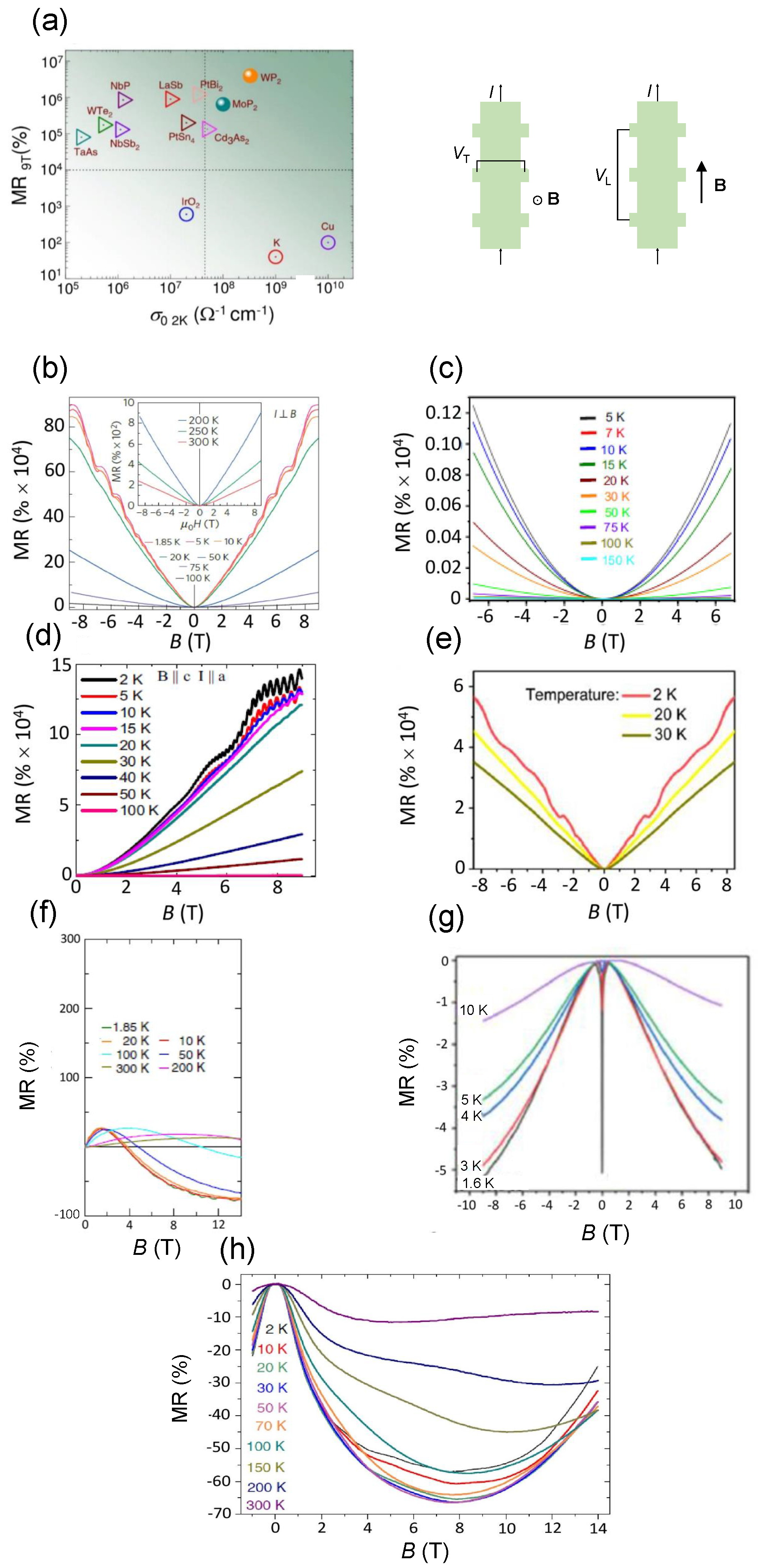
| Semimetal | Mobility (cm V s) | Resistivity ( cm) | MR (%) |
|---|---|---|---|
| [94] | (1.85 K) | (2 K) | (1.85 K, 9 T) |
| [149,150] | (5 K) | (2 K) | (2 K, 9 T) |
| [151] | (2 K) | (2 K) | (2 K, 9 T) |
| [122,152,153] | (2 K) | (2.5 K) | (5 K, 6 T) |
| [99] | (2 K) | (1 K) | (10 K, 9 T) |
| [108] | (2 K) | (2 K) | (2 K, 9 T) |
| [142,154] | (1.6 K) | (2 K) | (4.5 K, 14.7 T) |
| [155,156] | (2 K) | (2 K) | (1.8 K, 14 T) |
| [157] | (2 K) | (2 K) | (1.8 K, 33 T) |
| [140] | (5 K) | (2 K) | (2 K, 9 T) |
| [108] | (2 K) | (2 K) | (2 K, 9 T) |
| [100] | (2 K) | (2 K) | (2 K, 14 T) |
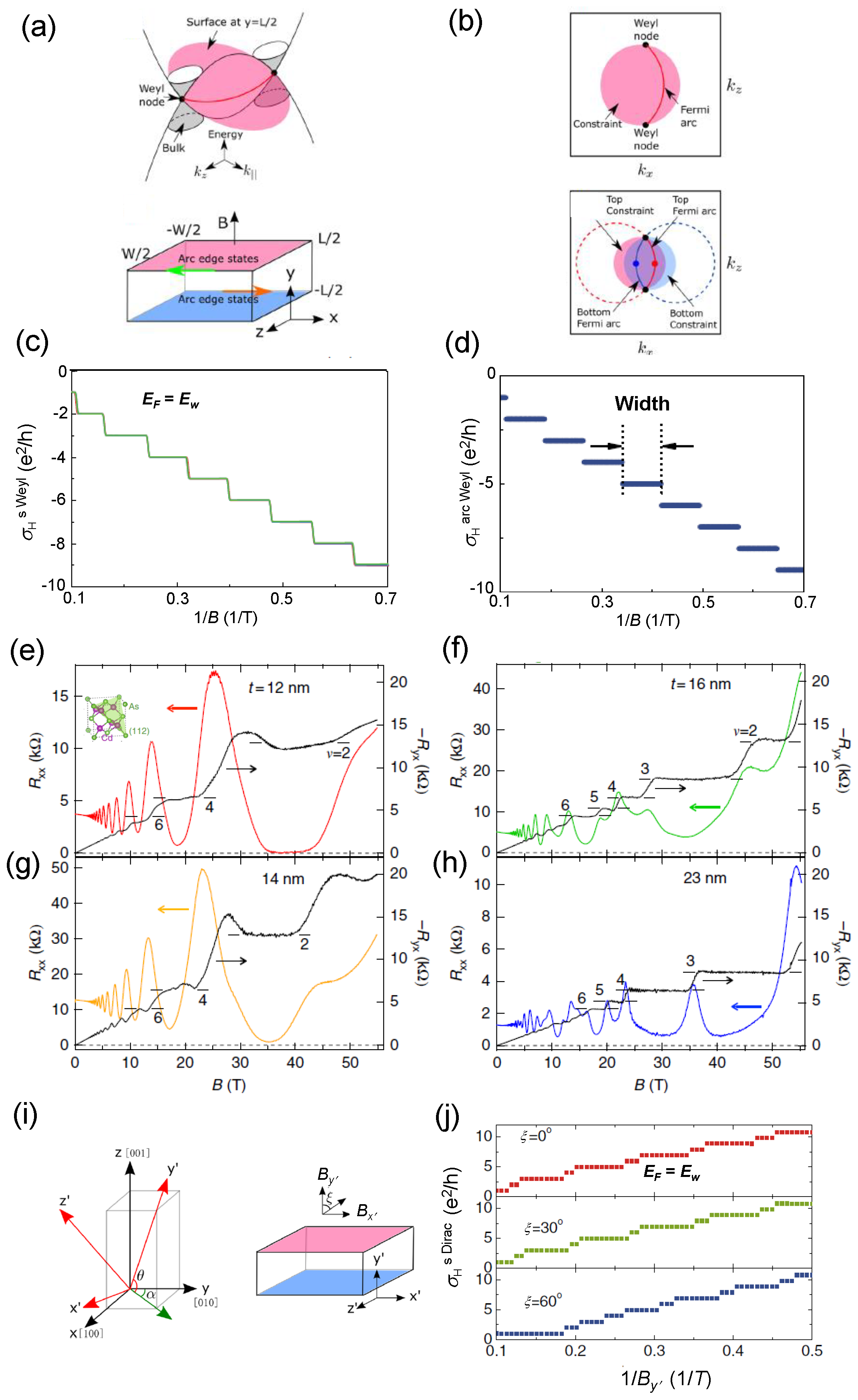
3.2. Novel Type of Quantum Hall Effect in 3D Topological Semimetals
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMR | Anisotropic magnetoresistance |
| BZ | Brillouin Zone |
| CMR | Colossal magnetoresistance |
| DFT | Density functional theory |
| EMR | Extraordinary magnetoresistance |
| GMR | Giant magnetoresistance |
| MR | Magnetoresistance |
| MTE | Magneto-thermoelectric |
| TMR | Tunnel magnetoresistance |
References
- Harrison, W.A.W.A. Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond; Dover Publications: Mineola, NY, USA, 1980. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons Inc.: Hoboken, NY, USA, 2004. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Das Sarma, S.; Hwang, E.H. Density-dependent electrical conductivity in suspended graphene: Approaching the Dirac point in transport. Phys. Rev. B 2013, 87, 035415. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef]
- Cho, S.; Fuhrer, M.S. Charge transport and inhomogeneity near the minimum conductivity point in graphene. Phys. Rev. B 2008, 77, 081402. [Google Scholar] [CrossRef]
- Hwang, E.H.; Adam, S.; Sarma, S.D. Carrier Transport in Two-Dimensional Graphene Layers. Phys. Rev. Lett. 2007, 98, 186806. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Akerman, N.; Ulbricht, G.; Lohmann, T.; Smet, J.H.; von Klitzing, K.; Yacoby, A. Observation of electron–hole puddles in graphene using a scanning single-electron transistor. Nat. Phys. 2008, 4, 144–148. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Hone, J.; Stormer, H.L.; Kim, P. Temperature-Dependent Transport in Suspended Graphene. Phys. Rev. Lett. 2008, 101, 096802. [Google Scholar] [CrossRef]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y. Topological Insulator Materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Moore, J.E. Three-Dimensional Topological Insulators. Annu. Rev. Condens. Matter Phys. 2011, 2, 55–78. [Google Scholar] [CrossRef]
- Zhu, Z.; Winkler, G.W.; Wu, Q.; Li, J.; Soluyanov, A.A. Triple Point Topological Metals. Phys. Rev. X 2016, 6, 031003. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, Y.; Song, Z.; Huang, H.; He, Y.; Fang, Z.; Weng, H.; Fang, C. Catalogue of topological electronic materials. Nature 2019, 566, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Jia, S. Crystal growth and electrical transport properties of niobium and tantalum monopnictide and dipnictide semimetals. Front. Phys. 2017, 12, 127211. [Google Scholar] [CrossRef]
- Niu, Q. Advances on topological materials. Front. Phys. 2020, 15, 43601. [Google Scholar] [CrossRef]
- Armitage, N.; Mele, E.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef]
- Lv, B.; Qian, T.; Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 2021, 93, 025002. [Google Scholar] [CrossRef]
- Mori, R.; Wang, K.; Morimoto, T.; Ciocys, S.; Denlinger, J.D.; Paglione, J.; Lanzara, A. Observation of a Flat and Extended Surface State in a Topological Semimetal. Materials 2022, 15, 2744. [Google Scholar] [CrossRef]
- Hyart, T.; Heikkilä, T.T. Momentum-space structure of surface states in a topological semimetal with a nexus point of Dirac lines. Phys. Rev. B 2016, 93, 235147. [Google Scholar] [CrossRef]
- Ma, G.; Xiao, M.; Chan, C.T. Topological phases in acoustic and mechanical systems. Nat. Rev. Phys. 2019, 1, 281–294. [Google Scholar] [CrossRef]
- Ma, S.; Yang, B.; Zhang, S. Topological photonics in metamaterials. Photonics Insights 2022, 1, R02. [Google Scholar] [CrossRef]
- Lv, B.; Weng, H.; Fu, B.; Wang, X.; Miao, H.; Ma, J.; Richard, P.; Huang, X.; Zhao, L.; Chen, G.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Alidoust, N.; Belopolski, I.; Yuan, Z.; Bian, G.; Chang, T.R.; Zheng, H.; Strocov, V.N.; Sanchez, D.S.; Chang, G.; et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat. Phys. 2015, 11, 748–754. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Yang, L.X.; Sun, Y.; Zhang, T.; Peng, H.; Yang, H.F.; Chen, C.; Zhang, Y.; Guo, Y.F.; Prabhakaran, D.; et al. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nat. Mater. 2016, 15, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Koepernik, K.; Kasinathan, D.; Efremov, D.V.; Khim, S.; Borisenko, S.; Büchner, B.; van den Brink, J. TaIrTe4: A ternary type-II Weyl semimetal. Phys. Rev. B 2016, 93, 201101. [Google Scholar] [CrossRef]
- Li, F.Y.; Luo, X.; Dai, X.; Yu, Y.; Zhang, F.; Chen, G. Hybrid Weyl semimetal. Phys. Rev. B 2016, 94, 121105. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Y.; Zhang, Y.; Shi, W.J.; Parkin, S.S.P.; Yan, B. Topological Weyl semimetals in the chiral antiferromagnetic materials Mn3Ge and Mn3Sn. New J. Phys. 2017, 19, 015008. [Google Scholar] [CrossRef]
- Kanagaraj, M.; Ning, J.; He, L. Topological Co3Sn2S2 magnetic Weyl semimetal: From fundamental understanding to diverse fields of study. Rev. Phys. 2022, 8, 100072. [Google Scholar] [CrossRef]
- Carbotte, J.P. Dirac cone tilt on interband optical background of type-I and type-II Weyl semimetals. Phys. Rev. B 2016, 94, 165111. [Google Scholar] [CrossRef]
- Lv, B.Q.; Feng, Z.L.; Xu, Q.N.; Gao, X.; Ma, J.Z.; Kong, L.Y.; Richard, P.; Huang, Y.B.; Strocov, V.N.; Fang, C.; et al. Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature 2017, 546, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Hein, P.; Jauernik, S.; Erk, H.; Yang, L.; Qi, Y.; Sun, Y.; Felser, C.; Bauer, M. Mode-resolved reciprocal space mapping of electron-phonon interaction in the Weyl semimetal candidate Td-WTe2. Nat. Commun. 2020, 11, 2613. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.R.; Xu, S.Y.; Chang, G.; Lee, C.C.; Huang, S.M.; Wang, B.; Bian, G.; Zheng, H.; Sanchez, D.S.; Belopolski, I.; et al. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1-xTe2. Nat. Commun. 2016, 7, 10639. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Wan, B.; Wang, D.; Sheng, L.; Duan, C.G.; Wan, X. Dirac and Weyl Semimetal in XYBi (X = Ba, Eu; Y = Cu, Ag and Au). Sci. Rep. 2015, 5, 14423. [Google Scholar] [CrossRef] [PubMed]
- Udagawa, M.; Bergholtz, E. Field-Selective Anomaly and Chiral Mode Reversal in Type-II Weyl Materials. Phys. Rev. Lett. 2016, 117, 086401. [Google Scholar] [CrossRef]
- Swekis, P.; Sukhanov, A.S.; Chen, Y.C.; Gloskovskii, A.; Fecher, G.H.; Panagiotopoulos, I.; Sichelschmidt, J.; Ukleev, V.; Devishvili, A.; Vorobiev, A.; et al. Magnetic and Electronic Properties of Weyl Semimetal Co2MnGa Thin Films. Nanomaterials 2021, 11, 251. [Google Scholar] [CrossRef] [PubMed]
- Hirschberger, M.; Kushwaha, S.; Wang, Z.; Gibson, Q.; Liang, S.; Belvin, C.A.; Bernevig, B.A.; Cava, R.J.; Ong, N.P. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nat. Mater. 2016, 15, 1161–1165. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; He, H.; Lu, H.Z.; Zhang, H.; Liu, H.; Ma, R.; Fan, Z.; Shen, S.Q.; Wang, J. Negative magnetoresistance in Dirac semimetal Cd3As2. Nat. Commun. 2016, 7, 10301. [Google Scholar] [CrossRef]
- Baidak, S.T.; Lukoyanov, A.V. Common Topological Features in Band Structure of RNiSb and RSb Compounds for R = Tb, Dy, Ho. Materials 2023, 16, 242. [Google Scholar] [CrossRef]
- Jia, S.; Xu, S.Y.; Hasan, M.Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nat. Mater. 2016, 15, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
- Balents, L. Weyl electrons kiss. Physics 2011, 4, 36. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Fang, C.; Gilbert, M.J.; Dai, X.; Bernevig, B.A. Multi-Weyl Topological Semimetals Stabilized by Point Group Symmetry. Phys. Rev. Lett. 2012, 108, 266802. [Google Scholar] [CrossRef]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P.; et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Mullen, K.; Uchoa, B.; Glatzhofer, D.T. Line of Dirac Nodes in Hyperhoneycomb Lattices. Phys. Rev. Lett. 2015, 115, 026403. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.S.; Schoop, L.M.; Seibel, E.M.; Gibson, Q.D.; Xie, W.; Cava, R.J. A new form of Ca3P2 with a ring of Dirac nodes. APL Mater. 2015, 3, 083602. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, M.; Zhang, H.; Huang, H.; Arita, M.; Sun, Z.; Duan, W.; Wu, Y.; Zhou, S. Experimental evidence for type-II Dirac semimetal in PtSe2. Phys. Rev. B 2017, 96, 125102. [Google Scholar] [CrossRef]
- Vafek, O.; Vishwanath, A. Dirac Fermions in Solids: From High-Tc Cuprates and Graphene to Topological Insulators and Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2014, 5, 83–112. [Google Scholar] [CrossRef]
- Yan, M.; Huang, H.; Zhang, K.; Wang, E.; Yao, W.; Deng, K.; Wan, G.; Zhang, H.; Arita, M.; Yang, H.; et al. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. Nat. Commun. 2017, 8, 257. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef]
- Gibson, Q.D.; Schoop, L.M.; Muechler, L.; Xie, L.S.; Hirschberger, M.; Ong, N.P.; Car, R.; Cava, R.J. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Phys. Rev. B 2015, 91, 205128. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, R.; Fang, Z.; Dai, X.; Weng, H. Topological nodal line semimetals in the CaP3 family of materials. Phys. Rev. B 2017, 95, 045136. [Google Scholar] [CrossRef]
- Yang, M.X.; Luo, W.; Chen, W. Quantum transport in topological nodal-line semimetals. Adv. Phys. X 2022, 7, 2065216. [Google Scholar] [CrossRef]
- Chang, T.R.; Pletikosic, I.; Kong, T.; Bian, G.; Huang, A.; Denlinger, J.; Kushwaha, S.K.; Sinkovic, B.; Jeng, H.T.; Valla, T.; et al. Realization of a Type-II Nodal-Line Semimetal in Mg3Bi2. Adv. Sci. 2019, 6, 1800897. [Google Scholar] [CrossRef]
- Du, Y.; Tang, F.; Wang, D.; Sheng, L.; Kan, E.j.; Duan, C.G.; Savrasov, S.Y.; Wan, X. CaTe: A new topological node-line and Dirac semimetal. NPJ Quantum Mater. 2017, 2, 3. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.; Zhao, H.; Wu, M.; Pan, H. Magneto-Optical Transport Properties of Type-II Nodal Line Semimetals. Materials 2021, 14, 3035. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Saigusa, K.; Wada, T.; Yamakawa, Y.; Yamakage, A.; Sasagawa, T.; Katayama, N.; Takatsu, H.; Kageyama, H.; Takenaka, K. High-mobility carriers induced by chemical doping in the candidate nodal-line semimetal CaAgP. Phys. Rev. B 2020, 102, 115101. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Dai, X.; Liu, G. Topological Type-II Nodal Line Semimetal and Dirac Semimetal State in Stable Kagome Compound Mg3Bi2. J. Phys. Chem. Lett. 2017, 8, 4814–4819. [Google Scholar] [CrossRef] [PubMed]
- Chang, G.; Xu, S.Y.; Sanchez, D.S.; Huang, S.M.; Lee, C.C.; Chang, T.R.; Bian, G.; Zheng, H.; Belopolski, I.; Alidoust, N.; et al. A strongly robust type II Weyl fermion semimetal state in Ta3S2. Sci. Adv. 2016, 2, e1600295. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, T.; Fang, Z.; Fang, C. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 2018, 9, 3530. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, T.; Fang, C. Diagnosis for Nonmagnetic Topological Semimetals in the Absence of Spin-Orbital Coupling. Phys. Rev. X 2018, 8, 031069. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties; Graduate Texts in Physics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Goringe, C.M.; Bowler, D.R.; Hernández, E. Tight-binding modelling of materials. Rep. Prog. Phys. 1997, 60, 1447. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Slater, J.C. Wave Functions in a Periodic Potential. Phys. Rev. 1937, 51, 846–851. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Dreizler, R.M.; Gross, E.K.U. Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Singh, D.J.; Nordström, L. Planewaves, Pseudopotentials and the LAPW Method; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A.J. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Phys. Rev. B 1981, 24, 864–875. [Google Scholar] [CrossRef]
- Burkov, A.A. Topological semimetals. Nat. Mater. 2016, 15, 1145–1148. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Venderbos, J.W.; Kim, Y.; Rappe, A.M. Topological Semimetals from First Principles. Annu. Rev. Mater. Res. 2019, 49, 153–183. [Google Scholar] [CrossRef]
- Tang, F.; Wan, X. Effective models for nearly ideal Dirac semimetals. Front. Phys. 2019, 14, 43603. [Google Scholar] [CrossRef]
- He, L.; Hong, X.; Dong, J.; Pan, J.; Zhang, Z.; Zhang, J.; Li, S. Quantum Transport Evidence for the Three-Dimensional Dirac Semimetal Phase in Cd3As2. Phys. Rev. Lett. 2014, 113, 246402. [Google Scholar] [CrossRef] [PubMed]
- Fei, F.; Bo, X.; Wang, R.; Wu, B.; Jiang, J.; Fu, D.; Gao, M.; Zheng, H.; Chen, Y.; Wang, X.; et al. Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2. Phys. Rev. B 2017, 96, 041201. [Google Scholar] [CrossRef]
- Guo, P.J.; Yang, H.C.; Liu, K.; Lu, Z.Y. Type-II Dirac semimetals in the YPd2Sn. Phys. Rev. B 2017, 95, 155112. [Google Scholar] [CrossRef]
- Shekhar, C.; Nayak, A.K.; Sun, Y.; Schmidt, M.; Nicklas, M.; Leermakers, I.; Zeitler, U.; Skourski, Y.; Wosnitza, J.; Liu, Z.; et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 2015, 11, 645–649. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Zhu, Z.; Yan, D.; Nie, X.A.; Xu, H.K.; Yang, X.; Guan, D.D.; Wang, S.; Li, Y.Y.; Liu, C.; Liu, J.W.; et al. Scanning tunneling microscopic investigation on morphology of magnetic Weyl semimetal YbMnBi2. Chin. Phys. B 2019, 28, 077302. [Google Scholar] [CrossRef]
- Sie, E.J.; Nyby, C.M.; Pemmaraju, C.D.; Park, S.J.; Shen, X.; Yang, J.; Hoffmann, M.C.; Ofori-Okai, B.K.; Li, R.; Reid, A.H.; et al. An ultrafast symmetry switch in a Weyl semimetal. Nature 2019, 565, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef]
- Zhang, C.L.; Yuan, Z.; Jiang, Q.D.; Tong, B.; Zhang, C.; Xie, X.C.; Jia, S. Electron scattering in tantalum monoarsenide. Phys. Rev. B 2017, 95, 085202. [Google Scholar] [CrossRef]
- Kumar, N.; Sun, Y.; Nicklas, M.; Watzman, S.J.; Young, O.; Leermakers, I.; Hornung, J.; Klotz, J.; Gooth, J.; Manna, K.; et al. Extremely high conductivity observed in the triple point topological metal MoP. Nat. Commun. 2019, 10, 2475. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.G.; Zhang, C.; Zou, Y.; Zhang, E.; Yang, L.; Hong, M.; Xiu, F.; Zou, J. Scalable Growth of High Mobility Dirac Semimetal Cd3As2 Microbelts. Nano Lett. 2015, 15, 5830–5834. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, K.; Kawamuma, K.; Tsuzuku, T. Temperature Dependence of the Average Mobility in Graphite. J. Phys. Soc. Jpn. 1979, 47, 1210–1215. [Google Scholar] [CrossRef]
- Pendrys, L.A.; Zeller, C.; Vogel, F.L. Electrical transport properties of natural and synthetic graphite. J. Mater. Sci. 1980, 15, 2103–2112. [Google Scholar] [CrossRef]
- Ibach, H.; Lüth, H. Solid-State Physics: An Introduction to Principles of Materials Science; with 100 Problems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014, 5, 3786. [Google Scholar] [CrossRef] [PubMed]
- Hosur, P.; Qi, X. Recent developments in transport phenomena in Weyl semimetals. Comptes Rendus Phys. 2013, 14, 857–870. [Google Scholar] [CrossRef]
- Khim, S.; Koepernik, K.; Efremov, D.V.; Klotz, J.; Förster, T.; Wosnitza, J.; Sturza, M.I.; Wurmehl, S.; Hess, C.; van den Brink, J.; et al. Magnetotransport and de Haas–van Alphen measurements in the type-II Weyl semimetal TaIrTe4. Phys. Rev. B 2016, 94, 165145. [Google Scholar] [CrossRef]
- Kumar, N.; Sun, Y.; Xu, N.; Manna, K.; Yao, M.; Süss, V.; Leermakers, I.; Young, O.; Förster, T.; Schmidt, M.; et al. Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2. Nat. Commun. 2017, 8, 1642. [Google Scholar] [CrossRef]
- Singha, R.; Pariari, A.K.; Satpati, B.; Mandal, P. Large nonsaturating magnetoresistance and signature of nondegenerate Dirac nodes in ZrSiS. Proc. Natl. Acad. Sci. USA 2017, 114, 2468–2473. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Song, Z.Y.; Guo, L.; Gao, H.; Dong, Z.; Yu, Q.; Zheng, R.K.; Kang, T.T.; Zhang, K. Nontrivial Giant Linear Magnetoresistance in Nodal-Line Semimetal ZrGeSe 2D Layers. Nano Lett. 2021, 21, 10139–10145. [Google Scholar] [CrossRef] [PubMed]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.G.; Felser, C.; Cava, R.J.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353, aaf5037. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yu, Z.M.; Yao, Y.; Yang, S.A. Type-II topological metals. Front. Phys. 2020, 15, 43201. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; He, X.; Zhang, Q.; Xia, C.; Yu, Z.M.; Yang, S.A.; Zhu, Z.; Alshareef, H.N.; Zhang, X.X. Evidence for topological type-II Weyl semimetal WTe2. Nat. Commun. 2017, 8, 2150. [Google Scholar] [CrossRef] [PubMed]
- Autès, G.; Gresch, D.; Troyer, M.; Soluyanov, A.; Yazyev, O. Robust Type-II Weyl Semimetal Phase in Transition Metal Diphosphides XP2 (X = Mo, W). Phys. Rev. Lett. 2016, 117, 066402. [Google Scholar] [CrossRef] [PubMed]
- Tamai, A.; Wu, Q.; Cucchi, I.; Bruno, F.; Riccò, S.; Kim, T.; Hoesch, M.; Barreteau, C.; Giannini, E.; Besnard, C.; et al. Fermi Arcs and Their Topological Character in the Candidate Type-II Weyl Semimetal MoTe2. Phys. Rev. X 2016, 6, 031021. [Google Scholar] [CrossRef]
- Belopolski, I.; Sanchez, D.S.; Ishida, Y.; Pan, X.; Yu, P.; Xu, S.Y.; Chang, G.; Chang, T.R.; Zheng, H.; Alidoust, N.; et al. Discovery of a new type of topological Weyl fermion semimetal state in MoxW1-xTe2. Nat. Commun. 2016, 7, 13643. [Google Scholar] [CrossRef]
- Zyuzin, A.A.; Tiwari, R.P. Intrinsic anomalous Hall effect in type-II Weyl semimetals. JETP Lett. 2016, 103, 717–722. [Google Scholar] [CrossRef]
- Haubold, E.; Koepernik, K.; Efremov, D.; Khim, S.; Fedorov, A.; Kushnirenko, Y.; van den Brink, J.; Wurmehl, S.; Büchner, B.; Kim, T.K.; et al. Experimental realization of type-II Weyl state in noncentrosymmetric TaIrTe4. Phys. Rev. B 2017, 95, 241108. [Google Scholar] [CrossRef]
- Islam, M.R.; Mojumder, M.R.H.; Moghal, B.K.; Islam, A.S.M.J.; Miah, M.R.; Roy, S.; Kumar, A.; Shihavuddin, A.S.M.; Ashique, R.H. Impact of strain on the electronic, phonon, and optical properties of monolayer transition metal dichalcogenides XTe2 (X = Mo and W). Phys. Scr. 2022, 97, 045806. [Google Scholar] [CrossRef]
- Borisenko, S.; Evtushinsky, D.; Gibson, Q.; Yaresko, A.; Koepernik, K.; Kim, T.; Ali, M.; van den Brink, J.; Hoesch, M.; Fedorov, A.; et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nat. Commun. 2019, 10, 3424. [Google Scholar] [CrossRef]
- Tchoumakov, S.; Civelli, M.; Goerbig, M.O. Magnetic-Field-Induced Relativistic Properties in Type-I and Type-II Weyl Semimetals. Phys. Rev. Lett. 2016, 117, 086402. [Google Scholar] [CrossRef]
- Bedoya-Pinto, A.; Pandeya, A.K.; Liu, D.; Deniz, H.; Chang, K.; Tan, H.; Han, H.; Jena, J.; Kostanovskiy, I.; Parkin, S.S.P. Realization of Epitaxial NbP and TaP Weyl Semimetal Thin Films. ACS Nano 2020, 14, 4405–4413. [Google Scholar] [CrossRef] [PubMed]
- Lv, H.Y.; Lu, W.J.; Shao, D.F.; Liu, Y.; Tan, S.G.; Sun, Y.P. Perfect charge compensation in WTe2 for the extraordinary magnetoresistance: From bulk to monolayer. Europhys. Lett. 2015, 110, 37004. [Google Scholar] [CrossRef]
- Tian, W.; Yu, W.; Liu, X.; Wang, Y.; Shi, J. A Review of the Characteristics, Synthesis, and Thermodynamics of Type-II Weyl Semimetal WTe2. Materials 2018, 11, 1185. [Google Scholar] [CrossRef] [PubMed]
- Rosmus, M.; Olszowska, N.; Bukowski, Z.; Starowicz, P.; Piekarz, P.; Ptok, A. Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2. Materials 2022, 15, 7168. [Google Scholar] [CrossRef] [PubMed]
- Wadge, A.S.; Grabecki, G.; Autieri, C.; Kowalski, B.J.; Iwanowski, P.; Cuono, G.; Islam, M.F.; Canali, C.M.; Dybko, K.; Hruban, A.; et al. Electronic properties of TaAs2 topological semimetal investigated by transport and ARPES. J. Phys. Condens. Matter 2022, 34, 125601. [Google Scholar] [CrossRef] [PubMed]
- Mathur, P.C.; Kataria, N.D.; Jain, S.; Sharma, V. Electron mobility in n-InSb from 77 to 300 K. J. Phys. C Solid State Phys. 1975, 9, L89. [Google Scholar] [CrossRef]
- Pei, Q.L.; Luo, X.; Chen, F.C.; Lv, H.Y.; Sun, Y.; Lu, W.J.; Tong, P.; Sheng, Z.G.; Han, Y.Y.; Song, W.H.; et al. Mobility spectrum analytical approach for the type-II Weyl semimetal Td-MoTe2. Appl. Phys. Lett. 2018, 112, 072401. [Google Scholar] [CrossRef]
- Ishiwata, S.; Shiomi, Y.; Lee, J.S.; Bahramy, M.S.; Suzuki, T.; Uchida, M.; Arita, R.; Taguchi, Y.; Tokura, Y. Extremely high electron mobility in a phonon-glass semimetal. Nat. Mater. 2013, 12, 512–517. [Google Scholar] [CrossRef]
- Coleman, R.V.; Isin, A. Magnetoresistance in Iron Single Crystals. J. Appl. Phys. 1966, 37, 1028–1029. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Grünberg, P.; Schreiber, R.; Pang, Y.; Brodsky, M.B.; Sowers, H. Layered Magnetic Structures: Evidence for Antiferromagnetic Coupling of Fe Layers across Cr Interlayers. Phys. Rev. Lett. 1986, 57, 2442–2445. [Google Scholar] [CrossRef] [PubMed]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Van Dau, F.N.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.P. Colossal magnetoresistance. J. Phys. Condens. Matter 1997, 9, 8171. [Google Scholar] [CrossRef]
- Sun, J.; Kosel, J. Extraordinary Magnetoresistance in Semiconductor/Metal Hybrids: A Review. Materials 2013, 6, 500–516. [Google Scholar] [CrossRef]
- Pippard, A. Magnetoresistance in Metals. In Magnetoresistance in Metals; Pippard, A.B., Ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Solin, S.A.; Thio, T.; Hines, D.R.; Heremans, J.J. Enhanced Room-Temperature Geometric Magnetoresistance in Inhomogeneous Narrow-Gap Semiconductors. Science 2000, 289, 1530–1532. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.M.; Sun, H.P.; Lu, H.Z.; Xie, X.C. 3D Quantum Hall Effect of Fermi Arcs in Topological Semimetals. Phys. Rev. Lett. 2017, 119, 136806. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Ali, M.N.; Liu, M.; Cava, R.J.; Ong, N.P. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 2015, 14, 280–284. [Google Scholar] [CrossRef]
- Feng, J.; Pang, Y.; Wu, D.; Wang, Z.; Weng, H.; Li, J.; Dai, X.; Fang, Z.; Shi, Y.; Lu, L. Large linear magnetoresistance in Dirac semimetal Cd3As2 with Fermi surfaces close to the Dirac points. Phys. Rev. B 2015, 92, 081306. [Google Scholar] [CrossRef]
- Pletikosić, I.; Ali, M.N.; Fedorov, A.V.; Cava, R.J.; Valla, T. Electronic structure basis for the extraordinary magnetoresistance in WTe2. Phys. Rev. Lett. 2014, 113, 216601. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.N.; Xiong, J.; Flynn, S.; Tao, J.; Gibson, Q.D.; Schoop, L.M.; Liang, T.; Haldolaarachchige, N.; Hirschberger, M.; Ong, N.P.; et al. Large, non-saturating magnetoresistance in WTe2. Nature 2014, 514, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.M.; Yao, Y.; Yang, S.A. Predicted Unusual Magnetoresponse in Type-II Weyl Semimetals. Phys. Rev. Lett. 2016, 117, 077202. [Google Scholar] [CrossRef]
- Adhikari, R.; Adhikari, S.; Faina, B.; Terschanski, M.; Bork, S.; Leimhofer, C.; Cinchetti, M.; Bonanni, A. Positive Magnetoresistance and Chiral Anomaly in Exfoliated Type-II Weyl Semimetal Td-WTe2. Nanomaterials 2021, 11, 2755. [Google Scholar] [CrossRef]
- Shekhar, C.; Ouardi, S.; Nayak, A.K.; Fecher, G.H.; Schnelle, W.; Felser, C. Ultrahigh mobility and nonsaturating magnetoresistance in Heusler topological insulators. Phys. Rev. B 2012, 86, 155314. [Google Scholar] [CrossRef]
- Singleton, J.; Singleton, J. Band Theory and Electronic Properties of Solids; Oxford Master Series in Physics; Oxford University Press: Oxford, NY, USA, 2001. [Google Scholar]
- Arnold, F.; Shekhar, C.; Wu, S.C.; Sun, Y.; dos Reis, R.D.; Kumar, N.; Naumann, M.; Ajeesh, M.O.; Schmidt, M.; Grushin, A.G.; et al. Negative magnetoresistance without well-defined chirality in the Weyl semimetal TaP. Nat. Commun. 2016, 7, 11615. [Google Scholar] [CrossRef] [PubMed]
- Son, D.T.; Spivak, B.Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 2013, 88, 104412. [Google Scholar] [CrossRef]
- Wang, K.; Graf, D.; Li, L.; Wang, L.; Petrovic, C. Anisotropic giant magnetoresistance in NbSb2. Sci. Rep. 2014, 4, 7328. [Google Scholar] [CrossRef]
- Li, P.; Qiu, P.; Xu, Q.; Luo, J.; Xiong, Y.; Xiao, J.; Aryal, N.; Li, Q.; Chen, L.; Shi, X. Colossal Nernst power factor in topological semimetal NbSb2. Nat. Commun. 2022, 13, 7612. [Google Scholar] [CrossRef]
- Ghimire, N.J.; Luo, Y.; Neupane, M.; Williams, D.J.; Bauer, E.D.; Ronning, F. Magnetotransport of single crystalline NbAs. J. Phys. Condens. Matter 2015, 27, 152201. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Sudesh; Patnaik, S. Exceptional magnetoresistance in Weyl semimetal TaP. AIP Conf. Proc. 2019, 2115, 030409. [Google Scholar] [CrossRef]
- Shekhar, C.; Süss, V.; Schmidt, M. Mobility induced unsaturated high linear magnetoresistance in transition-metal monopnictides Weyl semimetals. arXiv 2016, arXiv:1606.06649. [Google Scholar]
- Wang, Y.; Wang, L.; Liu, X.; Wu, H.; Wang, P.; Yan, D.; Cheng, B.; Shi, Y.; Watanabe, K.; Taniguchi, T.; et al. Direct Evidence for Charge Compensation-Induced Large Magnetoresistance in Thin WTe2. Nano Lett. 2019, 19, 3969–3975. [Google Scholar] [CrossRef]
- Mun, E.; Ko, H.; Miller, G.J.; Samolyuk, G.D.; Bud’ko, S.L.; Canfield, P.C. Magnetic field effects on transport properties of PtSn4. Phys. Rev. B 2012, 85, 035135. [Google Scholar] [CrossRef]
- Fu, C.; Guin, S.N.; Scaffidi, T.; Sun, Y.; Saha, R.; Watzman, S.J.; Srivastava, A.K.; Li, G.; Schnelle, W.; Parkin, S.S.P.; et al. Largely Suppressed Magneto-Thermal Conductivity and Enhanced Magneto-Thermoelectric Properties in PtSn4. Research 2020, 2020, 4643507. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Hao, N.; Zheng, F.W.; Ning, W.; Wu, M.; Zhu, X.; Zheng, G.; Zhang, J.; Lu, J.; Zhang, H.; et al. Extremely Large Magnetoresistance in a Topological Semimetal Candidate Pyrite PtBi2. Phys. Rev. Lett. 2017, 118, 256601. [Google Scholar] [CrossRef]
- Uchida, M.; Nakazawa, Y.; Nishihaya, S.; Akiba, K.; Kriener, M.; Kozuka, Y.; Miyake, A.; Taguchi, Y.; Tokunaga, M.; Nagaosa, N.; et al. Quantum Hall states observed in thin films of Dirac semimetal Cd3As2. Nat. Commun. 2017, 8, 2274. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Yuan, X.; Lu, S.; Zhang, J.; Narayan, A.; Liu, Y.; Zhang, H.; Ni, Z.; Liu, R.; et al. Quantum Hall effect based on Weyl orbits in Cd3As2. Nature 2019, 565, 331–336. [Google Scholar] [CrossRef]
- Weis, J. Quantum Hall Effect. In Encyclopedia of Condensed Matter Physics; Bassani, F., Liedl, G.L., Wyder, P., Eds.; Elsevier: Oxford, UK, 2005; pp. 22–29. [Google Scholar] [CrossRef]
- Klitzing, K.v.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Laughlin, R.B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 1981, 23, 5632–5633. [Google Scholar] [CrossRef]
- Feng, T.; Wang, P.; Han, Z.; Zhou, L.; Zhang, W.; Liu, Q.; Liu, W. Large Transverse and Longitudinal Magneto-Thermoelectric Effect in Polycrystalline Nodal-Line Semimetal Mg3Bi2. Adv. Mater. 2022, 34, 2200931. [Google Scholar] [CrossRef]
- Walukiewicz, W.; Ruda, H.E.; Lagowski, J.; Gatos, H.C. Electron mobility in modulation-doped heterostructures. Phys. Rev. B 1984, 30, 4571–4582. [Google Scholar] [CrossRef]
- Xia, F.; Perebeinos, V.; Lin, Y.m.; Wu, Y.; Avouris, P. The origins and limits of metal–graphene junction resistance. Nat. Nanotechnol. 2011, 6, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Umansky, V.; Heiblum, M.; Levinson, Y.; Smet, J.; Nübler, J.; Dolev, M. MBE growth of ultra-low disorder 2DEG with mobility exceeding 35×106 cm2/V s. J. Cryst. Growth 2009, 311, 1658–1661. [Google Scholar] [CrossRef]
- Shur, M.S.; Maki, P. Advanced High Speed Devices; World Scientific: Singapore, 2009. [Google Scholar] [CrossRef]
- Hurtado-Aviles, E.; Trejo-Valdez, M.; Torres, J.; Ramos-Torres, C.; Martínez-Gutiérrez, H.; Torres-Torres, C. Photo-induced structured waves by nanostructured topological insulator Bi2Te3. Opt. Laser Technol. 2021, 140, 107015. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zivieri, R.; Lumetti, S.; Létang, J. High-Mobility Topological Semimetals as Novel Materials for Huge Magnetoresistance Effect and New Type of Quantum Hall Effect. Materials 2023, 16, 7579. https://doi.org/10.3390/ma16247579
Zivieri R, Lumetti S, Létang J. High-Mobility Topological Semimetals as Novel Materials for Huge Magnetoresistance Effect and New Type of Quantum Hall Effect. Materials. 2023; 16(24):7579. https://doi.org/10.3390/ma16247579
Chicago/Turabian StyleZivieri, Roberto, Stefano Lumetti, and Jérémy Létang. 2023. "High-Mobility Topological Semimetals as Novel Materials for Huge Magnetoresistance Effect and New Type of Quantum Hall Effect" Materials 16, no. 24: 7579. https://doi.org/10.3390/ma16247579
APA StyleZivieri, R., Lumetti, S., & Létang, J. (2023). High-Mobility Topological Semimetals as Novel Materials for Huge Magnetoresistance Effect and New Type of Quantum Hall Effect. Materials, 16(24), 7579. https://doi.org/10.3390/ma16247579






