A Review on Nonlocal Theories in Fatigue Assessment of Solids
Abstract
1. Introduction
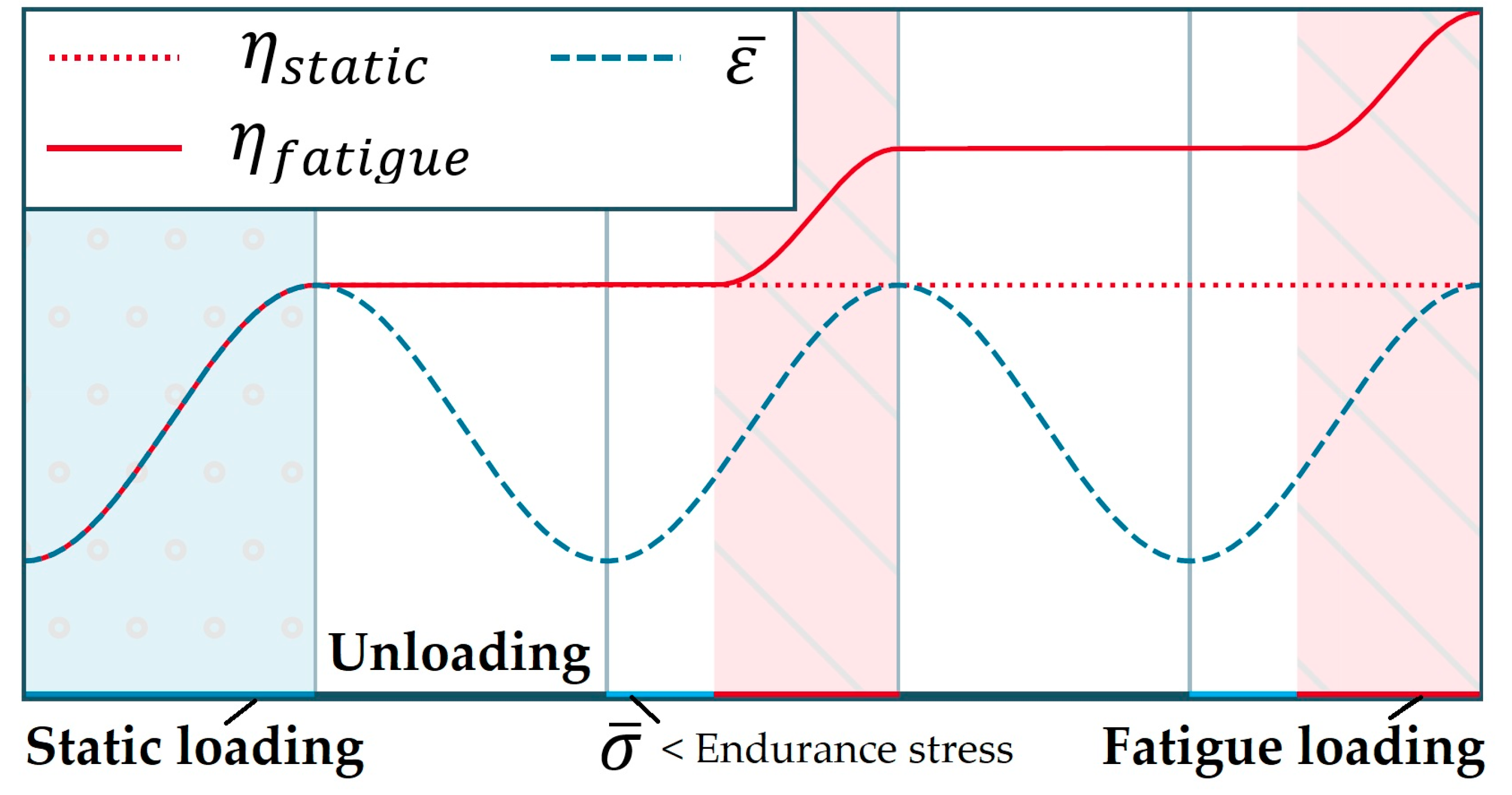
2. Nonlocal Theories in Fatigue Evaluation
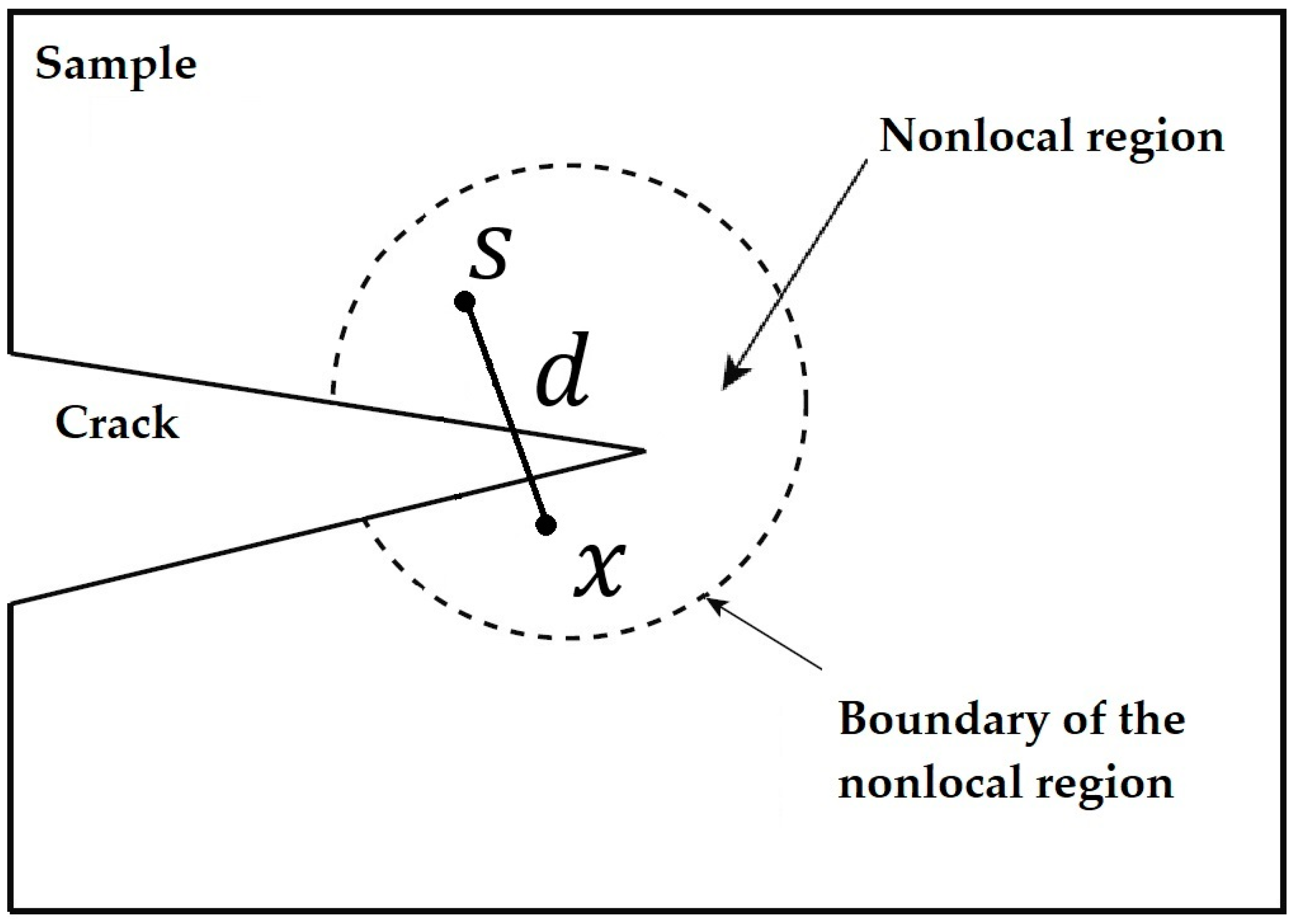
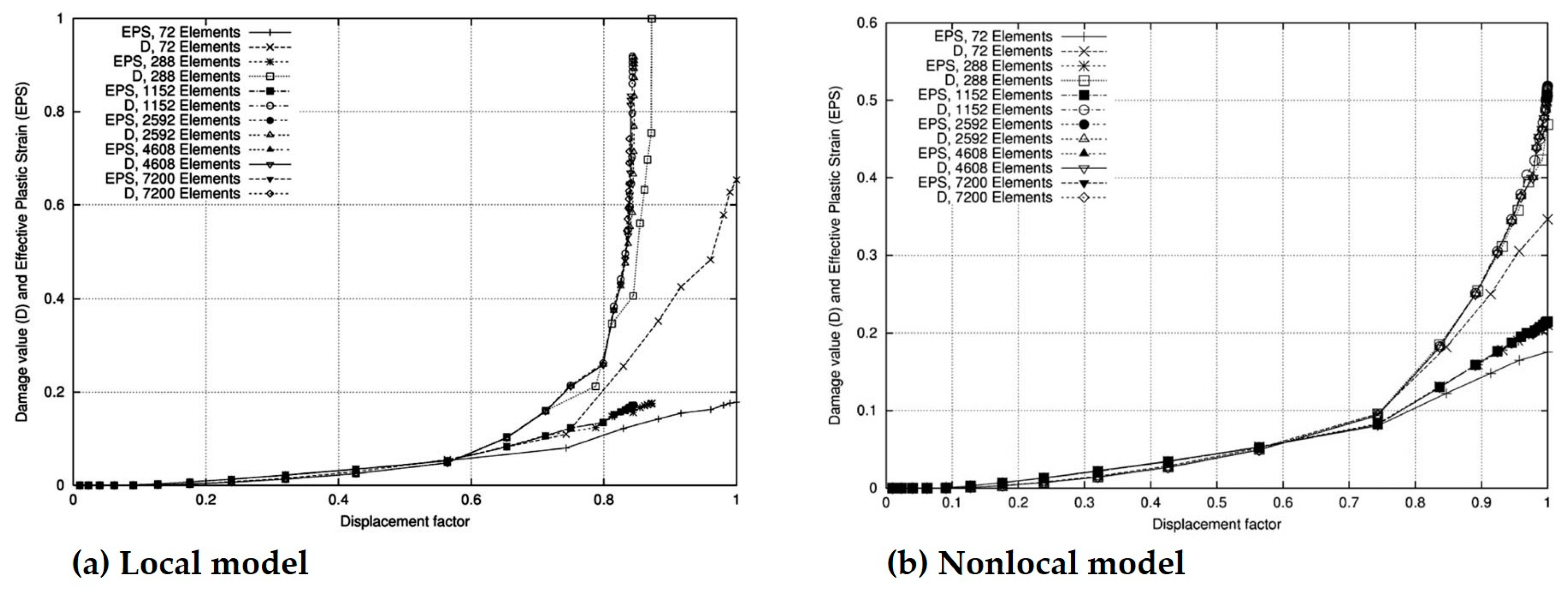
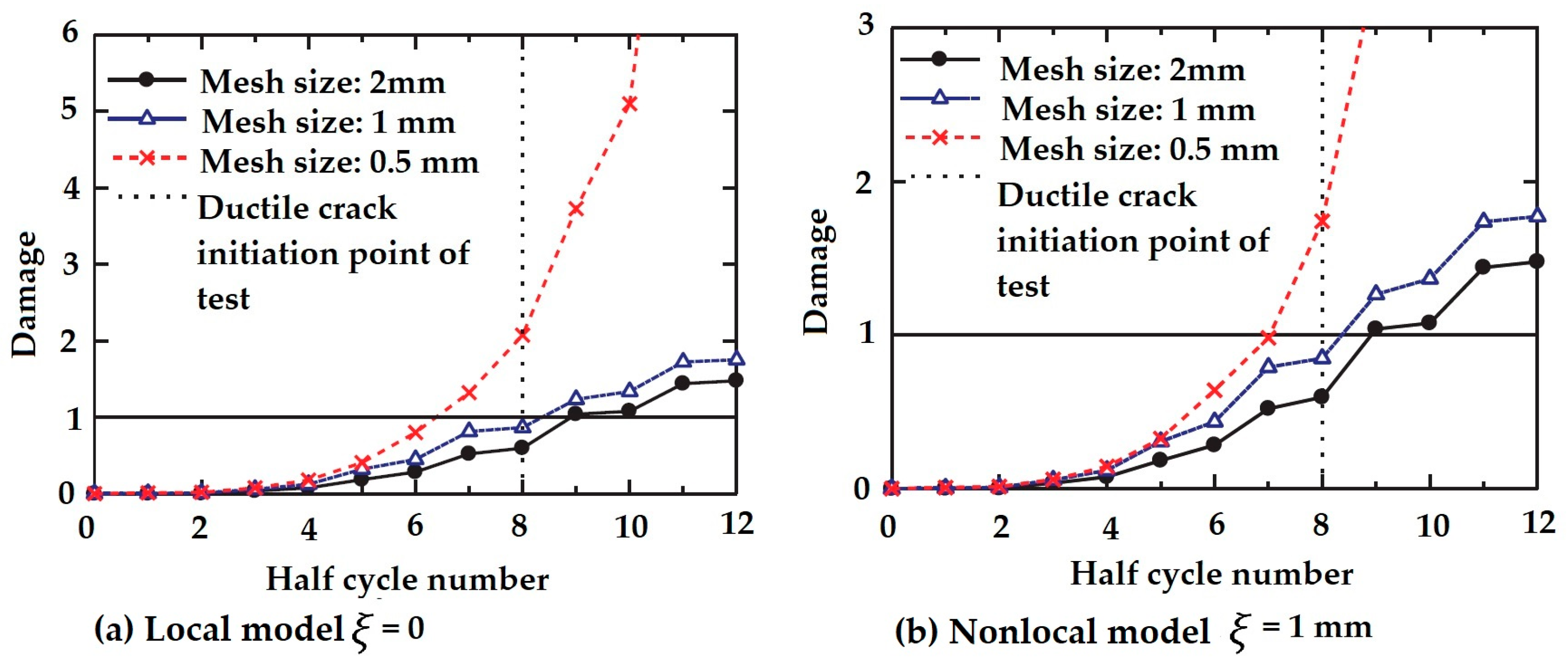
2.1. Nonlocal Continuum Damage Model
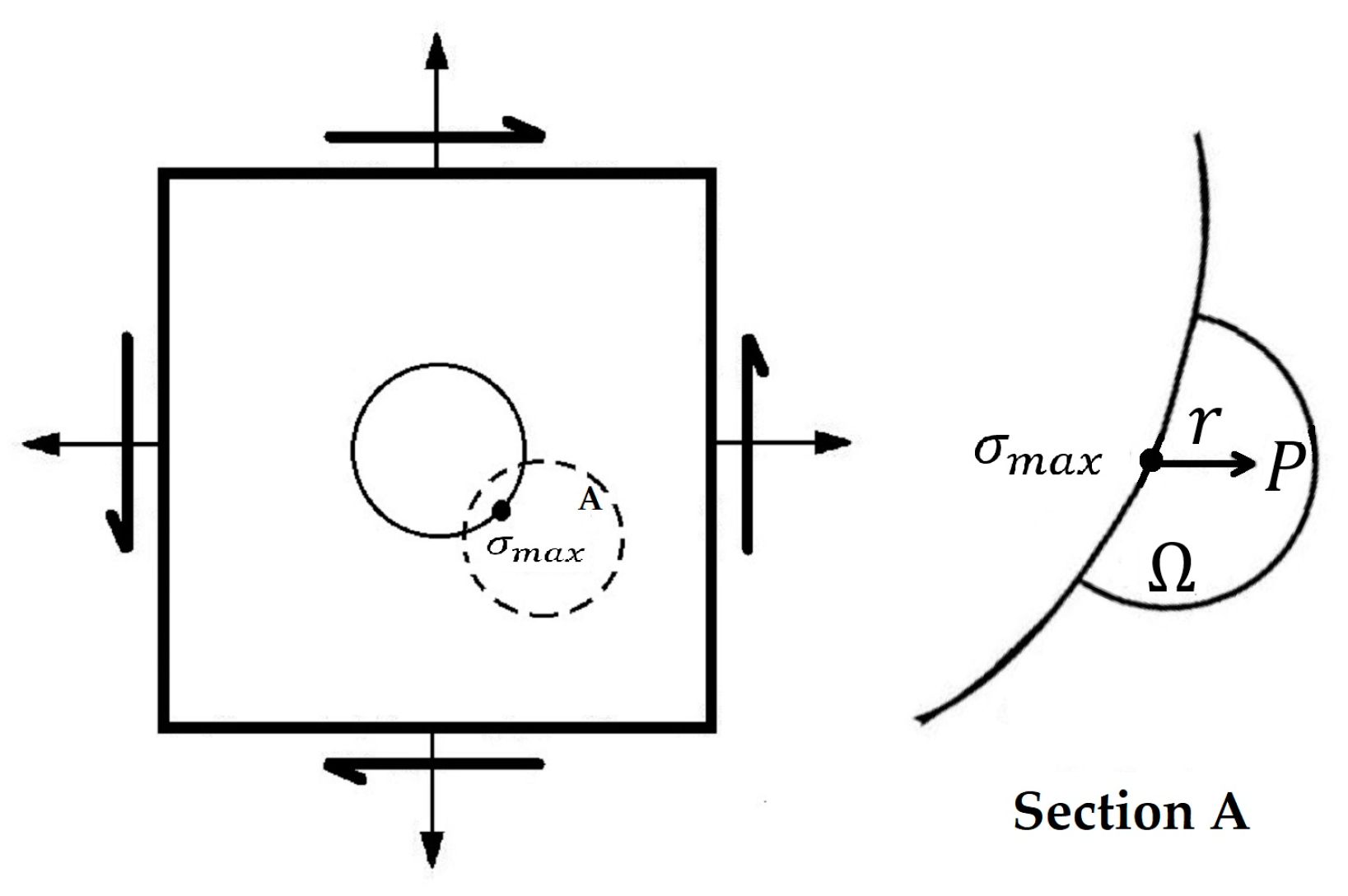
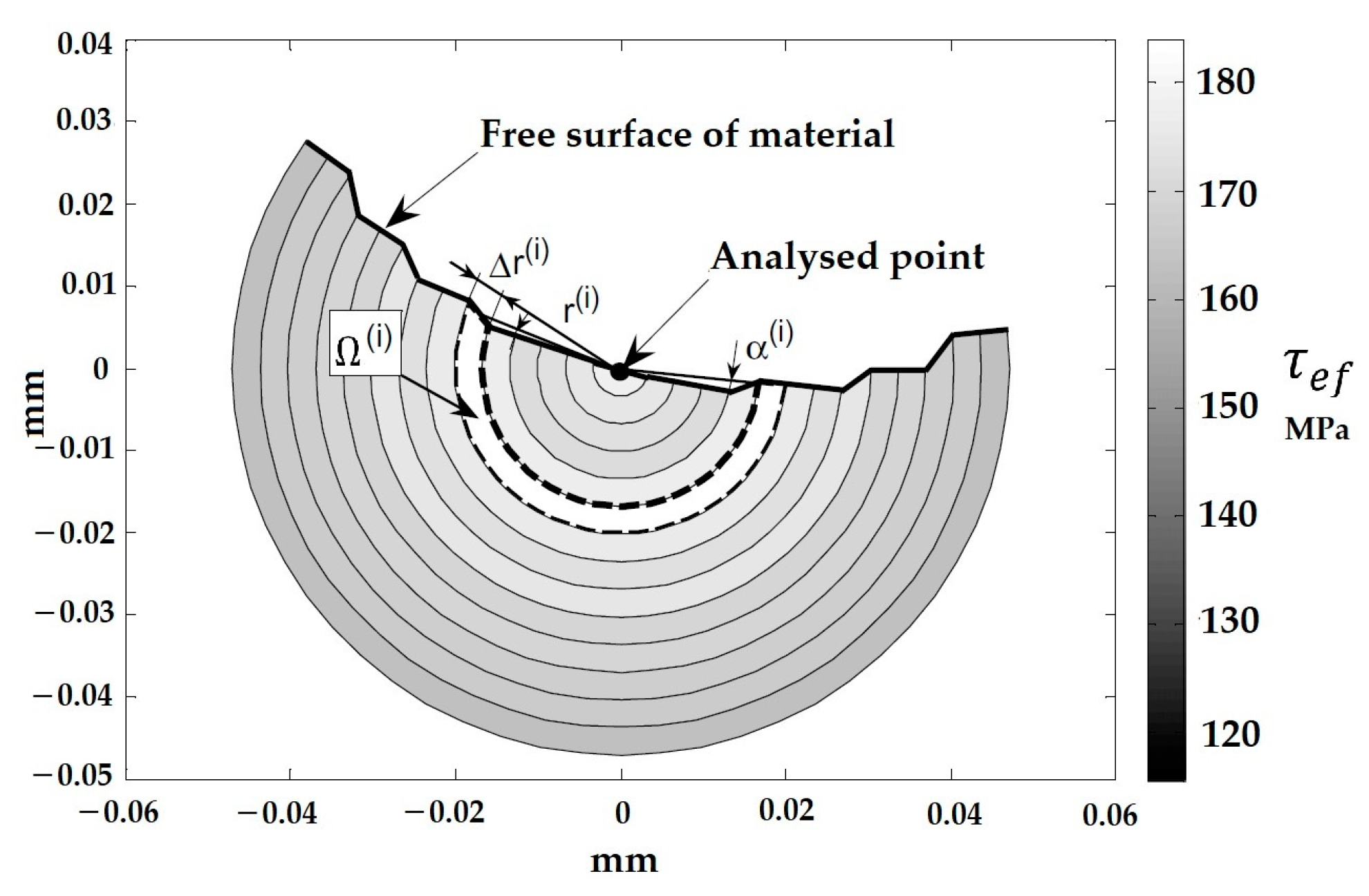
2.2. Stress Field Intensity Factor
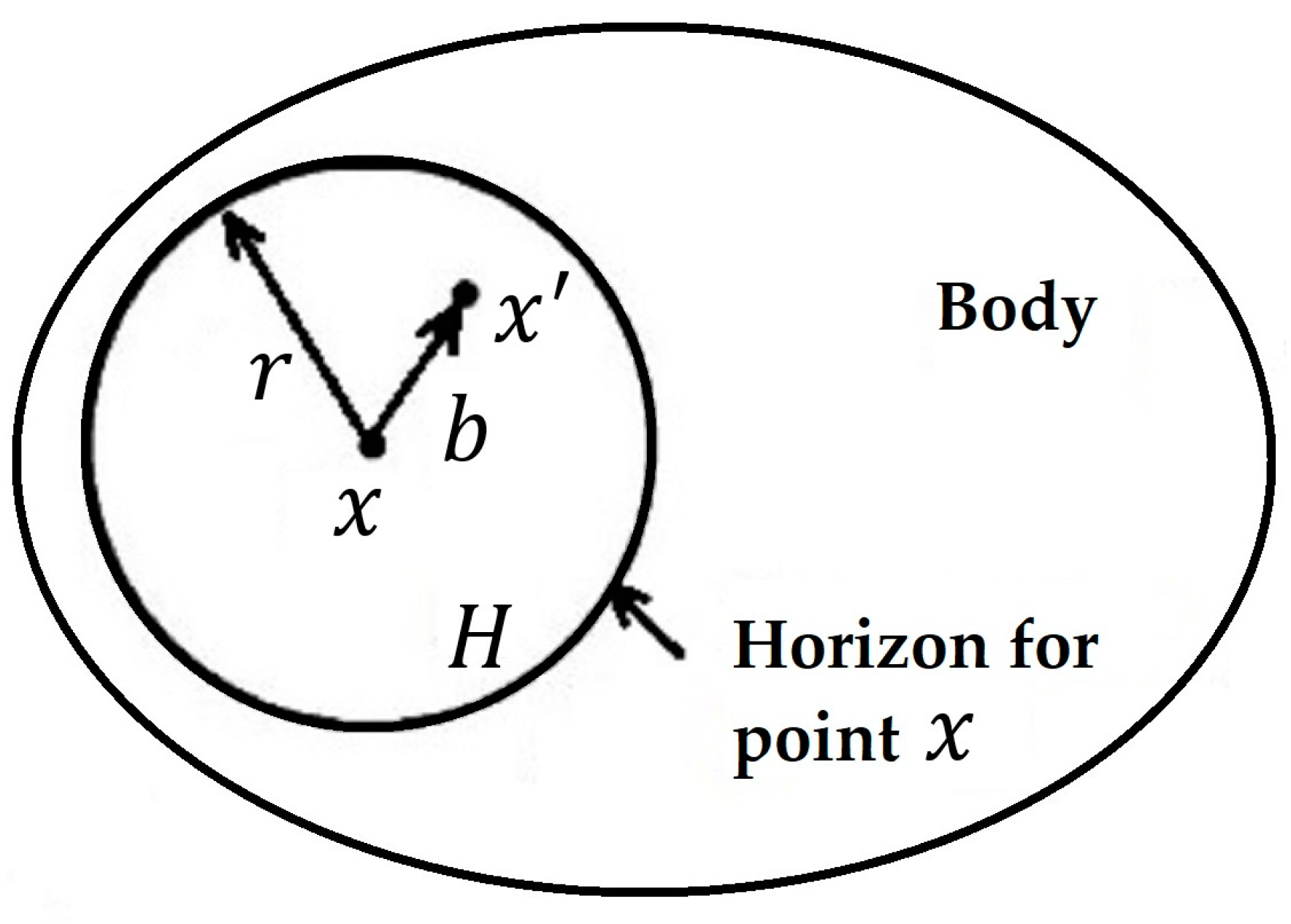
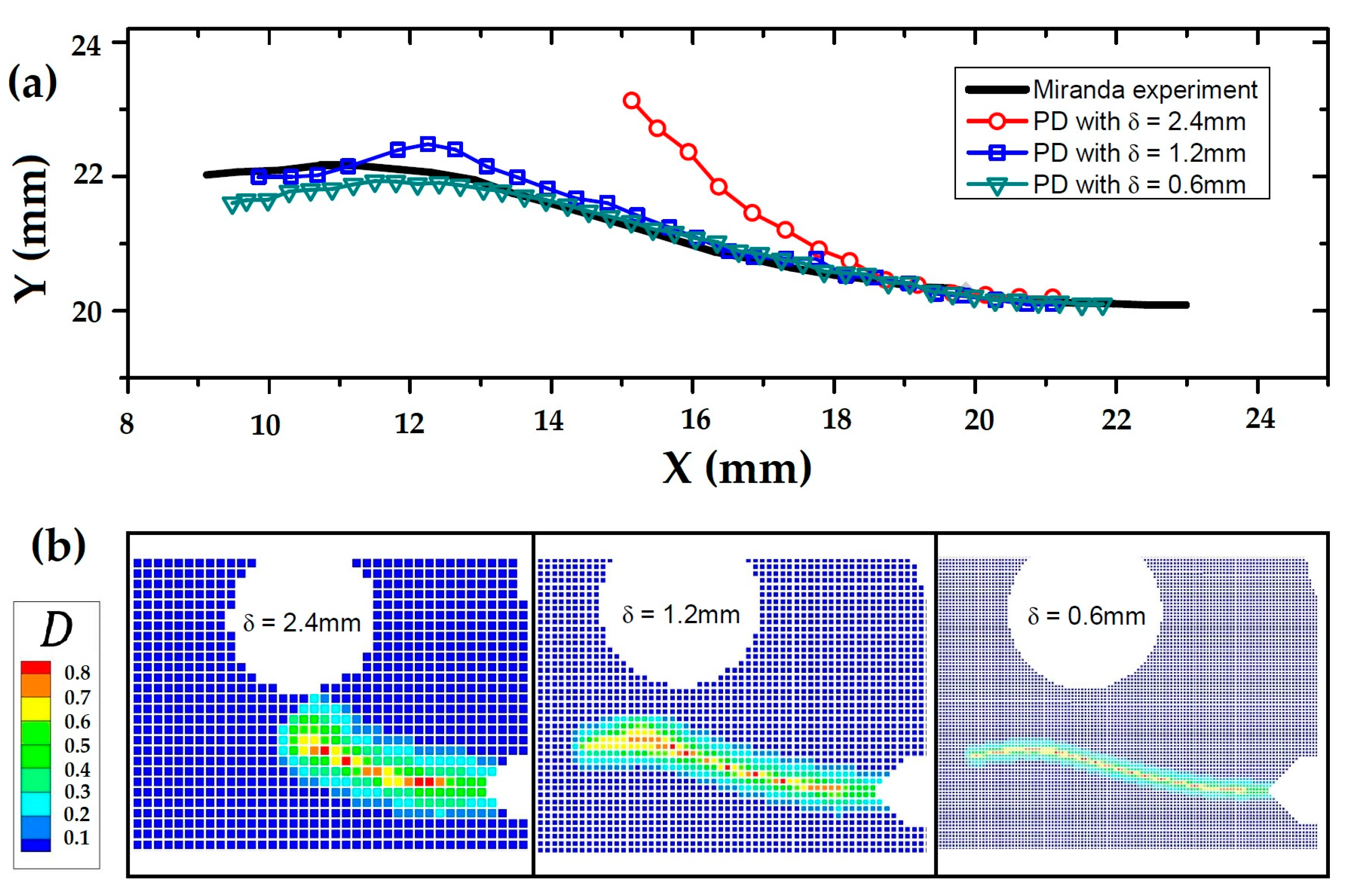
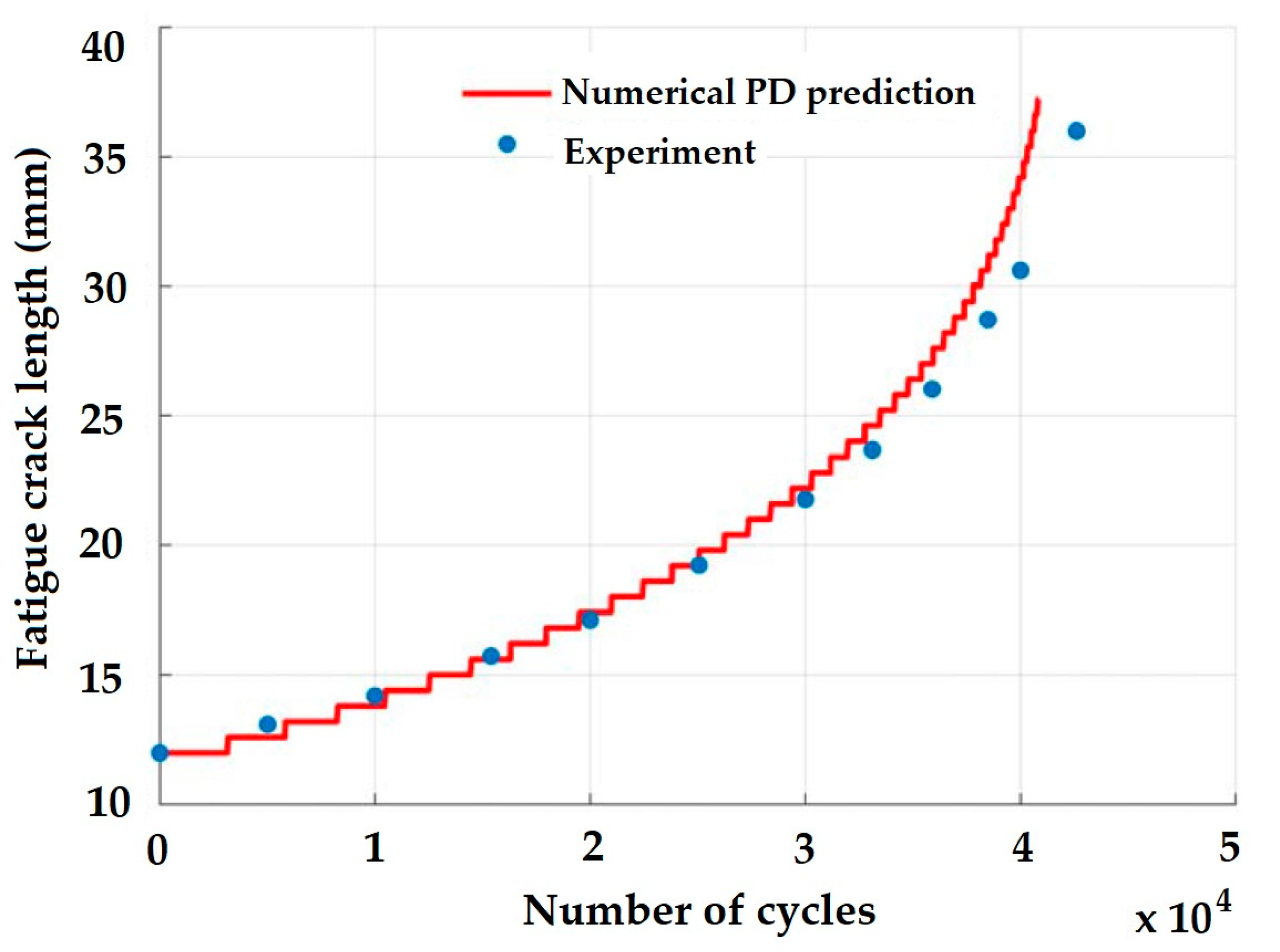
2.3. Peridynamics Model
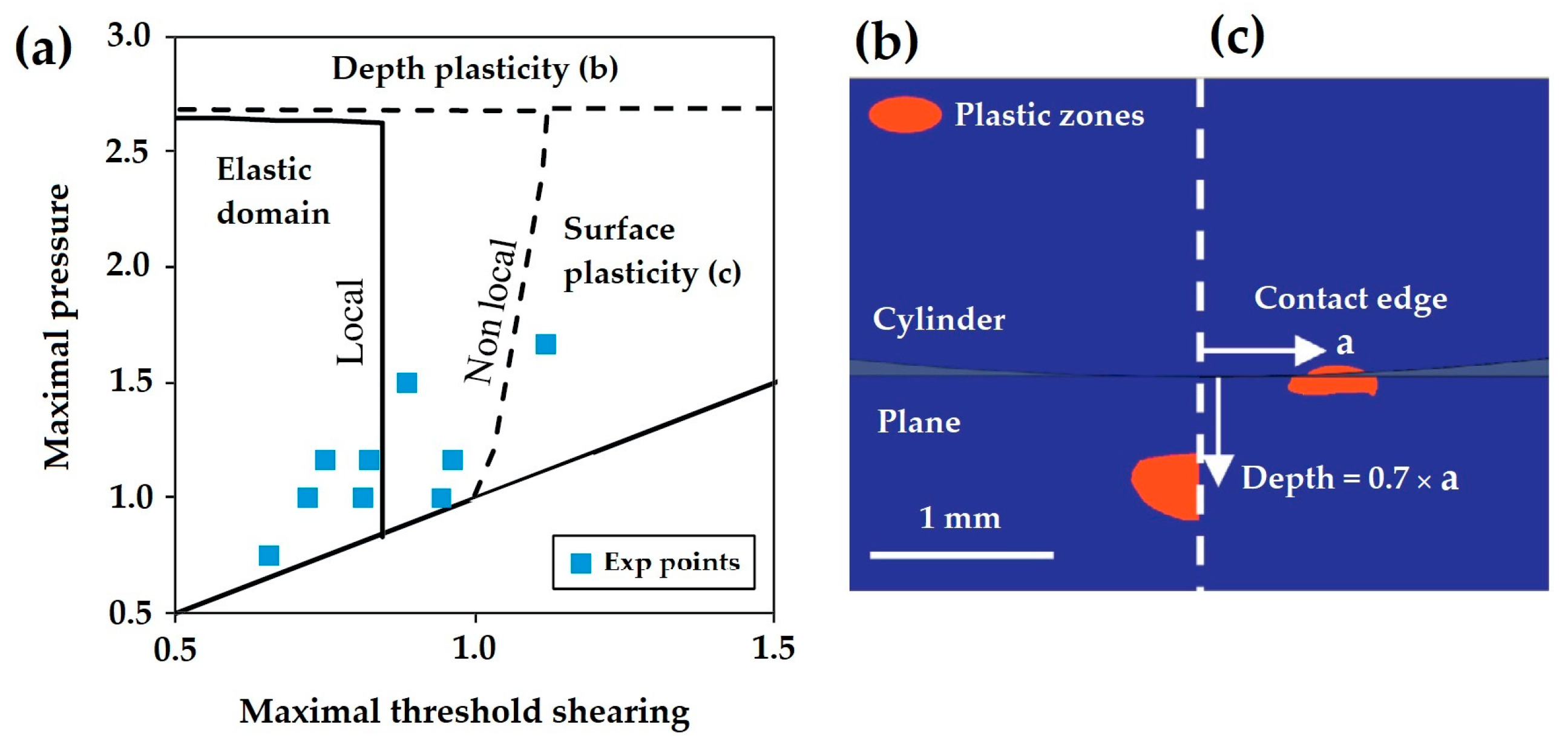
2.4. Elastic-Plastic Models
2.5. Energy-Based Nonlocal Models
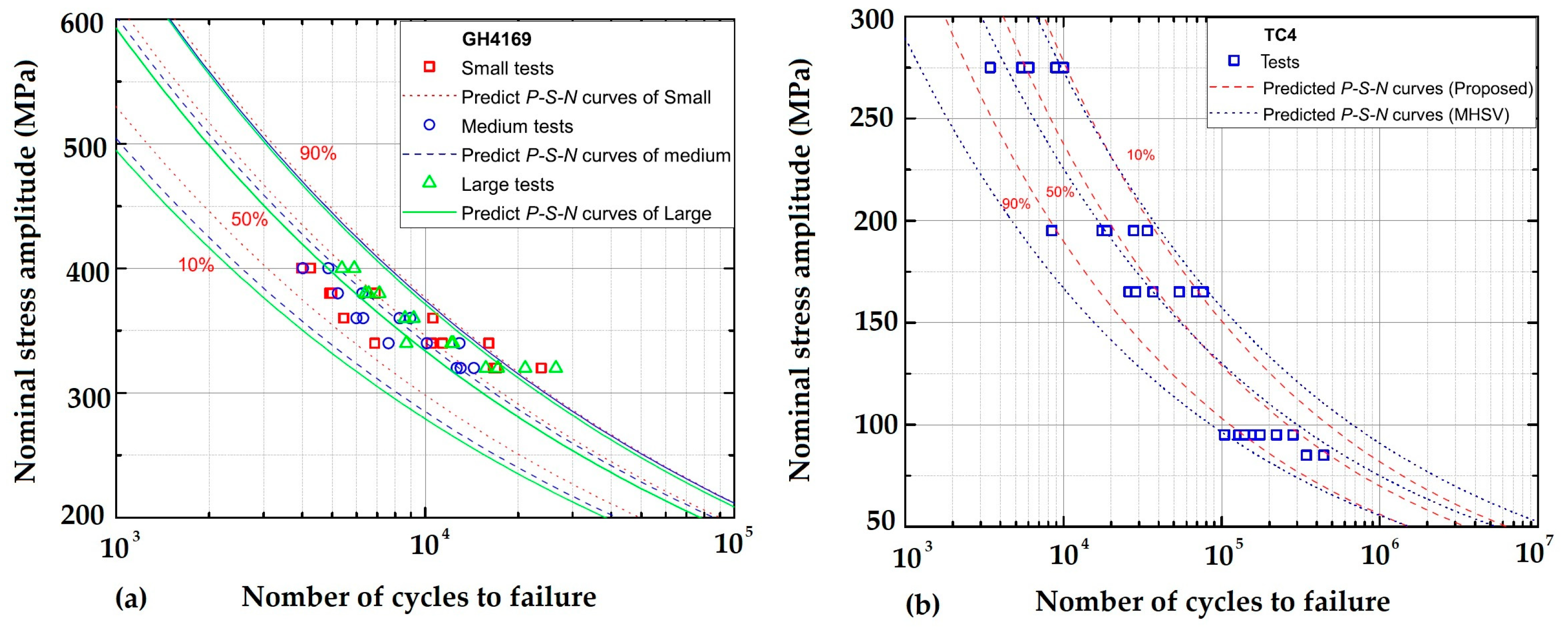
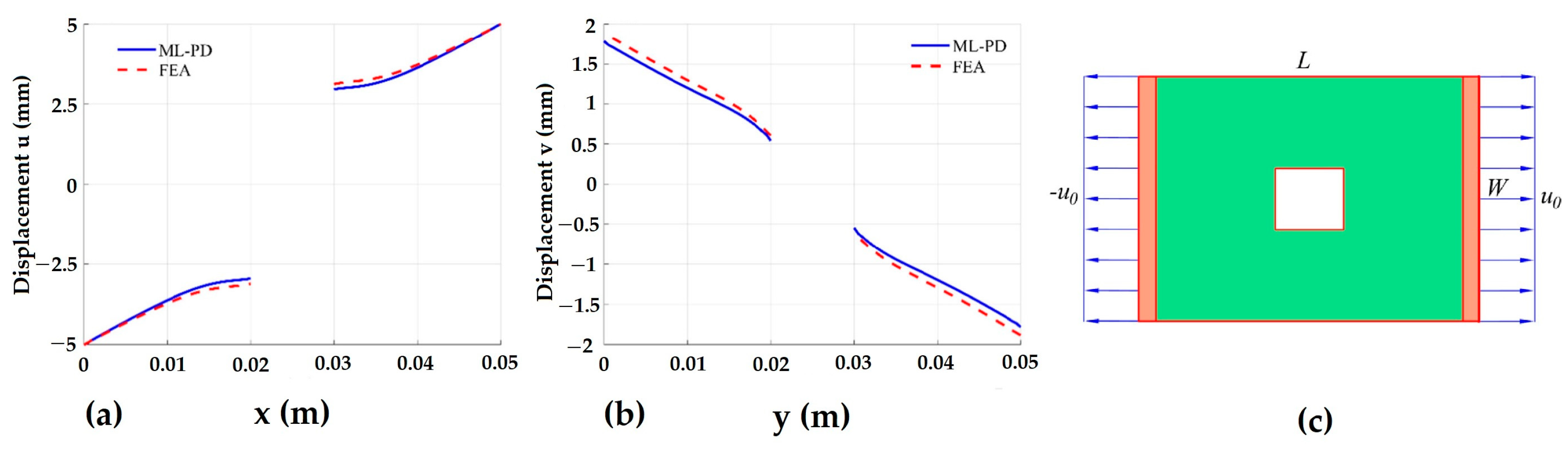
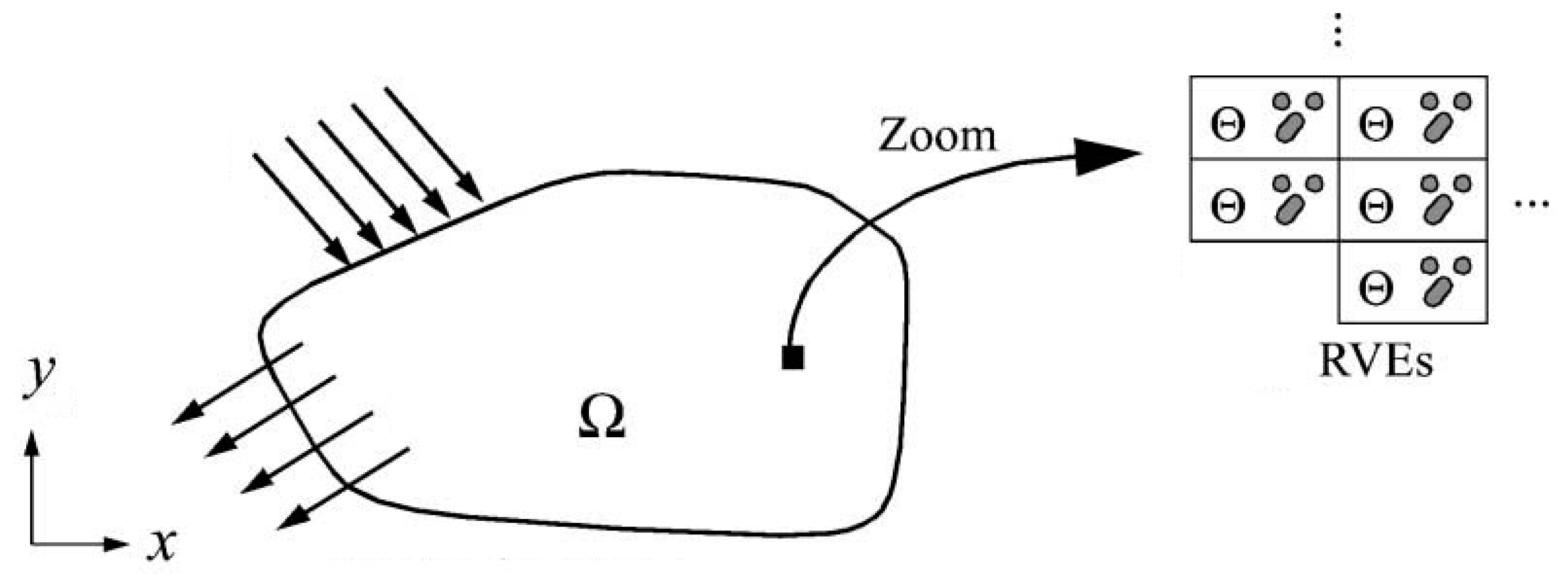
2.6. Nonlocal Multiscale Model
3. Extension of Nonlocal Models
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, Z.; Berto, F.; Hong, Y.; Susmel, L. Comparison of TCD and SED Methods in Fatigue Lifetime Assessment. Int. J. Fatigue 2019, 123, 105–134. [Google Scholar] [CrossRef]
- Orenes Moreno, B.; Bessone, A.; Solazzi, S.; Vanti, F.; Bagnera, F.; Riva, A.; Botto, D. Linear Elastic Fracture Mechanics Assessment of a Gas Turbine Vane. Materials 2022, 15, 4694. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Z.; Zhong, Z.; Huang, Y. Fatigue Factor Assessment and Life Prediction of Concrete Based on Bayesian Regularized BP Neural Network. Materials 2022, 15, 4491. [Google Scholar] [CrossRef]
- Masoudi Nejad, R.; Berto, F. Fatigue Fracture and Fatigue Life Assessment of Railway Wheel Using Non-linear Model for Fatigue Crack Growth. Int. J. Fatigue 2021, 153, 106516. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Ai, Y.; Liao, D.; Correia, J.A.F.O.; De Jesus, A.M.P.; Wang, Q. Recent Advances on Size Effect in Metal Fatigue under Defects: A Review. Int. J. Fract. 2022, 234, 21–43. [Google Scholar] [CrossRef]
- Ye, X.W.; Su, Y.H.; Han, J.P. A State-of-the-Art Review on Fatigue Life Assessment of Steel Bridges. Math. Probl. Eng. 2014, 2014, 956473. [Google Scholar] [CrossRef]
- Chin, C.H.; Abdullah, S.; Singh, S.S.K.; Ariffin, A.K.; Schramm, D. On the Need to Evaluate the Probabilistic of Fatigue Life Assessment of Random Strain Loading Considering Load Sequence Effects. Eng. Fail. Anal. 2023, 145, 107013. [Google Scholar] [CrossRef]
- Civalek, Ö.; Uzun, B.; Yaylı, M.Ö. Nonlocal Free Vibration of Embedded Short-Fiber-Reinforced Nano-/Micro-Rods with Deformable Boundary Conditions. Materials 2022, 15, 6803. [Google Scholar] [CrossRef]
- Shi, F.; Fantuzzi, N.; Trovalusci, P.; Li, Y.; Wei, Z. Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum. Materials 2022, 15, 6196. [Google Scholar] [CrossRef]
- Moghtaderi, S.H.; Faghidian, S.A.; Asghari, M. Nonlinear Vibrations of Gradient and Nonlocal Elastic Nano-Bars. Mech. Based Des. Struct. Mach. 2020, 15, 1–19. [Google Scholar] [CrossRef]
- Hrytsyna, O.R. Applications of the Local Gradient Elasticity to the Description of the Size Effect of Shear Modulus. SN Appl. Sci. 2020, 2, 1453. [Google Scholar] [CrossRef]
- Tang, F.; He, S.; Shi, S.; Xue, S.; Dong, F.; Liu, S. Analysis of Size-Dependent Linear Static Bending, Buckling, and Free Vibration Based on a Modified Couple Stress Theory. Materials 2022, 15, 7583. [Google Scholar] [CrossRef]
- Krysko, A.v.; Papkova, I.v.; Rezchikov, A.F.; Krysko, V.A. A New Mathematical Model of Functionally Graded Porous Euler–Bernoulli Nanoscaled Beams Taking into Account Some Types of Nonlinearities. Materials 2022, 15. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. Theory of Nonlocal Elasticity and Some Applications; Princeton University: Princeton, NJ, UAS, 1984. [Google Scholar]
- Fazlali, M.; Moghtaderi, S.H.; Faghidian, S.A. Nonlinear Flexure Mechanics of Beams: Stress Gradient and Nonlocal Integral Theory. Mater. Res. Express 2021, 8, 035011. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal Nonlinear Formulations for Bending of Classical and Shear Deformation Theories of Beams and Plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal Theories for Bending, Buckling and Vibration of Beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Reddy, J.N.; Pang, S.D. Nonlocal Continuum Theories of Beams for the Analysis of Carbon Nanotubes. J. Appl. Phys. 2008, 103, 023511. [Google Scholar] [CrossRef]
- Ni, Z.; Xiong, T.; Lei, J.; Wang, L.; Gao, T.; Yu, J.; Mi, C. Life Prediction Method of Dissimilar Lightweight Materials Welded Joints with Precrack under Coupled Impact-Fatigue Loading. Materials 2022, 15, 5077. [Google Scholar] [CrossRef]
- Choi, W.K.; Ha, S.; Kim, J.C.; Park, J.C.; Gong, A.; Kim, T.W. Oxidation Damage Evolution in Low-Cycle Fatigue Life of Niobium-Stabilized Austenitic Stainless Steel. Materials 2022, 15, 4073. [Google Scholar] [CrossRef]
- Strohmann, T.; Breitbarth, E.; Besel, M.; Zaunschirm, S.; Witulski, T.; Requena, G. Damage Mechanisms and Anisotropy of an AA7010-T7452 Open-Die Forged Alloy: Fatigue Crack Propagation. Materials 2022, 15, 3771. [Google Scholar] [CrossRef]
- Sheng, J.; Yu, Z.; Dou, G.; Liu, H. Fatigue Damage Behaviors of TRC-Strengthened RC Beams. Materials 2022, 15, 5113. [Google Scholar] [CrossRef] [PubMed]
- Pijaudier-Cabot, G.; Bažant, Z.P. Nonlocal Damage Theory. J. Eng. Mech. 1987, 113, 1512–1533. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Pijaudier-Cabot, G. Nonlocal Continuum Damage, Localization Instability and Convergence. J. Appl. Mech. 1988, 55, 287–293. [Google Scholar] [CrossRef]
- Jirásek, M. Nonlocal Models for Damage and Fracture: Comparison of Approaches. Int. J. Solids Struct. 1998, 35, 4133–4145. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Brekelmans, W.A.M.; de Borst, R.; Geers, M.G.D. Gradient-Enhanced Damage Modelling of High-Cycle Fatigue. Int. J. Numer. Methods Eng. 2000, 49, 1547–1569. [Google Scholar] [CrossRef]
- de Borst, R.; Geers, M.G.D.; Peerlings, R.H.J.; Benallal, A. Some Remarks on Gradient and Nonlocal Damage Theories; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A Critical Comparison of Nonlocal and Gradient-Enhanced Softening Continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; de Borst, R.; Brekelmans, W.A.M.; Geers, M.G.D. Localisation Issues in Local and Nonlocal Continuum Approaches to Fracture. Eur. J. Mech. A Solids 2002, 21, 175–189. [Google Scholar] [CrossRef]
- Borino, G.; Failla, B.; Parrinello, F. A Symmetric Nonlocal Damage Theory. Int. J. Solids Struct. 2003, 40, 3621–3645. [Google Scholar] [CrossRef]
- Bodin, D.; Pijaudier-Cabot, G.; de La Roche, C.; Piau, J.-M.; Chabot, A. Continuum Damage Approach to Asphalt Concrete Fatigue Modeling. J. Eng. Mech. 2004, 130, 700–708. [Google Scholar] [CrossRef]
- Bodin, D.; de La Roche, C.; Pijaudier-Cabot, G. Size Effect Regarding Fatigue Evaluation of Asphalt Mixtures: Laboratory Cantilever Bending Tests. Road Mater. Pavement Des. 2006, 7, 181–200. [Google Scholar] [CrossRef]
- César de Sá, J.M.A.; Areias, P.M.A.; Zheng, C. Damage Modelling in Metal Forming Problems Using an Implicit Non-Local Gradient Model. Comput. Methods Appl. Mech. Eng. 2006, 195, 6646–6660. [Google Scholar] [CrossRef]
- Ubachs, R.L.J.M.; Schreurs, P.J.G.; Geers, M.G.D. Elasto-Viscoplastic Nonlocal Damage Modelling of Thermal Fatigue in Anisotropic Lead-Free Solder. Mech. Mater. 2007, 39, 685–701. [Google Scholar] [CrossRef]
- Desmorat, R.; Gatuingt, F.; Ragueneau, F. Nonlocal Anisotropic Damage Model and Related Computational Aspects for Quasi-Brittle Materials. Eng. Fract. Mech. 2007, 74, 1539–1560. [Google Scholar] [CrossRef]
- Tovo, R.; Livieri, P. An Implicit Gradient Application to Fatigue of Sharp Notches and Weldments. Eng. Fract. Mech. 2007, 74, 515–526. [Google Scholar] [CrossRef]
- Mallardo, V. Integral Equations and Nonlocal Damage Theory: A Numerical Implementation Using the BDEM. Int. J. Fract. 2009, 157, 13–32. [Google Scholar] [CrossRef]
- Kang, L.; Ge, H. Predicting Ductile Crack Initiation of Steel Bridge Structures Due to Extremely Low-Cycle Fatigue Using Local and Non-Local Models. J. Earthq. Eng. 2013, 17, 323–349. [Google Scholar] [CrossRef]
- Lorentz, E. A Nonlocal Damage Model for Plain Concrete Consistent with Cohesive Fracture. Int. J. Fract. 2017, 207, 123–159. [Google Scholar] [CrossRef]
- Nguyen, H.T.T.; Nguyen, N.H. Using a Non-Local Elastic Damage Model to Predict the Fatigue Life of Asphalt Pavement Structure. In Lecture Notes in Mechanical Engineering; Pleiades Publishing: New York, NY, USA, 2018; Volume PartF3, pp. 47–63. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Q.; Wu, D.; Gao, W.; Tin-Loi, F. Stochastic Nonlocal Damage Analysis by a Machine Learning Approach. Comput. Methods Appl. Mech. Eng. 2020, 372, 113371. [Google Scholar] [CrossRef]
- Livieri, P.; Tovo, R. Overview of the Geometrical Influence on the Fatigue Strength of Steel Butt Welds by a Nonlocal Approach. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 502–514. [Google Scholar] [CrossRef]
- Livieri, P.; Tovo, R. Fatigue Strength of Aluminium Welded Joints by a Non-Local Approach. Int. J. Fatigue 2021, 143, 106000. [Google Scholar] [CrossRef]
- Titscher, T.; Unger, J.F. Efficient Higher-Order Cycle Jump Integration of a Continuum Fatigue Damage Model. Int. J. Fatigue 2020, 141, 105863. [Google Scholar] [CrossRef]
- Mareau, C. A Non-Local Damage Model for the Fatigue Behaviour of Metallic Polycrystals. Philos. Mag. 2020, 100, 955–981. [Google Scholar] [CrossRef]
- Pandey, V.B.; Samant, S.S.; Singh, I.V.; Mishra, B.K. An Improved Methodology Based on Continuum Damage Mechanics and Stress Triaxiality to Capture the Constraint Effect during Fatigue Crack Propagation. Int. J. Fatigue 2020, 140, 105823. [Google Scholar] [CrossRef]
- Kamei, K.; Khan, M.A. Current Challenges in Modelling Vibrational Fatigue and Fracture of Structures: A Review. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 77. [Google Scholar] [CrossRef]
- Reiner, J. A Practical Approach for the Non-Local Simulation of Progressive Damage in Quasi-Isotropic Fibre-Reinforced Composite Laminates. Compos. Struct. 2021, 265, 113761. [Google Scholar] [CrossRef]
- Soni, A.; Negi, A.; Kumar, S.; Kumar, N. An IGA Based Nonlocal Gradient-Enhanced Damage Model for Failure Analysis of Cortical Bone. Eng. Fract. Mech. 2021, 255, 107976. [Google Scholar] [CrossRef]
- Huang, J.S.; Liew, J.X.; Liew, K.M. Data-Driven Machine Learning Approach for Exploring and Assessing Mechanical Properties of Carbon Nanotube-Reinforced Cement Composites. Compos. Struct. 2021, 267. [Google Scholar] [CrossRef]
- Weixing, Y. Stress Field Intensity Approach for Predicting Fatigue Life. Int. J. Fatigue 1993, 15, 243–246. [Google Scholar] [CrossRef]
- Qylafku, G.; Azari, Z.; Kadi, N.; Gjonaj, M.; Pluvinage, G. Application of a New Model Proposal for Fatigue Life Prediction on Notches and Key-Seats. Int. J. Fatigue 1999, 21, 753–760. [Google Scholar] [CrossRef]
- Morel, F.; Palin-Luc, T. A Non-Local Theory Applied to High Cycle Multiaxial Fatigue. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 649–665. [Google Scholar] [CrossRef]
- Wormsen, A.; Sjödin, B.; Härkegård, G.; Fjeldstad, A. Non-Local Stress Approach for Fatigue Assessment Based on Weakest-Link Theory and Statistics of Extremes. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 1214–1227. [Google Scholar] [CrossRef]
- Chamat, A.; Abbadi, M.; Gilgert, J.; Cocheteux, F.; Azari, Z. A New Non-Local Criterion in High-Cycle Multiaxial Fatigue for Non-Proportional Loadings. Int. J. Fatigue 2007, 29, 1465–1474. [Google Scholar] [CrossRef]
- Karolczuk, A. Non-Local Area Approach to Fatigue Life Evaluation under Combined Reversed Bending and Torsion. Int. J. Fatigue 2008, 30, 1985–1996. [Google Scholar] [CrossRef]
- Karolczuk, A.; Nadot, Y.; Dragon, A. Non-Local Stress Gradient Approach for Multiaxial Fatigue of Defective Material. Comput. Mater. Sci. 2008, 44, 464–475. [Google Scholar] [CrossRef]
- Karolczuk, A.; Blacha. Fatigue Life Estimation under Variable Amplitude Bending Using the Non-Local Damage Parameter and Multisurface Plasticity Model. Int. J. Fatigue 2011, 33, 1376–1383. [Google Scholar] [CrossRef]
- Marmi, A.K.; Habraken, A.M.; Duchene, L. Multiaxial Fatigue Damage Modelling at Macro Scale of Ti-6Al-4V Alloy. Int. J. Fatigue 2009, 31, 2031–2040. [Google Scholar] [CrossRef]
- Zhang, G. Method of Effective Stress for Fatigue: Part i—A General Theory. Int. J. Fatigue 2012, 37, 17–23. [Google Scholar] [CrossRef]
- Ferré, R.; Fouvry, S.; Berthel, B.; Ruiz-Sabariego, J.A. Stress Gradient Effect on the Crack Nucleation Process of a Ti-6Al-4V Titanium Alloy under Fretting Loading: Comparison between Non-Local Fatigue Approaches. Int. J. Fatigue 2013, 54, 56–67. [Google Scholar] [CrossRef]
- Baumgartner, J.; Schmidt, H.; Ince, E.; Melz, T.; Dilger, K. Fatigue Assessment of Welded Joints Using Stress Averaging and Critical Distance Approaches. Weld. World 2015, 59, 731–742. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Liao, D.; Niu, X.P. Probabilistic Fatigue Assessment of Notched Components under Size Effect Using Critical Distance Theory. Eng. Fract. Mech. 2020, 235, 107150. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.P.; Keshtegar, B.; Qian, G.; Wang, Q. Probabilistic Framework for Fatigue Life Assessment of Notched Components under Size Effects. Int. J. Mech. Sci. 2020, 181, 105685. [Google Scholar] [CrossRef]
- Kang, G.; Luo, H. Review on Fatigue Life Prediction Models of Welded Joint. Acta Mech. Sin. 2020, 36, 701–726. [Google Scholar] [CrossRef]
- Mei, J.; Xing, S.; Vasu, A.; Chung, J.; Desai, R.; Dong, P. The Fatigue Limit Prediction of Notched Components—A Critical Review and Modified Stress Gradient Based Approach. Int. J. Fatigue 2020, 135, 105531. [Google Scholar] [CrossRef]
- Zhu, S.P.; Wu, Y.L.; Yi, X.; Fu, S.; Correia, J.A.F.O. Probabilistic Fatigue Assessment of Notched Components under Size Effect Using Generalized Weakest-Link Model. Int. J. Fatigue 2022, 162, 107005. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of Elasticity Theory for Discontinuities and Long-Range Forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A Meshfree Method Based on the Peridynamic Model of Solid Mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Littlewood, D.J. A Nonlocal Approach to Modeling Crack Nucleation in AA 7075-T651. In Mechanics of Solids, Structures and Fluids, Vibration, Acoustics and Wave Propagation; ASMEDC: New York, NY, USA, 2011; Volume 8, pp. 567–576. [Google Scholar] [CrossRef]
- Martowicz, A.; Ruzzene, M.; Staszewski, W.J.; Uhl, T. Non-Local Modeling and Simulation of Wave Propagation and Crack Growth. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2014; Volume 1581, pp. 513–520. [Google Scholar] [CrossRef]
- Zhang, G.; Le, Q.; Loghin, A.; Subramaniyan, A.; Bobaru, F. Validation of a Peridynamic Model for Fatigue Cracking. Eng. Fract. Mech. 2016, 162, 76–94. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Roy, P.; Roy, D.; Reddy, J.N. A Peridynamic Theory for Linear Elastic Shells. Int. J. Solids Struct. 2016, 84, 110–132. [Google Scholar] [CrossRef]
- Rokkam, S.; Gunzburger, M.; Brothers, M.; Phan, N.; Goel, K. A Nonlocal Peridynamics Modeling Approach for Corrosion Damage and Crack Propagation. Theor. Appl. Fract. Mech. 2019, 101, 373–387. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Oterkus, S.; Oterkus, E. An Energy-Based Peridynamic Model for Fatigue Cracking. Eng. Fract. Mech. 2021, 241, 107373. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Oterkus, S.; Oterkus, E. A Peridynamic-Based Machine Learning Model for One-Dimensional and Two-Dimensional Structures. Contin. Mech. Thermodyn. 2020. [Google Scholar] [CrossRef]
- Hattori, G.; Hobbs, M.; Orr, J. A Review on the Developments of Peridynamics for Reinforced Concrete Structures. In Archives of Computational Methods in Engineering; Springer Science and Business Media B.V.: Berlin/Heidelberg, Germany, 2021; Volume 28, pp. 4655–4686. [Google Scholar] [CrossRef]
- Ma, J.-X.; Zhou, X.-P. Data-Driven Bond-Based Peridynamics with Nonlocal Influence Function for Crack Propagation. Eng. Fract. Mech. 2022, 272, 108681. [Google Scholar] [CrossRef]
- Javili, A.; Morasata, R.; Oterkus, E.; Oterkus, S. Peridynamics Review. Math. Mech. Solids 2019, 24, 3714–3739. [Google Scholar] [CrossRef]
- Polizzotto, C. Thermodynamics and Continuum Fracture Mechanics for Nonlocal-Elastic Plastic Materials. Eur. J. Mech. A Solids 2002, 21, 85–103. [Google Scholar] [CrossRef]
- Belnoue, J.P.; Nguyen, G.D.; Korsunsky, A.M. Consistent Tangent Stiffness for Local-Nonlocal Damage Modelling of Metals. In Procedia Engineering; Elsevier Ltd.: Amsterdam, The Netherlands, 2009; Volume 1. [Google Scholar] [CrossRef]
- Boeff, M.; Gutknecht, F.; Engels, P.S.; Ma, A.; Hartmaier, A. Formulation of Nonlocal Damage Models Based on Spectral Methods for Application to Complex Microstructures. Eng. Fract. Mech. 2015, 147, 373–387. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Meng, Q. A Non-Local Approach Based on the Hypothesis of Damage Dissipation Potential Equivalence to the Effect of Stress Gradient in Fretting Fatigue. Int. J. Fatigue 2016, 90, 125–138. [Google Scholar] [CrossRef]
- Kolwankar, S.; Kanvinde, A.; Kenawy, M.; Kunnath, S. Uniaxial Nonlocal Formulation for Geometric Nonlinearity–Induced Necking and Buckling Localization in a Steel Bar. J. Struct. Eng 2017, 143, 04017091. [Google Scholar] [CrossRef]
- Banvillet, A.; Palin-Luc, T.; Lasserre, S. A Volumetric Energy Based High Cycle Multiaxial Fatigue Citerion. Int. J. Fatigue 2003, 25, 755–769. [Google Scholar] [CrossRef]
- Saintier, N.; Palin-Luc, T.; Bénabes, J.; Cocheteux, F. Non-Local Energy Based Fatigue Life Calculation Method under Multiaxial Variable Amplitude Loadings. Int. J. Fatigue 2013, 54, 68–83. [Google Scholar] [CrossRef]
- Krzyzak, D.; Łagoda, T. Fatigue Life Estimation of Notched Elements with Use of Non-Local Volumetric Method. Int. J. Fatigue 2014, 61, 59–66. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; de Castro, J.T.P.; Wu, H. Non-Linear Incremental Fatigue Damage Calculation for Multiaxial Non-Proportional Histories. Int. J. Fatigue 2017, 100, 502–511. [Google Scholar] [CrossRef]
- Maurel, V.; Köster, A.; Rémy, L.; Rambaudon, M.; Missoum-Benziane, D.; Fontanet, V.; Salgado-Goncalves, F.; Heudt, A.; Wang, H.; Trabelsi, M. Fatigue Crack Growth under Large Scale Yielding Condition: The Need of a Characteristic Length Scale. Int. J. Fatigue 2017, 102, 184–201. [Google Scholar] [CrossRef]
- Maurel, V.; Rémy, L.; Dahmen, F.; Haddar, N. An Engineering Model for Low Cycle Fatigue Life Based on a Partition of Energy and Micro-Crack Growth. Int. J. Fatigue 2009, 31, 952–961. [Google Scholar] [CrossRef]
- Raphael, I.; Saintier, N.; Rolland, H.; Robert, G.; Laiarinandrasana, L. A Mixed Strain Rate and Energy Based Fatigue Criterion for Short Fiber Reinforced Thermoplastics. Int. J. Fatigue 2019, 127, 131–143. [Google Scholar] [CrossRef]
- Maurel, V.; Chiaruttini, V.; Koster, A.; Missoum-Benziane, D. Fatigue Crack Growth under Large Scale Yielding Condition: A Tool Based on Explicit Crack Growth. J. Theor. Comput. Appl. Mech. 2022. Available online: https://hal.science/hal-03628416v2 (accessed on 30 July 2022).
- Fish, J.; Yu, Q. Computational Mechanics of Fatigue and Life Predictions for Composite Materials and Structures. Comput. Methods Appl. Mech. Eng. 2002, 191, 4827–4849. [Google Scholar] [CrossRef]
- Fish, J.; Oskay, C. A Nonlocal Multiscale Fatigue Model. Mech. Adv. Mater. Struct. 2005, 12, 485–500. [Google Scholar] [CrossRef]
- Sorić, J.; Lesičar, T.; Putar, F.; Tonković, Z. On Multiscale Damage Modelling of Heterogeneous Materials Using Nonlocal Continuum Theory. Brodogradnja 2021, 72, 121–139. [Google Scholar] [CrossRef]
- Owolabi, G.M.; Prasannavenkatesan, R.; McDowell, D.L. Probabilistic Framework for a Microstructure-Sensitive Fatigue Notch Factor. Int. J. Fatigue 2010, 32, 1378–1388. [Google Scholar] [CrossRef]
- McDowell, D.L.; Dunne, F.P.E. Microstructure-Sensitive Computational Modeling of Fatigue Crack Formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y. A Non-Local 3D Lattice Particle Framework for Elastic Solids. Int. J. Solids Struct. 2016, 81, 411–420. [Google Scholar] [CrossRef]
- Gao, Y.; Yao, H.; Wei, H.; Liu, Y. Physics-Based Deep Learning for Probabilistic Fracture Analysis of Composite Materials. In AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics Inc. (AIAA): Reston, VA, USA, 2020; Volume 1. [Google Scholar] [CrossRef]
- el May, M.; Saintier, N.; Palin-Luc, T.; Devos, O. Non-Local High Cycle Fatigue Strength Criterion for Metallic Materials with Corrosion Defects. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1017–1025. [Google Scholar] [CrossRef]
- Li, D.; Hu, D.; Wang, R.; Ma, Q.; Liu, H. A Non-Local Approach for Probabilistic Assessment of LCF Life Based on Optimized Effective-Damage-Parameter. Eng. Fract. Mech. 2018, 199, 188–200. [Google Scholar] [CrossRef]
- Suknev, S.v. Nonlocal and Gradient Fracture Criteria for Quasi-Brittle Materials under Compression. Phys. Mesomech. 2019, 22, 504–513. [Google Scholar] [CrossRef]
- Nguyen, G.D.; Korsunsky, A.M.; Belnoue, J.P.H. A Nonlocal Coupled Damage-Plasticity Model for the Analysis of Ductile Failure. Int. J. Plast. 2015, 64, 56–75. [Google Scholar] [CrossRef]
- Khodabakhshi, P.; Reddy, J.N.; Srinivasa, A. GraFEA: A Graph-based Finite Element approach for the Study of Damage and Fracture in Brittle Materials. Meccanica 2016, 51, 3129–3147. [Google Scholar] [CrossRef]
- Khodabakhshi, P.; Reddy, J.N.; Srinivasa, A. A Nonlocal Fracture Criterion and Its Effect on the Mesh Dependency of GraFEA. Acta Mech. 2019, 230, 3593–3612. [Google Scholar] [CrossRef]
- Alebrahim, R.; Thamburaja, P.; Srinivasa, A.; Reddy, J.N. A Robust Moore–Penrose Pseudoinverse-Based Static Finite-Element Solver for Simulating Non-Local Fracture in Solids. Comput. Methods Appl. Mech. Eng. 2023, 403, 115727. [Google Scholar] [CrossRef]
- Shin, H.Y.; Thamburaja, P.; Srinivasa, A.R.; Reddy, J.N. Modeling Impact Fracture in a Quasi-Brittle Solids Using a 3D Nonlocal Graph-Based Finite Element Analysis: Theory, Finite Element Simulations, and Experimental Verification. J. Mech. Phys. Solids 2023, 170, 105097. [Google Scholar] [CrossRef]
- Shin, H.Y.; Thamburaja, P.; Srinivasa, A.; Reddy, J.N. On Simulating Impact Fracture in High-Strength Concrete Using GraFEA. Extrem. Mech. Lett. 2022, 52, 101618. [Google Scholar] [CrossRef]
- Thamburaja, P.; Sarah, K.; Srinivasa, A.; Reddy, J.N. Fracture of Viscoelastic Materials: FEM Implementation of a Non-local & Rate Form-based Finite-deformation Constitutive Theory. Comput. Methods Appl. Mech. Eng. 2019, 354, 871–903. [Google Scholar] [CrossRef]
- Sarah, K.; Thamburaja, P.; Srinivasa, A.; Reddy, J.N. Numerical Simulations of Damage and Fracture in Viscoelastic Solids Using a Nonlocal Fracture Criterion. Mech. Adv. Mater. Struct. 2020, 27, 1085–1097. [Google Scholar] [CrossRef]
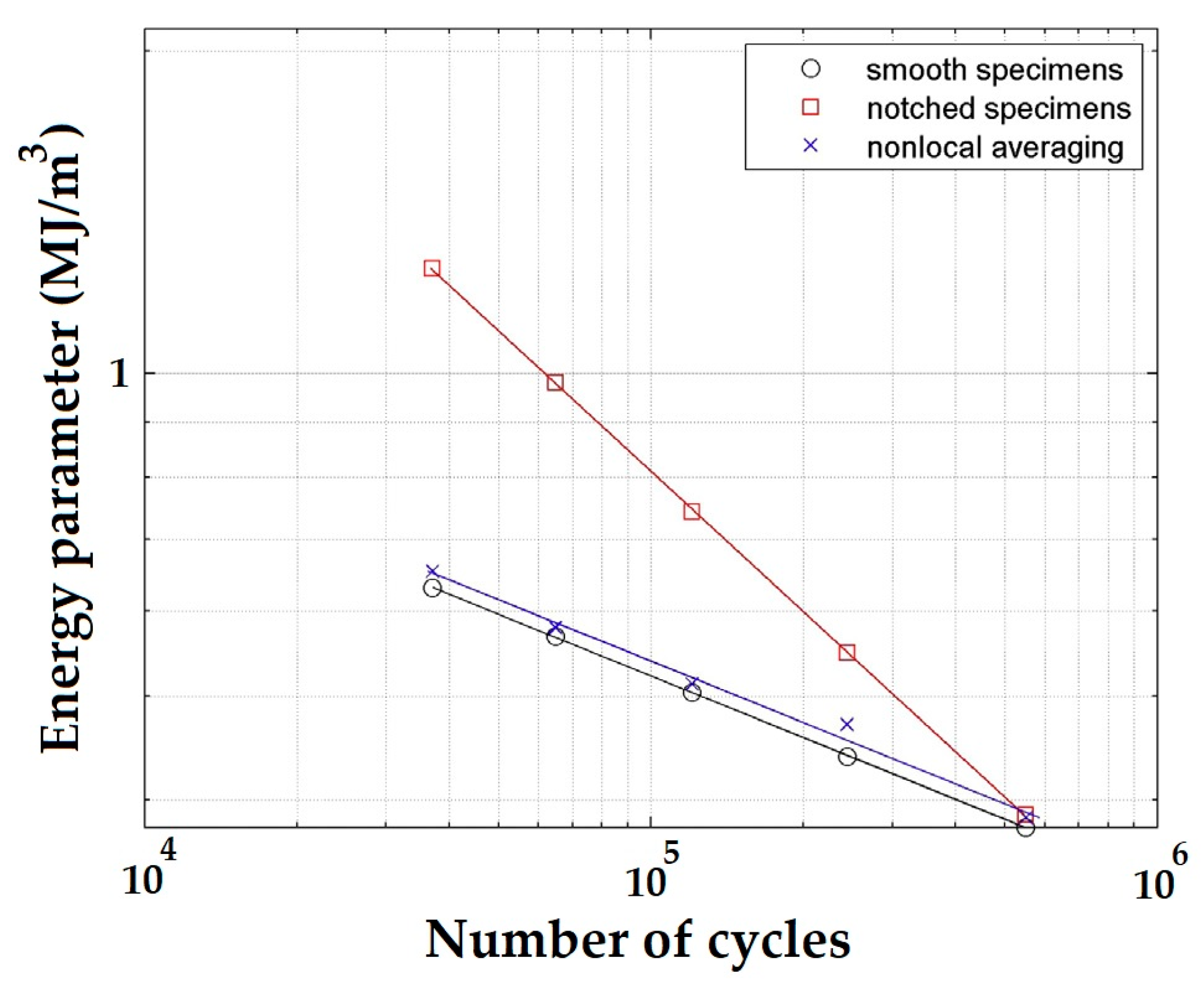

| Number of cycles | 1 × 104 | 5 × 104 | 1 × 105 | 5 × 105 | 1 × 106 | ||
|---|---|---|---|---|---|---|---|
| En3B | V-notched | (MPa) | 200 | 131 | 107 | 66 | 52 |
| (mm) | 3.315 | 1.785 | 1.350 | 0.720 | 0.566 | ||
| Hole 4 mm | (MPa) | 190 | 147 | 133 | 101 | 84 | |
| (mm) | 3.360 | 2.740 | 2.560 | 2.020 | 1.500 | ||
| Hole 1.75 mm | (MPa) | 251 | 195 | 172 | 130 | 106 | |
| (mm) | 2.640 | 2.060 | 1.815 | 1.420 | 1.030 | ||
| Al2024-T351 | Radius 1.5 mm | (MPa) | 157 | 118 | 104 | 79 | 71 |
| (mm) | 0.750 | 0.588 | 0.526 | 0.446 | 0.456 | ||
| Radius 0.25 mm | (MPa) | 211 | 161 | 143 | 101 | 97 | |
| (mm) | 0.307 | 0.236 | 0.219 | 0.206 | 0.201 | ||
| Radius 0.12 mm | (MPa) | 225 | 171 | 151 | 114 | 101 | |
| (mm) | 0.182 | 0.156 | 0.110 | 0.106 | 0.103 | ||
| Nonlocal Theories | Applications | Parameters | Materials and Structures | Ref. |
|---|---|---|---|---|
| NCDM | Damage analysis, Crack analysis, and Life prediction. | Elastic bar, Asphalt concrete, Sheet metals, Composites, and Laminates. | [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50] | |
| SFI | Fatigue life assessment, Size effect. | Elastoplastic materials, Steel, Cast iron. | [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67] | |
| PD | Crack analysis, Plastic deformation, Corrosion. | Elastic-viscoelastic materials, 2D plates, Composites. | [68,69,70,71,72,73,74,75,76,77,78,79] | |
| Elastic-Plastic | Damage analysis, Crack analysis. | Prismatic steel bars | [80,81,82,83,84] | |
| Energy-based | Multiaxial and high cycle fatigue, Crack analysis. | Λ | Industrial components, Steel. | [85,86,87,88,89,90,91,92] |
| Multiscale model | Damage analysis, Crack analysis, Life prediction. | Φ | Heterogeneous materials, Quasi-brittle materials. | [93,94,95] |
| Microstructural sensitive model | Life prediction. | Microstructures. | [96,97] | |
| LPM | Fracture analysis. | Composite materials. | [98,99] | |
| Volumetric HCF | Corrosion. | Martensitic stainless steels. | [100] | |
| OEDP | Low cycle fatigue. | Industrial components. | [101] | |
| Nonlocal and gradient fracture criteria | Fracture analysis. | Brittle, Quasi-brittle, Ductile materials. | [102] | |
| coupled damage-plasticity model | Fracture analysis. | Ductile materials. | [103] | |
| Nonlocal fracture criterion | Fracture analysis, Crack analysis, Computer Simulations. | Quasi-brittle materials, Viscoelastic materials. | [104,105,106,107,108,109,110] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghtaderi, S.H.; Jedi, A.; Ariffin, A.K. A Review on Nonlocal Theories in Fatigue Assessment of Solids. Materials 2023, 16, 831. https://doi.org/10.3390/ma16020831
Moghtaderi SH, Jedi A, Ariffin AK. A Review on Nonlocal Theories in Fatigue Assessment of Solids. Materials. 2023; 16(2):831. https://doi.org/10.3390/ma16020831
Chicago/Turabian StyleMoghtaderi, Saeed H., Alias Jedi, and Ahmad Kamal Ariffin. 2023. "A Review on Nonlocal Theories in Fatigue Assessment of Solids" Materials 16, no. 2: 831. https://doi.org/10.3390/ma16020831
APA StyleMoghtaderi, S. H., Jedi, A., & Ariffin, A. K. (2023). A Review on Nonlocal Theories in Fatigue Assessment of Solids. Materials, 16(2), 831. https://doi.org/10.3390/ma16020831







