Numerical Modelling of the Nonlinear Shear Creep Behavior of FRP-Concrete Bonded Joints
Abstract
1. Introduction
2. Nonlinear Creep Model
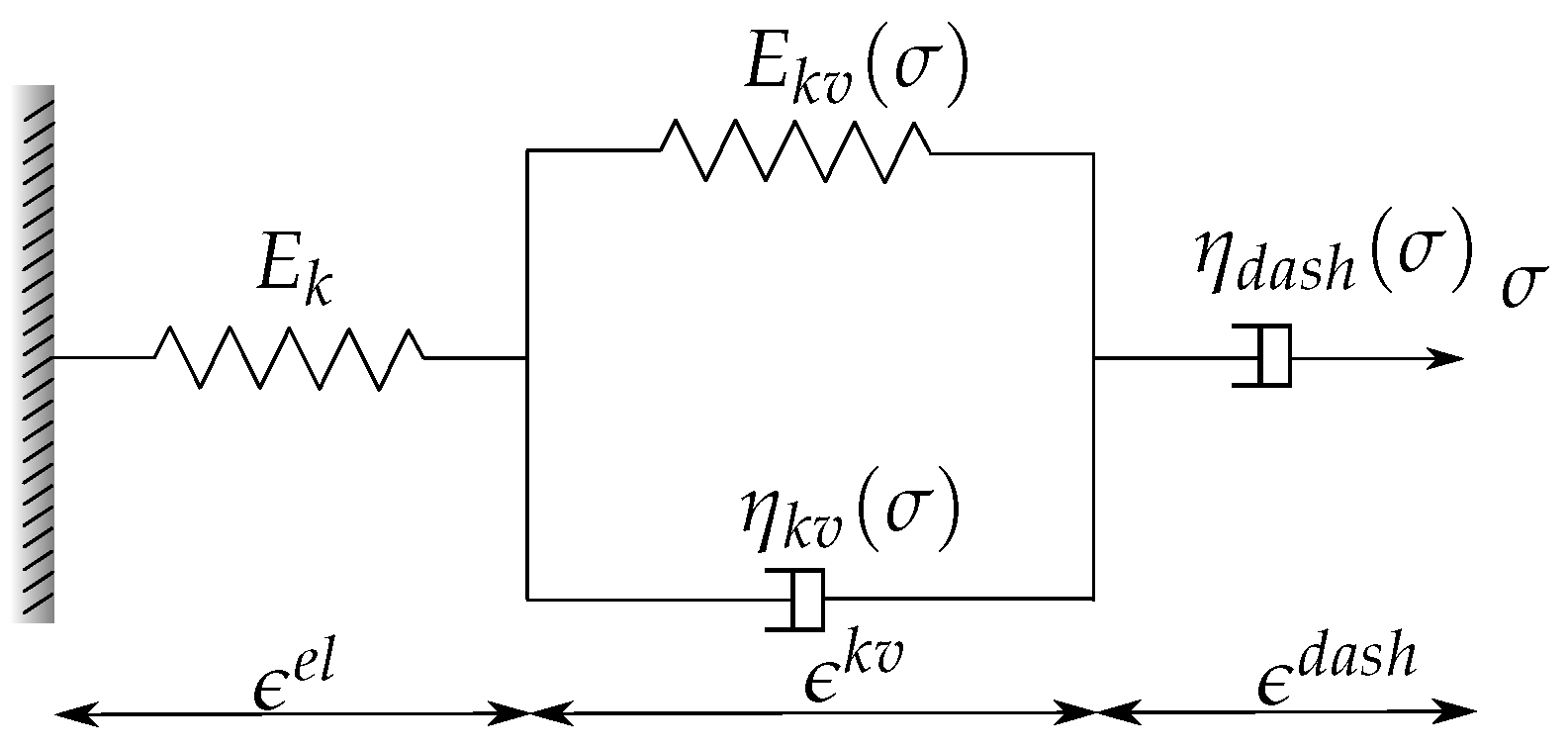
2.1. Constitutive Equations
2.1.1. Elastic and Viscous Strains
2.1.2. Nonlinearity
2.2. Implementation
2.2.1. Implicit Scheme
- -
- The increment of total strain:
- -
- The increment of elastic strain:
- -
- The increment of the two viscous strains:
- For a given time t in between and , is known. At the beginning of the time step, the elastic stress increment is computed:with the fourth order elastic tensor explicitly given in Appendix B.
- With this first estimation of the stress increment , the Newton minimization starts. The effective stress is computed (Equation (7)) at .
- If the minimization criterion is reached with the computed stress increment, then the minimization process stops, otherwise it returns to stage 2.
- i is incremented and the process goes to stage 1.
2.2.2. Implementation with MFront
- At the beginning of the time step, the nonlinear parameters (, and ) are computed on each Gauss point.
- Then, one must find the stress increment which verifies the structural equilibrium for a given strain increment from the incremental relationship given in the Section 2.2.1.
- Once the equilibrium is reached, the variables , and are updated.
3. Practical Case Studies
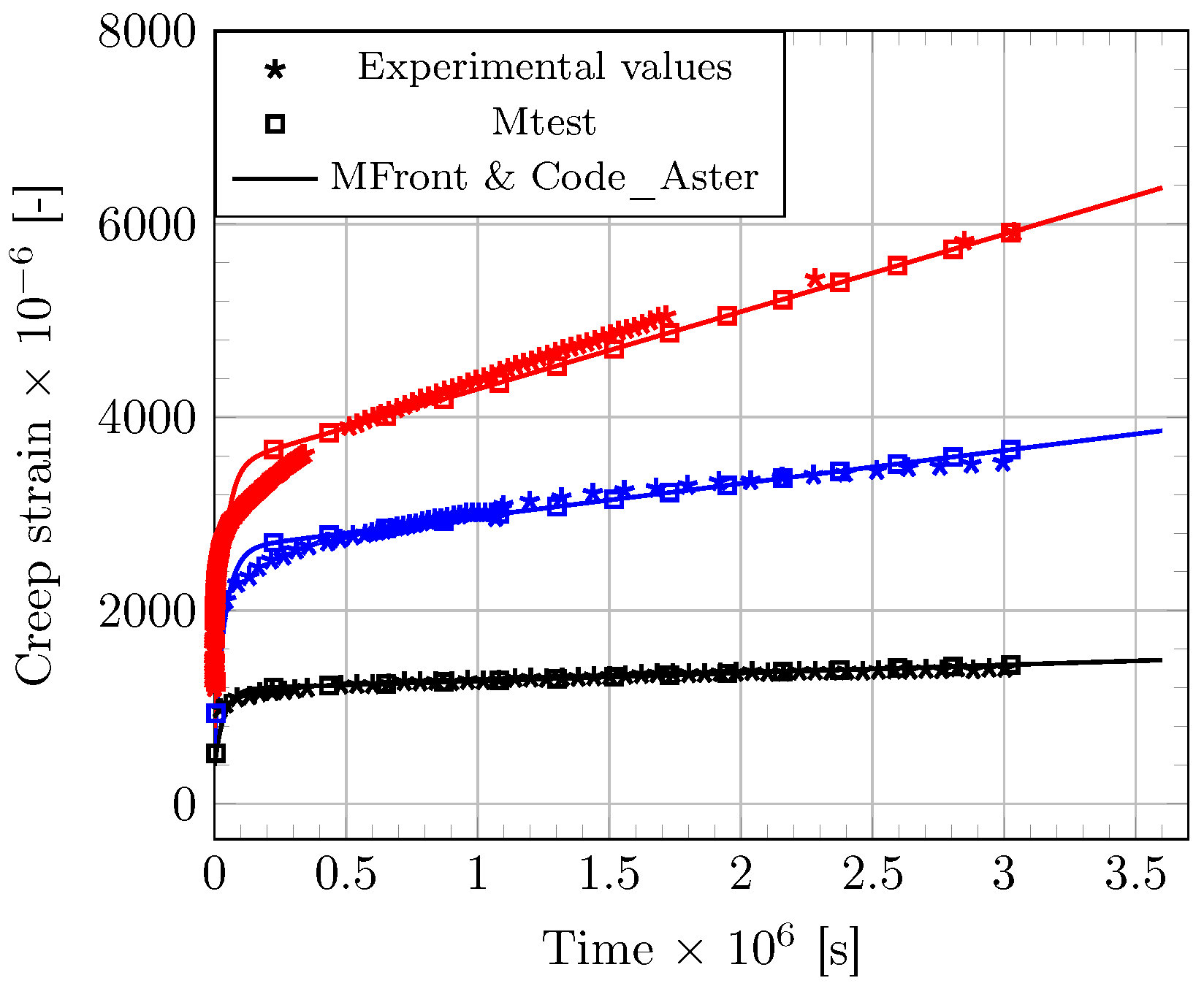
3.1. Samples of Bulk Epoxy Adhesive Subjected to Uniaxial Creep Loading
3.2. Structural Modelling
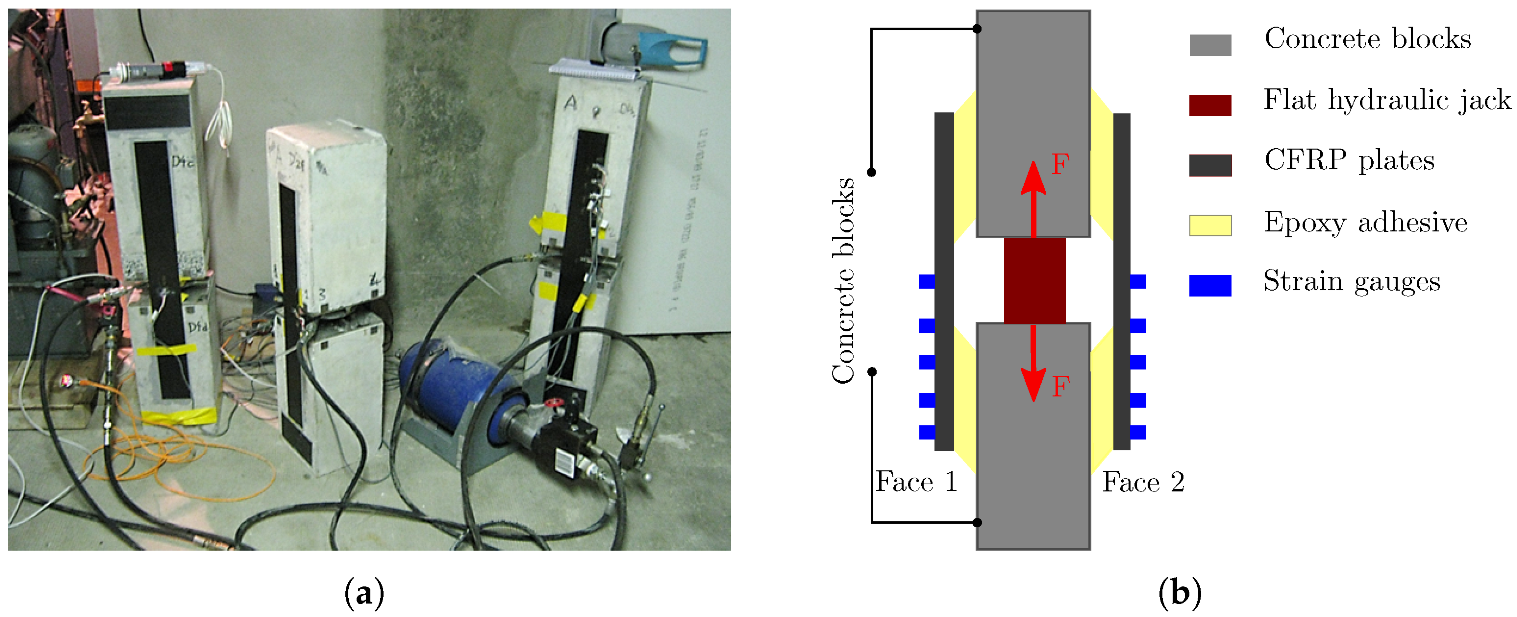
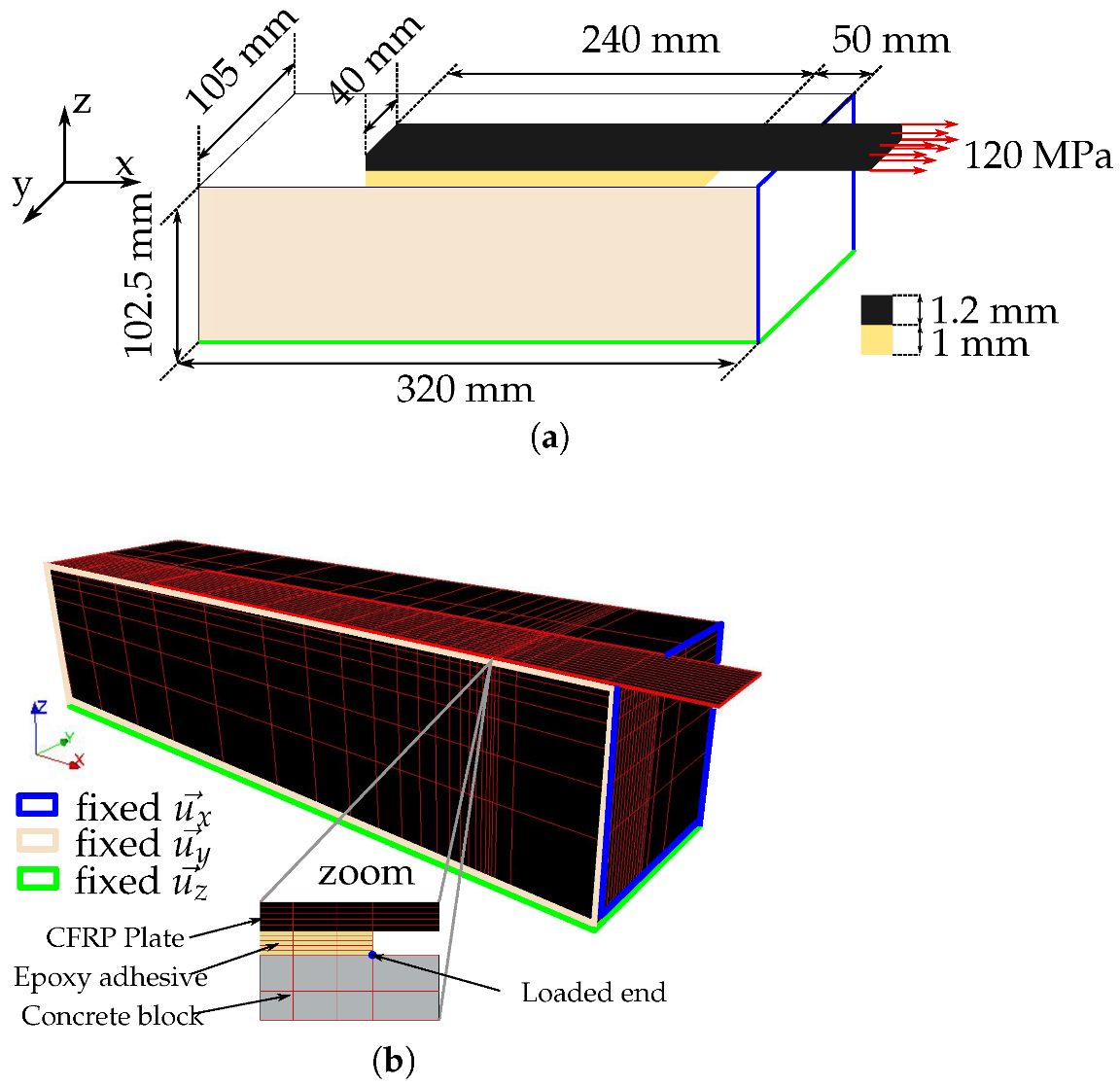
3.2.1. Experimental Setup
3.2.2. Description of the FE Model
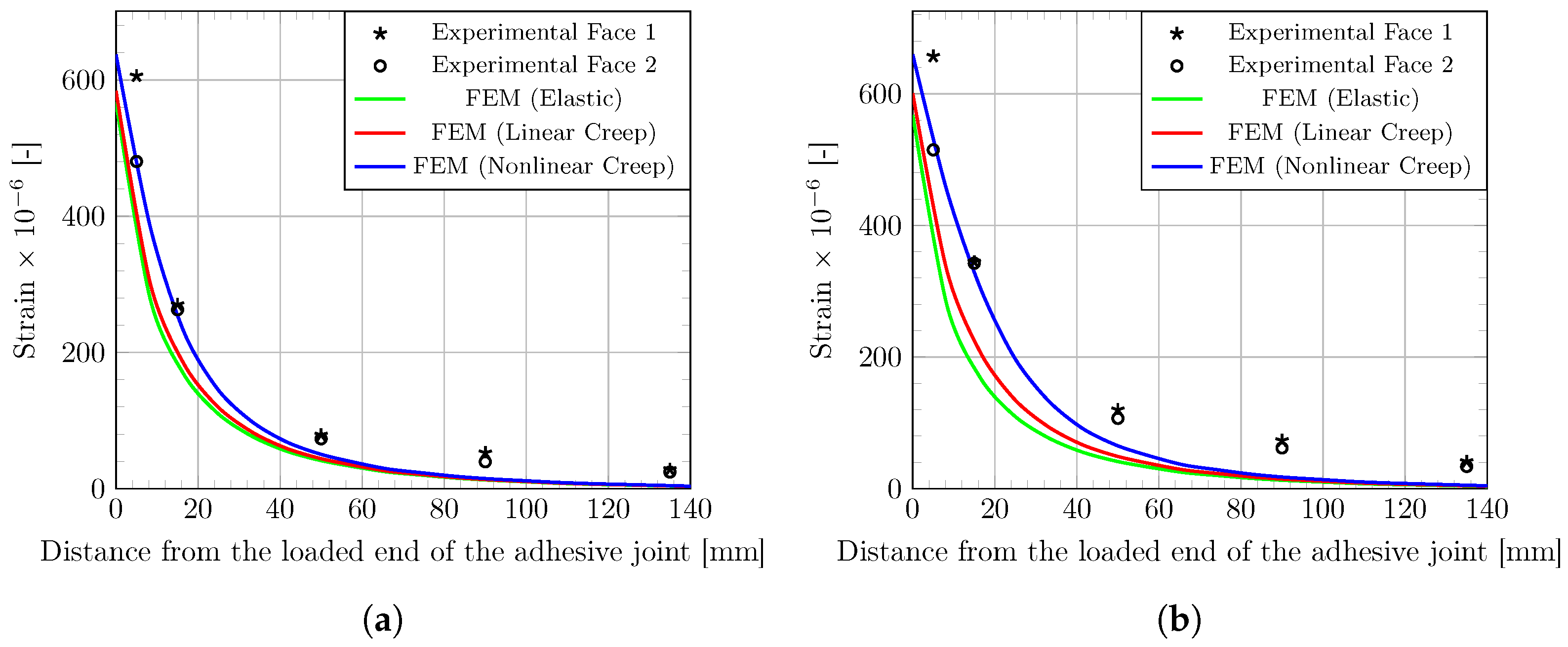
3.2.3. Confrontation between FE Model and Experimental Results
3.2.4. Sensitivity Analysis of the Elastic Parameters
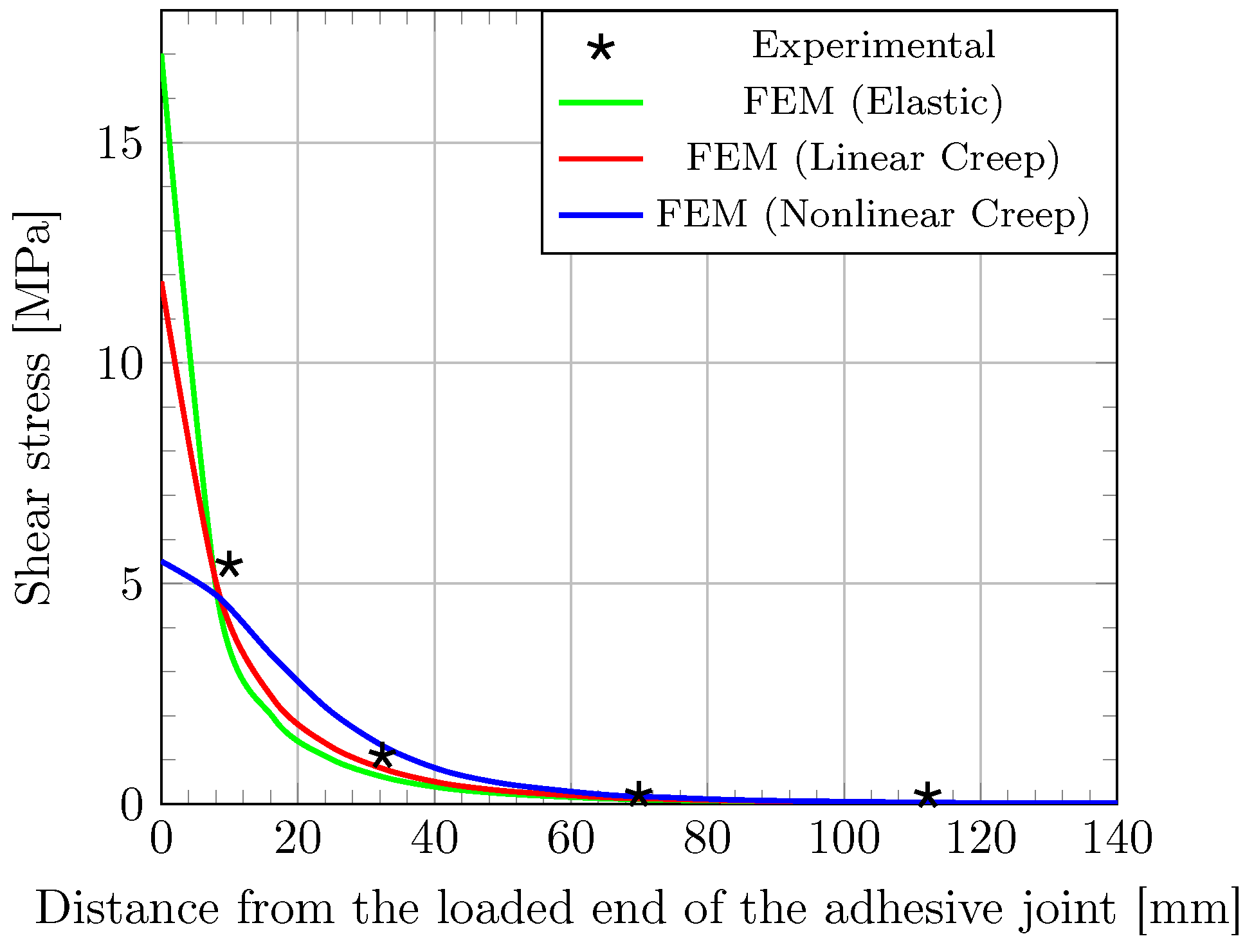
3.2.5. Impact of Adhesive Creep on Stress Transfer Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EB | Externally Bonded |
| FE | Finite Element |
| FRP | Fiber Reinforced Polymer |
| RC | Reinforced Concrete |
| TTSP | Time Temperature Superposition Principle |
Appendix A. Unit Tensor of Elastic Compliance
Appendix B. Unit Tensor of Elastic Stiffness
References
- Nanni, A.; Dolan, C. Fibre-Reinforced-Plastic (FRP) Reinforcement for Concrete Structures: Properties and Application; Developements in Civil Engineering; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Karbhari, V.M.; Seible, F. Fiber Reinforced composites–advanced materials for the renewal of civil infrastructure. Appl. Compos. Mater. 2000, 7, 95–124. [Google Scholar] [CrossRef]
- Smith, S.T.; Teng, J. FRP-strengthened RC beams I: Review of debonding strength models. Eng. Struct. 2002, 24, 385–395. [Google Scholar] [CrossRef]
- Wu, H.C.; Eamon, C.D. Strengthening of Concrete Structures Using Fiber Reinforced Polymers (FRP): Design, Construction and Practical Applications; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Al-Mahaidi, R.; Kalfat, R. Rehabilitation of Concrete Structures with Fiber-Reinforced Polymer; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Fayyadh, M.M.; Razak, H.A. Externally bonded FRP applications in RC structures: A state-of-the-art review. Jordan J. Civ. Eng. 2021, 15, 157–179. [Google Scholar]
- Japan Society of Civil Engineers (JSCE). Recommendations for Upgrading of Concrete Structures with Use of Continuous Fiber Sheet; Concrete Engineering Series (41); Japan Society of Civil Engineers: Tokyo, Japan, 2001. [Google Scholar]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; 440.2R-17; ACI: Farmington Hills, MI, USA, 2017. [Google Scholar]
- ISIS Canada Corporation. FRP Rehabilitation of Reinforced Concrete Structures; ISIS Design Manual No. 4; ISIS Canada Corporation: Winnipeg, MB, Canada, 2008. [Google Scholar]
- CNR—Advisory Committee on Technical Recommendations for Construction. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; National Research Council: Rome, Italy, 2013. [Google Scholar]
- Association Française de Génie Civil (AFGC). Seismic Retrofitting of Reinforced Concrete Structures Using Composites: Temporary Recommendations; AFGC: Paris, France, 2015. [Google Scholar]
- Fib Bulletin 90. Externally Applied FRP Reinforcement for Concrete Structures; The International Federation for Structural Concrete (Fib): Lausanne, Switzerland, 2019. [Google Scholar]
- Mazzotti, C.; Savoia, M. Stress redistribution along the interface between concrete and FRP subject to long-term loading. Adv. Struct. Eng. 2009, 12, 651–661. [Google Scholar] [CrossRef]
- Hamed, H.; Bradford, M. Flexural time-dependent cracking and post-cracking behavior of FRP strengthened concrete beams. Int. J. Solids Struct. 2012, 49, 1595–1607. [Google Scholar] [CrossRef]
- Hamed, E.; Chang, Z.T. Effect of creep on the edge debonding failure of FRP strengthened RC beams—A theoretical and experimental study. Compos. Sci. Technol. 2013, 74, 186–193. [Google Scholar] [CrossRef]
- Houachine, H.R.E.; Sereir, Z.; Amziane, S. Creep model for the long-term behaviour of combined cohesive-bridging model of FRP-concrete interface debonding under axial loading. Eur. J. Environ. Civ. Eng. 2021, 26, 5594–5616. [Google Scholar] [CrossRef]
- Houhou, N.; Benzarti, K.; Quiertant, M.; Chataigner, S.; Fléty, A.; Marty, C. Analysis of the nonlinear creep behavior of concrete/FRP-bonded assemblies. J. Adhes. Sci. Technol. 2014, 28, 1345–1366. [Google Scholar] [CrossRef]
- Benzarti, K.; Chataigner, S.; Quiertant, M.; Marty, C.; Aubagnac, C. Accelerated ageing behaviour of the adhesive bond between concrete specimens and CFRP overlays. Constr. Build. Mater. 2011, 25, 523–538. [Google Scholar] [CrossRef]
- Diab, H.; Wu, Z.; Iwashita, K. Short and long-term bond performance of prestressed FRP sheet anchorages. Eng. Struct. 2009, 31, 1241–1249. [Google Scholar] [CrossRef]
- Fischer, J.; Bradler, P.R.; Schmidtbauer, D.; Lang, R.W.; Wan-Wendner, R. Long-term creep behavior of resin-based polymers in the construction industry. Mater. Today Commun. 2019, 18, 60–65. [Google Scholar] [CrossRef]
- Silva, P.; Valente, T.; Azenha, M.; Sena-Cruz, J.; Barros, J. Viscoelastic response of an epoxy adhesive for construction since its early ages: Experiments and modelling. Compos. Part B Eng. 2017, 116, 266–277. [Google Scholar] [CrossRef]
- Emara, M.; Torres, L.; Baena, M.; Barris, C.; Moawad, M. Effect of sustained loading and environmental conditions on the creep behavior of an epoxy adhesive for concrete structures strengthened with CFRP laminates. Compos. Part B 2017, 129, 88–96. [Google Scholar] [CrossRef]
- Gómez, J.; Barris, C.; Jahani, Y.; Marta, B.; Torres, L. Experimental study and numerical prediction of the bond response of NSM CFRP laminates in RC elements under sustained loading. Constr. Build. Mater. 2021, 288, 123082. [Google Scholar] [CrossRef]
- Bradler, P.; Fischer, J.; Wan-Wendner, R.; Lang, R. Shear test equipment for testing various polymeric materials by using standardized multipurpose specimens with minor adaptions. Polym. Test. 2019, 75, 93–98. [Google Scholar] [CrossRef]
- Brinson, H. The viscoelastic constitutive modelling of adhesives. Composites 1982, 13, 377–382. [Google Scholar] [CrossRef]
- Zanni-Deffarges, M.; Shanahan, M. Diffusion of water into an epoxy adhesive: Comparison between bulk behaviour and adhesive joints. Int. J. Adhes. Adhes. 1995, 15, 137–142. [Google Scholar] [CrossRef]
- Ferrier, E.; Michel, L.; Jurkiewiez, B.; Hamelin, P. Creep behavior of adhesives used for external FRP strengthening of RC structures. Constr. Build. Mater. 2011, 25, 461–467. [Google Scholar] [CrossRef]
- Jeong, Y.; Lopez, M.; Bakis, C. Effects of temperature and sustained loading on the mechanical response of CFRP bonded to concrete. Constr. Build. Mater. 2016, 124, 442–452. [Google Scholar] [CrossRef]
- Zehsaz, M.; Vakili-Tahami, F.; Saeimi-Sadigh, M.A. Parametric study of the creep failure of double lap adhesively bonded joints. Mater. Des. 2014, 64, 520–526. [Google Scholar] [CrossRef]
- Hadjazi, K.; Sereir, Z.; Amziane, S. Creep response of intermediate flexural cracking behavior of reinforced concrete beam strengthened with an externally bonded FRP plate. Int. J. Solids Struct. 2016, 94–95, 196–205. [Google Scholar] [CrossRef]
- Hamed, E.; Bradford, M.A. Creep in concrete beams strengthened with composite materials. Eur. J. Mech. A/Solids 2010, 29, 951–965. [Google Scholar] [CrossRef]
- European Committee for Standardisation (CEN). Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings (EN 1992-1-1:2004); European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- Bouziadi, F.; Boulekbache, B.; Haddi, A.; Hamrat, M.; Djelal, C. Finite element modeling of creep behavior of FRP-externally strengthened reinforced concrete beams. Eng. Struct. 2020, 204, 109908. [Google Scholar] [CrossRef]
- Akpinar, S.; Aydin, M.D.; Özel, A. A study on 3-D stress distributions in the bi-adhesively bonded T-joints. Appl. Math. Model. 2013, 37, 10220–10230. [Google Scholar] [CrossRef]
- Houhou, N.; Benzarti, K.; Quiertant, M.; Chataigner, S.; Youssef, G.; Rabasse, M.; Aubagnac, C.; Gagnon, A.; Flety, A. Durability of concrete/FRP bonded assemblies subjected to hydrothermal coupled creep ageing mechanisms: Experimental and numerical investigations. In Proceedings of the TRA 2014, Paris, France, 14–17 April 2014; p. 10. [Google Scholar]
- Wineman, A.S.; Rajagopal, K.R. Mechanical Response of Polymers: An Introduction; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Jiang, S.; Yao, W.; Jin, C.; Cai, T. Finite Element Modeling of FRP-Strengthened RC Beam under Sustained Load. Adv. Mater. Sci. Eng. 2018, 45, 1368–1376. [Google Scholar] [CrossRef]
- Findley, W.N.; Laiand, J.S.; Onaran, K.; Christensen, R.M. Creep and relaxation of nonlinear viscoelastic materials. J. Appl. Mech. 1977, 44, 364. [Google Scholar] [CrossRef]
- Dean, G. Modelling non-linear creep behaviour of an epoxy adhesive. Int. J. Adhes. Adhes. 2007, 27, 636–646. [Google Scholar] [CrossRef]
- Tervoort, T.; Klompen, E.; Govaert, L. A multi-mode approach to finite, three-dimensional, nonlinear viscoelastic behavior of polymer glasses. J. Rheol. 1996, 40, 779–797. [Google Scholar] [CrossRef]
- Majda, P.; Skrodzewicz, J. A modified creep model of epoxy adhesive at ambient temperature. Int. J. Adhes. Adhes. 2009, 29, 396–404. [Google Scholar] [CrossRef]
- Helfer, T.; Michel, B.; Proix, J.M.; Salvo, M.; Sercombe, J.; Casella, M. Introducing the open-source mfront code generator: Application to mechanical behaviours and material knowledge management within the PLEIADES fuel element modelling platform. Comput. Math. Appl. 2015, 70, 994–1023. [Google Scholar] [CrossRef]
- Helfer, T.; Fandeur, O.; Haboussa, D.; Deloison, D.; Jamond, O.; Munier, R.; Berthon, L.; CASTELIER, E.; Ramière, I. New functionalities of the 3.0 version of TFEL, MFront and MTest. In Proceedings of the 13e Colloque National en Calcul des Structures, Université Paris-Saclay, Giens, France, 14–19 September 2017. [Google Scholar]
- CEA and EDF. MFront Web Site. Available online: http://www.tfel.sourceforge.net (accessed on 11 January 2023).
- Houhou, N. Durabilité des Interfaces Collées Béton/Renforts Composites: Développement d’une Méthodologie D’étude basée sur un Dispositif de Fluage Innovant Conçu pour être Couplé à un Vieillissement Hygrothermique. Ph.D. Thesis, Université Paris-Est, Créteil, France, 2012. [Google Scholar]
- Ascione, F.; Berardi, V.; Feo, L.; Giordano, A. An experimental study on the long-term behavior of CFRP pultruded laminates suitable to concrete structures rehabilitation. Compos. Part B Eng. 2008, 39, 1147–1150. [Google Scholar] [CrossRef]
- Yuan, H. Improved theoretical solutions of FRP-to-concrete interfaces. In Proceedings of the International Symposium on Bond Behaviour of FRP in Structures, BBFS, Hong Kong, China, 7–9 December 2005; pp. 97–102. [Google Scholar]
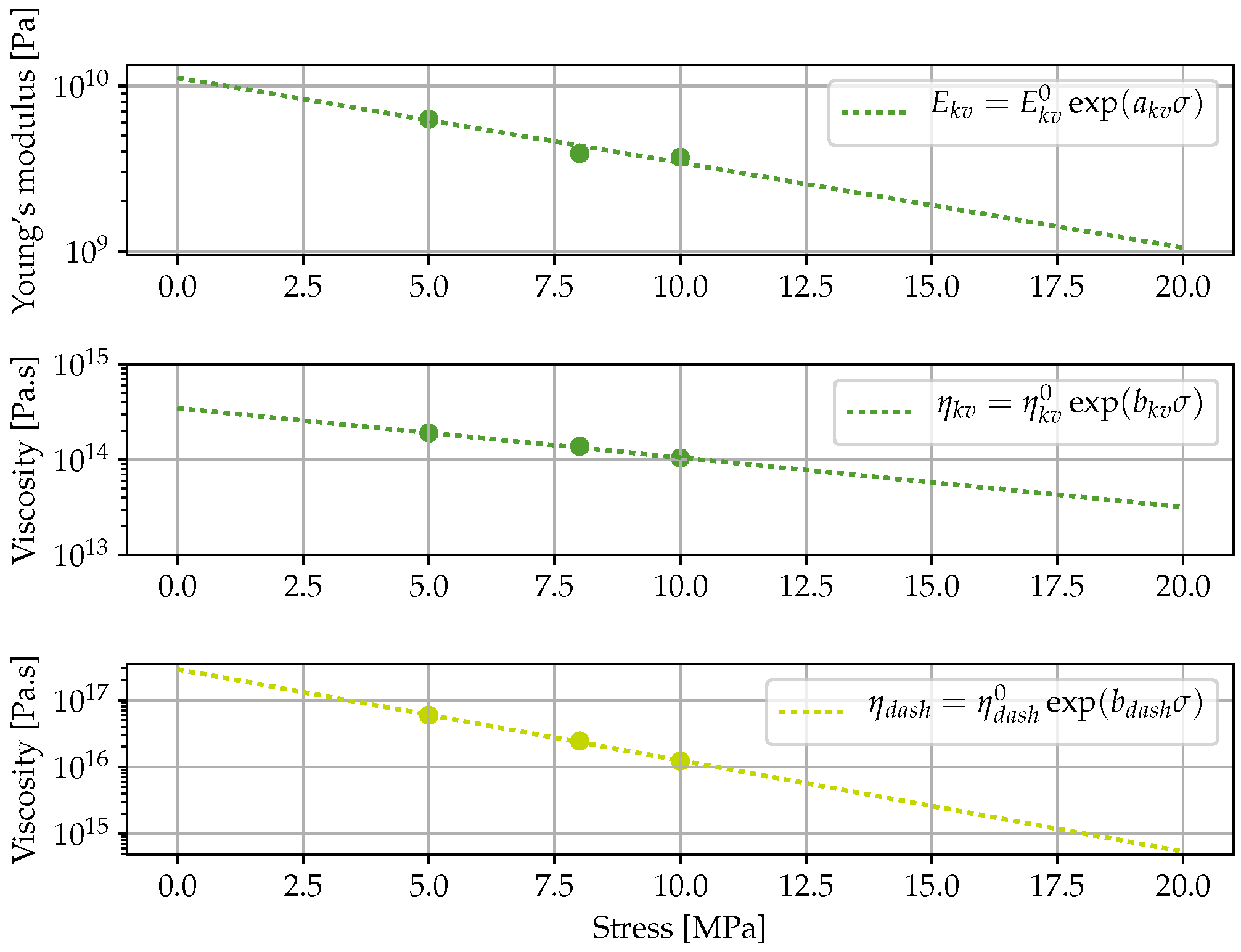

| E (GPa) | (MPa) | (GPa s) | (MPa) | (GPa s) | (MPa) |
|---|---|---|---|---|---|
| 10.8 | −1.10 × 10−1 | 3.47 × 105 | −1.19 × 10−1 | 2.88 × 108 | −3.14 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleilhet, F.; Quiertant, M.; Benzarti, K. Numerical Modelling of the Nonlinear Shear Creep Behavior of FRP-Concrete Bonded Joints. Materials 2023, 16, 801. https://doi.org/10.3390/ma16020801
Soleilhet F, Quiertant M, Benzarti K. Numerical Modelling of the Nonlinear Shear Creep Behavior of FRP-Concrete Bonded Joints. Materials. 2023; 16(2):801. https://doi.org/10.3390/ma16020801
Chicago/Turabian StyleSoleilhet, François, Marc Quiertant, and Karim Benzarti. 2023. "Numerical Modelling of the Nonlinear Shear Creep Behavior of FRP-Concrete Bonded Joints" Materials 16, no. 2: 801. https://doi.org/10.3390/ma16020801
APA StyleSoleilhet, F., Quiertant, M., & Benzarti, K. (2023). Numerical Modelling of the Nonlinear Shear Creep Behavior of FRP-Concrete Bonded Joints. Materials, 16(2), 801. https://doi.org/10.3390/ma16020801








