Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Thermogravimetry of PP
2.2. Kinetic Theory
3. Results and Discussion
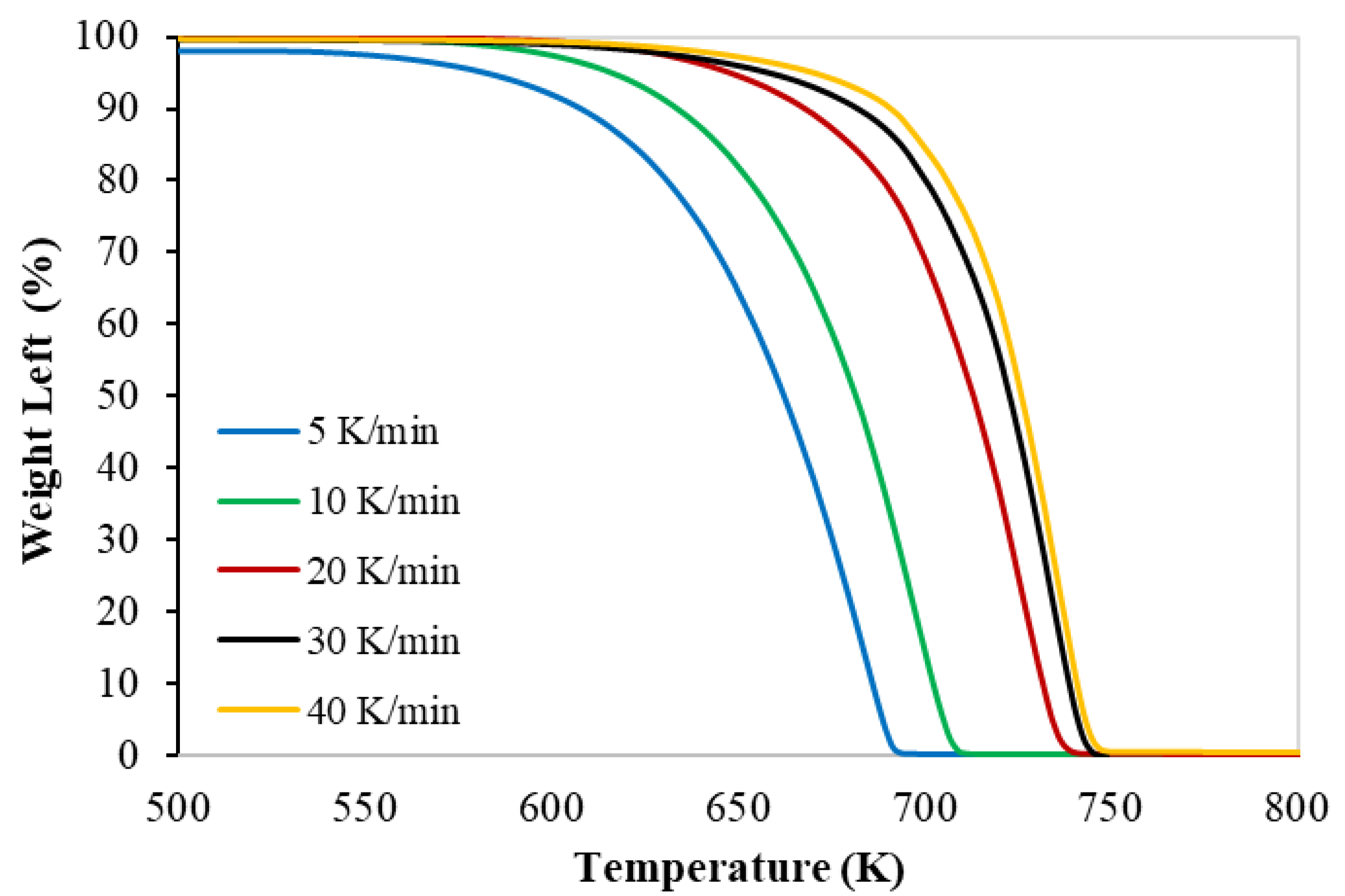
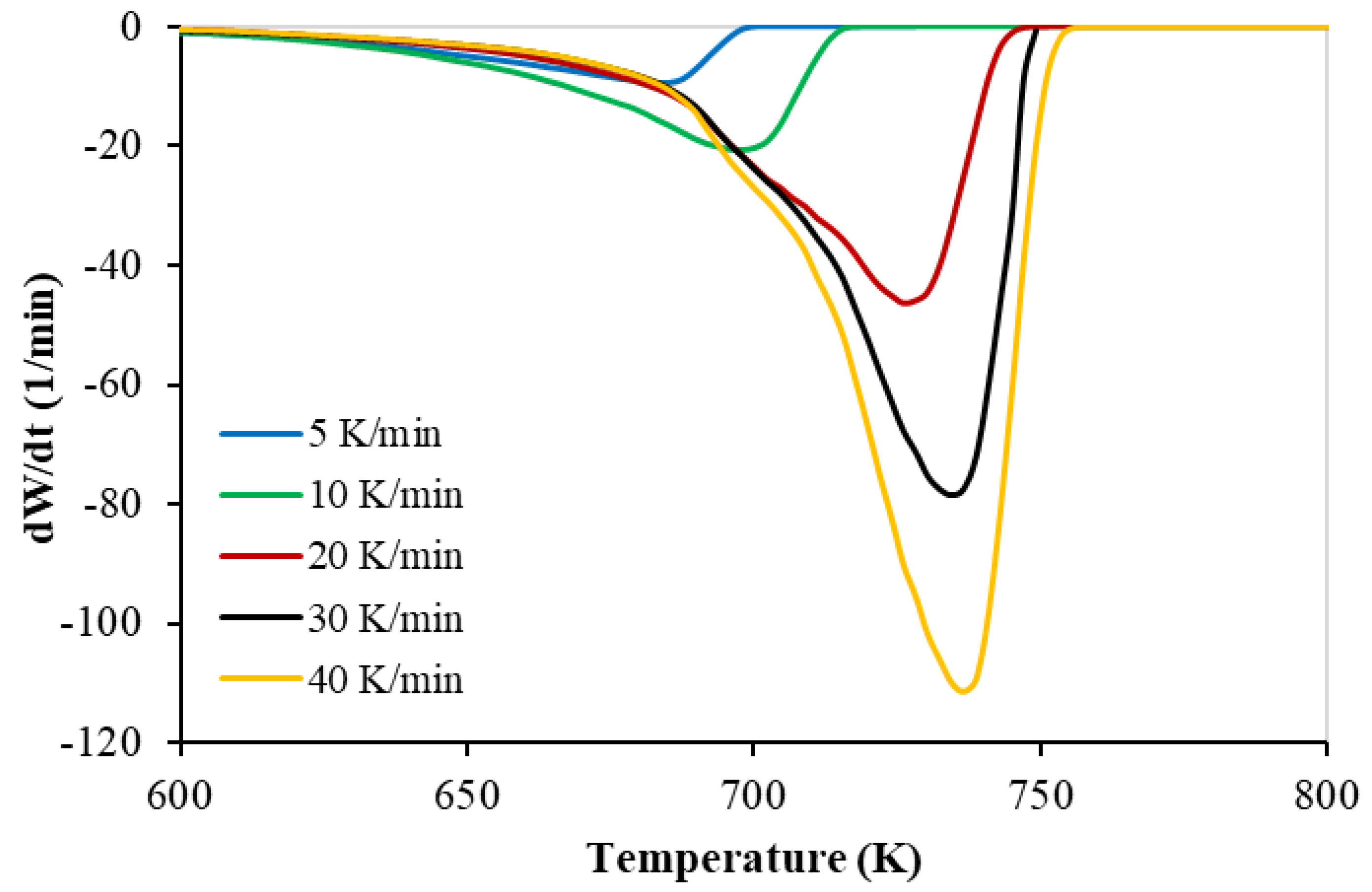
3.1. Thermogravimetry of PP
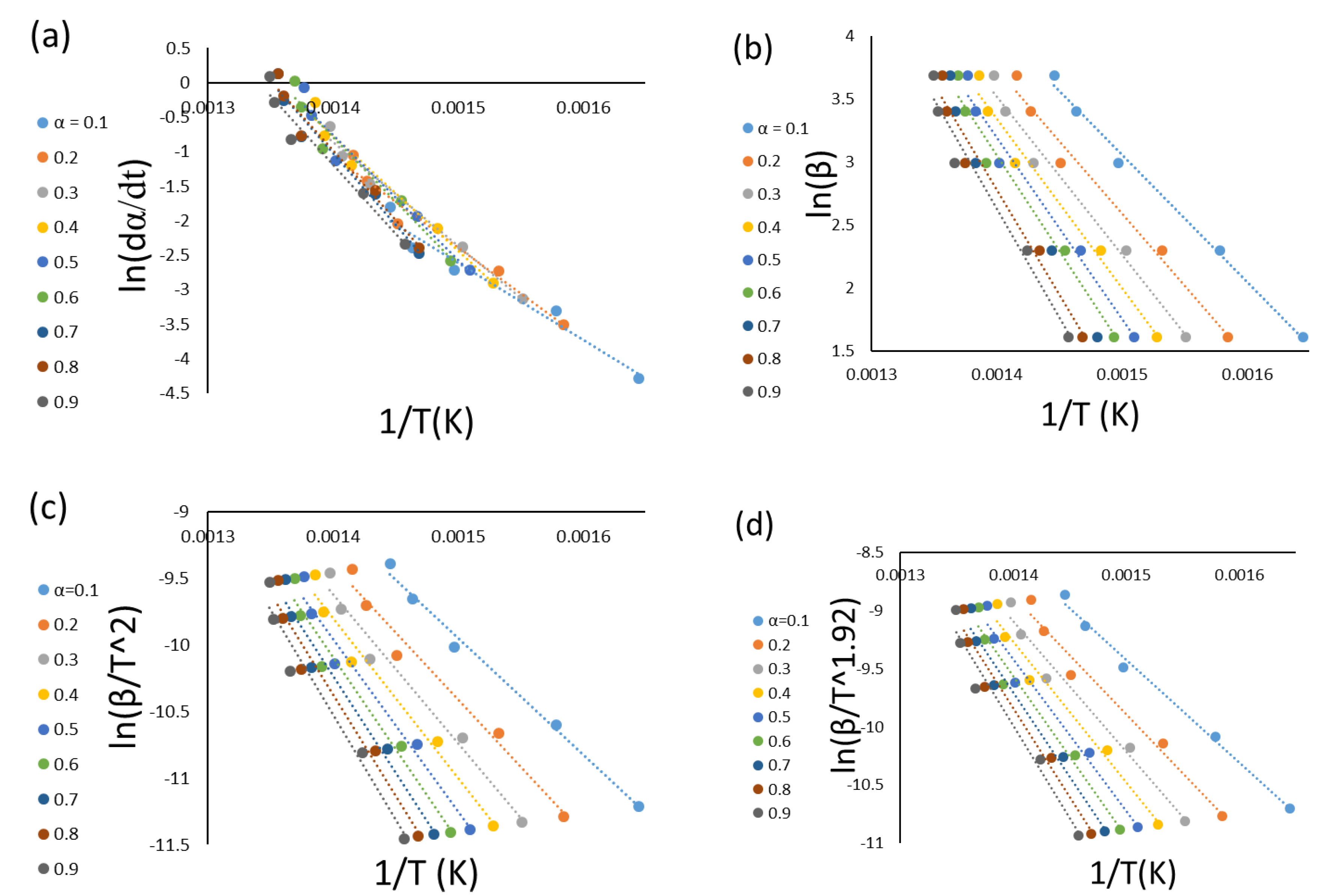
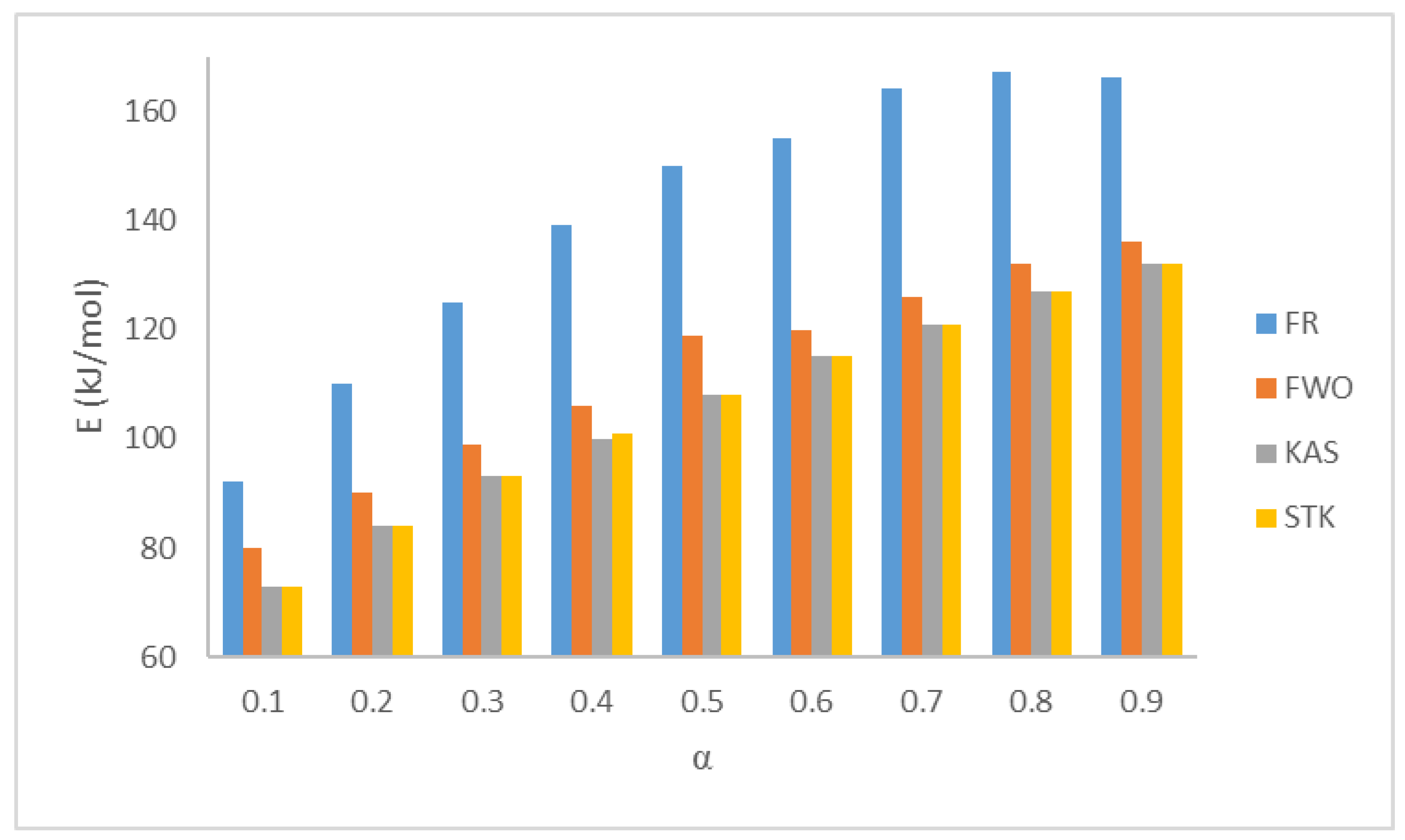
3.2. Model-Free Kinetics Calculation
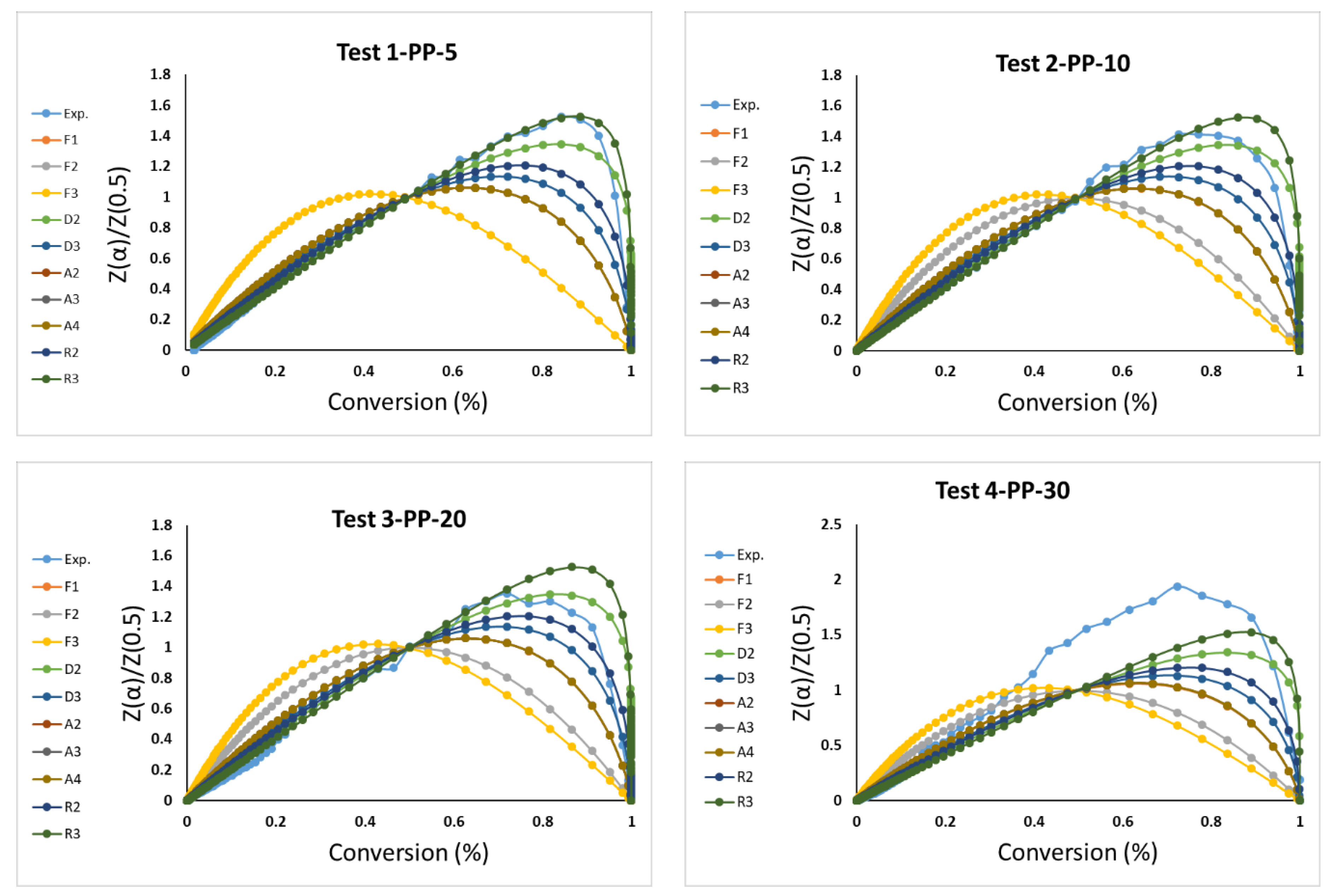
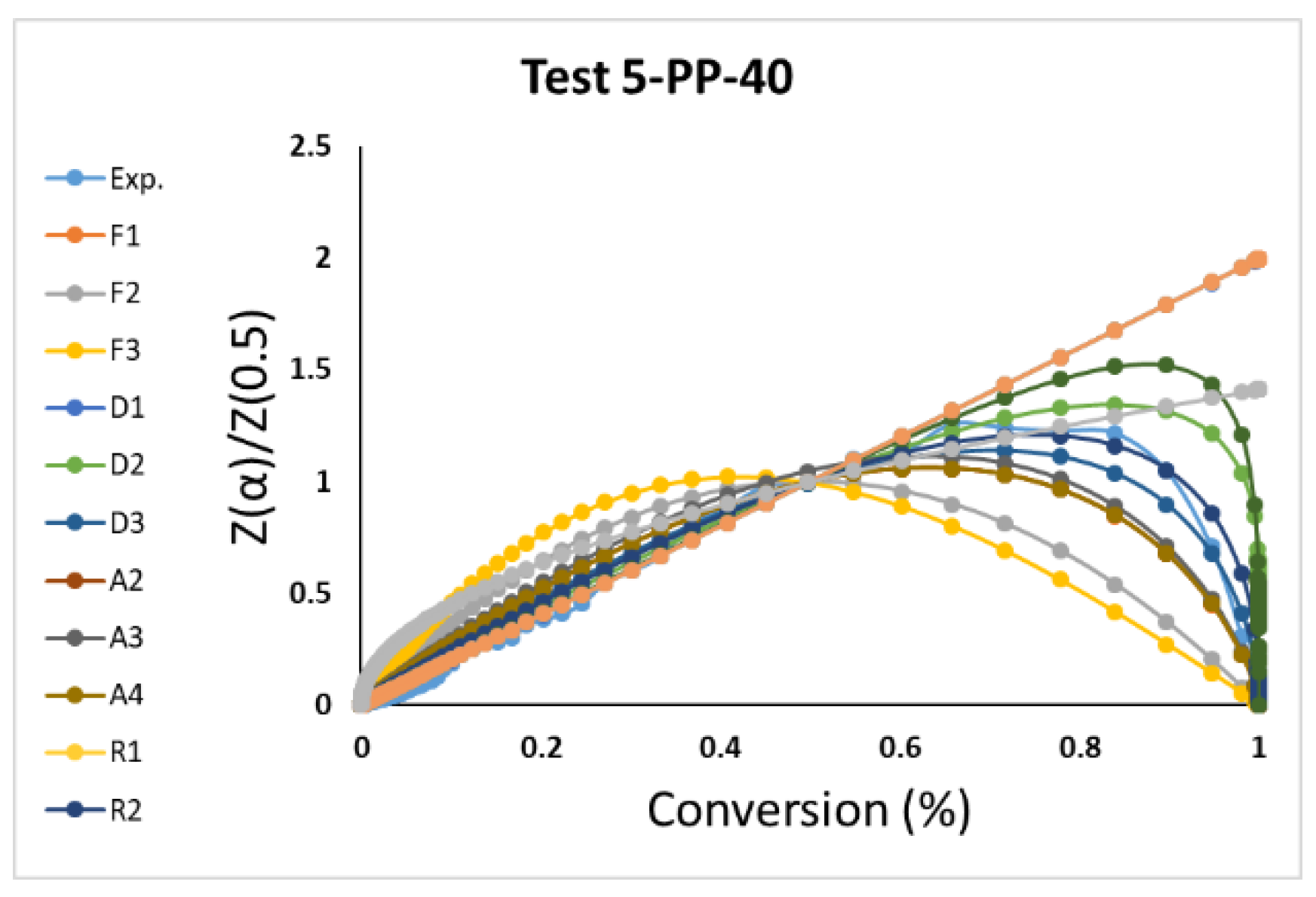
3.3. Model-Fitting Kinetics Parameters Calculation
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubdub, I.; Al-Yaari, M. Pyrolysis of Low Density Polyethylene: Kinetic Study Using TGA Data and ANN Prediction. Polymers 2020, 12, 891. [Google Scholar] [CrossRef] [PubMed]
- Dubdub, I.; Al-Yaari, M. Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics. Polymers 2021, 13, 3413. [Google Scholar] [CrossRef] [PubMed]
- Kaminsky, W.; Schlesselmann, B.; Simon, C.M. Thermal degradation of mixed plastic waste to aromatic and gas. Polym. Degrad. Stab. 1996, 53, 189–197. [Google Scholar] [CrossRef]
- Wu, C.H.; Chang, C.Y.; Hor, J.L.; Shih, S.M.; Chen, L.W.; Chang, F.W. On The Thermal Treatment of Plastic Mixtures of MSW: Pyrolysis Kinetics. Waste Manag. 1993, 13, 221–235. [Google Scholar]
- Diaz Silvarrey, L.S.; Phan, A.N. Kinetic study of municipal plastic waste. Int. J. Hydrogen Energy 2016, 41, 16352–16364. [Google Scholar] [CrossRef]
- Chowlu, A.C.K.; Reddy, P.K.; Ghoshal, A.K. Pyrolytic decomposition and model-free kinetics analysis of mixture of polypropylene (PP) and low-density polyethylene (LDPE). Thermochim. Acta 2009, 485, 20–25. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; El Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I Pyrolysis kinetics and mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Yu, J.; Sun, L.; Ma, C.; Qiao, Y.; Yao, H. Thermal degradation of PVC: A review. Waste Manag. 2016, 48, 300–314. [Google Scholar] [CrossRef]
- Anene, A.F.; Fredriksen, S.B.; Sætre, K.A.; Tokheim, L.A. Experimental Study of Thermal and Catalytic Pyrolysis of Plastic Waste Components. Sustainability 2018, 10, 3979. [Google Scholar] [CrossRef]
- Mumbach, G.D.; Alves, J.L.F.; Silva, J.C.G.D.; Sena, R.F.D.; Marangoni, C.; Machado, R.A.F.; Bolzan, A. Thermal investigation of plastic solid waste pyrolysis via the deconvolution technique using the asymmetric double sigmoidal function: Determination of the kinetic triplet, thermodynamic parameters, thermal lifetime and pyrolytic oil composition for clean energy recovery. Energy Convers. Manag. 2019, 200, 112031. [Google Scholar] [CrossRef]
- Galiwango, E.; Gabbar, H. Synergistic interactions, kinetic and thermodynamic analysis of co-pyrolysis of municipal paper and polypropylene waste. Waste Manag. 2022, 146, 86–93. [Google Scholar] [CrossRef]
- Osman, A.I.; Fawzy, S.; Farrell, C.; Al-Muhtaseb, A.H.; Harrison, J.; Al-Mawali, S.; Rooney, D.W. Comprehensive thermokinetic modelling and predictions of cellulose decomposition in isothermal, non-isothermal, and stepwise heating modes. J. Anal. Appl. Pyrolysis 2022, 161, 105427. [Google Scholar] [CrossRef]
- Nawaz, A.; Pradeep Kumar, P. Pyrolysis behavior of low value biomass (Sesbania bispinosa) to elucidate its bioenergy potential: Kinetic, thermodynamic and prediction modelling, using artificial neural network. Renew. Energy 2022, 200, 257–270. [Google Scholar] [CrossRef]
- Hayoune, F.; Chelouche, S.; Trache, D.; Zitouni, S.; Grohensc, Y. Thermal decomposition kinetics and lifetime prediction of a PP/PLA blend supplemented with iron stearate during artificial aging. Thermochim. Acta 2020, 690, 178700. [Google Scholar] [CrossRef]
- Yang, J.; Miranda, R.; Roy, C. Using the DTG curve fitting method to determine the apparent kinetic parameters of thermal decomposition of polymers. Polym. Degrad. Stab. 2001, 73, 455–461. [Google Scholar] [CrossRef]
- Park, J.W.; Oh, S.C.; Lee, H.P.; Kim, H.T.; Yoo, K.O. A kinetic analysis of thermal degradation of polymers using a dynamic method. Polym. Degrad. Stab. 2000, 67, 535–540. [Google Scholar] [CrossRef]
- Chan, J.H.; Balke, S.T. The thermal degradation kinetics of polypropylene: Part III. thermogravimetric analyses. Polym. Degrad. Stabil. 1997, 57, 135–149. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data. Thermochim. Acta 1999, 340–341, 53–68. [Google Scholar] [CrossRef]
- Xu, F.; Wang, B.; Yang, D.; Hao, J.; Qiao, Y.; Tian, Y. Thermal degradation of typical plastics under high heating rate conditions by TG-FTIR: Pyrolysis behaviors and kinetic analysis. Energy Convers. Manag. 2018, 171, 1106–1115. [Google Scholar] [CrossRef]
- Singh, S.; Patil, T.; Tekade, S.P.; Gawande, M.B.; Sawarkar, A.N. Studies on individual pyrolysis and co-pyrolysis of corn cob and polyethylene: Thermal degradation behavior, possible synergism, kinetics, and thermodynamic analysis. Sci. Total Environ. 2021, 783, 147004. [Google Scholar] [CrossRef]
- Mishra, G.; Kumar, J.; Bhaskar, T. Kinetic studies on the pyrolysis of pinewood. Bioresour. Technol. 2015, 182, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Naqvi, S.R.; Tariq, R.; Hameed, Z.; Ali, I.; Taqvi, S.A.; Naqvi, M.; Niazi, M.B.K.; Noor, T.; Farooq, W. Pyrolysis of high-ash sewage sludge: Thermo-kinetic study using TGA and artificial neural networks. Fuel 2018, 233, 529–538. [Google Scholar] [CrossRef]
- Mortezaeikia, V.; Tavakoli, O.; Mohammad Saleh Khodaparasti, M.S. A review on kinetic study approach for pyrolysis of plastic wastes using thermogravimetric analysis. J. Anal. Appl. Pyrolysis 2021, 160, 105340. [Google Scholar] [CrossRef]
- Janković, B.; Manić, N. Kinetic analysis and reaction mechanism of p-alkoxybenzyl alcohol ([4-(hydroxymethyl)phenoxymethyl]polystyrene) resin pyrolysis: Revealing new information on thermal stability. Polym. Degrad. Stab. 2021, 189, 109606. [Google Scholar] [CrossRef]
- Paik, P.; Kar, K.K. Kinetics of thermal degradation and estimation of lifetime for polypropylene particles: Effects of particle size. Polym. Degrad. Stab. 2008, 93, 24–35. [Google Scholar] [CrossRef]
- Ali, G.; Nisar, J.; Iqbal, M.; Afzal Shah, A.; Abbas, M.; Shah, M.R.; Rashid, U.; Bhatti, I.A.; Khan, R.A.; Shah, F. Thermo-catalytic decomposition of polystyrene waste: Comparative analysis using different kinetic models. Waste Manag. Res. 2020, 38, 202–212. [Google Scholar] [CrossRef]
- Baloch, M.K.; Khurram, M.J.Z.; Durrani, G.F. Application of Different Methods for the Thermogravimetric Analysis of Polyethylene Samples. J. Appl. Polym. Sci. 2011, 120, 3511–3518. [Google Scholar] [CrossRef]
- Balsora, H.K.; Kartik, S.; Dua, V.; Joshi, J.B.; Kataria, G.; Sharma, A.; Chakinala, A.G. Machine learning approach for the prediction of biomass pyrolysis kinetics from preliminary analysis. J. Environ. Chem. Eng. 2022, 10, 108025. [Google Scholar] [CrossRef]
- Bu, Q.; Chen, K.; Xie, W.; Liu, Y.; Cao, M.; Kong, X.; Chu, Q.; Mao, H. Hydrocarbon rich bio-oil production, thermal behavior analysis and kinetic study of microwave-assisted co-pyrolysis of microwave-torrefied lignin with low density polyethylene. Bioresour. Technol. 2019, 291, 121860. [Google Scholar] [CrossRef]
- Lai, J.; Meng, Y.; Yan, Y.; Lester, E.; Wu, T.; Pang, C.H. Catalytic pyrolysis of linear low-density polyethylene using recycled coal ash: Kinetic study and environmental evaluation. Korean J. Chem. Eng. 2021, 38, 2235–2246. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Chena, S.; Xua, K.; Fana, B.; Yang, D.; Geng, L.; Qiao, H. Investigation on the co-pyrolysis of agricultural waste and high-density polyethylene using TG-FTIR and artificial neural network modelling. Process Saf. Environ. Prot. 2022, 160, 341–353. [Google Scholar] [CrossRef]
- Patidar, K.; Singathia, A.; Vashishtha, M.; Sangal, V.K.; Upadhyaya, S. Investigation of kinetic and thermodynamic parameters approaches to non-isothermal pyrolysis of mustard stalk using model-free and master plots methods. Mater. Sci. Energy Technol. 2022, 5, 6–14. [Google Scholar] [CrossRef]
- Khodaparasti, M.S.; Shirazvatan, M.R.; Tavakoli, O.; Khodadadi, A.A. Co-pyrolysis of municipal sewage sludge and microalgae Chlorella Vulgaris: Products’ optimization; thermo-kinetic study, and ANN modeling. Energy Convers. Manag. 2022, 254, 115258. [Google Scholar] [CrossRef]
- Wan, H.; Huang, Z. Kinetic Analysis of Pyrolysis and Thermo-Oxidative Decomposition of Tennis String Nylon Wastes. Materials 2021, 14, 7564. [Google Scholar] [CrossRef] [PubMed]
| Proximate Analysis, wt%. | Ultimate Analysis, wt% | |||||
|---|---|---|---|---|---|---|
| Moisture | Volatile | Ash | C | H | N | S |
| 0.01 | 99.63 | 0.29 | 85.00 | 14.73 | 0.04 | 0.23 |
| Method | Equation | Integral (I) or Differential (D) | Plot |
|---|---|---|---|
| Friedman | D | ||
| Flynn–Wall–Qzawa (FWO) | I | ||
| Kissinger–Akahira–Sunose (KAS) | I | ||
| Starink | I |
| Equation | |
|---|---|
| CR method | |
| Criado method |
| Reaction Mechanism | Code | f(α) | g(α) |
|---|---|---|---|
| Reaction order models—First order | F1 | ||
| Reaction order models—Second order | F2 | ||
| Reaction order models—Third order | F3 | ||
| Diffusion model—One-dimension diffusion | D1 | ||
| Diffusion model—Two-dimension diffusion | D2 | ||
| Diffusion model—Three-dimension diffusion | D3 | ||
| Nucleation models—Two-dimension nucleation | A2 | ||
| Nucleation models—Three-dimension nucleation | A3 | ||
| Nucleation models—four-dimension nucleation | A4 | ||
| Geometrical contraction models—One-dimension | R1 | 1 | |
| Geometrical contraction models—Contracting sphere | R2 | 1− | |
| Geometrical contraction models—Contracting cylinder | R3 | 1 | |
| Nucleation models—Power law | P2 | ||
| Nucleation models—Power law | P3 | ||
| Nucleation models—Power law | P4 |
| Test No. | Heating Rate (K min−1) | Onset Temp. (K) | Peak Temp. (K) | Final Temp. (K) |
|---|---|---|---|---|
| 1 | 5 | 625 | 687 | 694 |
| 2 | 10 | 630 | 700 | 713 |
| 3 | 20 | 650 | 725 | 740 |
| 4 | 30 | 663 | 734 | 747 |
| 5 | 40 | 670 | 737 | 750 |
| Conversion | FR | FWO | KAS | STK | ||||
|---|---|---|---|---|---|---|---|---|
| Ea (kJ mol−1) | R2 | Ea (kJ mol−1) | R2 | Ea (kJ mol−1) | R2 | Ea (kJ mol−1) | R2 | |
| 0.1 | 92 | 0.9634 | 80 | 0.9937 | 73 | 0.9920 | 71 | 0.9921 |
| 0.2 | 110 | 0.9637 | 90 | 0.9829 | 84 | 0.9784 | 84 | 0.9786 |
| 0.3 | 125 | 0.9818 | 99 | 0.9825 | 93 | 0.9783 | 109 | 0.9785 |
| 0.4 | 139 | 0.9739 | 106 | 0.9809 | 100 | 0.9765 | 101 | 0.9767 |
| 0.5 | 150 | 0.9573 | 119 | 0.9775 | 108 | 0.9726 | 108 | 0.9729 |
| 0.6 | 155 | 0.9597 | 120 | 0.9747 | 115 | 0.9695 | 115 | 0.9697 |
| 0.7 | 164 | 0.9671 | 126 | 0.9723 | 121 | 0.9669 | 121 | 0.9671 |
| 0.8 | 167 | 0.9643 | 132 | 0.9703 | 127 | 0.9647 | 127 | 0.9650 |
| 0.9 | 166 | 0.9535 | 136 | 0.9676 | 132 | 0.9618 | 132 | 0.9621 |
| Average | 141 | 0.9650 | 112 | 0.9780 | 106 | 0.9734 | 108 | 0.9736 |
| References | E (kJ mol−1) | Method |
|---|---|---|
| Aboulkas et al. (2010) [7] | 179–183 | FR, FWO, KAS |
| Wu et al. (1993) [4] | 184 | FR |
| Paik and Kar (2008) [24] | 67–241 125–224 | FR FWO |
| Galiwango and Gabbar (2022) [11] | 165.54 159.72 187.25 | FWO FR CR |
| Mortezaeikia et al. (2021) [25] | 261.22 196–214 | KAS KAS |
| Reaction Mechanism | Code | Test 1 PP-5 | Test 2 PP-10 | Test 3 PP-20 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ea (kJ mol−1) | ln (A0) | R2 | Ea (kJ mol−1) | ln (A0) | R2 | Ea (kJ mol−1) | ln (A0) | R2 | ||
| Reaction order models—First-order | F1 | 125 | 20.51 | 0.9994 | 143 | 23.85 | 0.9994 | 179 | 29.59 | 0.9988 |
| Reaction order models—Second-order | F2 | 168 | 29.13 | 0.9976 | 186 | 32.07 | 0.9972 | 214 | 35.93 | 0.9973 |
| Reaction order models—Third-order | F3 | 220 | 39.16 | 0.9953 | 236 | 41.5 | 0.9945 | 252 | 42.94 | 0.9955 |
| Diffusion models—One-dimension | D1 | 189 | 31.5 | 0.9999 | 225 | 37.76 | 0.9999 | 307 | 50.87 | 0.9996 |
| Diffusion models—Two-dimension | D2 | 210 | 35 | 1.0000 | 247 | 41.21 | 1 | 327 | 53.68 | 0.9995 |
| Diffusion models—Three-dimension | D3 | 235 | 38.32 | 0.9998 | 271 | 44.38 | 0.9998 | 348 | 55.96 | 0.9992 |
| Nucleation models—Two-dimension | A2 | 57 | 13.29 | 0.9993 | 66 | 12.9 | 0.9993 | 84 | 12.98 | 0.9982 |
| Nucleation models—Three-dimension | A3 | 34 | 16.82 | 0.9992 | 40 | 16.87 | 0.9992 | 52 | 16.26 | 0.9985 |
| Nucleation models—Fourth-dimension | A4 | 23 | 18.45 | 0.999 | 27 | 18.71 | 0.9993 | 36 | 18.54 | 0.9987 |
| Geometrical contraction models—One-dimension phase boundary | R1 | 89 | 13.33 | 0.9999 | 107 | 16.88 | 0.9999 | 148 | 23.91 | 0.9996 |
| Geometrical contraction models—Contracting sphere | R2 | 106 | 16.05 | 0.9999 | 124 | 19.52 | 0.9999 | 163 | 25.97 | 0.9993 |
| Geometrical contraction models—Contracting cylinder | R3 | 112 | 16.86 | 0.9998 | 130 | 20.29 | 0.9998 | 168 | 26.52 | 0.9992 |
| Nucleation models—Power law | P2 | 39 | 16.33 | 0.9999 | 48 | 15.92 | 0.9999 | 68 | 13.99 | 0.9996 |
| Nucleation models—Power law | P3 | 22 | 18.66 | 0.9998 | 28 | 18.74 | 0.9999 | 42 | 17.88 | 0.9995 |
| Nucleation models—Power law | P4 | 14 | 19.66 | 0.9997 | 18 | 19.97 | 0.9998 | 28 | 19.66 | 0.9994 |
| Reaction Mechanism | Code | Test 4 PP-30 | Test 5 PP-40 | |||||||
| Ea (kJ mol−1) | ln (A0) | R2 | Ea (kJ mol−1) | ln (A0) | R2 | |||||
| Reaction order models—First-order | F1 | 198 | 32.87 | 0.9989 | 212 | 35.29 | 0.9984 | |||
| Reaction order models—Second-order | F2 | 245 | 41.15 | 0.9972 | 251 | 42.14 | 0.9969 | |||
| Reaction order models—Third-order | F3 | 297 | 50.45 | 0.9953 | 293 | 49.67 | 0.9952 | |||
| Diffusion models—One-dimension | D1 | 328 | 53.87 | 0.9999 | 367 | 60.477 | 0.9995 | |||
| Diffusion models—Two-dimension | D2 | 352 | 57.59 | 0.9997 | 388 | 63.6 | 0.9993 | |||
| Diffusion models—Three-dimension | D3 | 380 | 60.95 | 0.9993 | 412 | 66.21 | 0.9989 | |||
| Nucleation models—Two-dimension | A2 | 93 | 14.85 | 0.9987 | 100 | 16.24 | 0.9983 | |||
| Nucleation models—Three-dimension | A3 | 58 | 15.88 | 0.9986 | 63 | 15.56 | 0.9981 | |||
| Nucleation models—Fourth-dimension | A4 | 41 | 18.41 | 0.9984 | 44 | 15.2 | 0.9978 | |||
| Geometrical contraction models—One-dimension phase boundary | R1 | 158 | 25.63 | 0.9998 | 177 | 29.13 | 0.9995 | |||
| Geometrical contraction models—Contracting sphere | R2 | 177 | 28.43 | 0.9995 | 194 | 31.43 | 0.9991 | |||
| Geometrical contraction models—Contracting cylinder | R3 | 184 | 29.24 | 0.9993 | 200 | 32.06 | 0.9989 | |||
| Nucleation models—Power law | P2 | 73 | 13.86 | 0.9998 | 83 | 13.07 | 0.9995 | |||
| Nucleation models—Power law | P3 | 45 | 17.97 | 0.9998 | 51 | 17.34 | 0.9994 | |||
| Nucleation models—Power law | P4 | 31 | 19.89 | 0.9998 | 35 | 19.52 | 0.9993 | |||
| Test No. | Ea (kJ/mol) | ln (A0) | R2 | Reaction Mechanism |
|---|---|---|---|---|
| 1 | 112 | 16.86 | 0.9998 | Geometrical contraction models—Contracting cylinder (R3) |
| 2 | 130 | 20.29 | 0.9998 | Geometrical contraction models—Contracting cylinder (R3) |
| 3 | 168 | 26.52 | 0.9993 | Geometrical contraction models—Contracting cylinder (R3) |
| 4 | 184 | 29.24 | 0.9993 | Geometrical contraction models—Contracting cylinder (R3) |
| 5 | 200 | 32.06 | 0.9989 | Geometrical contraction models—Contracting cylinder (R3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubdub, I. Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis. Materials 2023, 16, 584. https://doi.org/10.3390/ma16020584
Dubdub I. Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis. Materials. 2023; 16(2):584. https://doi.org/10.3390/ma16020584
Chicago/Turabian StyleDubdub, Ibrahim. 2023. "Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis" Materials 16, no. 2: 584. https://doi.org/10.3390/ma16020584
APA StyleDubdub, I. (2023). Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis. Materials, 16(2), 584. https://doi.org/10.3390/ma16020584






