Prediction of In-Flight Particle Properties and Mechanical Performances of HVOF-Sprayed NiCr–Cr3C2 Coatings Based on a Hierarchical Neural Network
Abstract
:1. Introduction
2. Experimental Procedures
2.1. HVOF Spray Process Parameters
2.2. Coating Microstructure Characterization
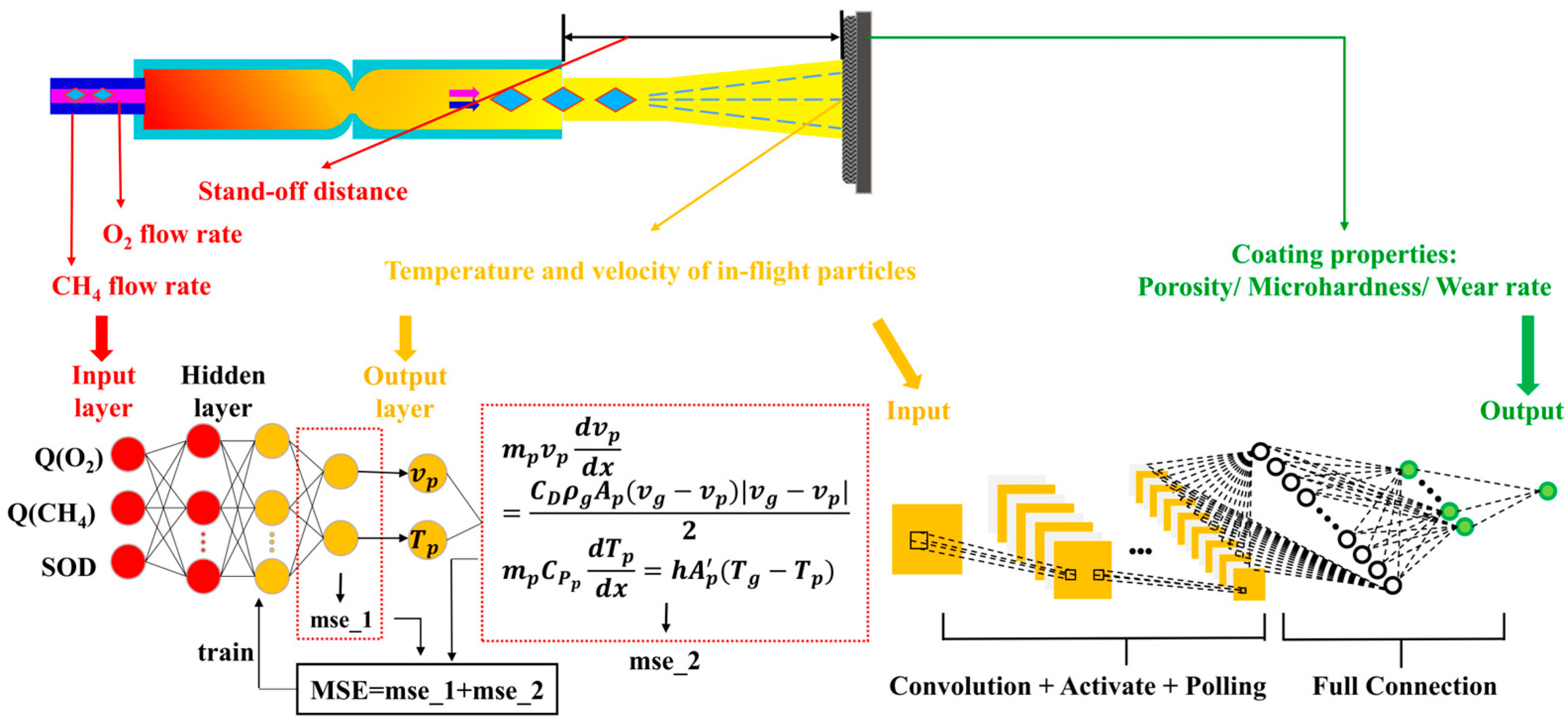
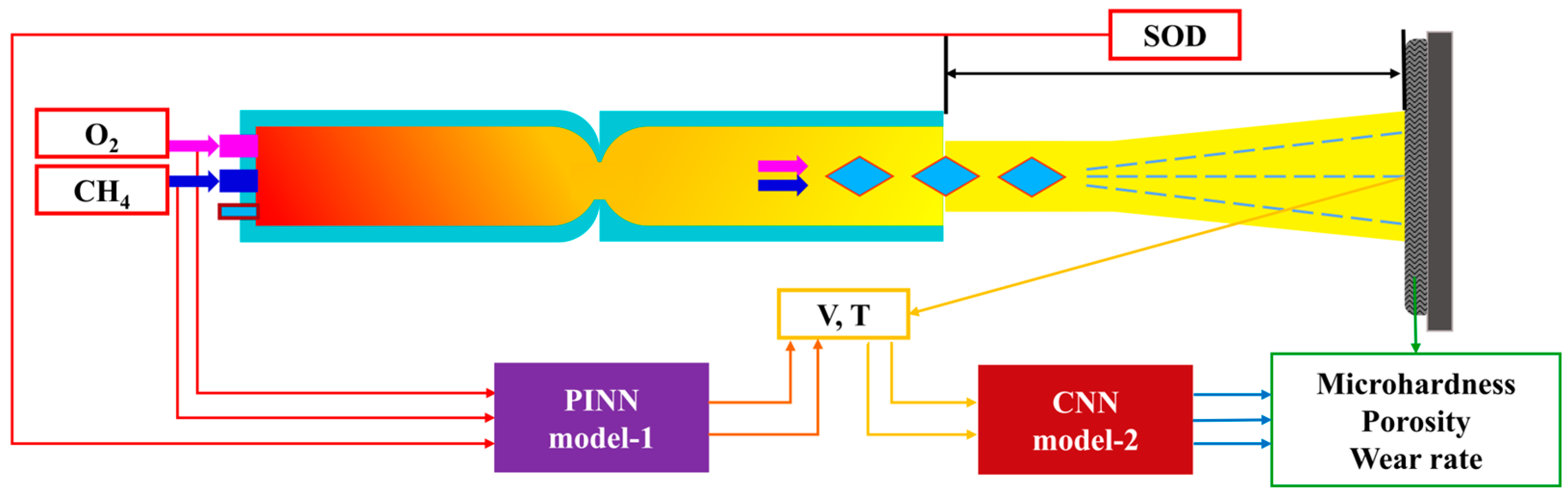
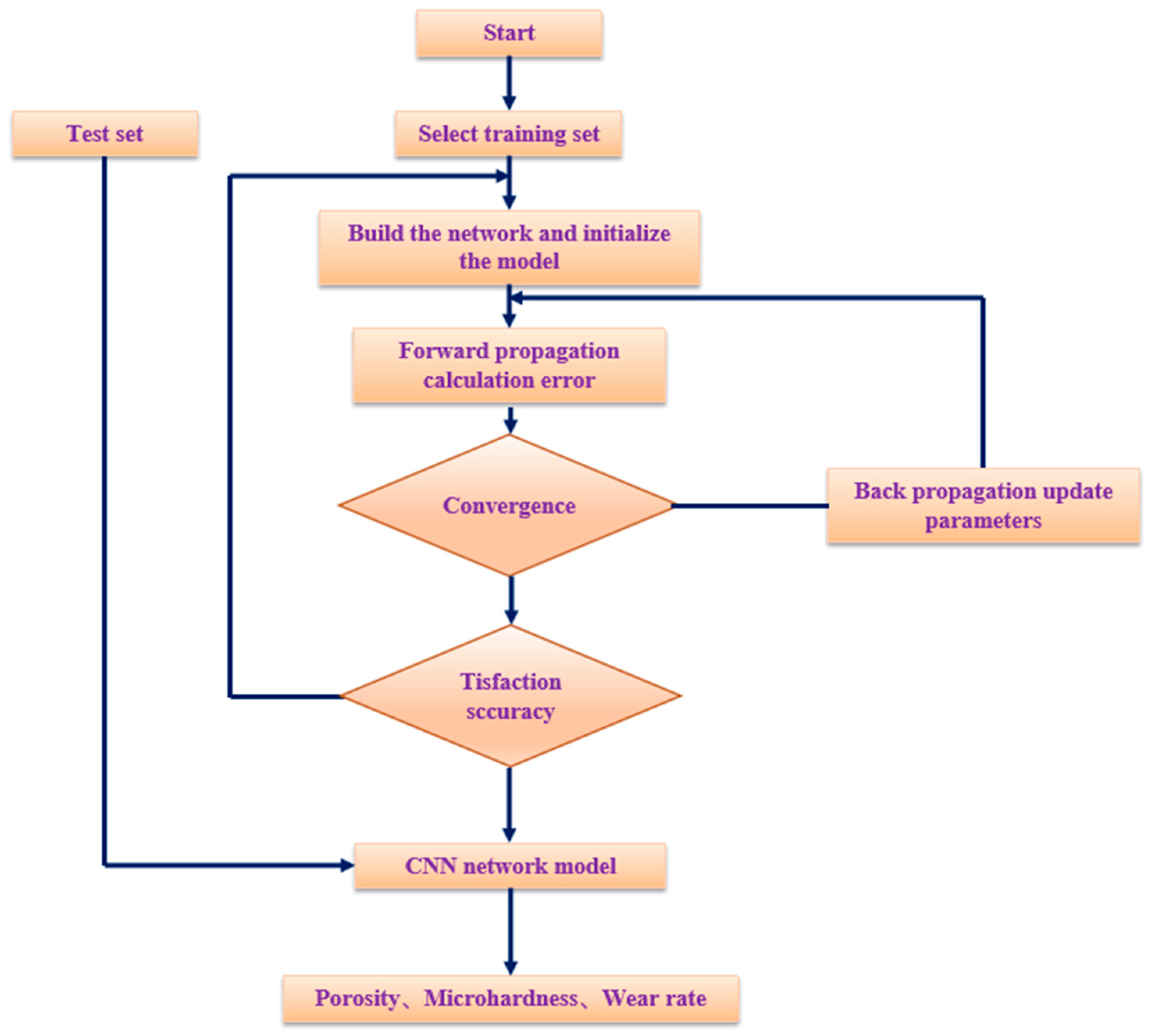
3. Hierarchical PINN-CNN Models and Their Implementations
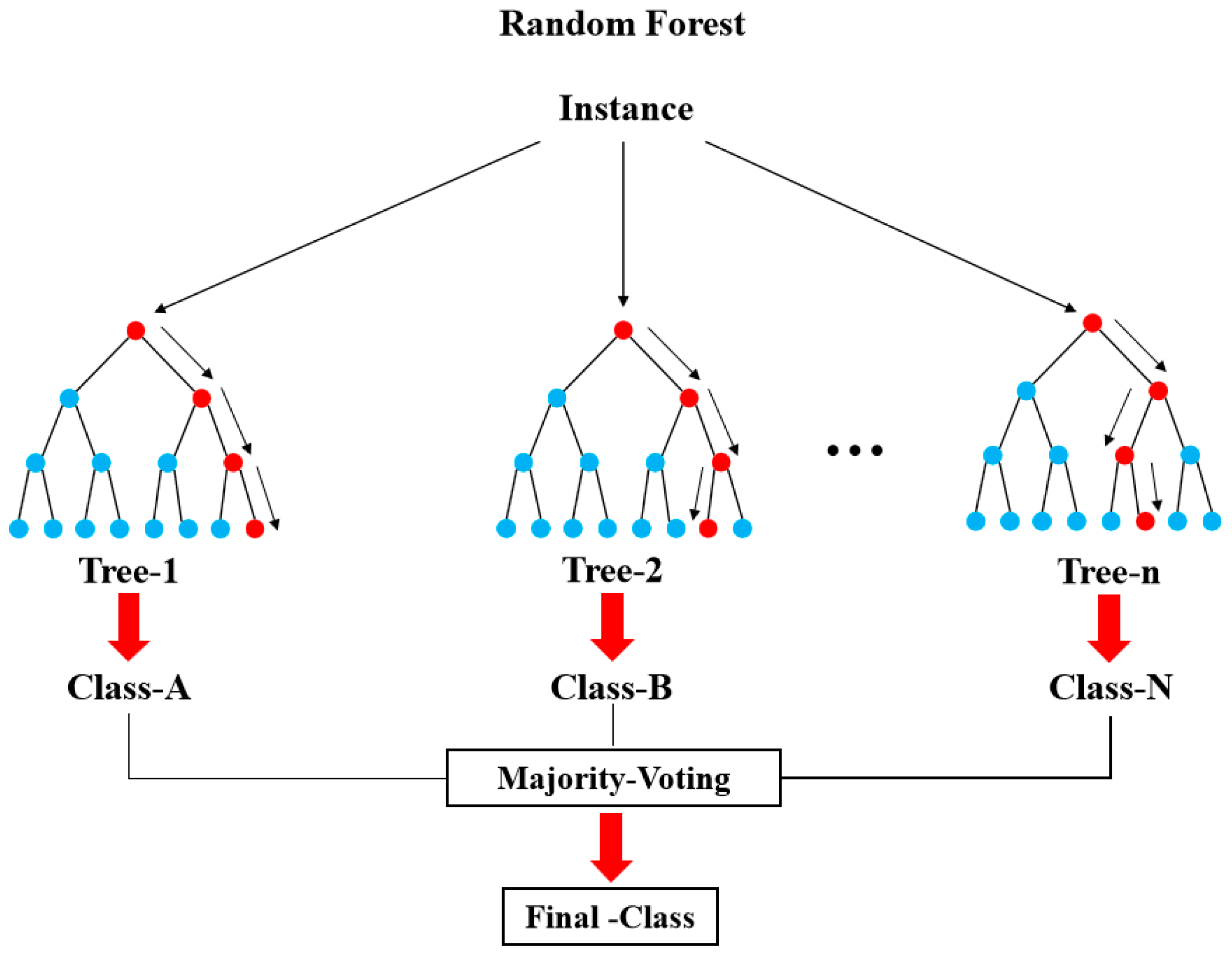
3.1. Feature Selection Based on the Random Forest (RF) Model
3.2. Data Collection and Preprocessing
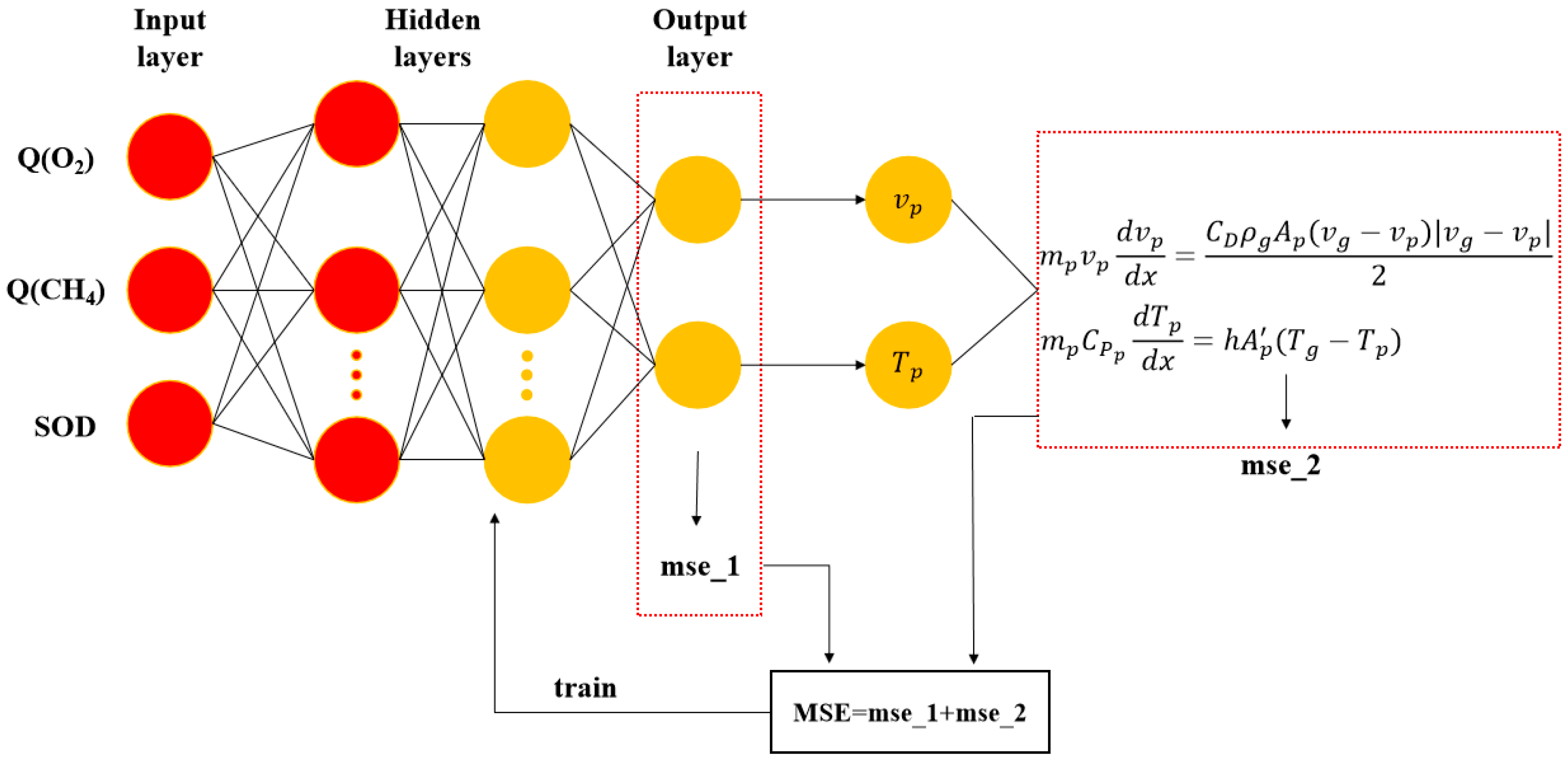
3.3. PINN Model: First-Layer Building, Training, and Validation
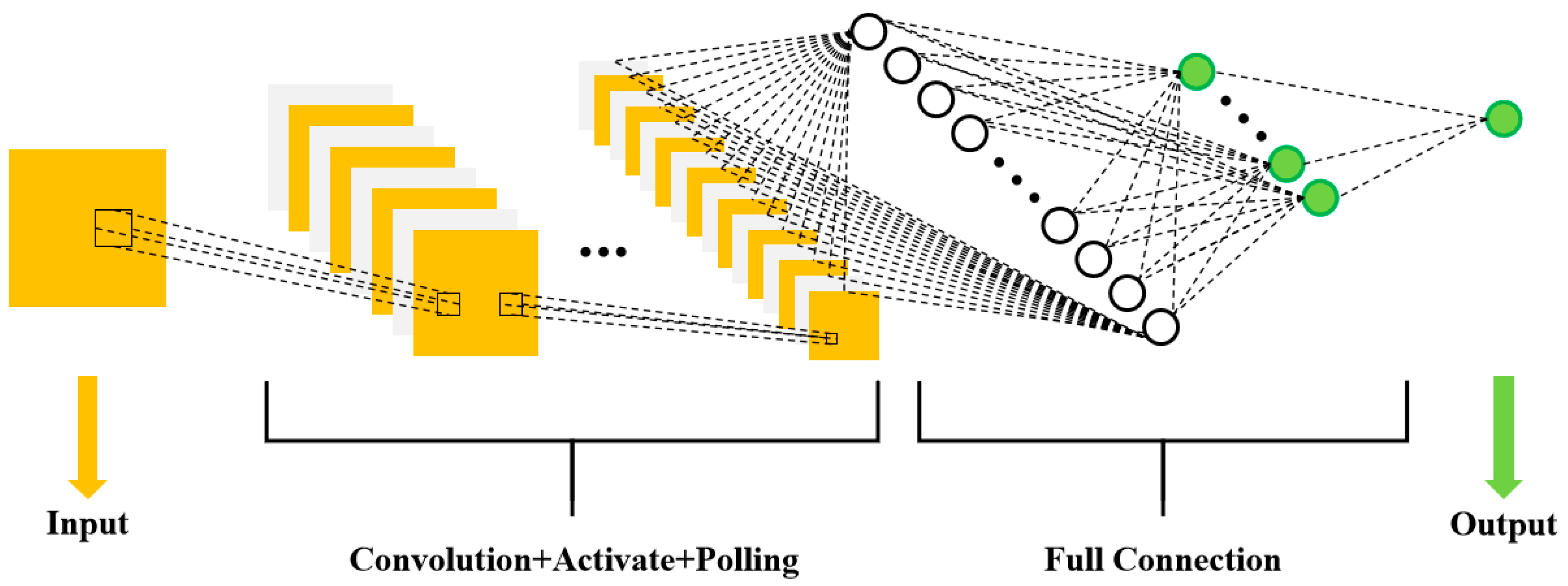
3.4. CNN Model: Building, Training, and Validation of the Second Layer
4. Results and Discussion
4.1. Analysis of RF Feature Selection Results
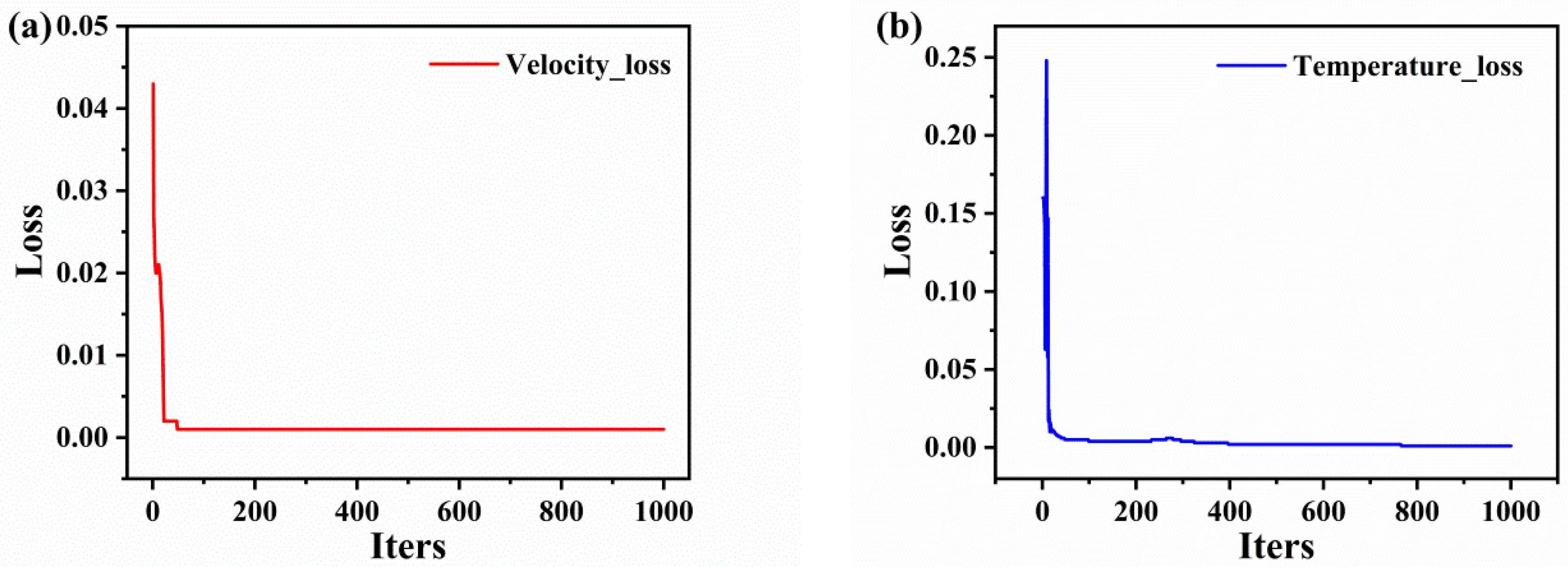
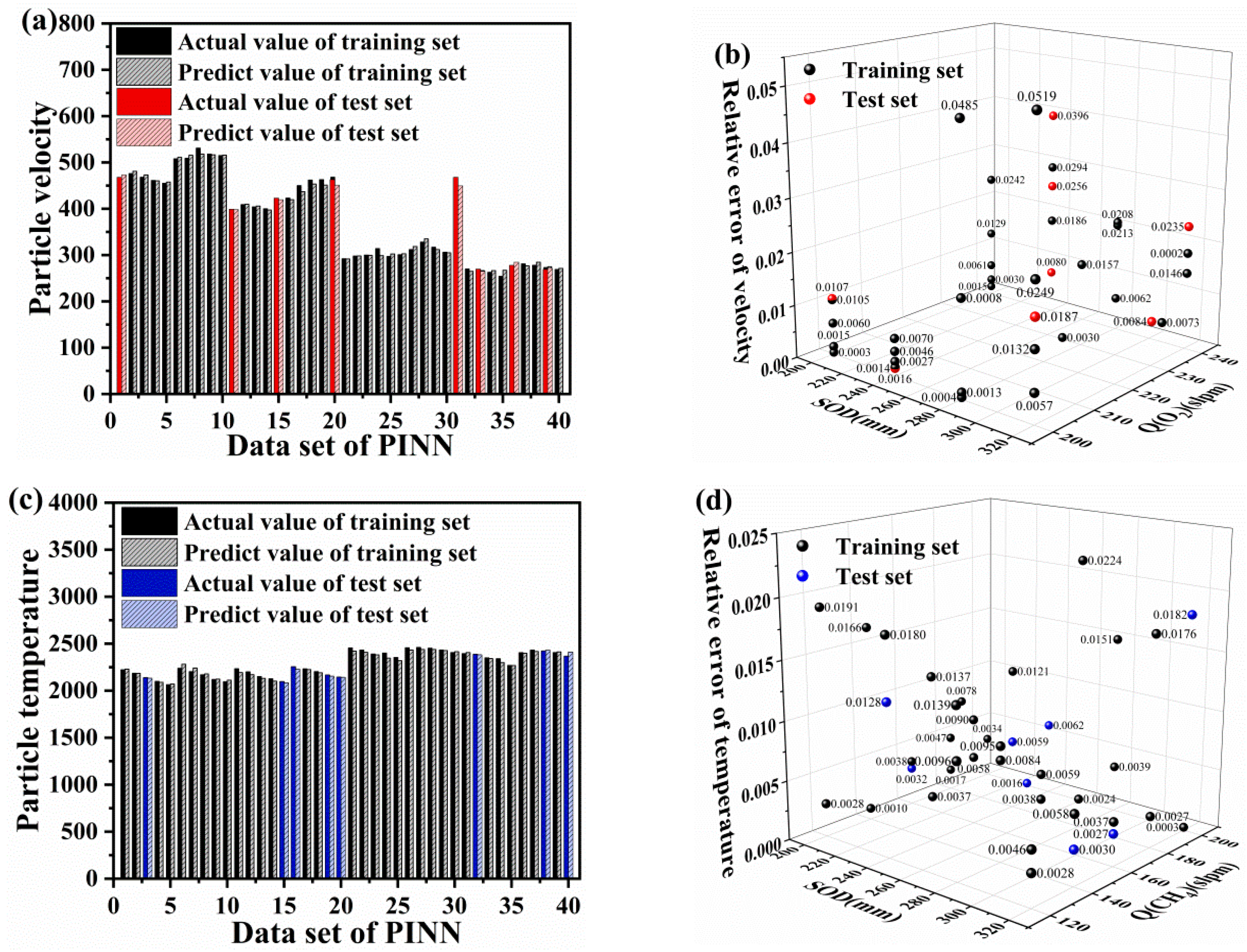
4.2. Analysis of the PINN Training Results
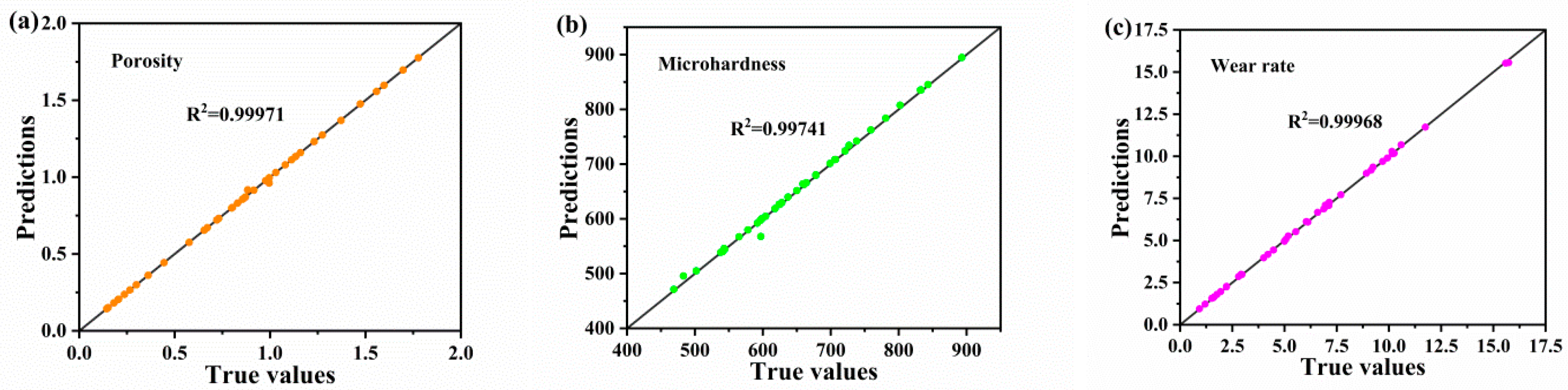
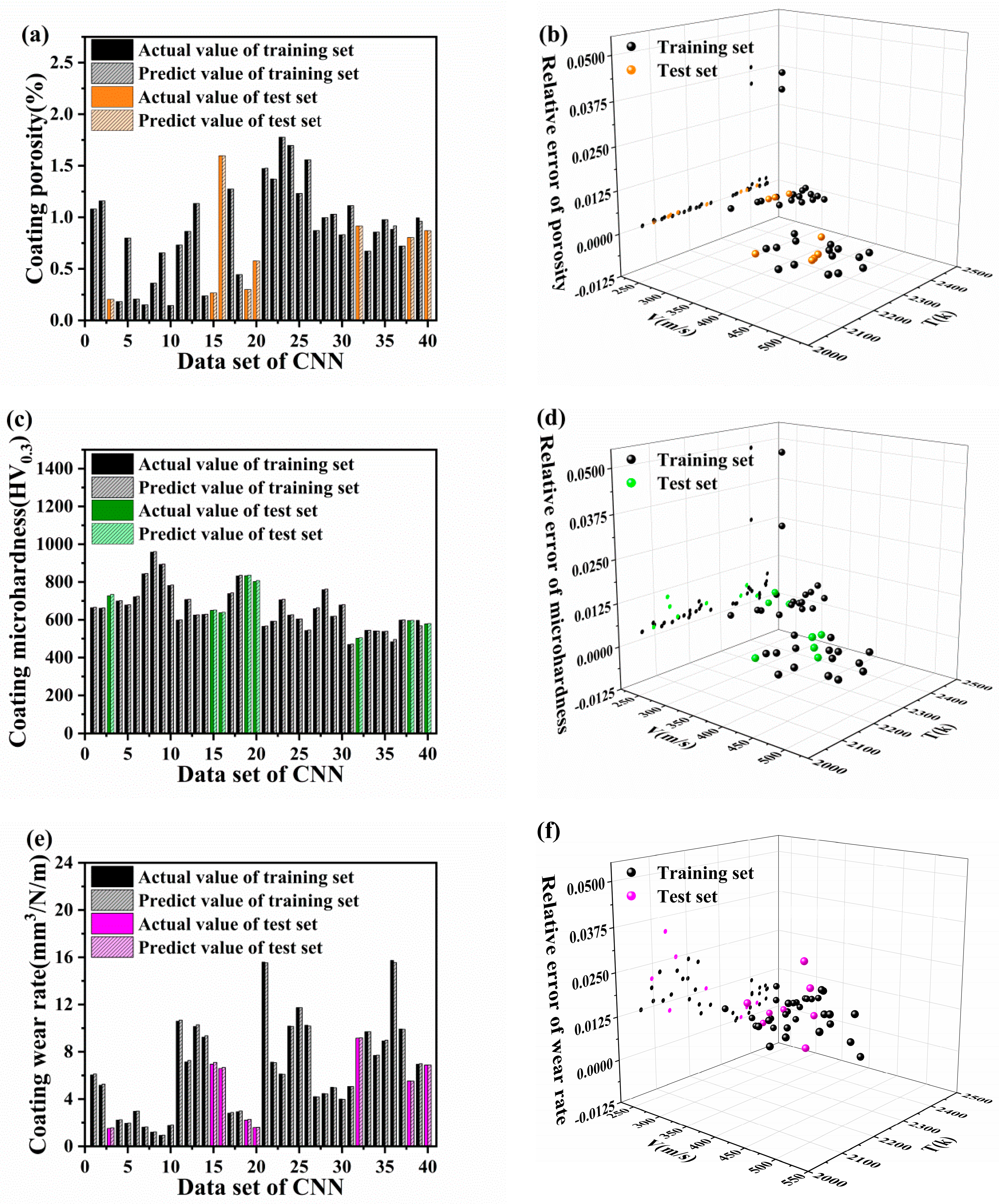
4.3. Analysis of the CNN Training Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raza, A.; Ahmad, F.; Badri, T.M.; Raza, M.; Malik, K. An influence of oxygen flow rate and spray distance on the porosity of HVOF coating and its effects on corrosion—A review. Materials 2022, 15, 6329. [Google Scholar] [CrossRef] [PubMed]
- Straffelini, G.; Federici, M. HVOF cermet coatings to improve sliding wear resistance in engineering systems. Coatings 2020, 10, 886. [Google Scholar] [CrossRef]
- Pradeep, D.; Venkatesh, C.; Nithin, H. Review on tribological and mechanical behavior in HVOF thermal-sprayed composite coatings. J. Bio-Tribo-Corros. 2022, 8, 30. [Google Scholar] [CrossRef]
- Silvello, A.; Cavaliere, P.; Yin, S.; Lupoi, R.; Garcia Cano, I.; Dosta, S. Microstructural, mechanical and wear behavior of HVOF and cold-sprayed high-entropy alloys (HEAs) coatings. J. Therm. Spray Technol. 2022, 31, 1184–1206. [Google Scholar] [CrossRef]
- Mittal, G.; Paul, S. Suspension and Solution Precursor Plasma and HVOF Spray: A Review. J. Therm. Spray Technol. 2022, 31, 1443–1475. [Google Scholar] [CrossRef]
- Kumar, R.; Kamaraj, M.; Seetharamu, S.; Pramod, T.; Sampathkumaran, P. Effect of spray particle velocity on cavitation erosion resistance characteristics of HVOF and HVAF processed 86WC-10Co4Cr hydro turbine coatings. J. Therm. Spray Technol. 2016, 25, 1217–1230. [Google Scholar] [CrossRef]
- Guo, X.; Planche, M.-P.; Chen, J.; Liao, H. Relationships between in-flight particle characteristics and properties of HVOF sprayed WC-CoCr coatings. J. Mater. Process. Technol. 2014, 214, 456–461. [Google Scholar] [CrossRef]
- Zhao, L.; Maurer, M.; Fischer, F.; Dicks, R.; Lugscheider, E. Influence of spray parameters on the particle in-flight properties and the properties of HVOF coating of WC-CoCr. Wear 2004, 257, 41–46. [Google Scholar] [CrossRef]
- Praveen, A.S.; Sarangan, J.; Suresh, S.; Channabasappa, B. Optimization and erosion wear response of NiCrSiB/WC–Co HVOF coating using Taguchi method. Ceram. Int. 2016, 42, 1094–1104. [Google Scholar] [CrossRef]
- Qiao, L.; Wu, Y.; Hong, S.; Zhang, J.; Shi, W.; Zheng, Y. Relationships between spray parameters, microstructures and ultrasonic cavitation erosion behavior of HVOF sprayed Fe-based amorphous/nanocrystalline coatings. Ultrason. Sonochem. 2017, 39, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Dongmo, E.; Wenzelburger, M.; Gadow, R. Analysis and optimization of the HVOF process by combined experimental and numerical approaches. Surf. Coat. Technol. 2008, 202, 4470–4478. [Google Scholar] [CrossRef]
- Pan, J.; Hu, S.; Yang, L.; Ding, K.; Ma, B. Numerical analysis of flame and particle behavior in an HVOF thermal spray process. Mater. Des. 2016, 96, 370–376. [Google Scholar] [CrossRef]
- Liu, M.; Yu, Z.; Wu, H.; Liao, H.; Zhu, Q.; Deng, S. Implementation of artificial neural networks for forecasting the HVOF spray process and HVOF sprayed coatings. J. Therm. Spray Technol. 2021, 30, 1329–1343. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Doan, T.H.; Tong, V.C. Multi-objective optimization of WC-12Co coating by high-velocity oxygen fuel spray using multiple regression-based weighted signal-to-noise ratio. Proc. Inst. Mech. Eng. Part B—J. Eng. Manuf. 2021, 235, 1168–1178. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Zhang, D.; Gao, H.; Han, X.; Zhang, B. Numerical Investigation on the Flame Characteristics and Particle Behaviors in a HVOF Spray Process Using Kerosene as Fuel. J. Therm. Spray Technol. 2021, 30, 725–738. [Google Scholar] [CrossRef]
- Oksa, M.; Turunen, E.; Suhonen, T.; Varis, T.; Hannula, S.P. Optimization and Characterization of High Velocity Oxy-fuel Sprayed Coatings: Techniques, Materials, and Applications. Coatings 2011, 1, 17–52. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Kou, L.; Zheng, L.; Zhang, H. Prediction of control parameters corresponding to in-flight particles in atmospheric plasma spray employing convolutional neural networks. Surf. Coat. Technol. 2020, 394, 125862. [Google Scholar] [CrossRef]
- Guessasma, S.; Montavon, G.; Coddet, C. Modeling of the APS plasma spray process using artificial neural networks: Basis, requirements and an example. Comput. Mater. Sci. 2004, 29, 315–333. [Google Scholar] [CrossRef]
- Sahraoui, T.; Guessasma, S.; Fenineche, N.; Montavon, G.; Coddet, C. Friction and wear behaviour prediction of HVOF coatings and electroplated hard chromium using neural computation. Mater. Lett. 2004, 58, 654–660. [Google Scholar] [CrossRef]
- Guessasma, S.; Montavon, G.; Coddet, C. Neural computation to predict in-flight particle characteristic dependences from processing parameters in the APS process. J. Therm. Spray Technol. 2004, 13, 570–585. [Google Scholar] [CrossRef]
- Guessasma, S.; Salhi, Z.; Montavon, G.; Gougeon, P.; Coddet, C. Artificial intelligence implementation in the APS process diagnostic. Mater. Sci. Eng. B 2004, 110, 285–295. [Google Scholar] [CrossRef]
- Choudhury, T.; Hosseinzadeh, N.; Berndt, C. Artificial Neural Network application for predicting in-flight particle characteristics of an atmospheric plasma spray process. Surf. Coat. Technol. 2011, 205, 4886–4895. [Google Scholar] [CrossRef]
- Zhang, C.; Kanta, A.F.; Li, C.X.; Li, C.J.; Planche, M.P.; Liao, H.L.; Coddet, C. Effect of in-flight particle characteristics on the coating properties of atmospheric plasma-sprayed 8 mol% Y2O3-ZrO2 electrolyte coating studying by artificial neural networks. Surf. Coat. Technol. 2009, 204, 463–469. [Google Scholar] [CrossRef]
- Mahendru, P.; Tembely, M.; Dolatabadi, A. Artificial Intelligence Models for Analyzing Thermally Sprayed Functional Coatings. J. Therm. Spray Technol. 2023, 32, 388–400. [Google Scholar] [CrossRef]
- Mojena, M.A.R.; Roca, A.S.; Zamora, R.S.; Orozco, M.S.; Fals, H.C.; Lima, C.R.C. Neural network analysis for erosive wear of hard coatings deposited by thermal spray: Influence of microstructure and mechanical properties. Wear 2017, 376, 557–565. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef] [PubMed]
- Finol, D.; Lu, Y.; Mahadevan, V.; Srivastava, A. Deep convolutional neural networks for eigenvalue problems in mechanics. Int. J. Numer. Methods Eng. 2019, 118, 258–275. [Google Scholar] [CrossRef]
- Zhang, J.S.; Jiang, Y.C.; Luo, H.; Yin, S. Prediction of material removal rate in chemical mechanical polishing via residual convolutional neural network. Control Eng. Pract. 2021, 107, 104673. [Google Scholar] [CrossRef]
- Lu, F.; Liang, Y.C.; Wang, X.Y.; Gao, T.H.; Chen, Q.; Liu, Y.C.; Zhou, Y.; Yuan, Y.K.; Liu, Y.T. Prediction of amorphous forming ability based on artificial neural network and convolutional neural network. Comput. Mater. Sci. 2022, 210, 111464. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Physics-informed deep learning for incompressible laminar flows. Theor. Appl. Mech. Lett. 2020, 10, 207–212. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Z.; Yan, J. Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput. Mech. 2021, 67, 619–635. [Google Scholar] [CrossRef]
- Zhang, X.C.; Gong, J.G.; Xuan, F.Z. A physics-informed neural network for creep-fatigue life prediction of components at elevated temperatures. Eng. Fract. Mech. 2021, 258, 108130. [Google Scholar] [CrossRef]
- Bobzin, K.; Wietheger, W.; Heinemann, H.; Dokhanchi, S.R.; Rom, M.; Visconti, G. Prediction of Particle Properties in Plasma Spraying Based on Machine Learning. J. Therm. Spray Technol. 2021, 30, 1751–1764. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Cai, S.; Chen, W.L.; Abd Ali, R.; Jin, K. Analysis of Critical Velocity of Cold Spray Based on Machine Learning Method with Feature Selection. J. Therm. Spray Technol. 2021, 30, 1213–1225. [Google Scholar] [CrossRef]




| Parameters | Scope |
|---|---|
| O2 flow (slpm) | 200–240 |
| CH4 flow (slpm) | 120–200 |
| Air flow (slpm) | 300 |
| Carrier gas flow (slpm) | 40 |
| stand-off distance (mm) | 200–320 |
| Spray gun speed (mm/s) | 400 |
| Powder feeding speed (g/min) | 30 |
| No. | Q(CH4) (slpm) | SOD (mm) | Q(O2) (slpm) | V (m/s) | T (K) | MH (HV0.3) | WR × 10−5 (mm3/N/m) | PO (% Area) |
|---|---|---|---|---|---|---|---|---|
| 1 | 120 | 200 | 200 | 467 | 2223 | 664 | 6.039 | 1.08 |
| 2 | 120 | 200 | 240 | 508 | 2239 | 721 | 2.962 | 0.206 |
| 3 | 120 | 240 | 200 | 389 | 2234 | 598 | 10.587 | 0.731 |
| 4 | 120 | 240 | 240 | 423 | 2256 | 637 | 6.585 | 1.597 |
| 5 | 120 | 280 | 200 | 292 | 2455 | 565 | 15.589 | 1.473 |
| 6 | 120 | 280 | 240 | 301 | 2457 | 543 | 10.249 | 1.558 |
| 7 | 120 | 320 | 200 | 269 | 2395 | 469 | 5.061 | 1.113 |
| 8 | 120 | 320 | 240 | 274 | 2405 | 483 | 15.732 | 0.883 |
| 9 | 140 | 200 | 200 | 476 | 2186 | 661 | 5.175 | 1.159 |
| 10 | 140 | 200 | 240 | 509 | 2204 | 843 | 1.624 | 0.151 |
| 11 | 140 | 240 | 200 | 409 | 2201 | 707 | 7.142 | 0.863 |
| 12 | 140 | 240 | 240 | 450 | 2233 | 738 | 2.802 | 1.274 |
| 13 | 140 | 280 | 200 | 298 | 2432 | 592 | 7.122 | 1.372 |
| 14 | 140 | 280 | 240 | 312 | 2460 | 659 | 4.203 | 0.871 |
| 15 | 140 | 320 | 200 | 270 | 2388 | 502 | 9.154 | 0.915 |
| 16 | 140 | 320 | 240 | 281 | 2432 | 598 | 9.927 | 0.721 |
| 17 | 160 | 200 | 200 | 468 | 2139 | 727 | 1.516 | 0.204 |
| 18 | 160 | 200 | 240 | 531 | 2170 | 958 | 1.197 | 0.361 |
| 19 | 160 | 240 | 200 | 404 | 2151 | 625 | 10.144 | 1.134 |
| 20 | 160 | 240 | 240 | 462 | 2204 | 832 | 2.926 | 0.444 |
| 21 | 160 | 280 | 200 | 300 | 2390 | 706 | 6.122 | 1.777 |
| 22 | 160 | 280 | 240 | 328 | 2453 | 759 | 4.467 | 0.996 |
| 23 | 160 | 320 | 200 | 265 | 2350 | 544 | 9.698 | 0.671 |
| 24 | 160 | 320 | 240 | 278 | 2423 | 596 | 5.54 | 0.803 |
| 25 | 180 | 200 | 200 | 461 | 2099 | 699 | 2.217 | 0.182 |
| 26 | 180 | 200 | 240 | 518 | 2120 | 893 | 0.926 | 0.655 |
| 27 | 180 | 240 | 200 | 400 | 2127 | 628 | 9.235 | 0.237 |
| 28 | 180 | 240 | 240 | 463 | 2167 | 833 | 2.221 | 0.299 |
| 29 | 180 | 280 | 200 | 314 | 2400 | 624 | 10.172 | 1.697 |
| 30 | 180 | 280 | 230 | 317 | 2433 | 618 | 4.997 | 1.03 |
| 31 | 180 | 320 | 200 | 263 | 2341 | 541 | 7.693 | 0.856 |
| 32 | 180 | 320 | 233 | 273 | 2406 | 597 | 6.941 | 0.995 |
| 33 | 186 | 200 | 240 | 515 | 2096 | 781 | 1.764 | 0.144 |
| 34 | 188 | 240 | 240 | 468 | 2145 | 802 | 1.59 | 0.576 |
| 35 | 200 | 200 | 200 | 455 | 2064 | 678 | 1.944 | 0.799 |
| 36 | 200 | 240 | 200 | 399 | 2097 | 650 | 6.955 | 0.266 |
| 37 | 200 | 280 | 200 | 297 | 2354 | 604 | 11.741 | 1.231 |
| 38 | 200 | 280 | 225 | 306 | 2406 | 678 | 4.001 | 0.83 |
| 39 | 200 | 320 | 200 | 254 | 2269 | 538 | 8.92 | 0.977 |
| 40 | 200 | 320 | 230 | 269 | 2368 | 578 | 6.881 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, L.; Wang, B.; Cai, R.; Yu, Z.; Liu, M.; Zhu, Q.; Xie, Y.; Liu, S.; Killinger, A. Prediction of In-Flight Particle Properties and Mechanical Performances of HVOF-Sprayed NiCr–Cr3C2 Coatings Based on a Hierarchical Neural Network. Materials 2023, 16, 6279. https://doi.org/10.3390/ma16186279
Gui L, Wang B, Cai R, Yu Z, Liu M, Zhu Q, Xie Y, Liu S, Killinger A. Prediction of In-Flight Particle Properties and Mechanical Performances of HVOF-Sprayed NiCr–Cr3C2 Coatings Based on a Hierarchical Neural Network. Materials. 2023; 16(18):6279. https://doi.org/10.3390/ma16186279
Chicago/Turabian StyleGui, Longen, Botong Wang, Renye Cai, Zexin Yu, Meimei Liu, Qixin Zhu, Yingchun Xie, Shaowu Liu, and Andreas Killinger. 2023. "Prediction of In-Flight Particle Properties and Mechanical Performances of HVOF-Sprayed NiCr–Cr3C2 Coatings Based on a Hierarchical Neural Network" Materials 16, no. 18: 6279. https://doi.org/10.3390/ma16186279
APA StyleGui, L., Wang, B., Cai, R., Yu, Z., Liu, M., Zhu, Q., Xie, Y., Liu, S., & Killinger, A. (2023). Prediction of In-Flight Particle Properties and Mechanical Performances of HVOF-Sprayed NiCr–Cr3C2 Coatings Based on a Hierarchical Neural Network. Materials, 16(18), 6279. https://doi.org/10.3390/ma16186279






