Study of Effective Stress Intensity Factor through the CJP Model Using Full-Field Experimental Data
Abstract
:1. Introduction
2. Mathematical Description of the Crack Tip Fields According to the CJP Model
3. Experimental Campaign
4. Experimental Methodology
4.1. Calculating Crack Tip Parameters from TSA and DIC Data
4.1.1. Methodology for Fitting Thermoelastic Data
4.1.2. Methodology for Fitting Digital Image Correlation Data
4.2. Determination of the Thermal Calibration Contants
5. Results and Discussion
6. Conclusions
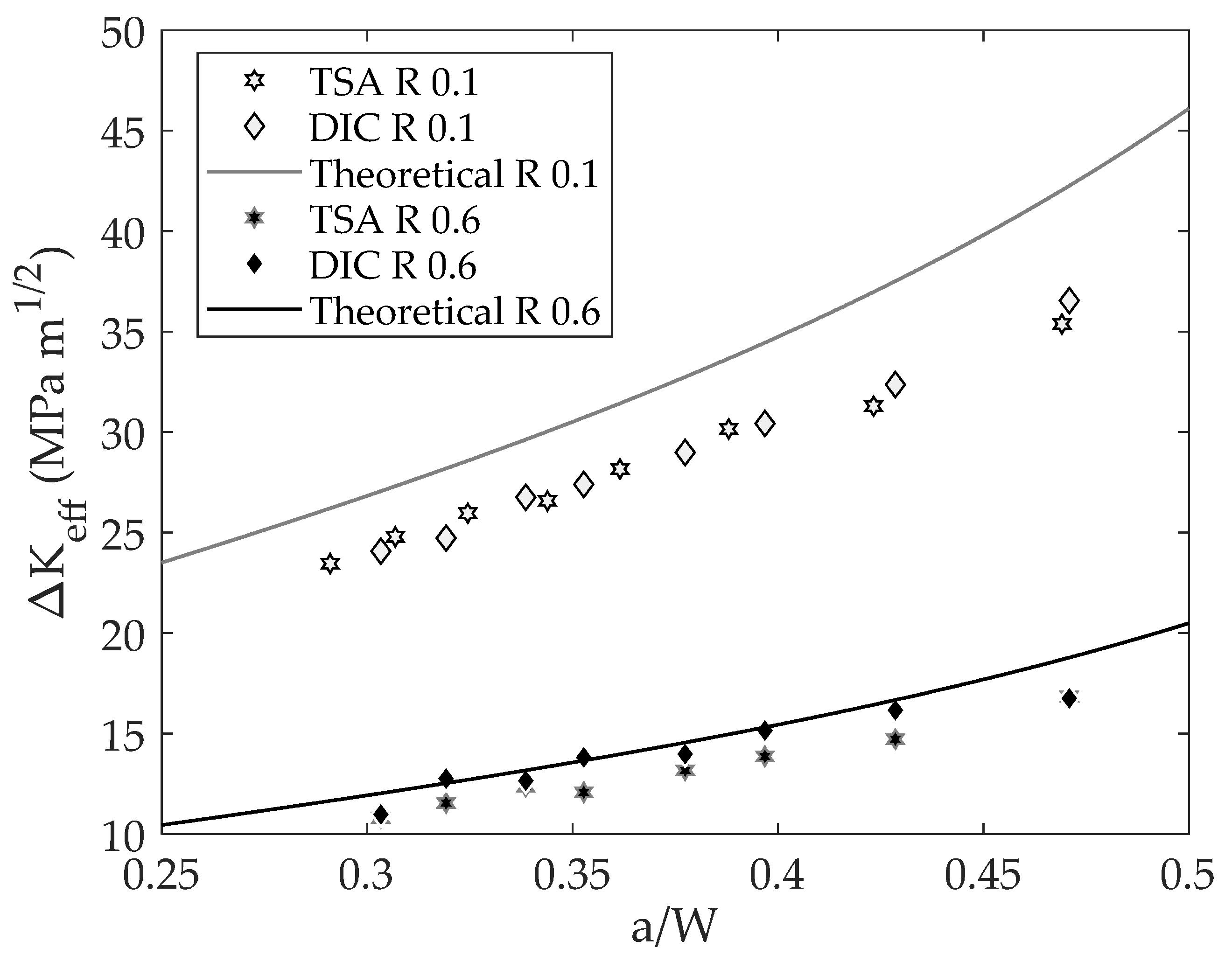
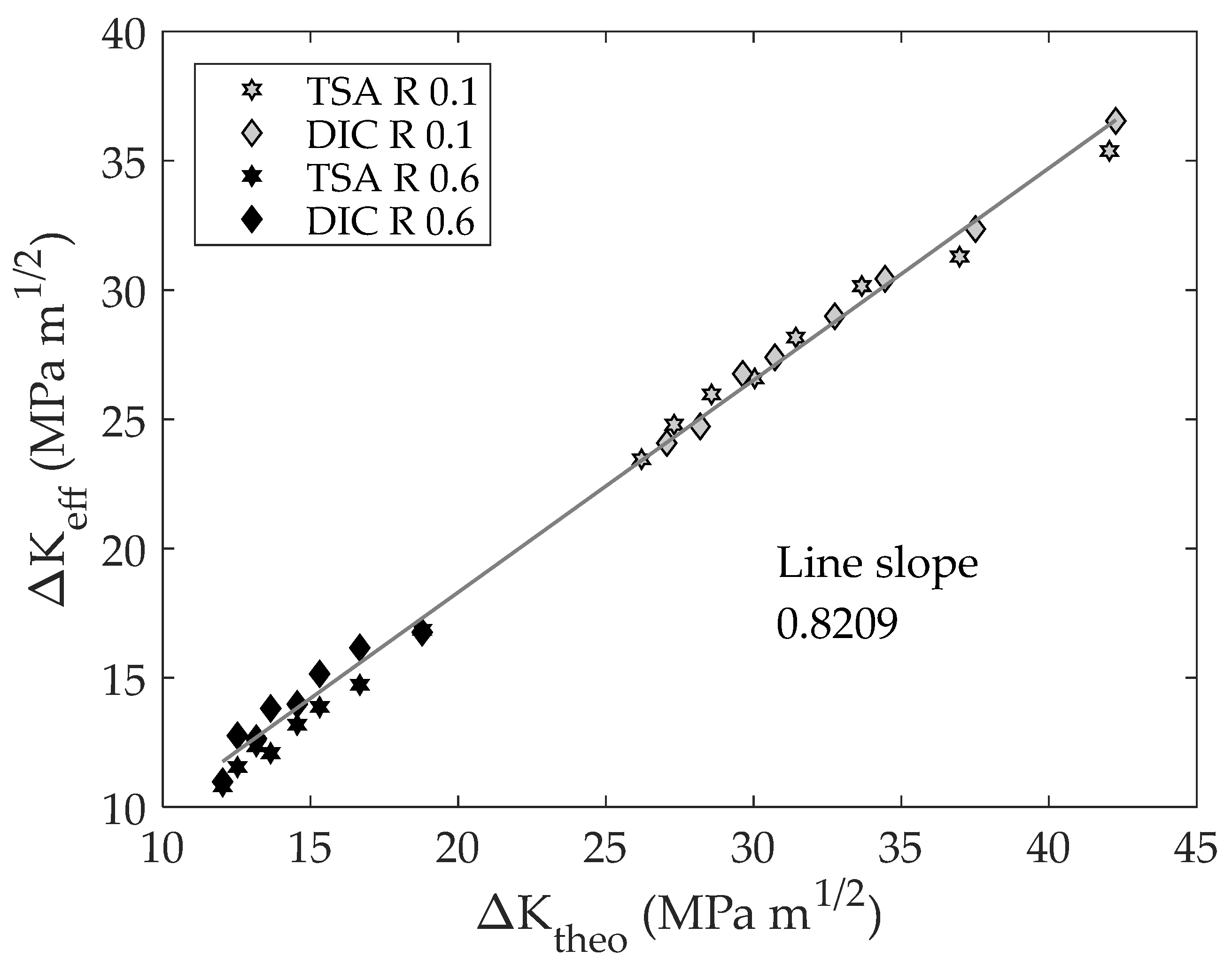
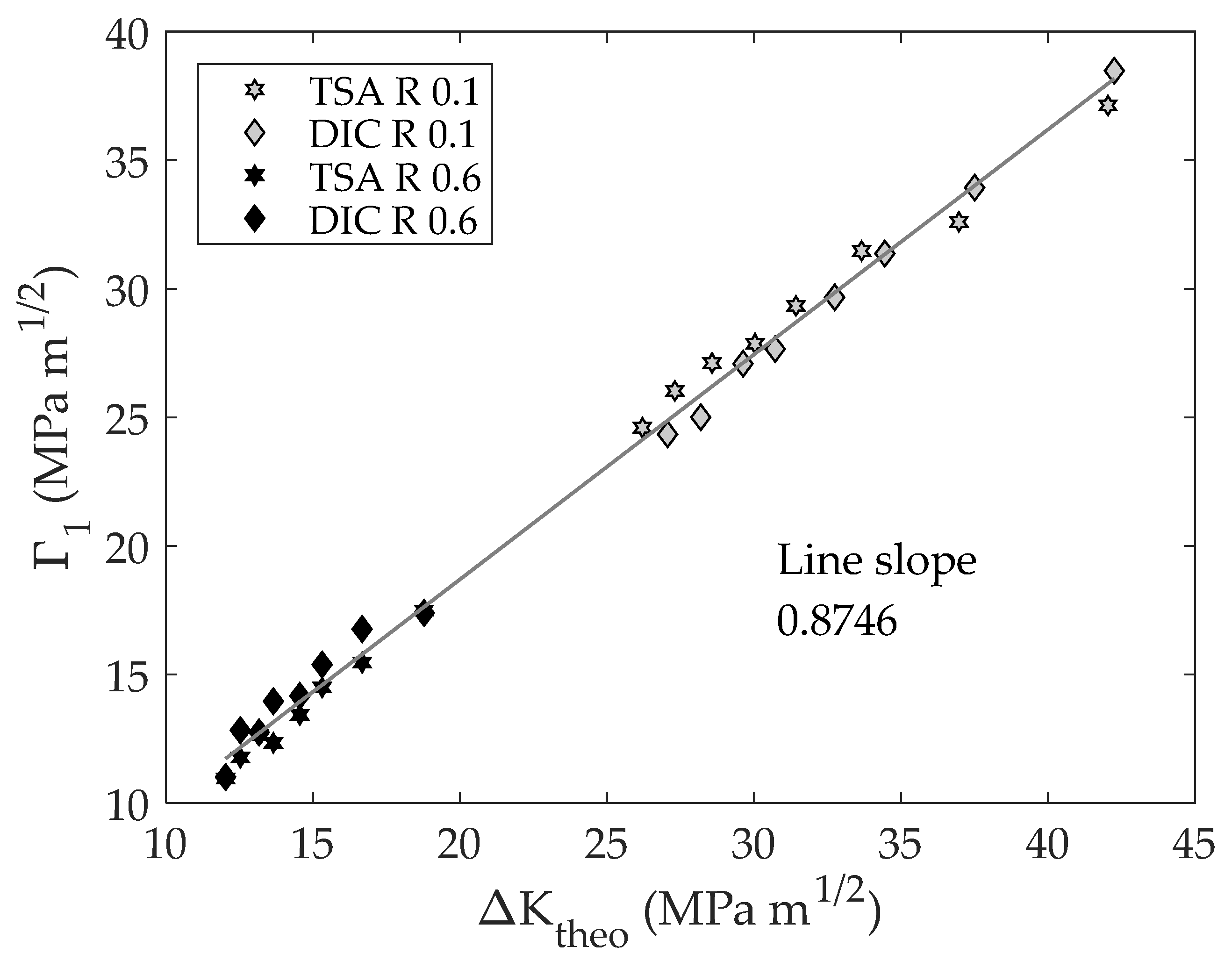
- There is convergence between the obtained SIF ranges from TSA and DIC data (mean deviation between data of around 2%) indicating the validity of the obtained results.
- The CJP model effective stress intensity factor range provides an effective rationalization of fatigue crack growth rates since those values fall along the same power law when ΔKeff is used as the fatigue crack driving force.
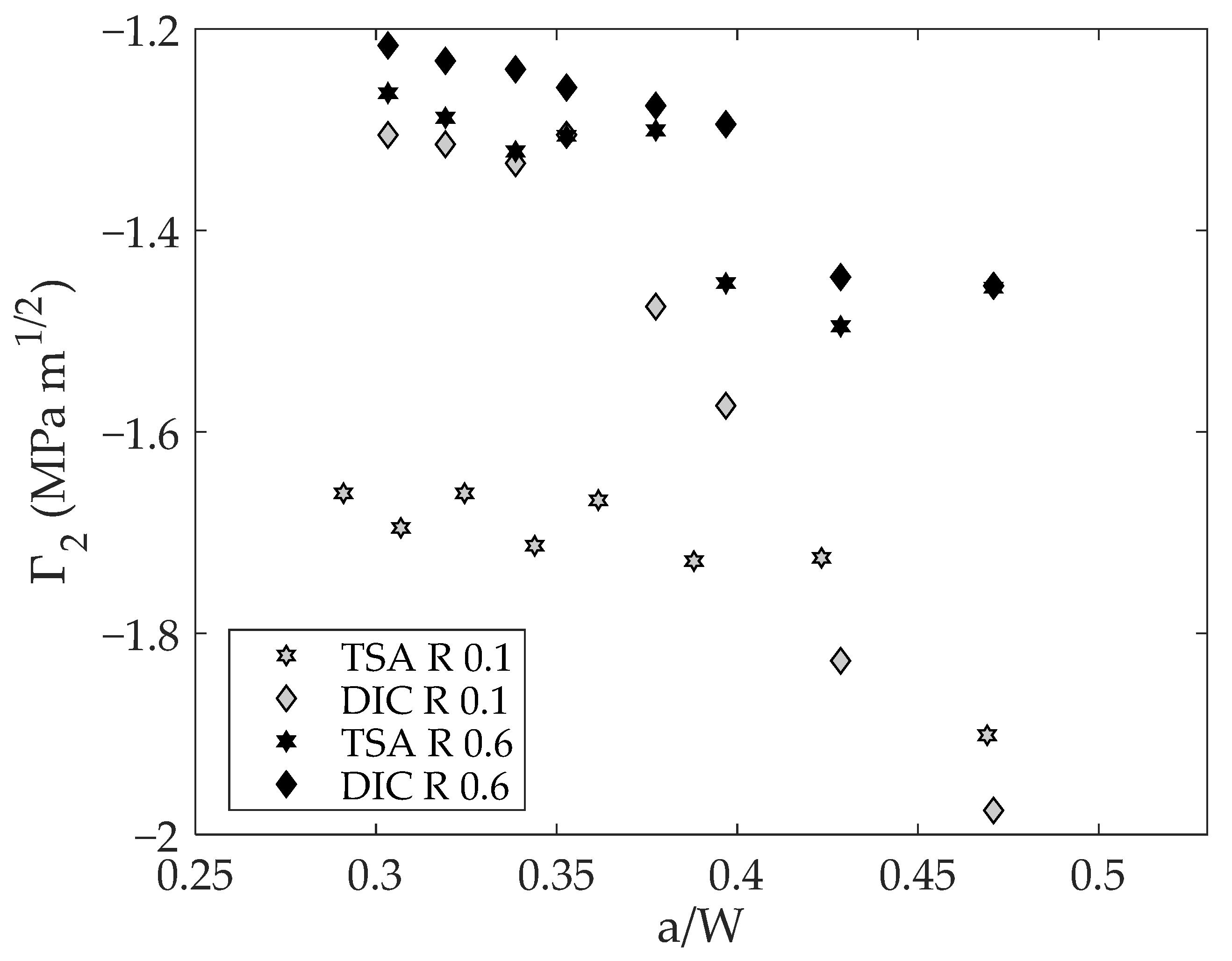
- The CJP model is able to quantify both the elastic and the retardation components of the stress intensity existing at the tip of a fatigue crack.
- The CJP model also demonstrates that crack closure is not the only factor involved in crack growth retardation, and it is important to consider the effects of the crack tip plasticity during fatigue crack growth (crack shielding), which can reduce the value of the effective SIF up to 7%, to a proper modelling of fatigue crack growth rates using Paris’s law.
- Further study might consider a recent and novel formulation of the CJP model also including the crack-blunting effect [41].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christopher, C.J.; James, M.N.; Patterson, E.A.; Tee, K.F. Towards a New Model of Crack Tip Stress Fields. Int. J. Fract. 2007, 148, 361–371. [Google Scholar] [CrossRef]
- Christopher, C.J.; James, M.N.; Patterson, E.A.; Tee, K.F. A Quantitative Evaluation of Fatigue Crack Shielding Forces Using Photoelasticity. Eng. Fract. Mech. 2008, 75, 4190–4199. [Google Scholar] [CrossRef]
- James, M.N.; Christopher, C.J.; Lu, Y.W.; Patterson, E.A. Local Crack Plasticity and Its Influences on the Global Elastic Stress Field. Int. J. Fatigue 2013, 46, 4–15. [Google Scholar] [CrossRef]
- Christopher, C.J.; Laboviciute, G.; James, M.N.; Patterson, E.A. Extension of the CJP Model to Mixed Mode I and Mode II. Frat. Integrita Strutt. 2013, 7, 161–166. [Google Scholar] [CrossRef]
- Elber, W. Fatigue Crack Closure under Cyclic Tension. Eng. Fract. Mech. 1970, 2, 37–44. [Google Scholar] [CrossRef]
- Elber, W. The Significance of Fatigue Crack Closure; ASTM Special Technical Publication; ASTM: West Conshohocken, PA, USA, 1971; pp. 230–242. [Google Scholar] [CrossRef]
- Ritchie, R.O. Mechanisms of Fatigue Crack Propagation in Metals, Ceramics and Composites: Role of Crack Tip Shielding. Mater. Sci. Eng. A 1988, 103, 15–28. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Plastic Stress and Strain Fields at a Crack Tip. J. Mech. Phys. Solids 1968, 16, 337–342. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Thomson, W.; Lord, K. On the Thermoelastic, Thermomagnetic and Pyro-Electric Properties of Matters. Philos. Mag. 1878, 5, 4–27. [Google Scholar] [CrossRef]
- Brewster, D. On the Communication of the Structure of Doubly Refracting Crystals to Glass, Muriate of Soda, Flour Spar and Other Substances by Mechanical Compression and Dilatation. Philos. Mag. 1816, 106, 156–178. [Google Scholar]
- Sutton, M.A.; Orteu, J.J.; Schreier, H.W. Image Correlation for Shape, Motion and Deformation Measurements; Springer: New York, NY, USA, 2009; ISBN 978-0-387-78746-6. [Google Scholar]
- Nurse, A.D.; Patterson, E.A. Photoelastic Determination of Fatigue-Crack Stress Intensity Factors. In Nondestructive Inspection of Aging Aircraft; Valley, M.T., DelGrande, N.K., Kobayashi, A., Eds.; SPIE: Bellingham, WA, USA, 1993; Volume 2001, pp. 155–162. [Google Scholar]
- Pacey, M.N.; James, M.N.; Patterson, E.A. A New Photoelastic Model for Studying Fatigue Crack Closure. Exp. Mech. 2005, 45, 42–52. [Google Scholar] [CrossRef]
- Lopez-Crespo, P.; Shterenlikht, A.; Yates, J.R.; Patterson, E.A.; Withers, P.J. Some Experimental Observations on Crack Closure and Crack-Tip Plasticity. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 418–429. [Google Scholar] [CrossRef]
- Rabbolini, S.; Beretta, S.; Foletti, S.; Cristea, M.E. Crack Closure Effects during Low Cycle Fatigue Propagation in Line Pipe Steel: An Analysis with Digital Image Correlation. Eng. Fract. Mech. 2015, 148, 441–456. [Google Scholar] [CrossRef]
- Diaz, F.A.; Vasco-Olmo, J.M.; Lopez-Alba, E.; Felipe-Sese, L.; Molina-Viedma, A.J.; Nowell, D. Experimental Evaluation of Effective Stress Intensity Factor Using Thermoelastic Stress Analysis and Digital Image Correlation. Int. J. Fatigue 2020, 135, 105567. [Google Scholar] [CrossRef]
- Camacho-Reyes, A.; Vasco-Olmo, J.M.; James, M.N.; Diaz, F.A. A Higher Order Thermoelastic Analysis of Fatigue Crack Growth Can Assess Crack Tip Shielding. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1596–1612. [Google Scholar] [CrossRef]
- Vasco-Olmo, J.M.; Diaz, F.A.; Garcia-Collado, A.; Dorado-Vicente, R. Experimental Evaluation of Crack Shielding during Fatigue Crack Growth Using Digital Image Correlation. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 223–237. [Google Scholar] [CrossRef]
- Robles, J.M.; Vasco-Olmo, J.M.; Cruces, A.S.; Diaz, F.A.; James, M.N.; Lopez-Crespo, P. Fatigue Crack Characterisation in 2024-T351 Aluminium Alloy through SEM Observation Combined with the CJP Model. Int. J. Fatigue 2023, 166, 107279. [Google Scholar] [CrossRef]
- Vasco-Olmo, J.M.; Diaz, F.A.; James, M.N.; Yang, B. Crack Tip Plastic Zone Evolution during an Overload Cycle and the Contribution of Plasticity-Induced Shielding to Crack Growth Rate Changes. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2172–2186. [Google Scholar] [CrossRef]
- Nowell, D.; Dragnevski, K.I.; O’Connor, S.J. Investigation of Fatigue Crack Models by Micro-Scale Measurement of Crack Tip Deformation. Int. J. Fatigue 2018, 115, 20–26. [Google Scholar] [CrossRef]
- Nowell, D.; Nowell, S.C. A Comparison of Recent Models for Fatigue Crack Tip Deformation. Theor. Appl. Fract. Mech. 2019, 103, 102299. [Google Scholar] [CrossRef]
- Pommier, S.; Hamam, R. Incremental Model for Fatigue Crack Growth Based on a Displacement Partitioning Hypothesis of Mode I Elastic-Plastic Displacement Fields. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 582–598. [Google Scholar] [CrossRef]
- Yang, B.; Vasco-Olmo, J.M.; Díaz, F.A.; James, M.N. A More Effective Rationalisation of Fatigue Crack Growth Rate Data for Various Specimen Geometries and Stress Ratios Using the CJP Model. Int. J. Fatigue 2018, 114, 189–197. [Google Scholar] [CrossRef]
- Nurse, A.D.; Patterson, E.A. Experimental Determination of Stress Intensity Factors for Cracks in Turbine Disks. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 315–325. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498728140. [Google Scholar]
- Available online: http://www.correlatedsolutions.com (accessed on 20 May 2022).
- Palumbo, D.; Galietti, U. Data Correction for Thermoelastic Stress Analysis on Titanium Components. Exp. Mech. 2016, 56, 451–462. [Google Scholar] [CrossRef]
- Robinson, A.F.; Dulieu-Barton, J.M.; Quinn, S.; Burguete, R.L. The Potential for Assessing Residual Stress Using Thermoelastic Stress Analysis: A Study of Cold Expanded Holes. Exp. Mech. 2012, 53, 299–317. [Google Scholar] [CrossRef]
- Galietti, U.; Palumbo, D. Thermoelastic Stress Analysis of Titanium Components and Simultaneous Assessment of Residual Stress. EPJ Web Conf. 2010, 6, 38015. [Google Scholar] [CrossRef]
- Sanford, R.J.; Dally, J.W. A General Method for Determining Mixed-Mode Stress Intensity Factors from Isochromatic Fringe Patterns. Eng. Fract. Mech. 1979, 11, 621–633. [Google Scholar] [CrossRef]
- Patki, A.S.; Patterson, E.A. Thermoelastic Stress Analysis of Fatigue Cracks Subject to Overloads. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 809–821. [Google Scholar] [CrossRef]
- Palumbo, D.; De Finis, R.; Di Carolo, F.; Vasco-Olmo, J.; Diaz, F.A.; Galietti, U. Influence of Second-Order Effects on Thermoelastic Behaviour in the Proximity of Crack Tips on Titanium. Exp. Mech. 2021, 62, 521–535. [Google Scholar] [CrossRef]
- Nurse, A.D.; Patterson, E.A. Determination of Predominantly Mode-II Stress Intensity Factors from Isochromatic Data. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 1339–1354. [Google Scholar] [CrossRef]
- Waltz, R.A.; Morales, J.L.; Nocedal, J.; Orban, D. An Interior Algorithm for Nonlinear Optimization That Combines Line Search and Trust Region Steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006; ISBN 978-0-387-30303-1. [Google Scholar]
- Vasco-Olmo, J.M.; Diaz, F.A.; Antunes, F.V.; James, M.N. Characterisation of Fatigue Crack Growth Using Digital Image Correlation Measurements of Plastic CTOD. Theor. Appl. Fract. Mech. 2019, 101, 332–341. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of Steel Sheets Containing Slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- ASTM E647; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM: West Conshohocken, PA, USA, 2000.
- Li, J.; Yang, B.; Wang, S.; James, M.N.; Xiao, S.; Zhu, T.; Yang, G. Modified Model of Crack Tip Stress Field Considering Dislocation Slip Accumulation and Crack Tip Blunting. Chin. J. Mech. Eng. 2023, 36, 47. [Google Scholar] [CrossRef]






| Fe | C | N | O | H | Ti |
|---|---|---|---|---|---|
| 0.1 | 0.01 | >0.01 | 0.12 | 0.002 | Balance |
| Young’s Modulus (GPa) | 0.2% Yield Stress (MPa) | Ultimate Tensile Strength (MPa) | Elongation at Failure (%) | Poisson’s Ratio |
|---|---|---|---|---|
| 105 | 390 | 448 | 20 | 0.34 |
| Amplitude (N) | Mean Component (N) |
|---|---|
| 700 | 1400 |
| 700 | 1600 |
| 700 | 1800 |
| 1000 | 1400 |
| 1000 | 1600 |
| 1000 | 1800 |
| 1200 | 1400 |
| 1200 | 1600 |
| 1200 | 1800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho-Reyes, A.; Vasco-Olmo, J.M.; Gómez Gonzales, G.L.; Diaz, F.A. Study of Effective Stress Intensity Factor through the CJP Model Using Full-Field Experimental Data. Materials 2023, 16, 5705. https://doi.org/10.3390/ma16165705
Camacho-Reyes A, Vasco-Olmo JM, Gómez Gonzales GL, Diaz FA. Study of Effective Stress Intensity Factor through the CJP Model Using Full-Field Experimental Data. Materials. 2023; 16(16):5705. https://doi.org/10.3390/ma16165705
Chicago/Turabian StyleCamacho-Reyes, Alonso, Jose Manuel Vasco-Olmo, Giancarlo Luis Gómez Gonzales, and Francisco Alberto Diaz. 2023. "Study of Effective Stress Intensity Factor through the CJP Model Using Full-Field Experimental Data" Materials 16, no. 16: 5705. https://doi.org/10.3390/ma16165705
APA StyleCamacho-Reyes, A., Vasco-Olmo, J. M., Gómez Gonzales, G. L., & Diaz, F. A. (2023). Study of Effective Stress Intensity Factor through the CJP Model Using Full-Field Experimental Data. Materials, 16(16), 5705. https://doi.org/10.3390/ma16165705







