Evaluation of Reinforced Concrete Structures with Magnetic Method and ACO (Amplitude-Correlation-Offset) Decomposition
Abstract
:1. Introduction
1.1. Nondestructive Testing (NDT) of Reinforced Concrete (RC) Structures
- Methods based on the ultrasonic frequencies (typically ≥ 20 kHz) may utilize mechanical and electromagnetic excitation systems. Mechanical excitation with piezo-ceramic transducers is much more popular. This group of methods is universal and can be used to detect rebar position [5,6], rebar parameters, or even rebar corrosion [7]. Applying a pulse compression technique and post-processing (e.g., Total Focusing Method—TFM) allows for obtaining reliable maps of reinforcement even for concrete cover thickness above 0.5 m. The methods are used primarily to determine the quality of the concrete [3,8,9,10,11,12]. External excitation can be unnecessary in some methods, such as Acoustic Emission (AE) testing. The AE is the passive technique that monitors the release of sonic waves generated when a material deforms under stress. The AE is commonly used in industrial applications to detect cracks, monitor weld quality, test structural integrity, detect leaks, and as a system for structural health monitoring (SHM). Systems of this kind can only qualitatively gauge structure damage and are noise-sensitive [3,13].
- Methods based on sound frequencies (typically from 20 Hz to 20 kHz) and low frequencies (typically < 20 Hz). These two groups have been combined because, in terms of frequency, the methods often cannot be classified into one of the groups and overlap with both. The methods can be categorized similarly to the previous group. An excellent example of the active sonic-frequency mechanical method is Impact-Echo (IE). IE is an NDT method for testing concrete and masonry structures. The method uses impact-generated stress waves that propagate through the structure and are reflected by the internal borders, flaws, and external surfaces. Transducers with electromagnetic excitation can usually work both sonic and ultrasonic frequencies. The lower frequency methods usually used in civil engineering are HIT (Hammer Impact Test) and shaker (vibration tester). The excitation is usually mechanical, but many methods with electromagnetic excitation are increasingly encountered. In these cases, the identification is mainly based on modal analysis (vibration testing of an object whereby the natural frequencies and damping ratios are determined). Good examples of mechanical methods with electromagnetic excitation are M5 [3,14,15,16] and EPAT [17]. Passive methods in the sonic-frequency range are usually used to study sounds generated during the regular operation of the device. A typical example is the noise test on transformers. In lower frequencies, the seismic vibration monitoring (VM) is working.
- Methods based on X and γ radiation frequencies (frequencies of the order of 1016 Hz to 1024 Hz). Radiography is a very effective method, but it has some limitations and is rarely used to evaluate RC structures. The method may create risks to human health. There is also a problem with accessing both sides of the tested element. The source and detector must usually be placed on both sides of the tested object (the exception is backscattering), which is, in many cases, challenging to implement [3].
- Methods based on visible light frequencies (frequencies of the order of 1014 Hz to 1015 Hz). In this frequency range, strictly electromagnetic methods are not often used. However, these frequencies are used in visual inspection (VI). VI is a preliminary technique commonly used before other, more accurate NDT methods. VI is limited to evaluating the external conditions of the structure [3,18].
- Methods based on infrared radiation frequencies (frequencies of the order of 1011 Hz to 1014 Hz). Similarly to the previous group, in this frequency range, electromagnetic methods are not often used. Infrared thermography (IR) is more popular. IR is an important method that can potentially be used to test reinforced concrete. This method is mainly used to test the concrete; however, it is one of the very few that can also be implemented as an area-testing method for the initial detection of rebars in large-sized structures [3] and sometimes to detect corrosion. The method’s effectiveness strongly depends on the thickness of the concrete cover. Essential for effectiveness is the method of heating. The method can be helpful when the cover thickness is lower than 5 cm. The method is not commonly used in practice [3,19,20,21,22,23,24].
- Methods based on terahertz frequencies (frequencies of the order of 1011 Hz to 1013 Hz). The terahertz technique is rarely used due to the very high equipment price and limited penetration of concrete (caused by water content in concrete which damps waves of that frequency) [3].
- Methods based on microwave frequencies (frequencies of the order of 109 Hz to 1011 Hz). The most crucial method in this group is ground-penetrating radar (GPR). GPR is an up-and-coming method. Rebars can be detected from several centimeters up to ten or more meters, while other electromagnetic methods usually have a maximum detection range below 20 cm. In some cases, GPR can be utilized to estimate the diameter of rebars, detect breaks and defects, or even for corrosion detection (debonding). The method may also be applied to mapping multilayer reinforced meshes. Many factors (such as voids or variable internal moisture conditions) may affect the results of this technique. The other disadvantages of GPR are the cost of the device, difficulties with results interpretation, and limited resolution [3,25,26,27,28,29,30].
- Methods based on low and medium frequencies (frequencies of the order of 102 Hz to 109 Hz). The eddy current (EC) method is one of the most important electromagnetic methods in civil engineering. The method can be applied to detect rebars’ presence and determine: position, diameter, and rebar alloy (due to different electrical properties) [31,32,33,34,35]. In some cases, the method can detect changes caused by corrosion [36,37,38,39]. Both single and multifrequency excitation can be applied in various types of methods [39]. Because the EC method is sensitive to external interferences, it is essential to use appropriate algorithms, especially when many parameters must be identified simultaneously [40,41,42,43]. The effective range of the method is from 0 to 60 mm [31,32,33,34,35,36,37,38,39,39,40,41,42,43,44]. Similarly, the capacitive method works in this frequency range like in the EC method case. Sensors of this type usually can detect smaller inhomogeneities, but their effective range is also smaller than that of the EC method [45,46,47].
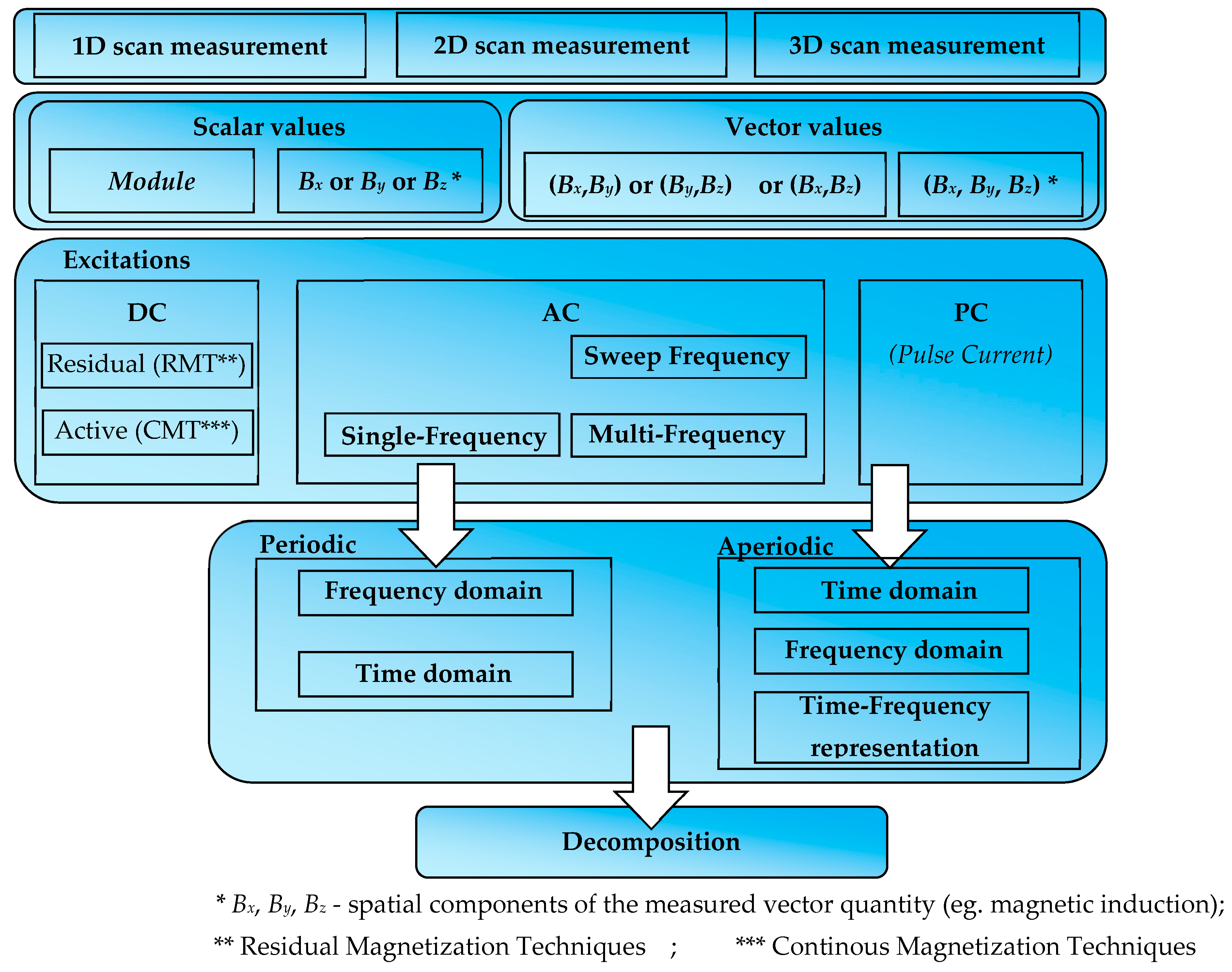
- Methods based on DC magnetic field—a large group of various methods. Generally, the methods can be divided into two groups: Continuous Magnetization Techniques (CMT), where an excitation device is utilized, and Residual Magnetization Techniques (RMT), which is passive. The main representative of CMT is the Magnetic Flux Leakage method (MFL). The method can be applied in civil engineering. However, the central area of use is in producing ferromagnetic parts and components. MFL can be used to localize rebars in the structure. Moreover, the propagation of magnetic flux can be obstructed by discontinuities in the material, such as breaks or cracks. Therefore, MFL may also be utilized to detect defects in rebars. In some cases, the MFL method can be used even to find out the material loss caused by corrosion. Other active magnetic methods, such as Barkhausen emission, magneto-acoustic emission, stress-induced magnetic anisotropy, or magnetic powder method, are usually not applied to evaluate RC structures. The CMT methods are more sensitive than RMT because the leakage field is higher when the magnetic flux is excited. However, the method poses some disadvantages, such as equipment deployment and power consumption. Residual magnetization methods are more economical and straightforward. One of the RMTs is the Magnetic Memory Method (MMM). The method can detect abnormal conditions arising from changes in crystalline structures of rebar material resulting from stress concentration, corrosion, or cracks [3,48,49,50,51,52,53,54,55]. The magneto-resistance (MR) and Hall effect sensors are most commonly used in the magnetic test. The MR sensors are usually susceptible and well-fitted for measuring small magnetic fields [56]. The Hall effect sensors are less sensitive and more appropriate for measuring relatively high magnetic fields. The magnetic method is one of the very few that can be implemented as an area-testing method for the initial detection of rebars in large-sized structures (e.g., with the use of a magneto-optical MO sensor) [48].
1.2. Knowledge Acquisition from the Experiment
2. Materials and Methods
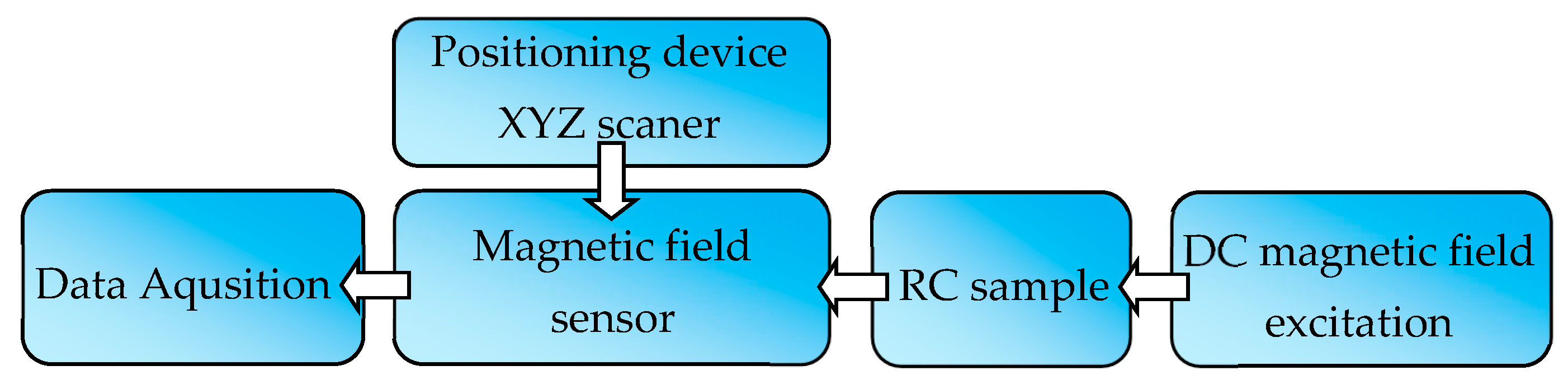
2.1. Measuring System for Magnetic Inspection
2.2. ACO (Amplitude-Correlation-Offset) Decomposition
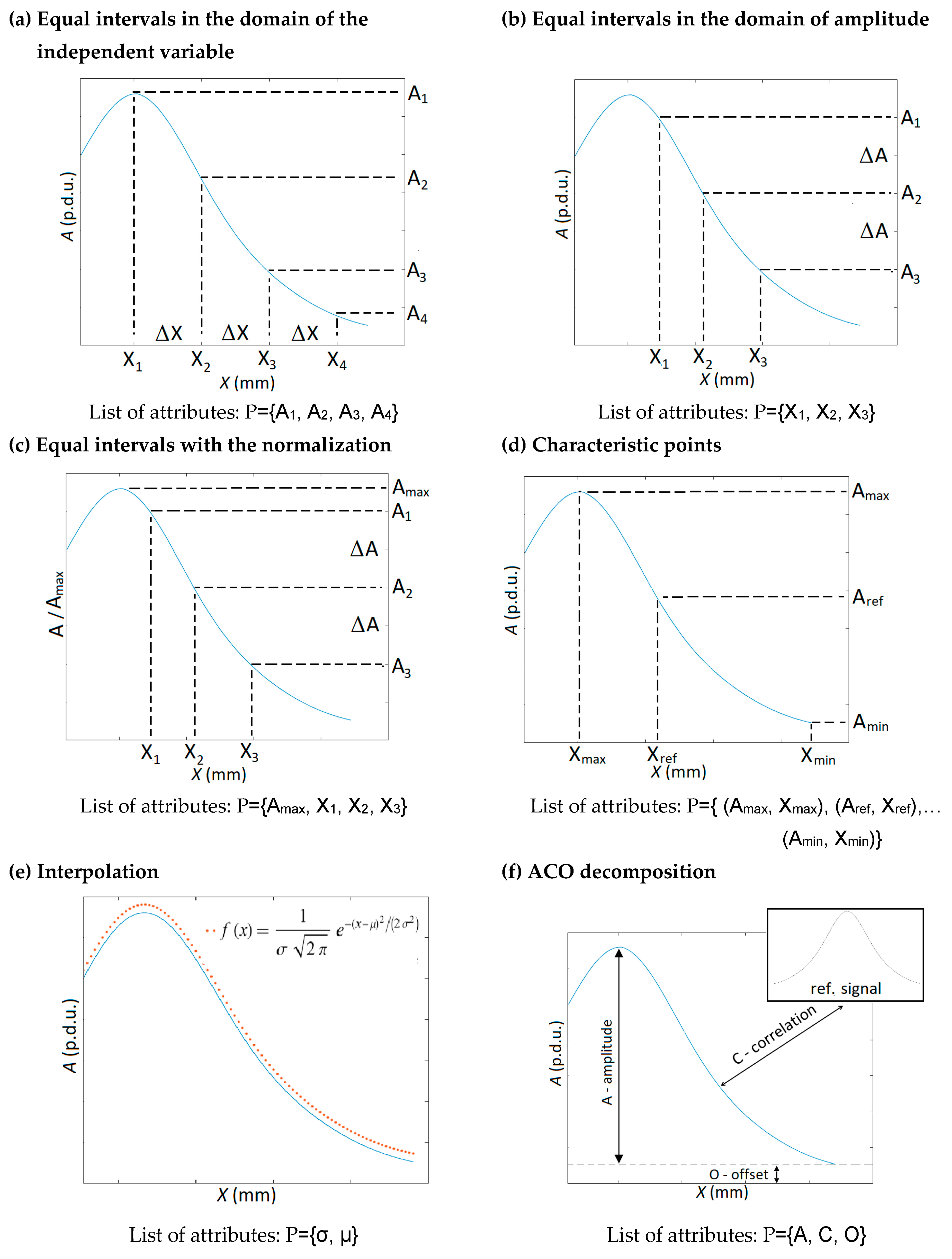
2.2.1. Motivation
2.2.2. Description of ACO Decomposition
- The cross-correlation between the windowed reference and tested signals is calculated in the first step. The results are utilized to determine the window’s lengths and position. The window with the reference signal is moved along the window with the tested signal (by one sample each time), and the cross-correlation is calculated for each setting. The setting when the absolute value of the cross-correlation achieves maximum is taken for further calculations. This step is used to find the rebar position precisely.
- The second step is devoted to determining the ACO attribute values using the later-mentioned algorithms.
- absolute offsets of the test signal: OT = min(abs(min(T)), abs(max(T))).
- absolute offsets of the reference signal: OR = min(abs(min(R)), abs(max(R))).
- absolute amplitude of the test signal:
- absolute amplitude of the reference signal:
- the corrected tested signal TC = T + αOT,
- the corrected reference signal RC = R + αOR,
- (1)
- α = 1, if all elements of the vector T are negative OR (elements of the vector have different signs AND abs(min(T)) < abs(max(T));
- (2)
- α = −1, if all elements of the vector T are positive OR (elements of the vector have different signs AND abs(min(T)) ≥ abs(max(T)).
2.3. ACO Decomposition in Comparison with Other Methods of Extracting Attributes
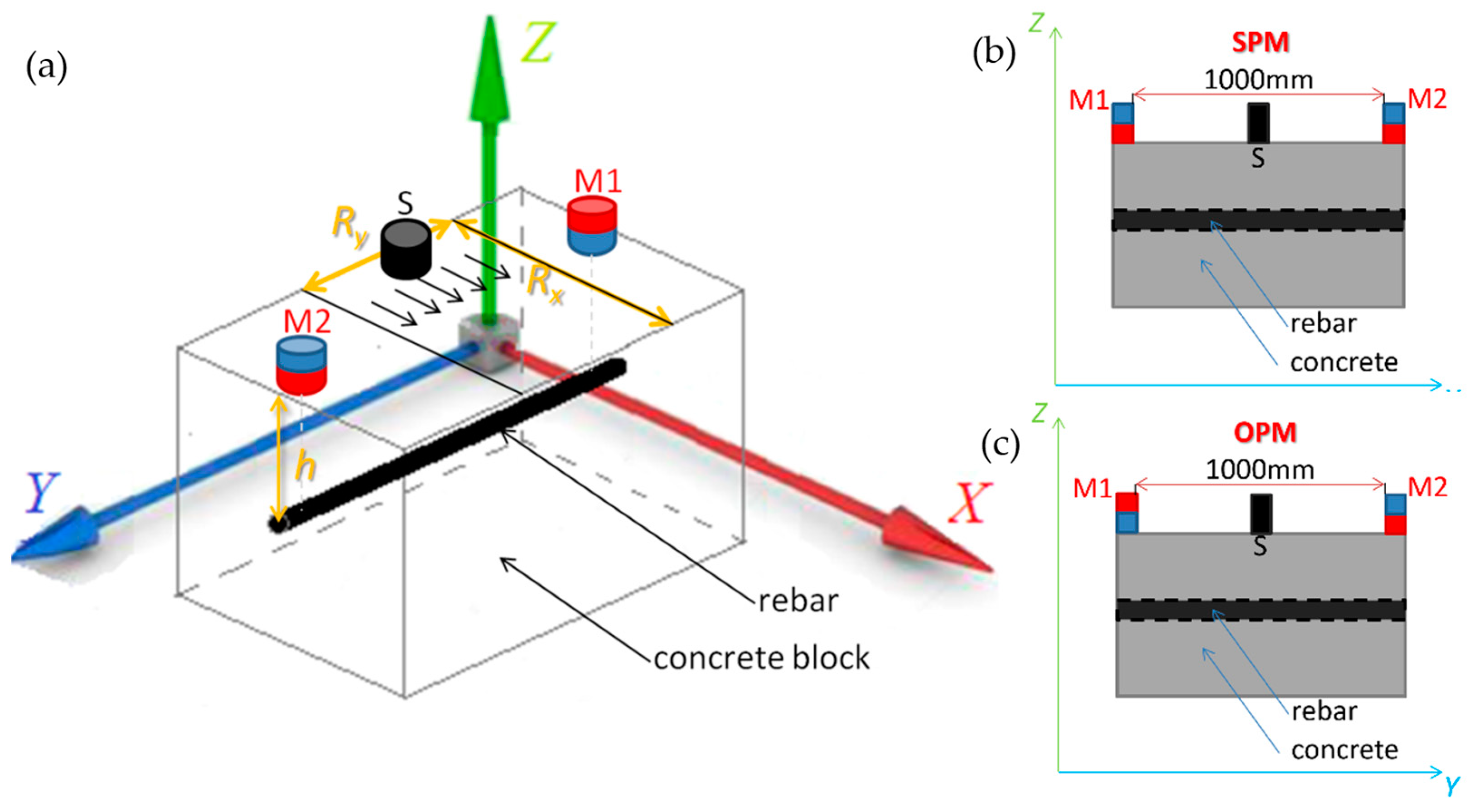
2.4. Description of the Experiments
- Designing the hardware (and usually software) layer of the system;
- Measurements and data processing;
- Attribute extraction from the obtained data;
- Identifying the structure parameters.
3. Results
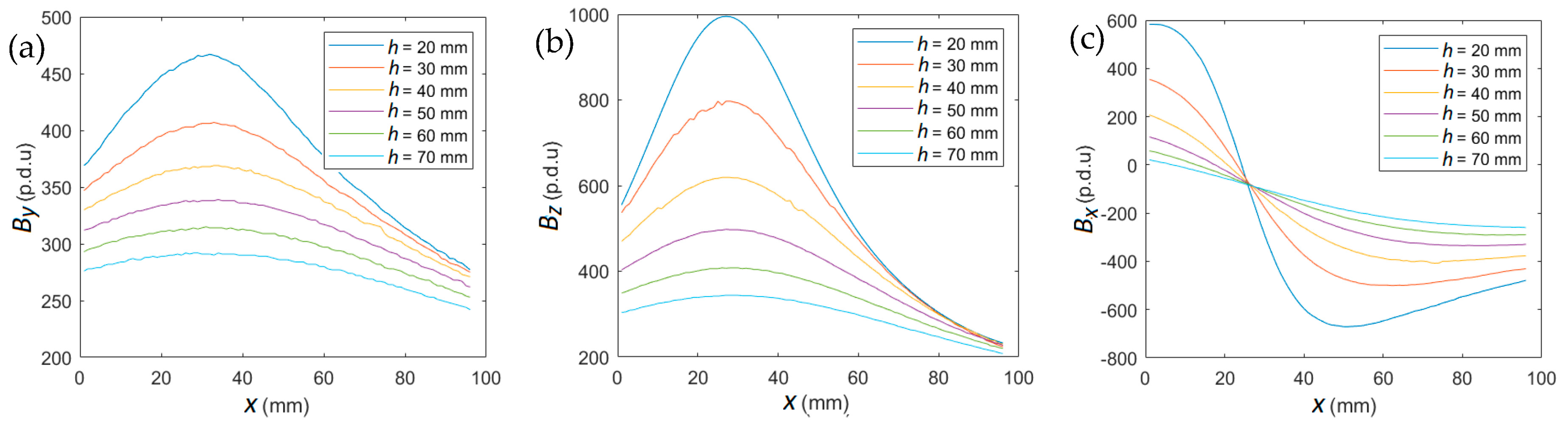
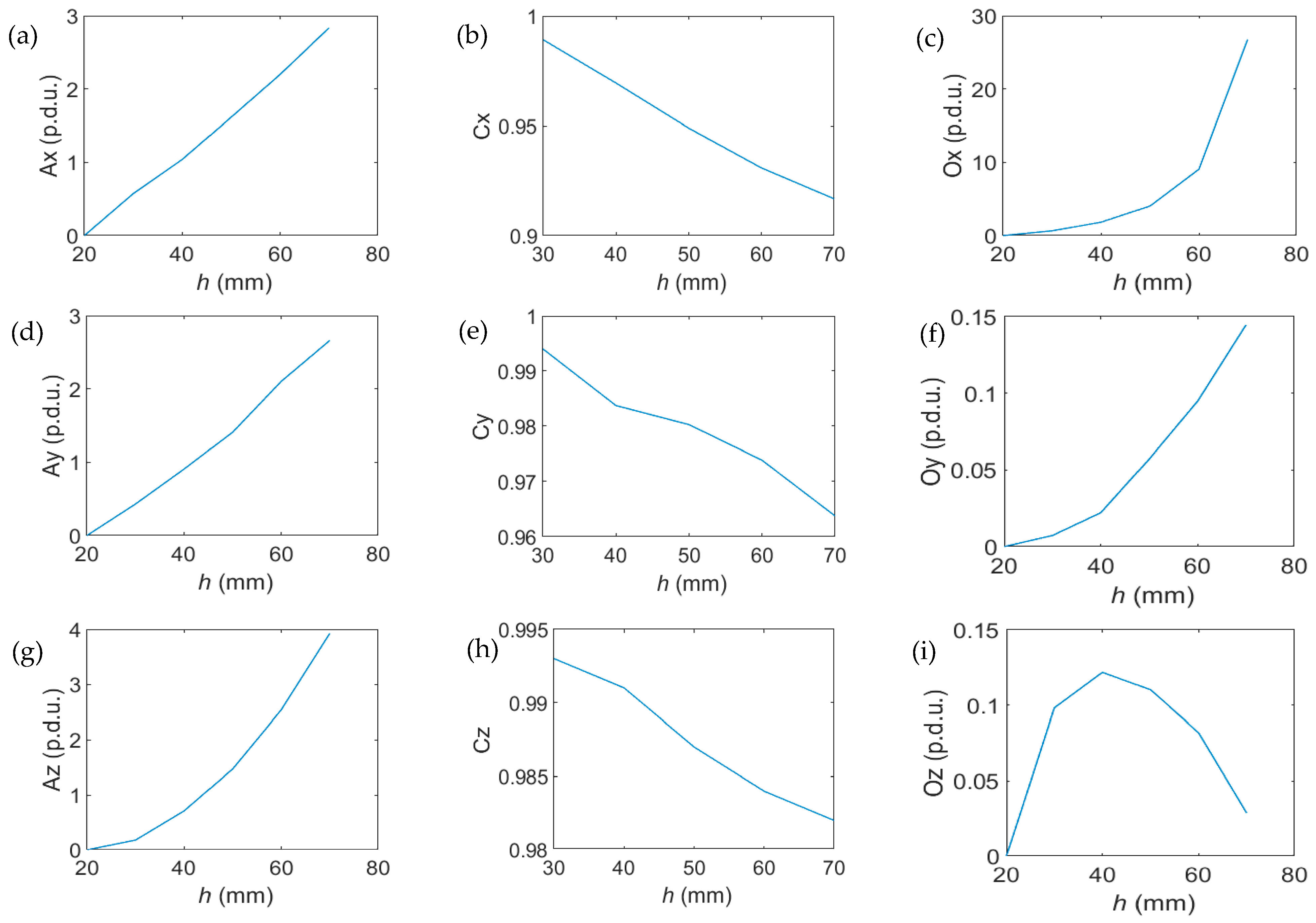
3.1. Evaluation of the Concrete Cover Thickness h
3.2. Evaluation of the Rebars Diameter D and Class
3.3. Simultaneous Identification of All Three Parameters (h, D, and Class)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wegen, G.; Polder, R.; Breugel, K. Guideline for service life design of structural concrete—A performance-based approach with regard to chloride induced corrosion. Heron 2012, 57, 153–168. [Google Scholar]
- Neville, A.M.; Neville, A.M. Properties of Concrete; Pearson Education Limited: London, UK, 2011; ISBN 9780273755807. [Google Scholar]
- Frankowski, P.K.; Chady, T.; Zieliński, A. Magnetic force induced vibration evaluation (M5) method for frequency analysis of rebar-debonding in reinforced concrete. Measurement 2021, 182, 109655. [Google Scholar] [CrossRef]
- Dixit, M.; Gupta, A.K. A Review of Different Assessment Methods of Corrosion of Steel Reinforcement in Concrete. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 735–752. [Google Scholar] [CrossRef]
- Laureti, S.; Ricci, M.; Mohamed MN, I.B.; Senni, L.; Davis, L.A.; Hutchins, D.A. Detection of rebars in concrete using advanced ultrasonic pulse compression techniques. Ultrasonics 2018, 85, 31–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcia, E.V.C. Identifying the onset, type, and location of deterioration in reinforced concrete using ultrasonic testing. Ph.D. Thesis, ETD collection for University of Nebraska—Lincoln, Lincoln, NE, USA, 2016. [Google Scholar]
- Mayakuntla, P.K.; Ganguli, A.; Smyl, D. Gaussian Mixture Model-Based Classification of Corrosion Severity in Concrete Structures Using Ultrasonic Imaging. J. Nondestruct. Eval. 2023, 42, 28. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, J. Monitoring Early Age Properties of Cementitious Material Using Ultrasonic Guided Waves in Embedded Rebar. J. Nondestruct. Eval. 2017, 36, 5. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T.; Trang, H.; Harada, K.; Hashimoto, C. Evaluation of corrosion induced crack and rebar corrosion by ultrasonic testing. Constr. Build. Mater. 2014, 67, 197–201. [Google Scholar] [CrossRef]
- Xu, Y.; Jin, R. Measurement of reinforcement corrosion in concrete adopting ultrasonic tests and artificial neural network. Constr. Build. Mater. 2018, 177, 125–133. [Google Scholar] [CrossRef]
- Mayakuntla, P.K.; Ghosh, D.; Ganguli, A. Nondestructive evaluation of rebar corrosion in concrete structures using ultrasonics and laser-based sensing. Nondestruct. Test. Eval. 2021, 37, 297–314. [Google Scholar] [CrossRef]
- Ghosh, D.; Kumar, R.; Ganguli, A.; Mukherjee, A. Nondestructive Evaluation of Rebar Corrosion–Induced Damage in Concrete through Ultrasonic Imaging. J. Mater. Civ. Eng. 2020, 32, 04020294. [Google Scholar] [CrossRef]
- Pourrastegar, A.; Marzouk, H. Vibration-Based Nondestructive Damage Detection for Concrete Plates. ACI Struct. J. 2021, 118, 117–129. [Google Scholar]
- Miwa, T. Nondestructive and Quantitative Evaluation of Rebar Corrosion by a Vibro-Doppler Radar Method. Sensors 2021, 21, 2546. [Google Scholar] [CrossRef] [PubMed]
- Miwa, T.; Nakazawa, Y. Nondestructive Evaluation of Localized Rebar Corrosion in Concrete Using Vibro-Radar Based on Pulse Doppler Imaging. Remote Sens. 2022, 14, 4645. [Google Scholar] [CrossRef]
- Blodgett, D.; Vojtech, G. Nondestructive Detection of Reinforcing Member Degradation. Patent U.S. US2004012 3665A1, 2004.
- Zhou, X.; Takeda, S.; Uchimoto, T.; Hashimoto, M.; Takagi, T. Electromagnetic pulse-induced acoustic testing enables reliable evaluation of debonding between rebar and concret. Cem. Concr. Compos. 2023, 142, 105170. [Google Scholar] [CrossRef]
- Li, V.; Demina, L.; Vlasenko, S. Identification of Defective Supports by Visual and Instrument Aids in the Operating Environment of a Railway Power Supply Division. In Technological Advancements in Construction; Mottaeva, A., Ed.; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2022; Volume 180. [Google Scholar] [CrossRef]
- Szymanik, B.; Chady, T.; Frankowski, P.K. Inspection of reinforcement concrete structures with active infrared thermography. In Proceedings of the 43rd Annual Review of Progress in Quantitative Nondestructive Evaluation, Volume 36, Atlanta, GA, USA, 17–22 July 2016; ISBN 9780735414747. [Google Scholar] [CrossRef]
- Keo, S.A.; Szymanik, B.; Le Roy, C.; Brachelet, F.; Defer, D. Defect Detection in CFRP Concrete Reinforcement Using the Microwave Infrared Thermography (MIRT) Method—A Numerical Modeling and Experimental Approach. Appl. Sci. 2023, 13, 8393. [Google Scholar] [CrossRef]
- Tran, H.Q. Passive and active infrared thermography techniques in nondestructive evaluation for concrete bridge. AIP Conf. Proc. 2021, 2420, 050008. [Google Scholar]
- Brachelet, F.; Keo, S.; Defer, D.; Breaban, F. Detection of reinforcement bars in concrete slabs by infrared thermography and microwaves excitation. In Proceedings of the QIRT 2014 Civil Engineering & Buildings, Bordeaux, France, 7–11 July 2014. [Google Scholar]
- Teo, S.A.; Brachelet, F.; Defer, D.; Breaban, F. Detection of Concrete Cover of Reinforcements in Reinforced Concrete Wall by Microwave Thermography with Transmission Approach. Appl. Sci. 2022, 12, 9865. [Google Scholar] [CrossRef]
- Garrido, I.; Solla, M.; Lagüela, S.; Rasol, M. Review of InfraRed Thermography and Ground-Penetrating Radar Applications for Building Assessment. Adv. Civ. Eng. 2022, 2022, 5229911. [Google Scholar] [CrossRef]
- Solla, M.; Lagüela, S.; Fernández, N.; Garrido, I. Assessing Rebar Corrosion through the Combination of Nondestructive GPR and IRT Methodologies. Remote Sens. 2019, 11, 1705. [Google Scholar] [CrossRef] [Green Version]
- Tešić, K.; Baricević, A.; Serdar, M. Nondestructive Corrosion Inspection of Reinforced Concrete Using Ground-Penetrating Radar: A Review. Materials 2021, 14, 975. [Google Scholar] [CrossRef] [PubMed]
- Tosti, F.; Benedetto, F.; Jagadissen Munisami, K.; Sofroniou, A.; Alani, A.M. A high-resolution velocity analysis to improve GPR data migration for rebars investigation. In Proceedings of the 20th EGU General Assembly, EGU2018, Vienna, Austria, 4–13 April 2018. [Google Scholar]
- Mechbal, Z.; Khamlichi, A. Determination of concrete rebars characteristics by enhanced post-processing of GPR scan raw data. NDT E Int. 2017, 89, 30–39. [Google Scholar] [CrossRef]
- Le, T.; Gibb, S.; Pham, N.; La, H.M.; Falk, L.; Berendsen, T. Autonomous robotic system using nondestructive evaluation methods for bridge deck inspection. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Ou, G.; Rashidi, A. Robust cascaded frequency filters to recognize rebar in GPR data with complex signal interference. Autom. Constr. 2021, 124, 103593. [Google Scholar] [CrossRef]
- Szymanik, B.; Frankowski, P.K.; Chady, T.; Chelliah, C.R.A.J. Detection and Inspection of Steel Bars in Reinforced Concrete Structures Using Active Infrared Thermography with Microwave Excitation and Eddy Current Sensors. Sensors 2016, 16, 234. [Google Scholar] [CrossRef] [Green Version]
- Rubinacci, G.; Tamburrino, A.; Ventre, S. Concrete rebars inspection by eddy current testing. Int. J. Appl. Electromagn. Mech. 2007, 25, 333–339. [Google Scholar] [CrossRef]
- Koido, J.; Hoshikawa, H. Covering Thickness and Diameter Measurement of Reinforcing Bars by Eddy Current Testing Using Neural Network. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Springer: Boston, MA, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Frankowski, P.K. Eddy current method for identification and analysis of reinforcement bars in concrete structures. In Proceedings of the Electrodynamic and Mechatronic Systems, Opole, Poland, 6–8 October 2011; pp. 105–109. [Google Scholar] [CrossRef]
- Drobiec, Ł.; Jasiński, R.; Mazur, W. Accuracy of Eddy-Current and Radar Methods Used in Reinforcement Detection. Materials 2019, 12, 1168. [Google Scholar] [CrossRef] [Green Version]
- Frankowski, P.K. Corrosion detection and measurement using eddy current method. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Świnouście, Poland, 9–12 May 2018. [Google Scholar] [CrossRef]
- Alcantara, N.P.; Silva, F.M.; Guimaraes, M.T.; Pereira, M.D. Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing. Sensors 2016, 16, 15. [Google Scholar] [CrossRef]
- Magistris, M.; Morozov, M.; Rubinacci, G.; Tamburrino, A.; Ventre, S. Electromagnetic inspection of concrete rebars. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2007, 26, 389–398. [Google Scholar] [CrossRef]
- Krause, T.; Krause, T.W. Pulsed Eddy Current Response to General Corrosion in Concrete Rebar. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2020, 24, 044501. [Google Scholar]
- Chia-Chia, C.; Chih-Peng, Y.; Yiching, L. Distinction between crack echoes and rebar echoes based on Morlet Wavelet Transform of impact echo signals. NDT E Int. 2019, 108, 102169. [Google Scholar]
- Frankowski, P.K.; Sikora, R.; Chady, T. Identification of rebars in a reinforced mesh using eddy current method. AIP Conf. Proc. 2016, 1706, 090008. [Google Scholar] [CrossRef] [Green Version]
- Xia, Z.; Huang, R.; Chen, Z.; Yu, K.; Zhang, Z.; Salas-Avila, J.R.; Yin, W. Eddy Current Measurement for Planar Structures. Sensors 2022, 22, 8695. [Google Scholar] [CrossRef]
- Frankowski, P.K.; Chady, T.; Sikora, R. Knowledge extraction algorithms dedicated for identification of steel bars in reinforced concrete structures. AIP Conf. Proc. 2014, 1581, 822–827. [Google Scholar] [CrossRef]
- Alcantara, N. Identification of steel bars immersed in reinforced concrete based on experimental results of eddy current testing and artificial neural network analysis. Nondestruct. Test. Eval. 2013, 28, 58–71. [Google Scholar] [CrossRef]
- Han, X.; Wang, P.; Cui, D.; Tawfik, T.A.; Chen, Z.; Tian, L.; Gao, Y. Rebar corrosion detection in concrete based on capacitance principle. Measurement 2023, 209, 112526. [Google Scholar] [CrossRef]
- Han, X.; Li, G.; Wang, P.; Chen, Z.; Cui, D.; Zhang, H.; Tian, L.; Zhou, X.; Jin, Z.; Zhao, T. A new method and device for detecting rebars in concrete based on capacitance. Measurement 2022, 202, 111721. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, L.; Soleimani, M. Magnetic induction tomography guided electrical capacitance tomography imaging with grounded conductors. Measurement 2014, 53, 171–181. [Google Scholar] [CrossRef] [Green Version]
- Frankowski, P.K.; Chady, T. Impact of Magnetization on the Evaluation of Reinforced Concrete Structures Using DC Magnetic Methods. Materials 2022, 15, 857. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Qiu, K.; Deng, B.; Zhang, G.; Ye, G. A NDT Method for Location and Buried Depth Measurement of Rebars in Concrete Pole. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Diogenes, A.G.; de Moura, E.P.; da Silveira Machado, A.; Gonçalves, L.L. Corrosion evaluation of carbon steel bars by magnetic nondestructive method. Nondestruct. Test. Eval. 2022, 37, 315–331. [Google Scholar] [CrossRef]
- Mosharafi, M.; Mahbaz, S.; Dusseault, M.B. Magnetic Data Pattern Features at Longitudinal Defect Sites in Rebars Scanned by a Passive Magnetic Inspection Technology. J. Environ. Eng. Geophys. 2020, 25, 513. [Google Scholar] [CrossRef]
- Mosharafi, M.; Mahbaz, S.B.; Dusseault, D. Bridge deck assessment using infrastructure corrosion assessment magnetic method (iCAMM™) technology, a case study of a culvert in Markham city, Ontario, Canada. NDT E Int. 2020, 116, 102356. [Google Scholar] [CrossRef]
- Mosharafi, M.; Mahbaz, S.B.; Dusseault, M.B.; Vanheeghe, P. Magnetic detection of corroded steel rebar: Reality and simulations. NDT E Int. 2020, 110, 102225. [Google Scholar] [CrossRef]
- Lo, C.C.H.; Nakagawa, N. Evaluation of eddy current and magnetic techniques for inspecting rebars in bridge barrier rails. AIP Conf. Proc. 2013, 1511, 1371–1377. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.H.; Wang, H.; Liu, A.Z. Rebar corrosion monitoring using magnetic gradient and partial modulus. Measurement 2020, 164, 107994. [Google Scholar] [CrossRef]
- Eslamlou, A.D.; Ghaderiaram, A.; Schlangen, E.; Fotouhi, M. A review on non-destructive evaluation of construction materials and structures using magnetic sensors. Constr. Build. Mater. 2023, 397, 132460. [Google Scholar] [CrossRef]
- Holmes, G.; Donkin, A.; Witten, I.H. Weka: A machine learning workbench. In Proceedings of the ANZIIS ′94—Australian New Zealnd Intelligent Information Systems Conference, Brisbane, Australia, 29 November–2 December 1994. [Google Scholar]
- PN-B-03264:2002; Concrete, Reinforced Concrete and Prestressed Structures. Static Calculations and Design. PKN: Warsaw, Poland, 2002.




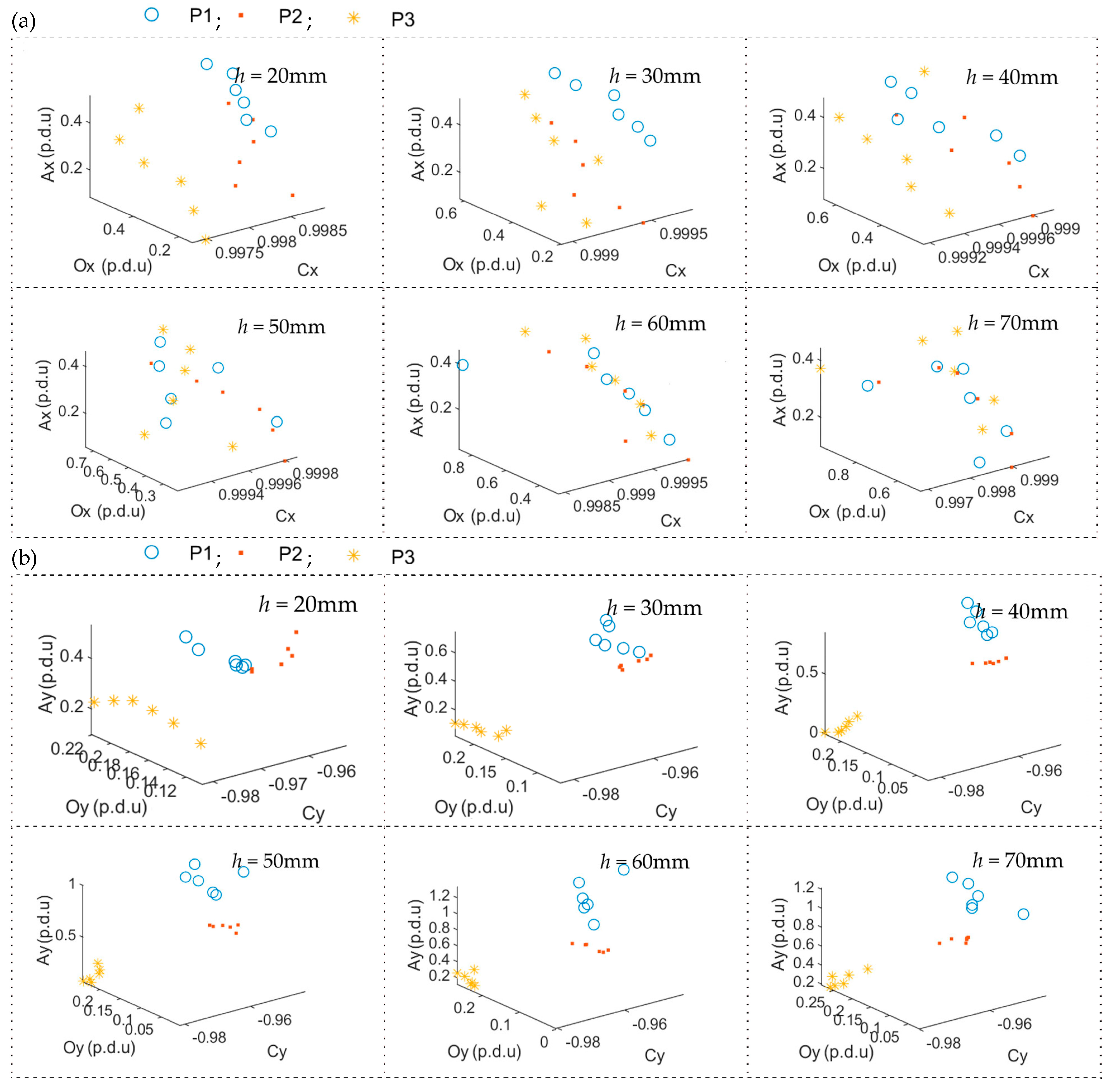


| P1 | P2 | P3 | P4 | |
|---|---|---|---|---|
| Diameter D (mm) | 10 | 10 | 12 | 12 |
| Class | AI | AIII | AIII | AIIIN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frankowski, P.K.; Chady, T. Evaluation of Reinforced Concrete Structures with Magnetic Method and ACO (Amplitude-Correlation-Offset) Decomposition. Materials 2023, 16, 5589. https://doi.org/10.3390/ma16165589
Frankowski PK, Chady T. Evaluation of Reinforced Concrete Structures with Magnetic Method and ACO (Amplitude-Correlation-Offset) Decomposition. Materials. 2023; 16(16):5589. https://doi.org/10.3390/ma16165589
Chicago/Turabian StyleFrankowski, Paweł Karol, and Tomasz Chady. 2023. "Evaluation of Reinforced Concrete Structures with Magnetic Method and ACO (Amplitude-Correlation-Offset) Decomposition" Materials 16, no. 16: 5589. https://doi.org/10.3390/ma16165589
APA StyleFrankowski, P. K., & Chady, T. (2023). Evaluation of Reinforced Concrete Structures with Magnetic Method and ACO (Amplitude-Correlation-Offset) Decomposition. Materials, 16(16), 5589. https://doi.org/10.3390/ma16165589






