Innovative Design of Bismuth-Telluride-Based Thermoelectric Transistors

Abstract

Conventional thermoelectric generators, predominantly based on the π-type structure, are severely limited in their applications due to the relatively low conversion efficiency. In response to the challenge, in this work, a Bi₂Te₃-based thermoelectric transistor driven by laser illumination is demonstrated. Under laser illumination, a temperature difference of 46.7 °C is produced between the two ends of the transistor structure. Further, the hole concentrations in each region redistribute and the built-in voltages decrease due to the temperature difference, leading to the formation of the transistor circuit. Additionally, the operation condition of the thermoelectric transistor is presented. The calculation results demonstrate that the maximum output power of such a designed thermoelectric transistor is 0.7093 μW.

1. Introduction

Fossil fuels, being the primary and nonrenewable energy source that has driven human society and industrial development since the Industrial Revolution, are facing an inevitable depletion due to the ever-growing demand. The resulting concerns over energy security have also contributed to escalated global conflicts [1]. Therefore, it is imperative to focus on the development of clean, low-carbon, secure, and efficient renewable energy sources.

Thermoelectric generators, capable of converting heat into electricity through the Seebeck effect, have emerged as a promising energy conversion technology [2]. Conventional thermoelectric generators typically consist of multiple thermoelectric modules, offering numerous advantages, such as high safety, extended service life, zero waste generation, no noise, and simple structure [3]. However, the applications of conventional thermoelectric generators are limited due to their relatively poor output performance. Therefore, thermoelectric generators can only be used in a few specific scenarios, such as medicine, aerospace, and military sectors.

In general, the output performance of thermoelectric generators was assessed based on the zT value of materials, output power, and conversion efficiency. To enhance the output performance, the combination of thermoelectric generators with transistor technology has been proposed [4,5]. Bejenari et al. studied the thermoelectric performance of Bi₂Te₃ nanowires in the transistor structure under the gate voltage. Theoretical results indicated that the zT value could reach 3.4 for Bi₂Te₃ nanowires [6]. Subsequently, Qin et al. found that the zT values of N-type and P-type Bi₂Te₃ films could reach 1.22 and 1.02 in the transistor structure through experimental measurement [7]. Furthermore, Nan et al. studied the output performance of a thermoelectric transistor driven by the Seebeck effect, in which the built-in electric field is perpendicular to the gradient temperature field. Results showed that the output power was 17.8 mW and conversion efficiency could reach 8.69% at a temperature difference of 50 °C [8,9].

These research results demonstrated that the output performance of thermoelectric generators could be significantly improved through the transistor effect. In this work, a Bi₂Te₃-based thermoelectric transistor driven by the laser illumination is presented. On the one hand, the short pulse width of a laser allows for rapid creation of a temperature difference between the two ends of the device, reaching nanosecond levels [10]. On the other hand, Bi₂Te₃-based materials exhibit excellent thermoelectric properties at room temperature [11]. Moreover, utilizing Bi₂Te₃-based materials as research subjects can improve the accuracy of theoretical calculations due to their comprehensive performance parameters [12,13]. As a result, in this work, theoretical results indicated that the maximum output power of a single Bi₂Te₃-based thermoelectric transistor could reach 0.7093 μW with a temperature difference of 46.7 °C. Conventional thermoelectric generators would require multiple thermoelectric modules connected in series to achieve such output performance [14,15,16].

2. Theoretical Foundations

The structure of the designed structure is depicted in the following Figure 1.

Considering the one-dimensional model, the length (x₁) of P₁ region (P₁-Bi₂Te₃) is 1 μm, while the length of (x₂) P₂ region (P₂-Si) is 4 μm. The scale of N region (N-Si) is the nanometer range, which can be neglected for calculation purposes.

Using a laser as the heat source, serving as the triggering condition, the P₁-Bi₂Te₃ is irradiated by the laser at one end, causing its temperature to rise. Subsequently, the heat is transmitted throughout the entire structure via thermal conduction, forming a temperature field along the X direction. The temperature field induces the redistribution of majority charge carriers (holes) within the structure. The holes in P₁ region and P₂ region diffuse from the hot end to the cold end, accumulating at the cold end. Simultaneously, the built-in voltage across P₁–N junction decreases from the cold end to the far end. Consequently, the balance between the diffusion potential and drift potential on both sides of P₁–N junction is disrupted, leading to the injection of holes from P₁ region into N-type region at the cold end. Additionally, since the length of N-type region is on the nanoscale, the holes further migrate towards P₂ region. Subsequently, the accumulated holes in P₂ region flow back to the N-type region along the wires. The migration of holes is consistent with the common base circuit of a bipolar transistor. Thus, it is inferred that the transistor circuit can be formed in the PNP structure under laser irradiation. In other words, the cold side of the P₁ region (x₁) functions as the emitter of the thermoelectric transistor, while the hot side of the P₂ region (x₂) serves as the collector, with the N-type region acting as the base [17].

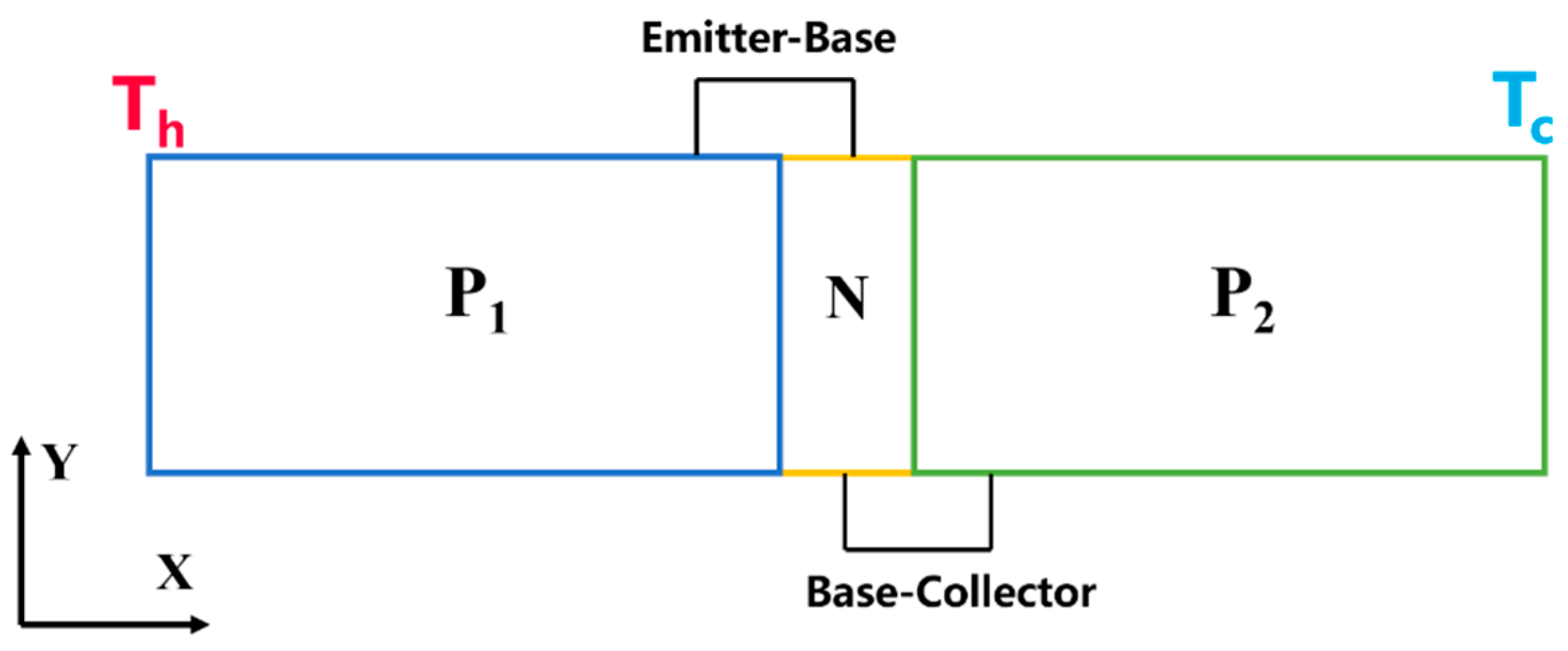
2.1. Temperature Distribution of Bi₂Te₃ and p-Type Si under Laser Irradiation

2.1.1. Calculation of Temperature Distribution in P₁-Bi₂Te₃

When a laser is incident upon Bi₂Te₃, according to Lambert’s law, it is known that the amount of light absorbed is closely related to the position in the one-dimensional model. The closer the position is to the source of light, the greater the light absorption. Assuming material thermal capacitance is uniform, a temperature gradient will form parallel to the direction of illumination. According to Fourier’s law, heat conduction will also occur along the direction of the incident light. Taking all these considerations into account under the one-dimensional condition, the following equation can be derived [18]:

$$\rho c\frac{\partial T_1}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T_1}{\partial x}\right)+\left(1-R\right)\alpha I_0{e}^{-\alpha x}$$

(1)

where ρ represents material density, c represents material-specific heat capacity, T₁ is the temperature, k represents thermal conductivity, R represents reflectivity, I₀ represents light intensity, t represents time, x is the material length along the direction of illumination, and α represents absorption coefficient.

Due to the extremely short duration of the pulse laser, it can be assumed that there is no heat transfer occurring at the ends of the sample. Therefore, the following conditions hold:

$$\frac{\partial T_1\left(x=0,t\right)}{\partial x}=0$$

(2)

$$\frac{\partial T_1\left(x=l,t\right)}{\partial x}=0$$

(3)

In addition, the initial temperature distribution of the sample is assumed to be uniform, with no heat transfer occurring between different parts of the sample. In other words, the temperature at each position is a constant, given by:

$$T_1\left(x,0\right)={\phi }_1\left(x\right)=constant$$

(4)

By solving these equations in MATLAB R2020a, the temperature distribution T₁(x₁) in P₁-Bi₂Te₃ can be obtained.

2.1.2. Calculation of Temperature Distribution in P₂-Si

Unlike the calculation of temperature distribution in Bi₂Te₃, the differential equation for the temperature distribution in P₂-Si does not include the influence of illumination; thus, it becomes a one-dimensional heat conduction problem without a heat source:

$$\rho c\frac{\partial T_2}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T_2}{\partial x}\right)$$

(5)

Similarly, the boundary conditions can be set as follows:

$$\frac{\partial T_2\left(x=0,t\right)}{\partial x}=0$$

(6)

$$\frac{\partial T_2\left(x=l,t\right)}{\partial x}=0$$

(7)

The initial condition for the P₂-Si sample is:

$$T_2\left(x,0\right)={\phi }_2\left(x\right)=constant$$

(8)

By solving these equations in MATLAB R2020a, the temperature distribution T₂(x₂) in P₂-Si can be obtained.

2.2. Hole Concentration Distribution in Bi₂Te₃ and P₂-Si

2.2.1. Hole Concentration Distribution in P₁-Bi₂Te₃

When P₁-Bi₂Te₃ is subjected to a stable temperature field at 20 °C, the hole concentration is uniformly distributed, which is equal to the acceptor concentration P_a. Subsequently, when P₁-Bi₂Te₃ is influenced by a temperature gradient (dx/dt ≠ 0), the holes redistribute, while the acceptor ions remain fixed. The redistribution of holes can be obtained through theoretical analysis, as shown below.

DC transport equation for current [19]:

$$J_p(x)={\sigma }_p(x)\left[E\left(x\right)-S_p\left(x\right)\nabla T\left(x\right)\right]$$

(9)

$$E\left(x\right)=\frac{d\phi \left(x\right)}{dx}$$

(10)

where J_p(x) represents the current density, ∇T(x) is the temperature gradient, E(x) denotes the electric field, φ(x) represents the electric potential, σ_p(x) is the electrical conductivity of P₁-Bi₂Te₃, and S_p(x) is the Seebeck coefficient p-type Bi₂Te₃.

One-dimensional Poisson equation [20]:

$$\frac{d^2\phi \left(x\right)}{d{x}^2}=-\frac{e}{{\epsilon }_r{\epsilon }_0}\left[p_1\left(x_1\right)-P_a\right]$$

(11)

where e is the electronic charge, ε_r is the relative permittivity, ε₀ is the vacuum permittivity, p₁(x₁) represents the hole concentration distribution in P₁-Bi₂Te₃, and P_a is the constant concentration of acceptor holes assuming complete ionization of Bi₂Te₃.

Continuity equation [21]:

$$\frac{\partial p_1\left(x_1\right)}{\partial t}=-\frac{1}{q}\frac{\partial J_p\left(x\right)}{\partial x}+\left(G_p-R_p\right)$$

(12)

where G_p is the hole carrier generation rate in Bi₂Te₃, and R_p is the hole carrier recombination rate.

Since P₁-Bi₂Te₃ discussed in this work is a degenerate semiconductor, σ_p(x) and S_p(x) can be expressed as [11,22]:

$${\sigma }_P\left(x\right)=p\left(x\right)e{\mu }_p$$

(13)

$$S_p\left(x\right)=\left[\frac{8{\pi }^{\frac{8}{3}}{m}_p^{\mathrm{*}}{k_B}^2\left(r+\frac{3}{2}\right)}{3^{\frac{5}{3}}{h}^{2}e}\right]\frac{T_1\left(x_1\right)}{{p_1\left(x_1\right)}^{\frac{2}{3}}}$$

(14)

where μ_p represents the hole mobility of P₁-Bi₂Te₃, r is the scattering factor (= −1/2), h is the Planck constant, $m_p^{\mathrm{*}}$ denotes the effective mass, and T₁(x₁) is temperature distribution of P₁-Bi₂Te₃ along the x direction.

Since the simulated temperature distribution is significantly lower than the intrinsic excitation temperature of Bi₂Te₃, it can be assumed that G_p = R_p and the total hole concentration in Bi₂Te₃ remains constant after applying the temperature gradient:

$${\int }_0^{l_x}{P}_{a}dx={\int }_0^{l_x}{p}_1\left(x_1\right)dx$$

(15)

Substituting the above equation into Equation (10) can obtain:

$$E\left(x\right)=\frac{d\phi \left(x\right)}{dx}={\int }_0^{l_x}\frac{-e}{{\epsilon }_r{\epsilon }_0}\left[p_1\left(x_1\right)-P_a\right]dx=0$$

(16)

Substituting Equation (16) into Equation (9) yields:

$$J_p\left(x\right)=-{\sigma }_p\left(x\right)S_p\left(x\right)\nabla T\left(x\right)$$

(17)

Furthermore, assuming that the entire P₁-Bi₂Te₃ reaches a stable state after the temperature distribution is established, Equation (12) can be written as:

$$\frac{\partial p}{\partial t}=-\frac{1}{q}\frac{\partial J_p\left(x\right)}{\partial x}=0$$

(18)

By solving these equations in MATLAB, the hole concentration distribution of P₁-Bi₂Te₃ can be obtained under a temperature gradient.

2.2.2. Hole Concentration Distribution in P₂-Si

Since the carrier concentration of P₂-Si studied in this work is less than 10¹⁸ cm⁻³, it is considered a nondegenerate semiconductor. Therefore, the Seebeck coefficient can be expressed as [23]:

$$S_p\left(x\right)=\frac{k_B}{e}\left[\left(r+\frac{5}{2}\right)+\mathit{ln}\frac{2{\left(2\pi m^{\mathrm{*}}{k}_B{T}_2\left(x_2\right)\right)}^{3/2}}{h^{3}n}\right]$$

(19)

Then, based on the temperature distribution T₂(x₂) in P₂-Si and Equations (13), (15), (17), and (18), the hole concentration distribution of P₂-Si can be derived.

2.3. Operation Conditions of Thermoelectric Transistor

In order for the thermoelectric transistor to operate properly, it must be in a forward-active mode [17]. Since the formation for the circuit of the thermoelectric transistor is only based on the Seebeck effect, the potential within it can be represented by the concentration distribution in each region. Therefore, it is crucial to determine appropriate concentration ranges within each region to ensure the normal operation of the thermoelectric transistor.

Firstly, the thermoelectric transistor is composed of P₁-Bi₂Te₃, N-Si, and P₂-Si materials. Before applying a temperature gradient (the entire transistor is at T = 20 °C), the respective donor or acceptor doping ion concentrations must be greater than their intrinsic carrier concentrations. Mathematically, it can be expressed as follows:

$$P_{a1}>p_{i1}\left(T=20 °\mathrm{C}\right)$$

(20)

$$N_d>n_i\left(T=20 °\mathrm{C}\right)$$

(21)

$$P_{a2}>p_{i2}\left(T=20 °\mathrm{C}\right)$$

(22)

where P_a1, N_d, and P_a2 represent the doping concentrations in P₁ region (P₁-Bi₂Te₃, emitter), N region (N-Si, base), and P₂ region (P₂-Si, collector), respectively. p_i1, n_i, and p_i2 represent the intrinsic carrier concentrations in the respective regions at T = 20 °C.

2.3.1. Implementation of Forward Bias and Forward Conduction at the Emitter–Base

After applying a temperature gradient, the emitter (P₁ region) and the base (N region) should simultaneously satisfy the forward bias and forward conduction. The temperature distribution T₁(x₁) between P₁ region and N region can be obtained from the previous section. According to the relevant literature [24], the built-in voltage at the emitter–base junction varies with temperature:

$$V_{bi1}\left(x_1\right)=\frac{k_B{T}_1\left(x_1\right)}{q}\left[\mathit{ln}\frac{P_{a1}}{p_{i1}\left(x_1\right)}+\mathit{ln}\frac{N_d}{n_i\left(x_1\right)}\right]$$

(23)

where k_B is the Boltzmann constant, p_i1(x₁) is the intrinsic carrier concentration affected by the temperature distribution T₁(x₁), while P_a1 and N_d remain constant regardless of the applied temperature gradient. The variations in p_i1(x₁) and n_i(x₁) with the temperature distribution can be described by the following [25,26]:

$$p_{i1}\left(x_1\right)={\left(\frac{m_{p1}^{\mathrm{*}}}{m_e}\right)}^{\frac{3}{2}}\times ({\frac{T_1\left(x_1\right)}{300})}^{\frac{3}{2}}\times \mathit{exp}\left(-\frac{E_{gp1}}{T_1\left(x_1\right)}\right)\times 2.5\times {10}^{19}$$

(24)

$$n_i\left(x_1\right)=5.23\times {10}^{15}\times {T_1\left(x_1\right)}^{\frac{3}{2}}\times \mathit{exp}\left(\frac{6395.39}{T_1\left(x_1\right)}\right)$$

(25)

where $m_{p1}^{\mathrm{*}}$ is the effective mass of the emitter, m_e is the electron mass, and E_gp1 is the bandgap of the emitter.

To achieve forward bias and forward conduction at the emitter–base junction, the built-in voltage V_bi1(x₁) should satisfy:

$$V_{bi1}\left(x_1\right)>0$$

(26)

Additionally, after applying the temperature gradient, the potential of the emitter should be higher than that of the base:

$${\phi }_{p1}\left(x_1\right)>{\phi }_n\left(x_1\right)$$

(27)

Since the potential of each region in this work is mainly determined by its carrier concentration, Equation (27) can be written as:

$$p_1\left(x_1\right)>N_d$$

(28)

where p₁(x₁) is the hole concentration distribution of the emitter after applying the temperature gradient. However, the concentration of the base remains constant (N_d) because it is completely depleted.

Finally, in order to ensure the forward conduction in the thermoelectric transistor, the generated voltage due to the Seebeck effect (the Seebeck voltage V_s1(x₁)) should be greater than the built-in voltage V_bi1(x₁). In other words, the emitter voltage V_e(x₁) should be greater than 0:

$$V_e\left(x_1\right)=V_{s1}\left(x_1\right)-V_{bi1}\left(x_1\right)>0$$

(29)

$$V_{s1}\left(x_1\right)=∆T\left(x_1\right)\times S_1$$

(30)

$$S_1=\left[\frac{8{\pi }^{\frac{8}{3}}{m}_{p1}^{\mathrm{*}}{k}_B^2\left(r+\frac{3}{2}\right)}{3^{\frac{5}{3}}{h}^{2}e}\right]\left[\frac{T_1\left(x_1\right)}{{p_1\left(x_1\right)}^{\frac{2}{3}}}\right]$$

(31)

where S₁ represents the Seebeck coefficient of the emitter and ∆T(x₁) is the temperature distribution between the emitter and the base. By combining these equations, the forward bias and forward conduction at the emitter–base can be achieved.

2.3.2. Realization of Reverse Bias at the Base–Collector

Similarly, the intrinsic carrier concentration distribution of P₂-type region (P₂-Si) under the applied temperature gradient can be expressed [25]:

$$p_{i2}\left(x_2\right)=5.23\times {10}^{15}\times {T_2\left(x_2\right)}^{\frac{3}{2}}\times \mathit{exp}\left(\frac{6395.39}{T_2\left(x_2\right)}\right)$$

(32)

In order ensure the normal operation of the thermoelectric transistor, the base–collector junction should be the reverse bias. Under the influence of the temperature distribution T₂(x₂), the built-in voltage at the base–collector junction can be expressed as:

$$V_{bi2}\left(x_2\right)=\frac{k_{B}T\left(x_2\right)}{q}\left[\mathit{ln}\frac{P_{a2}}{p_{i2}\left(x_2\right)}+\mathit{ln}\frac{N_d}{n_i\left(x_2\right)}\right]$$

(33)

To ensure proper operation, V_bi2(x₂) must be positive:

$$V_{bi2}\left(x_2\right)>0$$

(34)

Similar to the emitter–base junction, the potential of the base should be higher than that of the collector:

$${\phi }_n\left(x_2\right)>{\phi }_{p2}\left(x_2\right)$$

(35)

$$N_d>p_2\left(x_2\right)$$

(36)

Furthermore, the Seebeck coefficient and the Seebeck voltage for P₂-Si are expressed as follows:

$$V_{s2}\left(x_2\right)=∆T\left(x_2\right)\times S_2$$

(37)

$$S_2=\frac{k_B}{e}\left[\left(r+\frac{5}{2}\right)+\mathit{ln}\frac{2{\left(2\pi m_{p2}^{*}{k}_B{T}_2\left(x_2\right)\right)}^{3/2}}{h^3{p}_2\left(x_2\right)}\right]$$

(38)

where p₂(x₂) is the hole concentration distribution in the collector region after applying the temperature gradient.

By solving these equations, the operation conditions of the base–collector junction can be determined.

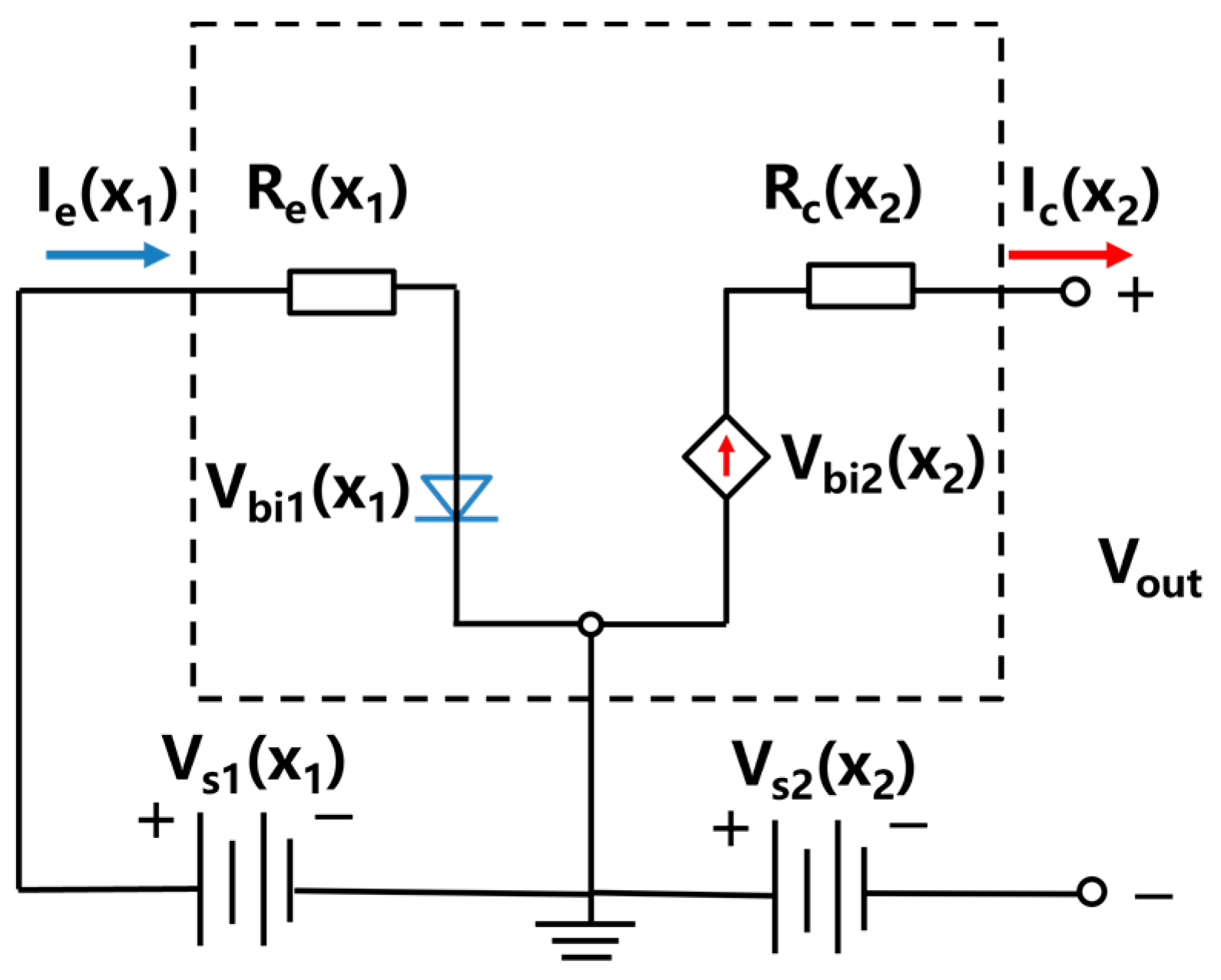
2.4. The Output Performance of Thermoelectric Transistors

For bipolar thermoelectric transistors, the base–collector circuit can be considered as the output circuit. In this work, the early voltage effects of the emitter, base, and collector, as well as the contact resistance between the transistor and the electrodes, can be neglected. The corresponding equivalent DC circuit diagram is shown in Figure 2. The left side of the circuit diagram represents the equivalent circuit of the emitter–base junction. V_s1(x₁) denotes the Seebeck voltage generated in the P₁ region, serving as the external voltage at the emitter. R_e(x₁) represents the resistance of the P₁ region of the emitter. V_bi1(x₁) is assumed to be the forward voltage. On the right side of the circuit, the equivalent circuit of the base–collector junction is shown. V_s2(x₂) signifies the Seebeck voltage generated in the P₂ region, acting as the external voltage at the collector. R_c(x₂) corresponds to the resistance of the P₂ region of the collector. V_bi2(x₂) is the voltage influenced by the emitter current I_e(x₁). Furthermore, considering that the thickness of the base can be neglected compared to the emitter and collector and that it is fully depleted, the collector current I_c(x₂) can be assumed to be equal to the emitter current I_e(x₁).

According to the Kirchhoff’s law, the relationships among these electrical parameters can be expressed:

$$V_e\left(x_1\right)=V_{s1}\left(x_1\right)-V_{bi1}\left(x_1\right)=I_e\left(x_1\right)R_e\left(x_1\right)$$

(39)

$$V_c\left(x_2\right)=V_{bi2}\left(x_2\right)-V_{s2}\left(x_2\right)=I_c\left(x_2\right)R_c\left(x_2\right)$$

(40)

$$I_e\left(x_1\right)=I_c\left(x_2\right)$$

(41)

$$R_e\left(x_1\right)=\frac{1}{p_{a1}e{\mu }_{p1}}\times \frac{l_{x1}}{w_y{h}_z}$$

(42)

$$R_c\left(x_2\right)=\frac{1}{p_{a2}e{\mu }_{p2}}\times \frac{l_{x2}}{w_y{h}_z}$$

(43)

where V_e(x₁) is the emitter voltage, V_c(x₂) is the collector voltage, and μ_p1 and μ_p2 are the hole mobility of the P₁-type material (P₁-Bi₂Te₃) and P₂-type material (P₂-Si), respectively. lx₁ and lx₂ represent the lengths of the P₁-type and P₂-type materials along the x direction, while w_y and h_z denote the lengths of the device in y and z directions, respectively, with values set to 1 μm. S_p2 is the Seebeck coefficient of the collector and m*_p2 is the effective mass of the collector.

The output power of the transistor can be expressed as the product of the open-circuit voltage and the short-circuit current:

$$P_{out}=I_e\left(x_1\right)\times V_{out}=I_e\left(x_1\right)\times V_c\left(x_2\right)=I_e\left(x_1\right)\times [V_{bi2}\left(x_2\right)-V_{s2}\left(x_2\right)]$$

(44)

2.5. The Material Parameters of Thermoelectric Transistor

In this work, P₁-Bi₂Te₃, N-Si, and P₂-Si are selected as the emitter material, base material, and collector material, respectively. The material parameters of the thermoelectric transistor studied are listed in

Table 1. Material parameters of thermoelectric transistor.

Parameter	Emitter	Base	Collector	Ref.
Eg (eV)	0.18	1.12	1.12	[25,27]
m*/me	1.4671	0.43	0.2601	[28,29,30]
εr	90	11.7	11.7	[6,25]
μp (cm2/V s)	510	-	480	[21,25]

.

3. Results and Discussion

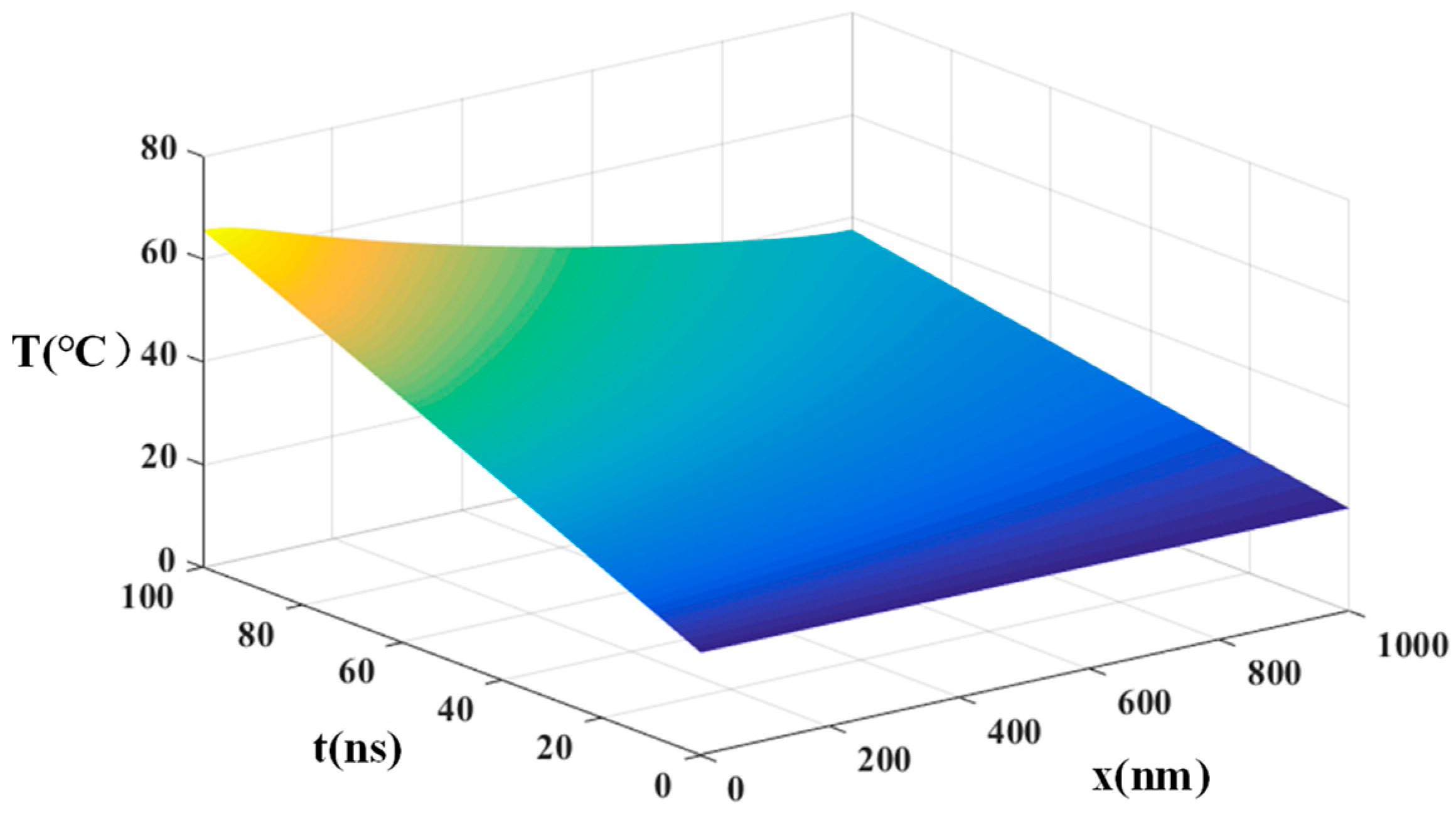
3.1. Temperature Distribution in Thermoelectric Transistor

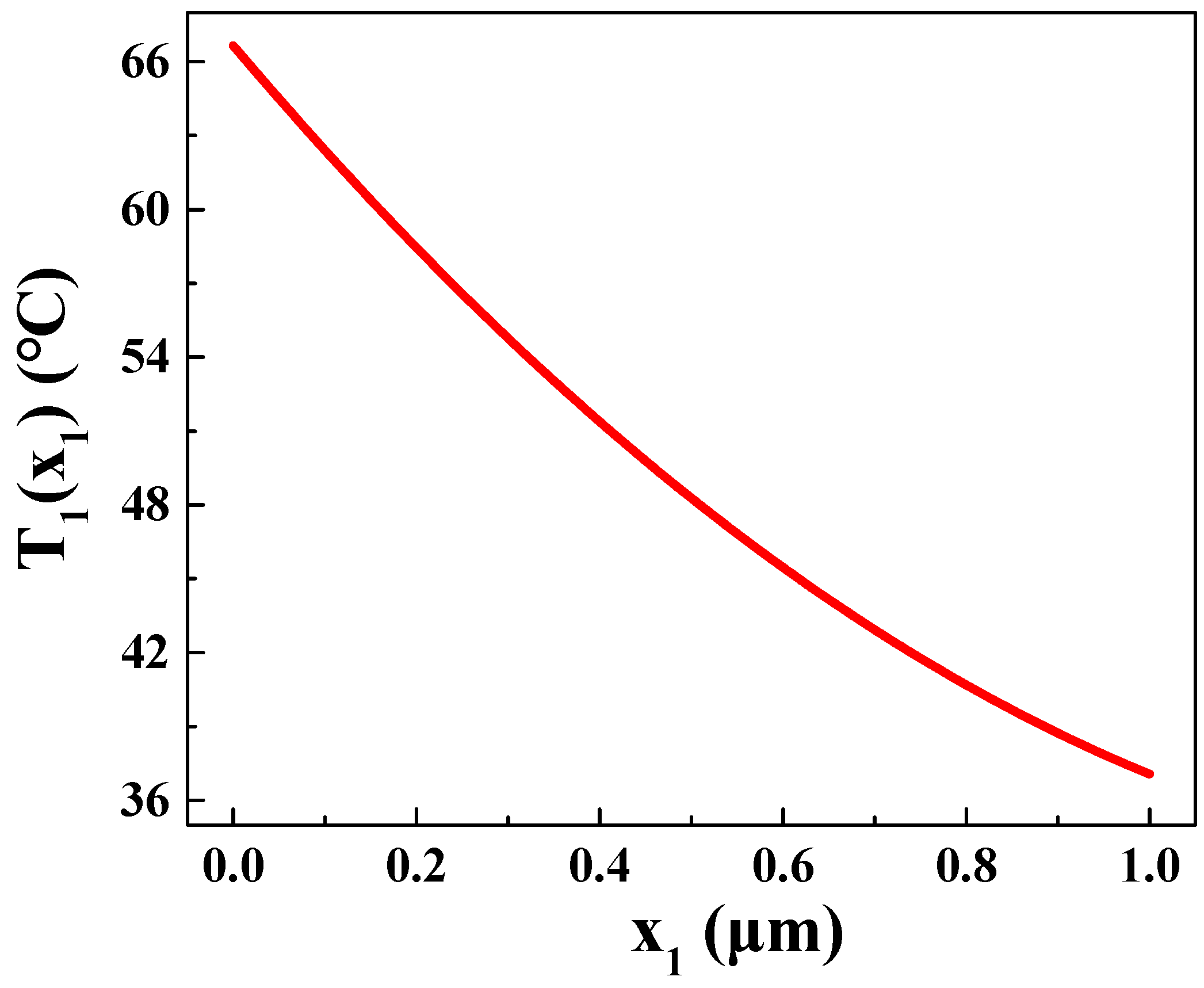
3.1.1. Temperature Distribution in p-Type Bi₂Te₃

It is assumed that P₁-Bi₂Te₃ is in the temperature of 20 °C. Under the condition of illuminating with an incident optical power of =3 × 10⁷(W·cm⁻²) for a duration of 100 ns, the temperature distribution within Bi₂Te₃ is obtained as shown in Figure 3.

As depicted in Figure 3, it is apparent that, with an increase in laser irradiation time, the sample initiates heating from the irradiated surface at x = 0 μm. Subsequently, the heat gradually propagates throughout the entire device, and the lowest temperature is observed at x = 1 μm within P₁ region. Figure 4 illustrates the temperature distribution in P₁ region at T = 100 ns. Notably, after 100 ns of illumination, the temperature distribution in P₁ region (Bi₂Te₃) exhibits a pattern of decreasing temperature as the distance from the laser increases. Specifically, at x = 0 μm, the temperature at 100 ns is T_b1 = 66.7 °C, whereas, at x = 1 μm, the temperature reaches its minimum value of T_b2 = 37 °C. By employing a quadratic function, the temperature variation T₁(x₁) in P₁ region as a function of x can be obtained:

$$T_1\left(x_1\right)=14.35x_1^2-43.95x_1+66.7$$

(45)

3.1.2. Temperature Distribution in p-Si

By solving the equations in MATLAB, the temperature distribution in P₂ region (P₂-Si) along the x direction can be obtained. After 100 ns, the temperature distribution is shown in Figure 5.

Based on Figure 5, it can be observed that the temperature distribution in P₂-type region gradually decreases with increasing x. It is important to note that n-type region in this work is extremely thin. Therefore, the length of the n-type region along the x direction is assumed to be 0, implying that x₁ = 1 μm coincides with x₂ = 0 μm. At x₂ = 0 μm, P₂-Si exhibits the highest temperature, T_s1 = 37 °C, while, at x₂ = 4 μm, p-Si reaches its lowest temperature, T_s2 = 20 °C. By fitting a curve to the data in the figure, a fitting function T₂(x₂) for the temperature distribution in P₂-Si can be obtained:

$$T_2\left(x_2\right)=-0.1982x_2^3+{2.798x}_2^2-12.48x_2+37$$

(46)

3.2. Hole Concentration Distribution within Thermoelectric Transistor

The thermoelectric transistor consists of P₁-type region, N-type region, and P₂-type region. As mentioned in the previous section, the temperature distribution along the x direction of the transistor is represented by Equations (45) and (46).

Considering that N-type region is assumed to be completely depleted, it contains no free mobile carriers. However, for both P₁-type region and P₂-type region, under the influence of temperature distribution, the holes migrate from the hot end to the cold end, leading to their accumulation at the cold end. By utilizing the calculation formula from the previous section, the concentration distribution of holes in P₁-type region can be obtained:

$$p_1\left(x_1\right)=\frac{P_{a1}\times \left(-6.429\times {10}^{-13}\right)}{{\left(x_1-1.532\times {10}^{-4}\right)}^3}$$

(47)

From Figure 6, it is evident that p₁(x₁) increases with increasing x₁. This indicates that the hole concentration in P₁-type region gradually increases from the hot end to the cold end. Additionally, as P_a1 increases, p₁(x₁) also increases. Of note, p₁(x₁) = P_a1 is near the midpoint of the P₁-type region (x₁₀ = 0.501 μm), as shown in the dashed line in Figure 6. This is because the hole carriers in the P₁-type region (Bi₂Te₃) redistribute only along the x direction, and the temperature difference is fixed. Therefore, the position x₁₀ remains constant. As a result, it can be inferred that, for x₁ < x₁₀, p₁(x₁) < P_a1, and, for x₁₀ ≤ x₁ ≤ 1 μm, p₁(x₁) ≥ P_a1, with equality only at x₁ = x₁₀.

Similarly, hole concentration distribution of P₂-Si can be obtained:

$$p_2\left(x_2\right)=\frac{P_{a2}\times \left(5.773\times {10}^4\right)}{{\left(1.858\times {10}^8\times x_2^2-1.749\times {10}^5\times x_2+39\right)}^3}$$

(48)

Figure 7 illustrates the variation in p₂(x₂) with respect to x₂ for different P_a2. It can be observed that p₂(x₂) also increases with the increase in x₂. Additionally, as P_a2 increases, p₂(x₂) increases. Similarly, at x₂₀ = 2.009 μm, p₂(x₂) equals P_a2, as indicated by the dashed line in Figure 7. In other words, for 0 ≤x₂ < x₂₀ = 2.009 μm, P_a2 > p₂(x₂), and, for x₂₀ ≤ x₂ ≤ 4 μm, p₂(x₂) ≥ P_a2, with equality only at x₂ = x₂₀.

Thus, it can be inferred that the Seebeck effect causes the redistribution of hole concentrations in both P₁-type and P₂-type regions, with holes diffusing from the hot end to the cold end. Consequently, the built-in voltage at both the P₁–N junction and the N–P₂ junction decreases from the cold end to the hot end. This unique characteristic enables such PNP heterojunctions to function as thermoelectric transistors. The emitter corresponds to the region with x₁₀ ≤ x₁ ≤ 1 μm in the P₁-type region, the base corresponds to the entire N-type region, and the collector corresponds to the region with 0 ≤ x₂ < x₂₀ = 2.009 μm in the P₂-type region.

3.3. Operarion Conditions in Thermoelectric Transistor

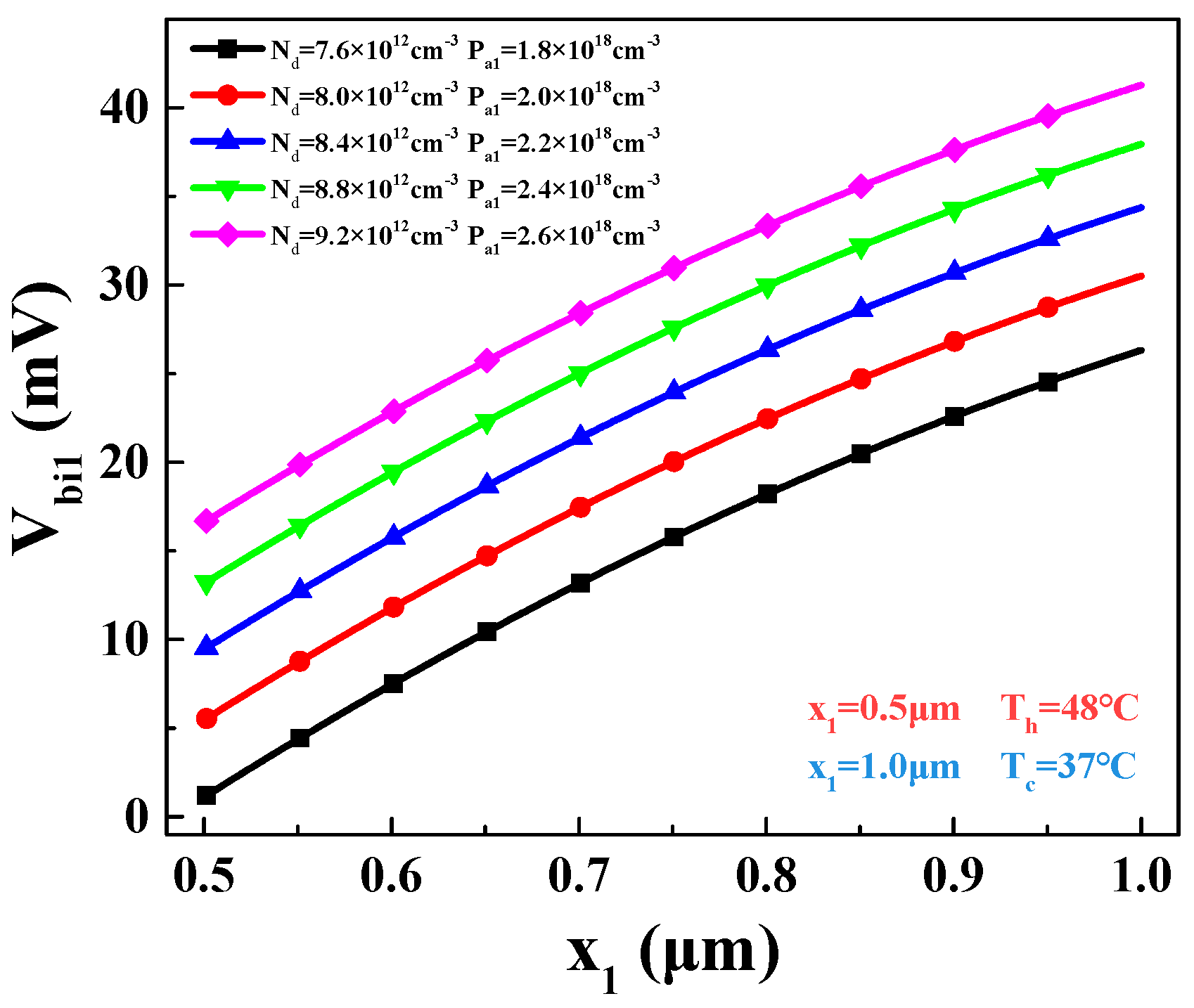
3.3.1. Forward Bias of Emitter–Base Junction

When the entire thermoelectric transistor is at 20 °C, based on Equations (20)–(22), the required values for P_a1, N_d, and P_a2 can be determined:

$$P_{a1}>p_{i1}=1.609\times {10}^{18}\left({\mathrm{c}\mathrm{m}}^{-3},T=20 °\mathrm{C}\right)$$

(49)

$$N_d>n_i=3.179\times {10}^{10}\left({\mathrm{c}\mathrm{m}}^{-3},T=20 °\mathrm{C}\right)$$

(50)

$$P_{a2}>p_{i2}=9.268\times {10}^9\left({\mathrm{c}\mathrm{m}}^{-3},T=20 °\mathrm{C}\right)$$

(51)

For simplicity, their values are assumed to be 1.61 × 10¹⁸ cm⁻³, 3.2 × 10¹⁰ cm⁻³, and 1.0 × 10¹⁰ cm⁻³, respectively.

The temperature distribution T₁(x₁) and the temperature difference ΔT₁(x₁) for the emitter–base junction can be written:

$$T_1\left(x_1\right)=14.35x_1^2-43.95x_1+66.7$$

(52)

$${∆T}_1\left(x_1\right)=-14.35x_1^2-43.95x_1$$

(53)

$$x_1\in \left[\mathrm{0.501,1}\right]\left(\mathsf{\mu }\mathrm{m}\right)$$

(54)

Under this temperature distribution, the calculated values for the Seebeck coefficient S₁ and the Seebeck voltage V_s1 in P₁ region are shown in Figure 8.

As shown in Figure 8, the Seebeck coefficient S₁ of P₁ region increases with the temperature T₁(x₁). Moreover, for different doping concentrations P_a1, the smaller doping concentration leads to a larger Seebeck coefficient. As for the Seebeck voltage V_s1, it exhibits a trend where it increases as the distance from the hot end (x₁ = 0) increases due to the larger temperature difference.

Additionally, the built-in voltage V_bi1 within P₁-N region can be obtained, as shown in Figure 9.

Under different values of P_a1 and N_d, the built-in voltage increases with the increase in x₁. This means that, as the temperature decreases, the built-in voltage increases. The increase is primarily attributed to the decrease in intrinsic carrier concentration with decreasing temperature.

Based on Section 2.3.1, it can be concluded that achieving the forward bias and forward conduction of the emitter–base junction depends on three conditions: V_bi1(x₁) > 0, V_e(x₁) = V_s1(x₁)–V_bi1(x₁) > 0, and p₁(x₁) > N_d. These conditions are all influenced by P_a1, x₁, and N_d. The appropriate concentration ranges for P_a1 and N_d are shown in Figure 10.

It can be observed that the suitable range for N_d is 3.2 × 10¹⁰ cm⁻³~15.8 × 10¹⁰ cm⁻³. As the range of N_d increases, the range of P_a1 decreases. When N_d is 3.2 × 10¹⁰ cm⁻³, the range of P_a1 is 1.61 × 10¹⁸ cm⁻³~5.6 × 10¹⁸ cm⁻³, as indicated by the black line. When N_d increases to 15.8 × 10¹⁰ cm⁻³, the range of P_a1 is only 1.61 × 10¹⁸ cm⁻³~2.0 × 10¹⁸ cm⁻³, as shown by the red line. This is because the built-in voltage V_bi1(x₁) is positively correlated with N_d and P_a1. As N_d and P_a1 increase, V_bi1(x₁) also increases, resulting in a smaller range of P_a1 for achieving V_s1(x₁)–V_bi1(x₁) > 0.

Additionally, it can be found that x₁ also changes with N_d and P_a1. As N_d and P_a1 increase, the range of x₁ gradually approaches 0.501 μm. This is because, at x₁ = 1 μm, both V_bi1(x₁) and V_s1(x₁) reach their maximum values. However, in comparison to V_s1(x₁), V_bi1(x₁) increases at a faster rate as x₁ increases. Therefore, it is relatively easier to achieve the operation conditions of the emitter–base junction at x₁ = 0.501 μm. Thus, when N_d = 3.2 × 10¹⁰ cm⁻³, the maximum range of x₁ is 0.608 μm to 1 μm. While N_d = 15.8 × 10¹⁰ cm⁻³, the maximum range of x₁ is 0.501 μm to 0.537 μm. Therefore, the forward bias and forward conduction of the emitter–base junction can be achieved by adjusting the concentrations of P_a1 and N_d. Such a deigned doping concentration for P₁-Bi₂Te₃ can be obtained directly by doping process, e.g., phosphorus as acceptor.

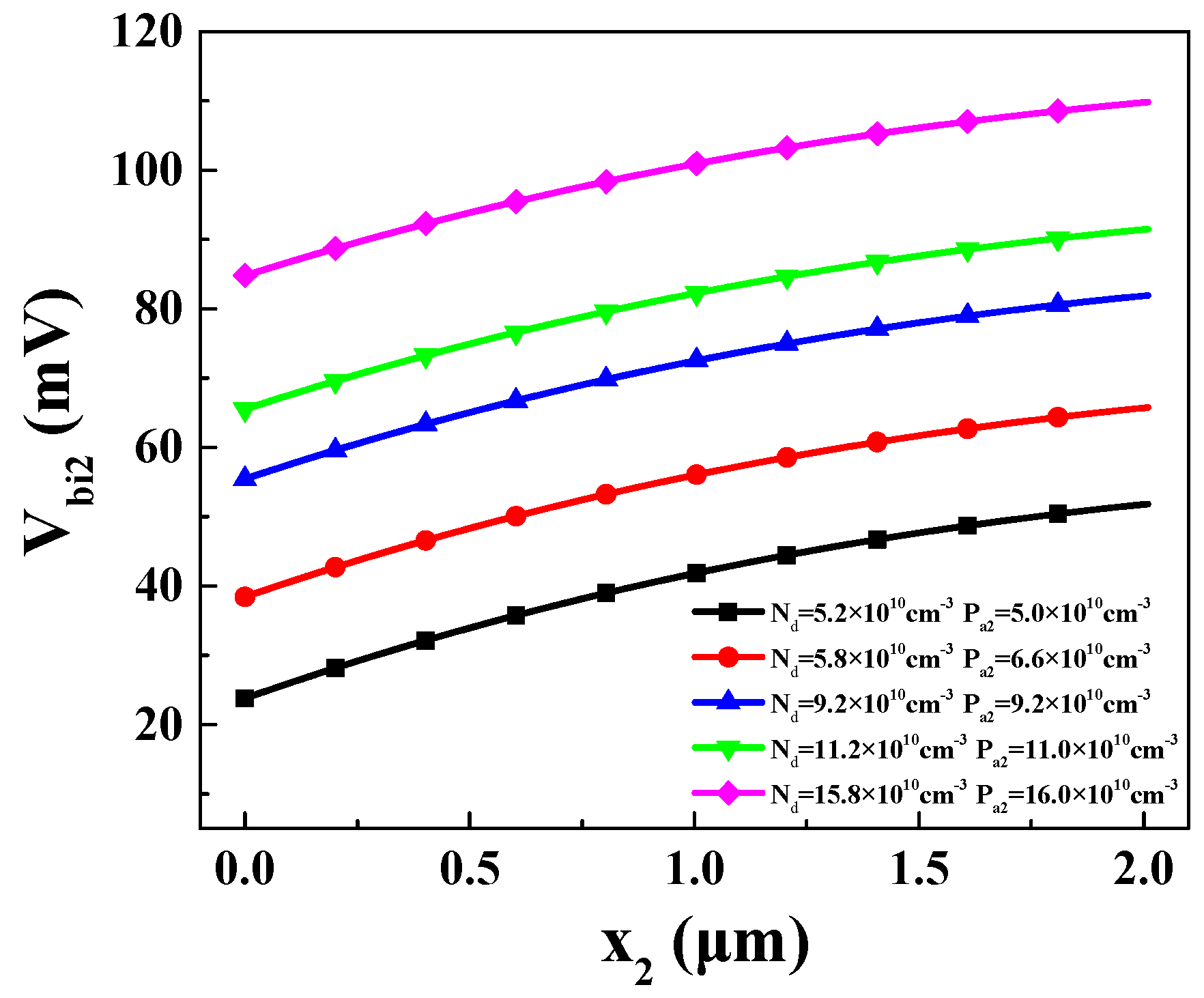
3.3.2. Reverse Bias of Base–Collector Junction

When a temperature gradient is applied in the base–collector junction, the temperature distribution equation T₂(x₂) and temperature difference ∆T₂(x₂) can be expressed as follows:

$$T_2\left(x_2\right)=-0.1982x_2^3+{2.798x}_2^2-12.48x_2+37$$

(55)

$${∆T}_2\left(x_2\right)=0.1982x_2^3-{2.798x}_2^2+12.48x_2-17$$

(56)

$$x_2\in \left[\mathrm{0,0.2}\right]\left(\mathsf{\mu }\mathrm{m}\right)$$

(57)

It should be noted that ∆T(x₁) represents the temperature difference between the emitter and base, with a positive value. However, ∆T₂(x₂) represents the temperature difference between the collector and base, with a negative value. Therefore, V_s1(x₁) has a positive value, while V_s2(x₂) has a negative value.

For P₂ region, the values of the Seebeck coefficient S₂ and the Seebeck voltage V_s2 are shown in Figure 11.

It can be observed that the Seebeck coefficient S₂ of P₂ region increases with temperature T₂(x₂). For different doping concentrations P_a2, a smaller doping concentration leads to a larger Seebeck coefficient. Regarding the Seebeck voltage V_s2, it exhibits a trend as the position approaches x₂ = 0 (closer to the hot end) due to the increasing temperature difference.

The built-in voltage V_bi2 in the N-P₂ region is depicted in Figure 12. It can be found that the built-in voltage V_bi2 increases with increasing x₂ at different values of P_a2 and N_d. In other words, as the temperature decreases, the built-in voltage increases. This increase primarily stems from the decrease in intrinsic charge carriers with decreasing temperature.

Based on Section 2.3.2, it can be concluded that achieving the forward bias and forward conduction of the emitter–base junction depends on three conditions: V_bi2(x₂) > 0 and p₂(x₂) < N_d. These conditions are all influenced by P_a2, x₂, and N_d. Therefore, the reverse bias in the base–collector junction can be achieved by adjusting the concentrations of P_a2 and N_d. The appropriate concentration ranges for P_a2 and N_d are shown in Figure 13.

Unlike the previous section, the range of N_d is from 5.2 × 10¹⁰ cm⁻³ to 15.8 × 10¹⁰ cm⁻³. It can be observed that, as N_d increases, the corresponding range of P_a2 also gradually increases. This is because higher values of N_d and P_a2 both lead to larger values of V_bi2(x₂), making it easier to satisfy the reverse biasing condition V_bi2(x₂) > 0.

To summarize, when N_d is within the range of 5.2 × 10¹⁰ cm⁻³ to 15.8 × 10¹⁰ cm⁻³, the thermoelectric transistor can be activated in the forward-active mode. The corresponding ranges of P_a1, P_a2, x₁, and x₂ are determined by the different values of N_d. By adjusting the concentrations of P_a1, N_d, and P_a2, the current can be generated in the thermoelectric transistor directly driven by the Seebeck effect.

3.4. Output Performance of Thermoelectric Transistor

It is evident that the output power of the transistor is primarily influenced by P_a1, N_d, P_a2, x₁, and x₂ based on Equation (44). Therefore, the impact of these parameters on the output power of the thermoelectric transistor is obtained in the following.

3.4.1. Impact of N_d on Output Power of Thermoelectric Transistor

Since the value of N_d directly affects the other four physical quantities, it is essential to initially examine the influence of N_d on the output power. Figure 14 illustrates the relationship between N_d and the maximum output power of the thermoelectric transistor.

It is evident that, as N_d gradually increases, P_outmax exhibits a trend of initially increasing and then decreasing. At N_d = 8.0 × 10¹⁰ cm⁻³, P_outmax reaches its maximum value of 0.7093 μW. It is important to note that different values of N_d correspond to various combinations of P_a1, P_a2, x₁, and x₂. Considering the multitude of possible parameter combinations, it is challenging to directly explain how N_d influences the output power. Therefore, a comprehensive enumeration of the parameters is necessary to identify the optimal solution, which, in this case, is N_d = 8.0 × 10¹⁰ cm⁻³ and P_outmax = 0.7093 μW.

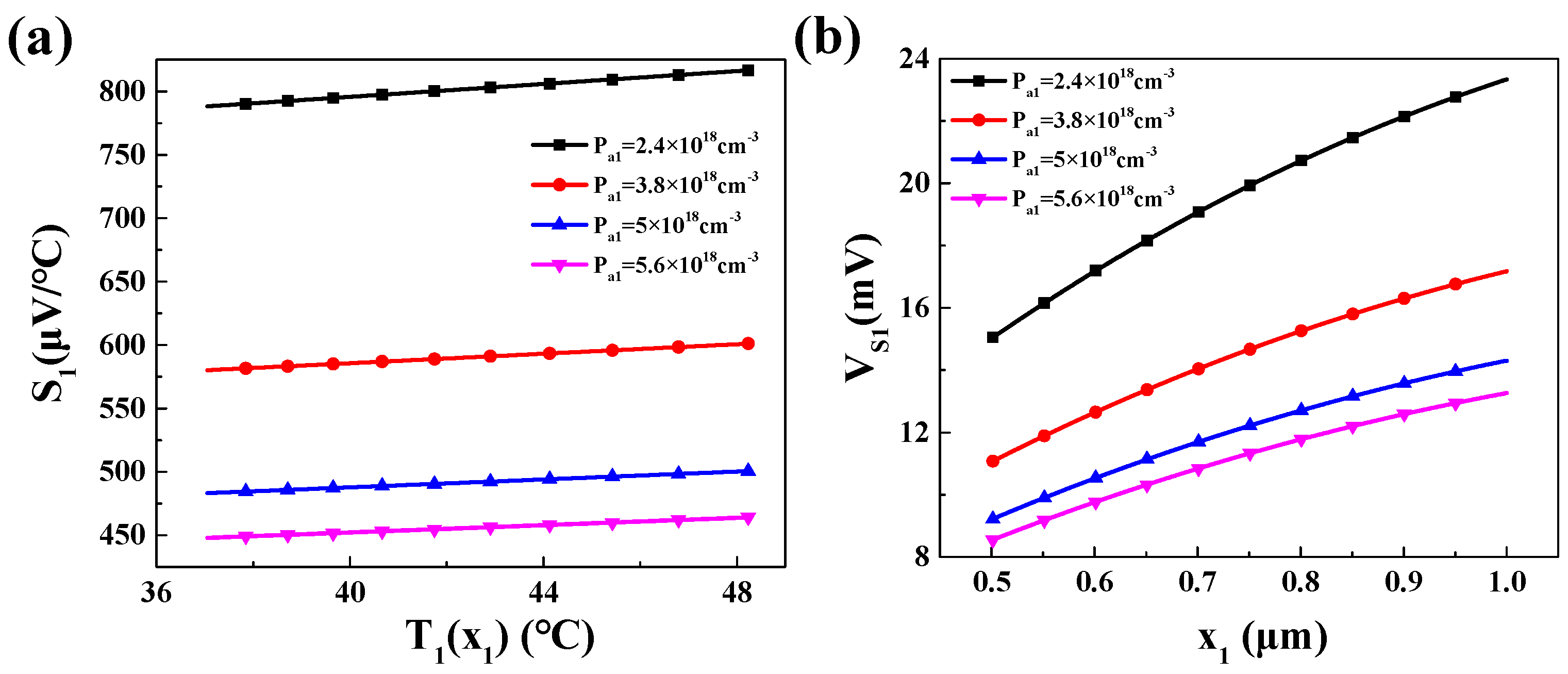
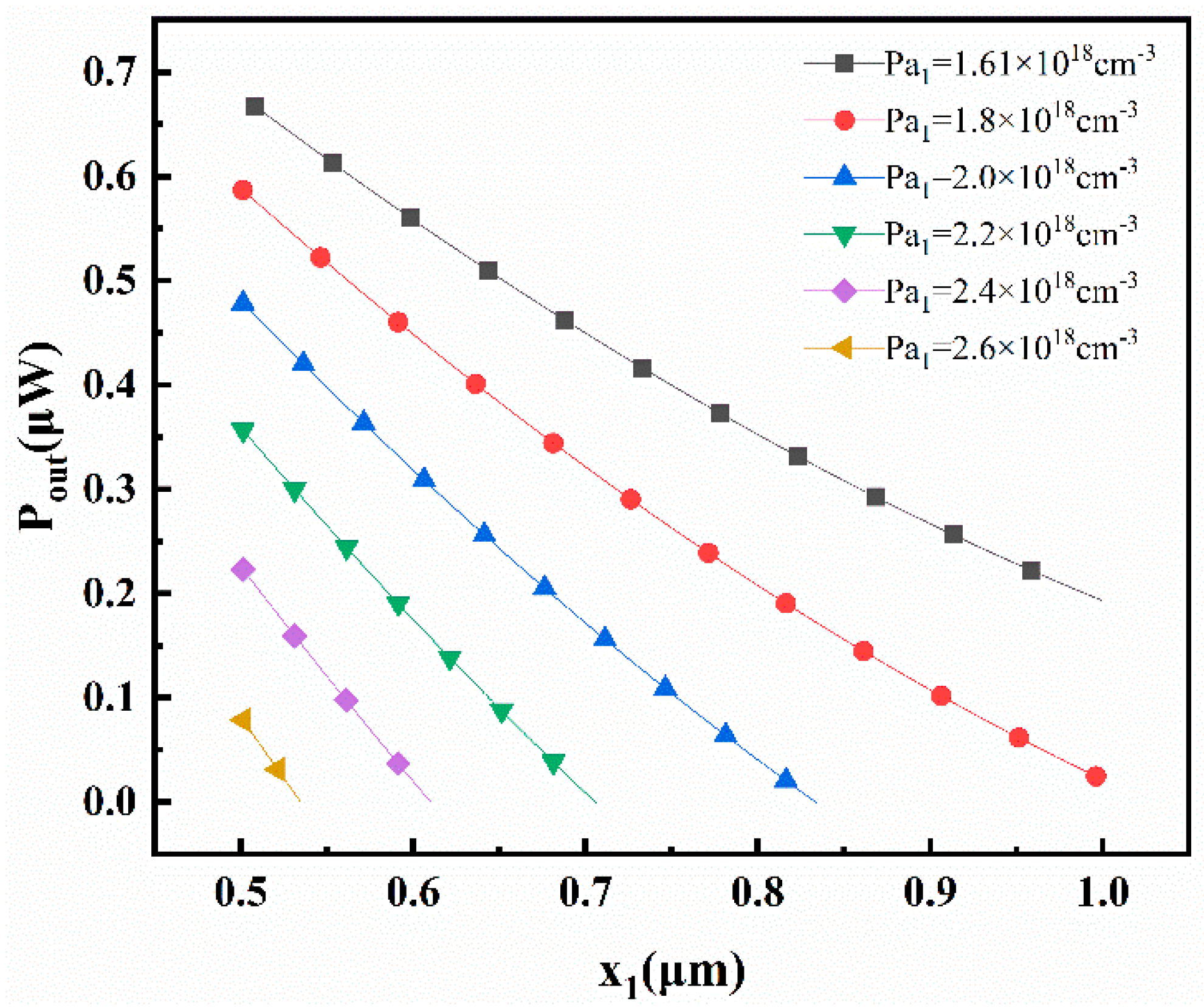
3.4.2. Impact of P_a1 and x₁ on Output Power of Thermoelectric Transistor

For N_d = 8.0 × 10¹⁰ cm⁻³, the range of P_a1 is from 1.61 × 10¹⁸ cm⁻³ to 2.6 × 10¹⁸ cm⁻³ and the range of P_a2 is from 1.0 × 10¹⁰ cm⁻³ to 8.2 × 10¹⁰ cm⁻³. Moreover, different values of P_a1 and P_a2 correspond to specific ranges of x₁ and x₂. Considering a fixed P_a2 value of 7.8 × 10¹⁰ cm⁻³ and x₂ value of 0.4 μm, the relationship between output power (P_out) and the variations in P_a1 and x₁ is illustrated in Figure 15.

It can be observed that the output power (P_out) increases as the concentration of P_a1 and x₁ decrease. These results can be derived from Equation (58):

$$P_{out}=I_e\left(x_1\right)\times [V_{bi2}\left(x_2\right)-V_{s2}\left(x_2\right)]$$

(58)

When N_d, P_a2, and x₂ remain constant, the value of P_out is primarily influenced by I_e(x₁):

$$I_e\left(x_1\right)=\frac{V_{s1}\left(x_1\right)-V_{bi1}\left(x_1\right)}{R_e\left(x_1\right)}$$

(59)

At x₁ = 1 μm, both V_bi1(x₁) and V_s1(x₁) reach their maximum values. However, compared to V_s1(x₁), V_bi1(x₁) increases more rapidly as x₁ increases. Therefore, at x₁ = 0.501 μm, V_s1(x₁)–V_bi1(x₁) reaches its maximum value. Thus, as x₁ decreases within the range of x₁ ∈ (0.501 μm, 1 μm), P_out increases. On the other hand, when other conditions remain unchanged, a larger P_a1 leads to a higher built-in voltage in the P₁ region (V_s1(x₁)–V_bi1(x₁)). As a result, with an increase in P_a1, P_out decreases.

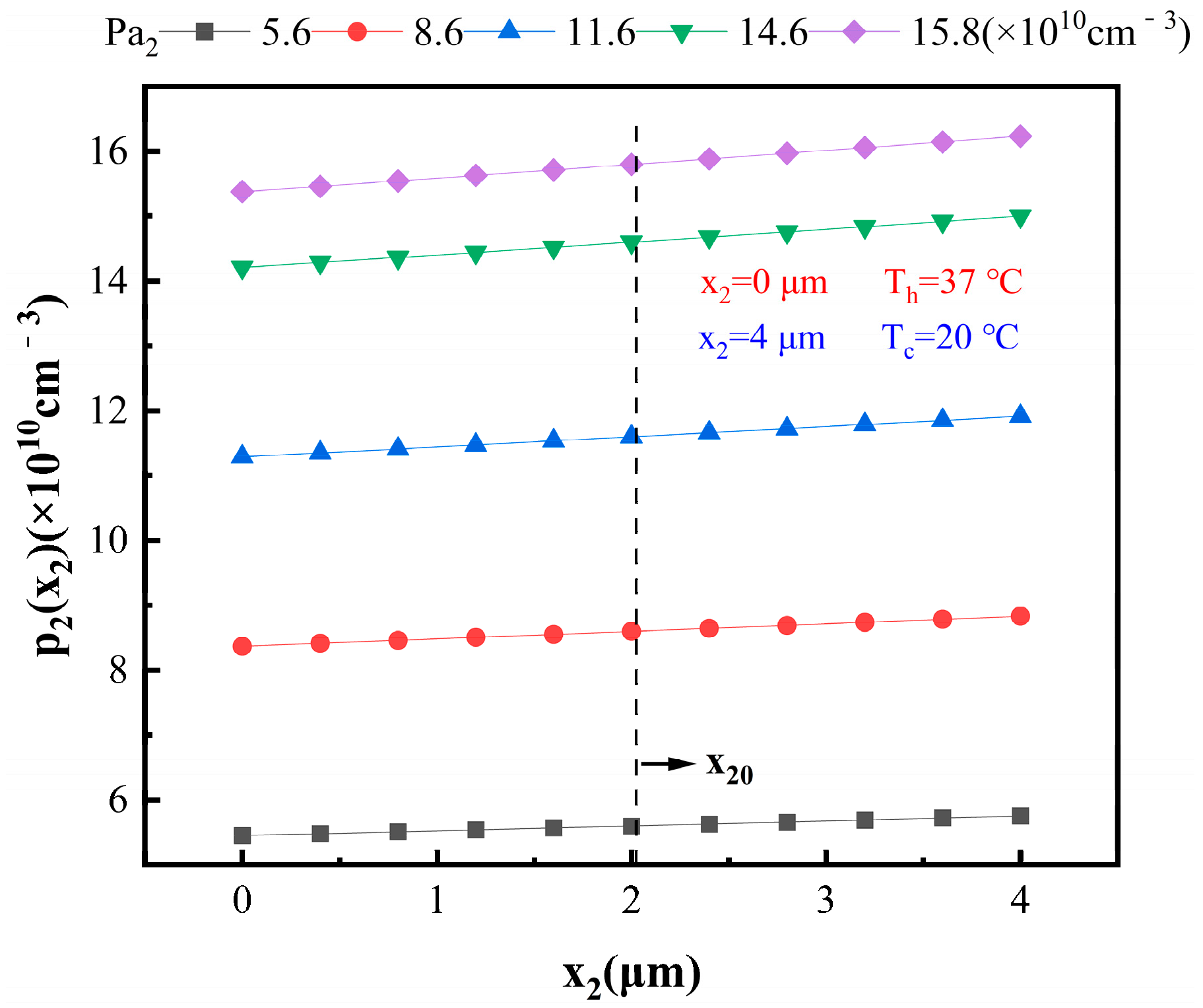
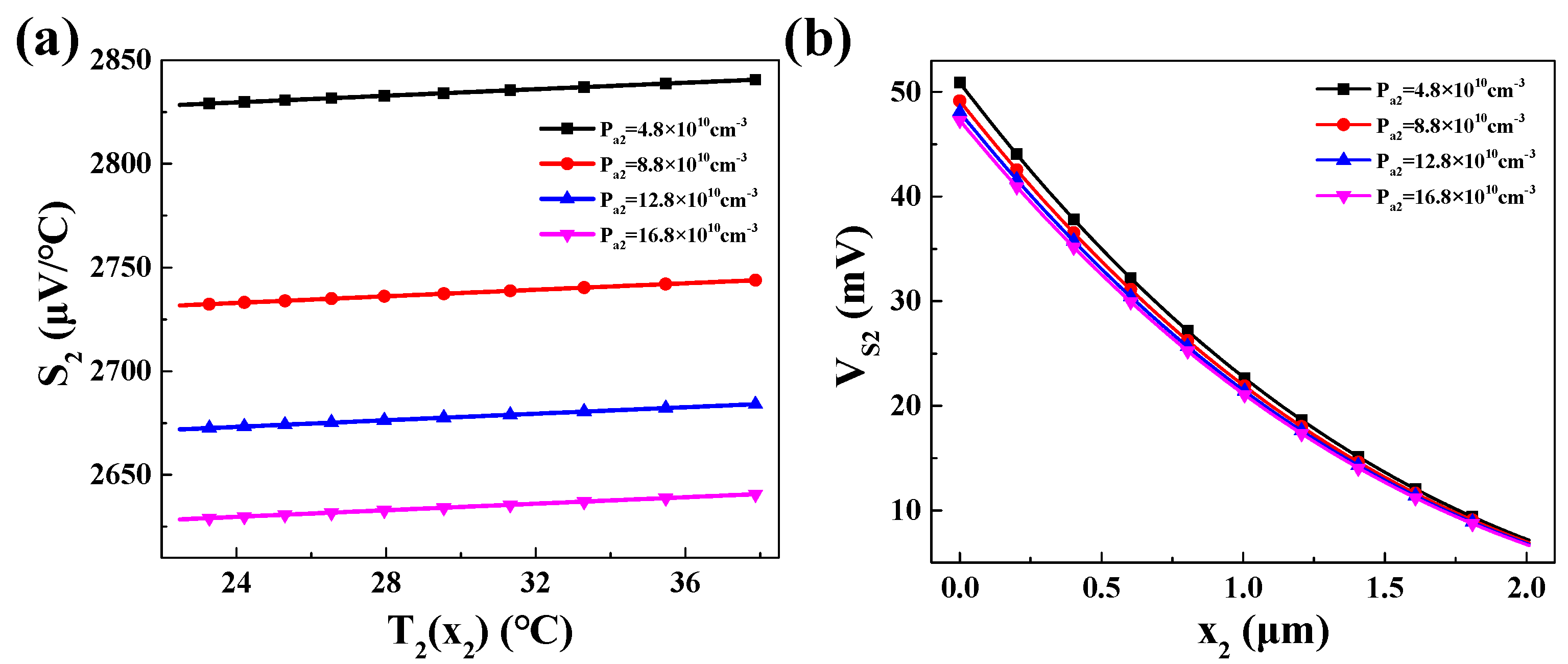
3.4.3. Impact of P_a2 and x₂ on Output Power of Thermoelectric Transistor

The impact of P_a2 and x₂ on the output power of the thermoelectric transistor is examined in the following when P_a1 = 1.61 × 10¹⁸ cm⁻³ and x₁ = 0.508 μm. As shown in Figure 16, it can be observed that P_out increases as P_a2 increases and x₂ decreases. Again, referring to the expression for P_out:

$$P_{out}=I_e\left(x_1\right)\times [V_{bi2}\left(x_2\right)-V_{s2}\left(x_2\right)]$$

(60)

When N_d, P_a1, and x₁ are constant, the value of P_out is mainly influenced by V_bi2(x₂)–V_s2(x₂). An increase in P_a2 leads to a higher value of V_bi2(x₂), resulting in a larger difference between V_bi2(x₂) and V_s2(x₂). Consequently, as P_a2 increases, P_out also increases. On the other hand, when x₂ increases, ∆T₂(x₂) decreases, resulting in a lower V_s2(x₂) and higher V_bi2(x₂). In this case, V_s2(x₂) dominates the relationship and the value of V_bi2(x₂)–V_s2(x₂) decreases, leading to a decrease in P_out.

3.4.4. Transistor Structure: Optimization of Output Power Effects

As deduced from the above analysis, when N_d = 8.0 × 10¹⁰ cm⁻³, P_a1 = 1.61 × 10¹⁸ cm⁻³, P_a2 = 8.2 × 10¹⁰ cm⁻³, x₁ = 0.508 μm, and x₂ = 0 μm, the maximum output power of this designed thermoelectric transistor can reach 0.7093 μW.

If only Bi₂Te₃ is used without the thermoelectric transistor structure, the output power, can be calculated as 0.1442 μW. It can be observed that the designed thermoelectric transistor structure in this work results in an increase in the output power compared to a single thermoelectric material, with an improvement of 391.9%.

4. Conclusions

In this work, the temperature distribution and hole concentration distribution within the thermoelectric transistor is obtained through theoretical calculations. By considering the variation in the built-in voltage with temperature, the formation principle of the thermoelectric transistor is demonstrated. Subsequently, based on the operation conditions of the thermoelectric transistor, suitable doping concentrations of the emitter, base, and collector can be determined. Furthermore, the maximum output power of the thermoelectric transistor is obtained. The main conclusions drawn from this work are as follows:

(i)

The thermoelectric transistor, composed of P₁-Bi₂Te₃, N-Si, and P₂-Si, is directly irradiated by the laser. Under laser illumination and heat conduction, the temperature decreases from 66.7 °C to 20 °C, creating a temperature difference of 46.7 °C at the two ends of the thermoelectric transistor. As a result of the temperature difference, holes inside P₁ and P₂ regions migrate from the hot end to the far end, leading to increased hole concentration at the cold end.

(ii)

The operation conditions of the thermoelectric transistor under laser irradiation are investigated. Based on the corresponding conditions, suitable doping concentrations of the emitter, base, and collector can be determined. By adjusting these concentrations, the current can be produced in the thermoelectric transistor only driven by the Seebeck effect.

(iii)

The influence of these parameters on the output power of the thermoelectric transistor is also investigated. The maximum output power of the thermoelectric transistor is 0.7093 μW under a temperature difference of 46.7 °C, which is nearly quadrupling the performance compared to the single thermoelectric material structure.

(iv)

Importantly, the operation conditions of the thermoelectric transistor established in this work are applicable to other material systems. By adjusting the doping concentration within each region, current can be generated, ensuring that the forward-active mode is achieved. Therefore, this novel thermoelectric generator concept can significantly contribute to the advancement of the thermoelectric field. Moreover, the combination with transistor technology can expand the range of applications for thermoelectric generators.