Numerical and Experimental Study on Carbon Segregation in Square Billet Continuous Casting with M-EMS
Abstract
:1. Introduction
2. Model Description
2.1. Assumptions
- The steel in the calculation domain is considered as incompressible Newtonian viscous fluid;
- The computing domain is considered vertical and the influence of mold oscillation and taper is ignored;
- The electromagnetic field in the effective zone of M-EMS does not affect the molten steel flow;
- While solving the solute diffusion, the interaction of solute elements can be ignored;
- The heat transfer phenomenon between the molten steel and the top slag of the meniscus is ignored.
2.2. Governing Equations
- (1)
- Fluid Flow Model
- (2)
- Heat Transfer Model
- (3)
- Solute Transport Model
- (4)
- Electromagnetic Field Model
2.3. Model Parameters and Boundary Conditions
3. Experimental Implementation
4. Results and Discussion
4.1. Model Validation
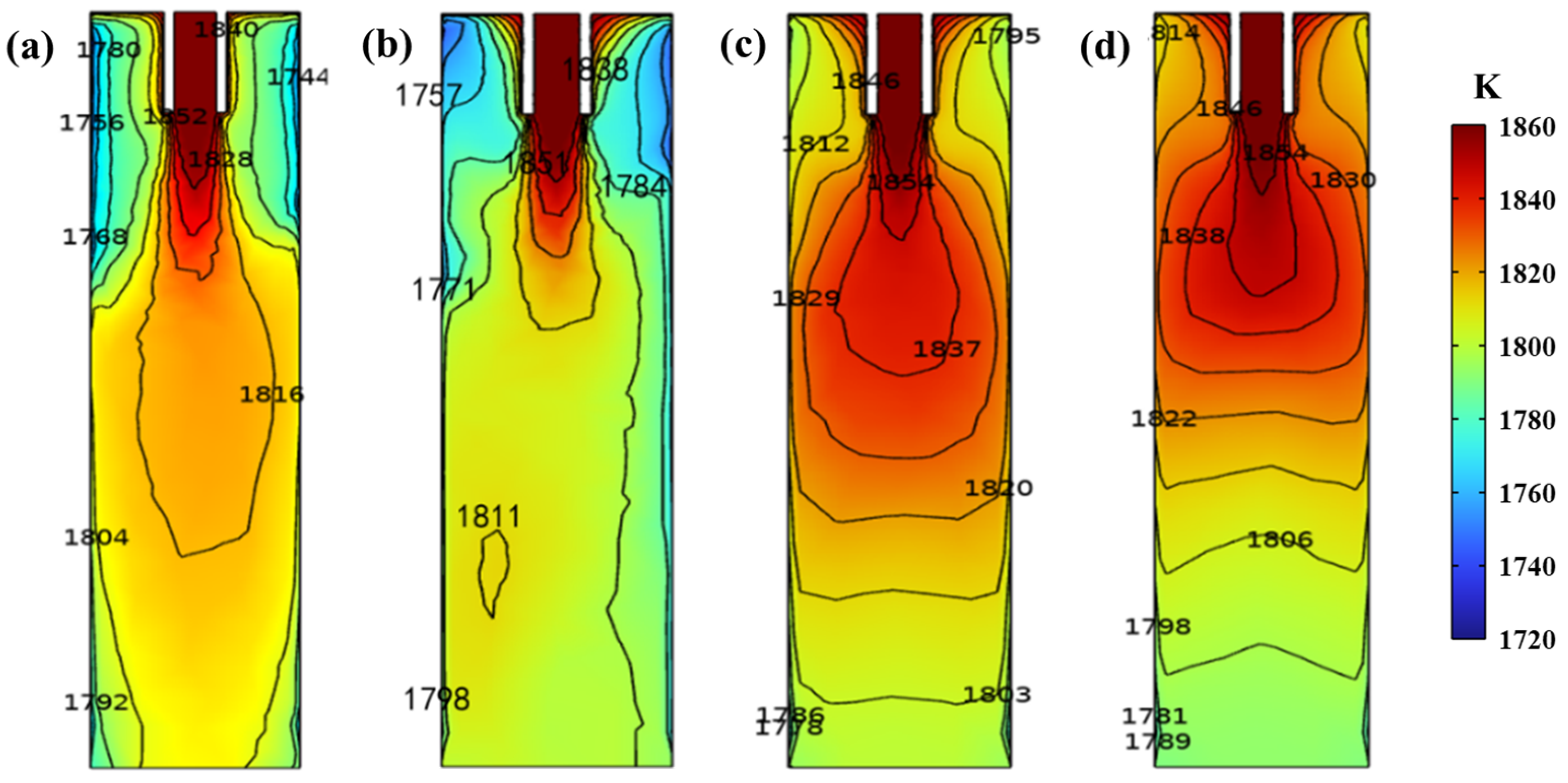
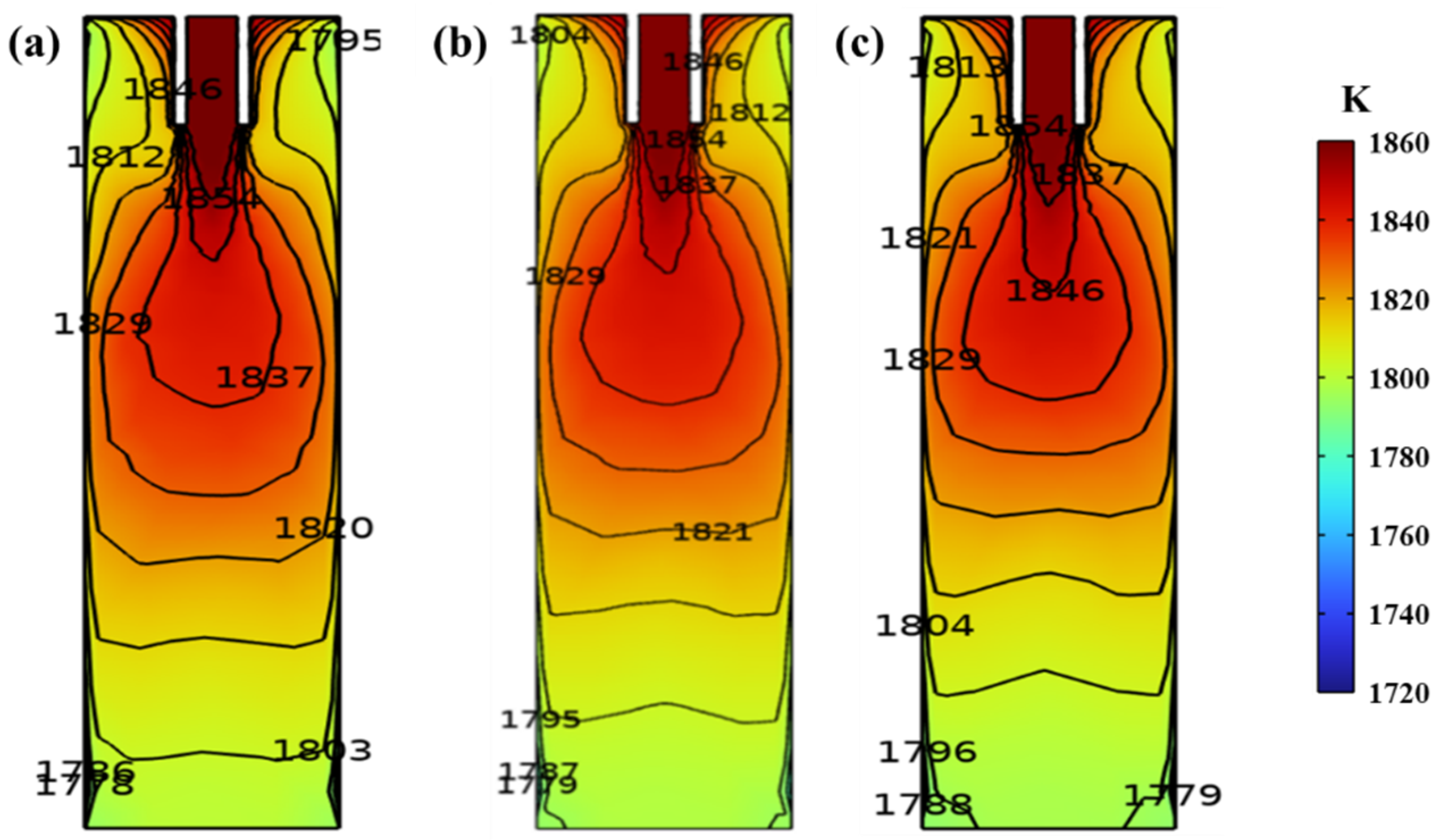
4.2. Melt Heat Transfer
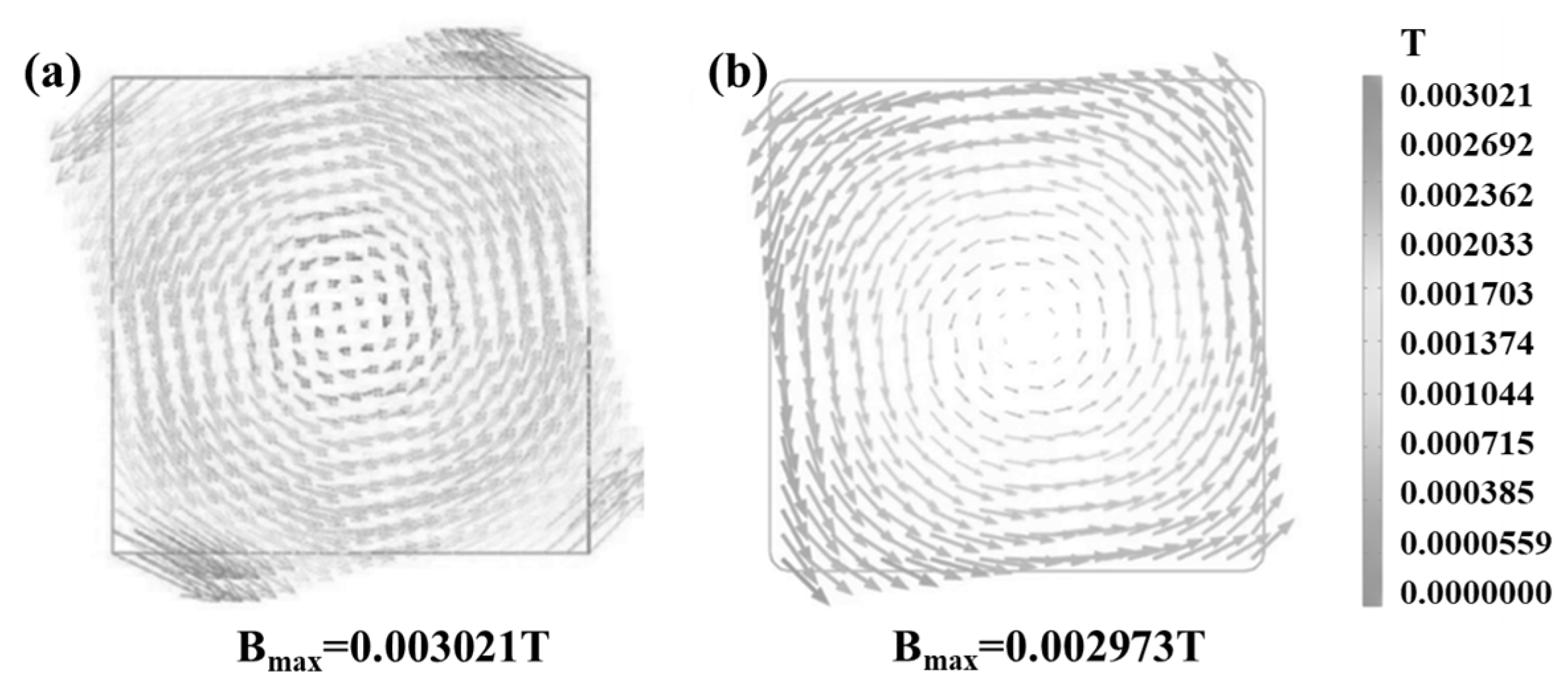
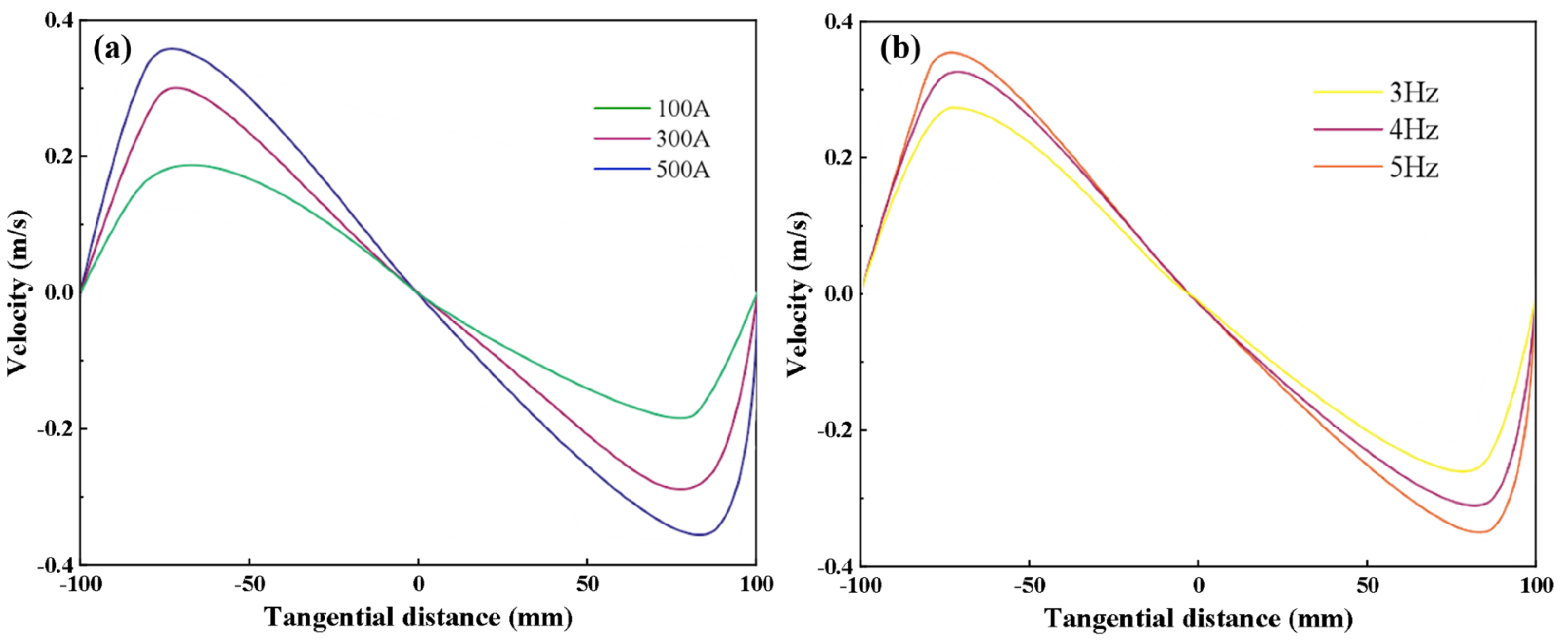
4.3. Melt Flow Field
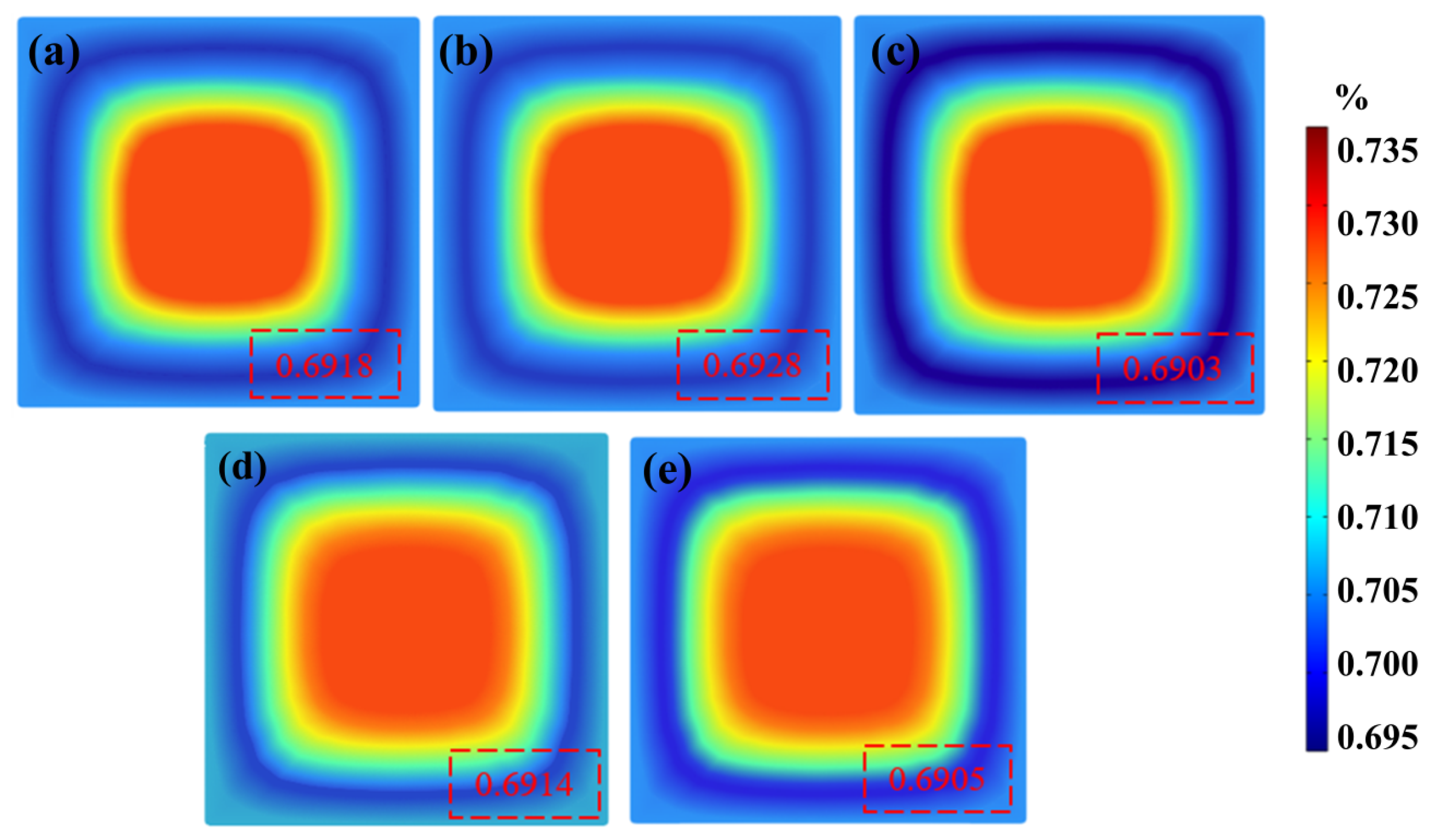
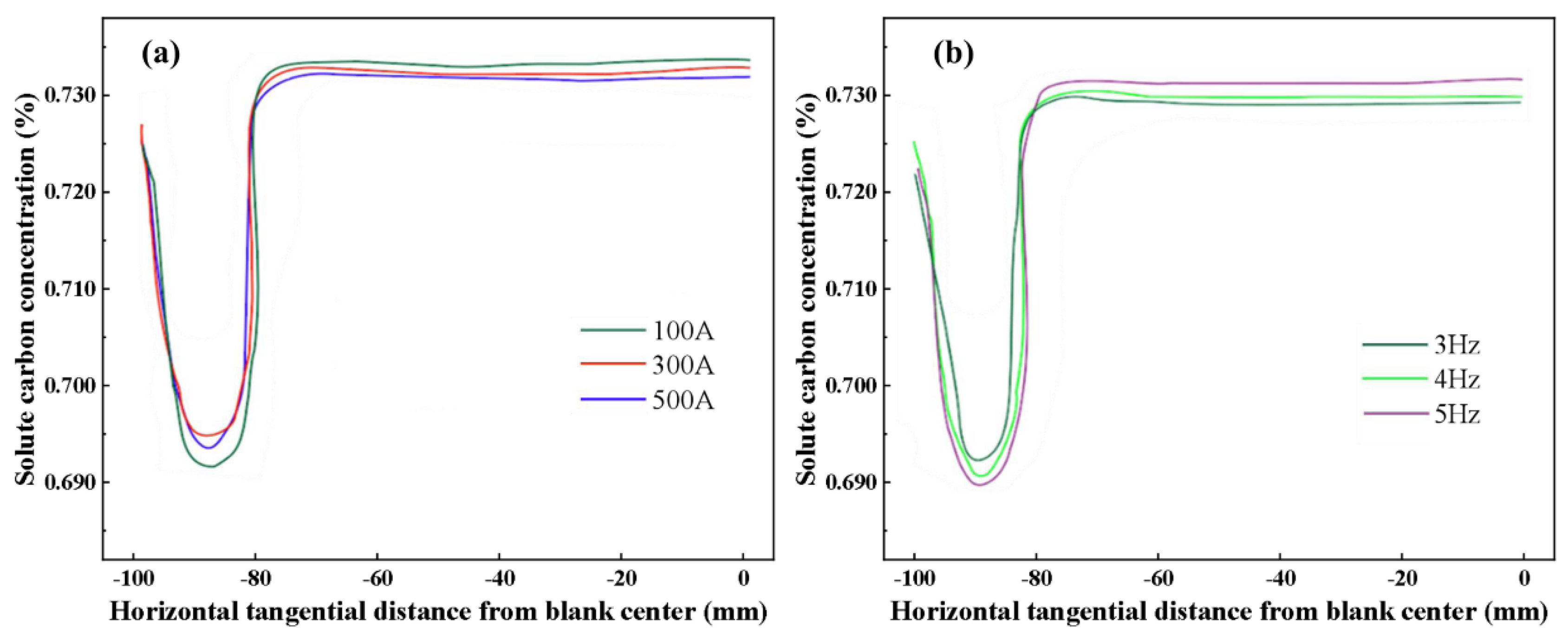
4.4. Distribution of Solute Carbon
4.5. Results for Solute Carbon inside Billet
5. Conclusions
- (1)
- With the increase in M−EMS frequency from 3 Hz to 5 Hz, the high−temperature zone is shifted upward, which is conducive to the rapid solidification of the cast billet. At the same time, as the M−EMS current increases from 100 A to 500 A, the maximum horizontal tangential velocity of the molten steel increases from 0.19 m/s to 0.38 m/s, which promotes the rotational flow of the steel in the horizontal plane.
- (2)
- When M−EMS is applied, the temperature of the molten steel near the mold walls decreases and the flow velocity near the mold walls increases. Hence, the wash−out effect on the initial solid created by the fluid flow and the variation of the solute transport rate produces a trend in the concentration of solute carbon first of a significant decrease and then of a rapid increase, with decreases in distance from the billet center.
- (3)
- When the M−EMS current is 300 A at a frequency of 3 Hz, producing a suitable mixing intensity and suitable current penetration depth effect, the negative segregation control of the carbon solute is controlled optimally. The carbon segregation index of the billet section is controlled at 0.92~1.1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.J.; Zhang, X.D.; Zhang, J.F.; Liu, X.H. Effect of CC Process on Macro Carbon Segregation in Steel Bloom. Contin. Cast. 2010, 3, 43–46. [Google Scholar]
- Wang, Y.D.; Zhang, L.F.; Zhang, H.J. Simulation of the macrosegregation in the gear steel billet continuous casting process. Chin. J. Eng. 2021, 43, 561–568. [Google Scholar]
- Zhang, Z.; Wu, M.; Zhang, H.; Hahn, S.; Wimmer, F.; Ludwig, A.; Kharicha, A. Modeling of the as−cast structure and macrosegregation in the continuous casting of a steel billet: Effect of M−EMS. J. Mater. Process. Technol. 2021, 301, 117434. [Google Scholar] [CrossRef]
- Chen, D.F.; Wei, Q.C. The Solute Transport and Segregation during Solidifying Process in Continuous Casting. J. Rare Earths 2000, 18, 206–208. [Google Scholar]
- Tzavaras, A.; Brody, H. Electromagnetic Stirring and Continuous Casting−Achievements, Problems, and Goals. JOM 1984, 36, 31–37. [Google Scholar] [CrossRef]
- Beitelman, L. Effect of mold EMS design on billet casting productivity and product quality. Can. Metall. Q. 1999, 38, 301–309. [Google Scholar] [CrossRef]
- Zhou, D.F.; Fu, J.; Wang, P.; Liu, Q. Effect of CC Process Parameters on Carbon Segregation of Bearing Steel. IronSteel 1999, 34, 22–26. [Google Scholar]
- Sun, H.B.; Zhang, J. Study on the macro segregation behavior for the bloom continuous casting: Model development and validation. Metall. Mater. Trans. B 2013, 45, 1133. [Google Scholar] [CrossRef]
- Jiang, D.; Zhu, M.Y. Solidification Structure and Macro segregation of Billet Continuous Casting Process with Dual Electromagnetic Stirrings in Mold and Final Stage of Solidification: A Numerical Study. Metall. Mater. Trans. B 2016, 47, 3446–3458. [Google Scholar] [CrossRef]
- Tao, J.J.; Zhu, H.G.; Wu, X.L. Effect of Carbon Segregation and Residual B on Hardenability of Bearing Steel 20CrMnTiH1. Spec. Steel 2007, 28, 58–59. [Google Scholar]
- Sasaki, K.; Sugitani, Y.; Kobayashi, S. Effect of fluid flow on the formation of the negative segative segregation zone in steel ingots. Tetsu Hagane 1979, 65, 60–69. [Google Scholar] [CrossRef] [Green Version]
- Asai, S.; Nishio, N.; Muchi, I. Theoretical analysis and model experiments on electromagnetically driven flow in continuous casting. Trans. Iron Steel Inst. Jpn. 1982, 22, 126. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.; Hou, Z.; Peng, Z.; Liu, Q.; Chang, Y.; Cao, J. Influence of Superheat on Macrosegregation in Continuously Cast Steel Billet from Statistical Maximum Viewpoint. ISIJ Int. 2021, 3, 515. [Google Scholar] [CrossRef]
- Ayata, K.; Mori, T.; Fujimoto, T.; Ohnishi, T.; Wakasugi, I. Improvement of macrosegregation in continuously cast bloom and billet by electromagnetic stirring. Trans. Iron Steel Inst. Jpn. 1984, 24, 931–939. [Google Scholar] [CrossRef]
- Wu, H.; Wei, N.; Bao, Y.; Wang, G.; Xiao, C.; Liu, J. Effect of M−EMS on the Solidification Structure of a Steel Billet. Int. J. Miner. Metall. Mater. 2011, 18, 159–164. [Google Scholar] [CrossRef]
- An, H.; Bao, Y.; Wang, M.; Zhao, L. Effects of electromagnetic stirring on fluid flow and temperature distribution in billet continuous casting mould and solidification structure of 55SiCr. Metall. Res. Technol. 2018, 115, 103–115. [Google Scholar] [CrossRef]
- Jiang, D.B. Numerical Investigation of Macrosegregation Formation and Influence Mechanisms of External Field During Continuous Casting Process. Ph.D. Thesis, Northeastern University, Shenyang, China, 2018. [Google Scholar]
- Okazawa, K.; Toh, T.; Fukuda, J. Fluid Flow in a Continuous Casting Mold Driven by Linear induction Motors. ISIJ Int. 2001, 41, 851–858. [Google Scholar] [CrossRef]
- Sun, H.B.; Zheng, L.; Li, L.J.; Nie, B.H. A Mathematical Model on Macro−Segregation Formation for Popular Bloom Continuous Casting Process. Mater. Sci. Forum 2019, 944, 770–777. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, S.; Chen, Y.; Wang, W.; Zhu, M. Numerical simulation of fluid flow, heat transfer, species transfer, and solidification in billet continuous casting mold with M−EMS. Metals 2019, 9, 66. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.Q.; Zhu, M.Y. Influence of electromagnetic stirring on transport phenomena in round billet continuous casting mould and macrostructure of high carbon steel billet. Ironmak. Steelmak. 2012, 39, 574–584. [Google Scholar] [CrossRef]
- Fang, Q.; Ni, H.W.; Wang, B.; Zhang, H.; Ye, F. Effects of EMS induced flow on solidification and solute transport in bloom mold. Metals 2017, 7, 72. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1990, 3, 269–289. [Google Scholar] [CrossRef]
- Wang, B.; Xie, Z.; Jia, G.L.; Lin, G.Q.; Ji, Z.P. Determination of Electromagnetic stirring Parameters at solidified End and Its Effect on Center Segregation. Iron Steel 2007, 3, 18–21. [Google Scholar]
- Chen, H.B.; Long, M.J.; Chen, D.F.; Liu, T.; Duan, H.M. Numerical study on the characteristics of solute distribution and the formation of centerline segregation in continuous casting (CC) slab. Int. J. Heat Mass Transf. 2018, 126, 843–853. [Google Scholar] [CrossRef]
- Wang, Y.D. Study on the Effect of Electromagnetic Stirring on the Macrosegregation of Steel Continuous Casting Blooms. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2021. [Google Scholar]
- Guo, S.Z.; Yang, W.Y.; Chen, G.A.; Sun, Z.Q. Effect of Nb on deformation enhanced ferrite transformation in low carbon steel. J. Univ. Sci. Technol. Beijing 2007, 29, 582–590. [Google Scholar]
- Li, Y.G.; Wang, H.B.; Bai, X.S.; Sun, Y.H.; Zhang, M.H.; Jia, J.P. Numerical Simulation of Electromagnetic Stirring in Billet Mold. Iron Steel Vanadium Titan. 2020, 41, 108–114. [Google Scholar]
- Bridge, M.R.; Rogers, G.D. Structural effects and band segregation formation during the electromagnetic stirring of strand−cast steel. Metall. Trans. B 1984, 15, 581–589. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.W. Application of EMS on Continuous Caster. Wide Heavy Plate 2009, 15, 7–11. [Google Scholar]
- Wang, Y.T.; Yang, Z.G.; Zhang, X.F.; Li, J.F.; Wang, B.; Liu, Q. Effects of electromagnetic stirring on the flow field and level fluctuation in bloom molds. J. Univ. Sci. Technol. Beijing 2014, 36, 7. [Google Scholar]
- Zhang, J.; Wang, E.G.; Deng, A.Y.; Zhang, X.W.; He, J.C. Influence of M−EMS Parameters on Distribution of Magnetic Field in Continuous Casting Bloom. China Metall. 2011, 21, 15–18. [Google Scholar]
- Sun, H.B.; Li, L.J.; Wu, X.X.; Liu, C.B. Effect of subsurface negative segregation induced by M−EMS on componential homogeneity for bloom continuous casting. Metall. Res. Technol. 2018, 115, 603. [Google Scholar] [CrossRef]
- Sun, Z.Q.; Zheng, L.Y.; Luo, B. Effect of Electromagnetic Stirring on Carbon Segregation in Blooms of Medium Carbon Steel. South. Met. 2019, 226, 8–13. [Google Scholar]
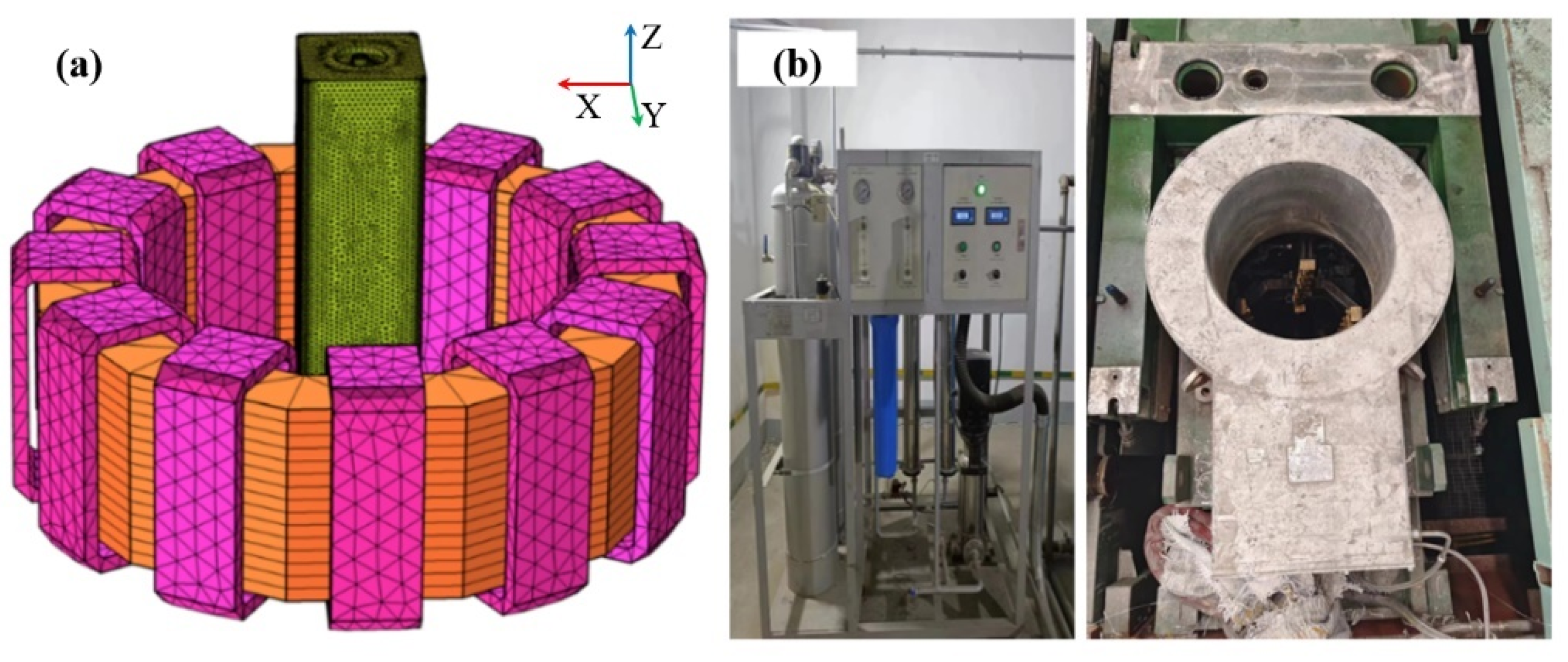
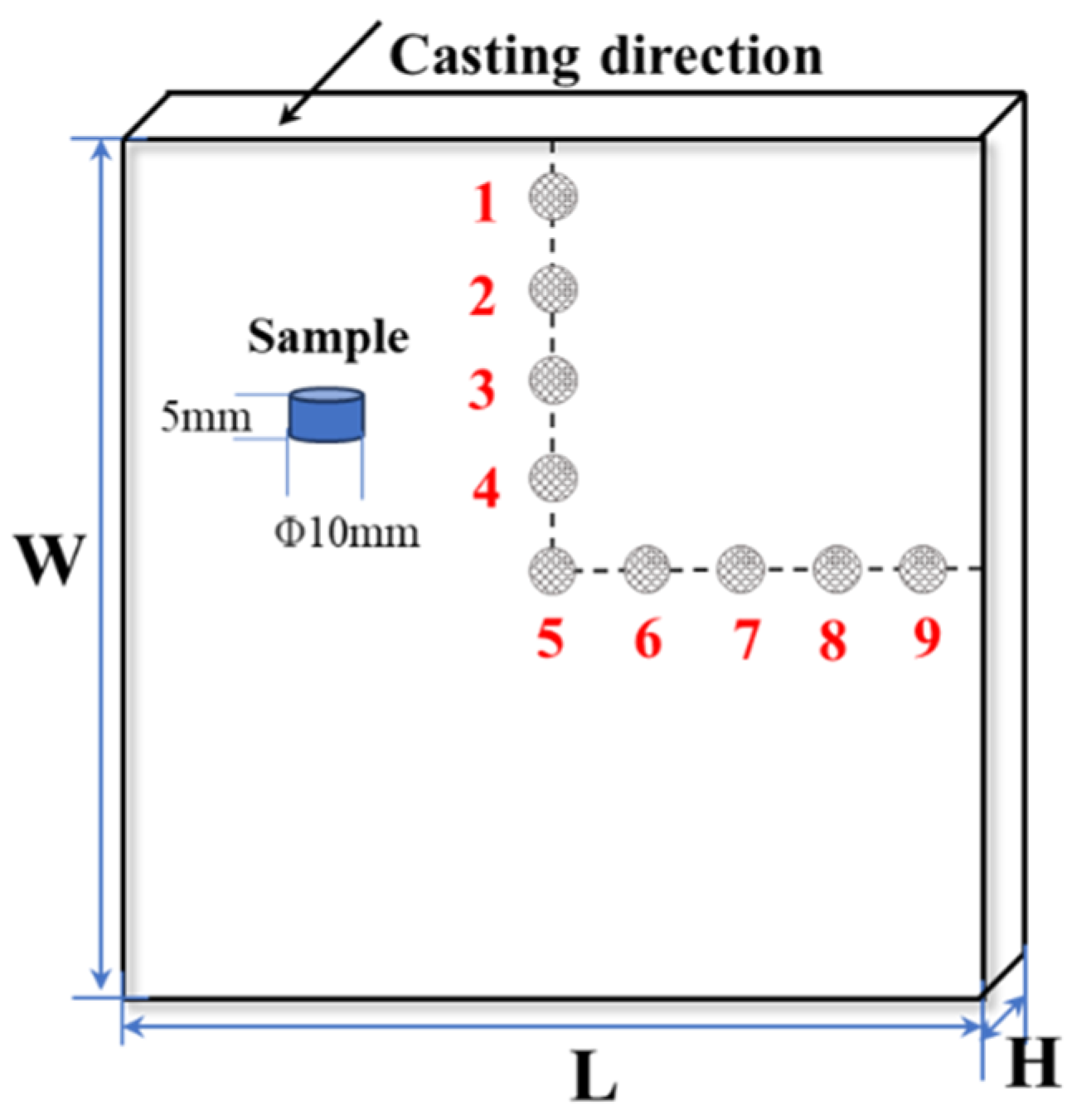


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nozzle inner diameter/mm | 40 | Equilibrium partition coefficient | 0.34 |
| Nozzle outer diameter/mm | 60 | Magnetic permeability/H·s−1 | 1.257 × 10−6 |
| Depth/mm | 120 | Electric conductivity/S·m−1 | 7.14 × 105 |
| Length of mold/mm | 900 | Latent heat of fusion/J·kg−1 | 271,000 |
| Casting speed/m·min−1 | 1.3 | Solidus temperature/K | 1762 |
| Frequency/Hz | 3, 4, 5 | Liquidus temperature/K | 1783 |
| Current/A | 100, 300, 500 | Diffusion coefficient of carbon in liquid phase/cm2·s−1 | 0.0052exp() |
| Inlet temperature/K | 1858 | Surface emissivity | 0.8 |
| Density of molten steel/kg/m3 | −0.823 × T + 7100 | Constant pressure heat capacity of molten steel/J·(kg·K)−1 | 0.0071 × T2 − 15.255 × T + 8959 |
| Dynamic viscosity of molten steel/Pa·s | 0.0065 | Thermal conductivity of molten steel/W·(m·K)−1 | 10−5 × T2 − 0.033 × T + 50.265 |
| C | Mn | P | S | Si | Cr | Ni |
|---|---|---|---|---|---|---|
| 0.725 | 0.3~0.5 | ≤0.035 | ≤0.008 | 0.25–0.50 | 12.10–12.60 | ≤0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhang, G.; Yan, P.; Zhang, P.; Tian, N.; Feng, Z. Numerical and Experimental Study on Carbon Segregation in Square Billet Continuous Casting with M-EMS. Materials 2023, 16, 5531. https://doi.org/10.3390/ma16165531
Li P, Zhang G, Yan P, Zhang P, Tian N, Feng Z. Numerical and Experimental Study on Carbon Segregation in Square Billet Continuous Casting with M-EMS. Materials. 2023; 16(16):5531. https://doi.org/10.3390/ma16165531
Chicago/Turabian StyleLi, Pengchao, Guifang Zhang, Peng Yan, Peipei Zhang, Nan Tian, and Zhenhua Feng. 2023. "Numerical and Experimental Study on Carbon Segregation in Square Billet Continuous Casting with M-EMS" Materials 16, no. 16: 5531. https://doi.org/10.3390/ma16165531
APA StyleLi, P., Zhang, G., Yan, P., Zhang, P., Tian, N., & Feng, Z. (2023). Numerical and Experimental Study on Carbon Segregation in Square Billet Continuous Casting with M-EMS. Materials, 16(16), 5531. https://doi.org/10.3390/ma16165531







