Study on In-Plane Initial Rotational Stiffness of Eccentric RHS Beam-Column Joints
Abstract
:1. Introduction
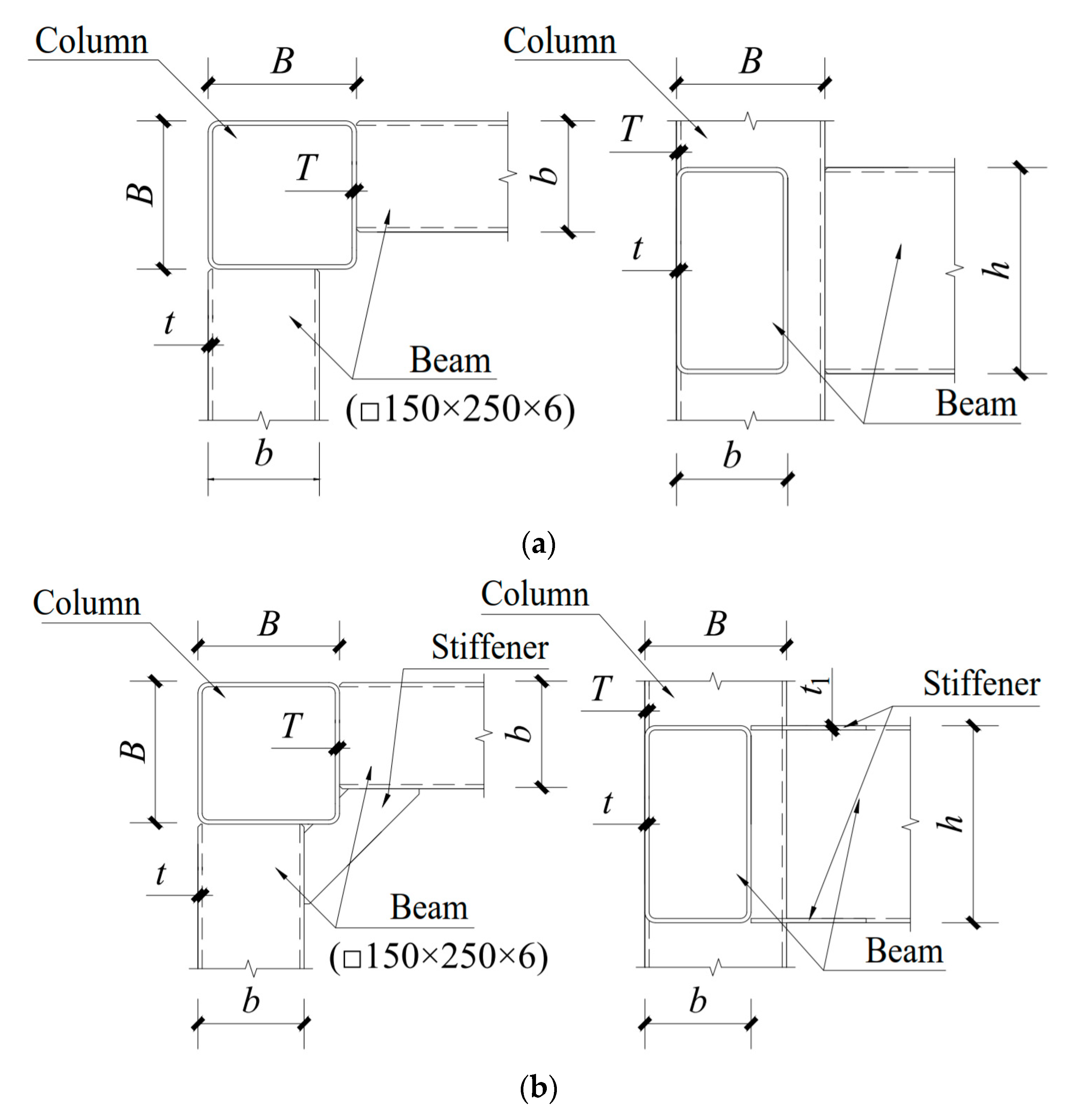
2. Construction and Finite Element Model
2.1. Construction
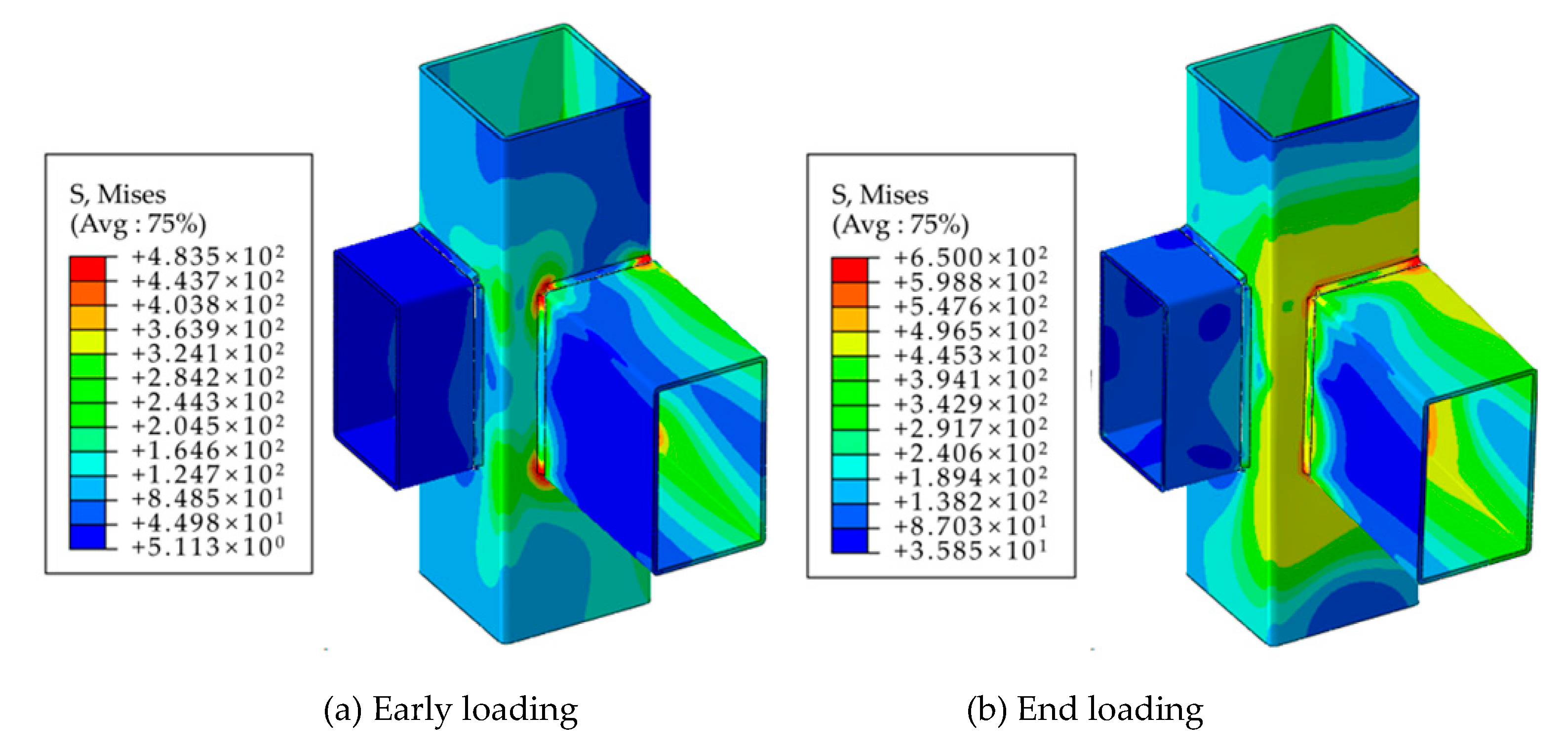
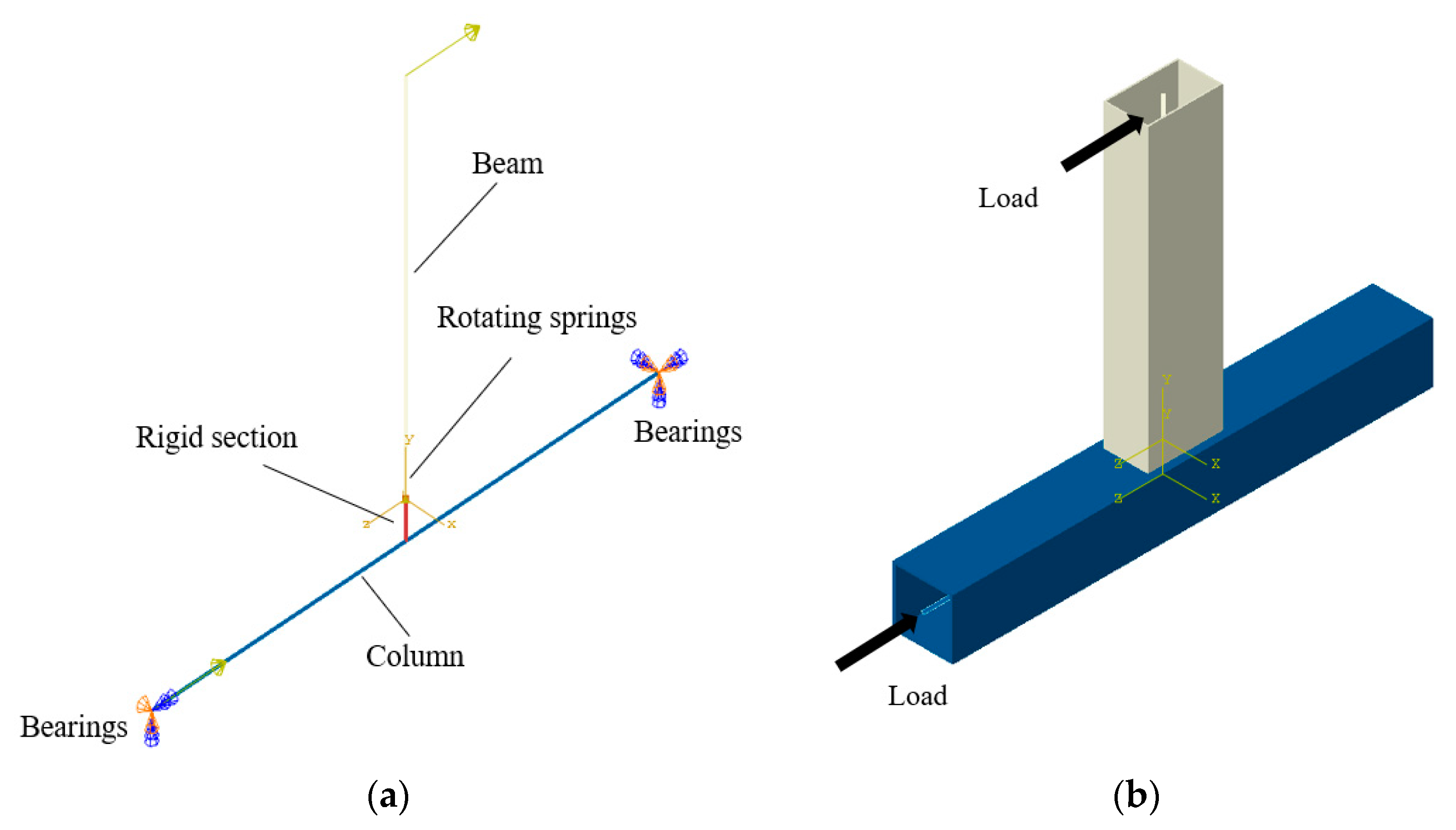
2.2. Finite Element Model
3. Initial Stiffness of the Joint
3.1. Eccentric RHS Joints without Stiffeners
3.2. Eccentric RHS Joints with Stiffeners
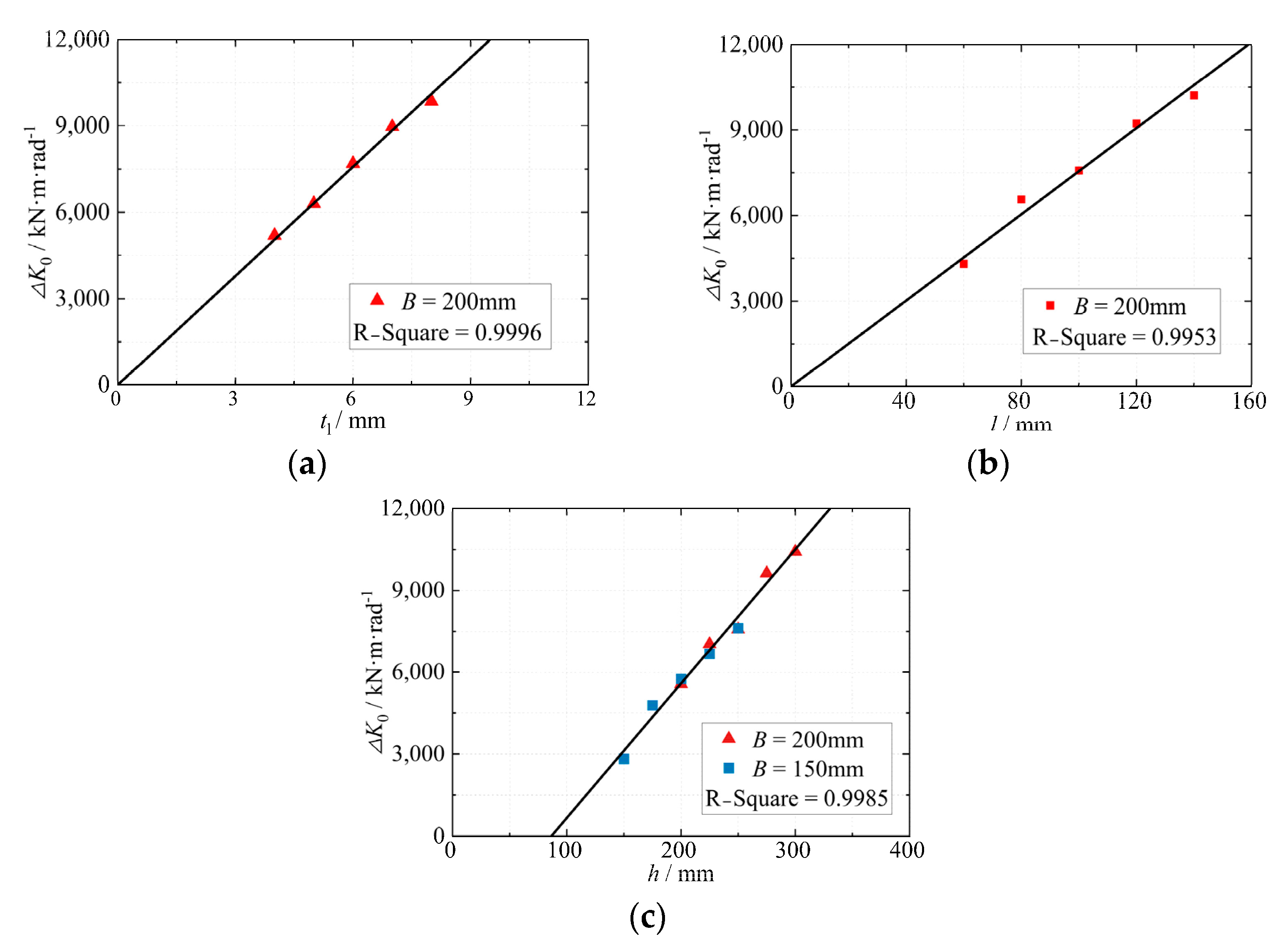
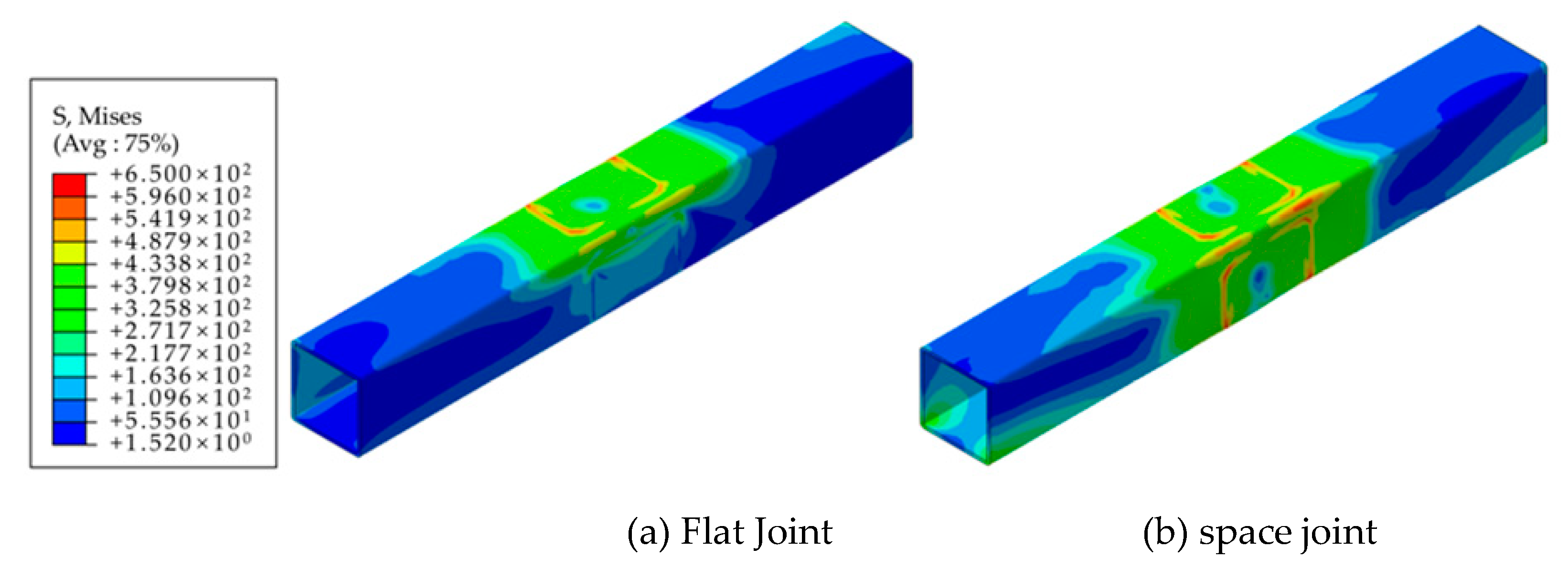
4. Spatial Effect
4.1. Geometric Effect
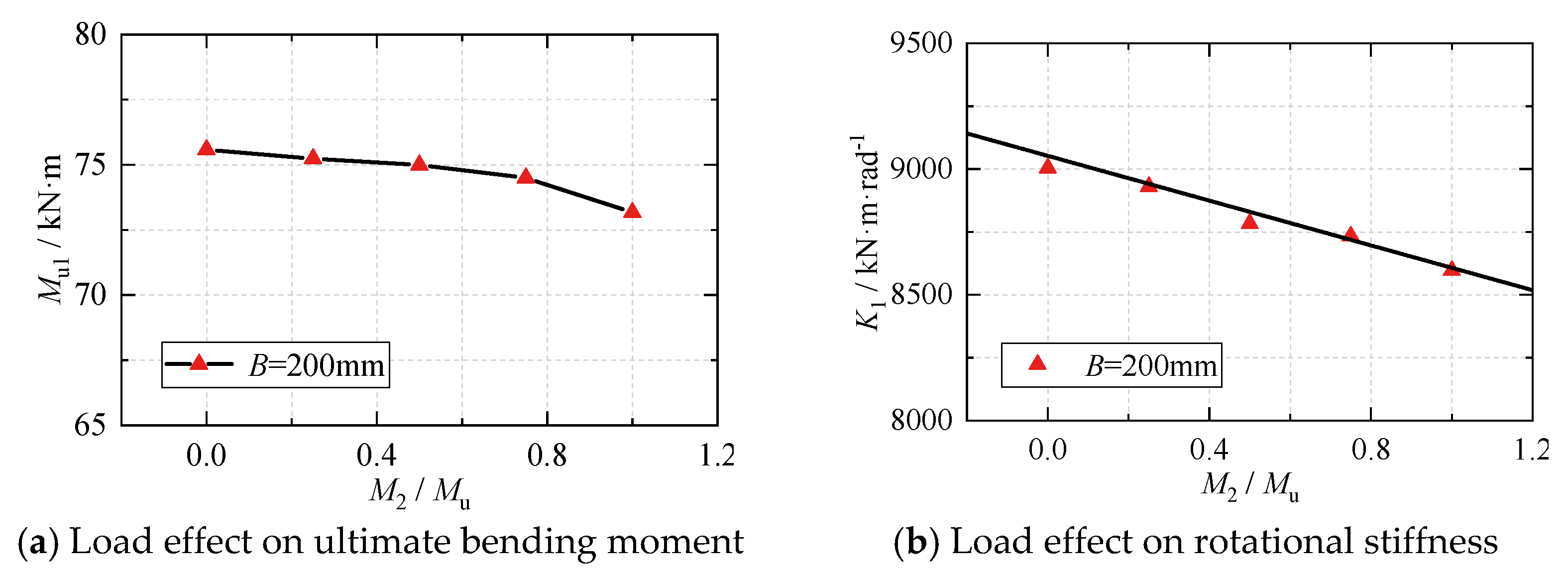
4.2. Load Effect
5. Mathematical Model of Eccentric RHS Beam-Column Joint
5.1. Selection of Mathematical Model
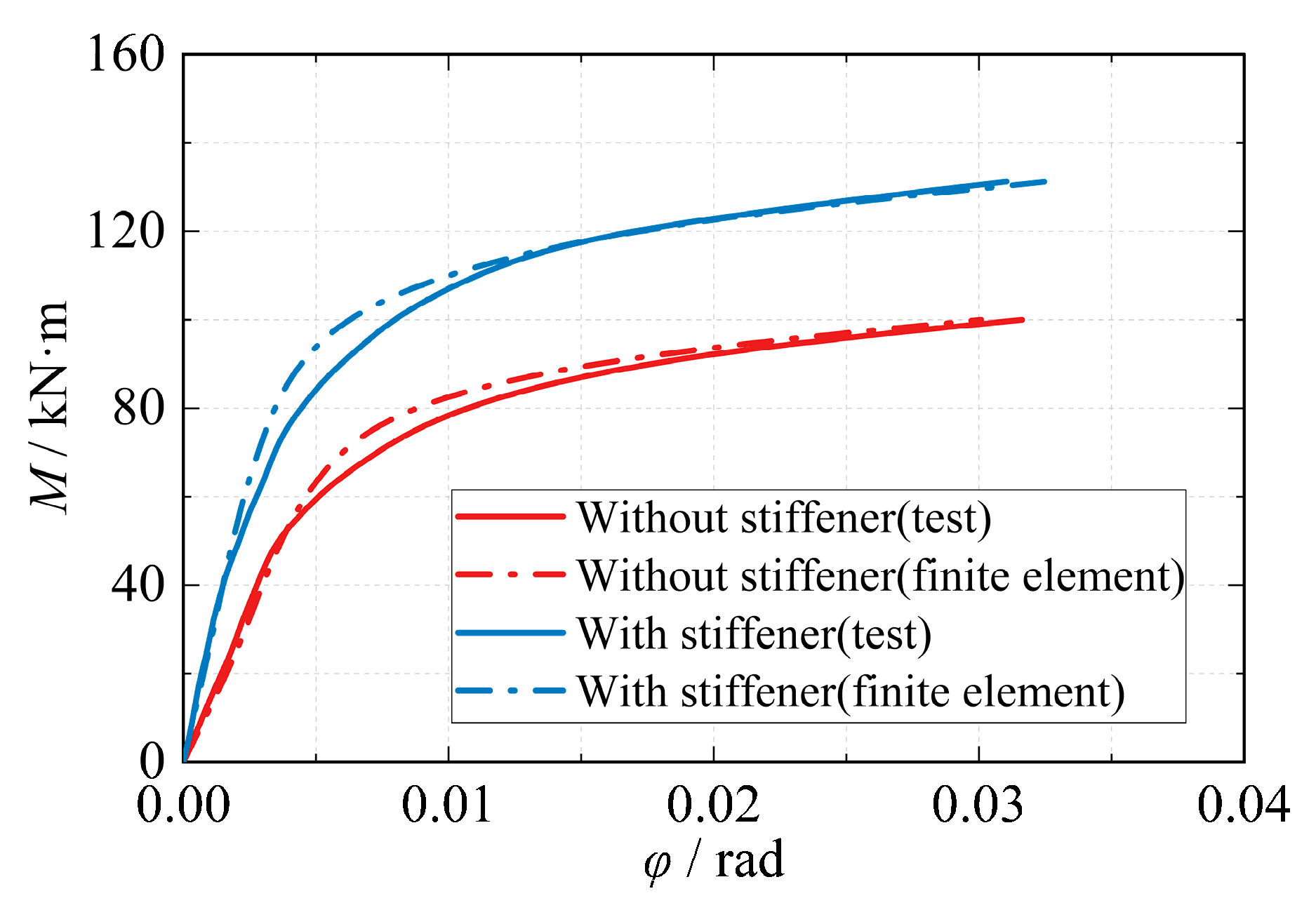
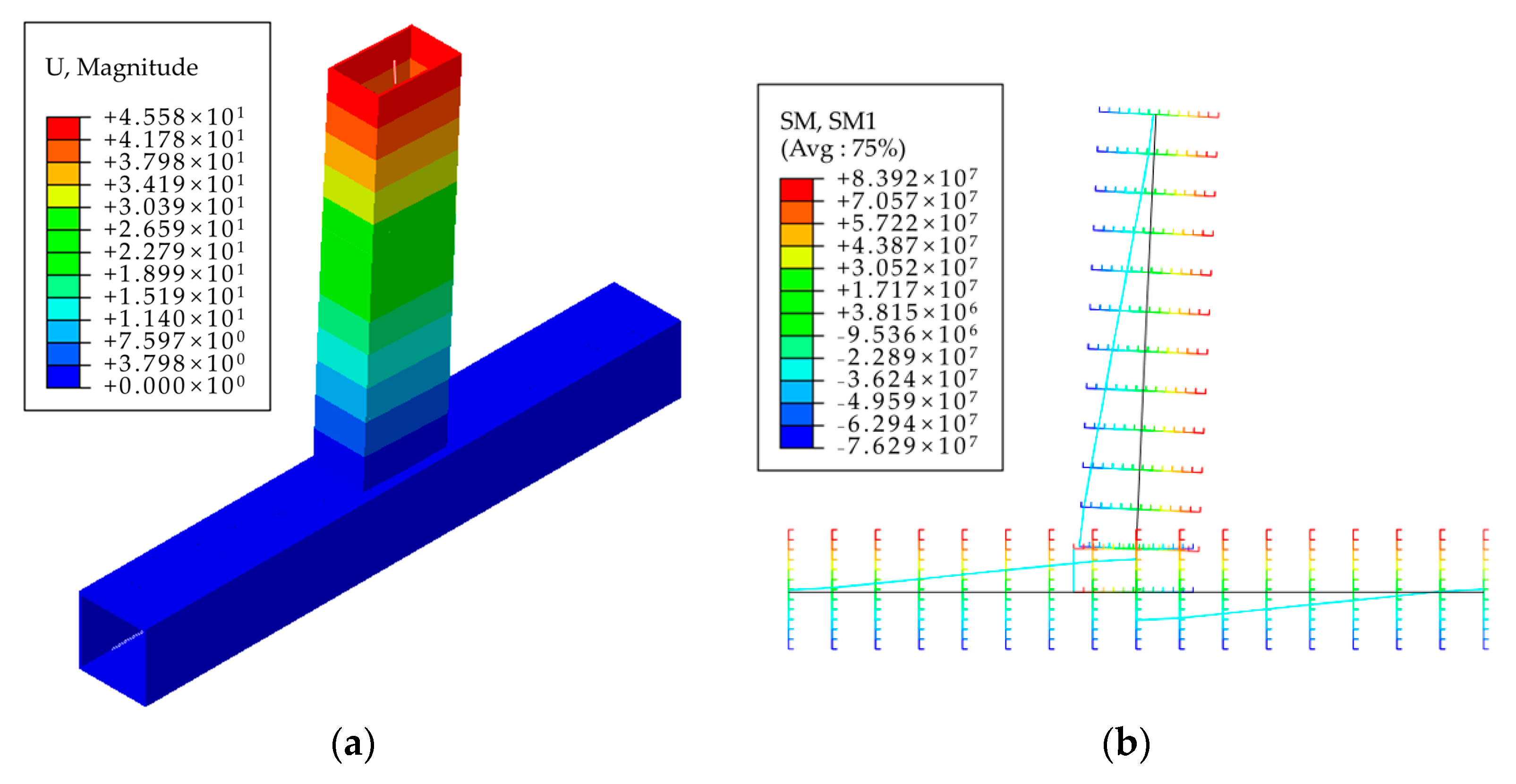
5.2. Joint-Level Finite Element Verification
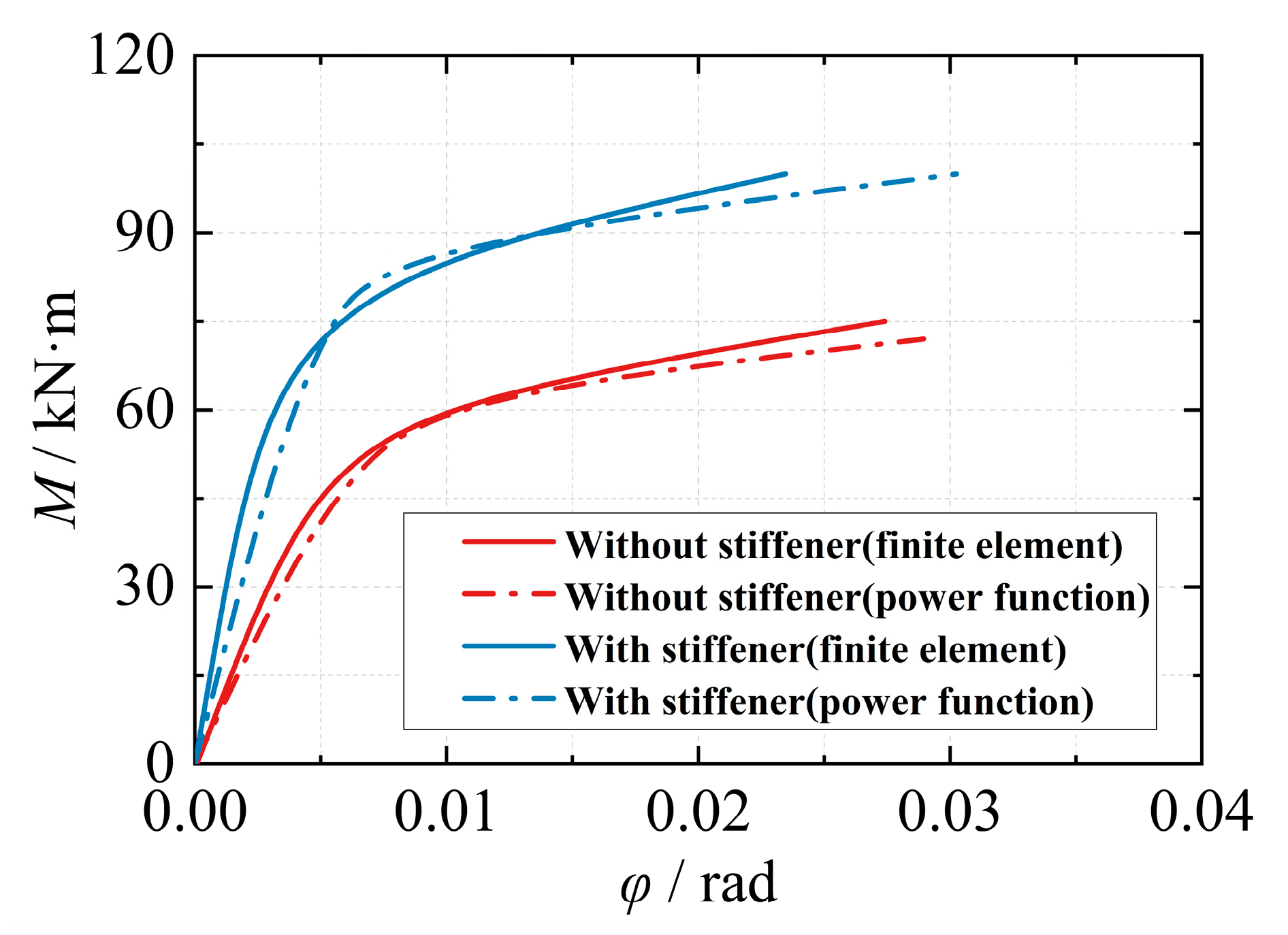
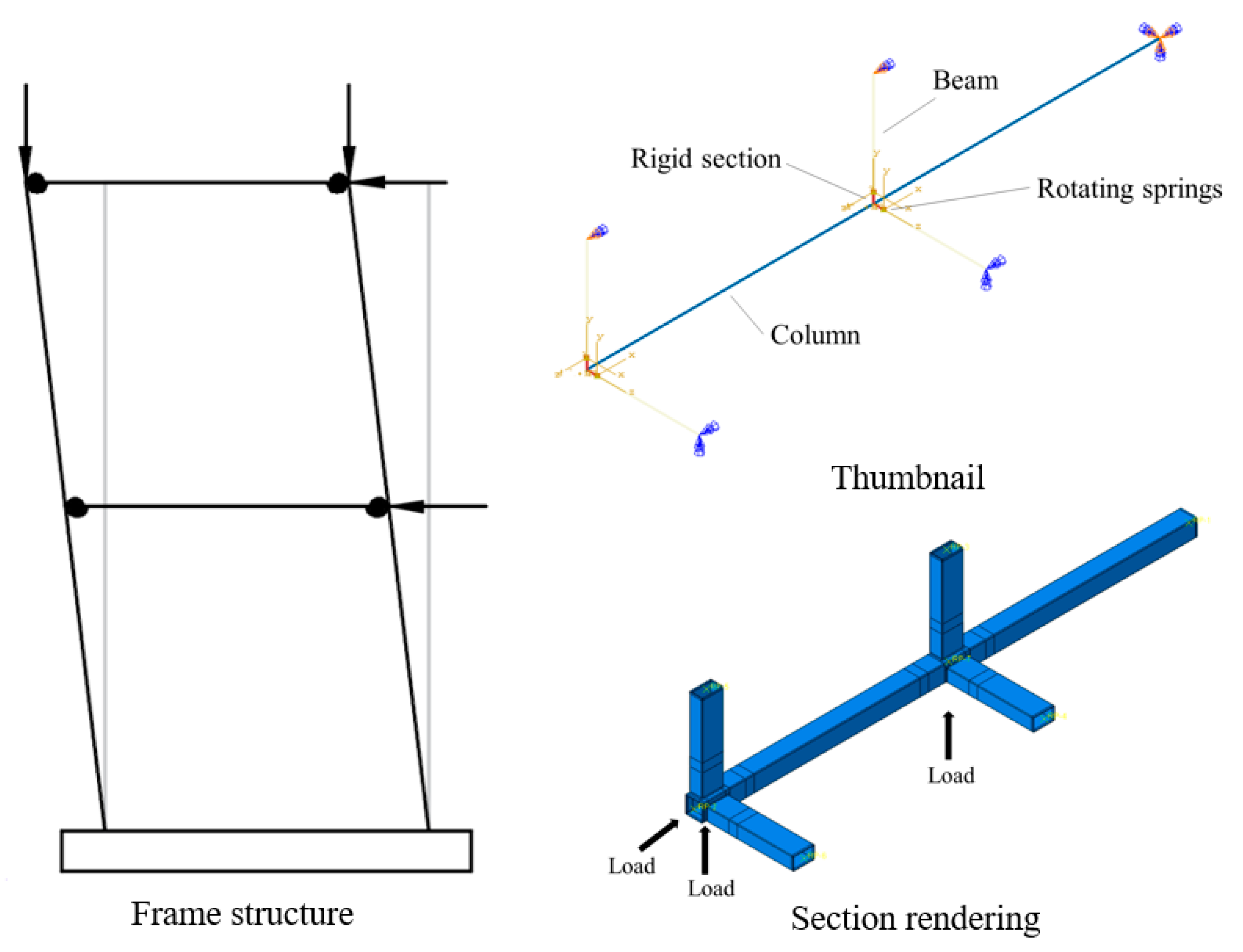
5.3. Structure-Level Finite Element Verification
6. Conclusions
- (1)
- The rotational stiffness (K0) of eccentric RHS joints is primarily influenced by the tension-compression deformation stiffness (kcw) of the web. It increases with the height-to-column flange width ratio (η) and the beam-to-column wall thickness ratio (τ). Meanwhile, the column’s wall width-to-thickness ratio (γ) increases with these ratios’ increments.
- (2)
- The rotational stiffness (K0) does not change significantly when the beam-column flange width ratio (β) is less than 0.5. It increases significantly with an increase in (β) when (β) is greater than 0.5, indicating that the bending moment distribution form of the joint changes.
- (3)
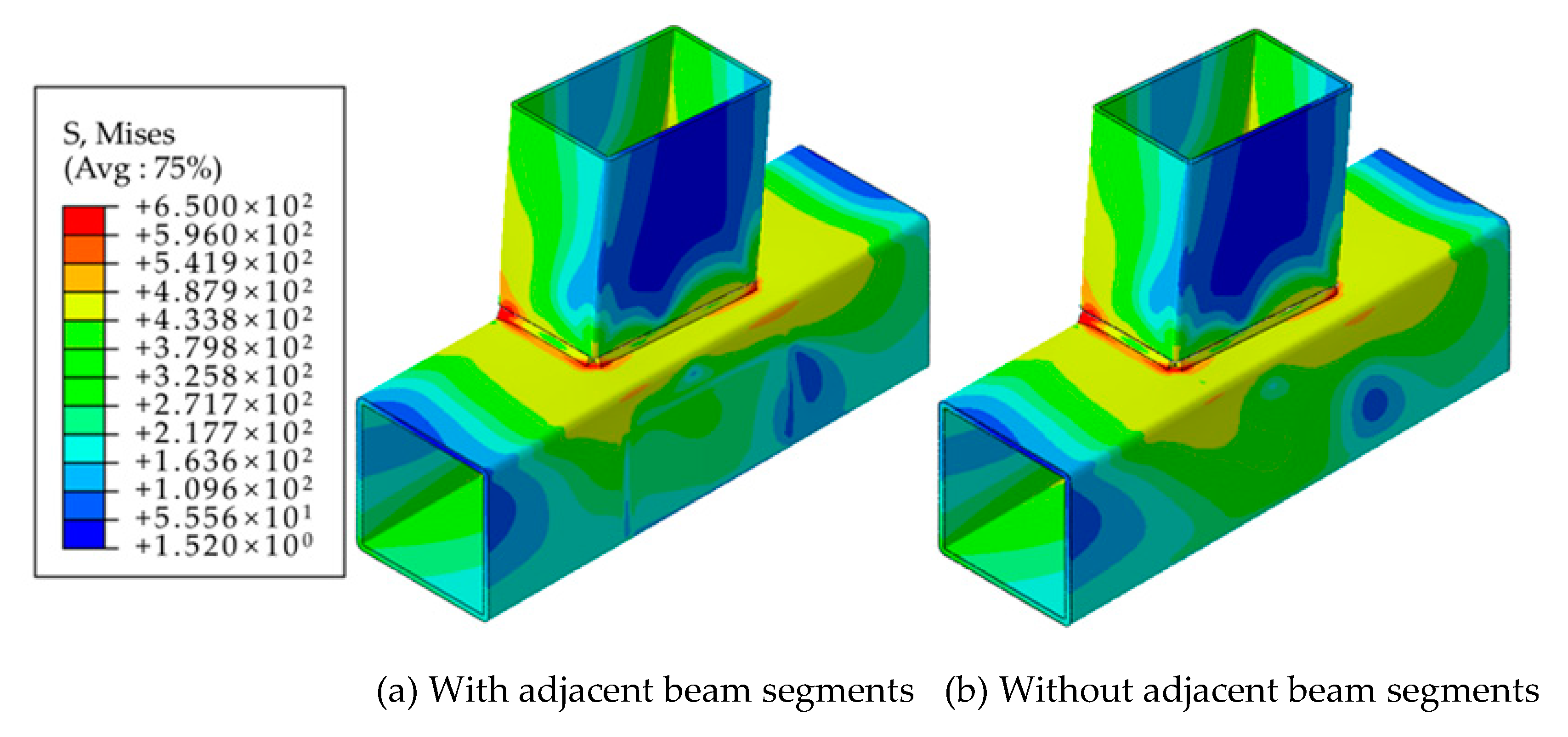
- Considering the force mechanism of the eccentric RHS joint, the side plate connected to the stressed beam and the web plate on the eccentric side bear most of the load, while the plates on the other two sides of the rectangular tubular column member are minimally affected. Therefore, for a T-shaped space joint with a 90° included angle, the mutual influence between the two stressed beams can be disregarded.
- (4)
- To simulate the semi-rigid effect of the joint, this study adopted a nonlinear corner spring model. Compared with the solid element analysis, the ultimate bending moment error of the joint is only 1.0%, the average lateral displacement error in the frame structure is only 2.5%. The finite element analysis confirmed the accuracy of the power function model in accurately simulating the static load behavior of the joint, particularly the bending moment-angle relationship.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | Implication |
| η | Beam height to column flange width ratio |
| β* | Beam-column width ratio correction |
| γ | Column tube wall width–thickness ratio |
| τ | Beam-column section wall-thickness ratio |
| β | Beam-column width ratio |
| Mu | Ultimate bending moment |
| tl l | The cross-sectional area of the plate corresponding to the stiffener |
| fy | The yield strength of the steel |
| K0 | The rotational stiffness |
| ΔK0 | The increment of the initial rotational stiffness |
| kcw | The tension-compression deformation stiffness |
| P | The vertical load at the loading point at the beam end |
| Δ | The vertical displacement at the loading point at the beam end |
| h | Indicates the moment arm provided by the upper and lower stiffeners |
References
- SAFRAJE. Encyclopedia Britannica (International Chinese Edition); Encyclopedia of China Publishing House: Beijing, China, 1999; Volume 5, p. 474. [Google Scholar]
- EN 1993-1-8; Design of Steel Structures: Design of Joints. European Committee for Standardization: Brussels, Belgium, 2005.
- Wang, Y.; Lei, H. Finite element analysis of static performance and stress concentration of T-shaped circular tube intersecting joints. Chin. Sci. Technol. Pap. 2018, 13, 1457–1461. [Google Scholar]
- Chen, J.; Huang, H. In-plane bending stiffness analysis of T-shaped joints in steel tube structures. J. Shijiazhuang Railw. Univ. Nat. Sci. Ed. 2015, 28, 1–6. [Google Scholar]
- Liu, J.; Guo, Y. Nonlinear finite element analysis of ultimate bearing capacity of intersecting joints of K-shaped square and circular tubes. Build. Sci. 2001, 17, 50–53. [Google Scholar]
- Weng, Y.; Guan, F.; Wang, X. Study on Failure Mode and Analysis Model of X-shaped Circular Tube Intersecting Joints. Steel Struct. 2006, 35, 11–15. [Google Scholar]
- Wang, L.; Wang, L. Ultimate strength analysis of TT-shaped circular tube joints on offshore platforms. Ship Ocean. Eng. 2008, 37, 83–86. [Google Scholar]
- Shu, X.; Zhu, Q. Finite element analysis of ultimate bearing capacity of intersecting joints of space KK steel tubes. J. South China Univ. Technol. Nat. Sci. Ed. 2002, 33, 102–106. [Google Scholar]
- Packer, J.A.; Davies, G.; Coutie, M.G. Ultimate strength of gapped joints in RHS trusses. J. Struct. Eng. ASCE 1982, 108, 411–431. [Google Scholar] [CrossRef]
- Wu, Z.; Tan, H. Calculation of initial flexural stiffness of T-shaped square steel tube joints with unequal widths. J. Harbin Inst. Technol. 2008, 40, 1517–1522. [Google Scholar]
- Hectors, K.; De Waele, W. A numerical framework for determination of stress concentration factor distributions in tubular joints. Int. J. Mech. Sci. 2020, 174, 105511. [Google Scholar] [CrossRef]
- Zhao, P.; Qian, J.; Zhao, J.; Ma, H.; Gu, L. Research on bearing capacity of intersecting joints of rectangular steel tubes under single stress state. J. Build. Struct. 2005, 26, 54–63. [Google Scholar]
- International Institute of Welding Subcommission XV-E. Static Design Procedure for Welded Hollow Section Joints: Recommendations, 3rd ed.; International Institute of Welding Subcommission XV-E: Paris, France, 2012. [Google Scholar]
- ISO 14346: 2013; Static Design Procedure for Welded Hollow Section Joints: Recommendations. International Standards Organization: Geneva, Switzerland, 2013.
- CECS 280: 2010; Technical Specification for Steel Tube Structure. China Planning Press: Beijing, China, 2010.
- GB 50017-2017; Design Standards for Steel Structures. China Architecture and Building Press: Beijing, China, 2017.
- Yang, Y. Application and Research of Eccentric Tubular Joints; Xi’an University of Architecture and Technology: Xi’an, China, 2015. [Google Scholar]
- Zhao, B.; Ke, K.; Jiang, W. Research on out-plane flexural performance of unstiffened eccentric RHS joints. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2018, 46, 29–35. [Google Scholar]
- Zhao, B.; Jiang, W.; Ke, K.; Liu, C. Out-OF-Plane Flexural Rigidity of Unstiffened Eccentric Rectangular Hollow Joints. J. Harbin Inst. Technol. 2019, 40, 1122–1127+1133. [Google Scholar]
- Guo, X.; Xu, Z.; Liu, J.; Luo, J. In-plane flexural capacity of rectangular steel tube eccentric intersecting beam-column joints. J. Hunan Univ. Nat. Sci. Ed. 2023, 50, 45–58. [Google Scholar]
- Nassiraei, H. Geometrical effects on the LJF of tubular T/Y-joints with doubler plate in offshore wind turbines. Ships Offshore Struct. 2022, 17, 481–491. [Google Scholar] [CrossRef]
- Nassiraei, H. Local joint flexibility of CHS X-joints reinforced with collar plates in jacket structures subjected to axial load. Appl. Ocean. Res. 2019, 93, 101961. [Google Scholar] [CrossRef]
- Rao, T.; Du, X.; Yuan, H.; Leng, Z.; Cao, H. Research on the mechanical performance of intersecting joints of equal-width KX-shaped rectangular steel tubes. Prog. Build. Steel Struct. 2022, 24, 79–87. [Google Scholar]










| Maximum Mesh Size | Ultimate Bending Moment Mu/(kN/m) | Error/% |
|---|---|---|
| 80 | 96.18 | 0.81 |
| 90 | 96.43 | 1.07 |
| 100 | 98.12 | 2.84 |
| 110 | 101.53 | 6.41 |
| 120 | 106.23 | 11.34 |
| Model Number | Column Size | Beam Size | |||
|---|---|---|---|---|---|
| Width B/mm | Thickness T/mm | Width b/mm | Height h/mm | Thickness t/mm | |
| J-β-200-130 | 200 | 8 | 130 | 250 | 6 |
| J-β-200-140 | 200 | 8 | 140 | 250 | 6 |
| J-β-200-150 | 200 | 8 | 150 | 250 | 6 |
| J-β-200-160 | 200 | 8 | 160 | 250 | 6 |
| J-β-200-170 | 200 | 8 | 170 | 250 | 6 |
| J-β-150-80 | 150 | 8 | 80 | 200 | 6 |
| J-β-150-90 | 150 | 8 | 90 | 200 | 6 |
| J-β-150-100 | 150 | 8 | 100 | 200 | 6 |
| J-β-150-110 | 150 | 8 | 110 | 200 | 6 |
| J-β-150-120 | 150 | 8 | 120 | 200 | 6 |
| J-β-250-160 | 250 | 8 | 160 | 300 | 6 |
| J-β-250-175 | 250 | 8 | 175 | 300 | 6 |
| J-β-250-190 | 250 | 8 | 190 | 300 | 6 |
| J-β-250-200 | 250 | 8 | 200 | 300 | 6 |
| J-β-250-210 | 250 | 8 | 210 | 300 | 6 |
| J-γ-200-6 | 200 | 6 | 150 | 250 | 6 |
| J-γ-200-7 | 200 | 7 | 150 | 250 | 7 |
| J-γ-200-8 | 200 | 8 | 150 | 250 | 8 |
| J-γ-200-9 | 200 | 9 | 150 | 250 | 9 |
| J-γ-200-10 | 200 | 10 | 150 | 250 | 10 |
| J-γ-150-6 | 150 | 6 | 100 | 200 | 6 |
| J-γ-150-7 | 150 | 7 | 100 | 200 | 7 |
| J-γ-150-8 | 150 | 8 | 100 | 200 | 8 |
| J-γ-150-9 | 150 | 9 | 100 | 200 | 9 |
| J-γ-150-10 | 150 | 10 | 100 | 200 | 10 |
| J-γ-250-8 | 250 | 8 | 180 | 300 | 8 |
| J-γ-250-9 | 250 | 9 | 180 | 300 | 9 |
| J-γ-250-10 | 250 | 10 | 180 | 300 | 10 |
| J-γ-250-11 | 250 | 11 | 180 | 300 | 11 |
| J-γ-250-12 | 250 | 12 | 180 | 300 | 12 |
| J-η-200-200 | 200 | 8 | 150 | 200 | 6 |
| J-η-200-225 | 200 | 8 | 150 | 225 | 6 |
| J-η-200-250 | 200 | 8 | 150 | 250 | 6 |
| J-η-200-275 | 200 | 8 | 150 | 275 | 6 |
| J-η-200-300 | 200 | 8 | 150 | 300 | 6 |
| J-η-150-150 | 150 | 8 | 100 | 150 | 6 |
| J-η-150-175 | 150 | 8 | 100 | 175 | 6 |
| J-η-150-200 | 150 | 8 | 100 | 200 | 6 |
| J-η-150-225 | 150 | 8 | 100 | 225 | 6 |
| J-η-150-250 | 150 | 8 | 100 | 250 | 6 |
| J-η-250-250 | 250 | 8 | 200 | 250 | 6 |
| J-η-250-275 | 250 | 8 | 200 | 275 | 6 |
| J-η-250-300 | 250 | 8 | 200 | 300 | 6 |
| J-η-250-325 | 250 | 8 | 200 | 325 | 6 |
| J-η-250-350 | 250 | 8 | 200 | 350 | 6 |
| J-τ-200-4 | 200 | 8 | 150 | 250 | 4 |
| J-τ-200-5 | 200 | 8 | 150 | 250 | 5 |
| J-τ-200-6 | 200 | 8 | 150 | 250 | 6 |
| J-τ-200-7 | 200 | 8 | 150 | 250 | 7 |
| J-τ-200-8 | 200 | 8 | 150 | 250 | 8 |
| J-τ-150-4 | 150 | 8 | 100 | 200 | 4 |
| J-τ-150-5 | 150 | 8 | 100 | 200 | 5 |
| J-τ-150-6 | 150 | 8 | 100 | 200 | 6 |
| J-τ-150-7 | 150 | 8 | 100 | 200 | 7 |
| J-τ-150-8 | 150 | 8 | 100 | 200 | 8 |
| J-τ-250-4 | 250 | 8 | 200 | 250 | 4 |
| J-τ-250-5 | 250 | 8 | 200 | 250 | 5 |
| J-τ-250-6 | 250 | 8 | 200 | 250 | 6 |
| J-τ-250-7 | 250 | 8 | 200 | 250 | 7 |
| J-τ-250-8 | 250 | 8 | 200 | 250 | 8 |
| Model Number | Column Size | Beam Size | Stiffener Size | ||||
|---|---|---|---|---|---|---|---|
| Width B/mm | Thickness T/mm | Width b/mm | Height h/mm | Thickness t/mm | Thickness tl/mm | Length l/mm | |
| J-t1-200-4+ | 200 | 8 | 150 | 250 | 8 | 4 | 100 |
| J-t1-200-5+ | 200 | 8 | 150 | 250 | 8 | 5 | 100 |
| J-t1-200-6+ | 200 | 8 | 150 | 250 | 8 | 6 | 100 |
| J-t1-200-7+ | 200 | 8 | 150 | 250 | 8 | 7 | 100 |
| J-t1-200-8+ | 200 | 8 | 150 | 250 | 8 | 8 | 100 |
| J-l-200-60+ | 200 | 8 | 150 | 250 | 6 | 6 | 60 |
| J-l-200-80+ | 200 | 8 | 150 | 250 | 6 | 6 | 80 |
| J-l-200-100+ | 200 | 8 | 150 | 250 | 6 | 6 | 100 |
| J-l-200-120+ | 200 | 8 | 150 | 250 | 6 | 6 | 120 |
| J-l-200-140+ | 200 | 8 | 150 | 250 | 6 | 6 | 140 |
| J-β-200-130+ | 200 | 8 | 130 | 250 | 6 | 6 | 100 |
| J-β-200-140+ | 200 | 8 | 140 | 250 | 6 | 6 | 100 |
| J-β-200-150+ | 200 | 8 | 150 | 250 | 6 | 6 | 100 |
| J-β-200-160+ | 200 | 8 | 160 | 250 | 6 | 6 | 100 |
| J-β-200-170+ | 200 | 8 | 170 | 250 | 6 | 6 | 100 |
| J-β-150-80+ | 150 | 8 | 80 | 200 | 6 | 6 | 100 |
| J-β-150-90+ | 150 | 8 | 90 | 200 | 6 | 6 | 100 |
| J-β-150-100+ | 150 | 8 | 100 | 200 | 6 | 6 | 100 |
| J-β-150-110+ | 150 | 8 | 110 | 200 | 6 | 6 | 100 |
| J-β-150-120+ | 150 | 8 | 120 | 200 | 6 | 6 | 100 |
| J-η-200-200+ | 200 | 8 | 150 | 200 | 6 | 6 | 100 |
| J-η-200-225+ | 200 | 8 | 150 | 225 | 6 | 6 | 100 |
| J-η-200-250+ | 200 | 8 | 150 | 250 | 6 | 6 | 100 |
| J-η-200-275+ | 200 | 8 | 150 | 275 | 6 | 6 | 100 |
| J-η-200-300+ | 200 | 8 | 150 | 300 | 6 | 6 | 100 |
| J-η-150-150+ | 150 | 8 | 100 | 150 | 6 | 6 | 100 |
| J-η-150-175+ | 150 | 8 | 100 | 175 | 6 | 6 | 100 |
| J-η-150-200+ | 150 | 8 | 100 | 200 | 6 | 6 | 100 |
| J-η-150-225+ | 150 | 8 | 100 | 225 | 6 | 6 | 100 |
| J-η-150-250+ | 150 | 8 | 100 | 250 | 6 | 6 | 100 |
| J-γ-200-6+ | 200 | 6 | 150 | 250 | 6 | 6 | 100 |
| J-γ-200-7+ | 200 | 7 | 150 | 250 | 6 | 6 | 100 |
| J-γ-200-8+ | 200 | 8 | 150 | 250 | 6 | 6 | 100 |
| J-γ-200-9+ | 200 | 9 | 150 | 250 | 6 | 6 | 100 |
| J-γ-200-10+ | 200 | 10 | 150 | 250 | 6 | 6 | 100 |
| J-γ-150-6+ | 150 | 6 | 100 | 200 | 6 | 6 | 100 |
| J-γ-150-7+ | 150 | 7 | 100 | 200 | 6 | 6 | 100 |
| J-γ-150-8+ | 150 | 8 | 100 | 200 | 6 | 6 | 100 |
| J-γ-150-9+ | 150 | 9 | 100 | 200 | 6 | 6 | 100 |
| J-γ-150-10+ | 150 | 10 | 100 | 200 | 6 | 6 | 100 |
| J-γ-200-6+ | 200 | 6 | 150 | 250 | 6 | 6 | 100 |
| J-τ-200-4+ | 200 | 8 | 150 | 250 | 4 | 4 | 100 |
| J-τ-200-5+ | 200 | 8 | 150 | 250 | 5 | 4 | 100 |
| J-τ-200-6+ | 200 | 8 | 150 | 250 | 6 | 4 | 100 |
| J-τ-200-7+ | 200 | 8 | 150 | 250 | 7 | 4 | 100 |
| J-τ-200-8+ | 200 | 8 | 150 | 250 | 8 | 4 | 100 |
| J-τ-150-4+ | 150 | 8 | 100 | 200 | 4 | 4 | 100 |
| J-τ-150-5+ | 150 | 8 | 100 | 200 | 5 | 4 | 100 |
| J-τ-150-6+ | 150 | 8 | 100 | 200 | 6 | 4 | 100 |
| J-τ-150-7+ | 150 | 8 | 100 | 200 | 7 | 4 | 100 |
| J-τ-150-8+ | 150 | 8 | 100 | 200 | 8 | 4 | 100 |
| Model Number | Beam–Column Flange Width Ratio β | Rotational Stiffness K0/(kN·m·rad−1) | ||
|---|---|---|---|---|
| Finite Element | Formula | Error/% | ||
| J-β-200-130 | 0.65 | 8435.53 | 8108.01 | −3.88 |
| J-β-200-140 | 0.70 | 8681.78 | 8423.72 | −2.97 |
| J-β-200-150 | 0.75 | 9004.52 | 8870.70 | −1.49 |
| J-β-200-160 | 0.80 | 9549.81 | 9448.95 | −1.06 |
| J-β-200-170 | 0.85 | 10,651.09 | 10,158.47 | −4.63 |
| J-β-150-80 | 0.53 | 5386.18 | 5526.39 | 2.60 |
| J-β-150-90 | 0.60 | 5508.9 | 5555.64 | 0.85 |
| J-β-150-100 | 0.67 | 5710.09 | 5748.51 | 0.67 |
| J-β-150-110 | 0.73 | 6156.72 | 6105.02 | −0.84 |
| J-β-150-120 | 0.80 | 7090.71 | 6625.16 | −6.57 |
| J-β-250-160 | 0.64 | 12,403.06 | 11,312.82 | −8.79 |
| J-β-250-175 | 0.70 | 12,123.24 | 11,822.41 | −2.48 |
| J-β-250-190 | 0.76 | 12,589.15 | 12,597.31 | 0.06 |
| J-β-250-200 | 0.80 | 13,458.62 | 13,261.29 | −1.47 |
| J-β-250-210 | 0.84 | 14,268.36 | 14,043.19 | −1.58 |
| Model Number | Beam Height to Column Flange Width Ratio η | Rotational Stiffness K0/(kN·m·rad−1) | ||
|---|---|---|---|---|
| Finite Element | Formula | Error/% | ||
| J-η-200-200 | 1.00 | 5655.36 | 5376.64 | −4.93 |
| J-η-200-225 | 1.13 | 6909.83 | 7016.18 | 1.54 |
| J-η-200-250 | 1.25 | 9004.52 | 8870.70 | −1.49 |
| J-η-200-275 | 1.38 | 10,786.44 | 10,940.21 | 1.43 |
| J-η-200-300 | 1.50 | 13,237.56 | 13,224.70 | −0.10 |
| J-η-150-150 | 1.00 | 3121.51 | 3022.32 | −3.18 |
| J-η-150-175 | 1.17 | 4228.32 | 4278.00 | 1.17 |
| J-η-150-200 | 1.33 | 5703.28 | 5748.51 | 0.79 |
| J-η-150-225 | 1.50 | 7100.36 | 7433.88 | 4.70 |
| J-η-150-250 | 1.67 | 8818.22 | 9334.08 | 5.85 |
| J-η-250-250 | 1.00 | 8602.05 | 8799.27 | 2.29 |
| J-η-250-275 | 1.10 | 11,142.91 | 10,917.69 | −2.02 |
| J-η-250-300 | 1.20 | 13,189.28 | 13,261.29 | 0.55 |
| J-η-250-325 | 1.30 | 15,711.35 | 15,830.08 | 0.76 |
| J-η-250-350 | 1.40 | 18,475.05 | 18,624.04 | 0.81 |
| Model Number | Column Tube Wall Width–Thickness Ratio γ | Rotational Stiffness K0/(kN·m·rad−1) | ||
|---|---|---|---|---|
| Finite Element | Formula | Error/% | ||
| J-γ-200-6 | 16.67 | 7164.19 | 7262.48 | 1.37 |
| J-γ-200-7 | 14.29 | 7785.08 | 7999.25 | 2.75 |
| J-γ-200-8 | 12.50 | 9004.52 | 8870.70 | −1.49 |
| J-γ-200-9 | 11.11 | 9973.64 | 9862.26 | −1.12 |
| J-γ-200-10 | 10.00 | 11,492.77 | 10,965.21 | −4.59 |
| J-γ-150-6 | 12.50 | 4347.77 | 4415.37 | 1.55 |
| J-γ-150-7 | 10.71 | 4694.31 | 5035.76 | 7.27 |
| J-γ-150-8 | 9.38 | 5710.09 | 5748.51 | 0.67 |
| J-γ-150-9 | 8.33 | 6901.66 | 6547.09 | −5.14 |
| J-γ-150-10 | 7.50 | 8195.46 | 7427.57 | −9.37 |
| J-γ-250-8 | 15.63 | 12,335.87 | 12,051.23 | −2.31 |
| J-γ-250-9 | 13.89 | 14,203.56 | 13,124.57 | −7.60 |
| J-γ-250-10 | 12.50 | 14,641.01 | 14,333.68 | −2.10 |
| J-γ-250-11 | 11.36 | 16,173.1 | 15,668.97 | −3.12 |
| J-γ-250-12 | 10.42 | 17,516.66 | 17,124.04 | −2.24 |
| Model Number | Beam–Column Section Wall–Thickness Ratio τ | Rotational Stiffness K0/(kN·m·rad−1) | ||
|---|---|---|---|---|
| Finite Element | Formula | Error/% | ||
| J-τ-200-4 | 0.50 | 7085.27 | 7919.16 | 11.77 |
| J-τ-200-5 | 0.63 | 8310.69 | 8394.87 | 1.01 |
| J-τ-200-6 | 0.75 | 9004.52 | 8870.70 | −1.49 |
| J-τ-200-7 | 0.88 | 9389.58 | 9346.63 | −0.46 |
| J-τ-200-8 | 1.00 | 9683.7 | 9822.67 | 1.44 |
| J-τ-150-4 | 0.50 | 4863.35 | 5131.88 | 5.52 |
| J-τ-150-5 | 0.63 | 5318.5 | 5440.16 | 2.29 |
| J-τ-150-6 | 0.75 | 5703.28 | 5748.51 | 0.79 |
| J-τ-150-7 | 0.88 | 5983.3 | 6056.94 | 1.23 |
| J-τ-150-8 | 1.00 | 6110.39 | 6365.43 | 4.17 |
| J-τ-250-4 | 0.50 | 6695.22 | 7855.39 | 17.33 |
| J-τ-250-5 | 0.63 | 8124.95 | 8327.28 | 2.49 |
| J-τ-250-6 | 0.75 | 8602.05 | 8799.27 | 2.29 |
| J-τ-250-7 | 0.88 | 9223.87 | 9271.37 | 0.51 |
| J-τ-250-8 | 1.00 | 9604.13 | 9743.58 | 1.45 |
| Model Number | Rotational Stiffness K0/(kN·m·rad−1) | ||
|---|---|---|---|
| Finite Element | Formula | Error/% | |
| J-t1-200-4+ | 14,880.21 | 14,915.25 | 0.24 |
| J-t1-200-5+ | 15,987.88 | 16,223.14 | 1.47 |
| J-t1-200-6+ | 17,373.82 | 17,531.02 | 0.90 |
| J-t1-200-7+ | 18,650.79 | 18,838.91 | 1.01 |
| J-t1-200-8+ | 19,533.17 | 20,146.8 | 3.14 |
| J-l-200-60+ | 13,313.45 | 13,712.91 | 3.00 |
| J-l-200-80+ | 15,567.45 | 15,282.38 | −1.83 |
| J-l-200-100+ | 16,579.87 | 16,851.84 | 1.64 |
| J-l-200-120+ | 18,229.8 | 18,421.31 | 1.05 |
| J-l-200-140+ | 19,216.52 | 19,990.77 | 4.03 |
| J-β-200-130+ | 16,367.13 | 16,282.85 | −0.51 |
| J-β-200-140+ | 16,712.04 | 16,529.1 | −1.09 |
| J-β-200-150+ | 16,579.71 | 16,851.84 | 1.64 |
| J-β-200-160+ | 17,218.84 | 17,397.13 | 1.04 |
| J-β-200-170+ | 18,244.75 | 18,498.41 | 1.39 |
| J-β-150-80+ | 9700.97 | 10,332.07 | 6.51 |
| J-β-150-90+ | 10,422.72 | 10,639.5 | 2.08 |
| J-β-150-100+ | 10,790.95 | 10,840.69 | 0.46 |
| J-β-150-110+ | 11,720.02 | 11,271.38 | −3.83 |
| J-β-150-120+ | 12,227.62 | 12,173.72 | −0.44 |
| J-η-200-200+ | 11,217.62 | 10,785.96 | −3.85 |
| J-η-200-225+ | 13,943.22 | 13,398.79 | −3.90 |
| J-η-200-250+ | 16,579.71 | 16,851.84 | 1.64 |
| J-η-200-275+ | 20,414.23 | 19,992.13 | −2.07 |
| J-η-200-300+ | 23,653.88 | 23,801.61 | 0.62 |
| J-η-150-150+ | 5941.52 | 5535.377 | −6.84 |
| J-η-150-175+ | 9010.61 | 8000.551 | −11.21 |
| J-η-150-200+ | 11,452.97 | 10,833.88 | −5.41 |
| J-η-150-225+ | 13,742.02 | 13,558.85 | −1.33 |
| J-η-150-250+ | 16,379.9 | 16,607.65 | 1.39 |
| J-γ-200-6+ | 15,002.93 | 15,011.51 | 0.06 |
| J-γ-200-7+ | 16,023.23 | 15,632.4 | −2.44 |
| J-γ-200-8+ | 16,579.71 | 16,851.84 | 1.64 |
| J-γ-200-9+ | 18,122.54 | 17,820.96 | −1.66 |
| J-γ-200-10+ | 19,006.86 | 19,340.09 | 1.75 |
| J-γ-150-6+ | 9189.39 | 9478.365 | 3.14 |
| J-γ-150-7+ | 9952.77 | 9824.905 | −1.28 |
| J-γ-150-8+ | 11,309.46 | 10,840.69 | −4.14 |
| J-γ-150-9+ | 12,203.30 | 11,972.49 | −1.89 |
| J-γ-150-10+ | 12,361.27 | 13,326.06 | 7.80 |
| J-γ-200-6+ | 15,002.93 | 15,011.51 | 0.06 |
| J-τ-200-4+ | 12,715.51 | 12,316.82 | −3.14 |
| J-τ-200-5+ | 13,780.39 | 13,542.24 | −1.73 |
| J-τ-200-6+ | 14,287.32 | 14,236.07 | −0.36 |
| J-τ-200-7+ | 14,777.89 | 14,621.13 | −1.06 |
| J-τ-200-8+ | 15,225.99 | 14,915.25 | −2.04 |
| J-τ-150-4+ | 7711.47 | 8283.747 | 7.42 |
| J-τ-150-5+ | 8991.67 | 8738.897 | −2.81 |
| J-τ-150-6+ | 9129.09 | 9123.677 | −0.06 |
| J-τ-150-7+ | 9533.8 | 9403.697 | −1.36 |
| J-τ-150-8+ | 9640.53 | 9530.787 | −1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Li, W.; Xv, Z. Study on In-Plane Initial Rotational Stiffness of Eccentric RHS Beam-Column Joints. Materials 2023, 16, 5103. https://doi.org/10.3390/ma16145103
Guo X, Li W, Xv Z. Study on In-Plane Initial Rotational Stiffness of Eccentric RHS Beam-Column Joints. Materials. 2023; 16(14):5103. https://doi.org/10.3390/ma16145103
Chicago/Turabian StyleGuo, Xiaonong, Weixin Li, and Zeyu Xv. 2023. "Study on In-Plane Initial Rotational Stiffness of Eccentric RHS Beam-Column Joints" Materials 16, no. 14: 5103. https://doi.org/10.3390/ma16145103
APA StyleGuo, X., Li, W., & Xv, Z. (2023). Study on In-Plane Initial Rotational Stiffness of Eccentric RHS Beam-Column Joints. Materials, 16(14), 5103. https://doi.org/10.3390/ma16145103





