Investigating the Impact of Electrolyte Flow Velocity on the Resistivity of Vanadium Redox Batteries: A Theoretical Analysis and Experimental Data Comparison
Abstract
:1. Introduction
2. The Modeling of the VR Cell
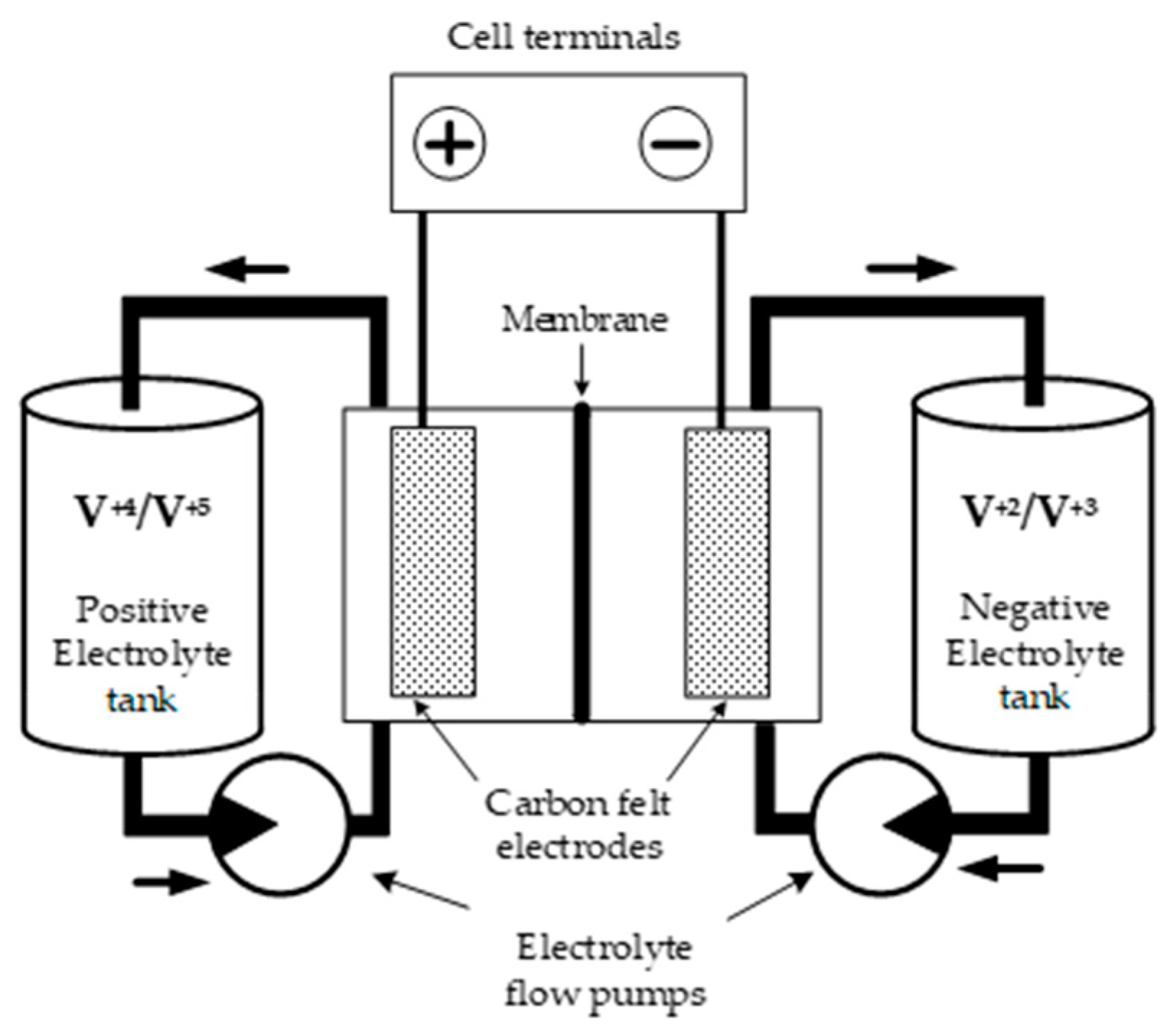
2.1. Principal Scheme of a Flow Battery Cell and Problem Definition
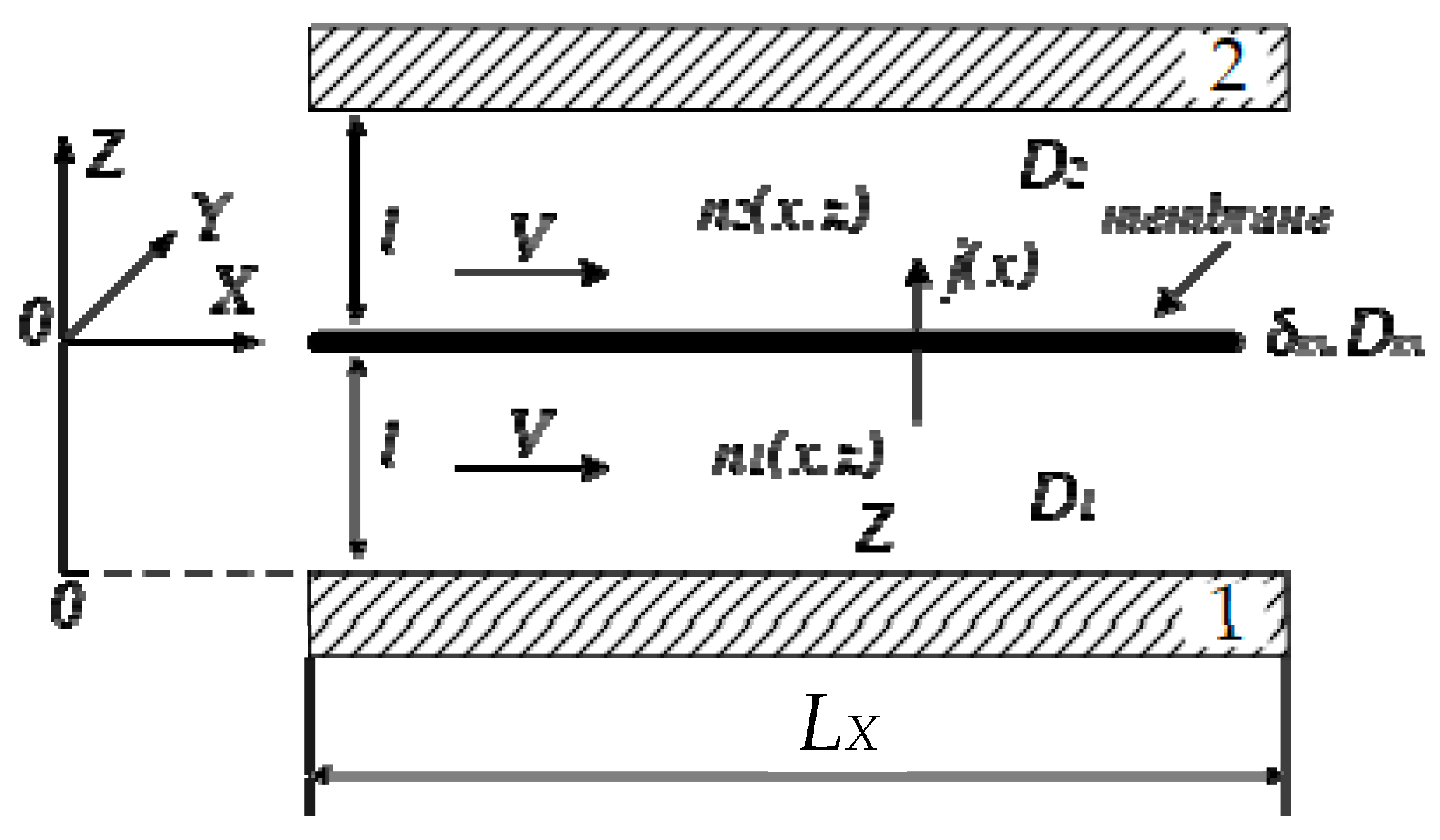
- X, Y, Z: geometric coordinates used to represent the spatial dimensions.
- Membrane m: the membrane with a thickness δm and a diffusion coefficient of ion conductivity, Dm.
- Diffusion coefficients: D1 and D2 represent the diffusion coefficients of proton ions within the negative and positive compartments, respectively.
- V—the electrolyte velocity over the membrane surface in the X direction.
- L—the distance between the membrane and electrodes.
- LX—the length of the cell in the X direction.
- In a vanadium redox flow battery, the individual cell voltage is relatively low, typically around 1.4 V. To achieve higher voltages, multiple vanadium cells are connected in series (N-serial connection). Consequently, the total battery voltage is determined by multiplying the voltage of a single cell, V0, by the total number of cells in the series string.
- On the other hand, the battery current is equal to the current of each individual cell. In other words, the current passing through the battery is the same as the current flowing through each cell in the series. The flow of current within each cell is facilitated by the movement of ions, specifically protons, through the proton-exchange membrane.
- The cell’s electrical behavior is primarily determined by the motion of protons, and therefore only protons are considered in the explanation.
- Protons are generated through the electrochemical transformation of vanadium ions on one electrode and are absorbed as an essential element required to continue the electrochemical reaction on another electrode.
- Protons move from one compartment to another under a concentration difference and electric field, which are mainly produced in the vicinity of electrodes and the membrane. The initial concentration is prescribed by the electrolyte velocity at the entrance of the cell.
- The membrane transportation property mainly defines the current density of the cell since its area is much lower than that of porous electrodes. In addition, the current density in the battery is influenced by the boundary conditions at the electrodes, which are defined by the potential difference between them.
2.2. The Density of Electric Charges and Proton Transportation
3. Estimation of the Model Parameters
3.1. The Assessment of the Electric Field Magnitude in the VRB
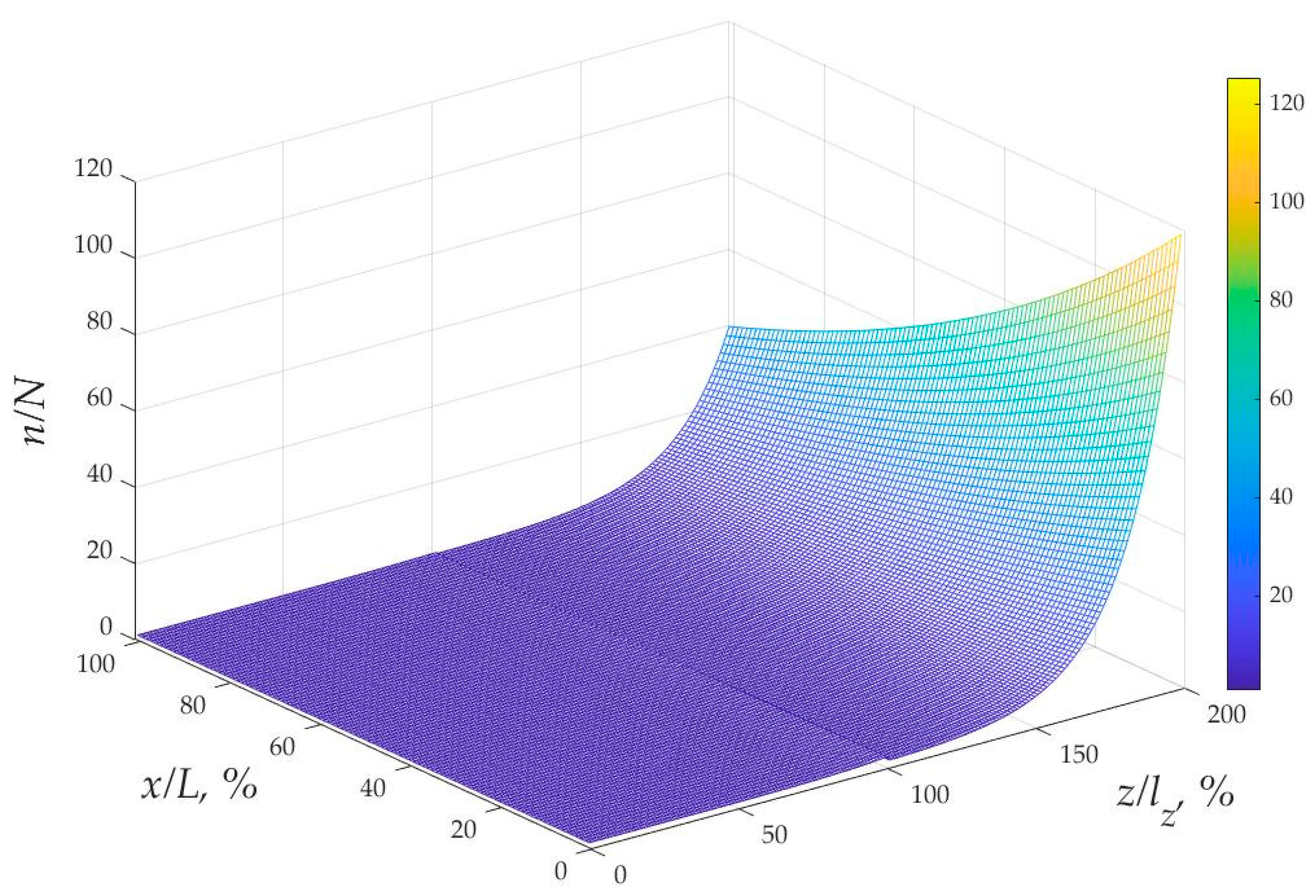
3.2. Solution for the Proton Concentration and Flux in Cell Compartments
3.3. Formulation for the Entire Battery Current and Resistance
3.4. Estimation of Model Parameters
- a1 = 0. It follows from three conditions. The first is that the coefficient r should be assigned a negative value as it is determined by the sign of the electric field, which is assumed to be negative in our investigation. The second condition is that the expression for the proton concentration (13) must always yield a positive value. The third condition is that the magnitude of the membrane current density should be kept below the allowable limit (~300 mA/cm2), as reported in [28,33,34].
- The sequential choosing of a2 in the range of more than 0 and less than 1, t.i. a2: 0 < a2 < 1. This is the consequence of the fact that δn1 should be less than N in consistency Condition (24).
- The sequential choosing of a4 among the range from (0.1∙a2) to a2. The reason for this is that the coefficient k should be assigned a positive value, as it aligns with the physical consideration of the decreasing proton concentration along the x-axis.
- Calculation of k using the Equality (36).
- The coefficients must adhere to the equality which is a consequence of (5) and (13):
- Calculation of a3 using Expression (40).
- Calculation of λ1 and λ2 based on (16).
- Calculation of the constants of integration A1−, A1+, A2−, and A2+ with (35).
- Calculation of total current through the membrane using (38).
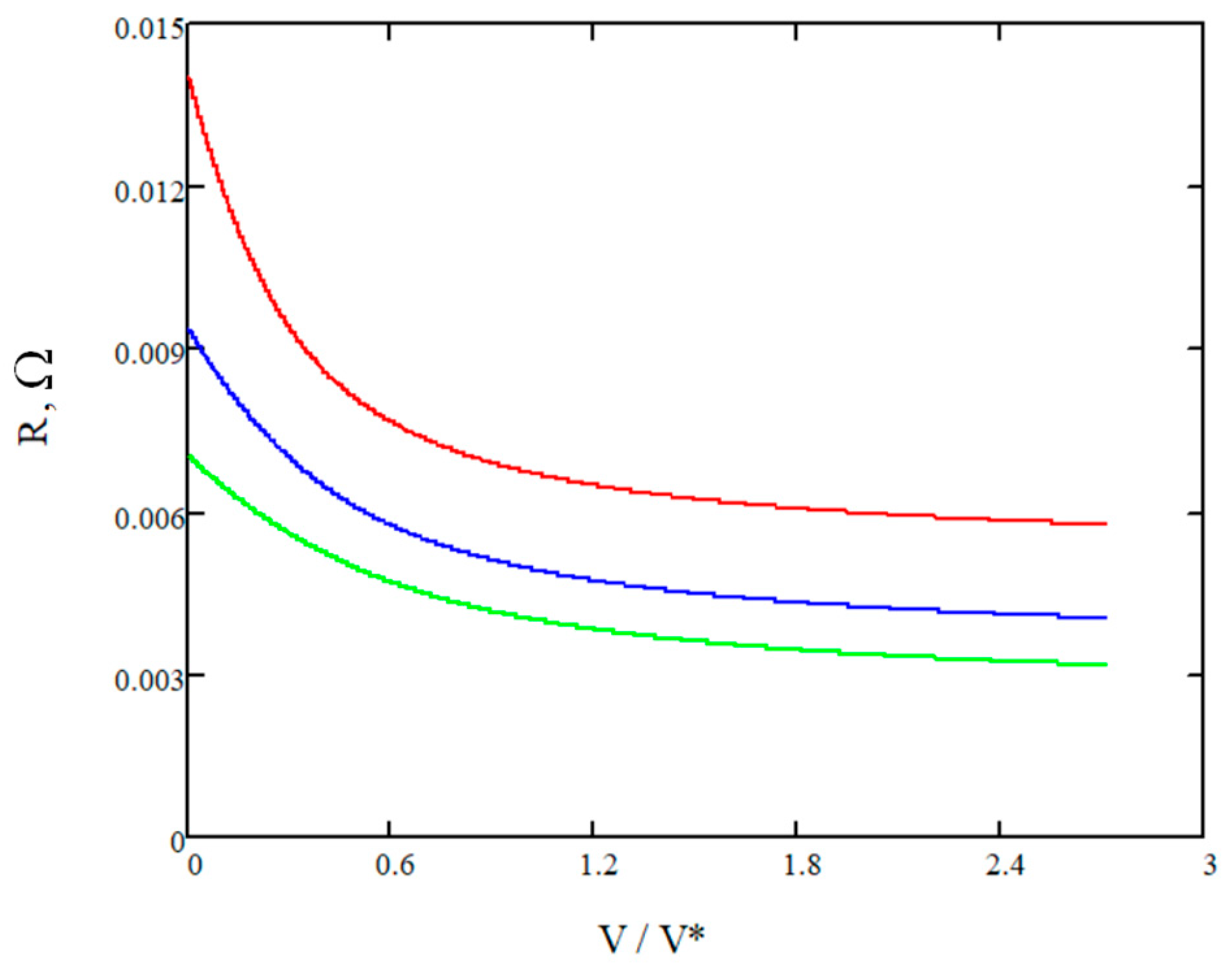
- The array of resistances of the vanadium cell for different electrolyte speeds is estimated by (39), and then the summarized error between modeled and real magnitudes is assessed.
- Compute model predictions: Using the current parameter values, compute the model predictions for the given experimental conditions. This involves solving the mathematical model that relates the battery resistance and electrolyte flow speed to the unknown parameters and other known variables.
- Evaluate the least mean square (LMS) for chosen a2 and a4 values providing a theoretical resistance curve with those obtained by the measurements. The LMS quantifies the mismatch between the model and the experimental data.
- Choosing the next combination of a2 and a4 values. Then, use the abovementioned algorithm from steps (a) to (l) to find the best combination of a2 and a4 values providing the minimum of LMS. The algorithm adjusts the values in a direction that minimizes the objective function, gradually improving the fit between the model and the experimental data.
- The combination of all variable parameters leading to the minimum of the summarized error (LMS) is recognized as the optimal for the math model.
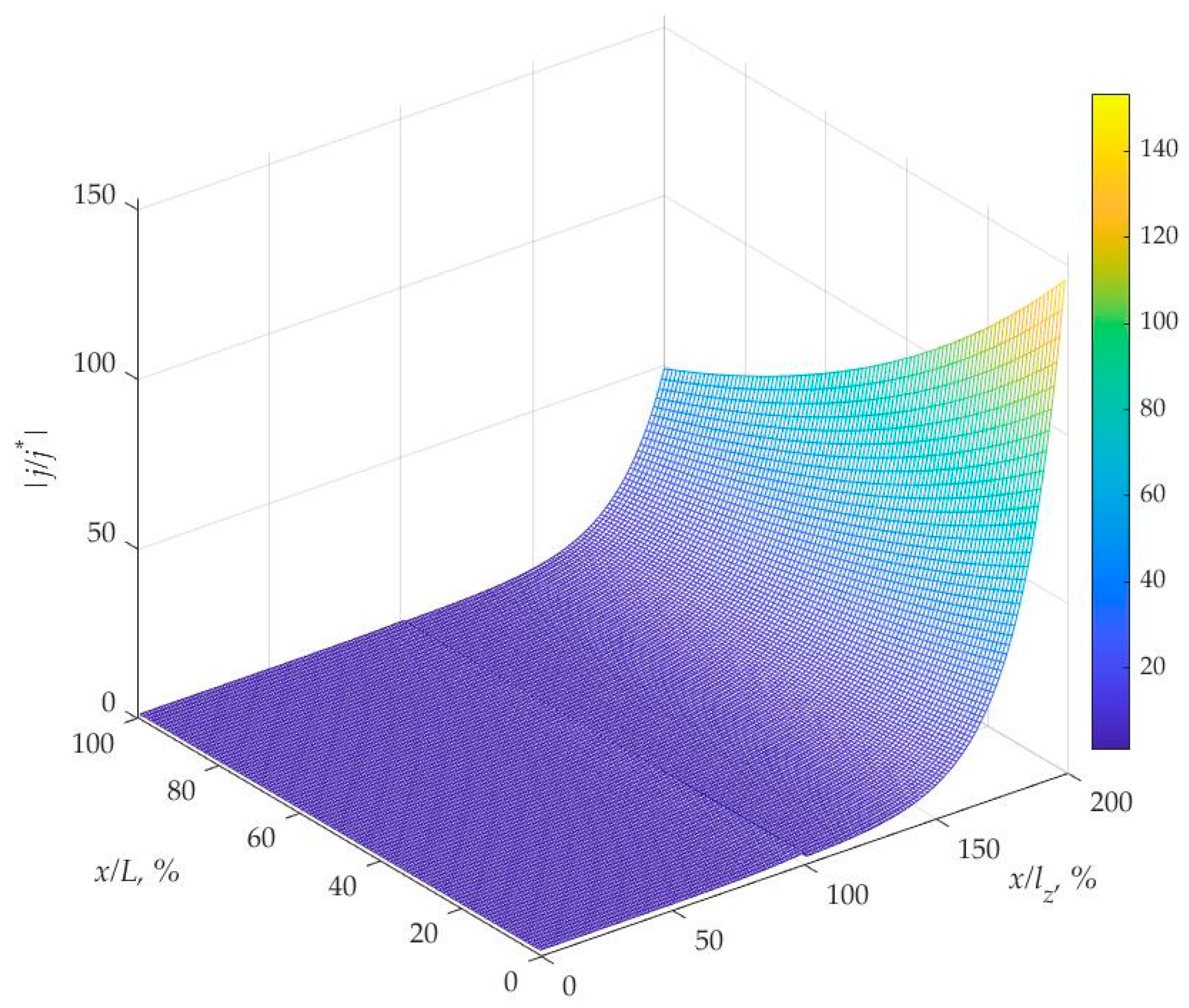
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| V, cm/s | R, mΩ | V, cm/s | R, mΩ | V, cm/s | R, mΩ | V, cm/s | R, mΩ | V, cm/s | R, mΩ |
|---|---|---|---|---|---|---|---|---|---|
| 2.755 | 90.8 | 2.637 | 107.3 | 2.447 | 106.6 | 2.159 | 112.5 | 1.851 | 126.9 |
| 2.754 | 91.0 | 2.614 | 106.4 | 2.403 | 108.3 | 2.132 | 114.3 | 1.846 | 128.9 |
| 2.756 | 94.4 | 2.611 | 105.5 | 2.379 | 108.6 | 2.117 | 114.9 | 1.846 | 129.7 |
| 2.755 | 92.6 | 2.611 | 100.6 | 2.374 | 108.2 | 2.088 | 115.2 | 1.846 | 131.6 |
| 2.756 | 93.9 | 2.611 | 107.6 | 2.373 | 108.2 | 2.081 | 116.0 | 1.846 | 128.1 |
| 2.756 | 95.5 | 2.611 | 104.5 | 2.373 | 107.3 | 2.081 | 116.5 | 1.846 | 132.9 |
| 2.755 | 97.9 | 2.611 | 104.2 | 2.373 | 110.9 | 2.080 | 111.6 | 1.830 | 134.6 |
| 2.755 | 98.0 | 2.596 | 106.2 | 2.372 | 107.9 | 2.080 | 119.5 | 1.785 | 130.3 |
| 2.739 | 99.6 | 2.570 | 104.4 | 2.328 | 108.6 | 2.081 | 117.0 | 1.756 | 132.7 |
| 2.731 | 99.1 | 2.537 | 104.3 | 2.295 | 110.5 | 2.080 | 116.6 | 1.737 | 133.9 |
| 2.722 | 95.9 | 2.533 | 108.5 | 2.294 | 110.1 | 2.066 | 120.1 | 1.734 | 134.4 |
| 2.722 | 98.1 | 2.533 | 104.8 | 2.294 | 110.5 | 2.020 | 114.0 | 1.733 | 139.3 |
| 2.723 | 102.7 | 2.533 | 104.7 | 2.294 | 110.4 | 1.969 | 123.0 | 1.733 | 137.9 |
| 2.723 | 100.0 | 2.533 | 105.0 | 2.294 | 110.1 | 1.962 | 121.1 | 1.733 | 137.3 |
| 2.723 | 101.8 | 2.533 | 107.5 | 2.294 | 110.6 | 1.961 | 121.2 | 1.730 | 139.6 |
| 2.723 | 100.1 | 2.523 | 106.3 | 2.289 | 111.2 | 1.961 | 124.5 | 1.684 | 141.3 |
| 2.707 | 104.3 | 2.502 | 108.5 | 2.253 | 113.8 | 1.961 | 121.7 | 1.654 | 141.4 |
| 2.695 | 99.9 | 2.480 | 108.5 | 2.201 | 109.8 | 1.961 | 125.0 | 1.639 | 143.8 |
| 2.687 | 102.7 | 2.470 | 105.8 | 2.179 | 111.9 | 1.961 | 123.3 | 1.636 | 142.6 |
| 2.687 | 103.4 | 2.460 | 109.5 | 2.179 | 111.5 | 1.961 | 125.1 | 1.636 | 144.0 |
| 2.687 | 105.6 | 2.460 | 106.3 | 2.179 | 112.2 | 1.961 | 121.9 | 1.636 | 148.9 |
| 2.687 | 101.1 | 2.460 | 107.6 | 2.179 | 113.7 | 1.960 | 128.3 | 1.635 | 148.8 |
| 2.687 | 101.1 | 2.460 | 108.5 | 2.179 | 113.3 | 1.923 | 123.5 | 1.627 | 145.8 |
| 2.687 | 104.1 | 2.460 | 108.3 | 2.179 | 115.0 | 1.899 | 124.4 | 1.601 | 148.3 |
| 2.666 | 101.4 | 2.460 | 110.0 | 2.179 | 112.2 | 1.870 | 123.5 |
References
- Dehghani-Sanij, A.R.; Tharumalingam, E.; Dusseault, M.B.; Fraser, R. Study of energy storage systems and environmental challenges of batteries. Renew. Sustain. Energy Rev. 2019, 104, 192–208. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Saleem, M.S.; Kalair, A.R.; Khan, N. Role of energy storage systems in energy transition from fossil fuels to renewables. Energy Storage 2021, 3, e135. [Google Scholar] [CrossRef] [Green Version]
- Xiong, B.; Zhao, J.; Wei, Z.; Skyllas-Kazacos, M. Extended Kalman filter method for state of charge estimation of vanadium redox flow battery using thermal-dependent electrical model. J. Power Sources 2014, 262, 50–61. [Google Scholar] [CrossRef]
- Rudolph, S.; Schröder, U.; Bayanov, I.M. On-line controlled state of charge rebalancing in vanadium redox flow battery. J. Electroanal. Chem. 2013, 703, 29–37. [Google Scholar] [CrossRef]
- Pozin, A.; Averbukh, M.; Sukoriansky, S. Power efficiency optimization of vanadium redox batteries based on experimental analysis of electrolyte flow through carbon felt of electrodes. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V06AT07A030. [Google Scholar]
- Xiong, B.; Zhao, J.; Li, J. Modeling of an all-vanadium redox flow battery and optimization of flow rates. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Lourenssen, K.; Williams, J.; Ahmadpour, F.; Clemmer, R.; Tasnim, S. Vanadium redox flow batteries: A comprehensive review. J. Energy Storage 2019, 25, 100844. [Google Scholar] [CrossRef]
- Tang, Z.; Keith, R.; Aaron, D.S.; Lawton, J.S.; Papandrew, A.P.; Zawodzinski, T.A. Proton exchange membrane performance characterization in VRFB. ECS Trans. 2012, 41, 25. [Google Scholar] [CrossRef]
- Tang, Z.; Svoboda, R.; Lawton, J.S.; Aaron, D.S.; Papandrew, A.B.; Zawodzinski, T.A. Composition and conductivity of membranes equilibrated with solutions of sulfuric acid and vanadyl sulfate. J. Electrochem. Soc. 2013, 160, F1040. [Google Scholar] [CrossRef] [Green Version]
- Schafner, K.; Becker, M.; Turek, T. Membrane resistance of different separator materials in a vanadium redox flow battery. J. Membr. Sci. 2019, 586, 106–114. [Google Scholar] [CrossRef]
- Waters, S.E.; Thurston, J.R.; Armstrong, R.W.; Robb, B.H.; Marshak, M.P.; Reber, D. Holistic design principles for flow batteries: Cation dependent membrane resistance and active species solubility. J. Power Sources 2022, 520, 230877. [Google Scholar] [CrossRef]
- Chen, D.; Hickner, M.A.; Agar, E.; Kumbur, E.C. Optimizing membrane thickness for vanadium redox flow batteries. J. Membr. Sci. 2013, 437, 108–113. [Google Scholar] [CrossRef]
- Bogdanov, S.; Pugach, M.; Parsegov, S.; Vlasov, V.; Ibanez, F.M.; Stevenson, K.J.; Vorobev, P. Dynamic modeling of vanadium redox flow batteries: Practical approaches, their applications and limitations. J. Energy Storage 2023, 57, 106191. [Google Scholar] [CrossRef]
- Pugach, M.; Parsegov, S.; Gryazina, E.; Bischi, A. Output feedback control of electrolyte flow rate for Vanadium Redox Flow Batteries. J. Power Sources 2020, 455, 227916. [Google Scholar] [CrossRef]
- Badrinarayanan, R.; Zhao, J.; Tseng, K.J.; Skyllas-Kazacos, M. Extended dynamic model for ion diffusion in all-vanadium redox flow battery including the effects of temperature and bulk electrolyte transfer. J. Power Sources 2014, 270, 576–586. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, H. Design and experimental validation of a generalised electrical equivalent model of Vanadium Redox Flow Battery for interfacing with renewable energy sources. J. Energy Storage 2017, 13, 220–232. [Google Scholar] [CrossRef]
- Yuan, C.; Xing, F.; Zheng, Q.; Zhang, H.; Li, X.; Ma, X. Factor analysis of the uniformity of the transfer current density in vanadium flow battery by an improved three-dimensional transient model. Energy 2020, 194, 116839. [Google Scholar] [CrossRef]
- Vlasov, V.I.; Gvozdik, N.A.; Mokrousov, M.D.; Ryazantsev, S.V.; Luchkin, S.Y.; Gorin, D.A.; Stevenson, K.J. Ion-exchange membrane impact on preferential water transfer in all-vanadium redox flow battery. J. Power Sources 2022, 540, 231640. [Google Scholar] [CrossRef]
- Sheng, J.; Li, L.; Wang, H.; Zhang, L.; Jiang, S.; Shi, H. An ultrahigh conductivity and efficiency of SPEEK-based hybrid proton exchange membrane containing amphoteric GO-VIPS nanofillers for vanadium flow battery. J. Membr. Sci. 2023, 669, 121326. [Google Scholar] [CrossRef]
- Ma, Q.; Xing, L.; Su, H.; Zhang, W.; Yang, W.; Xu, Q. Numerical investigation on the dispersion effect in vanadium redox flow battery. Chem. Eng. J. 2020, 393, 124753. [Google Scholar] [CrossRef]
- Chakrabarti, M.H.; Brandon, N.P.; Hajimolana, S.A.; Tariq, F.; Yufit, V.; Hashim, M.A.; Hussain, M.A.; Low, C.; Aravind, P.V. Application of carbon materials in redox flow batteries. J. Power Sources 2014, 253, 150–166. [Google Scholar] [CrossRef]
- Averbukh, M.; Kamanina, N. Improving vanadium redox cells efficiency by carbon nanotubes materials having enhanced conductivity and rapidity of electrode reactions. In Proceedings of the 14th Israeli-Russian Bi-National Workshop, Ariel, Israel, 12–16 July 2015; pp. 78–87. [Google Scholar]
- Ke, X.; Prahl, J.M.; Alexander, J.I.D.; Savinell, R.F. Redox flow batteries with serpentine flow fields: Distributions of electrolyte flow reactant penetration into the porous carbon electrodes and effects on performance. J. Power Sources 2018, 384, 295–302. [Google Scholar] [CrossRef]
- Xi, J.; Wu, Z.; Teng, X.; Zhao, Y.; Chen, L.; Qiu, X. Self-assembled polyelectrolyte multilayer modified Nafion membrane with suppressed vanadium ion crossover for vanadium redox flow batteries. J. Mater. Chem. 2008, 18, 1232–1238. [Google Scholar] [CrossRef]
- Rubinstein, I. Electro-Diffusion of Ions; SIAM: Philadelphia, PA, USA, 1990. [Google Scholar]
- Yamamura, T.; Watanabe, N.; Yano, T.; Shiokawa, Y. Electron-transfer kinetics of Np3+/Np4+, NpO2+/NpO22+, V2+/V3+, and VO2+/VO2+ at carbon electrodes. J. Electrochem. Soc. 2005, 152, A830. [Google Scholar] [CrossRef]
- Tamm, I.E. Fundamentals of the Theory of Electricity; Mir Publishers: Moscow, Russia, 1979. [Google Scholar]
- Averbukh, M.; Pozin, A.; Sukoriansky, S. Electrolyte pumping optimization in already manufactured vanadium redox battery based on experimentally determined electrical and hydrodynamic losses. J. Energy Eng. 2017, 143, 04016050. [Google Scholar] [CrossRef]
- Pintauro, P.N.; Verbrugge, M.W. The electric-potential profile in ion-exchange membrane pores. J. Membr. Sci. 1989, 44, 197–212. [Google Scholar] [CrossRef]
- Smirnov, B.M.; Son, E.E.; Tereshonok, D.V. Diffusion and mobility of atomic particles in a liquid. J. Exp. Theor. Phys. 2017, 125, 906–912. [Google Scholar] [CrossRef]
- Hemme, C.; Van Berk, W. Hydrogeochemical modeling to identify potential risks of underground hydrogen storage in depleted gas fields. Appl. Sci. 2018, 8, 2282. [Google Scholar] [CrossRef] [Green Version]
- Moradighadi, N.; Brown, B.; Nesic, S. Note on Selecting DC Potentials for EIS Measurements: An Example of Determining the Diffusion Coefficient of Hydrogen Ion in Aqueous Solutions. In Proceedings of the CORROSION 2021, Virtual, 19–30 April 2021; OnePetro: Richardson, TX, USA, 2021. [Google Scholar]
- De Leon, C.P.; Frías-Ferrer, A.; González-García, J.; Szánto, D.A.; Walsh, F.C. Redox flow cells for energy conversion. J. Power Sources 2006, 160, 716–732. [Google Scholar] [CrossRef] [Green Version]
- Pugach, M.; Kondratenko, M.; Briola, S.; Bischi, A. Zero dimensional dynamic model of vanadium redox flow battery cell incorporating all modes of vanadium ions crossover. Appl. Energy 2018, 226, 560–569. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kislov, R.; Danin, Z.; Averbukh, M. Investigating the Impact of Electrolyte Flow Velocity on the Resistivity of Vanadium Redox Batteries: A Theoretical Analysis and Experimental Data Comparison. Materials 2023, 16, 4845. https://doi.org/10.3390/ma16134845
Kislov R, Danin Z, Averbukh M. Investigating the Impact of Electrolyte Flow Velocity on the Resistivity of Vanadium Redox Batteries: A Theoretical Analysis and Experimental Data Comparison. Materials. 2023; 16(13):4845. https://doi.org/10.3390/ma16134845
Chicago/Turabian StyleKislov, Roman, Zekharya Danin, and Moshe Averbukh. 2023. "Investigating the Impact of Electrolyte Flow Velocity on the Resistivity of Vanadium Redox Batteries: A Theoretical Analysis and Experimental Data Comparison" Materials 16, no. 13: 4845. https://doi.org/10.3390/ma16134845
APA StyleKislov, R., Danin, Z., & Averbukh, M. (2023). Investigating the Impact of Electrolyte Flow Velocity on the Resistivity of Vanadium Redox Batteries: A Theoretical Analysis and Experimental Data Comparison. Materials, 16(13), 4845. https://doi.org/10.3390/ma16134845







