Figure 1.
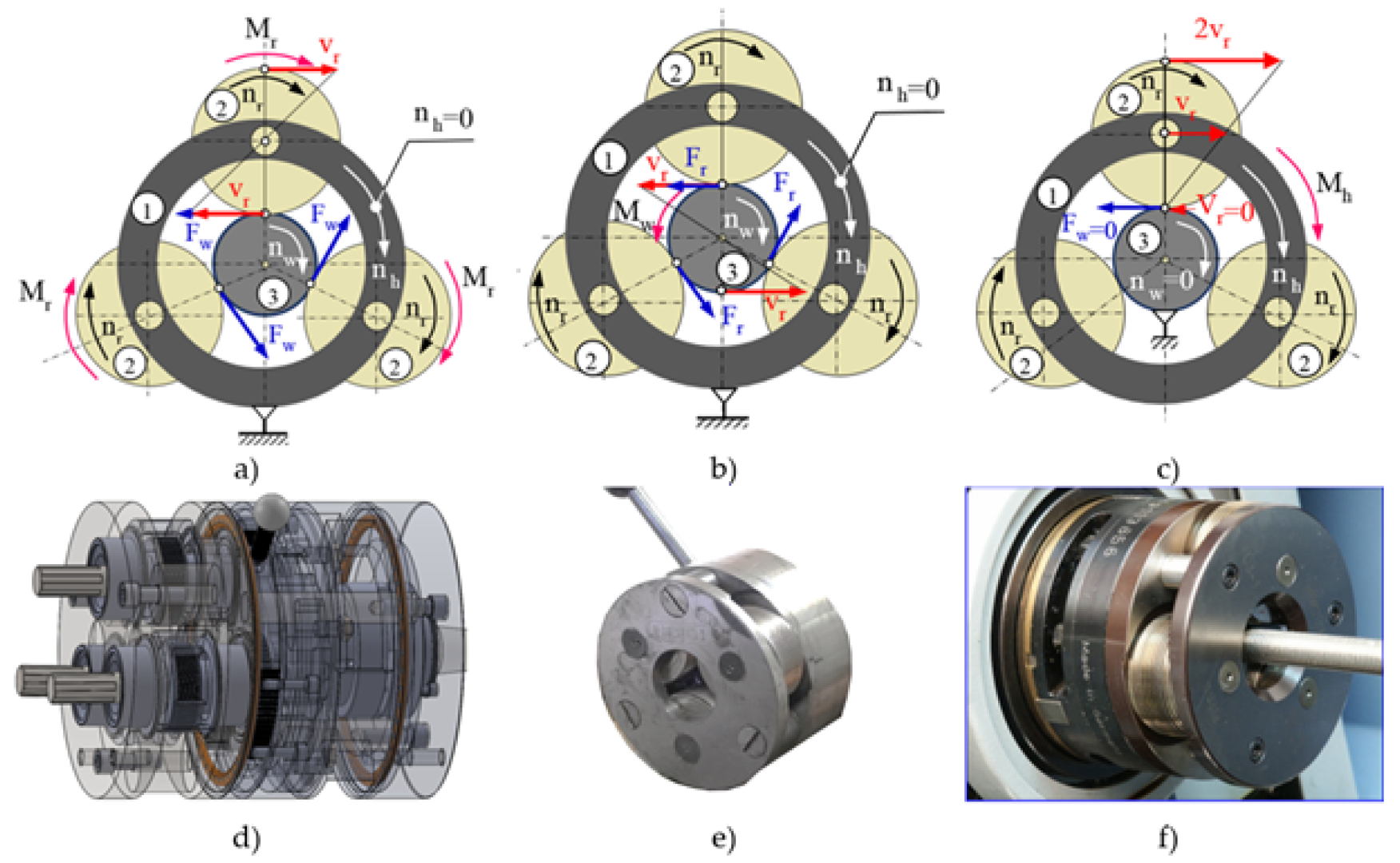
Kinematic diagrams (a–c) of three methods of rolling external threads and the rolling heads according to these methods (d–f): (a)—stationary basket of the head and rollers driven and a rotating non-driven workpiece that moves axially relative to the head; (b)—stationary head basket, rotating and non-driven rollers and rotating and driven workpiece; the head with the rollers moves axially relative to the workpiece; (c)—stationary object, rotating and driven basket of the head and rotating and non-powered rollers; the head with the rollers moves axially relative to the workpiece: 1—head basket, 2—rollers, 3—workpiece, —rolling speed, —peripheral speed of the head.
Figure 1.
Kinematic diagrams (a–c) of three methods of rolling external threads and the rolling heads according to these methods (d–f): (a)—stationary basket of the head and rollers driven and a rotating non-driven workpiece that moves axially relative to the head; (b)—stationary head basket, rotating and non-driven rollers and rotating and driven workpiece; the head with the rollers moves axially relative to the workpiece; (c)—stationary object, rotating and driven basket of the head and rotating and non-powered rollers; the head with the rollers moves axially relative to the workpiece: 1—head basket, 2—rollers, 3—workpiece, —rolling speed, —peripheral speed of the head.
Figure 2.
View of test stands for rolling external threads, equipped with angular heads according to the first (a) and second (b) and third (c) kinematic variations.
Figure 2.
View of test stands for rolling external threads, equipped with angular heads according to the first (a) and second (b) and third (c) kinematic variations.
Figure 3.
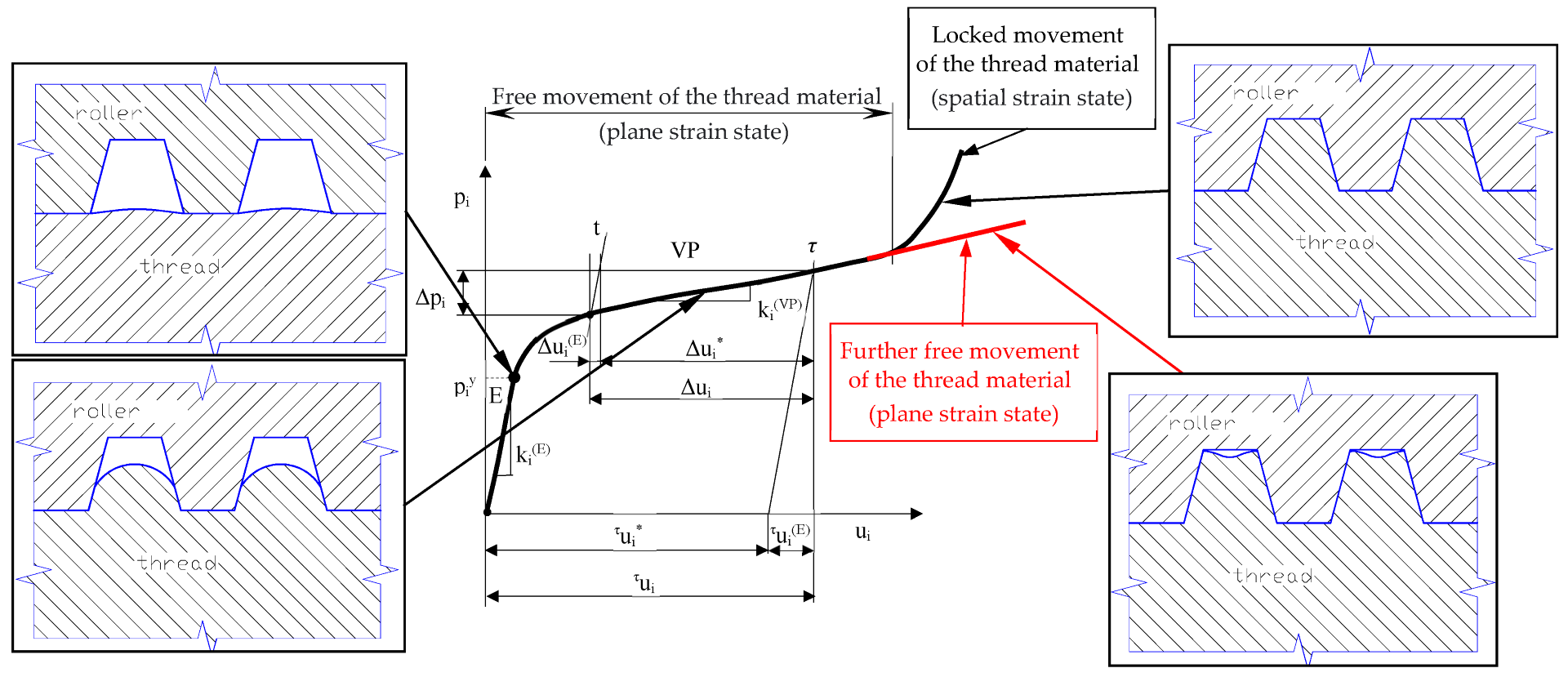
Diagram pi-ui for the contact of the shaped thread with roller, where Δui*—is the sum of visco-plastic increments, τui*—components of the node’s displacement in time.
Figure 3.
Diagram pi-ui for the contact of the shaped thread with roller, where Δui*—is the sum of visco-plastic increments, τui*—components of the node’s displacement in time.
Figure 4.
(a) View of a symmetrical roller with three shaping rings and two calibrating rings for trapezoidal thread Tr22×4 and a screw with a shaped thread. (b) View of the contact zone between the tool and the thread.
Figure 4.
(a) View of a symmetrical roller with three shaping rings and two calibrating rings for trapezoidal thread Tr22×4 and a screw with a shaped thread. (b) View of the contact zone between the tool and the thread.
Figure 5.
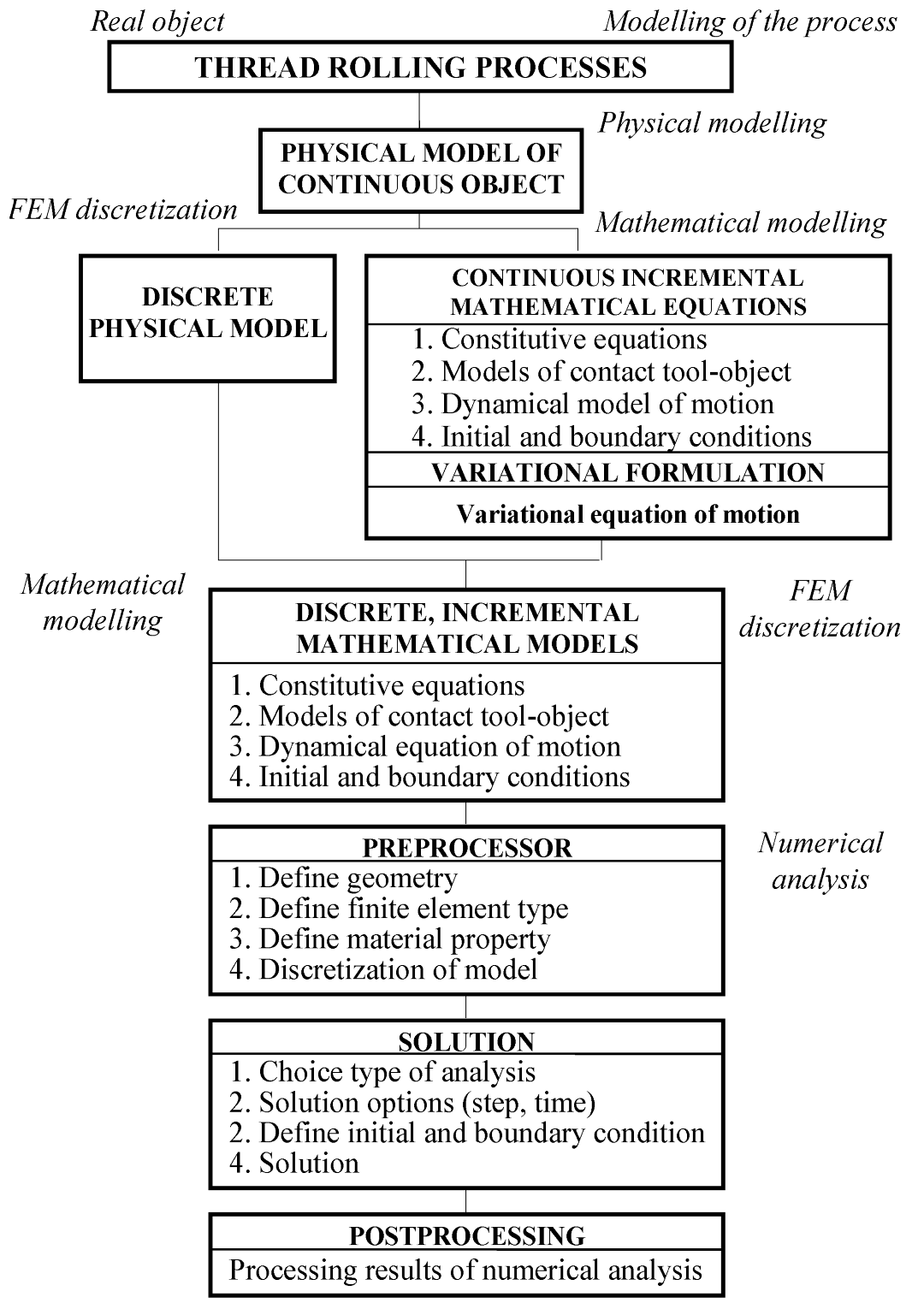
Scheme of modern modelling and analysis of thread rolling process.
Figure 5.
Scheme of modern modelling and analysis of thread rolling process.
Figure 6.
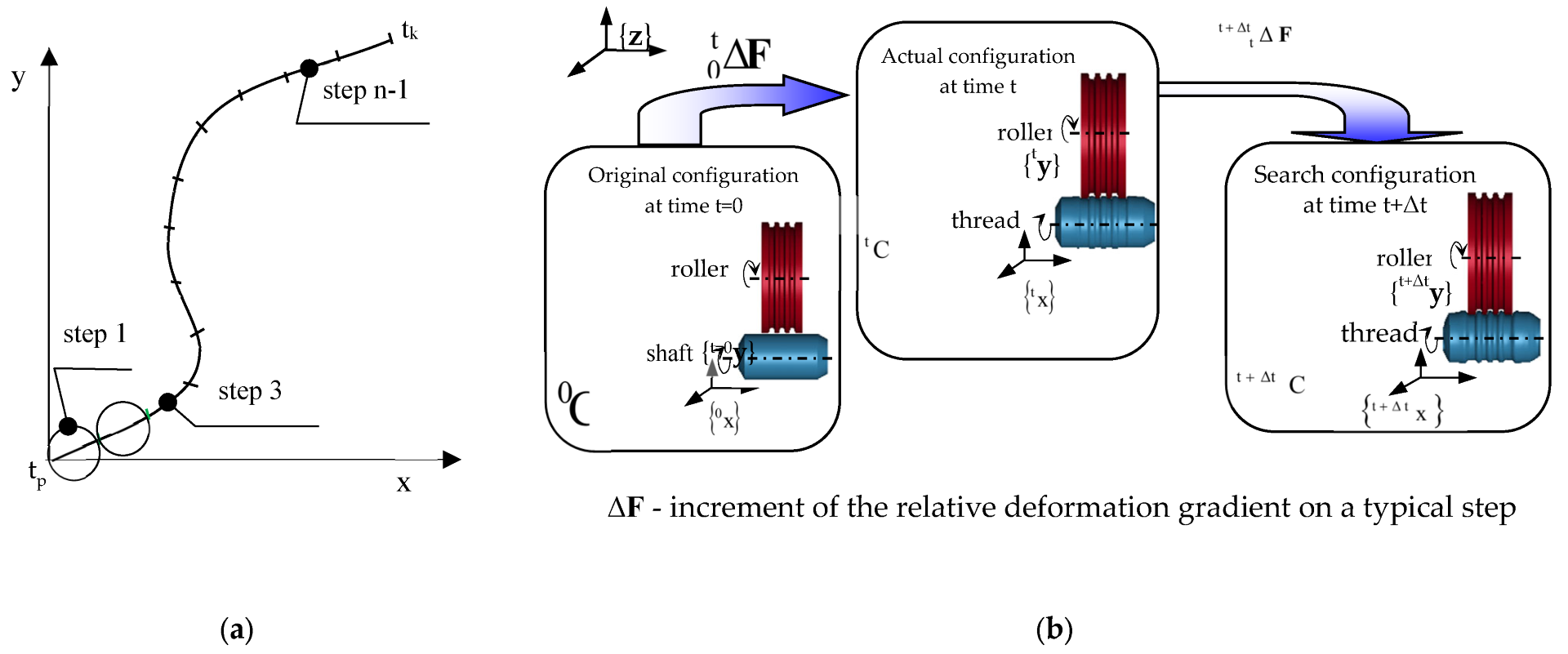
Schematic diagram of the step-by-step analysis of the thread rolling process (a) and the configurations adopted by the body in subsequent steps in the updated Lagrange description (b).
Figure 6.
Schematic diagram of the step-by-step analysis of the thread rolling process (a) and the configurations adopted by the body in subsequent steps in the updated Lagrange description (b).
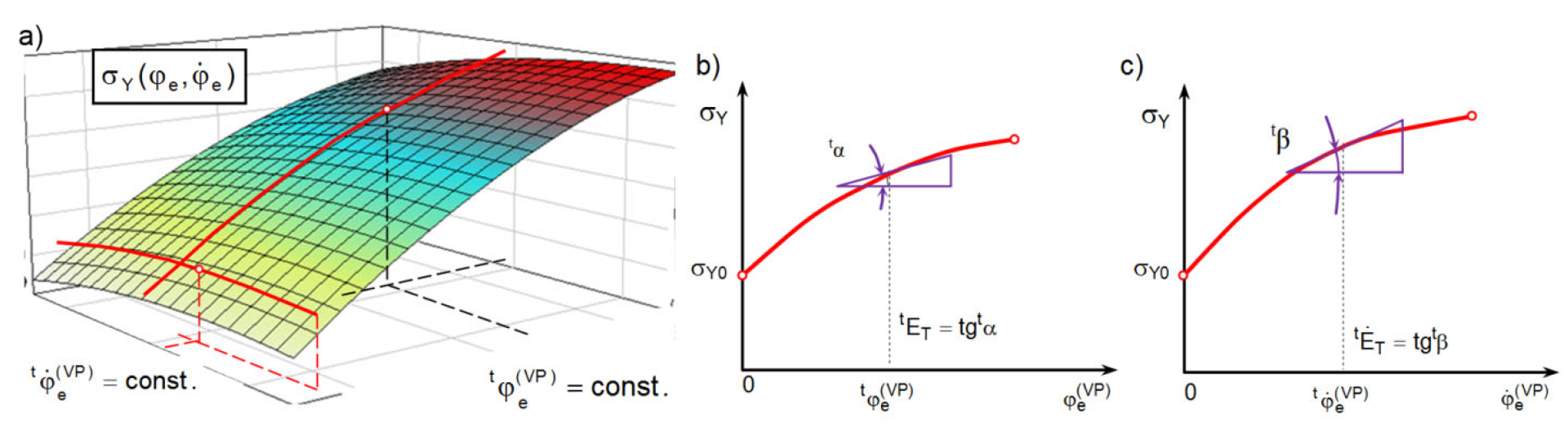
Figure 7.
The graph of relationship (a), and one parametric curve , for (b) and definition of the partial derivative and one parametric curve for definition of the partial derivative (c).
Figure 7.
The graph of relationship (a), and one parametric curve , for (b) and definition of the partial derivative and one parametric curve for definition of the partial derivative (c).
Figure 8.
The shape of a cylindrical sample normalized to tension (a) and the shape of a three-stage cylindrical sample for determining the constants n and K of the hardening curve (b).
Figure 8.
The shape of a cylindrical sample normalized to tension (a) and the shape of a three-stage cylindrical sample for determining the constants n and K of the hardening curve (b).
Figure 9.
View of samples for testing the mechanical properties of C45 steel: (a) one-stage sample, (b) one-stage sample after testing, (c) three-stage sample, (d) three-stage sample after testing.
Figure 9.
View of samples for testing the mechanical properties of C45 steel: (a) one-stage sample, (b) one-stage sample after testing, (c) three-stage sample, (d) three-stage sample after testing.
Figure 10.
Zwick Roell Z400E testing machine: (a) general view; (b) view of the traverses with a sample; (c) view of the ARAMIS device for optical measurement of the sample deformation.
Figure 10.
Zwick Roell Z400E testing machine: (a) general view; (b) view of the traverses with a sample; (c) view of the ARAMIS device for optical measurement of the sample deformation.
Figure 11.
Stress–strain engineering approximate, and true (hardening) curves: is the effective engineering plastic strain, is the effective true plastic strain, is the initial yield stress.
Figure 11.
Stress–strain engineering approximate, and true (hardening) curves: is the effective engineering plastic strain, is the effective true plastic strain, is the initial yield stress.
Figure 12.
Specimens with grid (
a) and speck (
b) coatings [
61].
Figure 12.
Specimens with grid (
a) and speck (
b) coatings [
61].
Figure 13.
Cylindrical specimens with grid (
a) and speck (
b) coatings during tension, with visible necking before the fracture [
62].
Figure 13.
Cylindrical specimens with grid (
a) and speck (
b) coatings during tension, with visible necking before the fracture [
62].
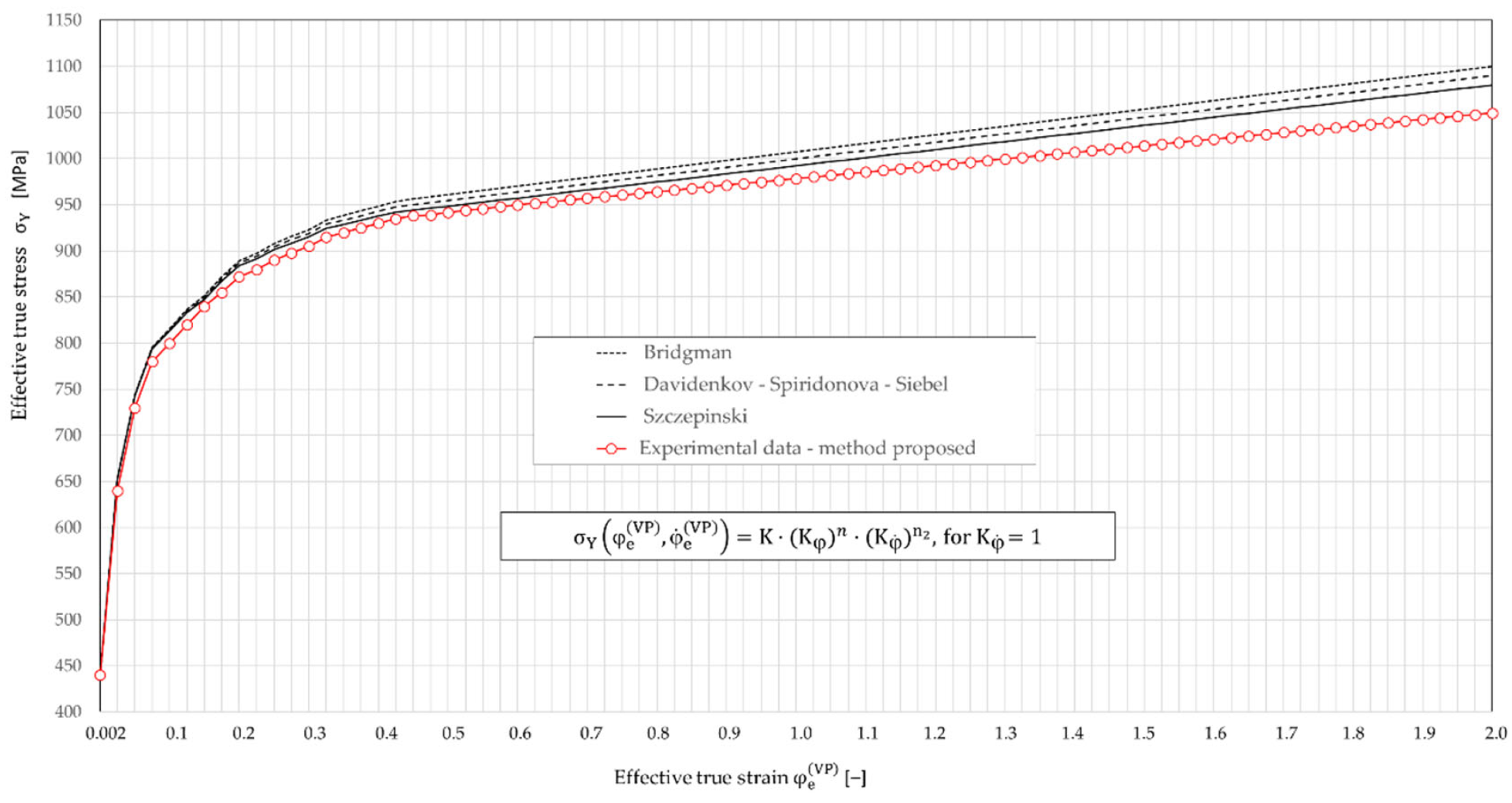
Figure 14.
The effective true stress–effective true strain curves developed from the proposed semi-empirical method (Experimental data) and from the Bridgman, Davidenkov–Spiridonova and Siebel, and Szczepiński methods for non-linear strain hardening material models, for C45 steel.
Figure 14.
The effective true stress–effective true strain curves developed from the proposed semi-empirical method (Experimental data) and from the Bridgman, Davidenkov–Spiridonova and Siebel, and Szczepiński methods for non-linear strain hardening material models, for C45 steel.
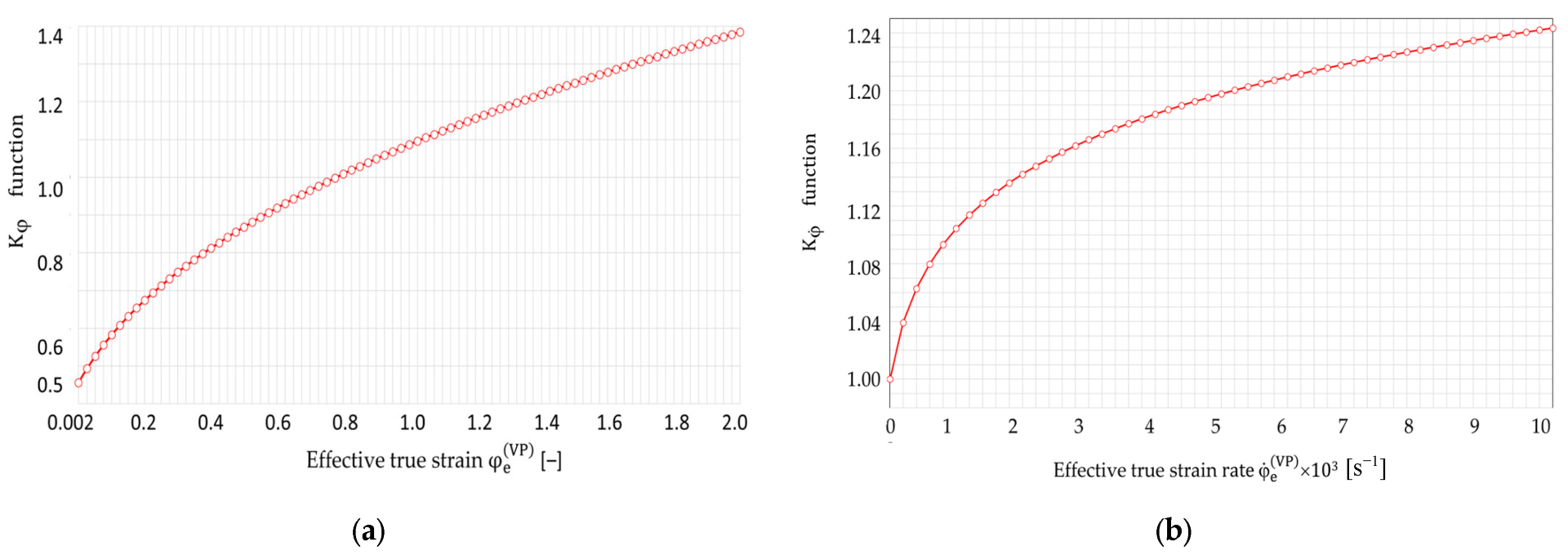
Figure 15.
Graphs of one-parameter functions (a) and (b) in models (8)–(10) for C45 steel, calculated from Formulas (24) and (25), respectively.
Figure 15.
Graphs of one-parameter functions (a) and (b) in models (8)–(10) for C45 steel, calculated from Formulas (24) and (25), respectively.
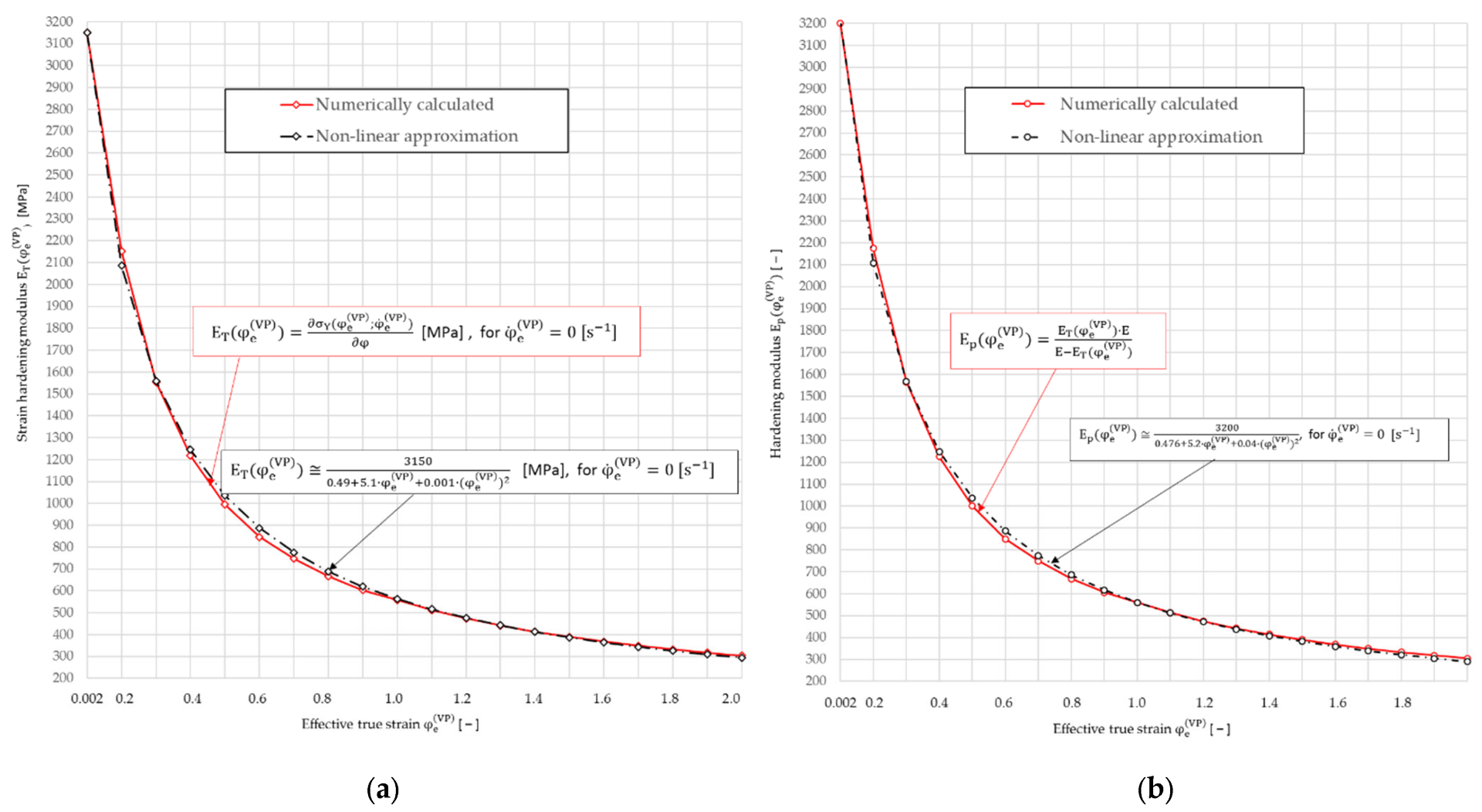
Figure 16.
The temporary strain-hardening modulus [MPa] (a) and temporary hardening modulus [] (b) for C45 steel, obtained numerically according to Formulas (28) and (27), respectively, and from approximation Equations (40) and (41), respectively.
Figure 16.
The temporary strain-hardening modulus [MPa] (a) and temporary hardening modulus [] (b) for C45 steel, obtained numerically according to Formulas (28) and (27), respectively, and from approximation Equations (40) and (41), respectively.
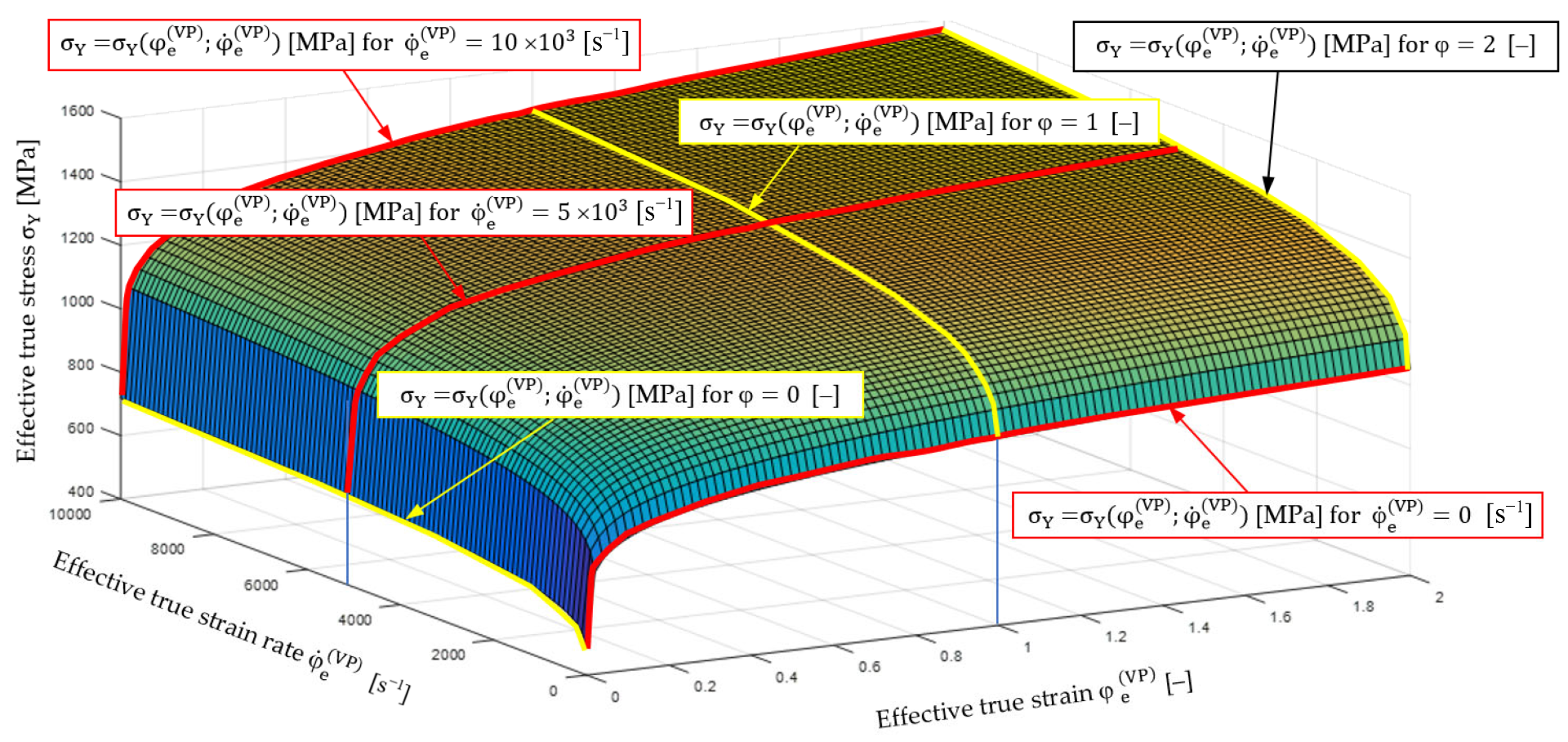
Figure 17.
Graphic dependence of yield stresses for C45 steel in the whole range of variability of true effective strain and true effective strain rate in the thread rolling process determined by the semi-empirical method.
Figure 17.
Graphic dependence of yield stresses for C45 steel in the whole range of variability of true effective strain and true effective strain rate in the thread rolling process determined by the semi-empirical method.
Figure 18.
Example graphical relations of plastic stresses for for C45 steel obtained on the basis of Equations (36) and (42) and determined by the semi-empirical method.
Figure 18.
Example graphical relations of plastic stresses for for C45 steel obtained on the basis of Equations (36) and (42) and determined by the semi-empirical method.
Figure 19.
Discretized model of cylindrical specimen.
Figure 19.
Discretized model of cylindrical specimen.
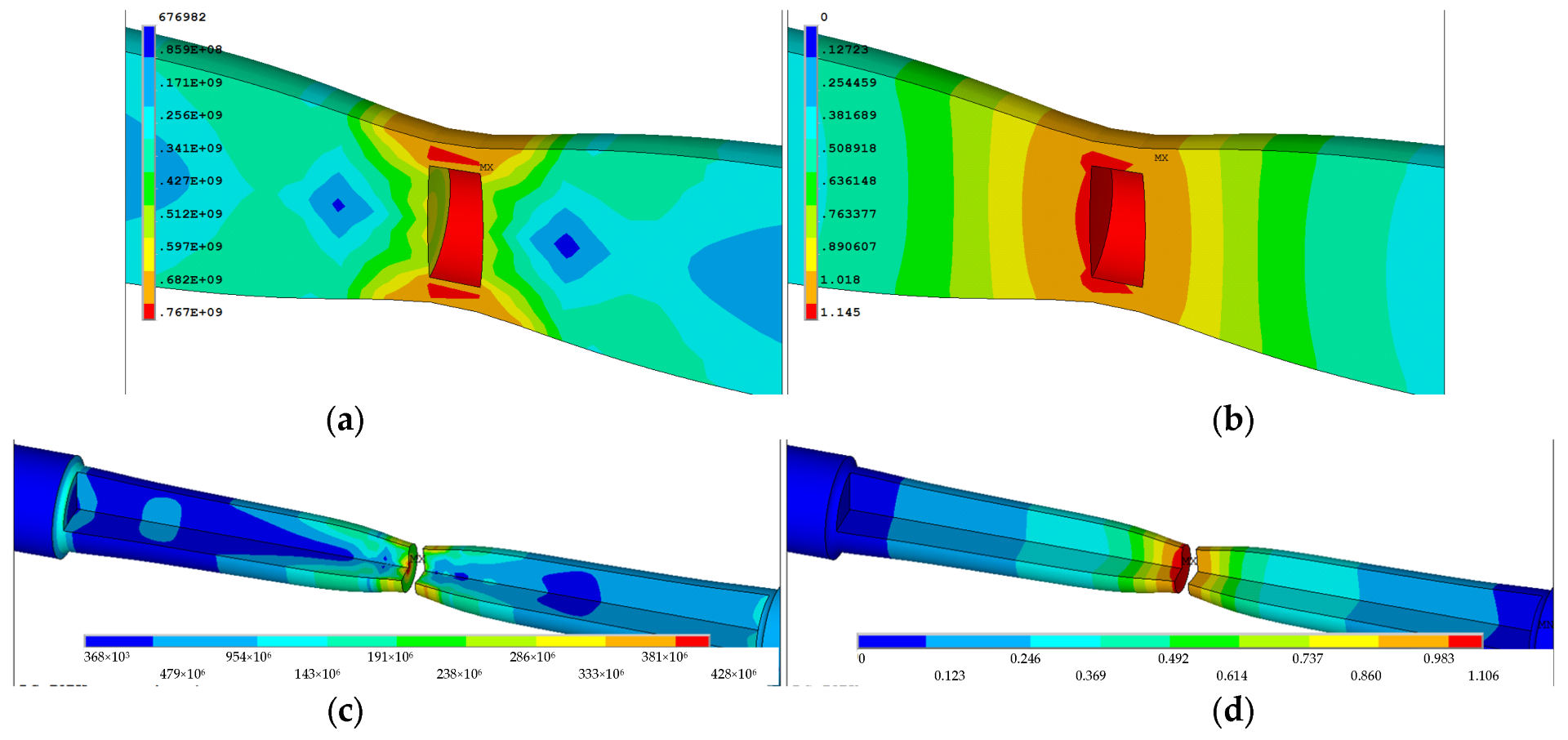
Figure 20.
Maps of effective stresses (a,c) and effective plastic strains (b,d) before fracture—steps 178 (a,b) and after fracture—steps 180 (c,d) in cylindrical specimen from C45 steel.
Figure 20.
Maps of effective stresses (a,c) and effective plastic strains (b,d) before fracture—steps 178 (a,b) and after fracture—steps 180 (c,d) in cylindrical specimen from C45 steel.
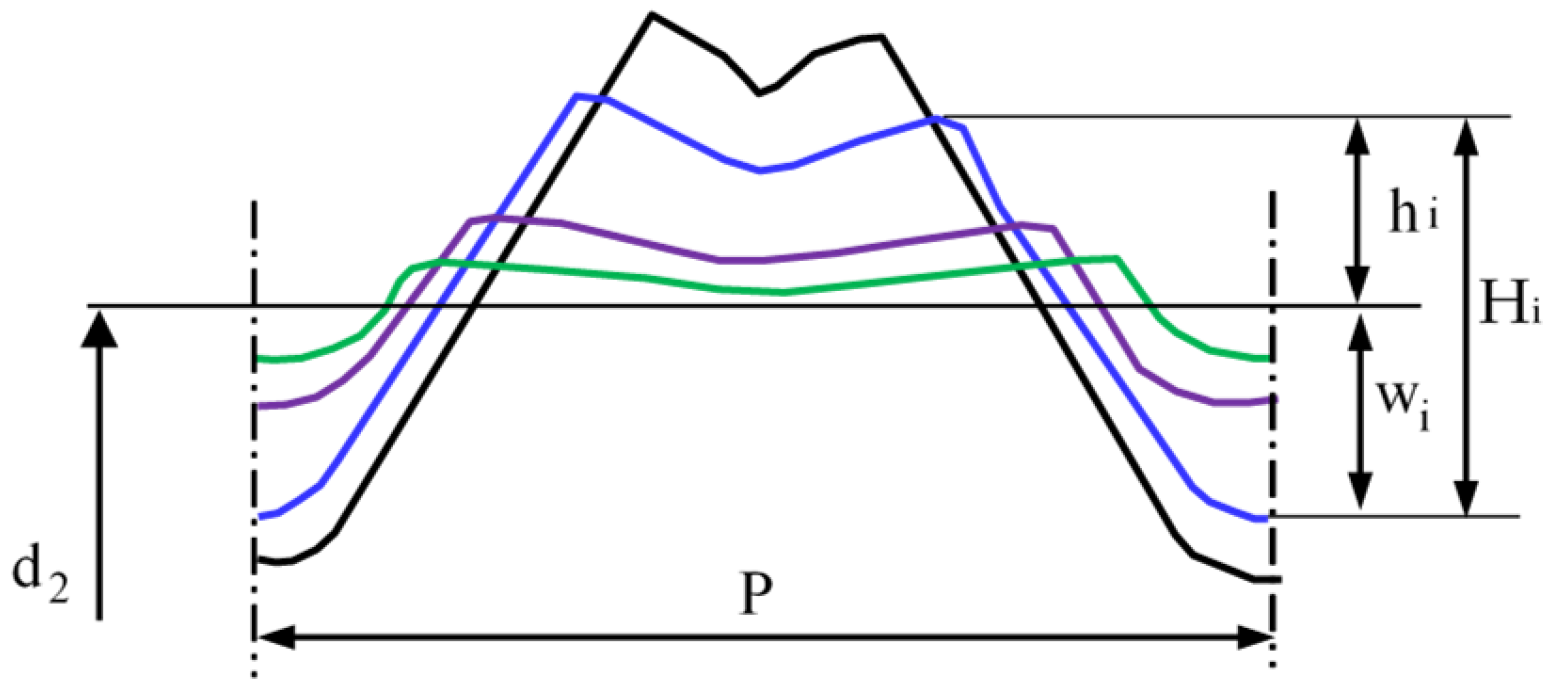
Figure 21.
Schema of the course of the thread outline forming: Hi—i-th height of the thread, wi—i-th penetration of the rings, hi—i-th hight of the flash, P—thread pitch, d2—shaft diameter.
Figure 21.
Schema of the course of the thread outline forming: Hi—i-th height of the thread, wi—i-th penetration of the rings, hi—i-th hight of the flash, P—thread pitch, d2—shaft diameter.
Figure 22.
View of a sample with a thread at various stages of the process and axial cross-sections of the thread resulting from the impact of successive rings of the embossing roller on the workpiece, during dry rolling (lower part) and with lubrication (upper part).
Figure 22.
View of a sample with a thread at various stages of the process and axial cross-sections of the thread resulting from the impact of successive rings of the embossing roller on the workpiece, during dry rolling (lower part) and with lubrication (upper part).
Figure 23.
Samples view for the thread rolling with axial inserts of flat steel C45 (a) and copper M1E (b).
Figure 23.
Samples view for the thread rolling with axial inserts of flat steel C45 (a) and copper M1E (b).
Figure 24.
View of the FETTE rolling mill for axial threading: 1—head, 2—workpiece, 3—cooling and lubricating system, 4—hydraulic feeder, 5—control system, 6—fixed headstock, 7—headstock shift control system, 8—control system for closing and opening the head, 9—hydraulic holder, 10—rolling mill motor.
Figure 24.
View of the FETTE rolling mill for axial threading: 1—head, 2—workpiece, 3—cooling and lubricating system, 4—hydraulic feeder, 5—control system, 6—fixed headstock, 7—headstock shift control system, 8—control system for closing and opening the head, 9—hydraulic holder, 10—rolling mill motor.
Figure 25.
View of the processing system of the FETTE rolling mill for thread-rolling using the axial method (a) and view of the rolling head using the axial method (b): 1—roller, 2—hydraulic holder, 3—roller axis, 4—thread diameter adjustment mechanism, 5—workpiece, 6—hydraulic vice, 7—three-roller head, 8—head closing and opening system, 9—cooling and lubricating system.
Figure 25.
View of the processing system of the FETTE rolling mill for thread-rolling using the axial method (a) and view of the rolling head using the axial method (b): 1—roller, 2—hydraulic holder, 3—roller axis, 4—thread diameter adjustment mechanism, 5—workpiece, 6—hydraulic vice, 7—three-roller head, 8—head closing and opening system, 9—cooling and lubricating system.
Figure 26.
View samples with the thread with flat steel C45 (a) and cooper M1E (b).
Figure 26.
View samples with the thread with flat steel C45 (a) and cooper M1E (b).
Figure 27.
View samples with flat steel insert after rolling and scanning pictures of cross-sectional of the sample at the edge of the groove before rolling (section I-I) and passing through the crest (section II-II) and the root of the thread (section III-III).
Figure 27.
View samples with flat steel insert after rolling and scanning pictures of cross-sectional of the sample at the edge of the groove before rolling (section I-I) and passing through the crest (section II-II) and the root of the thread (section III-III).
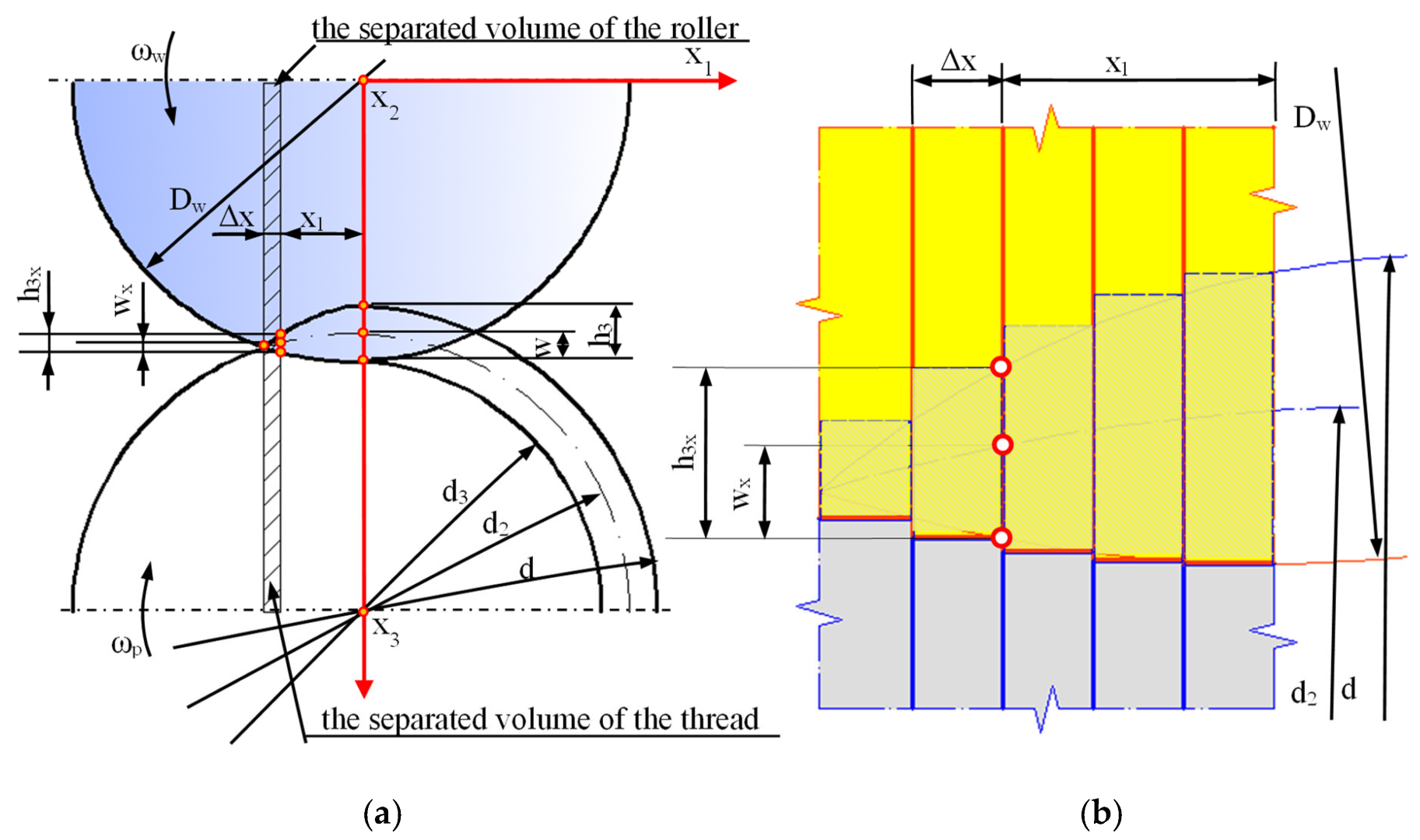
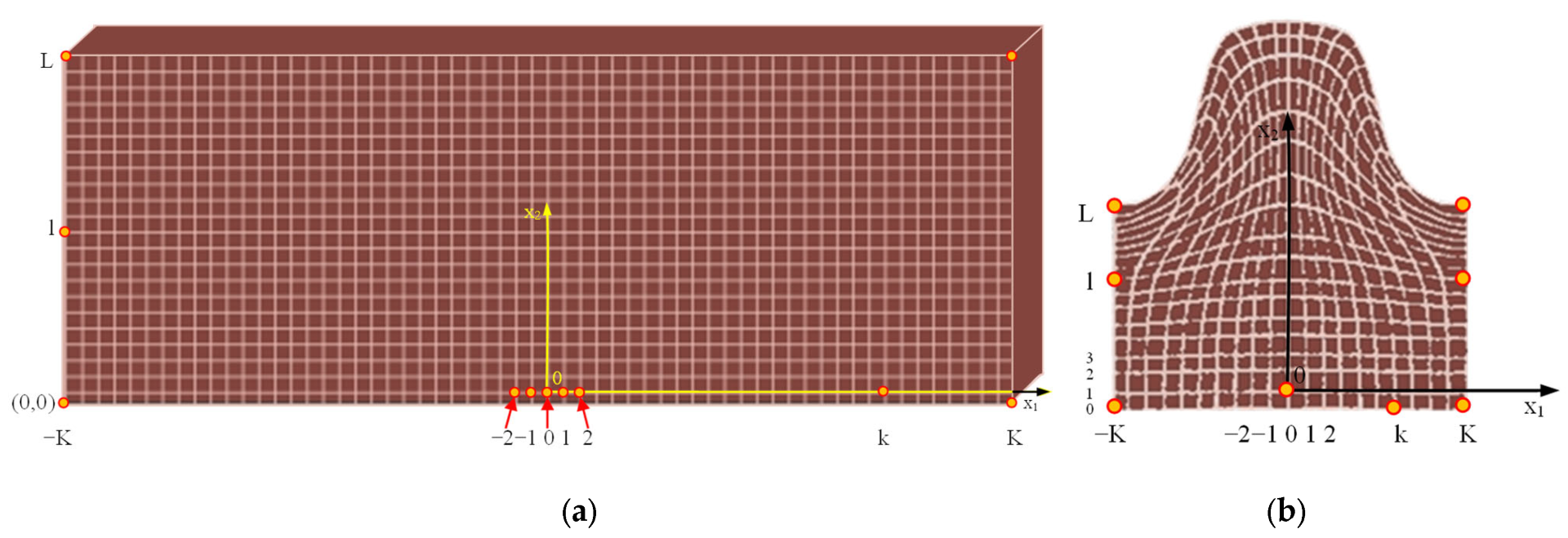
Figure 28.
Geometric dependencies in the deformation zone during thread rolling: (a) continuous model, (b) discrete model.
Figure 28.
Geometric dependencies in the deformation zone during thread rolling: (a) continuous model, (b) discrete model.
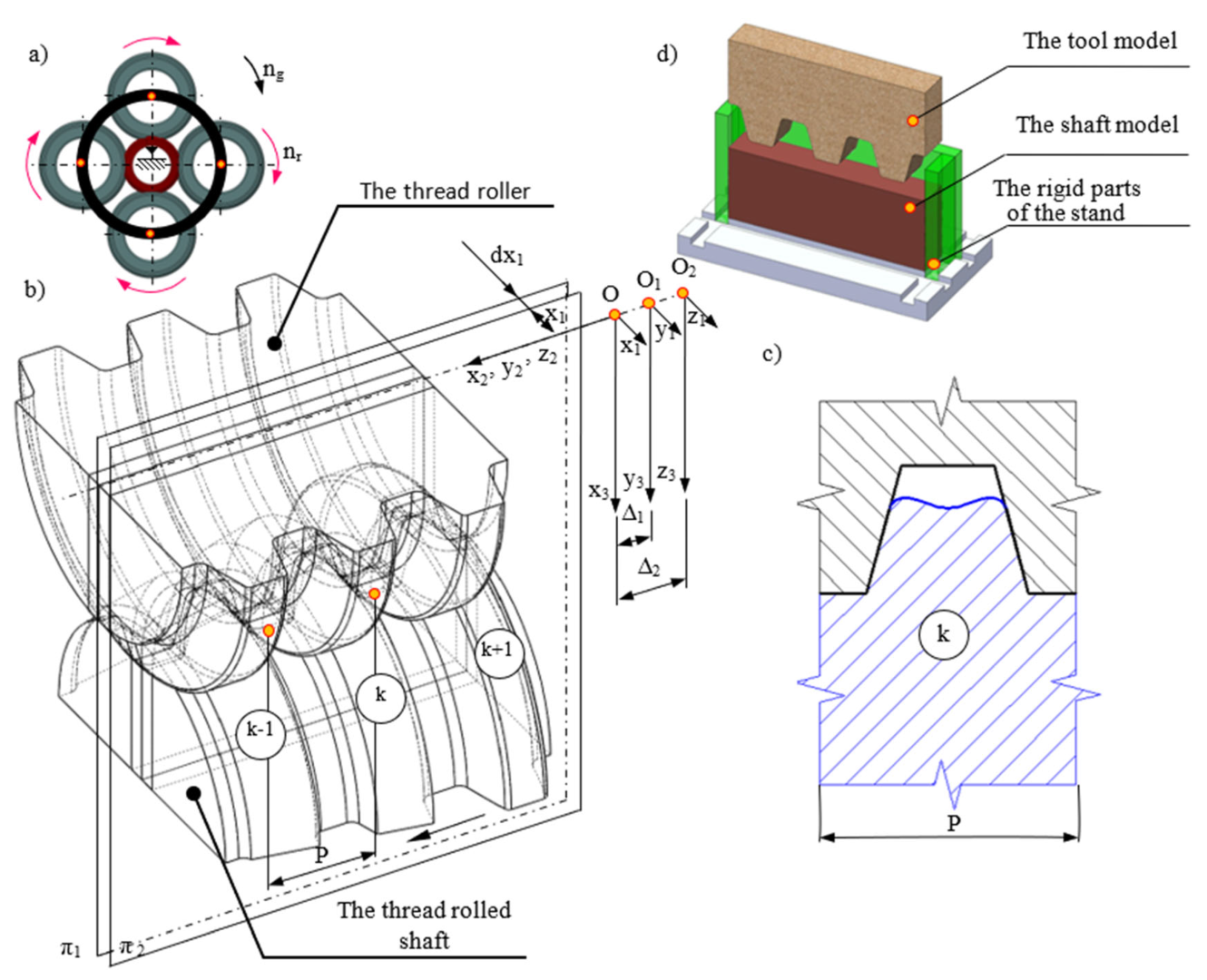
Figure 29.
Scheme of thread rolling process using four rolls by axial method (real object) (a); scheme of the division of the thread profile and roller rings into solids with a width of dx1 (b); cross-section of the k-th thread profile and the k-th roller ring with the plane (c); numerical simulation model implementation (d).
Figure 29.
Scheme of thread rolling process using four rolls by axial method (real object) (a); scheme of the division of the thread profile and roller rings into solids with a width of dx1 (b); cross-section of the k-th thread profile and the k-th roller ring with the plane (c); numerical simulation model implementation (d).
Figure 30.
Comparison of the material characteristics of plasticine with the characteristics of C45 steel.
Figure 30.
Comparison of the material characteristics of plasticine with the characteristics of C45 steel.
Figure 31.
An apparatus for forming the profile of a trapezoidal thread in a flat deformation state (a) and a sample for model investigations (b).
Figure 31.
An apparatus for forming the profile of a trapezoidal thread in a flat deformation state (a) and a sample for model investigations (b).
Figure 32.
View of the sample with a square mesh (a) and view of the sample with a deformed mesh after shaping the trapezoidal outline (b).
Figure 32.
View of the sample with a square mesh (a) and view of the sample with a deformed mesh after shaping the trapezoidal outline (b).
Figure 33.
View of the finite element mesh after the trapezoidal-thread-shaping process for different values of the friction coefficient: (a)— (b)— (c)—
Figure 33.
View of the finite element mesh after the trapezoidal-thread-shaping process for different values of the friction coefficient: (a)— (b)— (c)—
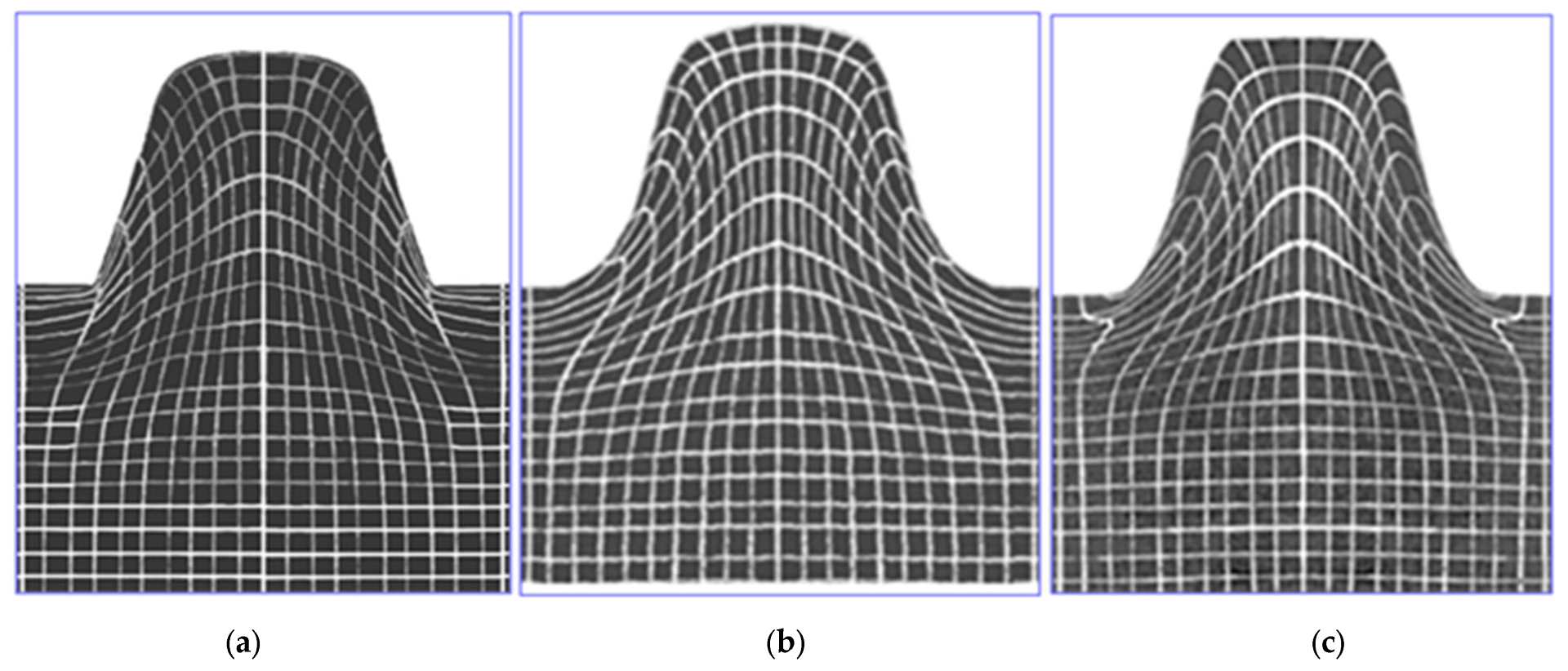
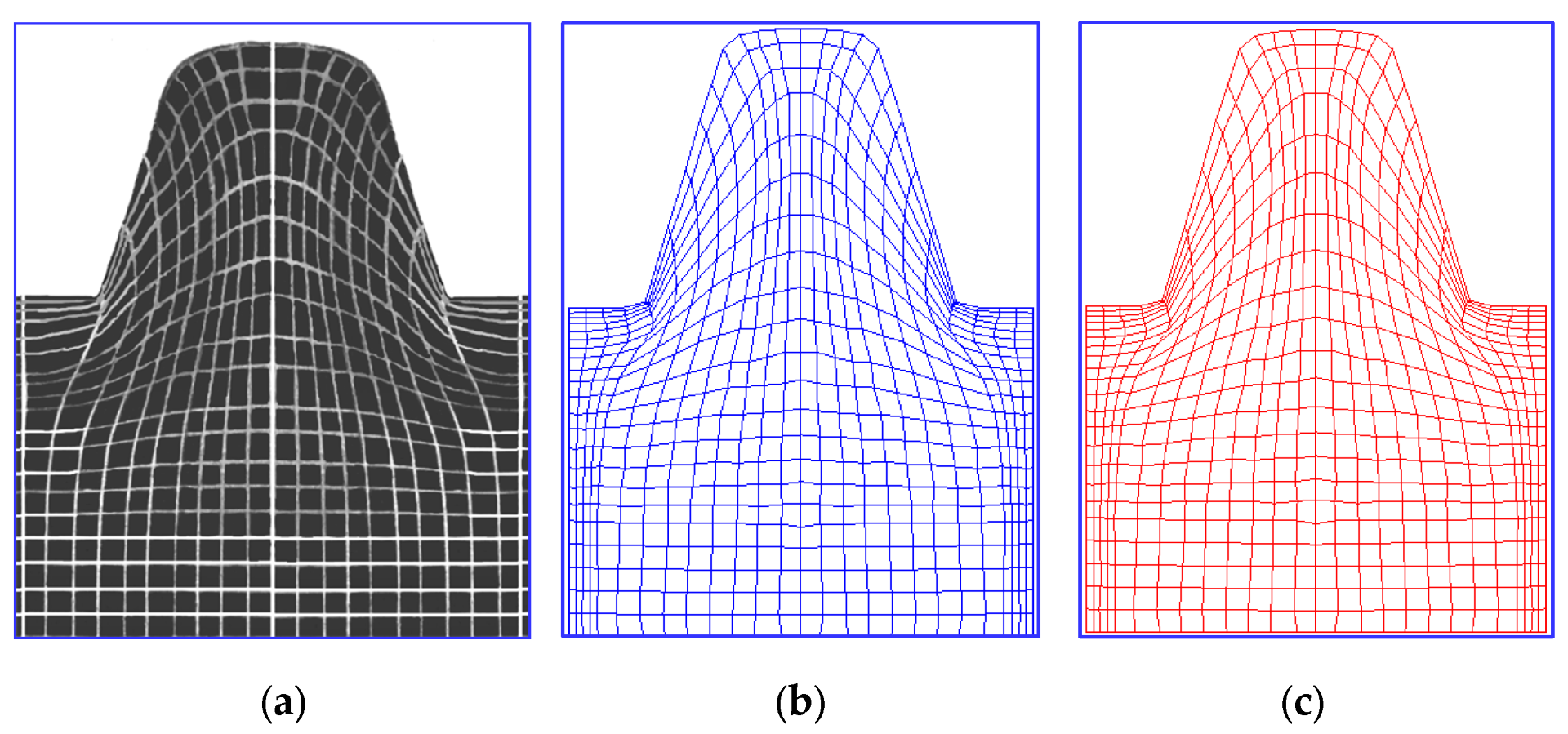
Figure 34.
View of exemplary finite element meshes after shaping a trapezoidal thread for the friction coefficient : (a) after model investigation, (b) after numerical simulation according to the first methodology, (c) after numerical simulation according to the second methodology.
Figure 34.
View of exemplary finite element meshes after shaping a trapezoidal thread for the friction coefficient : (a) after model investigation, (b) after numerical simulation according to the first methodology, (c) after numerical simulation according to the second methodology.
Figure 35.
View of the mesh deformation for different values of the shape factor SF.
Figure 35.
View of the mesh deformation for different values of the shape factor SF.
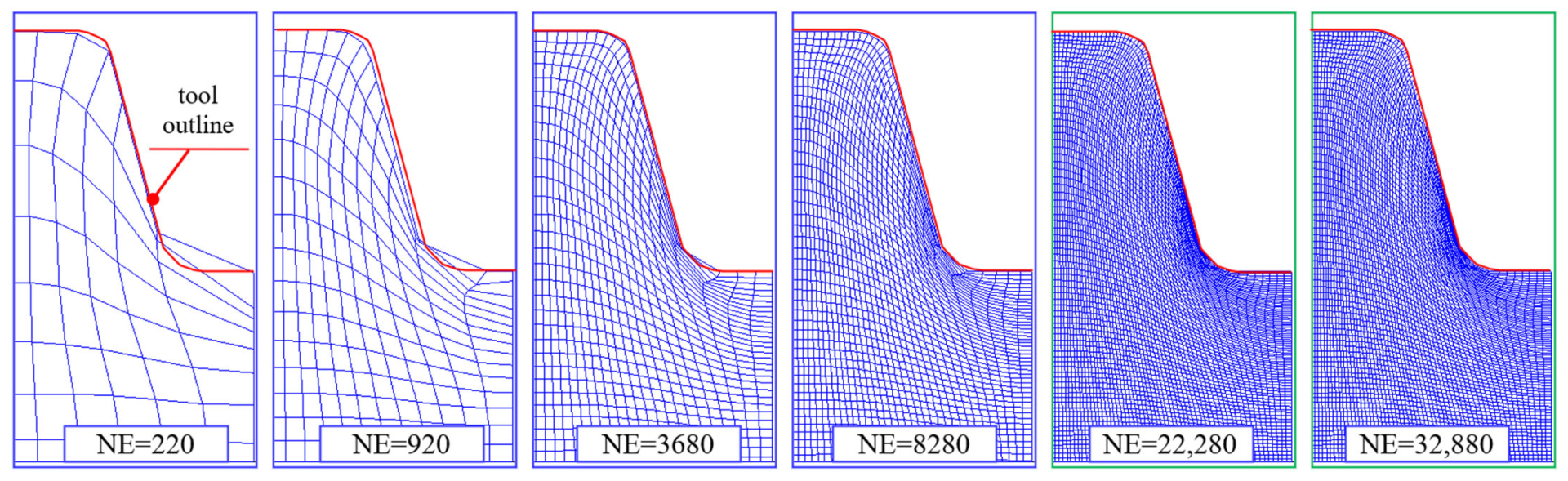
Figure 36.
View of the curvature of the finite element mesh (FEM) for a different element number (NE), for the shape factor of finite elements SF = 1.
Figure 36.
View of the curvature of the finite element mesh (FEM) for a different element number (NE), for the shape factor of finite elements SF = 1.
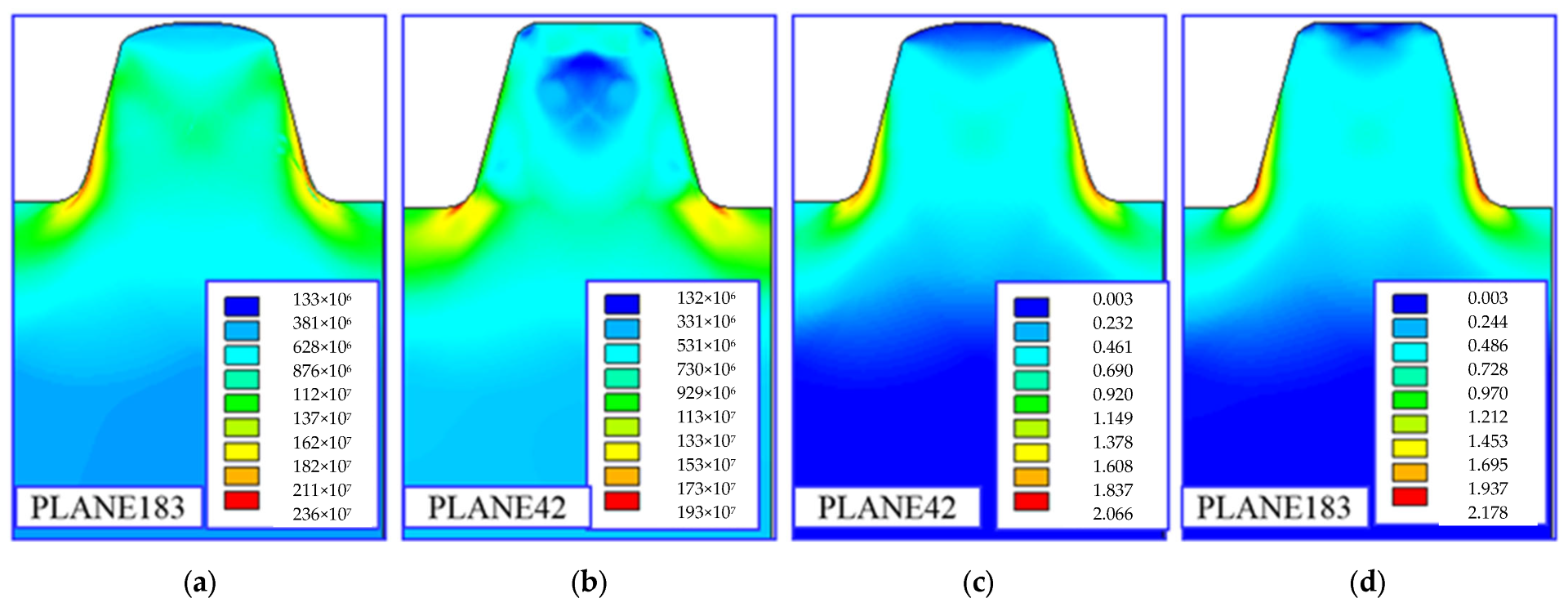
Figure 37.
Maps of effective stresses (a,b) and effective strains (c,d) for different types of finite elements—different than the shape element function (SEF).
Figure 37.
Maps of effective stresses (a,b) and effective strains (c,d) for different types of finite elements—different than the shape element function (SEF).
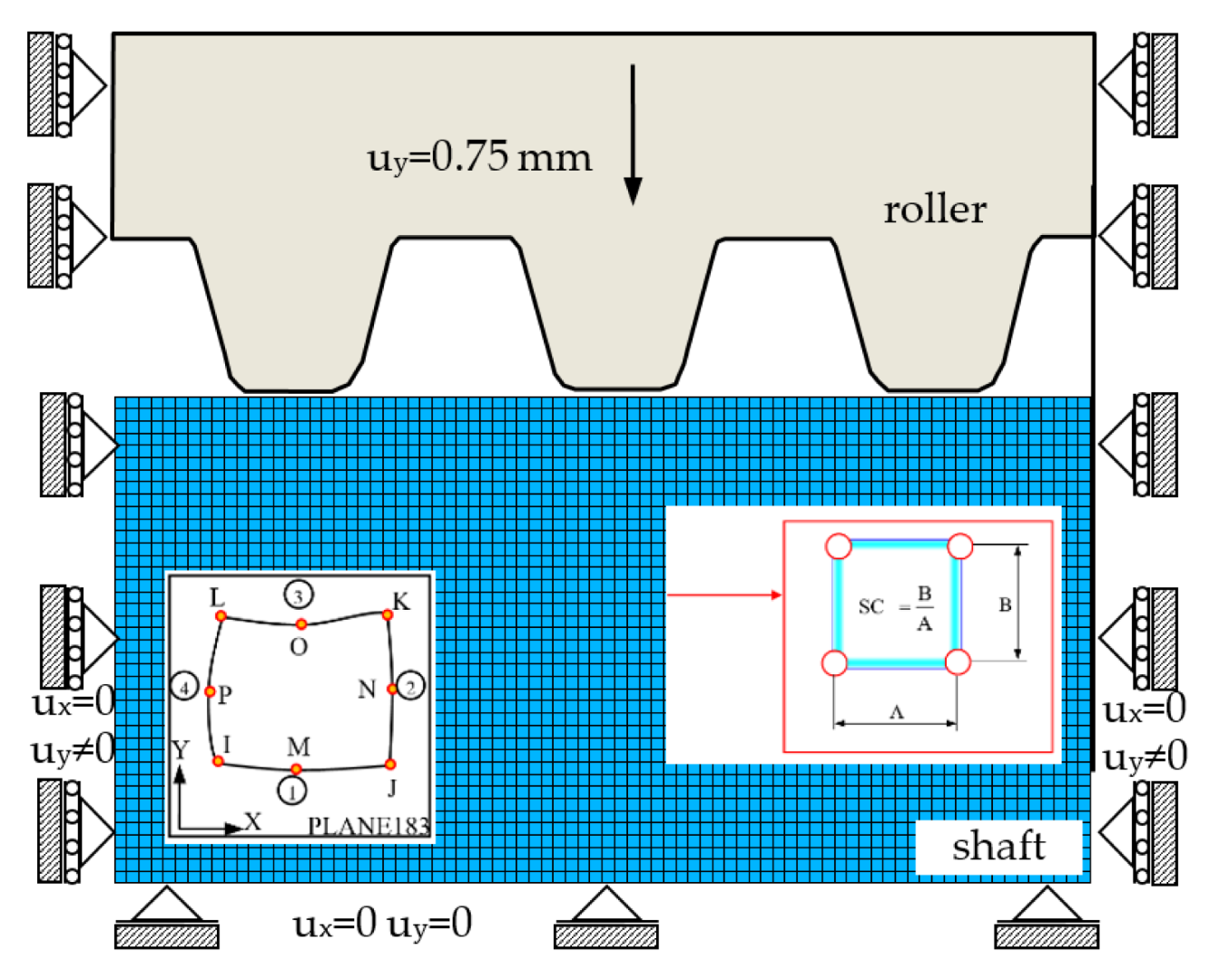
Figure 38.
Discrete model for trapezoidal thread rolling.
Figure 38.
Discrete model for trapezoidal thread rolling.
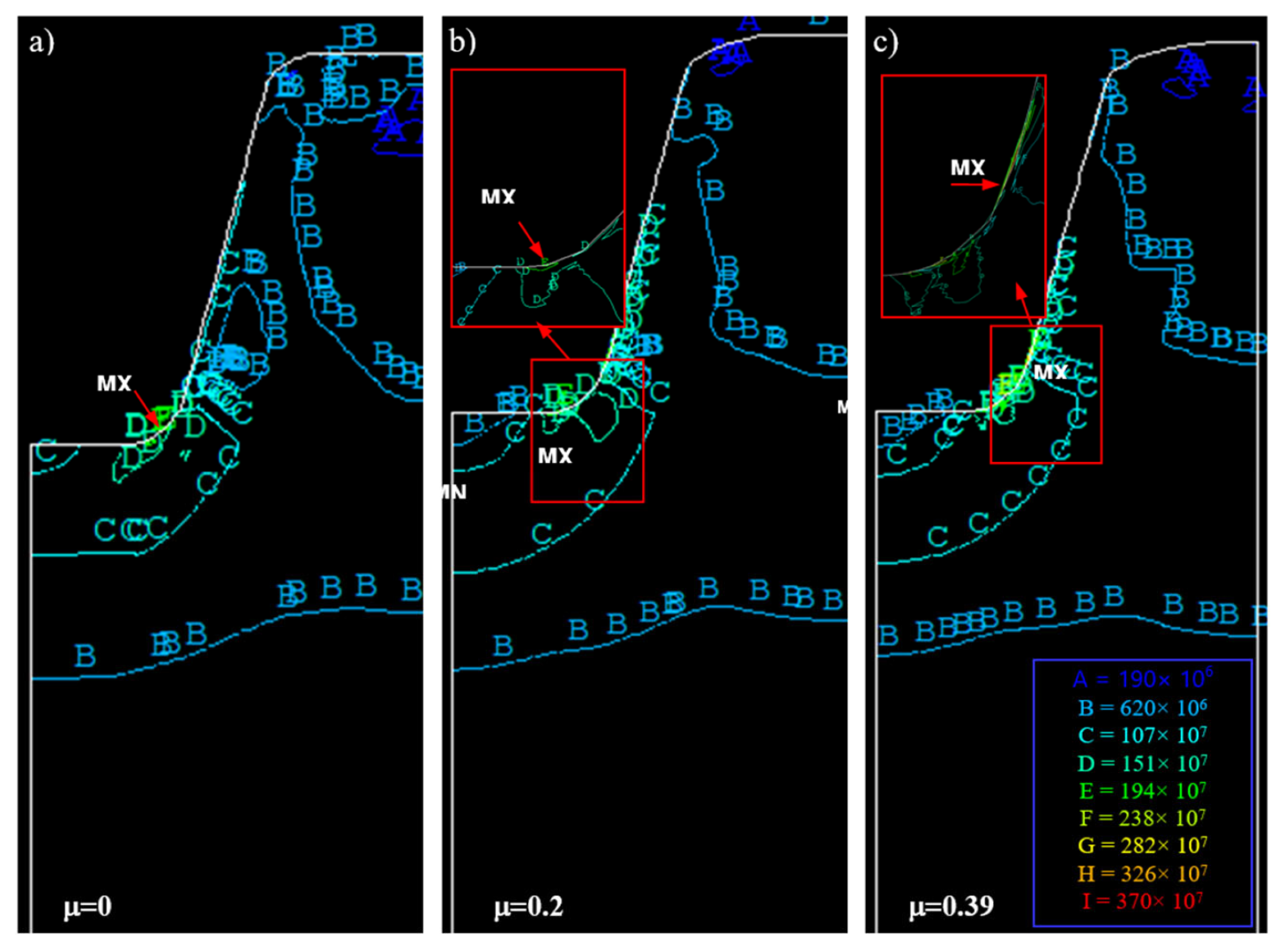
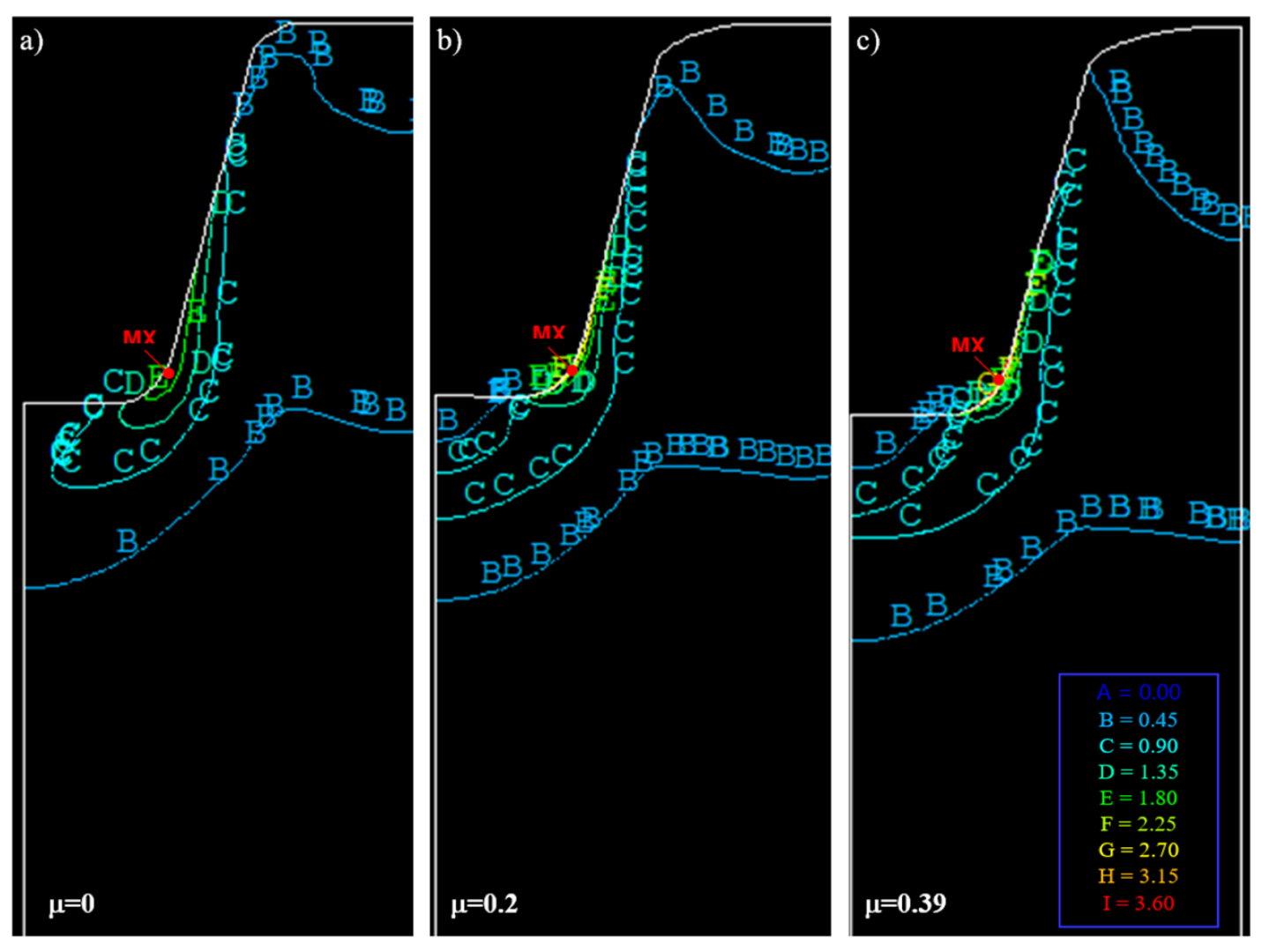
Figure 39.
Maps of effective stress for different values of the friction coefficient after a trapezoidal thread rolling, MPa. (a) µ = 0; (b) µ = 0.2; (c) µ = 0.39.
Figure 39.
Maps of effective stress for different values of the friction coefficient after a trapezoidal thread rolling, MPa. (a) µ = 0; (b) µ = 0.2; (c) µ = 0.39.
Figure 40.
Maps of effective strain for different values of the friction coefficient after a trapezoidal thread rolling. (a) µ = 0; (b) µ = 0.2; (c) µ = 0.39.
Figure 40.
Maps of effective strain for different values of the friction coefficient after a trapezoidal thread rolling. (a) µ = 0; (b) µ = 0.2; (c) µ = 0.39.
Table 1.
Chemical composition of C45 (1.0503) steel.
Table 1.
Chemical composition of C45 (1.0503) steel.
| | Chemical Composition [% Weight] | |
|---|
| | C [%] | Si [%] | Mn [%] | P [%] | S [%] | Cr [%] | Ni [%] | Mo [%] | Cu [%] | Co [%] |
|---|
| Measured | 0.44 | 0.19 | 0.63 | 0.007 | 0.009 | 0.07 | 0.06 | – | – | 0.01 |
According to the
EN 10083—2 norm | 0.42–0.5 | 0.1–0.4 | 0.5–0.8 | max 0.04 | max 0.04 | max 0.03 | max 0.03 | max 0.1 | max 0.03 | max 0.03 |
Table 2.
Chemical composition of Cu-ETP cooper according to the EN 1652/EN 13601/EN 1172 norms.
Table 2.
Chemical composition of Cu-ETP cooper according to the EN 1652/EN 13601/EN 1172 norms.
| Chemical Composition [% Weight] |
|---|
| Ni [%] | Sn [%] | Sb [%] | Pb [%] | Zn [%] | Fe [%] | As [%] | Bi [%] | Cu [%] |
|---|
| max 0.002 | max 0.002 | max 0.002 | max 0.005 | max 0.003 | max 0.005 | max 0.002 | max 0.001 | min 99.9 |
Table 3.
The two-level experiment plan.
Table 3.
The two-level experiment plan.
| Level Plan | Investigated Factors |
|---|
| Real Values | Coded Values |
|---|
| | | |
|---|
| 1 | | 0 | −1 | −1 |
| 2 | | 0 | +1 | −1 |
| 3 | | | −1 | +1 |
| 4 | | | +1 | +1 |
Table 4.
C45 steel material parameters used in the numerical simulation.
Table 4.
C45 steel material parameters used in the numerical simulation.
| Equations (8)–(10) | ρ [kg·m−3] | E [GPa] | ν [–] | K [MPa] | φ0 [–] | φf [–] (εf [–]) | n [–] | n1 [–] | n2 [–] |
| 7800 | 207 | 0.28 | 980 | 0.049 | 1.52 (2.88) | 0.2322 | 0.1222 | 0.39 |
| n3 [–] | a [–] | b [–] | c [–] | d [–] | e [–] | f [–] | g [–] | h [–] |
| 0.6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0.02 |
| Equation (26) | ρ [kg·m−3] | E [GPa] | Re [MPa] | ν [–] | C [s-1] | P [–] | φf [–] (εf [–]) | e [–] | f [–] |
| 7800 | 207 | 440 | 0.28 | 200 | 18 | 1.52 (2.88) | 0 | 0 |
| n [–] | n1 [–] | n2 [–] | n3 [–] | β [–] | a [–] | b [–] | c [–] | d [–] |
| 1 | m | 1 | 1 | 1 | 0 | 0 | | 0 |
| g [–] | h [–] | m [–] | | | | | | |
| 1/C | 0 | 0.055 | | | | | | |
Table 5.
The fracture stress value for various methods of calculation
Table 5.
The fracture stress value for various methods of calculation
| Method of Calculation | σe, MPa |
|---|
| Semi-empirical method | 1050 |
| Davidenkov N.N. | 1100 |
| Spiridonova N.E. and Siebel E. | 1090 |
| Szczepiński W. | 1080 |
Table 6.
An effective discrete model for trapezoidal thread.
Table 6.
An effective discrete model for trapezoidal thread.
| Name | Value |
|---|
| SF (shape function) | 1 |
| NE (number of finite elements) | 32,280 |
| NN (number of nodes) | 99,433 |
| DOF (number of degrees of freedom) | 198,866 |
| Type of finite element | PLANE183 |
Table 7.
Simulation parameters.
Table 7.
Simulation parameters.
| Simulation Parameters | Value |
|---|
| Process temperature | 20 °C |
| Type of thread | Tr12×3 |
| Thread-rolling depth | mm |
| Shaft Material | C45 |
| Roller (tool material) | a perfectly rigid body, E→∞ |
| Type of Finite Elements for shaft and roller | PLANE 183 |
| Type of Finite Elements for contact | TARGE169 and CONTA172 |
| Variety of the friction coefficient | , and |
| Shape coefficient | |
Table 8.
The maximum value of obtained numerical results for various values of the friction coefficient.
Table 8.
The maximum value of obtained numerical results for various values of the friction coefficient.
| Friction Coefficient | | |
|---|
| 0 | 2390 | 2.058 |
| 0.2 | 2410 | 2.803 |
| 0.39 | 3610 | 3.514 |