A Review on Controlling Grain Boundary Character Distribution during Twinning-Related Grain Boundary Engineering of Face-Centered Cubic Materials
Abstract
1. Introduction
2. Twinning-Related Grain Boundary Engineering
2.1. Coincident Site Lattice Model
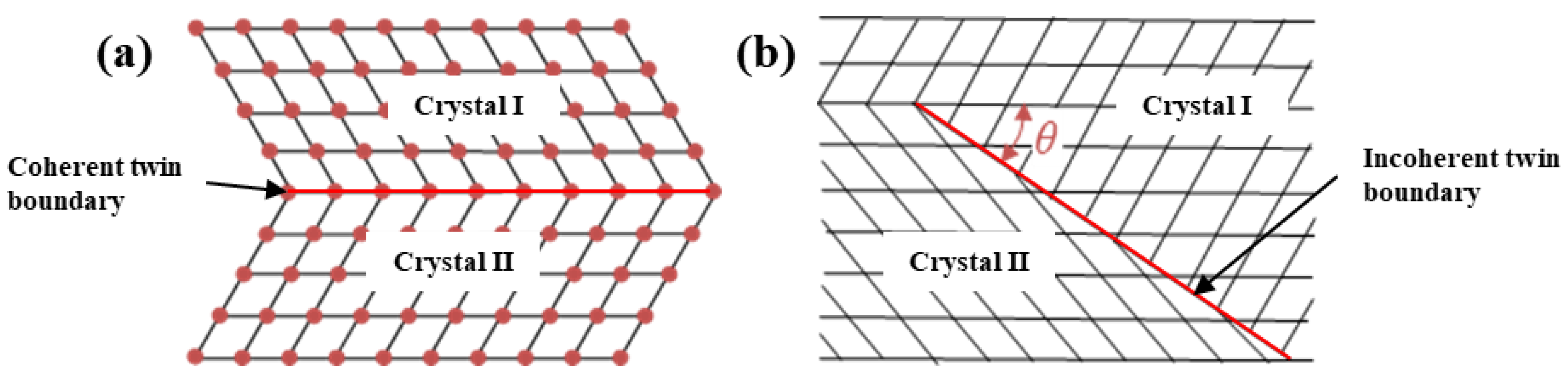
2.2. Morphology of Annealing Twin
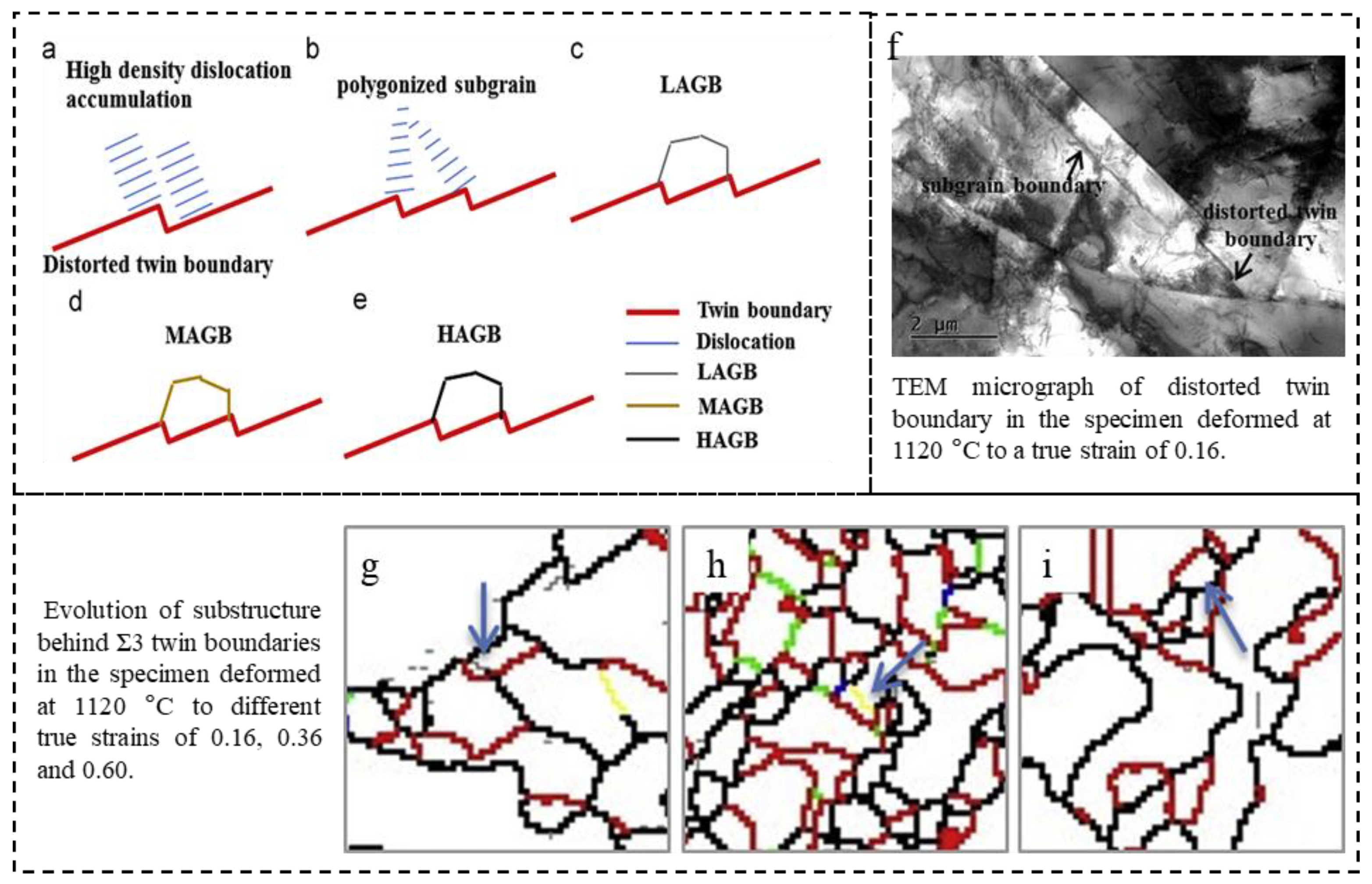
2.3. Microscopic Mechanisms for Optimizing Grain Boundary Character Distribution
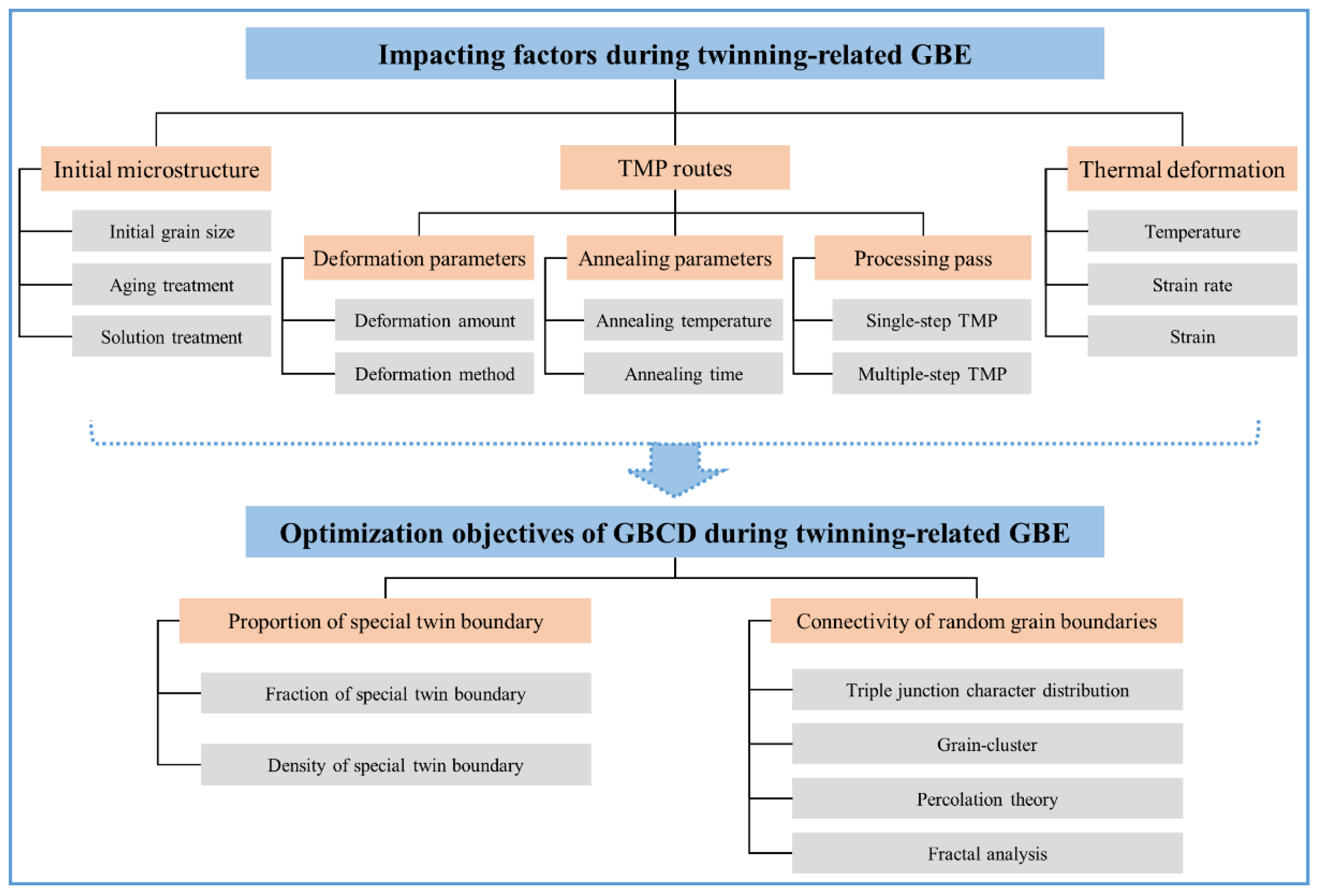
2.4. Optimization Objectives of Grain Boundary Character Distribution
2.4.1. Proportion of Special Twin Boundaries
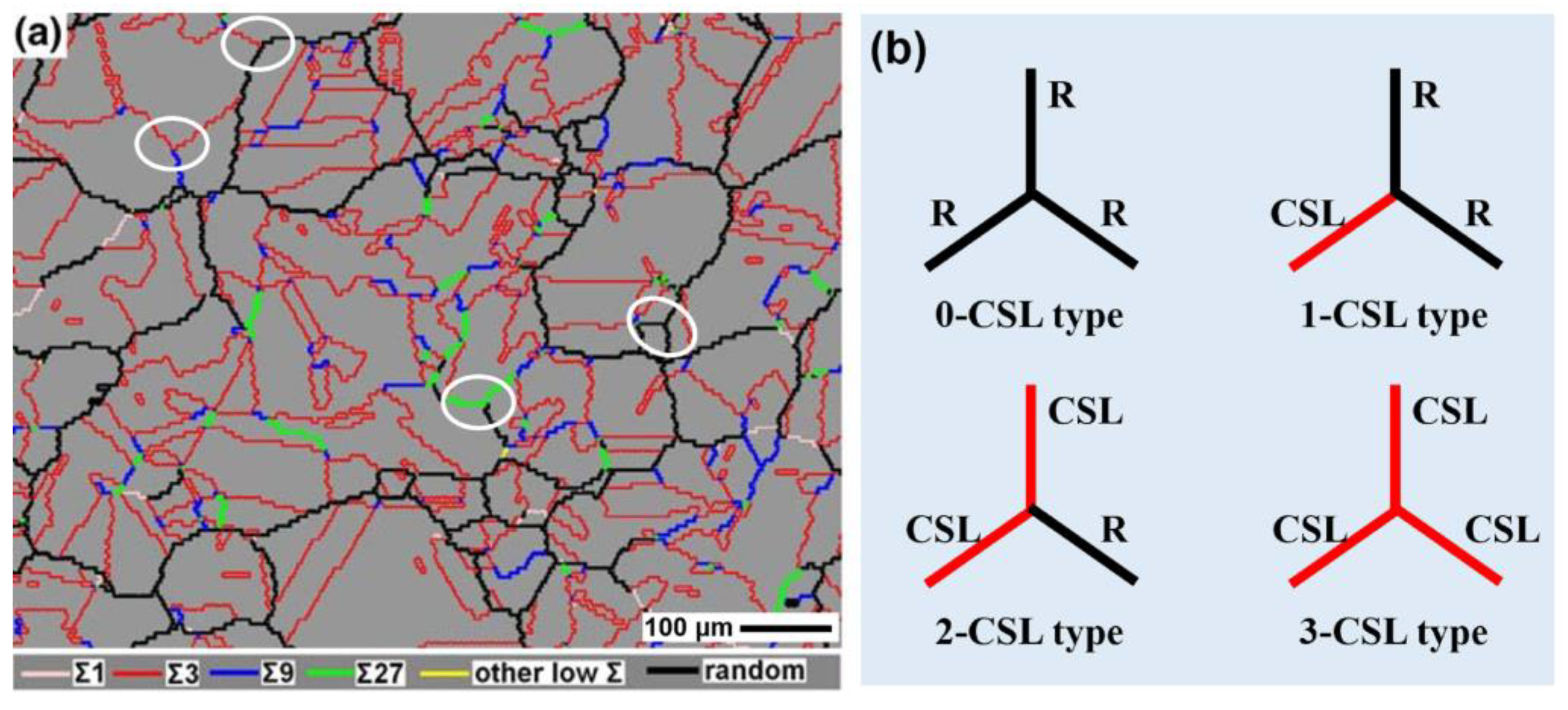
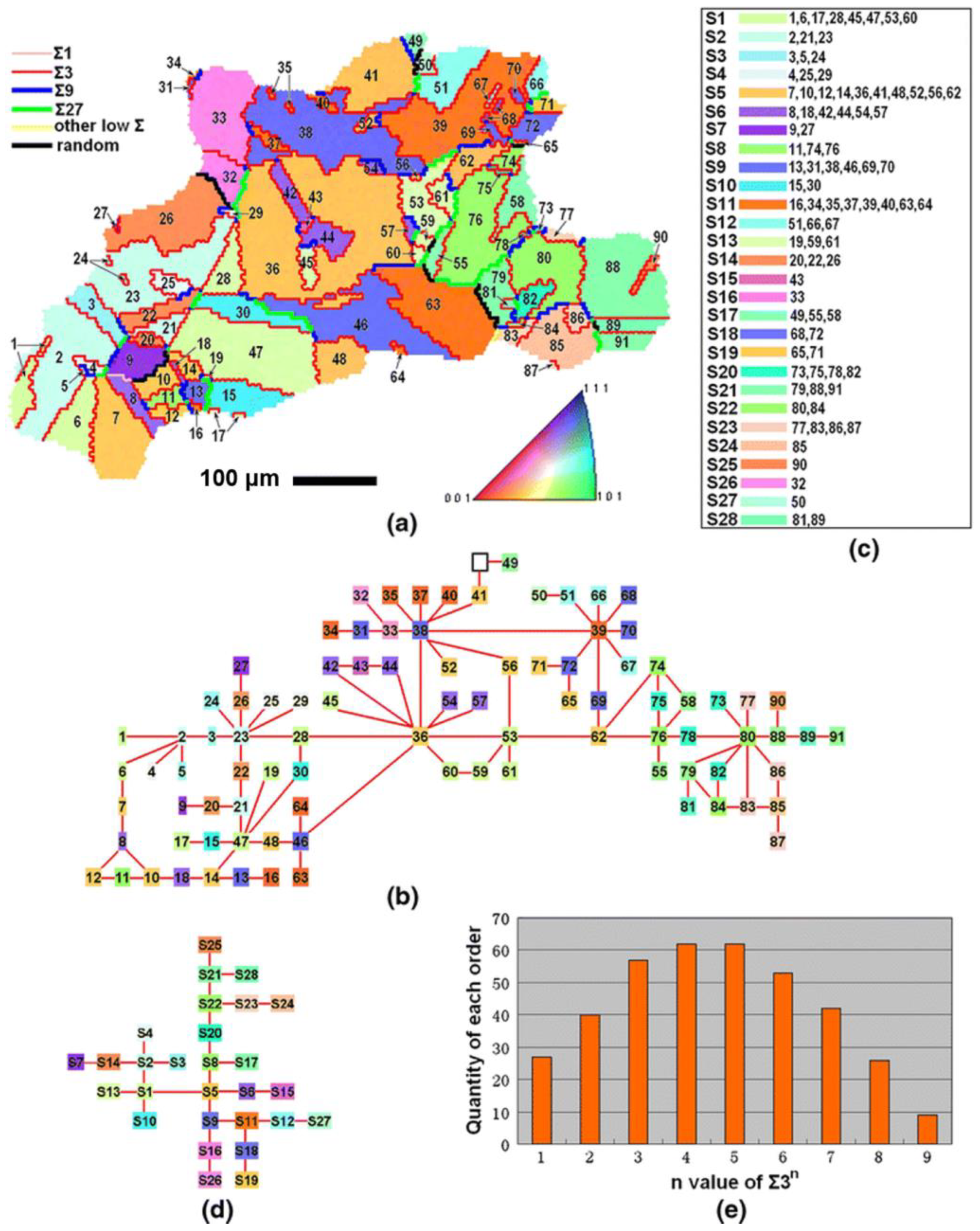
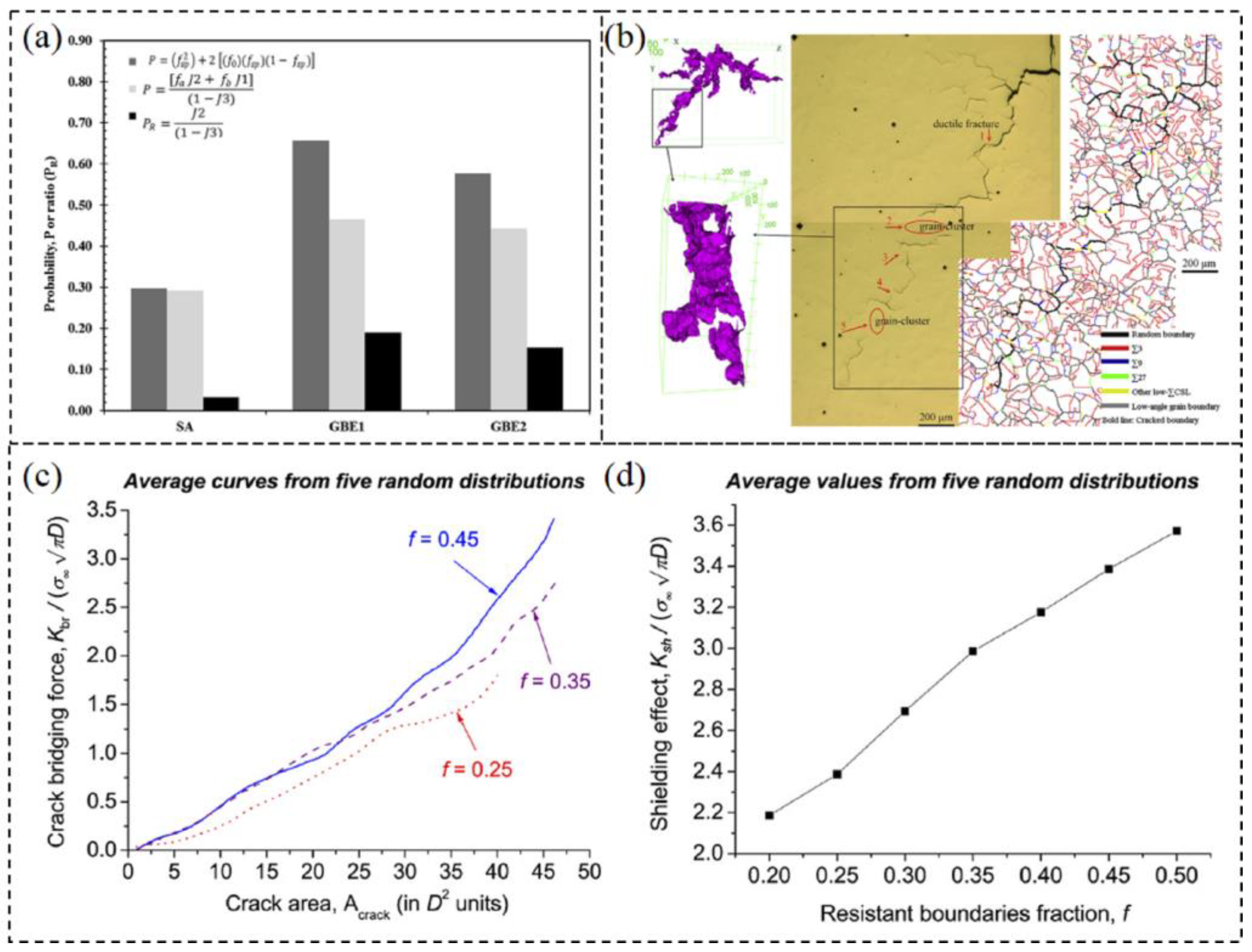
2.4.2. Connectivity of Random Boundary Network
- (a)
- Triple junction character distribution
- (b)
- Grain cluster
- (c)
- Percolation theory
- (d)
- Fractal analysis
3. Microstructure Control for Optimizing Grain Boundary Character Distribution
3.1. Influence of Initial Microstructure
3.2. Influence of Thermo-Mechanical Processing Routes
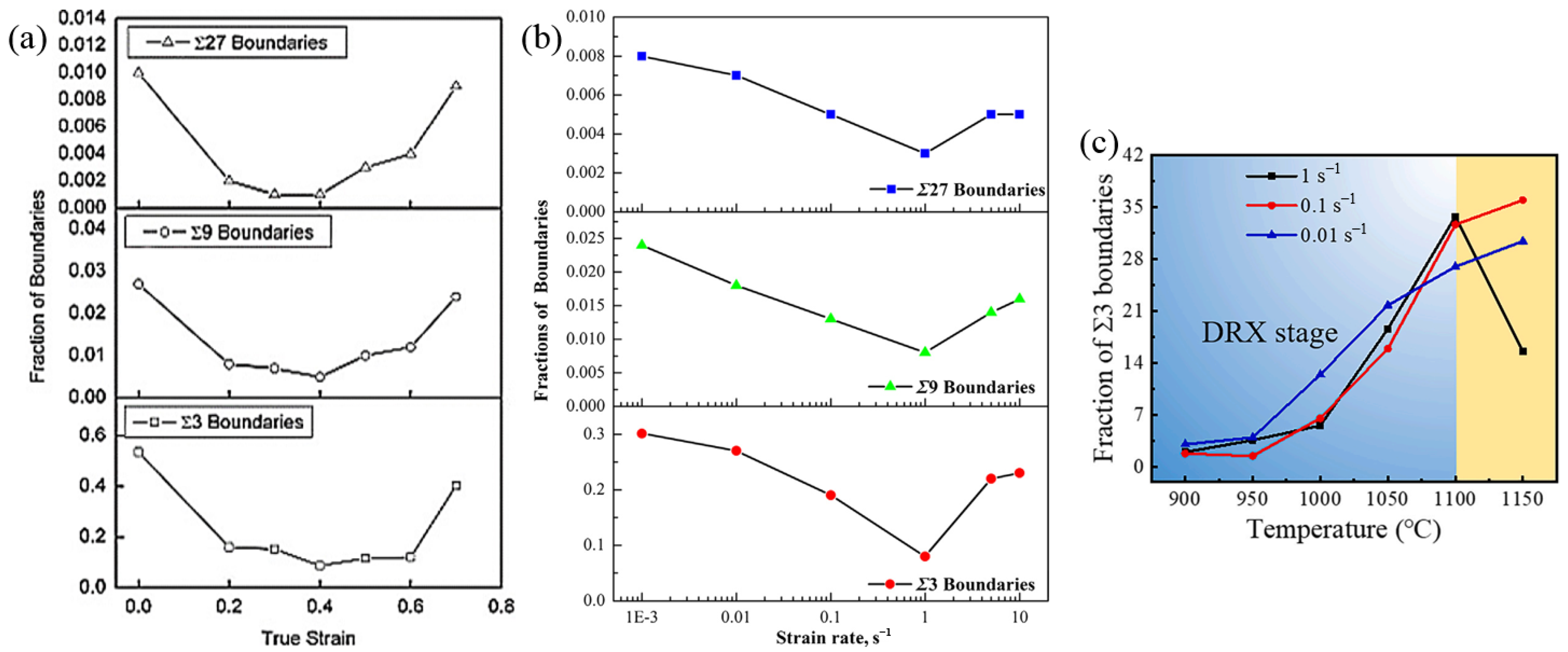
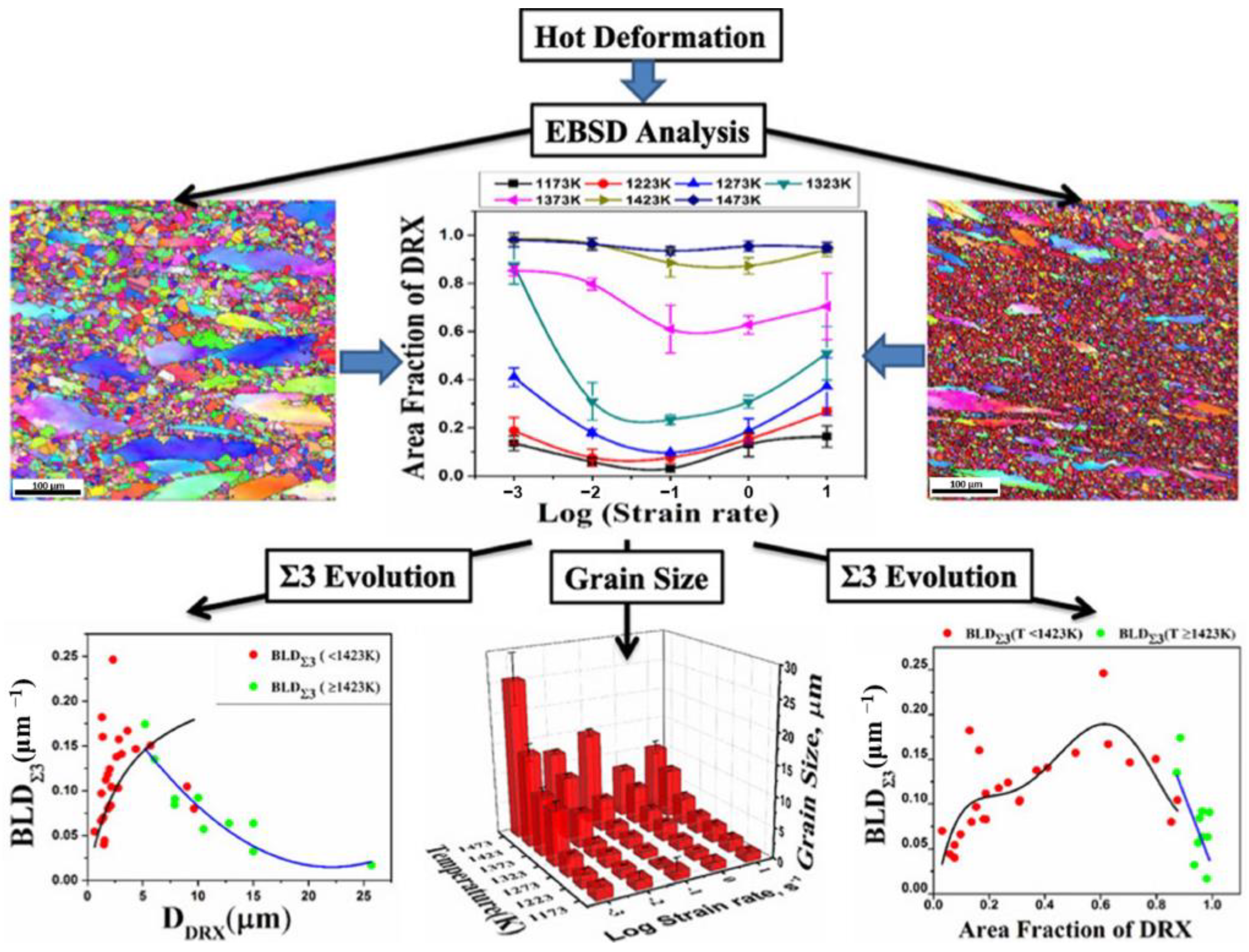
3.3. Influence of Thermal Deformation Parameters
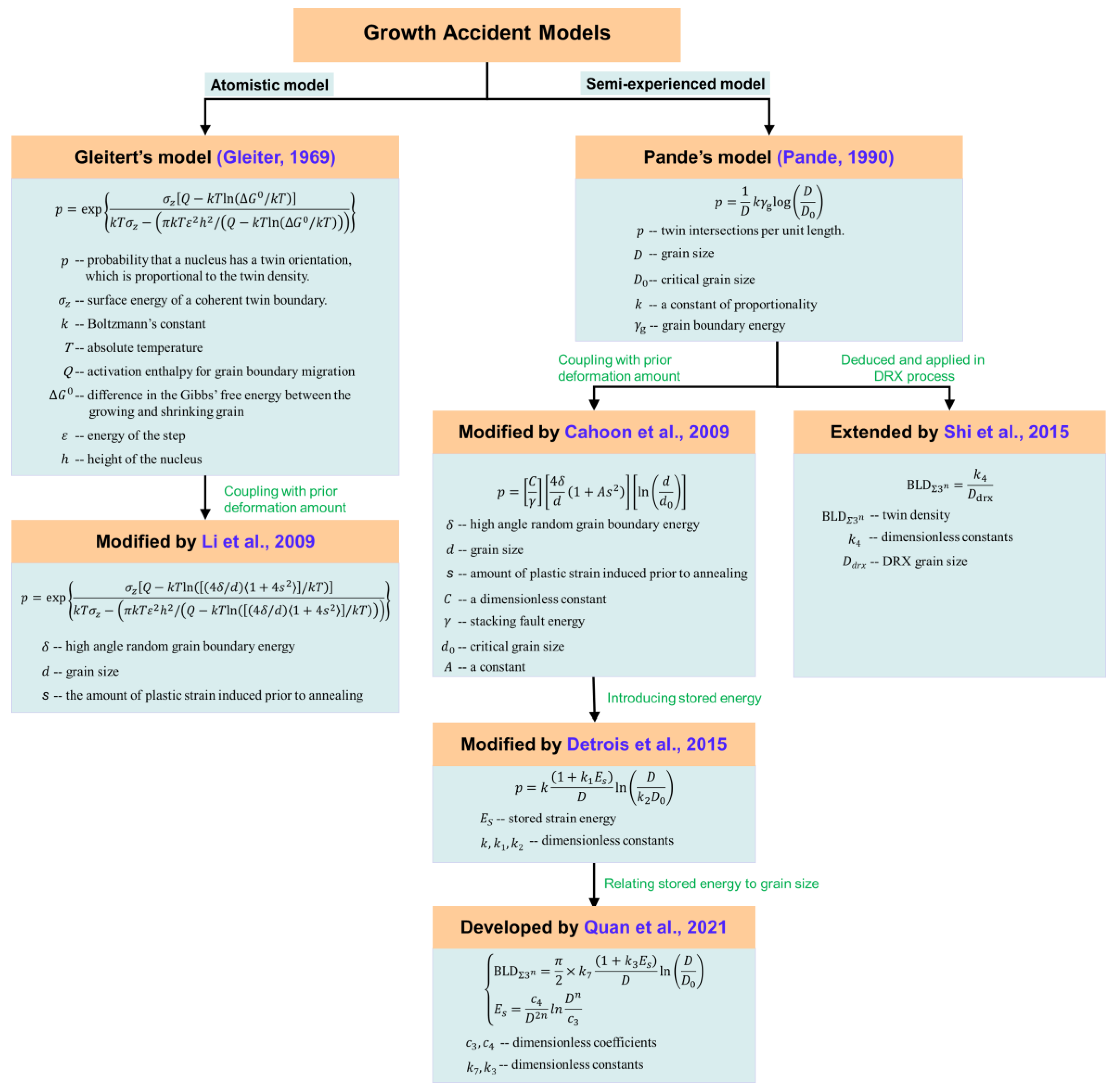
4. Development of Twinning-Related Kinetics Models
5. Application of Twinning-Related Grain Boundary Engineering
5.1. Improvement of Mechanical Properties
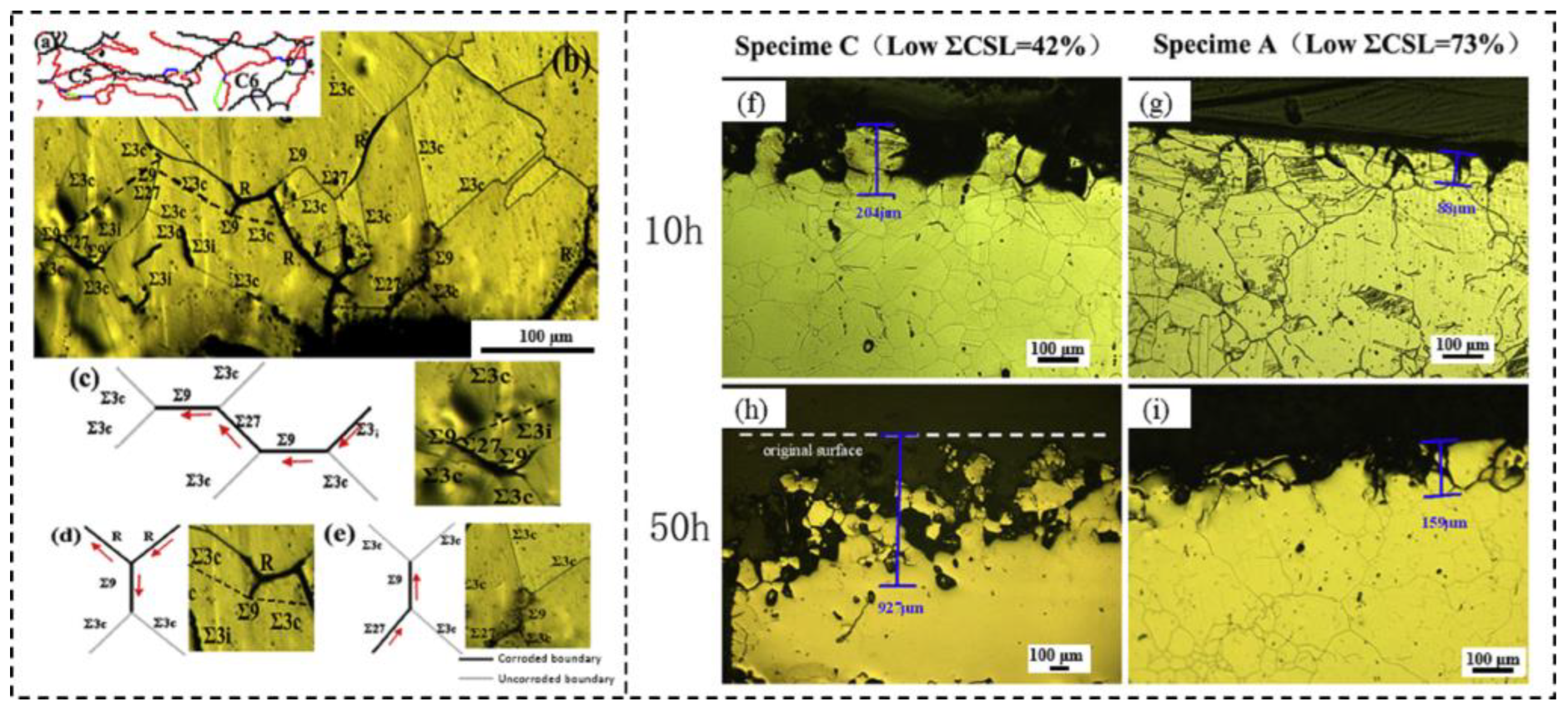
5.2. Improvement of Corrosion Resistance
6. Conclusions and Future Prospects
- (1)
- This review introduces the fundamentals of twinning-related GBE, encompassing the definition of special boundaries, the morphology of the annealing twin, the microscopic mechanisms required to optimize GBCD, and the optimization objectives of GBCD. The nature of optimizing GBCD in the twinning-related GBE of FCC materials is to improve the proportion of special twin boundaries and sufficiently interrupt the connectivity of the random boundary network.
- (2)
- The TMP treatment is the primary processing route used to achieve GBE. The initial microstructures, amount of deformation, annealing temperature and time, and processing pass are critical processing parameters that significantly impact the formation of special twin boundaries. Determining the optimal combination of TMP parameters still relies on trial-and-error or experience methods, and the control of GBCD through adjusting TMP parameters remains a challenging task that requires further attention.
- (3)
- This review addresses the influence of the deformation parameters on the evolution of special twin boundaries during the thermal deformation process of nickel-based alloys. Microstructural evolution mechanisms are extremely intricate, and the proportion of special twin boundaries exhibits a non-linear relationship with the deformation parameters and microstructural characteristics. To achieve the desired GBCD, the thermal deformation process of alloys can be designed within a favorable processing parameter window that yields a finer grain size and a higher proportion of special twin boundaries.
- (4)
- This review presents the development process of twinning-related kinetics models associated with processing parameters or microstructure characteristics. However, there is no universal model that can describe the evolution of twin density in all cases. The twinning-related kinetics model will be further developed in future studies.
- (5)
- This review provides some applications of twinning-related GBE in terms of enhancing the mechanical properties and corrosion resistance of FCC materials. The results suggest that the microstructures with a high proportion of special twin boundaries and the disrupted connectivity of the random boundary network contribute significantly to enhancing the mechanical properties and corrosion resistance of the materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Watanabe, T. An approach to grain boundary design of strong and ductile polycrystals. Res. Mech. 1984, 11, 47–84. [Google Scholar]
- Kobayashi, S.; Kobayashi, R.; Watanabe, T. Control of grain boundary connectivity based on fractal analysis for improvement of intergranular corrosion resistance in SUS316L austenitic stainless steel. Acta Mater. 2016, 102, 397–405. [Google Scholar] [CrossRef]
- Shimada, M.; Kokawa, H.; Wang, Z.J.; Sato, Y.S.; Karibe, I. Optimization of grain boundary character distribution for intergranular corrosion resistant 304 stainless steel by twin-induced grain boundary engineering. Acta Mater. 2002, 50, 2331–2341. [Google Scholar]
- Chen, C.-H.; Lai, Y.-C.; Chuang, T.-H. Grain growth and twin formation in a Ag-4Pd alloy ribbon after annealing treatments. J. Alloy. Compd. 2021, 863, 158619. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Wang, J.-J.; Gao, Y.-B.; Wang, X.-M.; Chen, J.-J.; Ding, Y.-T. Improving intergranular corrosion resistance in Inconel 625 via grain boundary character distribution optimization. J. Wuhan Univ. Technol. 2021, 36, 911–921. [Google Scholar]
- Wang, X.-M.; Ding, Y.-T.; Gao, Y.-B.; Ma, Y.-J.; Chen, J.-J.; Gan, B. Effect of grain refinement and twin structure on the strength and ductility of Inconel 625 alloy. Mater. Sci. Eng. A 2021, 823, 141739. [Google Scholar]
- Guan, X.-J.; Shi, F.; Ji, H.-M.; Li, X.-W. Gain boundary character distribution optimization of Cu-16at.%Al alloy by thermomechanical process: Critical role of deformation microstructure. Mater. Sci. Eng. A 2019, 765, 138299. [Google Scholar]
- Randle, V. Grain boundary engineering: An overview after 25 years. Mater. Sci. Technol. 2010, 26, 253–261. [Google Scholar] [CrossRef]
- Palumbo, G.; Lehockey, E.M.; Lin, P. Applications for grain boundary engineered materials. JOM 1998, 50, 40–43. [Google Scholar] [CrossRef]
- Guan, X.-J.; Shi, F.; Ji, H.-M.; Li, X.-W. A possibility to synchronously improve the high-temperature strength and ductility in face-centered cubic metals through grain boundary engineering. Scr. Mater. 2020, 187, 216–220. [Google Scholar]
- Guan, X.-J.; Jia, Z.-P.; Varkani, M.A.N.; Li, X.-W. Effect of grain boundary engineering on the work hardening behavior of Al6XN super-austenitic stainless steel. Acta Met. Sin. (Engl. Lett.) 2023, 36, 681–693. [Google Scholar]
- Lim, L.C.; Watanabe, T. Fracture toughness and brittle-ductile transition controlled by grain boundary character distribution (GBCD) in polycrystals. Acta Met. Mater. 1990, 38, 2507–2516. [Google Scholar] [CrossRef]
- Kobayashi, S.; Maruyama, T.; Tsurekawa, S.; Watanabe, T. Grain boundary engineering based on fractal analysis for control of segregation-induced intergranular brittle fracture in polycrystalline nickel. Acta Mater. 2012, 60, 6200–6212. [Google Scholar] [CrossRef]
- Athreya, C.N.; Deepak, K.; Kim, D.-I.; Boer, B.; Mandal, S.; Sarma, V.S. Role of grain boundary engineered microstructure on high temperature steam oxidation behaviour of Ni based superalloy alloy 617. J. Alloy. Compd. 2019, 778, 224–233. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Y.-J.; Yang, H.-S.; Su, Y.-J.; Qiao, L.-J. Study of the relationship between intergranular stress corrosion cracking and grain boundary characteristics in brass. Electrochem. Commun. 2021, 131, 107124. [Google Scholar]
- Xia, S.; Hui, L.; Liu, T.-G.; Bang, X.-Z. Appling grain boundary engineering to Alloy 690 tube for enhancing intergranular corrosion resistance. J. Nucl. Mater. 2011, 416, 303–310. [Google Scholar] [CrossRef]
- Lin, P.; Palumbo, G.; Erb, U.; Aust, K.T. Influence of grain-boundary-character-distribution on sensitization and intergranular corrosion of alloy-600. Scr. Met. Mater. 1995, 33, 1387–1392. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Prithiv, T.S.; Mandal, S. Through-thickness microstructural evolution during grain boundary engineering type thermomechanical processing and its implication on sensitization behavior in austenitic stainless steel. Mater. Charact. 2017, 134, 134–142. [Google Scholar]
- Tomozawa, M.; Miyahara, Y.; Kako, K. Solute segregation on Σ3 and random grain boundaries in type 316L stainless steel. Mater. Sci. Eng. A 2013, 578, 167–173. [Google Scholar] [CrossRef]
- Peng, Z.C.; Zou, J.W.; Wang, Y.; Zhou, L.; Tang, Y. Effects of solution temperatures on creep resistance in a powder metallurgy nickel-based superalloy. Mater. Today Commun. 2021, 28, 102573. [Google Scholar] [CrossRef]
- Gleiter, H. The formation of annealing twins. Acta Met. 1969, 17, 1421–1428. [Google Scholar] [CrossRef]
- Pande, C.S.; Imam, M.A.; Rath, B.B. Study of annealing twins in fcc metals and alloys. Met. Trans. A 1990, 21, 2891–2896. [Google Scholar] [CrossRef]
- Burgers, W.G. Crystal growth in the solid state (Recrystallization). Physica 1949, 15, 92–106. [Google Scholar]
- Nielsen, J.P. The origin of annealing twins. Acta Met. 1967, 15, 1083–1085. [Google Scholar] [CrossRef]
- Burgers, W.G. ‘Stimulation crystals’ and twin-formation in recrystallized aluminium. Nature 1946, 157, 76–77. [Google Scholar] [CrossRef]
- Goodhew, P. Annealing twin formation by boundary dissociation. Met. Sci. 1979, 13, 108–112. [Google Scholar] [CrossRef]
- Kumar, M.; Schwartz, A.J.; King, W.E. Microstructural evolution during grain boundary engineering of low to medium stacking fault energy fcc materials. Acta Mater. 2002, 50, 2599–2612. [Google Scholar] [CrossRef]
- Meyers, M.A.; Murr, L.E. A model for the formation of annealing twins in F.C.C. metals and alloys. Acta Met. 1978, 26, 951–962. [Google Scholar]
- Mahajan, S.; Pande, C.S.; Imam, M.A.; Rath, B.B. Formation of annealing twins in f.c.c. crystals. Acta Mater. 1997, 45, 2633–2638. [Google Scholar] [CrossRef]
- Dash, S.; Brown, N. An investigation of the origin and growth of annealing twins. Acta Met. 1963, 11, 1067–1075. [Google Scholar] [CrossRef]
- Randle, V. Mechanism of twinning-induced grain boundary engineering in low stacking-fault energy materials. Acta Mater. 1999, 47, 4187–4196. [Google Scholar] [CrossRef]
- Wang, W.; Guo, H. Effects of thermo-mechanical iterations on the grain boundary character distribution of Pb–Ca–Sn–Al alloy. Mater. Sci. Eng. A 2007, 445, 155–162. [Google Scholar] [CrossRef]
- Feng, W.; Yang, S.; Yan, Y.-B. Dependence of grain boundary character distribution on the initial grain size of 304 austenitic stainless steel. Philos. Mag. 2017, 97, 1057–1070. [Google Scholar] [CrossRef]
- Feng, W.; Yang, S.; Yan, Y.-B. Effects of deformation mode and strain level on grain boundary character distribution of 304 austenitic stainless steel. Met. Mater. Trans. A 2018, 49, 2257–2268. [Google Scholar] [CrossRef]
- Wang, Z.-G.; Tang, S.; Zhang, W.-N.; Gao, F.; Chen, J.; Liu, Z.-Y. Induction of large twin related domains and the grain boundary evolution during hot plate rolling and annealing of 316H-type stainless steel. Mater. Lett. 2022, 311, 131590. [Google Scholar]
- Liu, T.-G.; Xia, S.; Li, H.; Zhou, B.-X.; Bai, Q.; Su, C.; Cai, Z.-G. Effect of initial grain sizes on the grain boundary network during grain boundary engineering in Alloy 690. J. Mater. Res. 2013, 28, 1165–1176. [Google Scholar] [CrossRef]
- Lee, S.L.; Richards, N.L. The effect of single-step low strain and annealing of nickel on grain boundary character. Mater. Sci. Eng. A 2005, 390, 81–87. [Google Scholar] [CrossRef]
- Tan, L.; Sridharan, K.; Allen, T.R. Effect of thermomechanical processing on grain boundary character distribution of a Ni-based superalloy. J. Nucl. Mater. 2007, 371, 171–175. [Google Scholar] [CrossRef]
- Kaithwas, C.K.; Bhuyan, P.; Pradhan, S.K.; Mandal, S. Microstructure evolution during low-strain thermo-mechanical processing and its repercussion on intergranular corrosion in alloy 600H. Mater. Charact. 2018, 145, 582–593. [Google Scholar]
- Pradhan, S.K.; Bhuyan, P.; Kaithwas, C.; Mandal, S. Strain-annealing based grain boundary engineering to evaluate its sole implication on intergranular corrosion in extra-low carbon type 304L austenitic stainless steel. Met. Mater. Trans. A 2018, 49, 2817–2831. [Google Scholar] [CrossRef]
- Singh, R.; Chowdhury, S.G.; Ravi Kumar, B.; Das, S.K.; De, P.K.; Chattoraj, I. The importance of grain size relative to grain boundary character on the sensitization of metastable austenitic stainless steel. Scr. Mater. 2007, 57, 185–188. [Google Scholar]
- Li, Z.-G.; Zhang, L.-T.; Sun, N.-R.; Sun, Y.-L.; Shan, A.-D. Effects of prior deformation and annealing process on microstructure and annealing twin density in a nickel based alloy. Mater. Charact. 2014, 95, 299–306. [Google Scholar] [CrossRef]
- Lee, S.L.; Richards, N.L. Influence of long term annealing on grain boundary character distributions in nickel. Mater. Sci. Eng. A 2005, 405, 74–85. [Google Scholar]
- Randle, V.; Davies, H. Evolution of microstructure and properties in alpha-brass after iterative processing. Met. Mater. Trans. A 2002, 33, 1853–1857. [Google Scholar] [CrossRef]
- Mandal, S.; Bhaduri, A.K.; Sarma, V.S. One-step and iterative thermo-mechanical treatments to enhance Σ3n boundaries in a Ti-modified austenitic stainless steel. J. Mater. Sci. 2011, 46, 275–284. [Google Scholar] [CrossRef]
- Song, K.H.; Chun, Y.B.; Hwang, S.K. Direct observation of annealing twin formation in a Pb-base alloy. Mater. Sci. Eng. A 2007, 454, 629–636. [Google Scholar] [CrossRef]
- Kim, D.Y.; Ryu, S.H. Application of nimonic 80A to the hot forging of an exhaust valve head. J. Mater. Process. Technol. 2001, 113, 148–152. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Pan, J.; Wang, X.; Zhang, Z.-H.; Zhang, L.; Wang, T. Correspondence between grain refinements and flow softening behaviors at Nimonic 80A superalloy under different strain rates, temperatures and strains. Mater. Sci. Eng. A 2017, 679, 358–371. [Google Scholar]
- Chen, M.S.; Chen, Q.; Lou, Y.M.; Lin, Y.C.; Li, H.B.; Wang, G.Q.; Cai, H.W. Effect of deformation parameters of an initial aged GH4169 superalloy on its microstructural evolution during a new two-stage annealing. Materials 2022, 15, 5508. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Quan, G.-Z.; Zhao, J.; Xiong, W. Influence of variable loading path pattern on deformation and grain size in large-scale electric upsetting process of Nimonic superalloy. J. Adv. Manuf. Technol. 2022, 120, 5933–5954. [Google Scholar] [CrossRef]
- Souai, N.; Bozzolo, N.; Naze, L.; Chastel, Y.; Loge, R. About the possibility of grain boundary engineering via hot-working in a nickel-base superalloy. Scr. Mater. 2010, 62, 851–854. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Li, Y.-L.; Zhang, L.; Wang, X. Evolution of grain refinement degree induced by dynamic recrystallization for Nimonic 80A during hot compression process and its FEM analysis. Vacuum 2017, 139, 51–63. [Google Scholar] [CrossRef]
- Wang, W.; Lartigue-Korinek, S.; Brisset, F.; Helbert, A.L.; Bourgon, J.; Baudin, T. Formation of annealing twins during primary recrystallization of two low stacking fault energy Ni-based alloys. J. Mater. Sci. 2015, 50, 2167–2177. [Google Scholar] [CrossRef]
- Randle, V. The Role of Coincidence Site Lattice in Grain Boundary Engineering; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar]
- Bozzolo, N.; Bernacki, M. Viewpoint on the formation and evolution of annealing twins during thermomechanical processing of fcc metals and alloys. Met. Mater. Trans. A 2020, 51, 2665–2684. [Google Scholar]
- Prithiv, T.S.; Bhuyan, P.; Pradhan, S.K.; Sarma, V.S.; Mandal, S. A critical evaluation on efficacy of recrystallization vs. strain induced boundary migration in achieving grain boundary engineered microstructure in a Ni-base superalloy. Acta Mater. 2018, 146, 187–201. [Google Scholar] [CrossRef]
- Bai, Q.; Zhao, Q.; Xia, S.; Wang, B.-S.; Zhou, B.-X.; Su, C. Evolution of grain boundary character distributions in alloy 825 tubes during high temperature annealing: Is grain boundary engineering achieved through recrystallization or grain growth? Mater. Charact. 2017, 123, 178–188. [Google Scholar] [CrossRef]
- Yang, X.-Y.; Wang, P.; Huang, M. Grain boundary evolution during low-strain grain boundary engineering achieved by strain-induced boundary migration in pure copper. Mater. Sci. Eng. A 2021, 833, 142532. [Google Scholar] [CrossRef]
- Tokita, S.; Kokawa, H.; Sato, Y.S.; Fujii, H.T. In situ EBSD observation of grain boundary character distribution evolution during thermomechanical process used for grain boundary engineering of 304 austenitic stainless steel. Mater. Charact. 2017, 131, 31–38. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Zhang, Y.-Q.; Zhang, P.; Ma, Y.-Y.; Wang, W.-Y. Correspondence between low-energy twin boundary density and thermal-plastic deformation parameters in nickel-based superalloy. Trans. Nonferrous Met. Soc. China 2021, 31, 438–455. [Google Scholar] [CrossRef]
- Li, Q.-Y.; Cahoon, J.R.; Richards, N.L. Effects of thermo-mechanical processing parameters on the special boundary configurations of commercially pure nickel. Mater. Sci. Eng. A 2009, 527, 263–271. [Google Scholar] [CrossRef]
- Wang, W.; Brisset, F.; Helbert, A.L.; Solas, D.; Drouelle, I.; Mathon, M.H.; Baudin, T. Influence of stored energy on twin formation during primary recrystallization. Mater. Sci. Eng. A 2014, 589, 112–118. [Google Scholar] [CrossRef]
- Cahoon, J.R.; Li, Q.-Y.; Richards, N.L. Microstructural and processing factors influencing the formation of annealing twins. Mater. Sci. Eng. A 2009, 526, 56–61. [Google Scholar] [CrossRef]
- Detrois, M.; Goetz, R.L.; Helmink, R.C.; Tin, S. Modeling the effect of thermal-mechanical processing parameters on the density and length fraction of twin boundaries in Ni-base superalloy RR1000. Mater. Sci. Eng. A 2015, 647, 157–162. [Google Scholar] [CrossRef]
- Shi, H.; Chen, K.; Shen, Z.; Wu, J.-Q.; Dong, X.-P.; Zhang, L.-T.; Shan, A.-D. Twin boundary characters established during dynamic recrystallization in a nickel alloy. Mater. Charact. 2015, 110, 52–59. [Google Scholar] [CrossRef]
- Gao, J.; Tan, J.-B.; Wu, X.-Q.; Xia, S. Effect of grain boundary engineering on corrosion fatigue behavior of 316LN stainless steel in borated and lithiated high-temperature water. Corros. Sci. 2019, 152, 190–201. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nakamura, M.; Tsurekawa, S.; Watanabe, T. Effect of grain boundary microstructure on fatigue crack propagation in austenitic stainless steel. J. Mater. Sci. 2011, 46, 4254–4260. [Google Scholar] [CrossRef]
- Liu, T.-G.; Xia, S.; Du, D.-H.; Bai, Q.; Zhang, L.-F.; Lu, Y.-H. Grain boundary engineering of large-size 316 stainless steel via warm-rolling for improving resistance to intergranular attack. Mater. Lett. 2019, 234, 201–204. [Google Scholar] [CrossRef]
- Quan, S.-Y.; Song, R.-B.; Su, S.-R.; Huang, Y.; Cai, C.-H.; Wang, Y.-J.; Wang, K.-K. Grain boundary engineering prepared by iterative thermomechanical processing of nickel-saving austenitic stainless steel: Excellent corrosion resistance and mechanical properties. Mater. Charact. 2023, 196, 112601. [Google Scholar] [CrossRef]
- Shi, F.; Tian, P.C.; Ye, Z.H.; Qi, Y.; Liu, C.M.; Li, X.W. Improving intergranular corrosion resistance in a nickel-free and manganese-bearing high-nitrogen austenitic stainless steel through grain boundary character distribution optimization. Corros. Sci. 2016, 107, 49–59. [Google Scholar] [CrossRef]
- Kronberg, M.L.; Wilson, F.H. Secondary recrystallization in copper. JOM 1949, 1, 501–514. [Google Scholar] [CrossRef]
- Grimmer, H.; Bollmann, W.; Warrington, D.H. Coincidence-site lattices and complete pattern-shift in cubic crystals. Acta Crystallogr. 2010, 30, 197–207. [Google Scholar] [CrossRef]
- Hou, J.; Peng, Q.-J.; Lu, Z.-P.; Shoji, T.; Wang, J.-Q.; Han, E.-H.; Ke, W. Effects of cold working degrees on grain boundary characters and strain concentration at grain boundaries in Alloy 600. Corros. Sci. 2011, 53, 1137–1142. [Google Scholar] [CrossRef]
- Bennett, B.W.; Pickering, H.W. Effect of grain-boundary structure on sensitization and corrosion of stainless-steel. Met. Trans. A 1987, 18, 1117–1124. [Google Scholar] [CrossRef]
- Brandon, D.G. The structure of high-angle grain boundaries. Acta Met. 1966, 14, 1479–1484. [Google Scholar] [CrossRef]
- Palumbo, G.; Aust, K.T.; Lehockey, E.M.; Erb, U.; Lin, P. On a more restrictive geometric criterion for “special” CSL grain boundaries. Scr. Mater. 1998, 38, 1685–1690. [Google Scholar] [CrossRef]
- Randle, V. The effect of twinning interactions up to the seventh generation on the evolution of microstructure. J. Mater. Sci. 2006, 41, 653–660. [Google Scholar] [CrossRef]
- Hu, C.-L.; Shuang, X.; Hui, L.; Liu, T.-G.; Zhou, B.-X.; Chen, W.-J.; Ning, W. Improving the intergranular corrosion resistance of 304 stainless steel by grain boundary network control. Corros. Sci. 2011, 53, 1880–1886. [Google Scholar] [CrossRef]
- Thaveeprungsriporn, V.; Was, G.S. The role of coincidence-site-lattice boundaries in creep of Ni-16Cr-9Fe at 360 °C. Met. Mater. Trans. A 1997, 28, 2101–2112. [Google Scholar] [CrossRef]
- West, E.A.; Was, G.S. IGSCC of grain boundary engineered 316L and 690 in supercritical water. J. Nucl. Mater. 2009, 392, 264–271. [Google Scholar] [CrossRef]
- Yuan, Y.; Jiang, Y.-D.; Zhou, J.; Liu, G.-Y.; Ren, X. Influence of grain boundary character distribution and random high angle grain boundaries networks on intergranular corrosion in high purity copper. Mater. Lett. 2019, 253, 424–426. [Google Scholar] [CrossRef]
- Lehockey, E.M.; Brennenstuhl, A.M.; Thompson, I. On the relationship between grain boundary connectivity, coincident site lattice boundaries, and intergranular stress corrosion cracking. Corros. Sci. 2004, 46, 2383–2404. [Google Scholar] [CrossRef]
- Das, A. Grain boundary engineering: Fatigue fracture. Philos. Mag. 2017, 97, 867–916. [Google Scholar] [CrossRef]
- Hu, H.; Zhao, M.; Chen, S.; Rong, L. Effect of grain boundary character distribution on hydrogen embrittlement in Fe–Ni based alloy. Mater. Sci. Eng. A 2020, 780, 139201. [Google Scholar] [CrossRef]
- Tsurekawa, S.; Nakamichi, S.; Watanabe, T. Correlation of grain boundary connectivity with grain boundary character distribution in austenitic stainless steel. Acta Mater. 2006, 54, 3617–3626. [Google Scholar] [CrossRef]
- Xia, S.; Zhou, B.-X.; Chen, W.-J. Grain cluster microstructure and grain boundary character distribution in Alloy 690. Met. Trans. A 2009, 40, 3016–3030. [Google Scholar] [CrossRef]
- Liu, T.-G.; Xia, S.; Wang, B.-S.; Bai, Q.; Zhou, B.-X.; Su, C. Grain orientation statistics of grain-clusters and the propensity of multiple-twinning during grain boundary engineering. Mater. Des. 2016, 112, 442–448. [Google Scholar] [CrossRef]
- Liu, T.-G.; Xia, S.; Li, H.; Zhou, B.-X.; Bai, Q. The highly twinned grain boundary network formation during grain boundary engineering. Mater. Lett. 2014, 133, 97–100. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Z.; Sun, Q.; He, Y.-Q.; Sun, Y.-X. Effect of thermomechanical processing via rotary swaging on grain boundary character distribution and intergranular corrosion in 304 austenitic stainless steel. J. Mater. Res. Technol. 2022, 19, 2470–2482. [Google Scholar] [CrossRef]
- Schuh, C.A.; Minich, R.W.; Kumar, M. Connectivity and percolation in simulated grain-boundary networks. Philos. Mag. 2003, 83, 711–726. [Google Scholar] [CrossRef]
- Telang, A.; Gill, A.S.; Tammana, D.; Wen, X.; Kumar, M.; Teysseyre, S.; Mannava, S.R.; Dong, Q.; Vasudevan, V.K. Surface grain boundary engineering of Alloy 600 for improved resistance to stress corrosion cracking. Mater. Sci. Eng. A 2015, 648, 280–288. [Google Scholar] [CrossRef]
- Telang, A.; Gill, A.S.; Kumar, M.; Teysseyre, S.; Qian, D.; Mannava, S.R.; Vasudevan, V.K. Iterative thermomechanical processing of alloy 600 for improved resistance to corrosion and stress corrosion cracking. Acta Mater. 2016, 113, 180–193. [Google Scholar] [CrossRef]
- Shi, F.; Gao, R.-H.; Guan, X.-J.; Liu, C.-M.; Li, X.-W. Application of grain boundary engineering to improve intergranular corrosion resistance in a Fe–Cr–Mn–Mo–N high-nitrogen and nickel-free austenitic stainless steel. Acta Met. Sin. (Engl. Lett.) 2020, 33, 33–42. [Google Scholar] [CrossRef]
- Kumar, M.; King, W.E.; Schwartz, A.J. Modifications to the microstructural topology in f.c.c. materials through thermomechanical processing. Acta Mater. 2000, 48, 2081–2091. [Google Scholar] [CrossRef]
- Palumbo, G.; King, P.J.; Aust, K.T.; Erb, U.; Lichtenberger, P.C. Grain-boundary design and control for intergranular stress-corrosion resistance. Scr. Met. Mater. 1991, 25, 1775–1780. [Google Scholar] [CrossRef]
- Marrow, T.J.; Babout, L.; Jivkov, A.P.; Wood, P.; Engelberg, D.; Stevens, N.; Withers, P.J.; Newman, R.C. Three dimensional observations and modelling of intergranular stress corrosion cracking in austenitic stainless steel. J. Nucl. Mater. 2006, 352, 62–74. [Google Scholar] [CrossRef]
- Li, H.; Xia, S.; Zhou, B.-X.; Chen, W.-J.; Hu, C.-L. The dependence of carbide morphology on grain boundary character in the highly twinned Alloy 690. J. Nucl. Mater. 2010, 399, 108–113. [Google Scholar] [CrossRef]
- Cao, W.; Xia, S.; Bai, Q.; Zhang, W.-Z.; Zhou, B.-X.; Li, Z.-J.; Jiang, L. Effects of initial microstructure on the grain boundary network during grain boundary engineering in Hastelloy N alloy. J. Alloy. Compd. 2017, 704, 724–733. [Google Scholar] [CrossRef]
- Liu, J.X.; Wu, H.B.; Yang, S.W.; Yu, X.P.; Ding, C. Effect of hot rolling reduction and annealing treatment on grain boundary character distribution in austenitic low-density Fe-Mn-Al-C-Cr steel. Mater. Lett. 2021, 285, 128999. [Google Scholar] [CrossRef]
- Michiuchi, M.; Kokawa, H.; Wang, Z.-J.; Sato, Y.S.; Sakai, K. Twin-induced grain boundary engineering for 316 austenitic stainless steel. Acta Mater. 2006, 54, 5179–5184. [Google Scholar] [CrossRef]
- Xia, S.; Zhou, B.-X.; Chen, W.-J.; Wang, W.-G. Effects of strain and annealing processes on the distribution of Sigma 3 boundaries in a Ni-based superalloy. Scr. Mater. 2006, 54, 2019–2022. [Google Scholar] [CrossRef]
- Guyot, B.M.; Richards, N.L. A study on the effect of cold rolling and annealing on special grain boundary fractions in commercial-purity nickel. Mater. Sci. Eng. A 2005, 395, 87–97. [Google Scholar] [CrossRef]
- Qian, M.; Luo, H.-L.; Ding, C.-H.; Wang, J.-T. The effect of long term high temperature annealing on twinning and detwinning of the wrought Ni3Al-based alloy. Mater. Charact. 2017, 132, 458–466. [Google Scholar] [CrossRef]
- Lee, D.S.; Ryoo, H.S.; Hwang, S.K. A grain boundary engineering approach to promote special boundaries in Pb-base alloy. Mater. Sci. Eng. A 2003, 354, 106–111. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chun, Y.B.; Han, J.W.; Hwang, S.K. Effect of thermomechanical processing on grain boundary characteristics in two-phase brass. Mater. Sci. Eng. A 2003, 363, 307–315. [Google Scholar] [CrossRef]
- Lehockey, E.M.; Palumbo, G. On the creep behaviour of grain boundary engineered nickel. Mater. Sci. Eng. A 1997, 237, 168–172. [Google Scholar] [CrossRef]
- Zhu, Y.-L.; Cao, Y.; He, Q.-B.; Luo, R.; Di, H.-S.; Huang, G.-J.; Liu, Q.; Xiao, J. On the critical strain of thermal-mechanical processing to tailor grain boundary character distribution in Incoloy 925 alloy. Intermetallics 2022, 148, 107635. [Google Scholar] [CrossRef]
- Katnagallu, S.S.; Mandal, S.; Cheekur Nagaraja, A.; de Boer, B.; Vadlamani, S.S. Role of carbide precipitates and process parameters on achieving grain boundary engineered microstructure in a Ni-based superalloy. Met. Mater. Trans. A 2015, 46, 4740–4754. [Google Scholar] [CrossRef]
- King, W.E.; Schwartz, A.J. Toward optimization of the grain boundary character distribution in OFE copper. Scr. Mater. 1998, 38, 449–455. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chen, X.-M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Mandal, S.; Athreya, C.N.; Babu, K.A.; de Boer, B.; Sarma, V.S. Influence of processing parameters on dynamic recrystallization and the associated annealing twin boundary evolution in a nickel base superalloy. Mater. Sci. Eng. A 2017, 700, 49–58. [Google Scholar] [CrossRef]
- Chen, W.-X.; Jia, C.-N.; Hu, B.-J.; Zheng, C.-W.; Li, D.-Z. Evolution of twins and sub-boundaries at the early stage of dynamic recrystallization in a Ni-30%Fe austenitic model alloy. Mater. Sci. Eng. A 2018, 733, 419–428. [Google Scholar] [CrossRef]
- Yang, J.; Luo, J.; Li, X.-Y.; Li, M.-Q. Evolution mechanisms of recrystallized grains and twins during isothermal compression and subsequent solution treatment of GH4586 superalloy. J. Alloy. Compd. 2021, 850, 156732. [Google Scholar] [CrossRef]
- Li, H.Z.; Liu, X.A.; Wang, S.J.; Zhang, W.W.; Ke, Y.J.; Guo, Y.; Qin, H.Y.; Tian, Q. An evaluation of optimized grain boundary character distribution in hot-worked GH4698 superalloy. J. Mater. Sci. 2023, 58, 1382–1402. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, J.-X.; Zhang, M.-C.; Yao, Z.-H. Evolution of twins and substructures during low strain rate hot deformation and contribution to dynamic recrystallization in alloy 617B. Mater. Sci. Eng. A 2016, 649, 369–381. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Jia, Z.; Ji, J.-J.; Li, S.-D.; Liu, D.-X. Effect of twin nucleation and twin on the recrystallization of a nickel-based superalloy during hot compression. Mater. Charact. 2022, 194, 112362. [Google Scholar] [CrossRef]
- Cao, Y.; Di, H.-S.; Zhang, J.-Q.; Zhang, J.-C.; Ma, T.-J.; Misra, R.D.K. An electron backscattered diffraction study on the dynamic recrystallization behavior of a nickel-chromium alloy (800H) during hot deformation. Mater. Sci. Eng. A 2013, 585, 71–85. [Google Scholar] [CrossRef]
- Zhang, H.-B.; Zhang, K.-F.; Zhou, H.-P.; Lu, Z.; Zhao, C.-H.; Yang, X.-L. Effect of strain rate on microstructure evolution of a nickel-based superalloy during hot deformation. Mater. Des. 2015, 80, 51–62. [Google Scholar] [CrossRef]
- Zhang, H.-B.; Zhou, H.-P.; Qin, S.-X.; Liu, J.; Xu, X.-M. Effect of deformation parameters on twinning evolution during hot deformation in a typical nickel-based superalloy. Mater. Sci. Eng. A 2017, 696, 290–298. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Quan, G.-Z.; Zhao, J.; Xiong, W. Influencing mechanisms of prior cold deformation on mixed grain boundary network in the thermal deformation of Ni80A superalloy. Materials 2022, 15, 6426. [Google Scholar] [CrossRef] [PubMed]
- Detrois, M.; Rotella, J.; Goetz, R.L.; Helmink, R.C.; Tin, S. Grain boundary engineering of powder processed Ni-base superalloy RR1000: Influence of the deformation parameters. Mater. Sci. Eng. A 2015, 627, 95–105. [Google Scholar] [CrossRef]
- Shi, Z.-X.; Yan, X.-F.; Duan, C.-H.; Zhao, M.-H. Effect of strain rate on hot deformation characteristics of GH690 superalloy. Trans. Nonferrous Met. Soc. China 2017, 27, 538–550. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M.; Cabrera, J.M.; Calvo, J. Dynamic recrystallization mechanisms and twining evolution during hot deformation of Inconel 718. Mater. Sci. Eng. A 2016, 678, 137–152. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.-Z.; Zhen, L.; Zhang, X.-M. Microstructure evolution during dynamic recrystallization of hot deformed superalloy 718. Mater. Sci. Eng. A 2008, 486, 321–332. [Google Scholar] [CrossRef]
- Ebrahimi, G.R.; Momeni, A.; Ezatpour, H.R.; Jahazi, M.; Bocher, P. Dynamic recrystallization in Monel400 Ni-Cu alloy: Mechanism and role of twinning. Mater. Sci. Eng. A 2019, 744, 376–385. [Google Scholar] [CrossRef]
- Tang, X.-F.; Wang, B.-Y.; Ji, H.-C.; Fu, X.-B.; Xiao, W.-C. Behavior and modeling of microstructure evolution during metadynamic recrystallization of a Ni-based superalloy. Mater. Sci. Eng. A 2016, 675, 192–203. [Google Scholar] [CrossRef]
- Sinha, S.; Kim, D.I.; Fleury, E.; Suwas, S. Effect of grain boundary engineering on the microstructure and mechanical properties of copper containing austenitic stainless steel. Mater. Sci. Eng. A 2015, 626, 175–185. [Google Scholar] [CrossRef]
- Kumar, B.R.; Chowdhury, S.G.; Narasaiah, N.; Mahato, B.; Das, S.K. Role of grain boundary character distribution on tensile properties of 304L stainless steel. Met. Mater. Trans. A 2007, 38, 1136–1143. [Google Scholar] [CrossRef]
- Gao, Y.-B.; Ding, Y.-T.; Chen, J.-J.; Xu, J.-Y.; Ma, Y.-J.; Wang, X.-M. Effect of twin boundaries on the microstructure and mechanical properties of Inconel 625 alloy. Mater. Sci. Eng. A 2019, 767, 138361. [Google Scholar] [CrossRef]
- Guan, X.-J.; Jia, Z.-P.; Liang, S.-M.; Shi, F.; Li, X.-W. A pathway to improve low-cycle fatigue life of face-centered cubic metals via grain boundary engineering. J. Mater. Sci. Technol. 2022, 113, 82–89. [Google Scholar] [CrossRef]
- Bhat, R.S.; Manjunatha, K.B.; Prasanna, S.R.; Venkatakrishna, K.; Hegde, A.C. Electrochemical studies on the corrosion resistance of Zn-Ni-Co coating from acid chloride bath. Appl. Phys. A Mater. Sci. Process. 2020, 126, 772. [Google Scholar] [CrossRef]
- Bhat, R.S.; Venkatakrishna, K.; Hegde, C.A. Surface structure and electrochemical behavior of Zinc-Nickel anti-corrosive coating. Anal. Bioanal. Electrochem. 2023, 15, 90–101. [Google Scholar]
- Bhat, R.S.; Nagaraj, P.; Priyadarshini, S. Zn-Ni compositionally modulated multilayered alloy coatings for improved corrosion resistance. Surf. Eng. 2021, 37, 755–763. [Google Scholar] [CrossRef]
- Shi, F.; Yan, L.; Hu, J.; Wang, L.-F.; Li, T.-Z.; Li, W.; Guan, X.-J.; Liu, C.-M.; Li, X.-W. Improving intergranular stress corrosion cracking resistance in a Fe-18Cr-17Mn-2Mo-0.85N austenitic stainless steel through grain boundary character distribution optimization. Acta Met. Sin. (Engl. Lett.) 2022, 35, 1849–1861. [Google Scholar] [CrossRef]
- Liu, T.-G.; Xia, S.; Bai, Q.; Zhou, B.-X.; Zhang, L.-F.; Lu, Y.-H.; Shoji, T. Three-dimensional study of grain boundary engineering effects on intergranular stress corrosion cracking of 316 stainless steel in high temperature water. J. Nucl. Mater. 2018, 498, 290–299. [Google Scholar] [CrossRef]
- Jivkov, A.P.; Stevens, N.P.C.; Marrow, T.J. A three-dimensional computational model for intergranular cracking. Comput. Mater. Sci. 2006, 38, 442–453. [Google Scholar] [CrossRef]




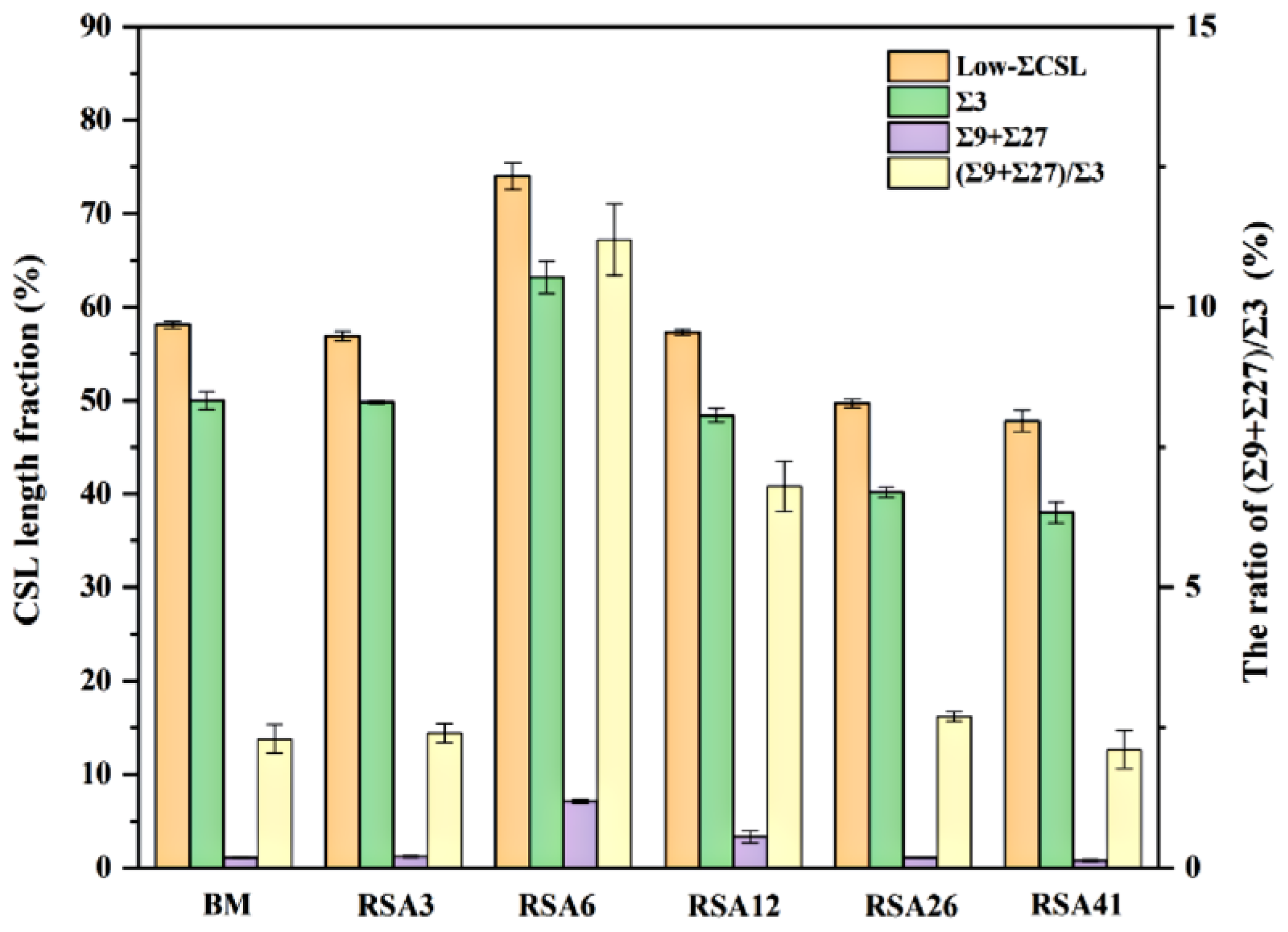
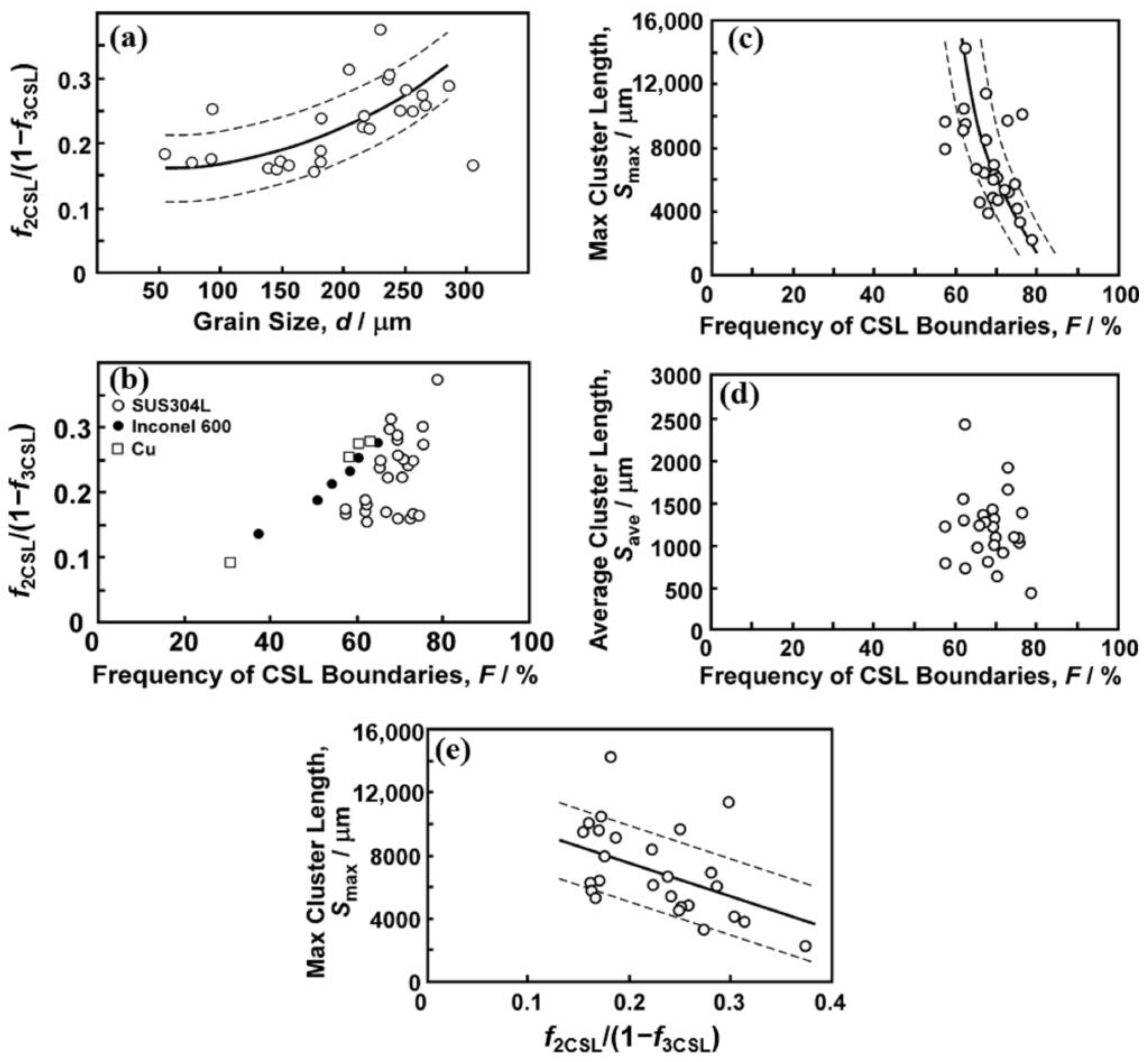
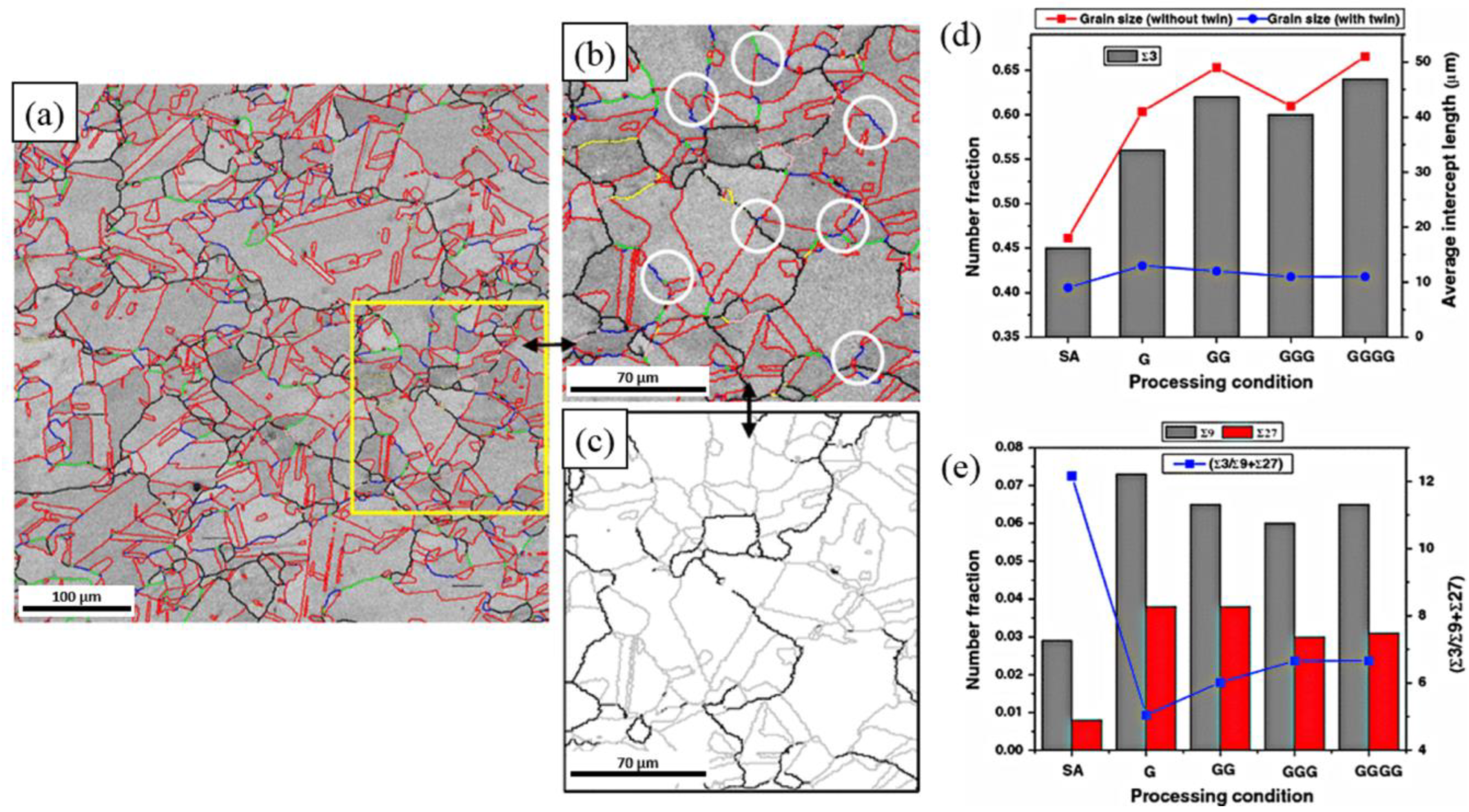




| Σ | θ | <uvw> | Σ | θ | <uvw> | Σ | θ | <uvw> |
|---|---|---|---|---|---|---|---|---|
| 1 | 0° | <111> | 13b | 27.8° | <111> | 21b | 44.4° | <211> |
| 3 | 60° | <111> | 15 | 48.2° | <210> | 23 | 40.5° | <311> |
| 5 | 36.9° | <100> | 17a | 28.1° | <100> | 25a | 16.3° | <100> |
| 7 | 38.2° | <111> | 17b | 61.9° | <221> | 25b | 51.7° | <331> |
| 9 | 38.9° | <110> | 19a | 26.5° | <311> | 27a | 31.6° | <110> |
| 11 | 50.5° | <110> | 19b | 46.8° | <100> | 27b | 35.4° | <210> |
| 13a | 22.6° | <100> | 21a | 21.8° | <331> | 29 | 46.3° | <100> |
| Material | Initial State or Pre-Treatment | Optimal TMP Route | GBCD Results | Grain Size /μm | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reduction /% | Temperature /°C | Time /min | Processing Pass/n | Fraction of Low-ΣCSL/% | |||||||
| Σ3 | Σ9 + 27 | Σ ≤ 29 | |||||||||
| Nickel-based alloy | 690 | 1100 °C/15 min + WQ | 5 | 1100 | 5 | 1 | 60.6 | 9.2 | 72.5 | - | [102] |
| 690 | 1100 °C/15 min + WQ + 750 °C/15 h | 5 | 1100 | 5 | 1 | 61.3 | 9.4 | 72.7 | - | [87] | |
| Ni-200 | Strips | 5 | 900 | 10 | 1 | 50.2 | 11.1 | 65.0 | 67 | [103] | |
| Ni | As-cast | 60 | 950~1150 | 1~15 | 1 | 46.7 | 5.5 | 66.2 | 25 | [107] | |
| 625 | 1150 °C/1 h + WQ | 5 | 1150 | 5 | 1 | 30.3 | 3.2 | 35.8 | 41.5 | [5] | |
| 600 | Bar | 20 | 1000 | 15 | 7 | ~34 | - | ~65 | - | [95] | |
| - | 1000 °C/1 h | 65 | 1020 | 180 | 1 | 40.3 | - | 41.5 | 31.3 | [42] | |
| Ni-200 | Sheet | 6 | 900 | 10 | 1 | - | - | 74.7 | 60 | [37] | |
| Pure nickel | Sheet | 6 | 700 | 2880 | 1 | 59.8 | 13.5 | 76.1 | 46 | [43] | |
| 600 H | 1130 °C + WQ | 7.5 | 1100 | 60 | 1 | ~64 | ~8 | 72 | 74 | [39] | |
| 825 | Solution-annealed | 5 | 1050 | 10 | 1 | - | - | 77.6 | 12.47 | [58] | |
| 925 | 1100 °C/2 h + WQ | 7 | 1075 | 10 | 1 | ~56 | ~5 | - | ~63 | [108] | |
| 617 | 1175 °C + WQ | 15 | 1100 | 30 | 1 | ~67 | - | - | ~74 | [109] | |
| Austenitic stainless steel | 316 | 1100 °C/0.5 h | 3 | 967 | 4320 | 1 | - | - | 86 | - | [101] |
| 304 | 1100 °C/15 min + WQ | 5 | 1100 | 5 | 1 | 59.2 | 8.7 | 73.1 | 33 | [79] | |
| 304 | 1050 °C/30 min | 5 | 927 | 4320 | 1 | - | - | 86.5 | - | [3] | |
| 304L | Hot rolling + 1050 °C/1 h + WQ | 5 | 1000 | 60 | 3 | 72 | 9 | - | 30 | [40] | |
| 304 L | 1070 °C/1 h + WQ | 90 | 950 | 30 | 1 | 37 | - | 41 | ~20 | [41] | |
| 316H | 1060 °C/1 h + WQ | 5 | 1010 | 120 | 1 | 67.4 | 8.9 | 76.3 | - | [35] | |
| D9 | Solution-annealed | 10 | 1000 | 30 | 2 | 62 | ~11 | 73 | ~50 | [45] | |
| Fe-Cr-Mn-Mo-N | 1050 °C/1 h + WQ | 5 | 1150 | 4320 | 1 | 74 | 5.2 | 79.4 | 25 | [94] | |
| Pb-alloy | Pb–Ca–Sn | Strip cast + 90% rolling | 30 | 270 | 10 | 2 | 63.9 | 25.8 | 96.1 | 60 | [105] |
| Pb–Ca–Sn–Al | 90% cold rolling + 270 °C/15 min | 30 | 270 | 10 | 3 | 59.9 | 11 | 80.0 | - | [32] | |
| Pb–Ca | 90% cold rolling + 270 °C/10 min | 30 | 270 | 10 | 3 | 53 | ~2 | ~57 | - | [46] | |
| Brass | Cu–Zn | 25% hot rolling + 800 °C/1 h | 20 | 680 | 20 | 2 | 73 | 5 | 79 | 42 | [106] |
| Ofe-Cu | Plate | 6 | 270 °C/14 h + 375 °C/7 h | 1 | 65 | 15 | 85 | - | [110] | ||
| Bar | 67 | 560 | 10 | 4 | 45 | - | 68 | 30 | [27] | ||
| 750 °C/15 min | 5 | 700 | 15 | 1 | - | - | ~83.5 | ~77 | [59] | ||
| Nickel-Based Alloy | Initial State or Pre-Treatment | Initial Grain Size/μm | Hot Compression Parameters | Maximum Value of Low-ΣCSL | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature /°C | Strain Rate /s−1 | True Strain or Reduction | Fraction of Low-ΣCSL/% | ||||||
| Σ3 | Σ9 | Σ27 | |||||||
| Ni80A | 1065 °C × 8 h | 170 | 1120–1180 | 0.1, 1 | 1.1 | 48 | ~2.6 | - | [66] |
| - | Ingot casting, 1150 °C × 30 min | 38.93 | 900–1150 | 0.01–1 | 50% | 35 | - | - | [117] |
| 617B | 1210 °C × 48 h | 94 | 1120–1210 | 0.001 | 0.16~0.84 | ~18 | ~1.4 | ~0.49 | [116] |
| 617 | - | - | 900–1200 | 0.001–10 | 50% | ~53 | - | - | [112] |
| 718 | 1025 °C × 1 h | 45 | 950–1100 | 0.001–1 | 0.05~0.7 | - | - | - | [124] |
| 718 | Wrought billet, 1100 °C × 30 min | 176 | 950–1120 | 10 | 0.7 | - | - | - | [125] |
| Monel 400 | - | 220 | 750–1150 | 0.01 | 0.7 | - | - | - | [126] |
| 800H | Hot forged | - | 850–1100 | 0.01–10 | 0.7 | ~40 | ~2.1 | ~0.9 | [118] |
| GH690 | Hot forged | 130 | 1000–1200 | 0.001–10 | 50% | ~28 | ~0.9 | ~0.2 | [123] |
| - | Wrought billet, 1100 °C × 30 min | 95 | 950–1100 | 0.01–1 | 0.357 | ~21 | - | - | [127] |
| - | Forging bar, 1100 °C × 30 min | 96.5 | 1100 | 0.001–10 | 0.7 | ~30 | ~2.4 | ~0.8 | [119] |
| - | Forging bar, 1100 °C × 0.5 h | 91.6 | 960–1160 | 0.001–1 | 50% | ~30 | ~2.4 | ~0.8 | [120] |
| RR1000 | As-consolidated billet, 1110 °C × 4 h | 3.2 | 1020–1100 | 0.001–0.05 | 0.5 | 33 | - | - | [122] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-Q.; Quan, G.-Z.; Zhao, J.; Yu, Y.-Z.; Xiong, W. A Review on Controlling Grain Boundary Character Distribution during Twinning-Related Grain Boundary Engineering of Face-Centered Cubic Materials. Materials 2023, 16, 4562. https://doi.org/10.3390/ma16134562
Zhang Y-Q, Quan G-Z, Zhao J, Yu Y-Z, Xiong W. A Review on Controlling Grain Boundary Character Distribution during Twinning-Related Grain Boundary Engineering of Face-Centered Cubic Materials. Materials. 2023; 16(13):4562. https://doi.org/10.3390/ma16134562
Chicago/Turabian StyleZhang, Yu-Qing, Guo-Zheng Quan, Jiang Zhao, Yan-Ze Yu, and Wei Xiong. 2023. "A Review on Controlling Grain Boundary Character Distribution during Twinning-Related Grain Boundary Engineering of Face-Centered Cubic Materials" Materials 16, no. 13: 4562. https://doi.org/10.3390/ma16134562
APA StyleZhang, Y.-Q., Quan, G.-Z., Zhao, J., Yu, Y.-Z., & Xiong, W. (2023). A Review on Controlling Grain Boundary Character Distribution during Twinning-Related Grain Boundary Engineering of Face-Centered Cubic Materials. Materials, 16(13), 4562. https://doi.org/10.3390/ma16134562








