Influence of Die Land Length on the Maximum Extrusion Force and Dry Ice Pellets Density in Ram Extrusion Process
Abstract
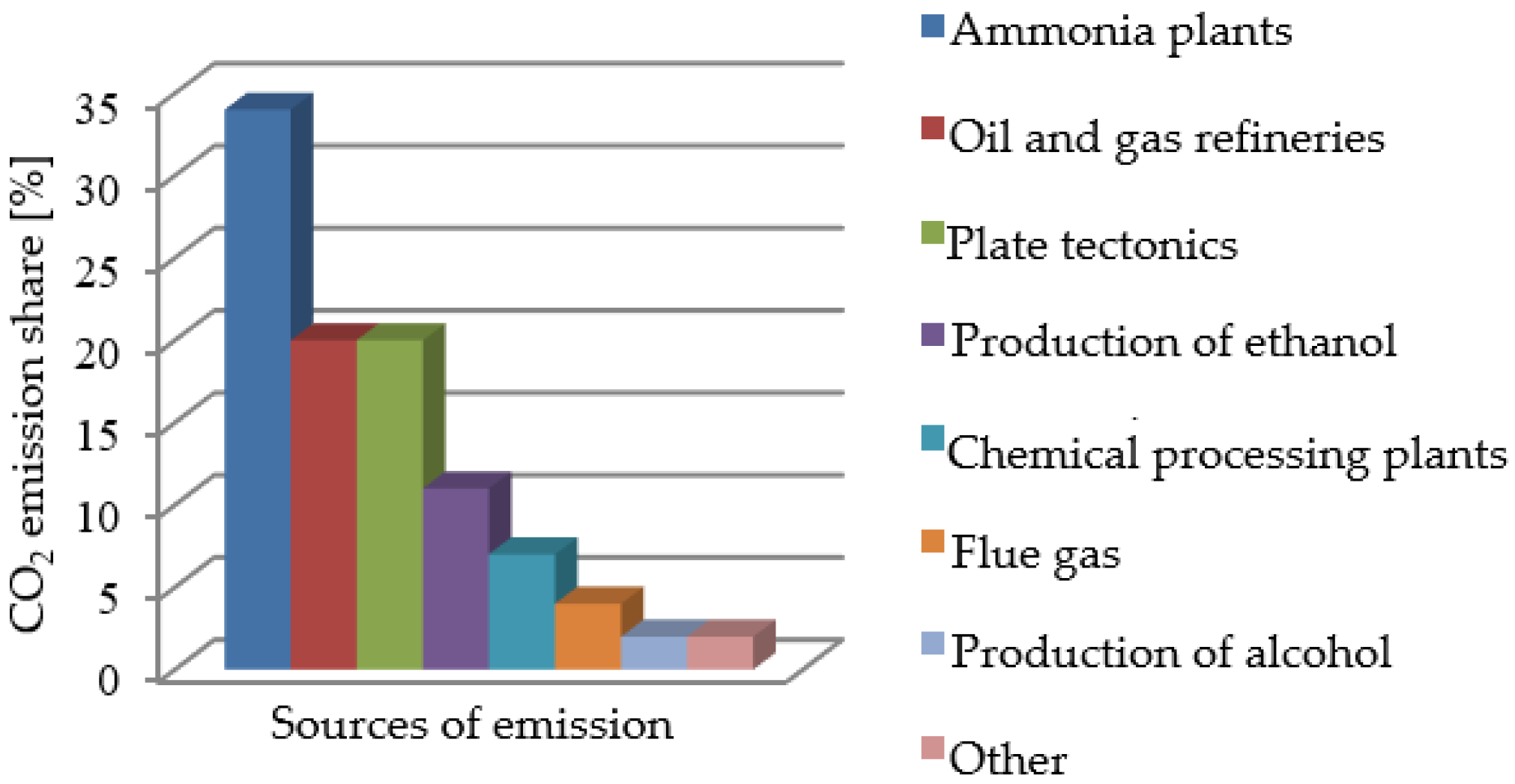
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Dry Ice Powder
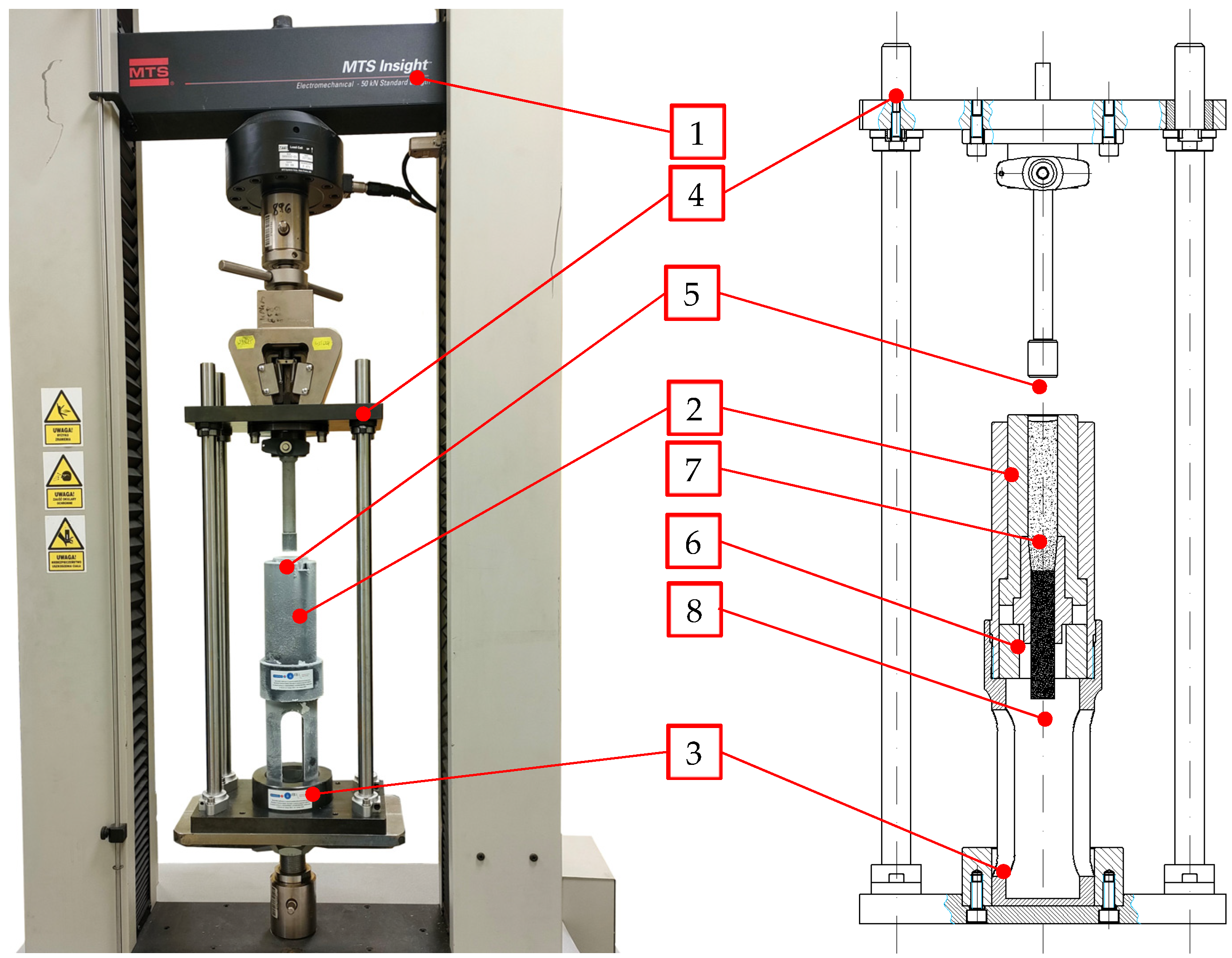
2.1.2. Compression and Extrusion
2.1.3. Dies
2.2. Method of Measurement of the Maximum Extrusion Force
2.3. Extrudate Density Measurement
2.4. Statistical Analysis
3. Results & Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wałęsa, K.; Talaśka, K.; Wilczyński, D.; Górecki, J.; Wojtkowiak, D. Experimental approach to modeling of the plasticizing operation in the hot plate welding process. Arch. Civ. Mech. Eng. 2022, 22, 16. [Google Scholar] [CrossRef]
- Dusaucy, J.; Gateuille, D.; Perrette, Y.; Naffrechoux, E. Microplastic pollution of worldwide lakes. Environ. Pollut. 2021, 284, 117075. [Google Scholar] [CrossRef]
- Piotrowska, K.; Kruszelnicka, W.; Bałdowska-Witos, P.; Kasner, R.; Rudnicki, J.; Tomporowski, A.; Flitzikowski, J.; Opielak, M. Assessmet of the environmental impact of a car tire throughout its life cycle using the Ica method. Materials 2019, 12, 4177. [Google Scholar] [CrossRef] [PubMed]
- Raza, S.; Ahmad, J. Composting process: A review. Int. J. Biol. Res. 2016, 4, 102–104. [Google Scholar] [CrossRef]
- Uhryński, A.; Bembenek, M. The Thermographic Analysis of the Agglomeration Process in the Roller Press of Pillow-Shaped Briquettes. Materials 2022, 15, 2870. [Google Scholar] [CrossRef]
- Wilczyński, D.; Berdychowski, M.; Talaśka, K.; Wojtkowiak, D. Experimental and numerical analysis of the effect of compaction conditions on briquette properties. Fuel 2021, 288, 119613. [Google Scholar] [CrossRef]
- Spur, G.; Uhlman, E.; Elbing, F. Dry-ice blasting for cleaning: Process, optimization and application. Wear 1999, 233–235, 402–411. [Google Scholar] [CrossRef]
- Górecki, J. Preliminary analysis of the sensitivity of the FEM model of the process of dry ice extrusion in the die with a circularly converging channel on the changing its geometrical parameters. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1199, 012006. [Google Scholar] [CrossRef]
- Berdychowski, M.; Górecki, J.; Biszczanik, A.; Wałęsa, K. Numerical Simulation of Dry Ice Compaction Process: Comparison of Drucker-Prager/Cap and Cam Clay Models with Experimental Results. Materials 2022, 15, 5771. [Google Scholar] [CrossRef] [PubMed]
- Hasanbeigi, A.; Price, L.; Lin, E. Emerging energy-efficiency and CO2 emission-reduction technologies for cement and concrete production: A technical review. Renew. Sustain. Energy Rev. 2012, 16, 6220–6238. [Google Scholar] [CrossRef]
- Yamasaki, H.; Wakimoto, H.; Kamimura, T.; Hattori, K.; Nekså, P.; Yamaguchi, H. Visualization and Measurement of Swirling Flow of Dry Ice Particles in Cyclone Separator-Sublimator. Energies 2022, 15, 4128. [Google Scholar] [CrossRef]
- Witte, A.K.; Bobal, M.; David, R.; Blättler, B.; Schoder, D.; Rossmanith, P. Investigation of the potential of dry ice blasting for cleaning and disinfection in the food production environment. LWT 2017, 75, 735–741. [Google Scholar] [CrossRef]
- Górecki, J.; Malujda, I.; Talaśka, K.; Wojtkowiak, K. Dry Ice Compaction in Piston Extrusion Process. Acta Mech. Autom. 2017, 11, 313–316. [Google Scholar] [CrossRef]
- Liu, Y.H.; Matsusaka, S.L. Formation of Dry Ice Particles and Their Application to Surface Cleaning. J. Aerosol Res. 2013, 28, 155–162. [Google Scholar] [CrossRef]
- Dzido, A.; Krawczyk, P.; Badyda, K.; Chondrokostas, P. Operational parameters impact on the performance of dry-ice blasting nozzle. Energy 2021, 214, 118847. [Google Scholar] [CrossRef]
- Górecki, J. Development of a testing station for empirical verification of the algebraic model of dry ice piston extrusion—Amoniak a CO2. Acta Mech. Autom. 2021, 15, 107–112. [Google Scholar] [CrossRef]
- Górecki, J.; Talaśka, K.; Wałęsa, K.; Wilczyński, D.; Wojtkowiak, D. Mathematical model describing the influence of geometrical parameters of multichannel dies on the limit force of dry ice extrusion process. Materials 2020, 13, 3317. [Google Scholar] [CrossRef]
- Wałęsa, K.; Górecki, J.; Berdychowski, M.; Biszczanik, A.; Wojtkowiak, D. Modelling of the Process of Extrusion of Dry Ice through a Single-Hole Die Using the Smoothed Particle Hydrodynamics (SPH) Method. Materials 2022, 15, 8242. [Google Scholar] [CrossRef]
- Biszczanik, A.; Wałęsa, K.; Kukla, M.; Górecki, J. The Influence of Density on the Value of Young’s Modulus for Dry Ice. Materials 2021, 14, 7763. [Google Scholar] [CrossRef]
- Górecki, J.; Malujda, I.; Talaśka, K.; Tarkowski, P.; Kukla, M. Influence of the value of limit densification stress on the quality of the pellets during the agglomeration proces of CO2. Procedia Eng. 2016, 136, 269–274. [Google Scholar] [CrossRef]
- Saloda, M.A. To Study the Influence of Frictional Conditions and Die Land Length on Component Error and Die Deflecion in Cold Extrusion by Finite Element Analysis. J. Metall. Eng. 2013, 2, 29–37. [Google Scholar]
- Berdychowski, M.; Górecki, J.; Wałęsa, K. Numerical Simulation of Dry Ice Compaction Process: Comparison of the Mohr–Coulomb Model with the Experimental Results. Materials 2022, 15, 7932. [Google Scholar] [CrossRef]
- Biszczanik, A.; Wojtkowiak, D.; Wałęsa, K. Influence of the geometric parameters of convergent extrusion channel of die on the maximum value of compaction stress of dry ice and on the quality of the obtained pellets. AIP Conf. Proc. 2023; in press. [Google Scholar]
- Górecki, J.; Wałęsa, K.; Biszczanik, A. Determination of the density of solid carbon dioxide using the hydrostatic method. AIP Conf. Proc. 2023; in press. [Google Scholar]
- Stasiak, M.; Molenda, M.; Bańda, M.; Gondek, E. Mechanical properties of sawdust and woodchips. Fuel 2015, 159, 900–908. [Google Scholar] [CrossRef]
- Lei, J.; Wang, D.; Zhang, Q.; Yang, X.; Li, L.; Li, C. Experiment on stress relaxation characteristics of intact rice straw during rotary compression. Trans. Chin. Soc. Agric. Eng. 2015, 31, 76–83. [Google Scholar] [CrossRef]
- Brewin, P.; Coube, O.; Doremus, P.; Tweed, J. Modeling of Powder Die Compaction; Springer: London, UK, 2008. [Google Scholar]
- Ostrowska-Maciejewska, J. Mechanika Ciał Odkształcalnych, 1st ed.; PWN Scientific Publishing House: Warsaw, Poland, 1994; pp. 181–194. [Google Scholar]
- Biszczanik, A.; Górecki, J.; Kukla, M.; Wałęsa, K.; Wojtkowiak, D. Experimental Investigation on the Effect of Dry Ice Compression on the Poisson Ratio. Materials 2022, 15, 1555. [Google Scholar] [CrossRef]
- Gawrońska, E.; Dyja, R.; Zych, M.; Domek, G. Selection of the Heat Transfer Coefficient Using Swarming Algorithms. Acta Mech. Autom. 2022, 16, 325–339. [Google Scholar] [CrossRef]
- Gawrońska, E.; Dyja, R. A Numerical Study of Geometry’s Impact on the Thermal and Mechanical Properties of Periodic Surface Structures. Materials 2021, 14, 427. [Google Scholar] [CrossRef]
- Wójcik, M.; Skrzat, A. The Coupled Eulerian-Lagrangian Analysis of the KOBO Extrusion Process. Adv. Sci. Technol. Res. J. 2021, 15, 197–208. [Google Scholar] [CrossRef]
- Greaves, G.; Greer, A.; Lakes, R.; Rouxel, T. Poissons’s ratio and modern materials. Nat. Mater. 2011, 10, 986. [Google Scholar] [CrossRef]
- Kaufmann, E.; Attree, N.; Bradwell, T.; Hagermann, A. Hardness and Yield Strength of CO2 Ice Under Martian Temperature Conditions. J. Geophys. Res. Planets 2020, 125, e2019JE006217. [Google Scholar] [CrossRef]






| DL | Min | Q25 | Q50 | Q75 | Max | AVR |
|---|---|---|---|---|---|---|
| 0 | 7.9 | 9.1 | 9.5 | 10.1 | 10.5 | 9.5 |
| 10 | 8.2 | 8.5 | 8.9 | 9.3 | 10.6 | 9.0 |
| 20 | 7.6 | 7.7 | 8.5 | 8.8 | 9.0 | 8.3 |
| 30 | 7.9 | 8.1 | 8.6 | 8.9 | 9.3 | 8.6 |
| 40 | 8.3 | 8.7 | 3.4 | 9.6 | 10.3 | 9.3 |
| 50 | 8.2 | 8.5 | 8.9 | 9.0 | 9.3 | 8.8 |
| DL | Min | Q25 | Q50 | Q75 | Max | AVR |
|---|---|---|---|---|---|---|
| 0 | 1170 | 1220 | 1300 | 1360 | 1480 | 1310 |
| 10 | 1440 | 1460 | 1480 | 1520 | 1560 | 1490 |
| 20 | 1310 | 1410 | 1430 | 1460 | 1530 | 1440 |
| 30 | 1380 | 1450 | 1520 | 1530 | 1550 | 1490 |
| 40 | 1280 | 1320 | 1360 | 1570 | 1660 | 1430 |
| 50 | 1310 | 1400 | 1430 | 1470 | 1490 | 1420 |
| DL | Min | Q25 | Q50 | Q75 | Max | AVR |
|---|---|---|---|---|---|---|
| 0 | 7.9 | 9.1 | 9.5 | 10.1 | 10.5 | 9.5 |
| 0.5 | 7.4 | 7.5 | 7.9 | 8.1 | 8.2 | 7.8 |
| 1 | 7.5 | 7.7 | 7.8 | 8.6 | 9.6 | 8.6 |
| 1.5 | 7.8 | 8.3 | 8.5 | 9.3 | 9.4 | 8.7 |
| 2.0 | 7.8 | 8.3 | 8.6 | 9.0 | 9.4 | 8.6 |
| 2.5 | 7.8 | 8 | 9.0 | 9.7 | 9.9 | 8.9 |
| DL | Min | Q25 | Q50 | Q75 | Max | AVR |
|---|---|---|---|---|---|---|
| 0 | 1170 | 1220 | 1300 | 1360 | 1480 | 1310 |
| 0.5 | 1310 | 1320 | 1380 | 1390 | 1500 | 1380 |
| 1 | 1310 | 1330 | 1370 | 1420 | 1440 | 1370 |
| 1.5 | 1430 | 1460 | 1490 | 1500 | 1540 | 1480 |
| 2.0 | 1450 | 1530 | 1530 | 1540 | 1560 | 1530 |
| 2.5 | 1410 | 1500 | 1530 | 1590 | 1640 | 1540 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górecki, J.; Łykowski, W. Influence of Die Land Length on the Maximum Extrusion Force and Dry Ice Pellets Density in Ram Extrusion Process. Materials 2023, 16, 4281. https://doi.org/10.3390/ma16124281
Górecki J, Łykowski W. Influence of Die Land Length on the Maximum Extrusion Force and Dry Ice Pellets Density in Ram Extrusion Process. Materials. 2023; 16(12):4281. https://doi.org/10.3390/ma16124281
Chicago/Turabian StyleGórecki, Jan, and Wiktor Łykowski. 2023. "Influence of Die Land Length on the Maximum Extrusion Force and Dry Ice Pellets Density in Ram Extrusion Process" Materials 16, no. 12: 4281. https://doi.org/10.3390/ma16124281
APA StyleGórecki, J., & Łykowski, W. (2023). Influence of Die Land Length on the Maximum Extrusion Force and Dry Ice Pellets Density in Ram Extrusion Process. Materials, 16(12), 4281. https://doi.org/10.3390/ma16124281