Properties of Accelerating Edge Dislocations in Arbitrary Slip Systems with Reflection Symmetry
Abstract
1. Introduction and Background
2. Most General Differential Equations for Pure Edge Dislocations
3. Cagniard–De Hoop Method
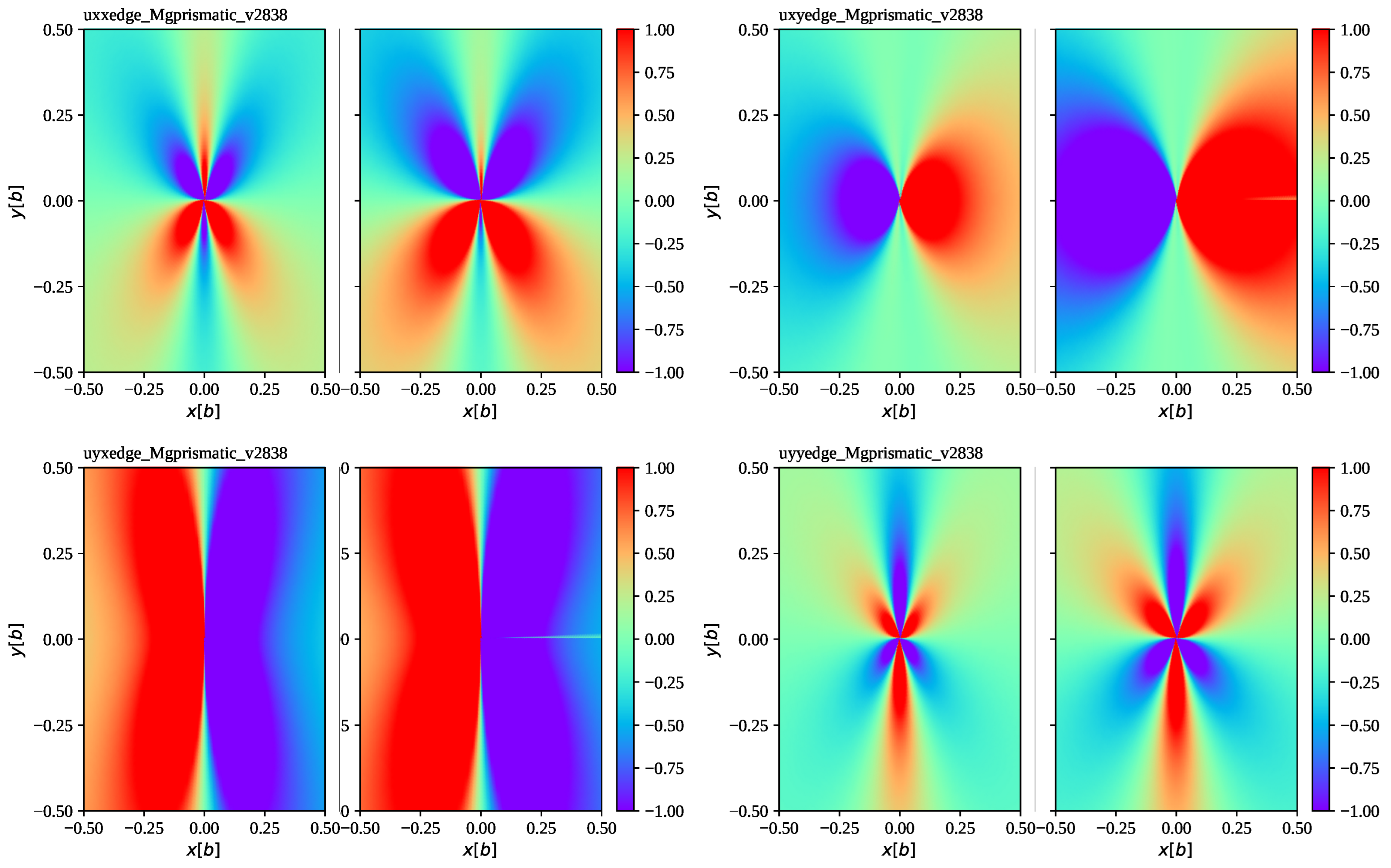
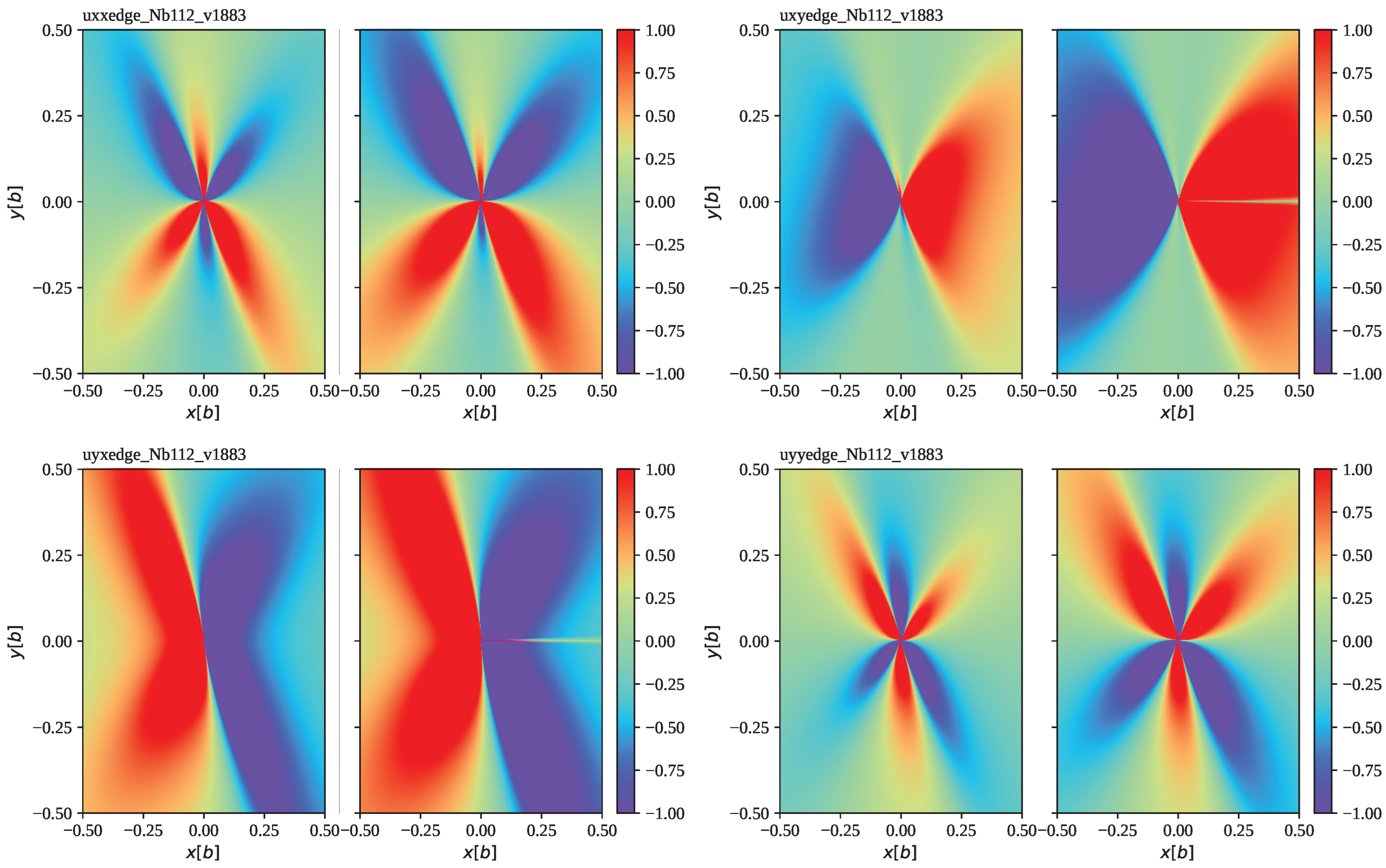
4. Special Cases: Constant Velocity and Constant Acceleration Rate
5. The Isotropic Limit
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Termentzidis, K.; Isaiev, M.; Salnikova, A.; Belabbas, I.; Lacroix, D.; Kioseoglou, J. Impact of screw and edge dislocations on the thermal conductivity of individual nanowires and bulk GaN: A molecular dynamics study. Phys. Chem. Chem. Phys. 2018, 20, 5159–5172. [Google Scholar] [CrossRef]
- Li, Y.; Krajňák, T.; Podaný, P.; Veselý, J.; Džugan, J. Thermal stability of dislocation structure and its effect on creep property in austenitic 316L stainless steel manufactured by directed energy deposition. Mater. Sci. Eng. 2023, A873, 144981. [Google Scholar] [CrossRef]
- Quansah, J.D.; Zhang, X.; Wasiullah, Q.; Yan, Q. Mechanical and thermophysical properties of energetic crystals: Evaluation methods and recent achievements. FirePhysChem 2022, in press. [Google Scholar] [CrossRef]
- Lubk, A.; Rossell, M.D.; Seidel, J.; Chu, Y.H.; Ramesh, R.; Hÿtch, M.J.; Snoeck, E. Electromechanical Coupling among Edge Dislocations, Domain Walls, and Nanodomains in BiFeO3 Revealed by Unit-Cell-Wise Strain and Polarization Maps. Nano Lett. 2013, 13, 1410–1415. [Google Scholar] [CrossRef] [PubMed]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Hansen, B.L.; Beyerlein, I.J.; Bronkhorst, C.A.; Cerreta, E.K.; Dennis-Koller, D. A dislocation-based multi-rate single crystal plasticity model. Int. J. Plast. 2013, 44, 129–146. [Google Scholar] [CrossRef]
- Luscher, D.J.; Mayeur, J.R.; Mourad, H.M.; Hunter, A.; Kenamond, M.A. Coupling continuum dislocation transport with crystal plasticity for application to shock loading conditions. Int. J. Plast. 2016, 76, 111–129. [Google Scholar] [CrossRef]
- Blaschke, D.N.; Hunter, A.; Preston, D.L. Analytic model of the remobilization of pinned glide dislocations: Including dislocation drag from phonon wind. Int. J. Plast. 2020, 131, 102750. [Google Scholar] [CrossRef]
- Gurrutxaga-Lerma, B.; Verschueren, J.; Sutton, A.P.; Dini, D. The mechanics and physics of high-speed dislocations: A critical review. Int. Mater. Rev. 2021, 66, 215–255. [Google Scholar] [CrossRef]
- Alshits, V.I. The Phonon-Dislocation Interaction and its Role in Dislocation Dragging and Thermal Resistivity. In Elastic Strain Fields and Dislocation Mobility; Indenbom, V.L., Lothe, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; Volume 31, pp. 625–697. [Google Scholar] [CrossRef]
- Blaschke, D.N.; Mottola, E.; Preston, D.L. Dislocation drag from phonon wind in an isotropic crystal at large velocities. Philos. Mag. 2020, 100, 571–600. [Google Scholar] [CrossRef]
- Blaschke, D.N. Velocity dependent dislocation drag from phonon wind and crystal geometry. J. Phys. Chem. Solids 2019, 124, 24–35. [Google Scholar] [CrossRef]
- Olmsted, D.L.; Hector, L.G., Jr.; Curtin, W.A.; Clifton, R.J. Atomistic simulations of dislocation mobility in Al, Ni and Al/Mg alloys. Mod. Simul. Mater. Sci. Eng. 2005, 13, 371. [Google Scholar] [CrossRef]
- Marian, J.; Caro, A. Moving dislocations in disordered alloys: Connecting continuum and discrete models with atomistic simulations. Phys. Rev. 2006, B74, 024113. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Accelerating dislocations to transonic and supersonic speeds in anisotropic metals. Appl. Phys. Lett. 2008, 92, 191909. [Google Scholar] [CrossRef]
- Oren, E.; Yahel, E.; Makov, G. Dislocation kinematics: A molecular dynamics study in Cu. Mod. Simul. Mater. Sci. Eng. 2017, 25, 025002. [Google Scholar] [CrossRef]
- Peng, S.; Wei, Y.; Jin, Z.; Yang, W. Supersonic Screw Dislocations Gliding at the Shear Wave Speed. Phys. Rev. Lett. 2019, 122, 045501. [Google Scholar] [CrossRef]
- Blaschke, D.N.; Chen, J.; Fensin, S.; Szajewski, B. Clarifying the definition of ‘transonic’ screw dislocations. Philos. Mag. 2021, 101, 997–1018. [Google Scholar] [CrossRef]
- Dang, K.; Blaschke, D.N.; Fensin, S.; Luscher, D.J. Limiting velocities and transonic dislocations in Mg. Comput. Mater. Sci. 2022, 215, 111786. [Google Scholar] [CrossRef]
- Katagiri, K.; Pikuz, T.; Fang, L.; Albertazzi, B.; Egashira, S.; Inubushi, Y.; Kamimura, G.; Kodama, R.; Koenig, M.; Kozioziemski, B.; et al. Transonic Dislocation Propagation in Diamond. arXiv 2023, arXiv:2303.04370. [Google Scholar]
- Wehrenberg, C.E.; McGonegle, D.; Bolme, C.; Higginbotham, A.; Lazicki, A.; Lee, H.J.; Nagler, B.; Park, H.S.; Remington, B.A.; Rudd, R.E.; et al. In situ X-ray diffraction measurement of shock-wave-driven twinning and lattice dynamics. Nature 2017, 550, 496–499. [Google Scholar] [CrossRef]
- Dresselhaus-Marais, L.E.; Winther, G.; Howard, M.; Gonzalez, A.; Breckling, S.R.; Yildirim, C.; Cook, P.K.; Kutsal, M.; Simons, H.; Detlefs, C.; et al. In situ visualization of long-range defect interactions at the edge of melting. Sci. Adv. 2021, 7, eabe8311. [Google Scholar] [CrossRef]
- Blaschke, D.N. How to determine limiting velocities of dislocations in anisotropic crystals. J. Phys. Cond. Mat. 2021, 33, 503005. [Google Scholar] [CrossRef]
- Teutonico, L.J. Dynamical Behavior of Dislocations in Anisotropic Media. Phys. Rev. 1961, 124, 1039–1045. [Google Scholar] [CrossRef]
- Teutonico, L.J. Uniformly Moving Dislocations of Arbitrary Orientation in Anisotropic Media. Phys. Rev. 1962, 127, 413–418. [Google Scholar] [CrossRef]
- Barnett, D.M.; Lothe, J.; Nishioka, K.; Asaro, R.J. Elastic surface waves in anisotropic crystals: A simplified method for calculating Rayleigh velocities using dislocation theory. J. Phys. F Met. Phys. 1973, 3, 1083–1096. [Google Scholar] [CrossRef]
- Markenscoff, X.; Huang, S. Analysis for a screw dislocation accelerating through the shear-wave speed barrier. J. Mech. Phys. Solids 2008, 56, 2225–2239. [Google Scholar] [CrossRef]
- Markenscoff, X.; Huang, S. The energetics of dislocations accelerating and decelerating through the shear-wave speed barrier. Appl. Phys. Lett. 2009, 94, 021906. [Google Scholar] [CrossRef]
- Huang, S.; Markenscoff, X. Is Intersonic Dislocation Motion Possible? Singularity Analysis for an Edge Dislocation Accelerating through the Shear Wave Speed Barrier. Exp. Mech. 2009, 49, 219–224. [Google Scholar] [CrossRef]
- Pillon, L.; Denoual, C.; Pellegrini, Y.P. Equation of motion for dislocations with inertial effects. Phys. Rev. B 2007, 76, 224105. [Google Scholar] [CrossRef]
- Pellegrini, Y.P. Dynamic Peierls-Nabarro equations for elastically isotropic crystals. Phys. Rev. B 2010, 81, 024101. [Google Scholar] [CrossRef]
- Pellegrini, Y.P. Equation of motion and subsonic-transonic transitions of rectilinear edge dislocations: A collective-variable approach. Phys. Rev. B 2014, 90, 054120. [Google Scholar] [CrossRef]
- Pellegrini, Y.P. Dynamic Peach-Koehler self-force, inertia, and radiation damping of a regularized dislocation. arXiv 2020, arXiv:2005.12704. [Google Scholar]
- Bacon, D.J.; Barnett, D.M.; Scattergood, R.O. Anisotropic continuum theory of lattice defects. Prog. Mater. Sci. 1980, 23, 51–262. [Google Scholar] [CrossRef]
- Pellegrini, Y.P. Causal Stroh formalism for uniformly-moving dislocations in anisotropic media: Somigliana dislocations and Mach cones. Wave Motion 2017, 68, 128–148. [Google Scholar] [CrossRef]
- Markenscoff, X.; Ni, L. The transient motion of a screw dislocation in an anisotropic medium. J. Elast. 1984, 14, 93–95. [Google Scholar] [CrossRef]
- Markenscoff, X.; Ni, L.Q. Nonuniform motion of an edge dislocation in an anisotropic solid. I. Quart. Appl. Math. 1984, 41, 475–494. [Google Scholar] [CrossRef]
- Markenscoff, X.; Ni, L. Nonuniform motion of an edge dislocation in an anisotropic solid. II. Quart. Appl. Math. 1985, 42, 425–432. [Google Scholar] [CrossRef]
- Markenscoff, X.; Ni, L. The transient motion of a dislocation in a solid of general anisotropy. Wave Motion 1987, 9, 191–199. [Google Scholar] [CrossRef]
- Payton, R.G. Transient stresses in a transversely isotropic elastic solid caused by a moving dislocation. Z. Angew. Math. Phys. 1985, 36, 191–203. [Google Scholar] [CrossRef]
- Payton, R.G. Steady state stresses induced in a transversely isotropic elastic solid by a moving dislocation. Z. Angew. Math. Phys. 1995, 46, 282–288. [Google Scholar] [CrossRef]
- Blaschke, D.N. A general solution for accelerating screw dislocations in arbitrary slip systems with reflection symmetry. J. Mech. Phys. Solids 2021, 152, 104448. [Google Scholar] [CrossRef]
- Foreman, A.J.E. Dislocation energies in anisotropic crystals. Acta Met. 1955, 3, 322–330. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Blaschke, D.N. PyDislocDyn, version 1.2.7, 2018–2023. Available online: https://github.com/dblaschke-LANL/PyDislocDyn (accessed on 22 May 2023).
- Markenscoff, X. The transient motion of a nonuniformly moving dislocation. J. Elast. 1980, 10, 193–201. [Google Scholar] [CrossRef]
- Cagniard, L. Réflexion et Réfraction Des Ondes Séismiques Progressives. Ph.D. Thesis, Université de Paris, Sorbonne, France, 1939. [Google Scholar]
- De Hoop, A.T. A modification of Cagniard’s method for solving seismic pulse problems. Appl. Sci. Res. 1960, 8, 349–356. [Google Scholar] [CrossRef]
- Freund, L.B. The Response of an Elastic Solid to Nonuniformly Moving Surface Loads. J. Appl. Mech. 1973, 40, 699–704. [Google Scholar] [CrossRef]
- Blaschke, D.N.; Luscher, D.J. Dislocation drag and its influence on elastic precursor decay. Int. J. Plast. 2021, 144, 103030. [Google Scholar] [CrossRef]
- Rumble, J.R. (Ed.) CRC Handbook of Chemistry and Physics, 102nd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Markenscoff, X.; Clifton, R.J. The nonuniformly moving edge dislocation. J. Mech. Phys. Solids 1981, 29, 253–262. [Google Scholar] [CrossRef]
- Eshelby, J.D. Uniformly Moving Dislocations. Proc. Phys. Soc. A 1949, 62, 307. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blaschke, D.N.; Dang, K.; Fensin, S.J.; Luscher, D.J. Properties of Accelerating Edge Dislocations in Arbitrary Slip Systems with Reflection Symmetry. Materials 2023, 16, 4019. https://doi.org/10.3390/ma16114019
Blaschke DN, Dang K, Fensin SJ, Luscher DJ. Properties of Accelerating Edge Dislocations in Arbitrary Slip Systems with Reflection Symmetry. Materials. 2023; 16(11):4019. https://doi.org/10.3390/ma16114019
Chicago/Turabian StyleBlaschke, Daniel N., Khanh Dang, Saryu J. Fensin, and Darby J. Luscher. 2023. "Properties of Accelerating Edge Dislocations in Arbitrary Slip Systems with Reflection Symmetry" Materials 16, no. 11: 4019. https://doi.org/10.3390/ma16114019
APA StyleBlaschke, D. N., Dang, K., Fensin, S. J., & Luscher, D. J. (2023). Properties of Accelerating Edge Dislocations in Arbitrary Slip Systems with Reflection Symmetry. Materials, 16(11), 4019. https://doi.org/10.3390/ma16114019








