Mechanics Characteristics of a 3D Star-Shaped Negative Poisson’s Ratio Composite Structure
Abstract
1. Introduction
2. Materials and Methods
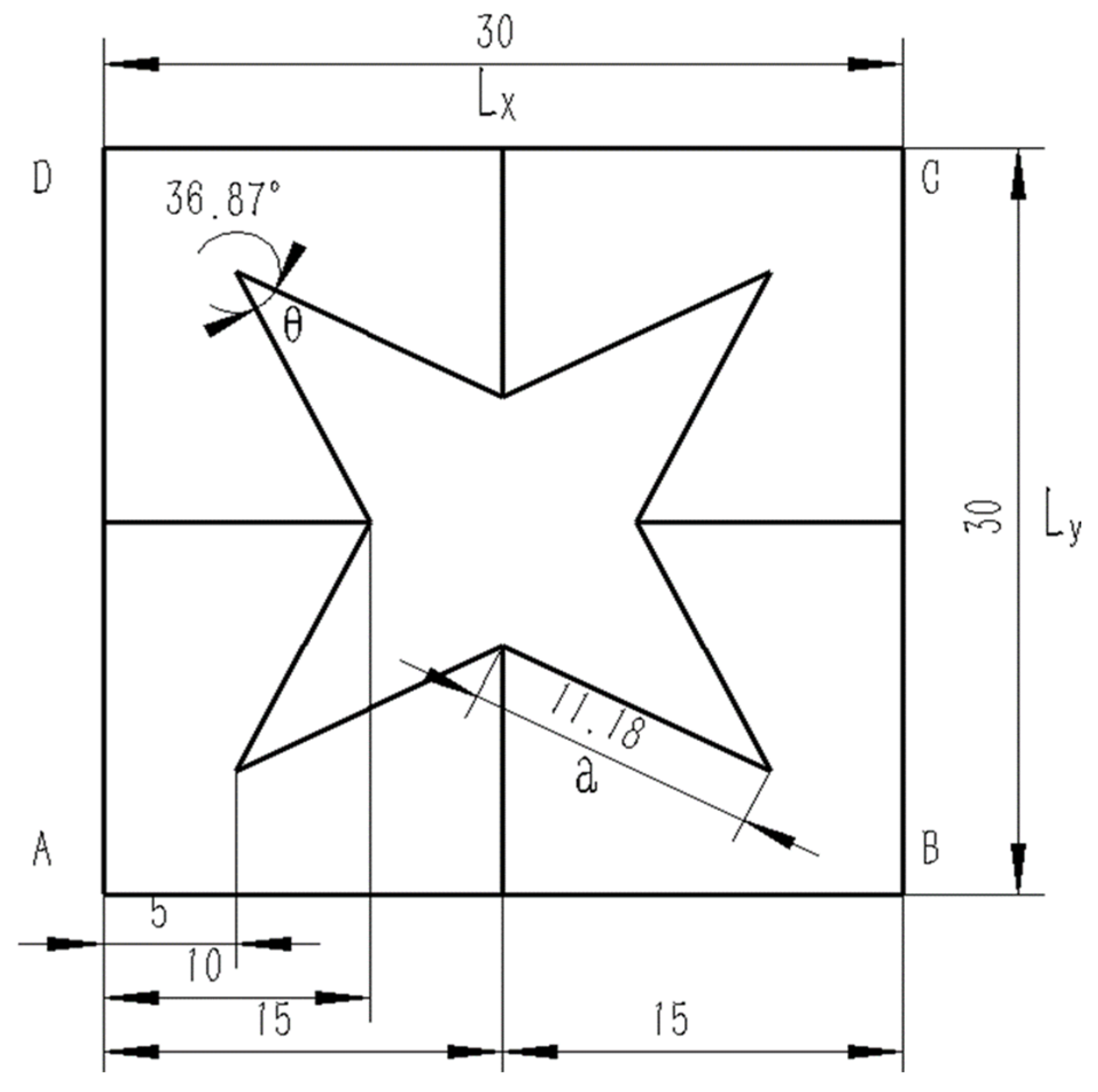
2.1. Three-Dimensional Star-Shaped Negative Poisson’s Ratio Structure
2.2. Numerical Simulation of Three-Dimensional Star-Shaped Negative Poisson’s Ratio Structures
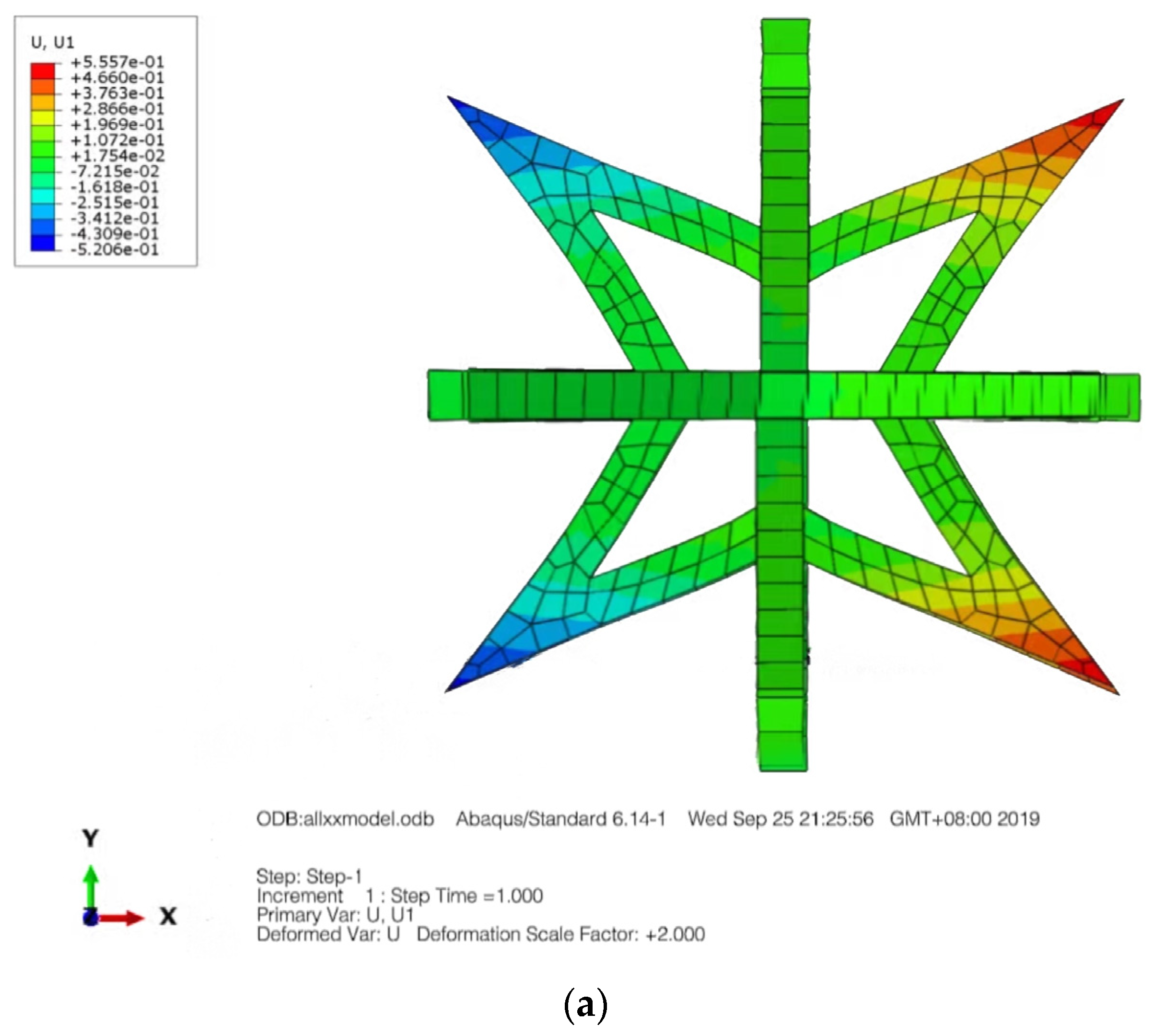
2.2.1. Numerical Simulation of Cellular Elements
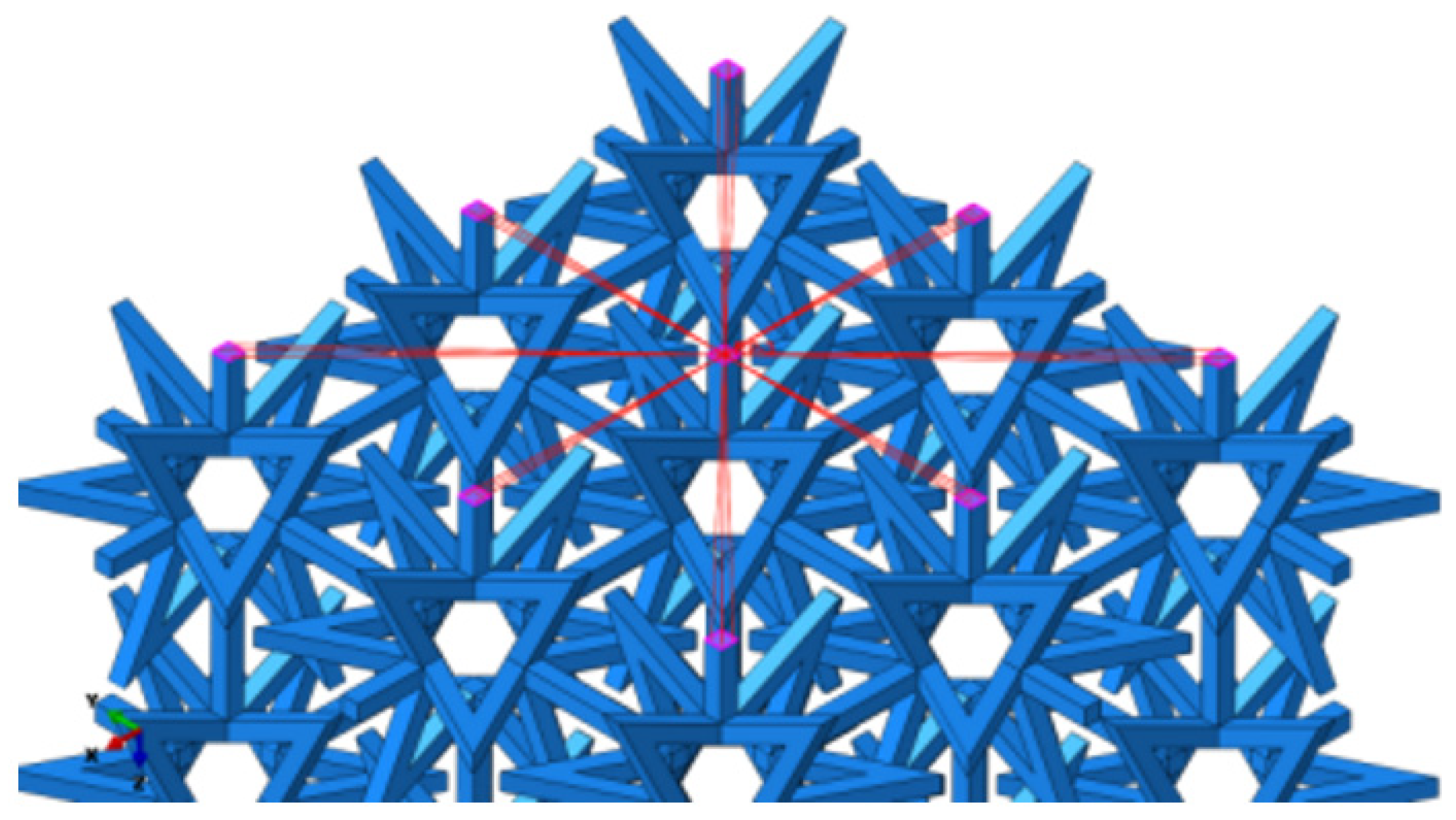
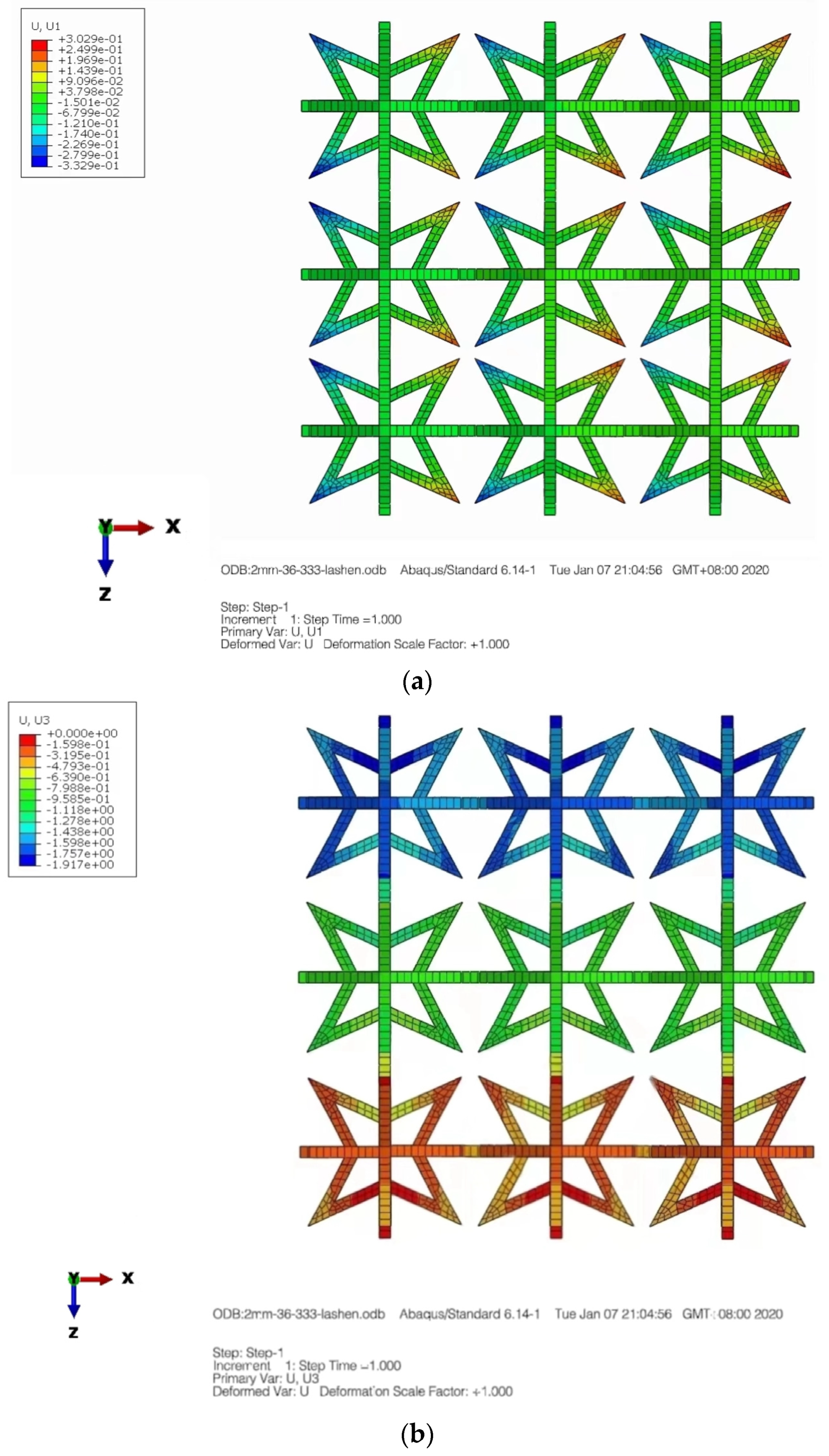
2.2.2. Numerical Simulation of Composite Structures
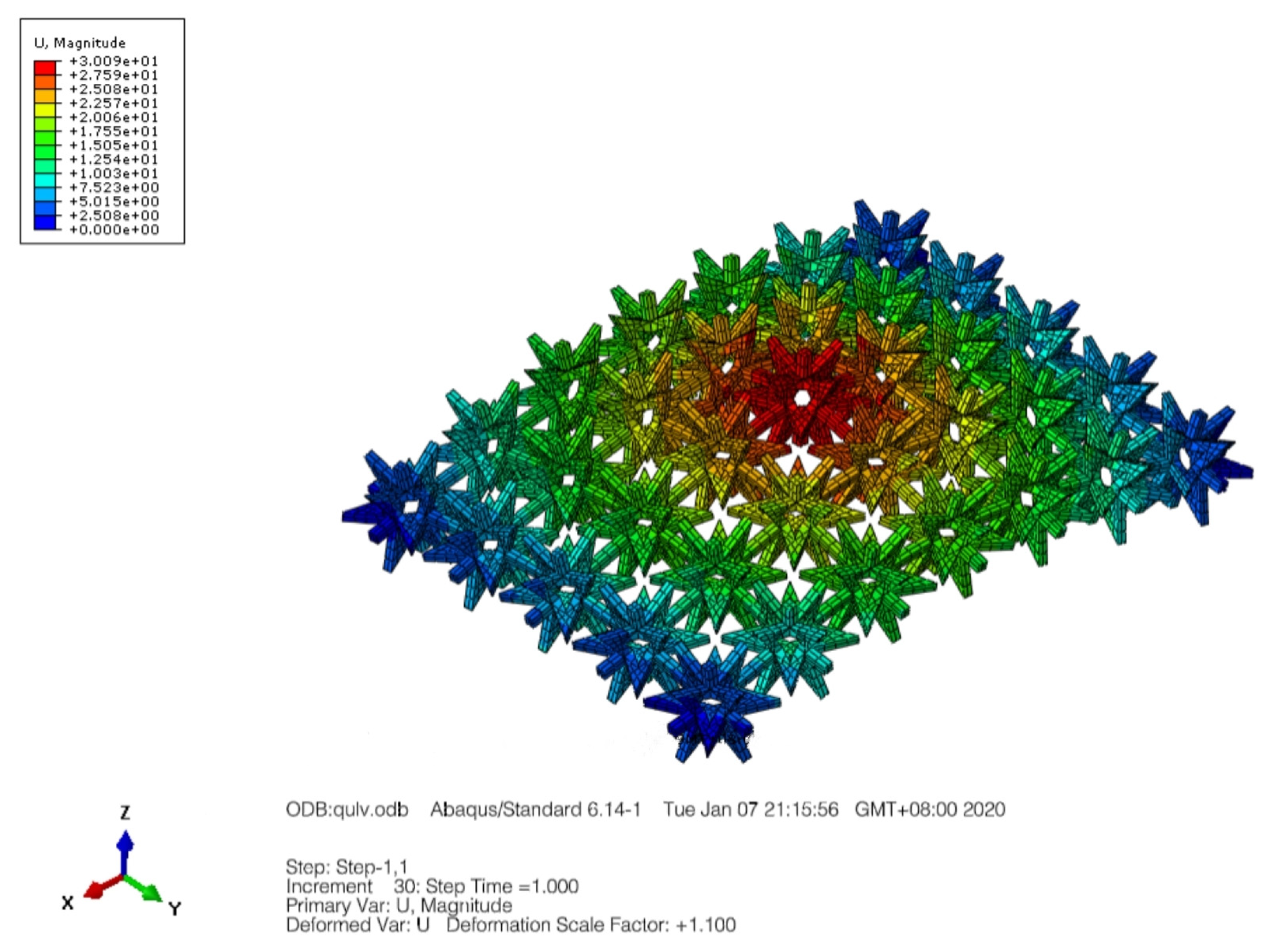
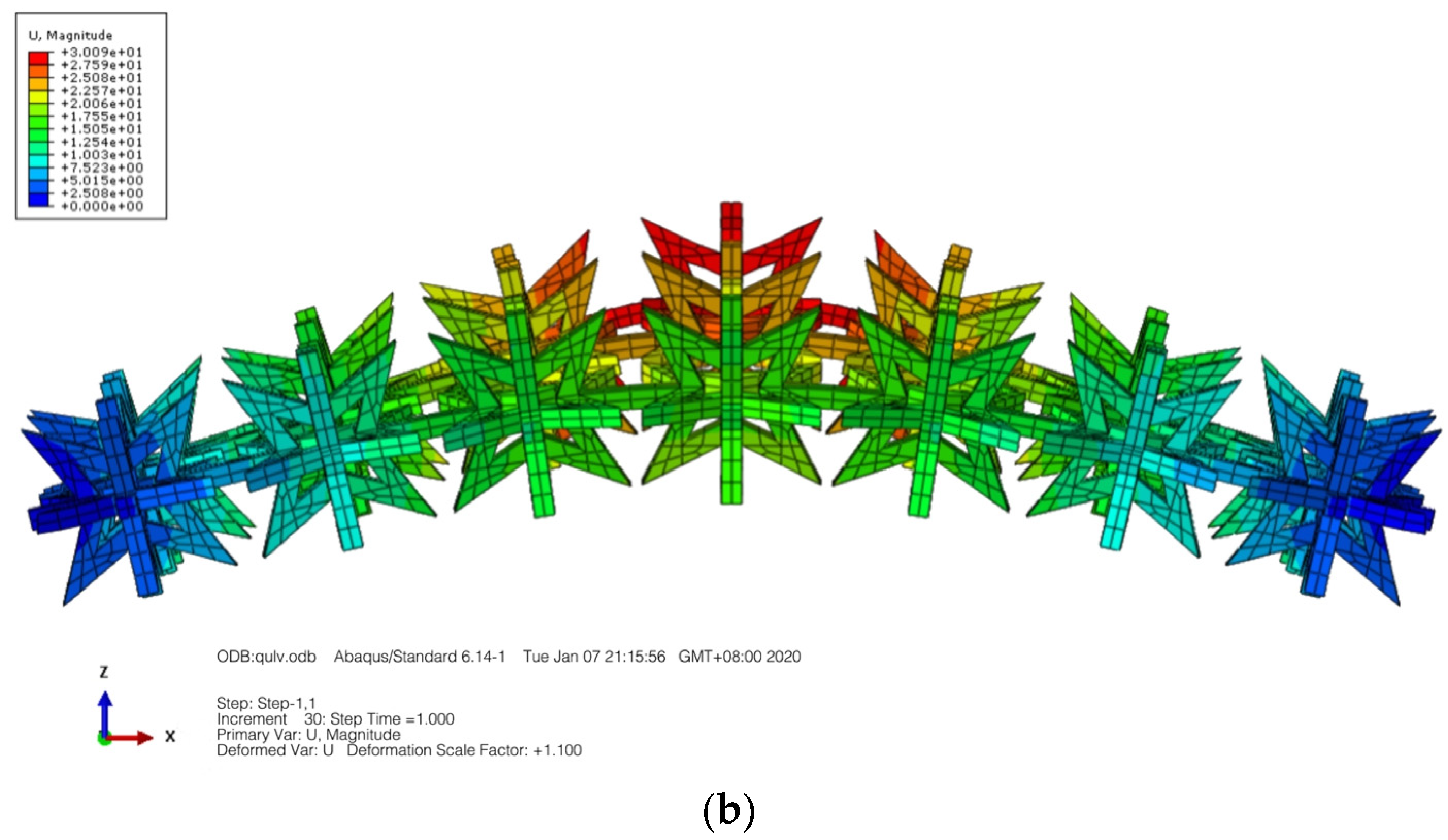
2.2.3. Bending Simulation of Composite Structures
2.3. Model Test of a New Three-Dimensional Star-Shaped Negative Poisson’s Ratio Structure
3. Results and Discussion
3.1. Equivalent Modulus of Elasticity and Equivalent Poisson’s Ratio
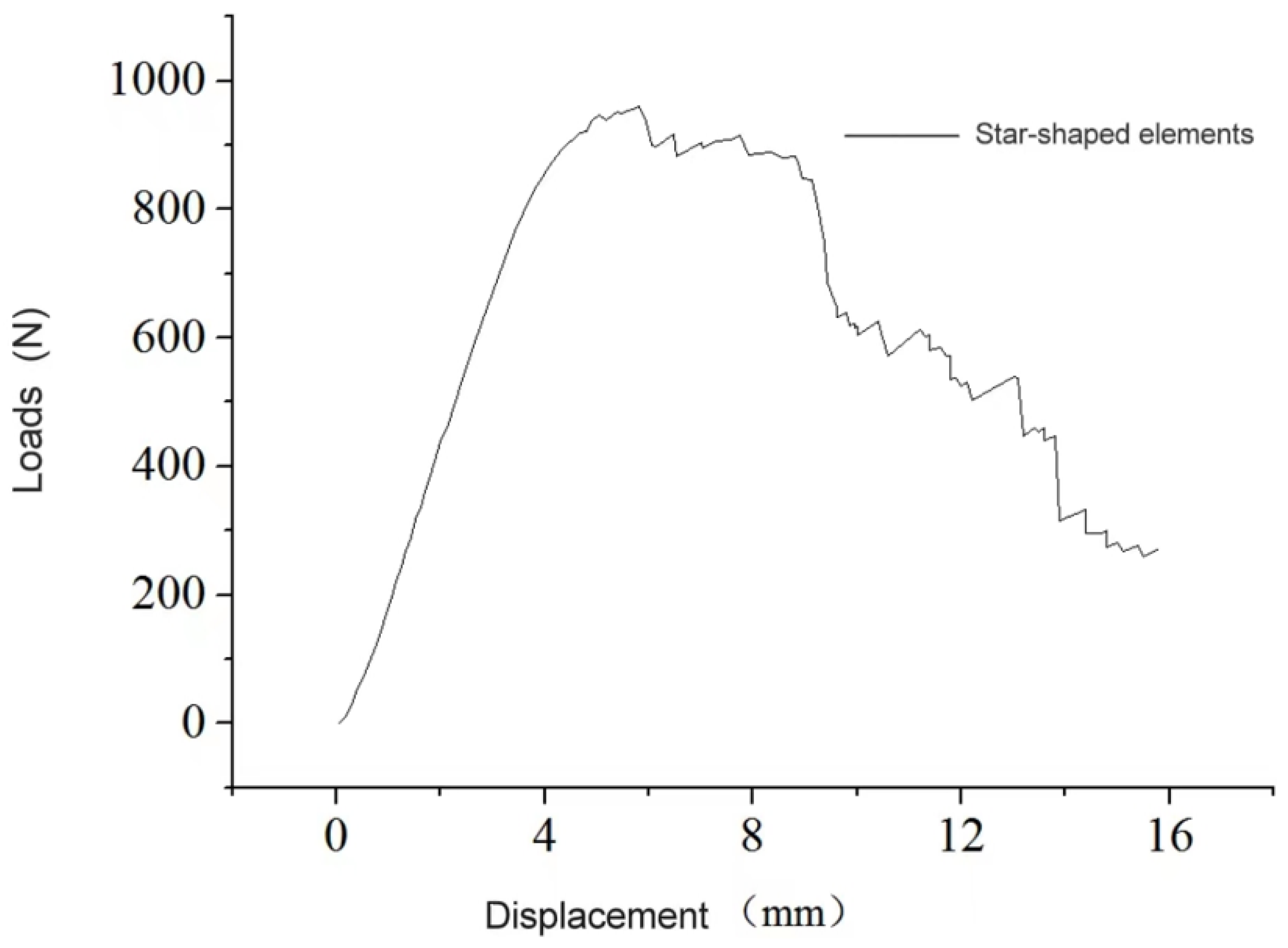
3.2. Three-Dimensional Star-Shaped Component Force–Displacement Curve
3.3. Key Parameter Analysis
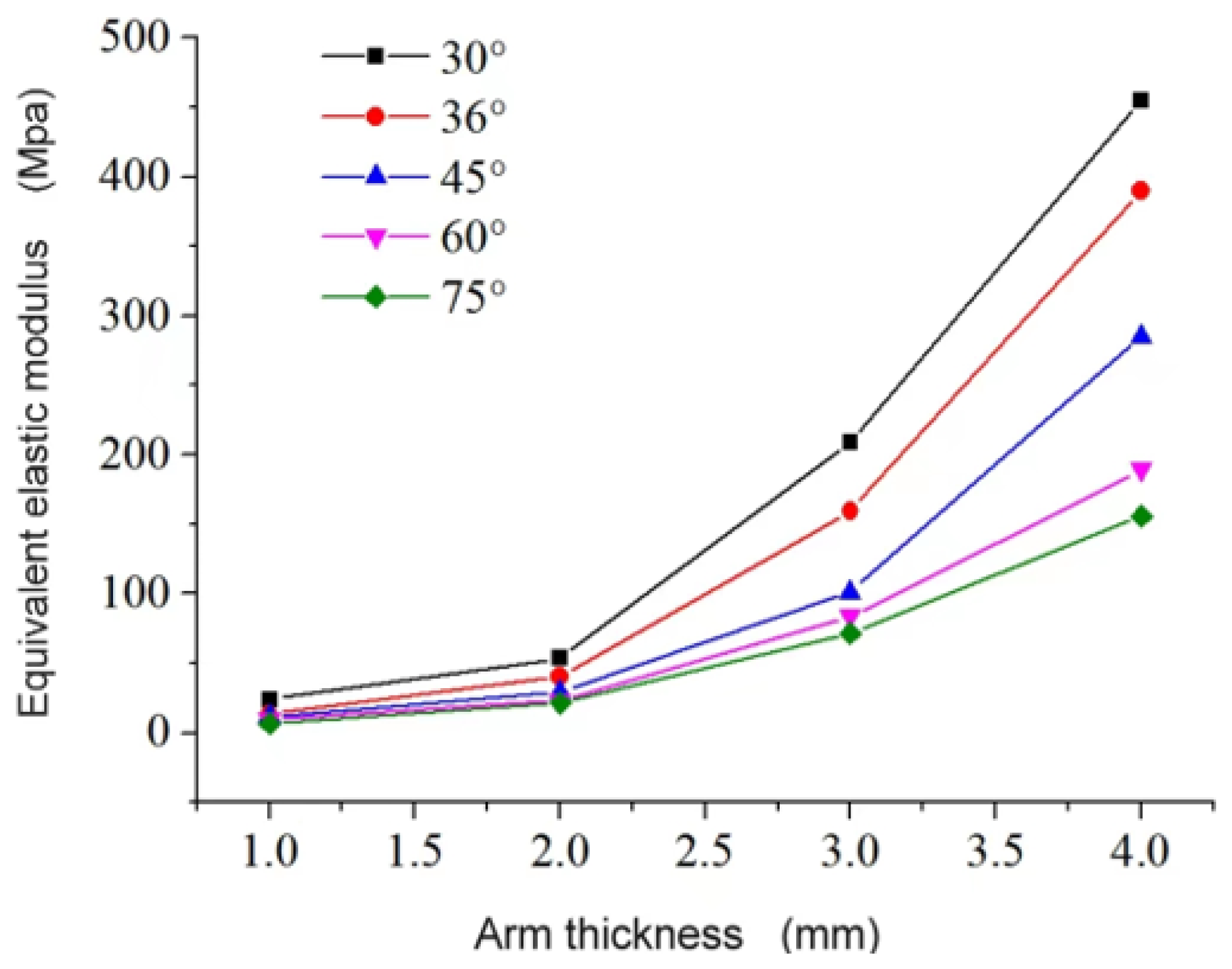
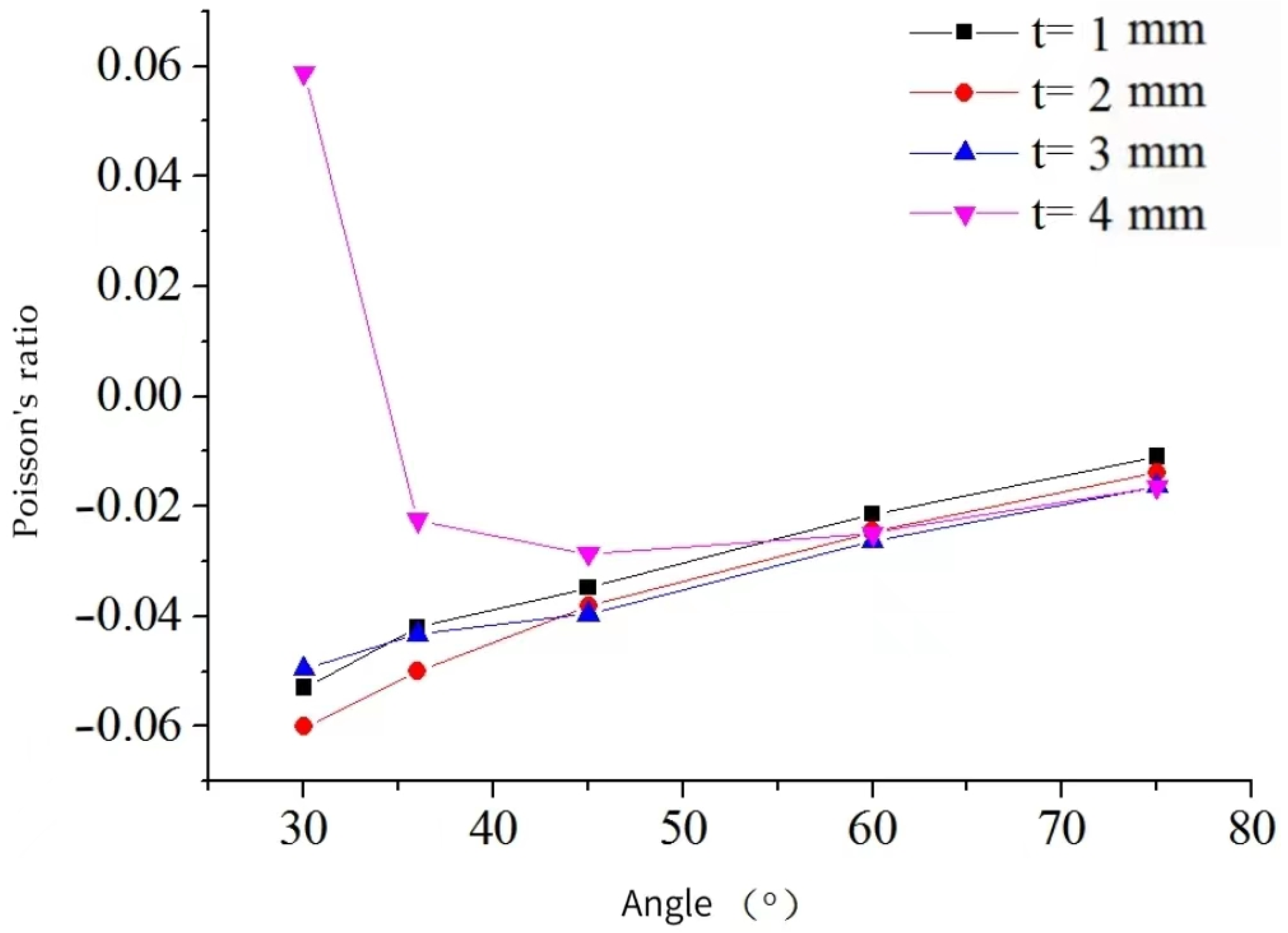
3.3.1. Effect of Structural Dimensions on the Mechanical Properties of the Star-Shaped Negative Poisson’s Ratio Composite Structures
3.3.2. Effect of Material Properties on the Mechanical Properties of the Star-Shaped Negative Poisson’s Ratio Composite Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 7534962014. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 38. [Google Scholar] [CrossRef]
- Xu, B.; Fang, H.; Jiang, S.; Hou, Y.; Lan, L. Geometry reconfiguration of a reflector with an auxetic material surface. In AIAA SCITECH 2022 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar]
- Luo, C.; Han, C.Z.; Zhang, X.Y.; Zhang, X.G.; Ren, X.; Xie, Y.M. Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Struct. 2021, 163, 107682. [Google Scholar] [CrossRef]
- Chen, F.; Du, Y.; He, M.; Sun, X.; Ma, T. Numerical experiment research on failure characteristics of anchored rock with negative Poisson’s ratio bolt. Front. Earth Sci. 2022, 10, 10. [Google Scholar] [CrossRef]
- Wu, Z.M.; Li, H.; Kong, X.S.; Deng, Z.H. A novel design of vibration isolator with high and frequency dependent damping characteristics based on a Large Negative Poisson’s Ratio (LNPR) structure. Mech. Syst. Signal Proc. 2023, 186, 182023. [Google Scholar] [CrossRef]
- Hewage, T.A.M.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson’s Ratio Properties. Adv. Mater. 2016, 28, 10116. [Google Scholar] [CrossRef]
- Liu, W.; Huang, S.; Xu, J. Engineering, Study on Negative Poisson Ratio and Energy Absorption Characteristics of Embedded Arrow Honeycomb Structure. Adv. Sci. Eng. 2020, 12, 47–57. [Google Scholar] [CrossRef]
- Xu, N.; Liu, H.T.; An, M.R.; Wang, L. Novel 2D star-shaped honeycombs with enhanced effective Young’s modulus and negative Poisson’s ratio. Extrem. Mech. Lett. 2021, 43, 92021. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Mousanezhad, D.; Nayeb-Hashemi, H.; Norato, J.; Vaziri, A. 3D cellular metamaterials with planar anti-chiral topology. Mater. Des. 2018, 145, 226–231. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. A three-dimensional rotating rigid units network exhibiting negative Poisson’s ratios. Phys. Status Solidi B-Basic Solid State Phys. 2012, 249, 1330–1338. [Google Scholar] [CrossRef]
- Mohanraj, H.; Ribeiro, S.; Panzera, T.H.; Scarpa, F.; Farrow, I.R.; Jones, R.; Davies-Smith, A.; Remillat, C.D.L.; Walters, P.; Peng, H.X. Hybrid auxetic foam and perforated plate composites for human body support. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1378–1386. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Guo, Z.V.; Dudte, L.; Liang, H.Y.; Mahadevan, L. Geometric Mechanics of Periodic Pleated Origami. Phys. Rev. Lett. 2013, 110, 5. [Google Scholar] [CrossRef] [PubMed]
- Li, T.T.; Liu, F.; Wang, L.F. Enhancing indentation and impact resistance in auxetic composite materials. Compos. Part B Eng. 2020, 198, 102020. [Google Scholar] [CrossRef]
- Tho, N.C.; Van Thom, D.; Cong, P.H.; Zenkour, A.M.; Doan, D.H.; Van Minh, P. Finite element modeling of the bending and vibration behavior of three-layer composite plates with a crack in the core layer. Compos. Struct. 2023, 305, 142023. [Google Scholar]
- Zhang, J.H.; Zhu, X.F.; Yang, X.D.; Zhang, W. Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads. Int. J. Impact Eng. 2019, 134, 102019. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, S.; Li, J.; Pokkalla, D.K.; Wang, Q.; Zhang, C. Novel Isotropic Anti-Tri-Missing Rib Auxetics with Prescribed In-Plane Mechanical Properties Over Large Deformations. Int. J. Appl. Mech. 2022, 13, 2150115. [Google Scholar] [CrossRef]
- Montgomery-Liljeroth, E.; Schievano, S.; Burriesci, G. Elastic properties of 2D auxetic honeycomb structures—A review. Appl. Mater. Today 2023, 30, 101722. [Google Scholar] [CrossRef]
- Yuan, H.; Huang, G.; Qin, G.Z.; Zhang, L.C.; Xie, Y.; Chen, Y.P. Two-Dimensional Carbon Networks with a Negative Poisson’s Ratio. Crystals 2023, 13, 10. [Google Scholar] [CrossRef]
- Jiang, Y.L.; Shi, K.; Zhou, L.A.; He, M.M.; Zhu, C.; Wang, J.C.; Li, J.H.; Li, Y.B.; Liu, L.M.; Sun, D.; et al. 3D-printed auxetic-structured intervertebral disc implant for potential treatment of lumbar herniated disc. Bioact. Mater. 2023, 20, 528–538. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, H.Y.; Kim, J.H.; Kim, J. 3D printing-based soft auxetic structures using PDMS-Ecoflex Hybrid. Funct. Compos. Struct. 2023, 5, 9. [Google Scholar] [CrossRef]
- Xue, B.Z.; Li, J.W.; Huang, R.; Yang, Y.Z.; Gong, H.S.; Zhang, Q.M.; Kong, L.H.; Li, D.M. A Study of Negative Poisson’s Ratio of 3D Printed Auxetic Structures. Mech. Sol. 2022, 57, 1524–1533. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, C. Technology, A double-plate finite-element model for the impact-induced delamination problem. Compos. Sci. Technol. 1995, 53, 111–118. [Google Scholar] [CrossRef]








| Parameter | Numerical Value |
|---|---|
| Ex(Ey,Ez) MPa | 24.34 |
| υxy (υyz,υxz) | −0.048 |
| Parameter | Finite Element Calculation |
|---|---|
| Ex(Ey,Ez) MPa | 23.58 |
| υxy(υyz,υxz) | −0.046 |
| Parameter | Test Value |
|---|---|
| Ey(Ex) MPa | 28.42 |
| υxy | −0.049 |
| Elastic Modulus of Material (MPa) | Poisson Ratio | Equivalent Elastic Modulus (MPa) | Equivalent Poisson’s Ratio |
|---|---|---|---|
| 160,000 | 0.3 | 7182.16 | −0.052 |
| 166,000 | 0.3 | 7451.02 | −0.052 |
| 172,000 | 0.3 | 7720.82 | −0.052 |
| 178,000 | 0.3 | 7990.16 | −0.052 |
| 184,000 | 0.3 | 8259.49 | −0.052 |
| 190,000 | 0.3 | 8528.82 | −0.052 |
| 196,000 | 0.3 | 8798.12 | −0.052 |
| 202,000 | 0.3 | 9067.49 | −0.052 |
| 208,000 | 0.3 | 9336.82 | −0.052 |
| 214,000 | 0.3 | 9606.15 | −0.052 |
| 220,000 | 0.3 | 9875.48 | −0.052 |
| Material Modulus (MPa) | Poisson Ratio | Equivalent Elastic Modulus (MPa) | Equivalent Poisson’s Ratio |
|---|---|---|---|
| 200,000 | 0.1 | 8536.97 | −0.0485 |
| 200,000 | 0.15 | 8633.74 | −0.0492 |
| 200,000 | 0.2 | 8738.98 | −0.0501 |
| 200,000 | 0.25 | 8853.32 | −0.0511 |
| 200,000 | 0.3 | 8977.71 | −0.0522 |
| 200,000 | 0.35 | 9113.17 | −0.0535 |
| 200,000 | 0.4 | 9261.19 | −0.0550 |
| 200,000 | 0.45 | 9423.77 | −0.0567 |
| Material | Elastic Modulus of Material | Poisson Ratio | Equivalent Elastic Modulus | Equivalent Poisson’s Ratio |
|---|---|---|---|---|
| rubber | 6.1 | 0.49 | 0.29 | −0.0582 |
| nylon | 1000 | 0.3 | 44.89 | −0.0522 |
| HT250 cast iron | 66,178.1 | 0.27 | 2945.53 | −0.0515 |
| 7075-T6 aluminum alloy | 72,000 | 0.33 | 3260.72 | −0.0530 |
| Titanium alloy | 110,000 | 0.3 | 4937.74 | −0.0522 |
| Copper alloy | 110,000 | 0.37 | 5043.92 | −0.0541 |
| KTB380-12 cast iron | 120,000 | 0.31 | 5402.32 | −0.0524 |
| Q235 | 210,000 | 0.27 | 9346.90 | −0.0515 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Ye, M.; Huang, Y.; Dong, J. Mechanics Characteristics of a 3D Star-Shaped Negative Poisson’s Ratio Composite Structure. Materials 2023, 16, 3950. https://doi.org/10.3390/ma16113950
Yang L, Ye M, Huang Y, Dong J. Mechanics Characteristics of a 3D Star-Shaped Negative Poisson’s Ratio Composite Structure. Materials. 2023; 16(11):3950. https://doi.org/10.3390/ma16113950
Chicago/Turabian StyleYang, Linyi, Mao Ye, Yonghui Huang, and Jingkun Dong. 2023. "Mechanics Characteristics of a 3D Star-Shaped Negative Poisson’s Ratio Composite Structure" Materials 16, no. 11: 3950. https://doi.org/10.3390/ma16113950
APA StyleYang, L., Ye, M., Huang, Y., & Dong, J. (2023). Mechanics Characteristics of a 3D Star-Shaped Negative Poisson’s Ratio Composite Structure. Materials, 16(11), 3950. https://doi.org/10.3390/ma16113950







