Development of the RF-MEAM Interatomic Potential for the Fe-C System to Study the Temperature-Dependent Elastic Properties
Abstract
1. Introduction
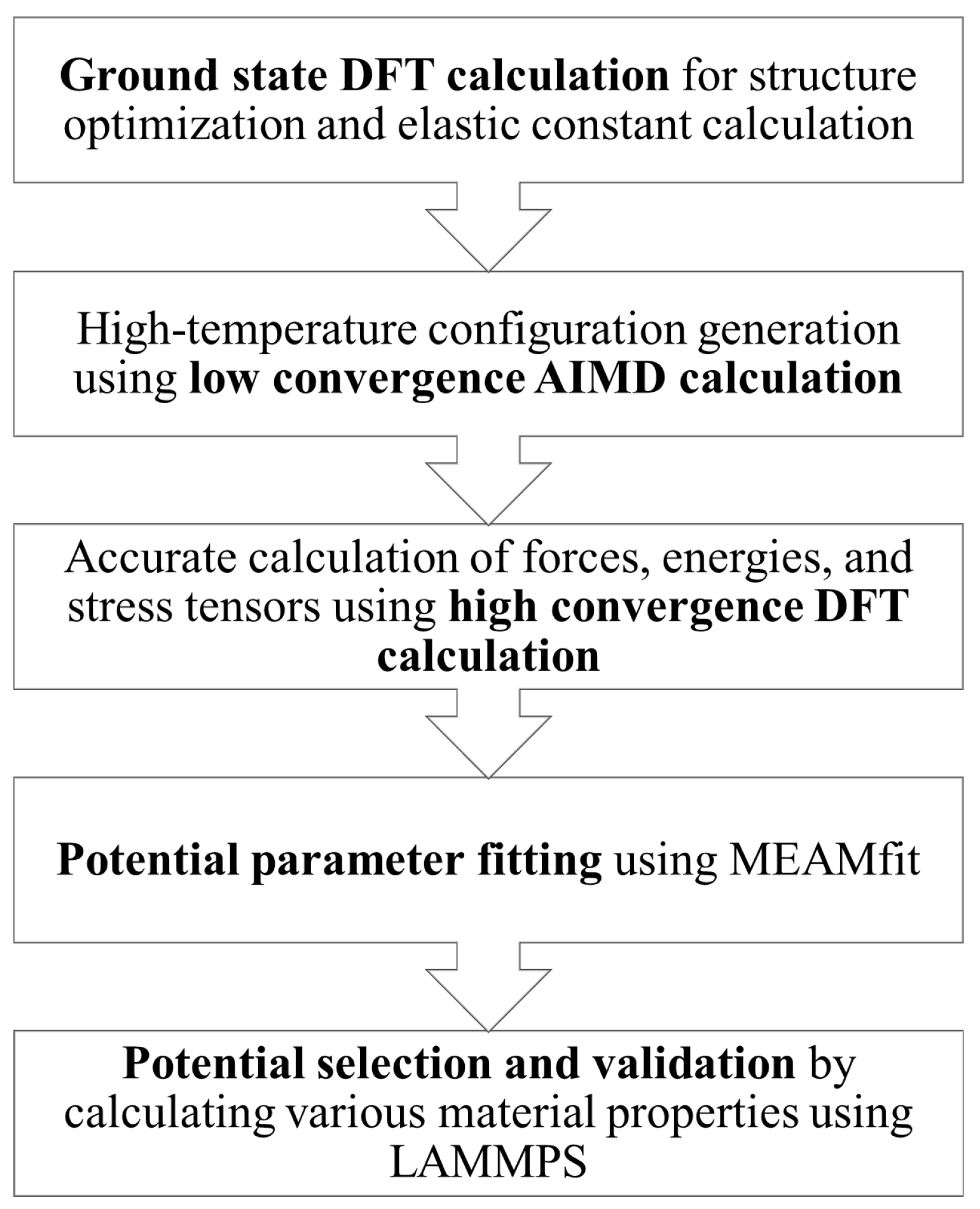
2. Materials and Methods
2.1. Ground State DFT Calculation
2.2. Low-Convergence AIMD Calculation
2.3. High-Convergence DFT Calculation
2.4. Potential Parameter Fitting
2.5. Potential Selection and Validation
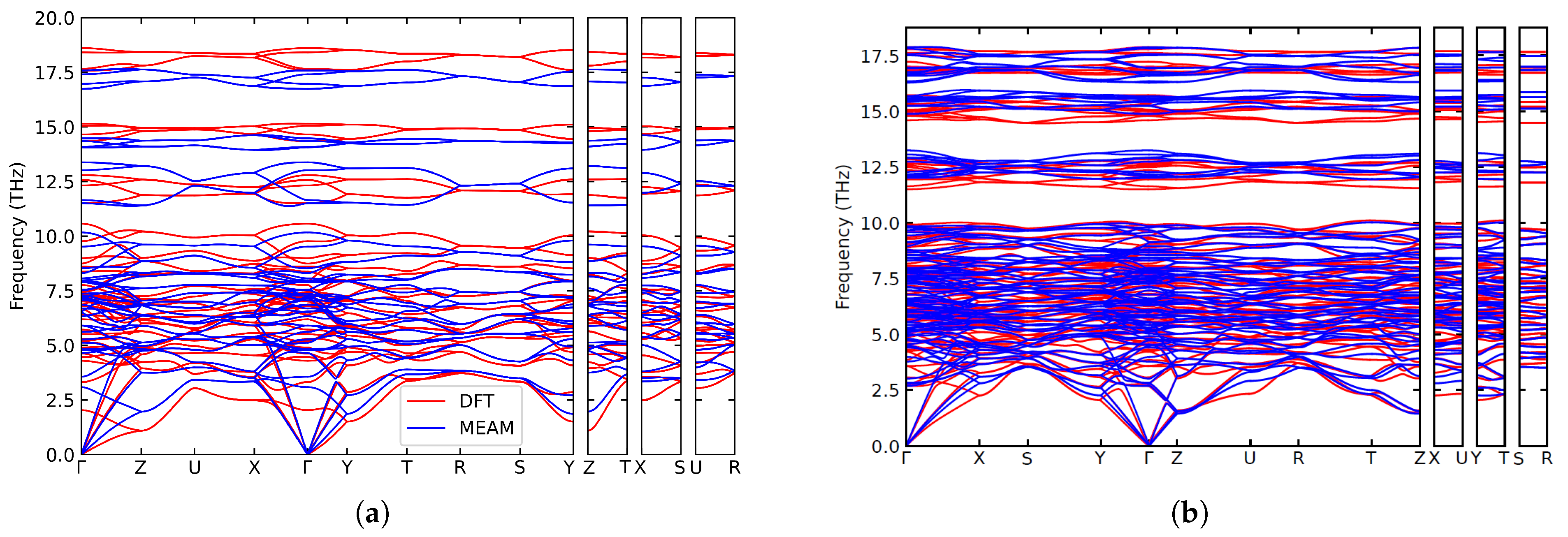
3. Results and Discussion
3.1. Parameters for AIMD Calculations
3.2. Ground State Elastic Calculation
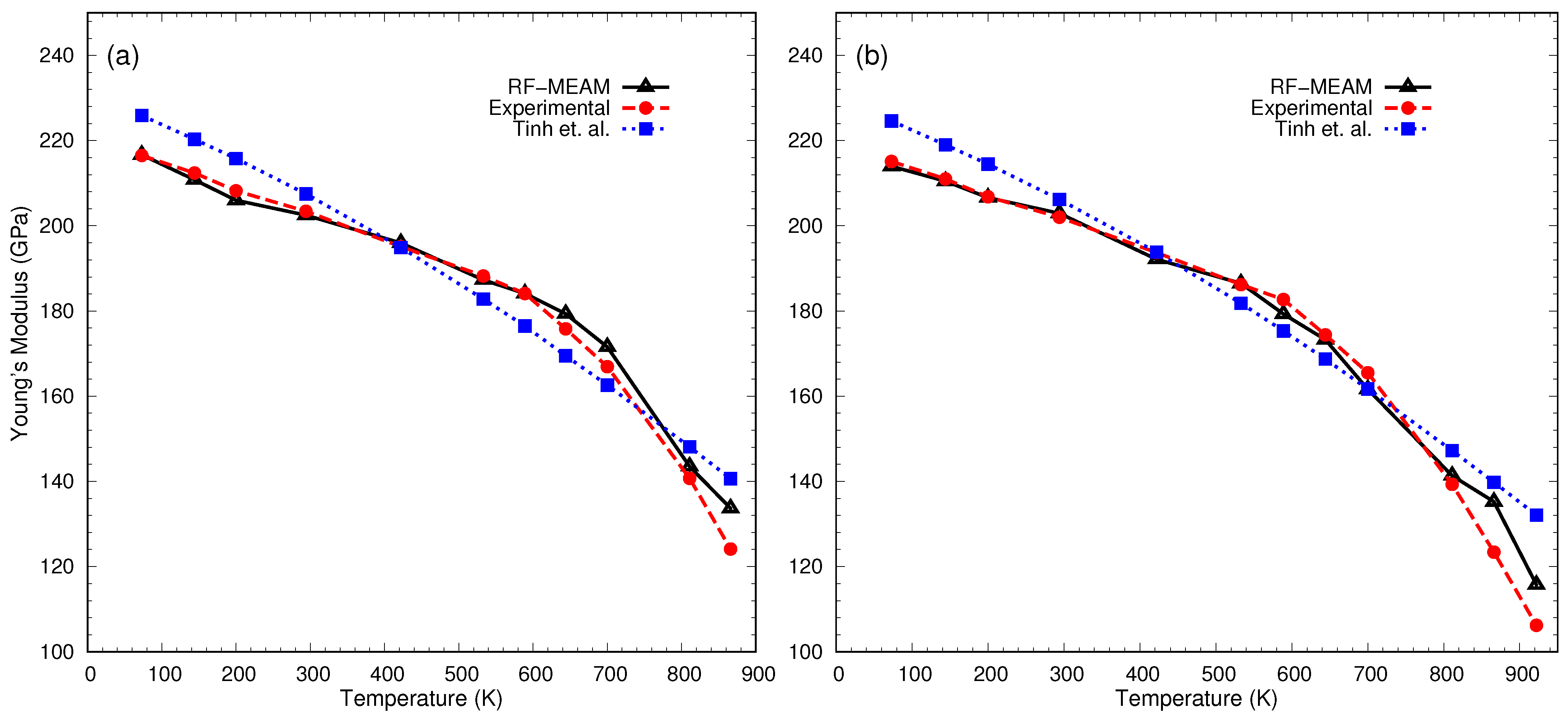
3.3. Finite-Temperature Elasticity Calculation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maraveas, C.; Fasoulakis, Z.; Tsavdaridis, K. Mechanical properties of High and Very High Steel at elevated temperatures and after cooling down. Fire Sci. Rev. 2017, 6, 1–13. [Google Scholar]
- Qiang, X.; Bijlaard, F.; Kolstein, H. Dependence of mechanical properties of high strength steel S690 on elevated temperatures. Constr. Build. Mater. 2012, 30, 73–79. [Google Scholar] [CrossRef]
- Qiang, X.; Jiang, X.; Bijlaard, F.; Kolstein, H. Mechanical properties and design recommendations of very high strength steel S960 in fire. Eng. Struct. 2016, 112, 60–70. [Google Scholar] [CrossRef]
- Azhari, F.; Heidarpour, A.; Zhao, X.; Hutchinson, C. Mechanical properties of ultra-high strength (Grade 1200) steel tubes under cooling phase of a fire: An experimental investigation. Constr. Build. Mater. 2015, 93, 841–850. [Google Scholar] [CrossRef]
- Mirmomeni, M.; Heidarpour, A.; Zhao, X.; Hutchinson, C.; Packer, J.; Wu, C. Mechanical properties of partially damaged structural steel induced by high strain rate loading at elevated temperatures—An experimental investigation. Int. J. Impact Eng. 2015, 76, 178–188. [Google Scholar] [CrossRef]
- Guo, W.; Crowther, D.; Francis, J.; Thompson, A.; Liu, Z.; Li, L. Microstructure and mechanical properties of laser welded S960 high strength steel. Mater. Des. 2015, 85, 534–548. [Google Scholar] [CrossRef]
- Cantwell, P.; Ma, S.; Bojarski, S.; Rohrer, G.; Harmer, M. Expanding time-temperature-transformation (TTT) diagrams to interfaces: A new approach for grain boundary engineering. Acta Mater. 2016, 106, 78–86. [Google Scholar] [CrossRef]
- Wang, W.; Liu, T.; Liu, J. Experimental study on post-fire mechanical properties of high strength Q460 steel. J. Constr. Steel Res. 2015, 114, 100–109. [Google Scholar] [CrossRef]
- Chen, J.; Young, B.; Uy, B. Behavior of high strength structural steel at elevated temperatures. J. Struct. Eng. 2006, 132, 1948–1954. [Google Scholar] [CrossRef]
- Greeley, J.; Nørskov, J. Large-scale, density functional theory-based screening of alloys for hydrogen evolution. Surf. Sci. 2007, 601, 1590–1598. [Google Scholar] [CrossRef]
- Karki, B.; Belbase, B.; Acharya, G.; Singh, S.; Ghimire, M. Pressure-induced creation and annihilation of Weyl points in Td − Mo0.5W0.5Te2 and 1T″ − Mo0.5W0.5Te2. Phys. Rev. B 2022, 105, 125138. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.; Bruno, P.; Galanakis, I. Exchange interactions and temperature dependence of magnetization in half-metallic Heusler alloys. Phys. Rev. B 2005, 72, 184415. [Google Scholar] [CrossRef]
- Kwee, H.; Zhang, S.; Krakauer, H. Finite-Size Correction in Many-Body Electronic Structure Calculations. Phys. Rev. Lett. 2008, 100, 126404. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.; Kermode, J.; Bernstein, N.; Csányi, G. Machine learning a general-purpose interatomic potential for silicon. Phys. Rev. X 2018, 8, 041048. [Google Scholar] [CrossRef]
- Mishin, Y. Machine-learning interatomic potentials for materials science. Acta Mater. 2021, 214, 116980. [Google Scholar] [CrossRef]
- Divi, S.; Agrahari, G.; Kadulkar, S.; Kumar, S.; Chatterjee, A. Improved prediction of heat of mixing and segregation in metallic alloys using tunable mixing rule for embedded atom method. Model. Simul. Mater. Sci. Eng. 2017, 25, 085011. [Google Scholar] [CrossRef]
- Jelinek, B.; Groh, S.; Horstemeyer, M.; Houze, J.; Kim, S.; Wagner, G.; Moitra, A.; Baskes, M. Modified embedded atom method potential for Al, Si, Mg, Cu, and Fe alloys. Phys. Rev. B 2012, 85, 245102. [Google Scholar] [CrossRef]
- Jelinek, B.; Houze, J.; Kim, S.; Horstemeyer, M.; Baskes, M.; Kim, S. Modified embedded-atom method interatomic potentials for the Mg- Al alloy system. Phys. Rev. B 2007, 75, 054106. [Google Scholar] [CrossRef]
- Pun, G.; Mishin, Y. Embedded-atom potential for hcp and fcc cobalt. Phys. Rev. B 2012, 86, 134116. [Google Scholar] [CrossRef]
- Lee, B.; Lee, T.; Kim, S. A modified embedded-atom method interatomic potential for the Fe–N system: A comparative study with the Fe–C system. Acta Mater. 2006, 54, 4597–4607. [Google Scholar] [CrossRef]
- Daw, M.; Baskes, M. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285–1288. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Chen, C.; Deng, Z.; Luo, J.; Ong, S. Quantum-accurate spectral neighbor analysis potential models for Ni-Mo binary alloys and fcc metals. Phys. Rev. B 2018, 98, 1–10. [Google Scholar] [CrossRef]
- Park, Y.; Hijazi, I. EAM Potentials for Hydrogen Storage Application. Am. Soc. Mech. Eng. Press. Vessel. Pip. Div. (Publ.) PVP 2017, 2, 1–5. [Google Scholar]
- Baskes, M.; Nelson, J.; Wright, A. Semiempirical modified embedded-atom potentials for silicon and germanium. Phys. Rev. B Condens. Matter 1989, 40, 6085–6100. [Google Scholar] [CrossRef]
- Lee, B.; Baskes, M. Second nearest-neighbor modified embedded-atom-method potential. Phys. Rev. B 2000, 62, 8564–8567. [Google Scholar] [CrossRef]
- Rose, J.; Smith, J.; Guinea, F.; Ferrante, J. Universal features of the equation of state of metals. Phys. Rev. B Condens. Matter 1984, 29, 2963–2969. [Google Scholar] [CrossRef]
- Li, J.; Liang, S.; Guo, H.; Liu, B. Four-parameter equation of state of solids. Appl. Phys. Lett. 2005, 87, 194111–194113. [Google Scholar] [CrossRef]
- Timonova, M.; Thijsse, B. Optimizing the MEAM potential for silicon. Model. Simul. Mater. Sci. Eng. 2010, 19, 015003. [Google Scholar] [CrossRef]
- Johnson, R.; Dienes, G.; Damask, A. Calculations of the energy and migration characteristics of carbon and nitrogen in α-iron and vanadium. Acta Metall. 1964, 12, 1215–1224. [Google Scholar] [CrossRef]
- Rosato, V. Comparative behavior of carbon in b.c.c. and f.c.c. iron. Acta Metall. 1989, 37, 2759–2763. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Abriata, J. Interatomic potentials for carbon interstitials in metals and intermetallics. Scr. Mater. 2002, 46, 349–355. [Google Scholar] [CrossRef]
- Henriksson, K.; Nordlund, K. Simulations of cementite: An analytical potential for the Fe-C system. Phys. Rev. B 2009, 79, 144107. [Google Scholar] [CrossRef]
- Lee, B. A modified embedded-atom method interatomic potential for the Fe–C system. Acta Mater. 2006, 54, 701–711. [Google Scholar] [CrossRef]
- Liyanage, L.; Kim, S.; Houze, J.; Kim, S.; Tschopp, M.; Baskes, M.; Horstemeyer, M. Structural, elastic, and thermal properties of cementite (Fe3 C) calculated using a modified embedded atom method. Phys. Rev. B 2014, 89, 094102. [Google Scholar] [CrossRef]
- Guziewski, M.; Coleman, S.; Weinberger, C. Atomistic investigation into the atomic structure and energetics of the ferrite-cementite interface: The Bagaryatskii orientation. Acta Mater. 2016, 119, 184–192. [Google Scholar] [CrossRef]
- Nguyen, T.; Sato, K.; Shibutani, Y. Development of Fe-C interatomic potential for carbon impurities in α-iron. Comput. Mater. Sci. 2018, 150, 510–516. [Google Scholar] [CrossRef]
- Pham, T.; Nguyen, T.; Terai, T.; Shibutani, Y.; Sugiyama, M.; Sato, K. Interaction of Carbon and Extended Defects in α-Fe Studied by First-Principles Based Interatomic Potential. Mater. Trans. 2022, 63, 475–483. [Google Scholar] [CrossRef]
- Daw, M.; Baskes, M. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Baskes, M. Modified embedded-atom potentials for cubic materials and impurities. Phys. Rev. B 1992, 46, 2727–2742. [Google Scholar] [CrossRef]
- Lee, B.; Baskes, M.; Kim, H.; Koo Cho, Y. Second nearest-neighbor modified embedded atom method potentials for bcc transition metals. Phys. Rev. B 2001, 64, 184102. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.; Ruzsinszky, A.; Csonka, G.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Ozoliņš, V.; Körling, M. Full-potential calculations using the generalized gradient approximation: Structural properties of transition metals. Phys. Rev. B 1993, 48, 18304–18307. [Google Scholar] [CrossRef]
- Bagno, P.; Jepsen, O.; Gunnarsson, O. Ground-state properties of third-row elements with nonlocal density functionals. Phys. Rev. B 1989, 40, 1997–2000. [Google Scholar] [CrossRef] [PubMed]
- Ziesche, P.; Kurth, S.; Perdew, J. Density functionals from LDA to GGA. Comput. Mater. Sci. 1998, 11, 122–127. [Google Scholar] [CrossRef]
- Xing, W.; Meng, F.; Ning, J.; Sun, J.; Yu, R. Comparative first-principles study of elastic constants of covalent and ionic materials with LDA, GGA, and meta-GGA functionals and the prediction of mechanical hardness. Sci. China Technol. Sci. 2021, 64, 2755–2761. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Grabowski, B.; Ismer, L.; Hickel, T.; Neugebauer, J. Ab initio up to the melting point: Anharmonicity and vacancies in aluminum. PHysical Rev. B Condens. Matter Mater. Phys. 2009, 79, 134106. [Google Scholar] [CrossRef]
- Srinivasan, P.; Duff, A.; Mellan, T.; Sluiter, M.; Nicola, L.; Simone, A. The effectiveness of reference-free modified embedded atom method potentials demonstrated for NiTi and NbMoTaW. Model. Simul. Mater. Sci. Eng. 2019, 27, 65013. [Google Scholar] [CrossRef]
- Duff, A. MEAMfit: A reference-free modified embedded atom method (RF-MEAM) energy and force-fitting code. Comput. Phys. Commun. 2016, 203, 354–355. [Google Scholar] [CrossRef]
- Carreras, A. Abelcarreras/Phonolammps: LAMMPS Interface for Phonon Calculations Using Phonopy. GitHub. Available online: https://github.com/abelcarreras/phonolammps (accessed on 25 April 2023).
- Parrinello, M.; Rahman, A. Crystal Structure and Pair Potentials: A Molecular-Dynamics Study. Phys. Rev. Lett. 1980, 45, 1196–1199. [Google Scholar] [CrossRef]
- Scott, R.; Allen, M.; Tildesley, D. Computer Simulation of Liquids. Math. Comput. 1991, 57, 442–444. [Google Scholar] [CrossRef]
- Henriksson, K.; Sandberg, N.; Wallenius, J. Carbides in stainless steels: Results from ab initio investigations. Appl. Phys. Lett. 2008, 93, 2006–2009. [Google Scholar] [CrossRef]
- Chihi, T.; Bouhemadou, A.; Reffas, M.; Khenata, R.; Ghebouli, M.; Ghebouli, B.; Louail, L. Structural, elastic and thermodynamic properties of iron carbide Fe7C3 phases: An ab initio study. Chin. J. Phys. 2017, 55, 977–988. [Google Scholar] [CrossRef]
- Fang, C.; Huis, M.; Zandbergen, H. Structural, electronic, and magnetic properties of iron carbide Fe7C3 phases from first-principles theory. Phys. Rev. B 2009, 80, 224108. [Google Scholar] [CrossRef]
- Villars, P.; Calvert, L. Pearson’s Handbook of Crystallographic Data for Intermediate Phases; American Society of Metals: Cleveland, OH, USA, 1985. [Google Scholar]
- Mouhat, F.; Coudert, F. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik: Teubner-Leipzig; Macmillan: New York, NY, USA, 1928. [Google Scholar]
- Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Jiang, C.; Srinivasan, S.; Caro, A.; Maloy, S. Structural, elastic, and electronic properties of Fe3C from first principles. J. Appl. Phys. 2008, 103, 43502. [Google Scholar] [CrossRef]
- Brakman, C.M. The Voigt model case. Philos. Mag. A 1987, 55, 39–58. [Google Scholar] [CrossRef]
- Engineering ToolBox. Metals and Alloys—Young’s Modulus of Elasticity. 2004. Available online: https://www.engineeringtoolbox.com/young-modulus-d_773.html (accessed on 25 April 2023).
- Tinh, B.; Hoc, N.; Vinh, D.; Cuong, T.; Hien, N. Thermodynamic and Elastic Properties of Interstitial Alloy FeC with BCC Structure at Zero Pressure. Adv. Mater. Sci. Eng. 2018, 2018, 5251741. [Google Scholar] [CrossRef]



| Fe-C Structure | k-Points (Gamma) | No. of Atoms | Supercell |
|---|---|---|---|
| B1 | 7 × 15 × 15 | 128 | 4 × 2 × 2 |
| B2 | 9 × 12 × 16 | 120 | 5 × 4 × 3 |
| B3 | 7 × 15 × 15 | 128 | 4 × 2 × 2 |
| Cementite | 23 × 10 × 7 | 64 | 1 × 2 × 2 |
| L12 | 10 × 15 × 15 | 48 | 3 × 2 × 2 |
| Fe-C Structure | k-Points (Gamma) | No. of Atoms | Supercell |
|---|---|---|---|
| B1 | 15 × 15 × 15 | 64 | 2 × 2 × 2 |
| B2 | 16 × 16 × 16 | 54 | 3 × 3 × 3 |
| B3 | 15 × 15 × 15 | 64 | 2 × 2 × 2 |
| Cementite | 23 × 10 × 7 | 64 | 1 × 2 × 2 |
| L12 | 10 × 15 × 15 | 48 | 3 × 2 × 2 |
| Structure | V (Å) | B (GPa) | B’ | |||
|---|---|---|---|---|---|---|
| RF-MEAM | Literature | RF-MEAM | Literature | RF-MEAM | Literature | |
| B1 (FeC) | 65 | 338 | 5.28 | |||
| B2 (FeC) | 16 | 302 | 4.12 | |||
| B3 (FeC) | 78 | 222 | 4.50 | |||
| Cementite (Fe3C) | 155 | 252 | 4.05 | |||
| O-FeC | 94 | , () | 288 | , | 3.10 | , |
| Elastic Constants (GPa) | Fe3C-Cementite | FeC-B1 | O-FeC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| This Study | Literature | This Study | Literature | This Study | Literature | ||||
| RF-MEAM | DFT | DFT/MEAM | RF-MEAM | DFT | DFT/MEAM | RF-MEAM | DFT | DFT/MEAM | |
| C11 | 399 | 296 | 585 | 584 | 399 | 344 | |||
| C22 | 459 | 392 | - | - | - | 469 | 428 | 445c | |
| C33 | 364 | 330 | - | - | - | 444 | 423 | ||
| C12 | 236 | 137 | 214 | 205 | 238 | 166 | |||
| C13 | 210 | 181 | - | - | - | 245 | 170 | ||
| C23 | 204 | 155 | - | - | - | 255 | 182 | ||
| C44 | 116 | 131 | 125 | 82 | 106 | 95 | |||
| C55 | 40 | 19 | - | - | - | 98 | 89 | ||
| C66 | 119 | 135 | - | - | - | 81 | 66 | ||
| - | |||||||||
| B | 280 | 218 | 338 | 331 | 310 | 247 | |||
| G | 93 | 93 | 149 | 125 | 95 | 95 | |||
| Y | 252 | 245 | 390 | 334 | 259 | 253 | |||
| T(K) | FeC-0.2% | FeC-0.4% | ||||
|---|---|---|---|---|---|---|
| B (GPa) | G (GPa) | E (GPa) | B (GPa) | G (GPa) | E (GPa) | |
| 73 | 215 | 81 | 217 | 214 | 80 | 214 |
| 144 | 211 | 79 | 211 | 210 | 79 | 210 |
| 200 | 206 | 77 | 206 | 204 | 78 | 207 |
| 294 | 202 | 76 | 203 | 202 | 76 | 203 |
| 422 | 195 | 74 | 196 | 194 | 72 | 192 |
| 533 | 186 | 70 | 187 | 185 | 70 | 186 |
| 589 | 186 | 69 | 184 | 183 | 67 | 179 |
| 644 | 179 | 67 | 179 | 180 | 65 | 173 |
| 700 | 173 | 64 | 172 | 174 | 60 | 162 |
| 811 | 167 | 53 | 144 | 169 | 52 | 141 |
| 866 | 165 | 49 | 134 | 162 | 50 | 135 |
| 922 | - | - | - | 154 | 42 | 116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Risal, S.; Singh, N.; Duff, A.I.; Yao, Y.; Sun, L.; Risal, S.; Zhu, W. Development of the RF-MEAM Interatomic Potential for the Fe-C System to Study the Temperature-Dependent Elastic Properties. Materials 2023, 16, 3779. https://doi.org/10.3390/ma16103779
Risal S, Singh N, Duff AI, Yao Y, Sun L, Risal S, Zhu W. Development of the RF-MEAM Interatomic Potential for the Fe-C System to Study the Temperature-Dependent Elastic Properties. Materials. 2023; 16(10):3779. https://doi.org/10.3390/ma16103779
Chicago/Turabian StyleRisal, Sandesh, Navdeep Singh, Andrew Ian Duff, Yan Yao, Li Sun, Samprash Risal, and Weihang Zhu. 2023. "Development of the RF-MEAM Interatomic Potential for the Fe-C System to Study the Temperature-Dependent Elastic Properties" Materials 16, no. 10: 3779. https://doi.org/10.3390/ma16103779
APA StyleRisal, S., Singh, N., Duff, A. I., Yao, Y., Sun, L., Risal, S., & Zhu, W. (2023). Development of the RF-MEAM Interatomic Potential for the Fe-C System to Study the Temperature-Dependent Elastic Properties. Materials, 16(10), 3779. https://doi.org/10.3390/ma16103779







