Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data
Abstract
1. Introduction
2. Samples and Measuring Equipment Used for Measuring the Sound Absorption Coefficient
2.1. Sample for Measuring the Sound Absorption Coefficient
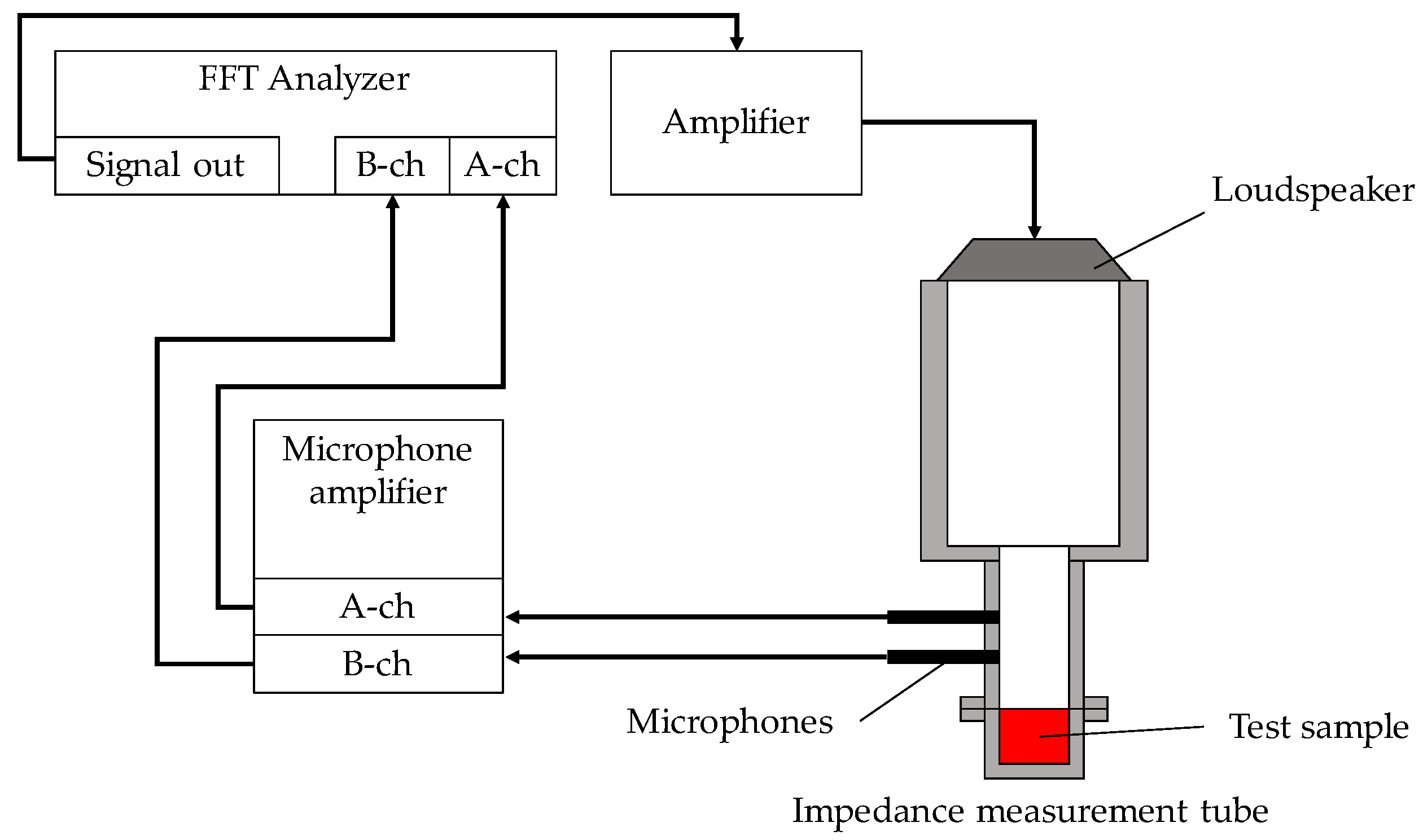
2.2. Equipment for Measuring the Sound Absorption Coefficient
3. Methods and Results of Measuring Tortuosity
3.1. Tortuosity Measurement Sample
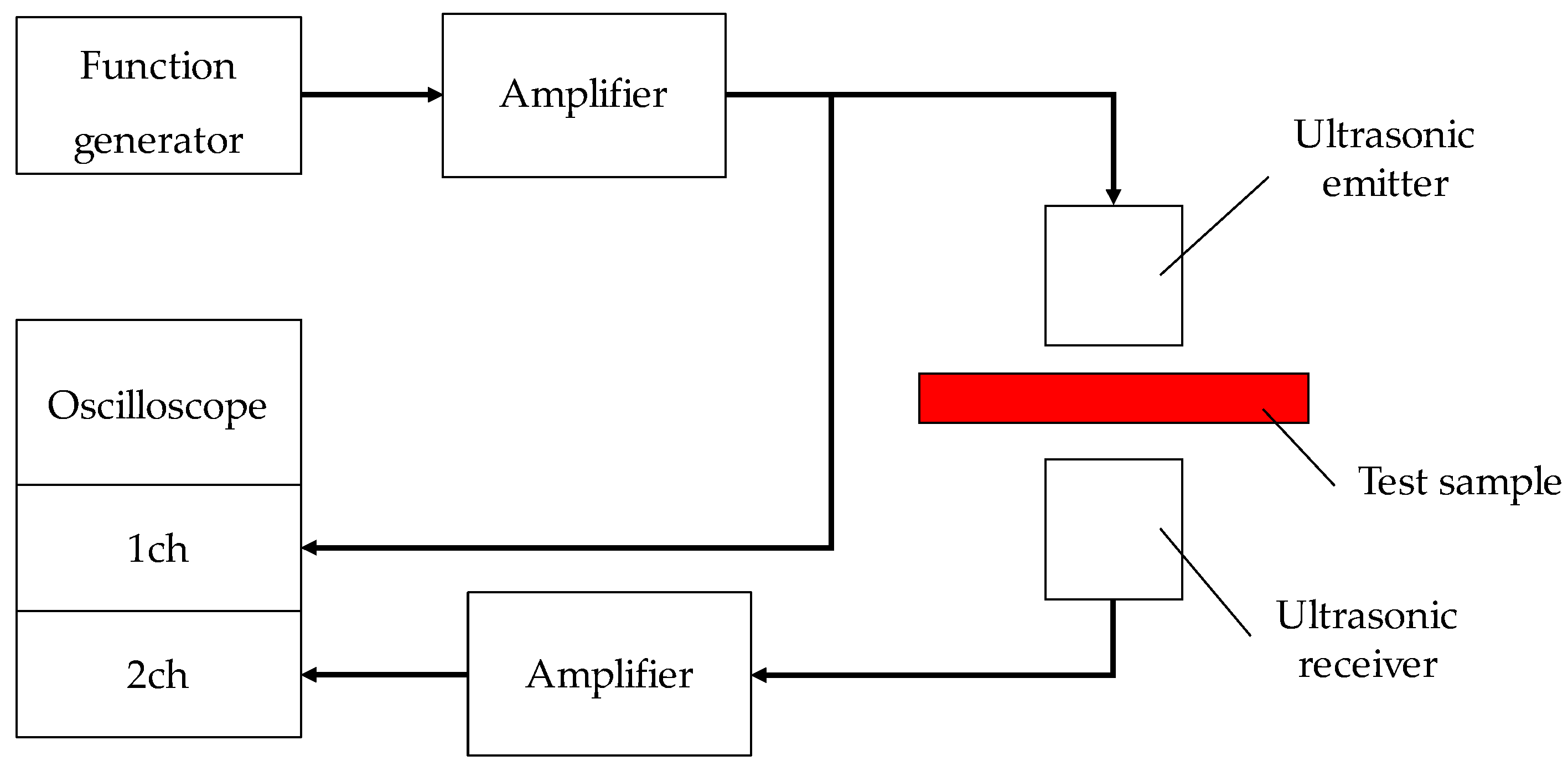
3.2. Tortuosity Measurement
4. Theoretical Analysis
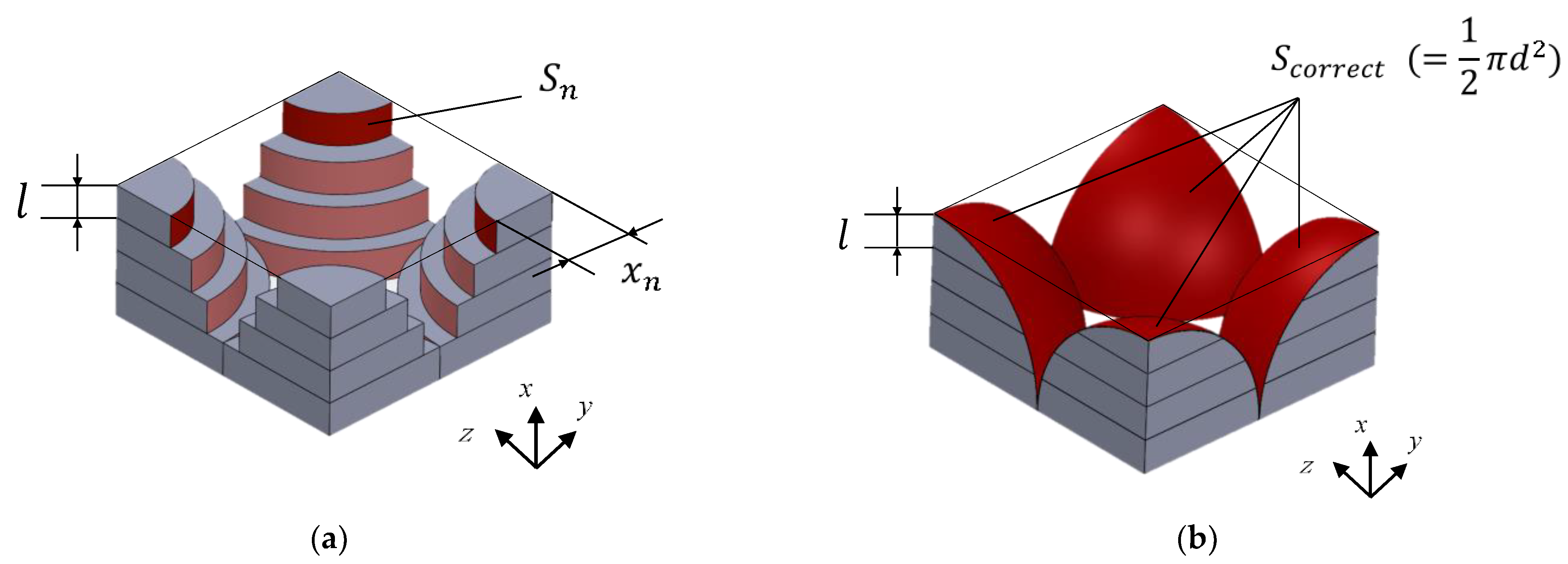
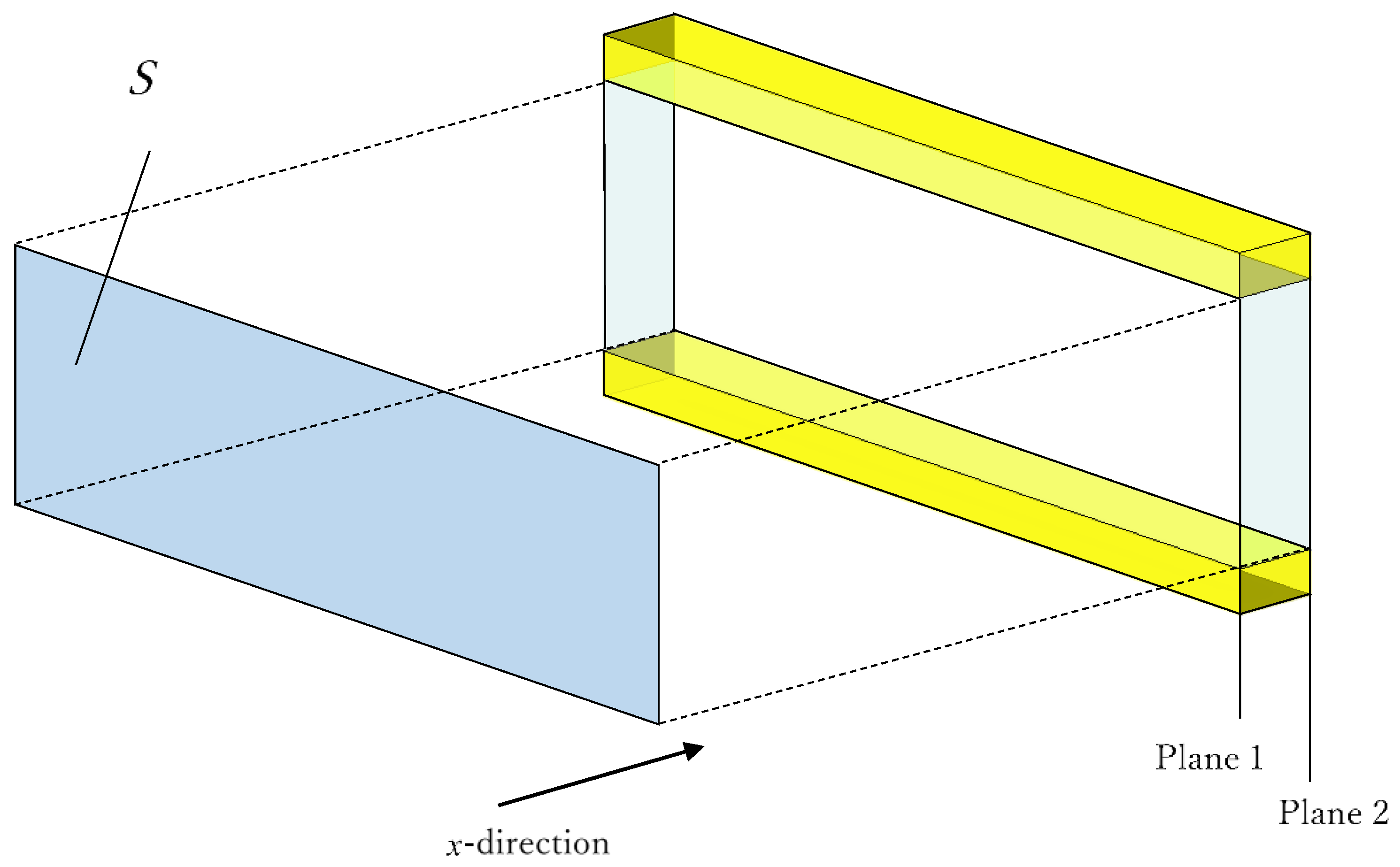
4.1. Analysis Unit and Element Division of the Packing Structure
4.2. Numerical Analysis of the Tomograms in Random Packing
4.3. Propagation Constants and Characteristic Impedance Considering the Tortuosity
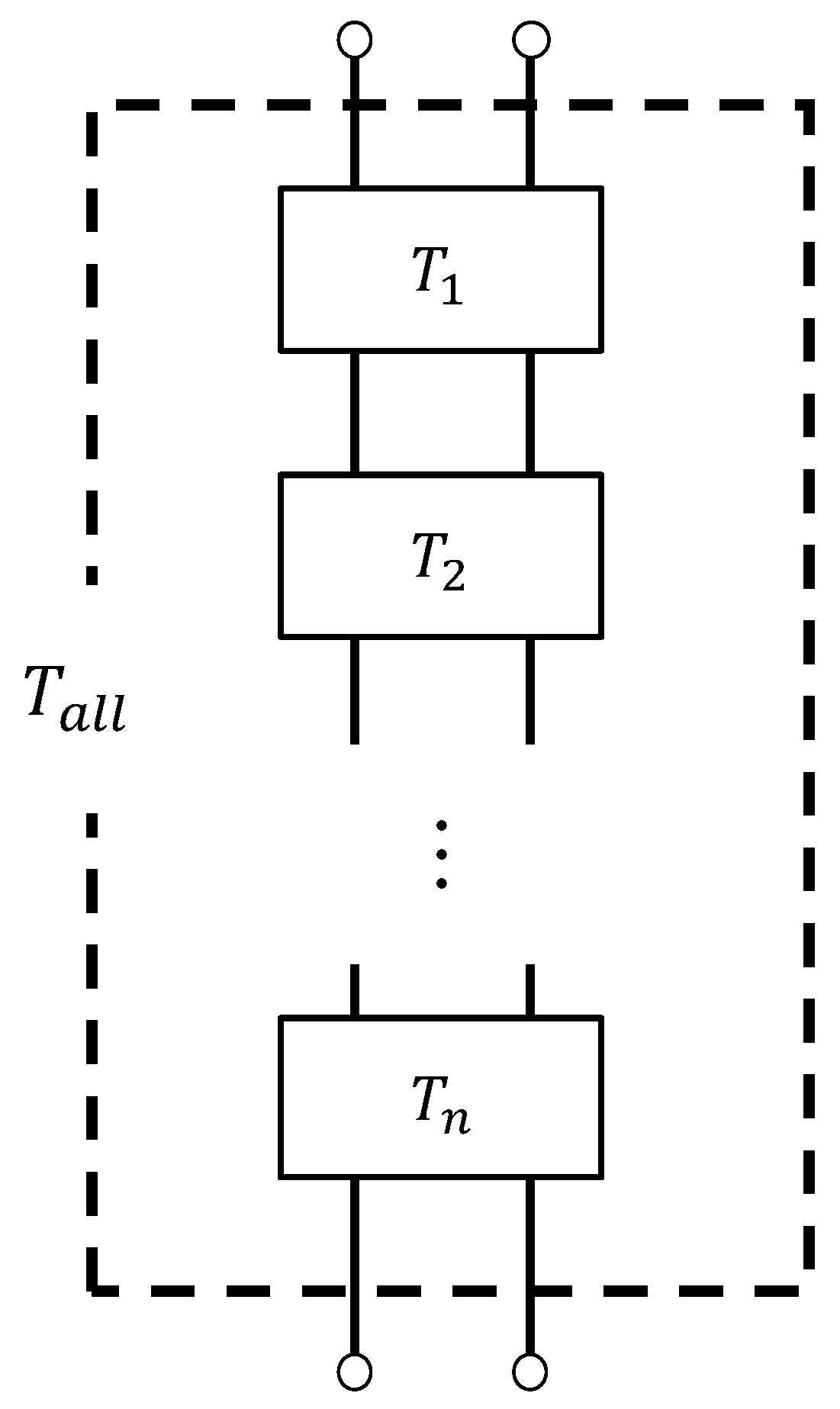
4.4. Transfer Matrix
4.5. Vertical Incident Sound Absorption Coefficient
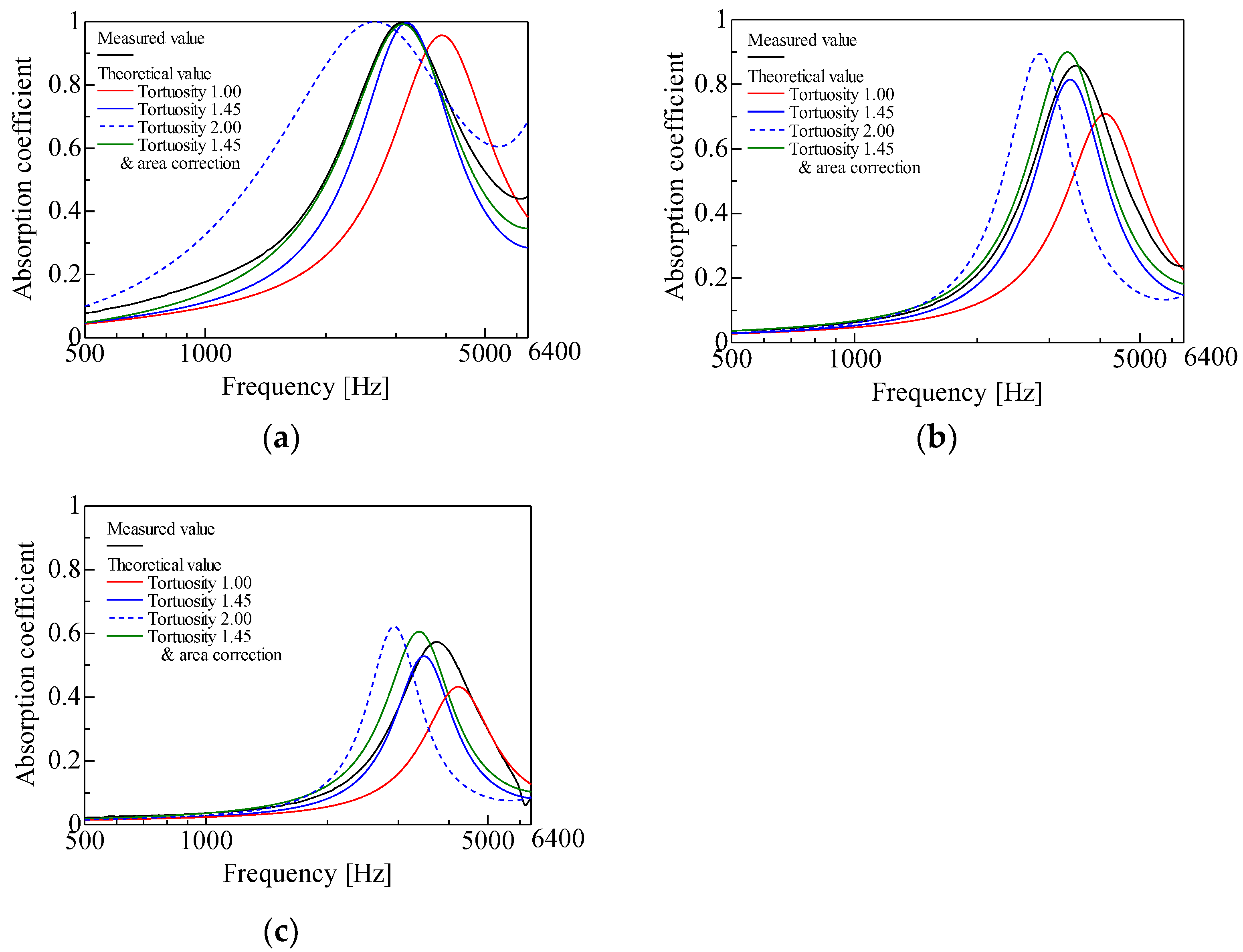
5. Comparison of the Measured and Theoretical Values
6. Conclusions
- 1.
- It is difficult to construct a mathematical model for random packing, as it has no structure periodicity. Therefore, the sound absorption coefficient was estimated using a theoretical analysis based on cross-sectional CT scan images.
- 2.
- For the theoretical values considering the tortuosity, the peak sound absorption values were higher, and the peak frequency moved to lower frequencies compared with the case without considering the tortuosity. As a result, in all cases, the theoretical values were closer to the measured values. Therefore, the measured tortuosity values are reasonable.
- 3.
- Regarding the theoretical values, when both the surface area and tortuosity were considered, the peak sound absorption frequency moved to a lower frequency compared with the theoretical value when only considering tortuosity, and was in general agreement with the measured values for the particle diameters of d = 1 mm and d = 2 mm. Therefore, the method of estimating the vertical incident sound absorption coefficient using computed tomographic images is useful. Moreover, this model can be applied even if the material changes, provided the granular material can be considered rigid. Additionally, the model can be applied without problems for general granular densities and grain sizes in the order of mm.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Sandberg, U. Low noise road surfaces—A state-of-the-art review. J. Acoust. Soc. Jpn. 1999, 20, 1–17. [Google Scholar] [CrossRef]
- Zhang, X.; Thompson, D.; Jeong, H.; Squicciarini, G. The effects of ballast on the sound radiation from railway track. J. Sound Vib. 2017, 339, 137–150. [Google Scholar] [CrossRef]
- Vašina, M.; Hughes, D.C.; Horoshenkov, K.V.; Lapčík, L., Jr. The acoustical properties of consolidated expanded clay granulates. Appl. Acoust. 2006, 67, 787–796. [Google Scholar] [CrossRef]
- Voronina, N.N.; Horoshenkov, K.V. A new empirical model for the acoustic properties of loose granular media. Appl. Acoust. 2003, 64, 415–432. [Google Scholar] [CrossRef]
- Dung, V.V.; Panneton, R.; Gagné, R. Prediction of effective properties and sound absorption of random close packings of monodisperse spherical particles: Multiscale approach. J. Acoust. Soc. Am. 2019, 145, 3606–3624. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Tsutsumi, Y.; Yanagimoto, K.; Watanabe, S. Study for Acoustic Characteristics Variation of Granular Material by Water Content. Trans. Jpn. Soc. Mech. Eng. 2009, 75, 2515–2520. [Google Scholar] [CrossRef]
- Sakamoto, S.; Ii, K.; Katayama, I.; Suzuki, K. Measurement and Theoretical Analysis of Sound Absorption of Simple Cubic and Hexagonal Lattice Granules. Noise Control. Eng. J. 2021, 69, 401–410. [Google Scholar] [CrossRef]
- Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of tortuosity in hexagonal close-packed and face-centered cubic lattices). Materials 2022, 15, 7393. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Sakuma, Y.; Yanagimoto, K.; Watanabe, S. Basic study for the acoustic characteristics of granular material (Normal incidence absorption coefficient for multilayer with different grain diameters). Trans. Jpn. Soc. Mech. Eng. 2008, 74, 2240–2245. [Google Scholar] [CrossRef]
- Gasser, S.; Paun, F.; Bréchet, Y. Absorptive properties of rigid porous media: Application to face centered cubic sphere packing. J. Acoust. Soc. Am. 2005, 117, 2090–2099. [Google Scholar] [CrossRef] [PubMed]
- Zieliński, T.G. Microstructure-based calculations and experimental results for sound absorbing porous layers of randomly packed rigid spherical beads. J. Appl. Phys. 2014, 116, 034905. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Leamy, M.J.; Nadler, J.H. Acoustic absorption calculation in irreducible porous media: A unified computational approach. J. Acoust. Soc. Am. 2009, 126, 1862–1870. [Google Scholar] [CrossRef] [PubMed]
- Allard, J.F.; Castagnede, B.; Henry, M. Evaluation of tortuosity in acoustic porous materials saturated by air. Rev. Sci. Instrum. 1994, 65, 754. [Google Scholar] [CrossRef]
- Stinson, M.R.; Champou, Y. Propagation of sound and the assignment of shape factors in model porous materials having simple pore geometries. J. Acoust. Soc. Am. 1992, 91, 685–695. [Google Scholar] [CrossRef]
- Allard, J.F. Propagation of sound in Porous Media Modeling Sound Absorbing Materials. J. Acoust. Soc. Am. 1994, 95, 2785. [Google Scholar] [CrossRef]
- Sakamoto, S.; Higuchi, K.; Saito, K.; Koseki, S. Theoretical analysis for sound-absorbing materials using layered narrow clearances between two planes. J. Adv. Mech. Des. Syst. Manuf. 2014, 8, 16. [Google Scholar] [CrossRef]

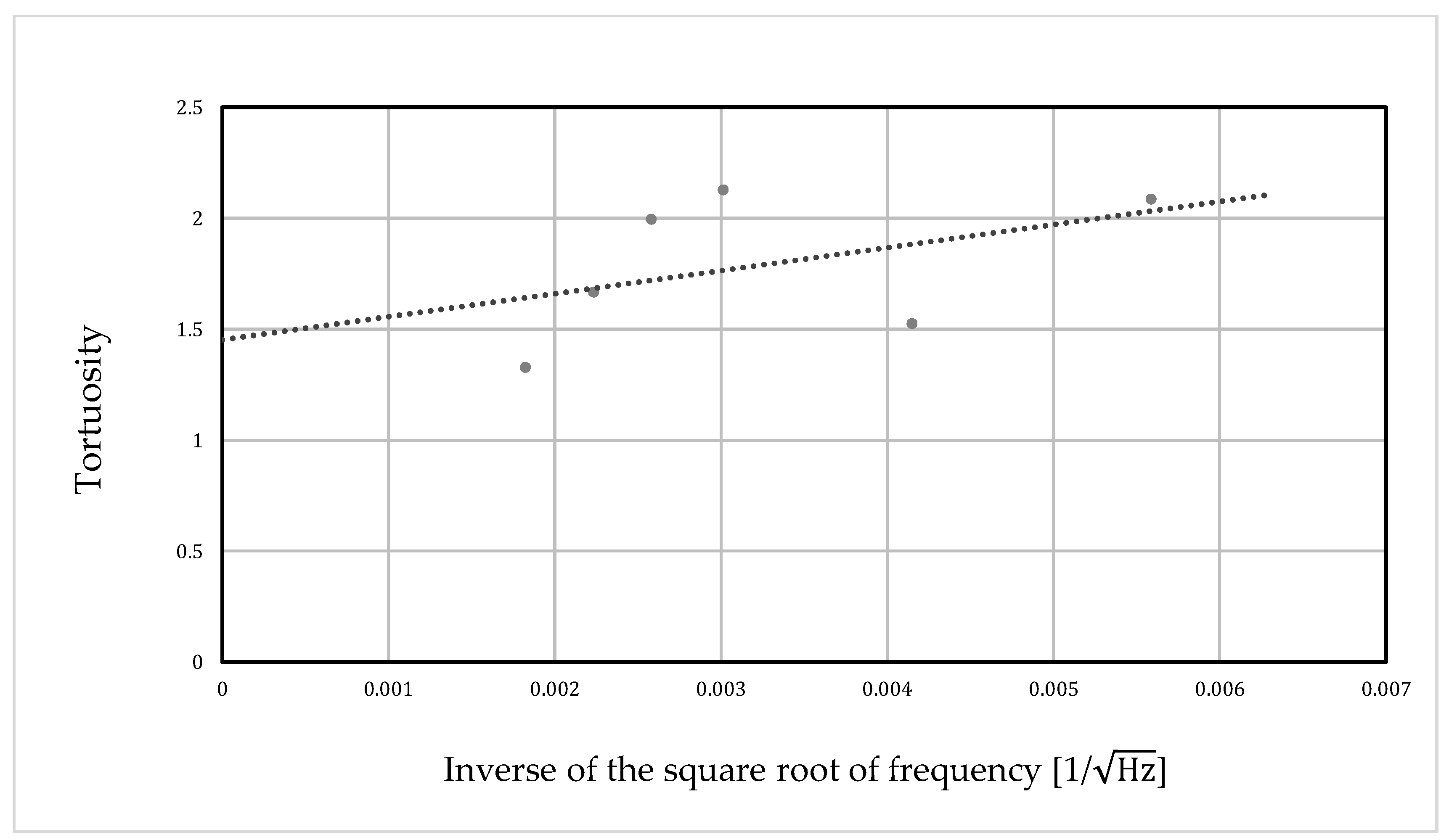


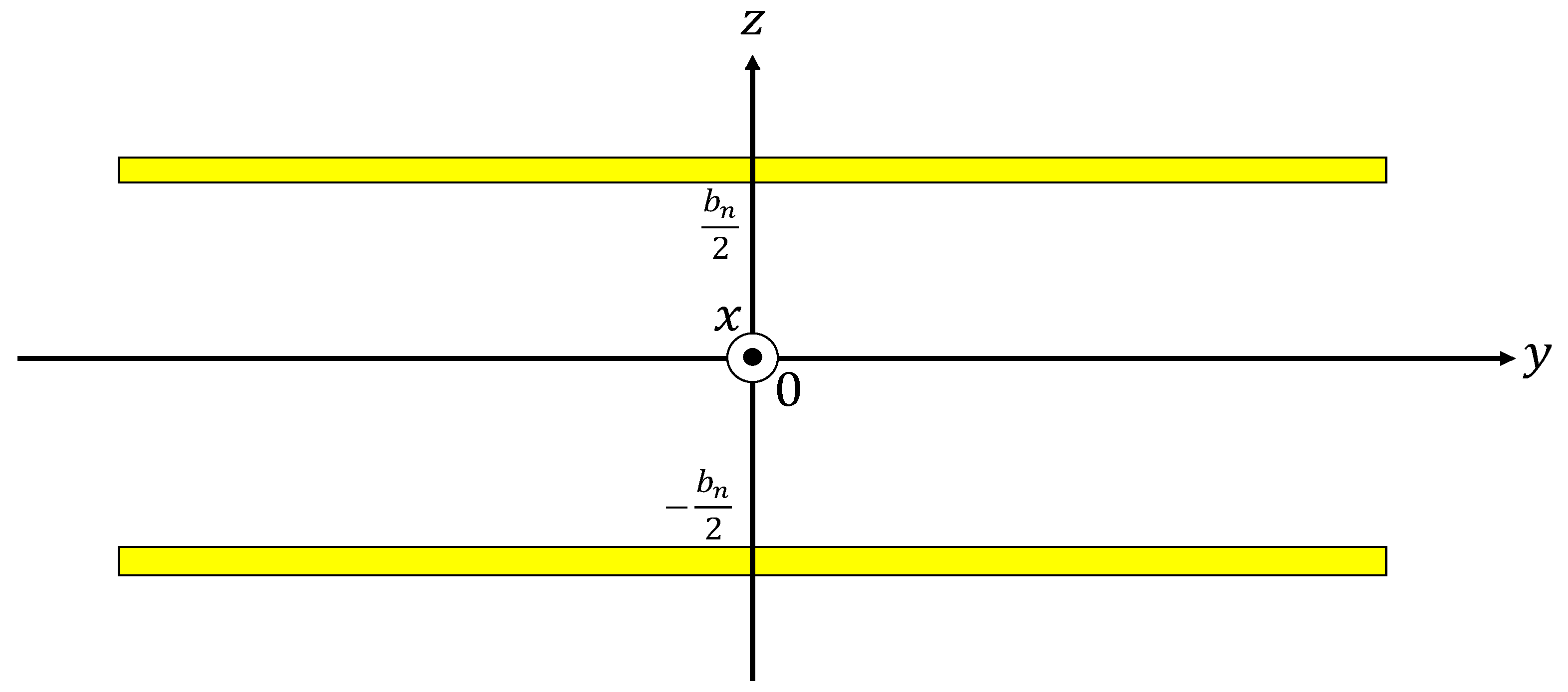
| Frequency [kHz] | Inverse of the Square Root of Frequency | Distance between Sensors [mm] | Transmission Time [ms] | Tortuosity |
|---|---|---|---|---|
| 32.7 | 0.00559 | 395 | 1.229 | 2.09 |
| 58 | 0.004152 | 395 | 1.199 | 1.53 |
| 110 | 0.003015 | 345 | 1.044 | 2.13 |
| 150 | 0.002582 | 204 | 0.626 | 2.00 |
| 200 | 0.002236 | 204 | 0.618 | 1.67 |
| 300 | 0.001826 | 204 | 0.615 | 1.33 |
| ∞ | 0 | - | - | 1.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials 2023, 16, 337. https://doi.org/10.3390/ma16010337
Sakamoto S, Suzuki K, Toda K, Seino S. Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials. 2023; 16(1):337. https://doi.org/10.3390/ma16010337
Chicago/Turabian StyleSakamoto, Shuichi, Kyosuke Suzuki, Kentaro Toda, and Shotaro Seino. 2023. "Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data" Materials 16, no. 1: 337. https://doi.org/10.3390/ma16010337
APA StyleSakamoto, S., Suzuki, K., Toda, K., & Seino, S. (2023). Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials, 16(1), 337. https://doi.org/10.3390/ma16010337






