Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
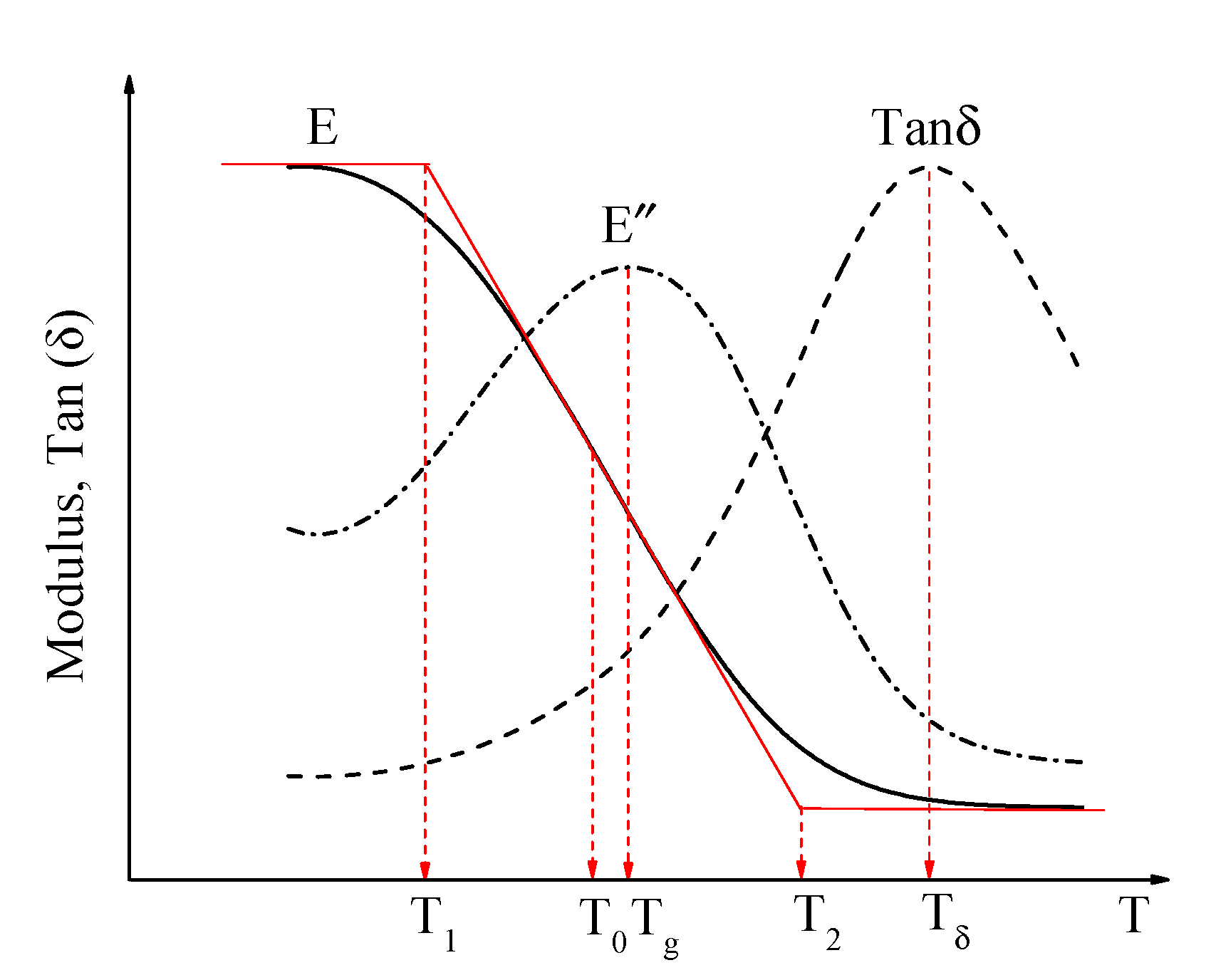
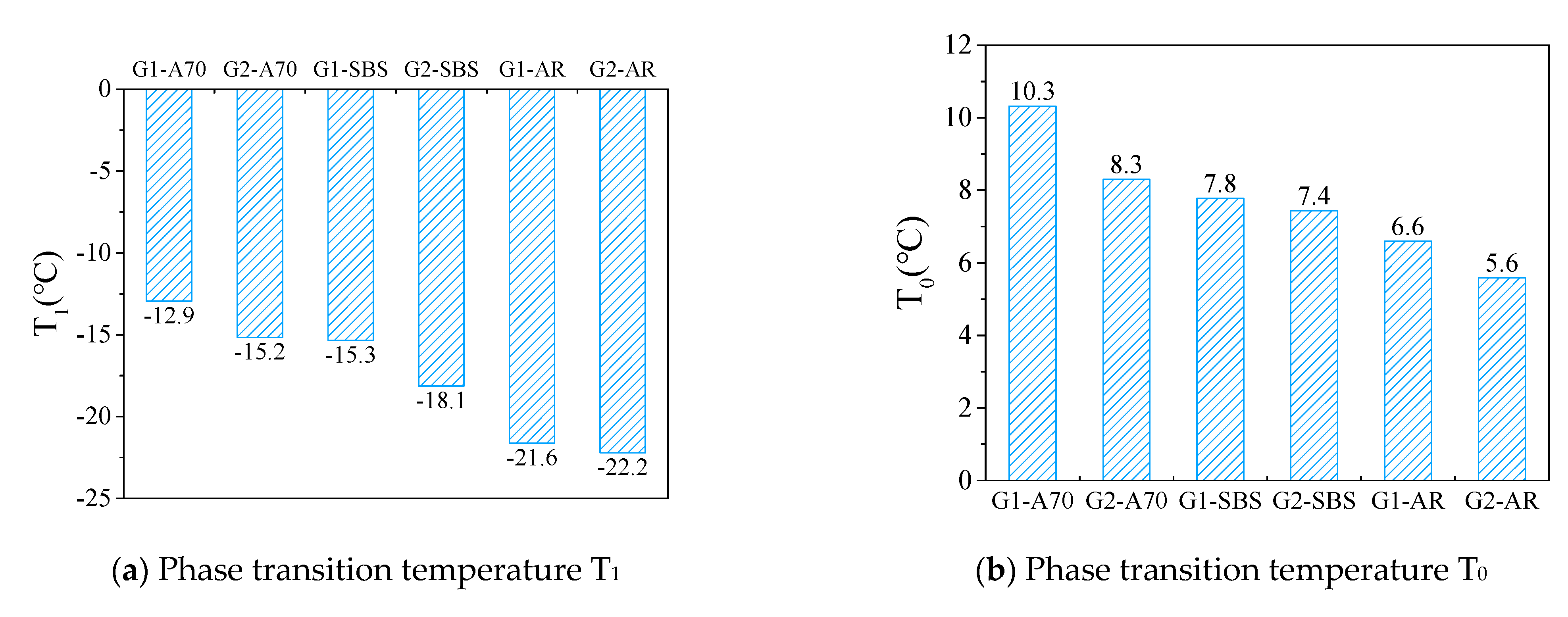
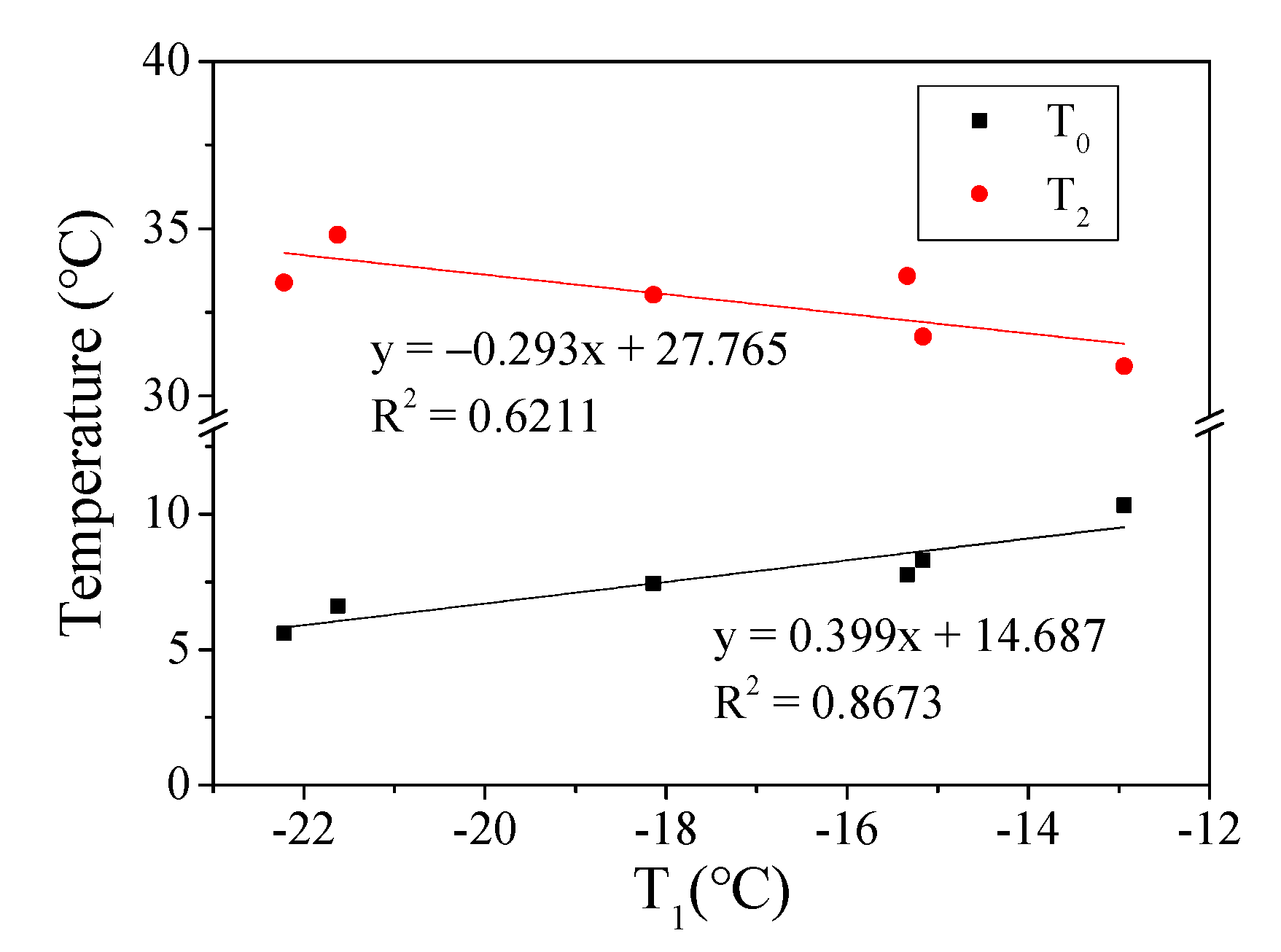
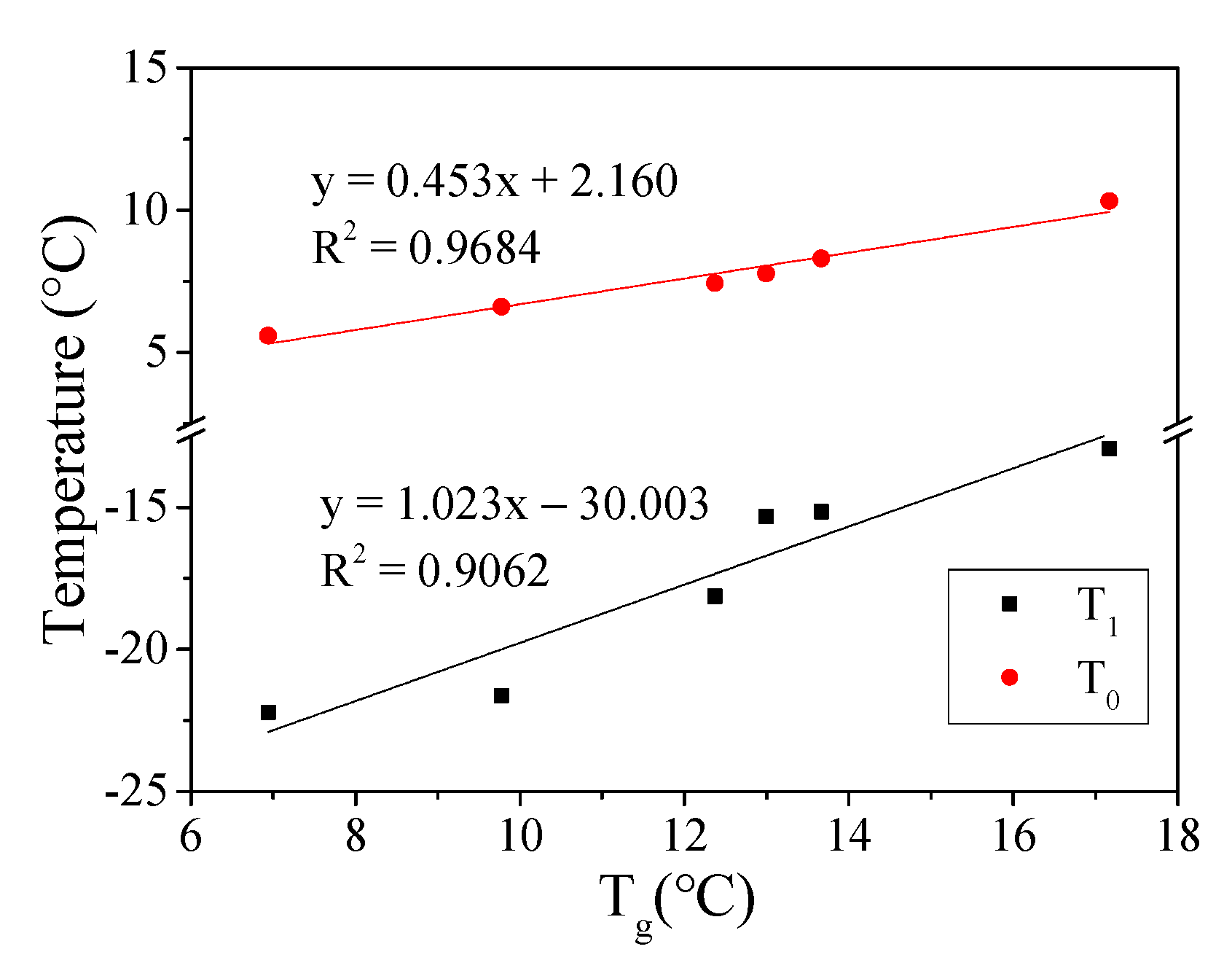
- The temperature corresponding to the midpoint () of the complex modulus curve is defined as T0, T0 = . This is also the temperature point where the complex modulus decreases the fastest with increasing temperature;
- The temperature corresponding to the intersection of the midpoint tangent of the complex modulus curve and the asymptote in the low-temperature zone is defined as , . T1 is the temperature corresponding to the change in asphalt mortar from a glassy to a rubbery state, which can be considered the glass transition temperature of the asphalt mortar;
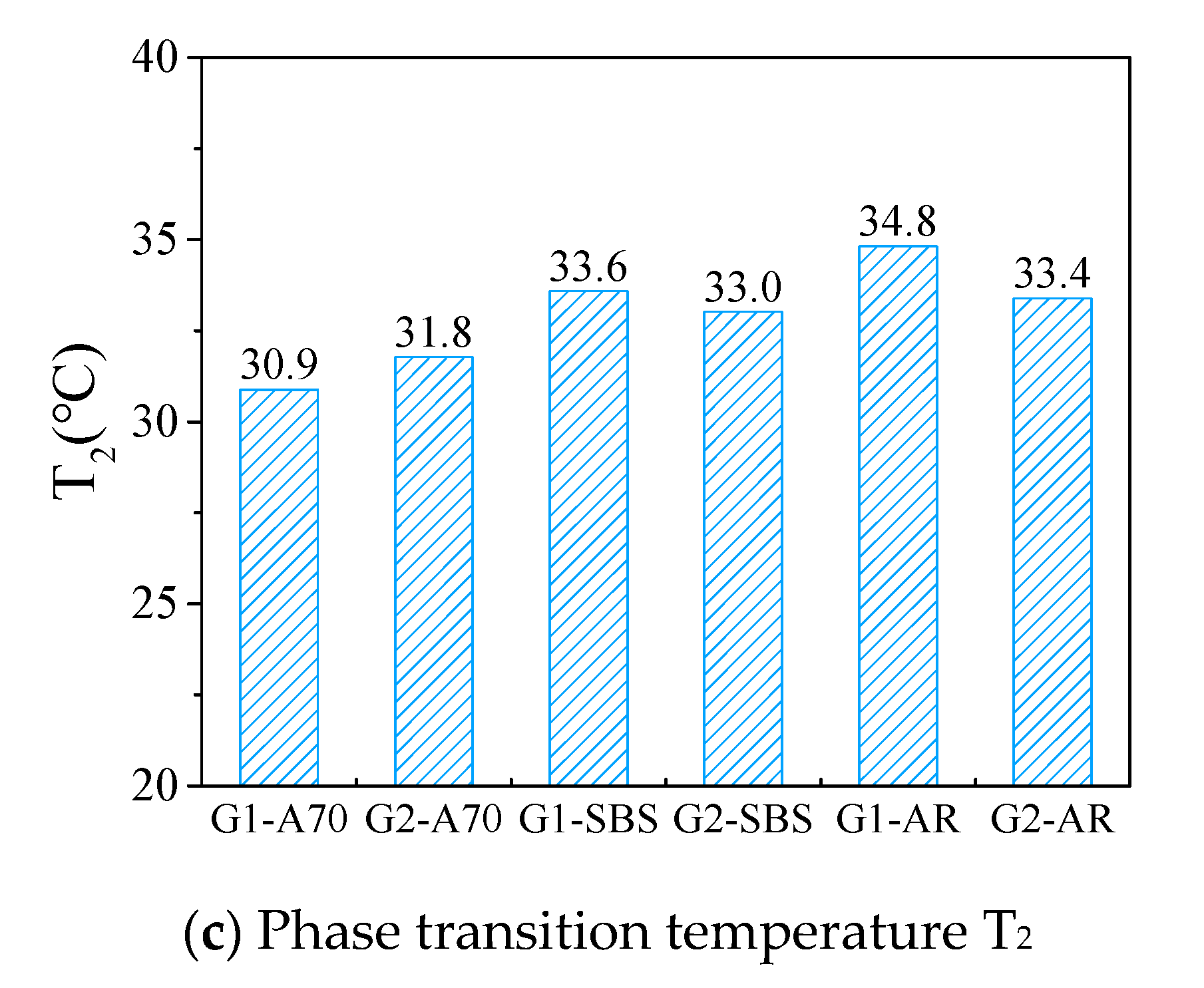
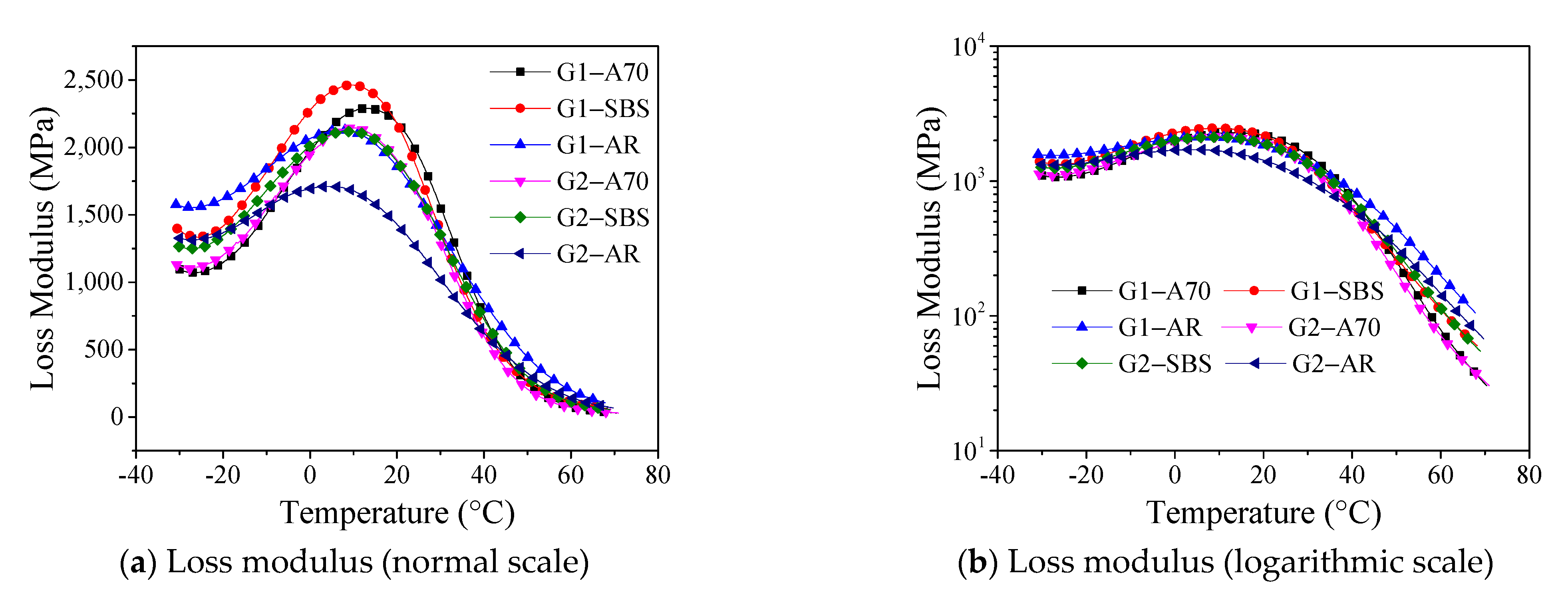
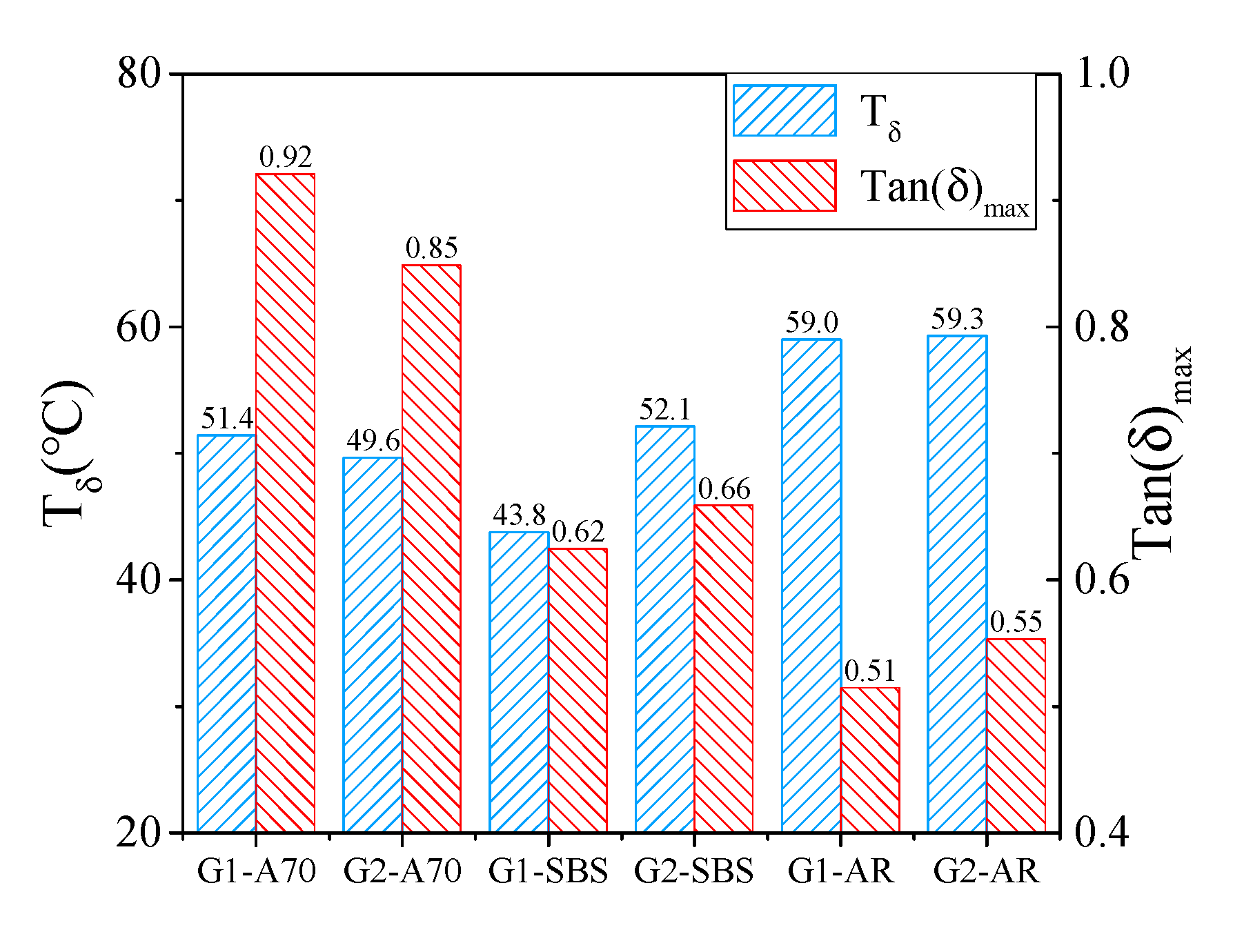
- The temperature corresponding to the intersection of the midpoint tangent of the complex modulus curve and the asymptote in the high-temperature zone is defined as , . This temperature reflects the phase behavior characteristics of asphalt mortar in the high-temperature zone. The loss modulus and tan(δ) curves have distinct peak points, and the temperatures corresponding to the peak points are denoted as Tg and Tδ, respectively, which can be referred to as the glass transition temperature [23,25].
3. Results and Discussion
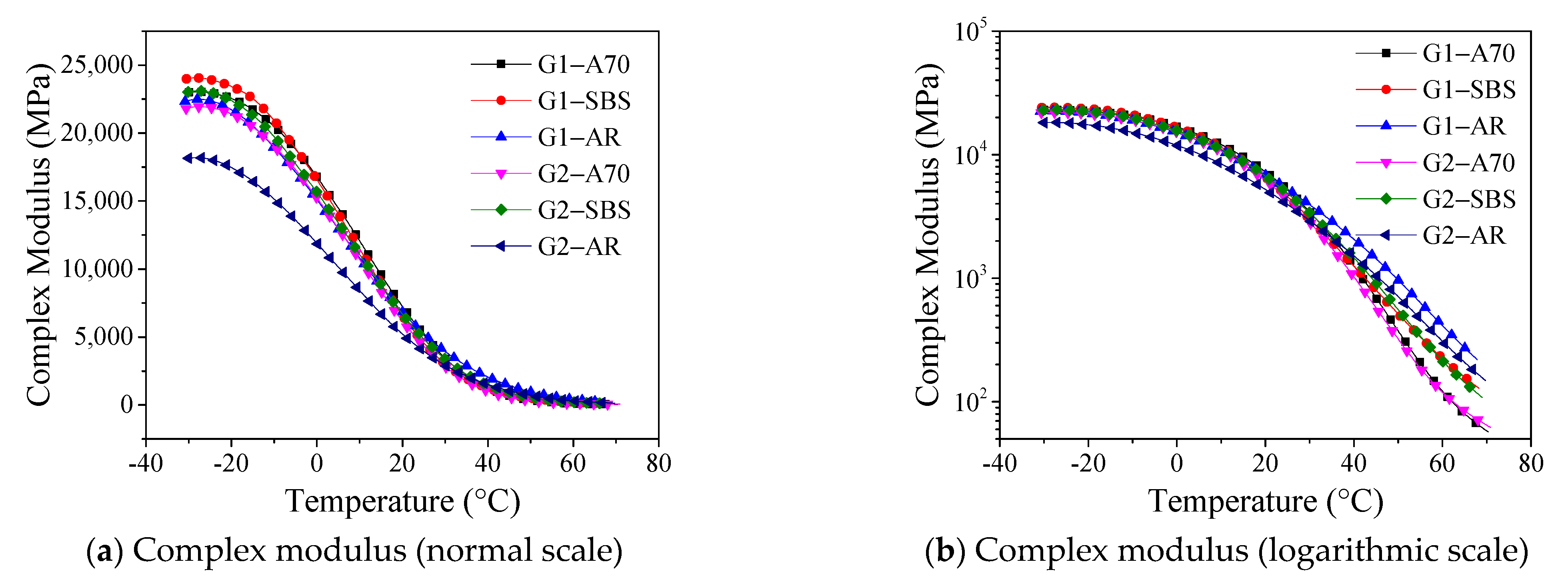
3.1. Complex Modulus
3.2. Loss Modulus
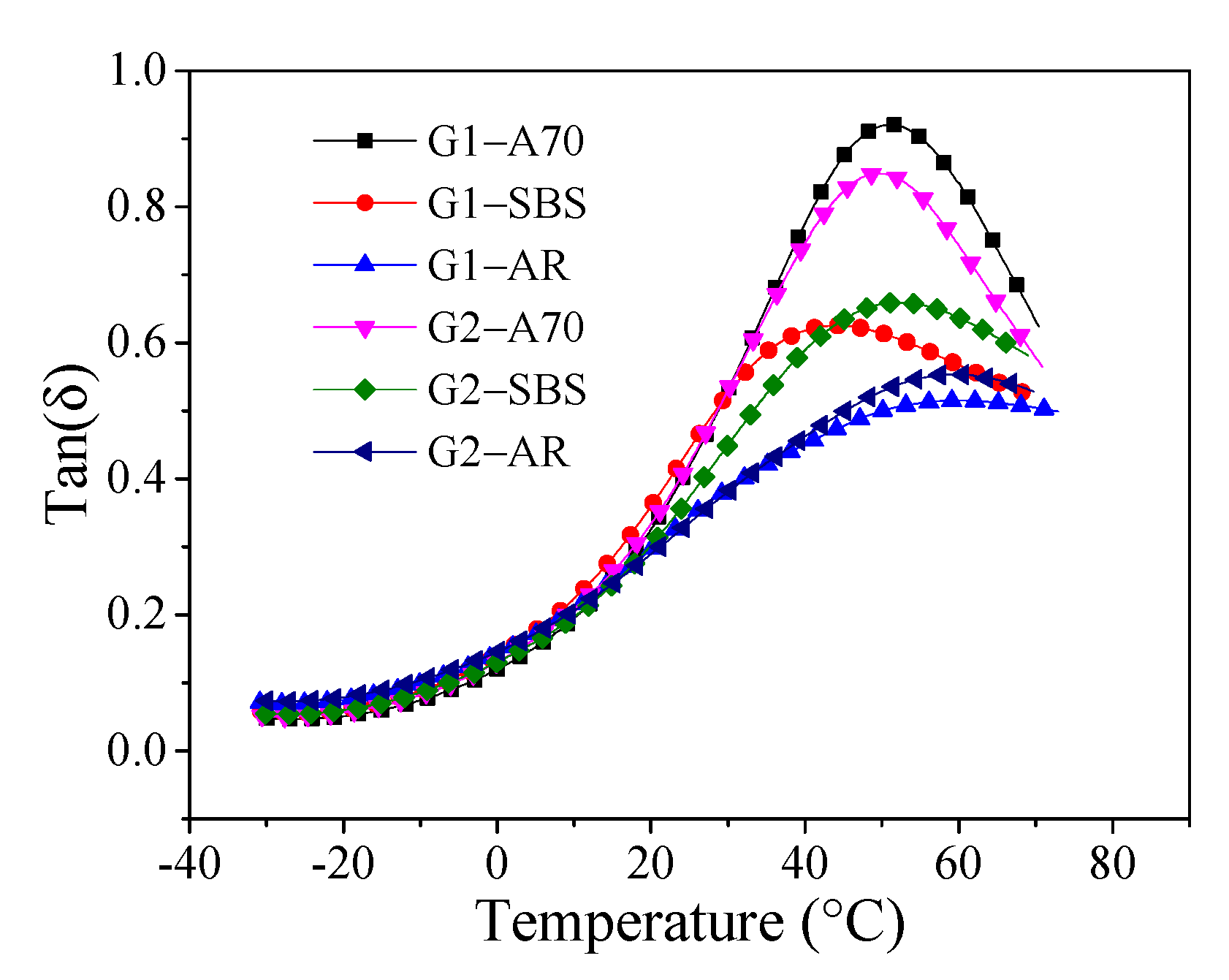
3.3. Tan(δ) (E″/E′)
4. Conclusions
- a)
- The phase transition temperatures T1, T0, and Tg can be used as the glass transition temperature of asphalt mortar, and they had a good linear relationship. T1, T0, and Tg effectively evaluated the low-temperature performance of asphalt mortar, and the evaluation results of the three indices were consistent. Mortars with neat asphalt A70 had a significantly higher T1, T0, and Tg and poor low-temperature performance, while mortars with modified asphalt AR had the best low-temperature performance. The finer gradation had a positive effect on the low-temperature performance of asphalt mortar.
- b)
- Phase transition temperature T2, complex modulus at 60 °C (E60), and the maximum tan(δ) (Tan(δ)max) can be used to evaluate the high-temperature performance of asphalt mortar. The mortar formed by asphalt AR had the best high-temperature performance, followed by asphalt SBS and A70. Coarser gradation had a good effect on the high-temperature performance of the modified asphalt, but it had the opposite effect on the neat asphalt A70.
- c)
- Asphalt plays a key role in the high- and low-temperature performance of asphalt mortar. In this study, the order of high- and low-temperature performance was AR > SBS > A70.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Ni, F.; Gu, X.; Yao, L.; Dong, Q. Evaluation of aggregate packing based on thickness distribution of asphalt binder, mastic and mortar within asphalt mixtures using multiscale methods. Constr. Build. Mater. 2019, 222, 717–730. [Google Scholar] [CrossRef]
- Arshadi, A.; Bahia, H. Development of an image-based multi-scale finite-element approach to predict mechanical response of asphalt mixtures. Road Mater. Pavement Des. 2015, 16, 214–229. [Google Scholar] [CrossRef]
- Suresha, S.; Ningappa, A. Recent trends and laboratory performance studies on FAM mixtures: A state-of-the-art review. Constr. Build. Mater. 2018, 174, 496–506. [Google Scholar] [CrossRef]
- Li, Q.; Chen, X.; Li, G.; Zhang, S. Fatigue resistance investigation of warm-mix recycled asphalt binder, mastic, and fine aggregate matrix. Fatigue Fract. Eng. Mater. Struct. 2017, 41, 400–411. [Google Scholar] [CrossRef]
- Nejad, F.M.; Habibi, M.; Hosseini, P.; Jahanbakhsh, H. Investigating the mechanical and fatigue properties of sustainable cement emulsified asphalt mortar. J. Clean. Prod. 2017, 156, 717–728. [Google Scholar] [CrossRef]
- Chen, M.; Javilla, B.; Hong, W.; Pan, C.; Riara, M.; Mo, L.; Guo, M. Rheological and Interaction Analysis of Asphalt Binder, Mastic and Mortar. Materials 2019, 12, 128. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Jiang, J.; Leng, Z.; Ni, F. Feasibility and performance of the Semi-circular Bending test in evaluating the low-temperature performance of asphalt mortar. Constr. Build. Mater. 2020, 269, 121305. [Google Scholar] [CrossRef]
- Niu, D.; Chen, H.; Kim, Y.R.; Sheng, Y.; Geng, J.; Guan, B.; Xiong, R.; Yang, Z. Damage assessment of asphalt concrete with composite additives at the FAM–coarse aggregate interfacial zone. Constr. Build. Mater. 2019, 198, 587–596. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; Daniel, G.C.; Erkens, S.; Scarpas, T. Effect of synthetic fibres on fracture performance of asphalt mortar. Road Mater. Pavement Des. 2019, 21, 1918–1931. [Google Scholar] [CrossRef] [Green Version]
- Chuanfeng, Z.; Yupeng, F.; Zhuang, M.; Xue, Y. Influence of mineral filler on the low-temperature cohesive strength of asphalt mortar. Cold Reg. Sci. Technol. 2017, 133, 1–6. [Google Scholar] [CrossRef]
- Underwood, B.S.; Kim, Y.R. Effect of volumetric factors on the mechanical behavior of asphalt fine aggregate matrix and the relationship to asphalt mixture properties. Constr. Build. Mater. 2013, 49, 672–681. [Google Scholar] [CrossRef]
- Osmari, P.H.; de Souza, R.C.; Nascimento, L.A.H.D.; Aragão, F.T.S. Evaluation of the relationship between the fatigue performance of FAM and AC mixtures based on volumetric characteristics and on the S-VECD theory. Constr. Build. Mater. 2020, 265, 120294. [Google Scholar] [CrossRef]
- Espinosa, L.; Caro, S.; Wills, J. Study of the influence of the loading rate on the fracture behaviour of asphalt mixtures and asphalt mortars. Constr. Build. Mater. 2020, 262, 120037. [Google Scholar] [CrossRef]
- Im, S.; Ban, H.; Kim, Y.-R. Characterization of mode-I and mode-II fracture properties of fine aggregate matrix using a semicircular specimen geometry. Constr. Build. Mater. 2014, 52, 413–421. [Google Scholar] [CrossRef]
- Aragão, F.T.S.; Badilla-Vargas, G.A.; Hartmann, D.A.; de Oliveira, A.D.; Kim, Y.-R. Characterization of temperature- and rate-dependent fracture properties of fine aggregate bituminous mixtures using an integrated numerical-experimental approach. Eng. Fract. Mech. 2017, 180, 195–212. [Google Scholar] [CrossRef]
- Gong, X.; Romero, P.; Dong, Z.; Li, Y. Investigation on the low temperature property of asphalt fine aggregate matrix and asphalt mixture including the environmental factors. Constr. Build. Mater. 2017, 156, 56–62. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Lv, J. Investigation on the Flexural–Tensile Rheological Behavior and Its Influence Factors of Fiber-reinforced Asphalt Mortar. Polymers 2020, 12, 1970. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.-J.; Niu, D.-T.; Long, G.; Luo, D.-M.; Yuan, Q.; Song, H. Integrated experimental measurement and computational analysis of relaxation behavior of cement and asphalt mortar. Constr. Build. Mater. 2016, 120, 137–146. [Google Scholar] [CrossRef]
- Zhu, J.; Alavi, M.Z.; Harvey, J.; Sun, L.; He, Y. Evaluating fatigue performance of fine aggregate matrix of asphalt mix containing recycled asphalt shingles. Constr. Build. Mater. 2017, 139, 203–211. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.; Long, G.; Niu, D.; Song, H. Dynamic mechanical thermo-analysis of cement and asphalt mortar. Powder Technol. 2017, 313, 36–43. [Google Scholar] [CrossRef]
- Yu, H.; Yao, D.; Qian, G.; Cai, J.; Gong, X.; Cheng, L. Effect of ultraviolet aging on dynamic mechanical properties of SBS modified asphalt mortar. Constr. Build. Mater. 2021, 281, 122328. [Google Scholar] [CrossRef]
- Fang, L.; Yuan, Q.; Deng, D.; Pan, Y.; Wang, Y. Effect of Mix Parameters on the Dynamic Mechanical Properties of Cement Asphalt Mortar. J. Mater. Civ. Eng. 2017, 29, 04017080. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, M. Study on the phase behavior of asphalt mastic. Constr. Build. Mater. 2013, 47, 311–317. [Google Scholar] [CrossRef]
- Yang, G.; Wang, X.; Zhou, X.; Wang, Y. Experimental Study on the Phase Transition Characteristics of Asphalt Mixture for Stress Absorbing Membrane Interlayer. Materials 2020, 13, 474. [Google Scholar] [CrossRef] [Green Version]
- Soliman, H.; Shalaby, A. Characterizing the Low-Temperature Performance of Hot-Pour Bituminous Sealants Using Glass Transition Temperature and Dynamic Stiffness Modulus. J. Mater. Civ. Eng. 2009, 21, 688–693. [Google Scholar] [CrossRef]
- Liu, H.; Luo, R.; Lv, H. Establishing continuous relaxation spectrum based on complex modulus tests to construct relaxation modulus master curves in compliance with linear viscoelastic theory. Constr. Build. Mater. 2018, 165, 372–384. [Google Scholar] [CrossRef]


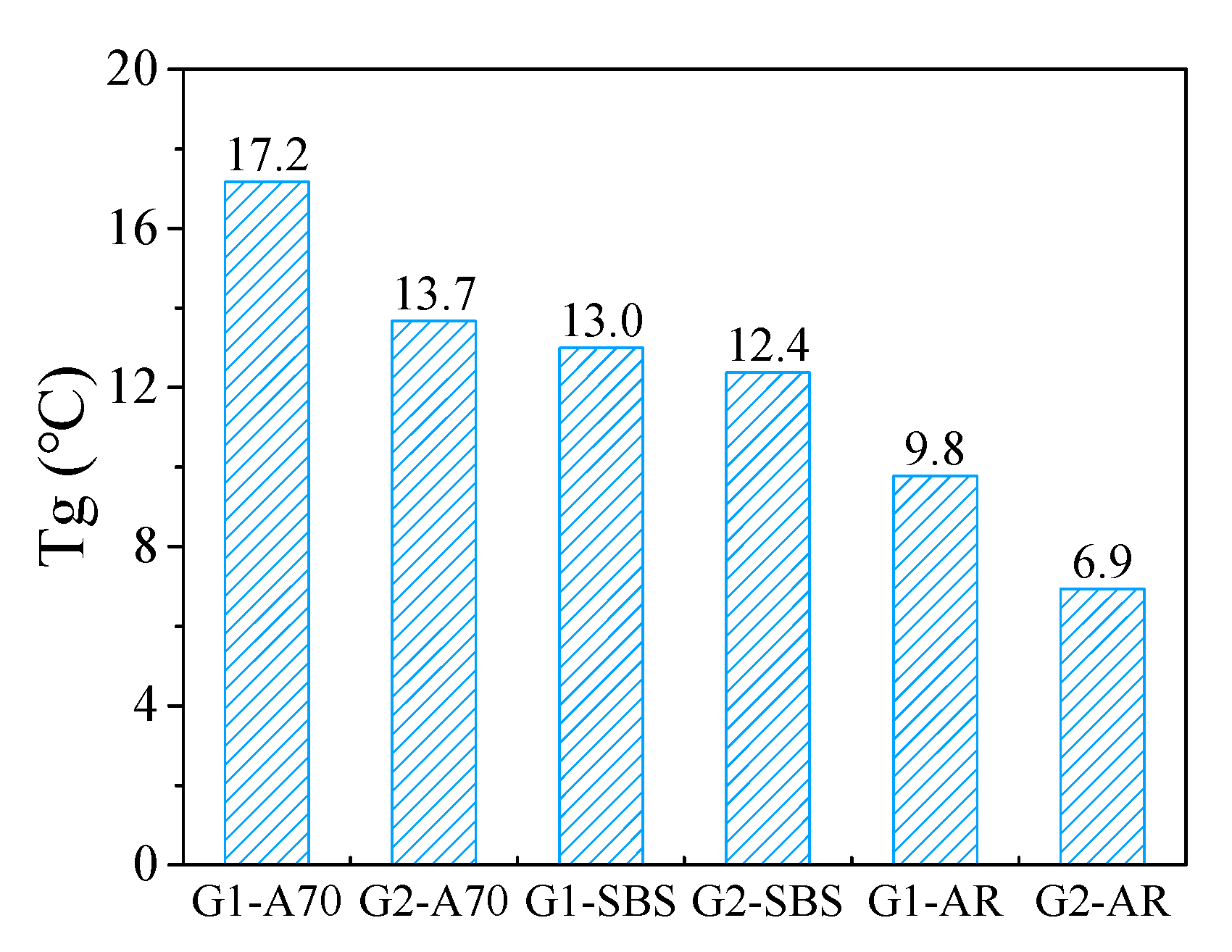
| Asphalt | Penetration (25 °C)/0.1 mm | Softening Point/°C | Ductility (5 cm/min, 10 °C) | PG Grade |
|---|---|---|---|---|
| A70 | 67 | 49.0 | 55 | PG64-22 |
| SBS | 63 | 72.7 | 49 | PG82-22 |
| AR | 39 | 72.6 | - | PG88-28 |
| Percent Passing /%wt | Sieve Size/mm | ||||||
|---|---|---|---|---|---|---|---|
| 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| G1 | 100 | 67.8 | 46.2 | 31.7 | 21.6 | 14.7 | 10 |
| G2 | 100 | 84.8 | 69.8 | 55.1 | 40.1 | 25 | 10 |
| Asphalt Mortar | Asphalt | Gradation | Asphalt–Aggregate Ratio/% | Porosity/% |
|---|---|---|---|---|
| G1-A70 | A70 | G1 | 6.5 | 3.6 |
| G1-SBS | SBS | G1 | 6.5 | 3.7 |
| G1-AR | AR | G1 | 6.5 | 3.4 |
| G2-A70 | A70 | G2 | 6.5 | 2.8 |
| G2-SBS | SBS | G2 | 6.5 | 2.8 |
| G2-AR | AR | G2 | 6.5 | 2.7 |
| Asphalt Mortar | E60/MPa |
|---|---|
| G1-A70 | 33 |
| G2-A70 | 41 |
| G1-SBS | 157 |
| G2-SBS | 150 |
| G1-AR | 450 |
| G2-AR | 330 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Ma, Z.; Shan, L.; Zhang, C. Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method. Materials 2022, 15, 3341. https://doi.org/10.3390/ma15093341
Wang Y, Wang X, Ma Z, Shan L, Zhang C. Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method. Materials. 2022; 15(9):3341. https://doi.org/10.3390/ma15093341
Chicago/Turabian StyleWang, Yanzhu, Xudong Wang, Zhimin Ma, Lingyan Shan, and Chao Zhang. 2022. "Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method" Materials 15, no. 9: 3341. https://doi.org/10.3390/ma15093341
APA StyleWang, Y., Wang, X., Ma, Z., Shan, L., & Zhang, C. (2022). Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method. Materials, 15(9), 3341. https://doi.org/10.3390/ma15093341






