Explicit Analysis of Nonuniform Irradiation Swelling Pressure Exerting on Dispersion Fuel Matrix Based on the Equivalent Inclusion Method
Abstract
:1. Introduction
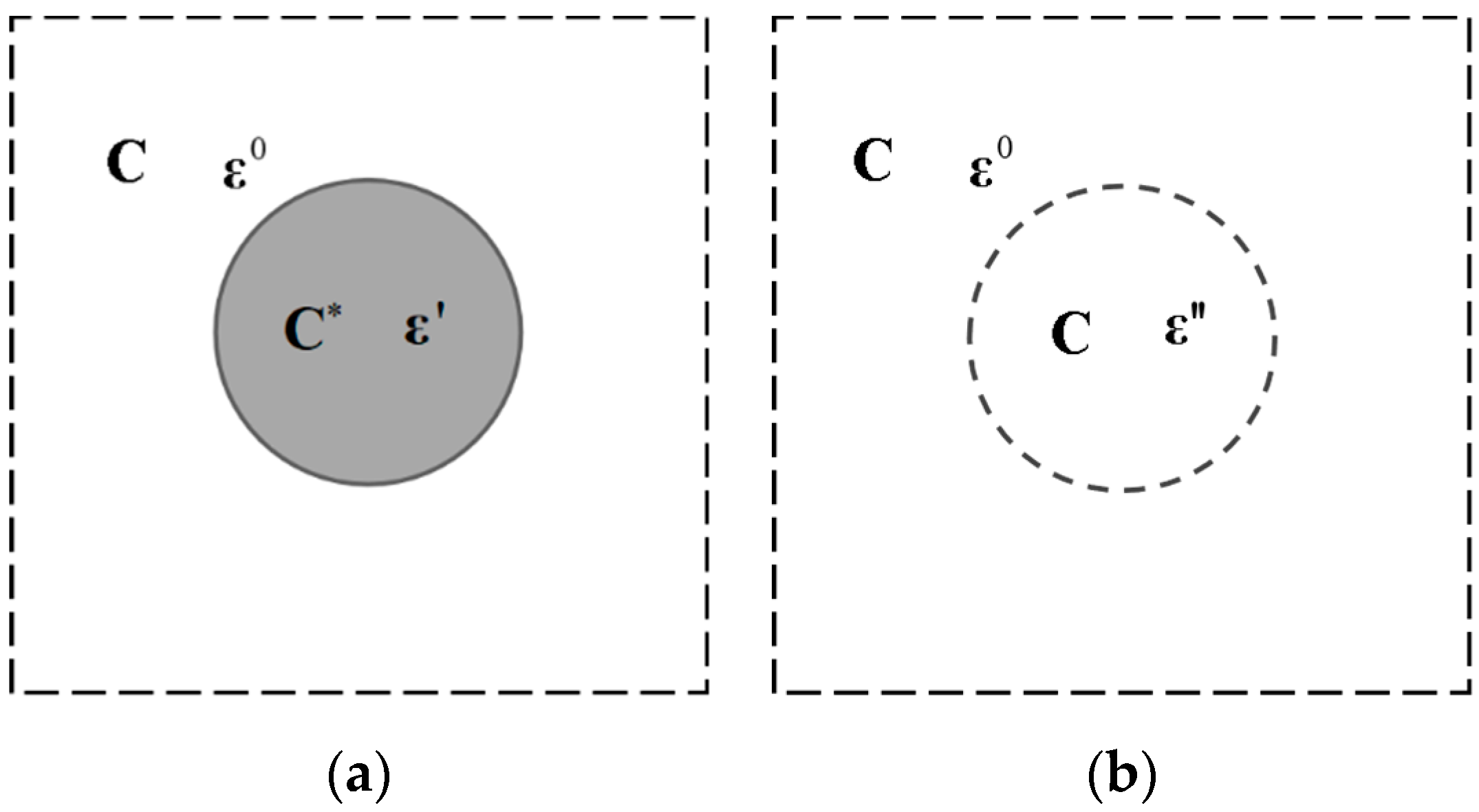
2. The Equivalent Inclusion Method
3. Formalism of Irradiation Swelling Pressure by Equivalent Inclusion Method
4. Numerical Examples
4.1. Analytical Solution
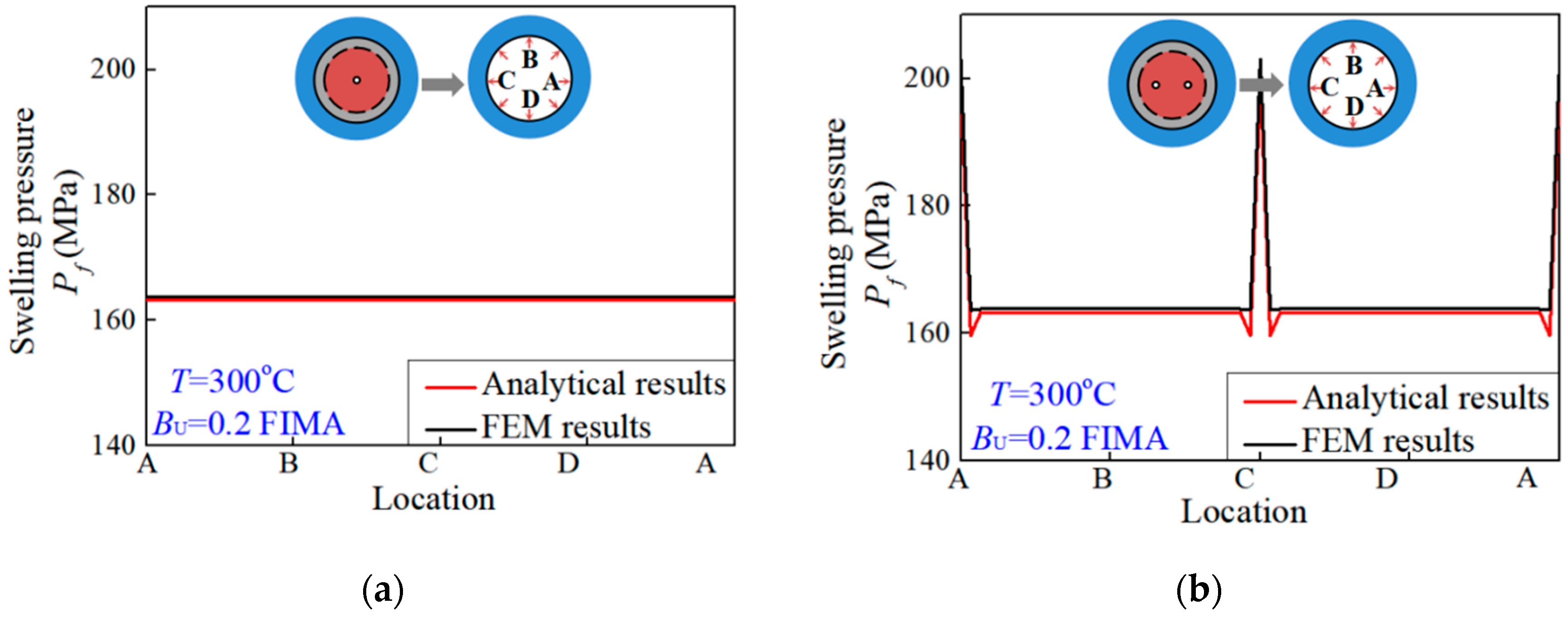
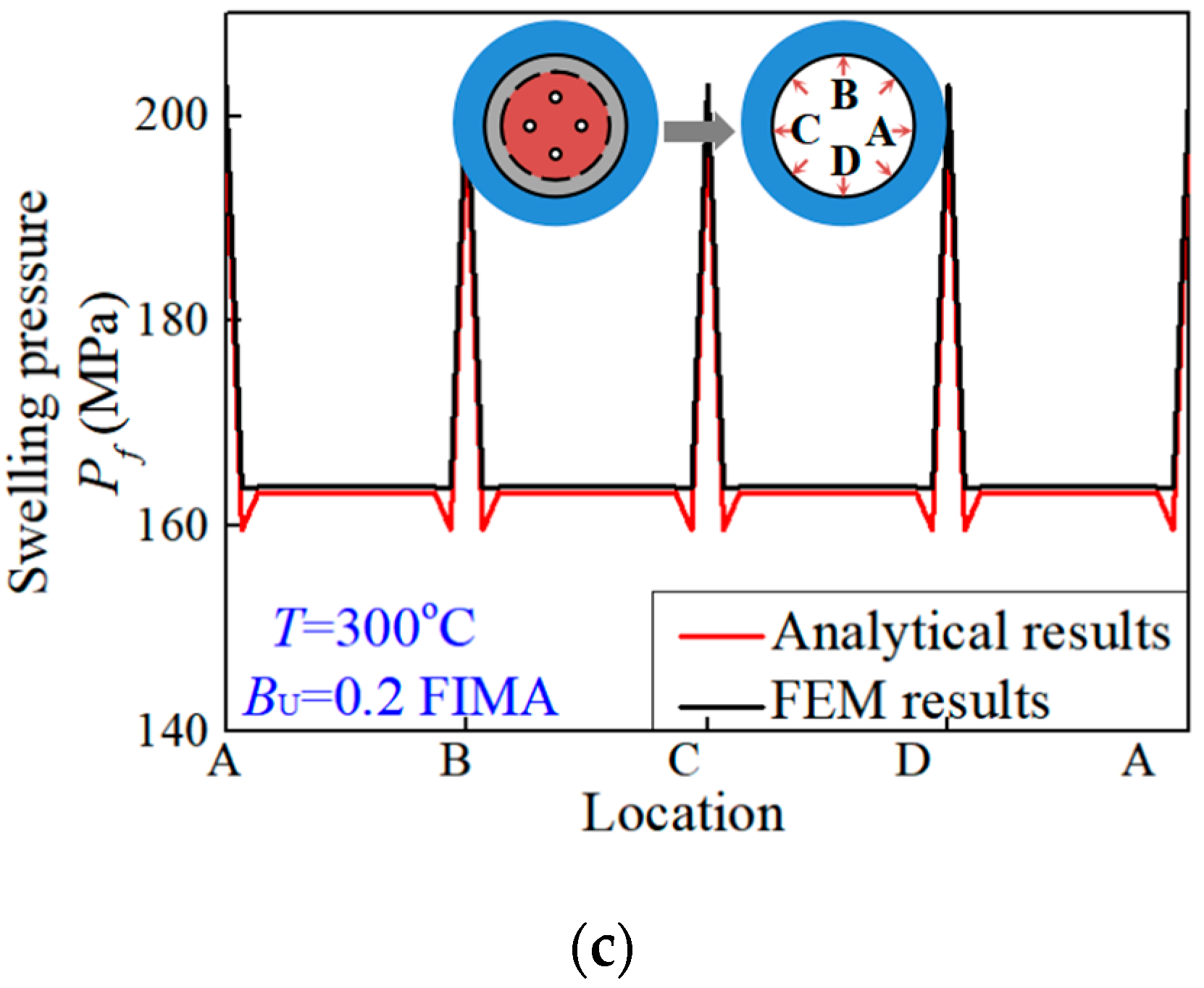
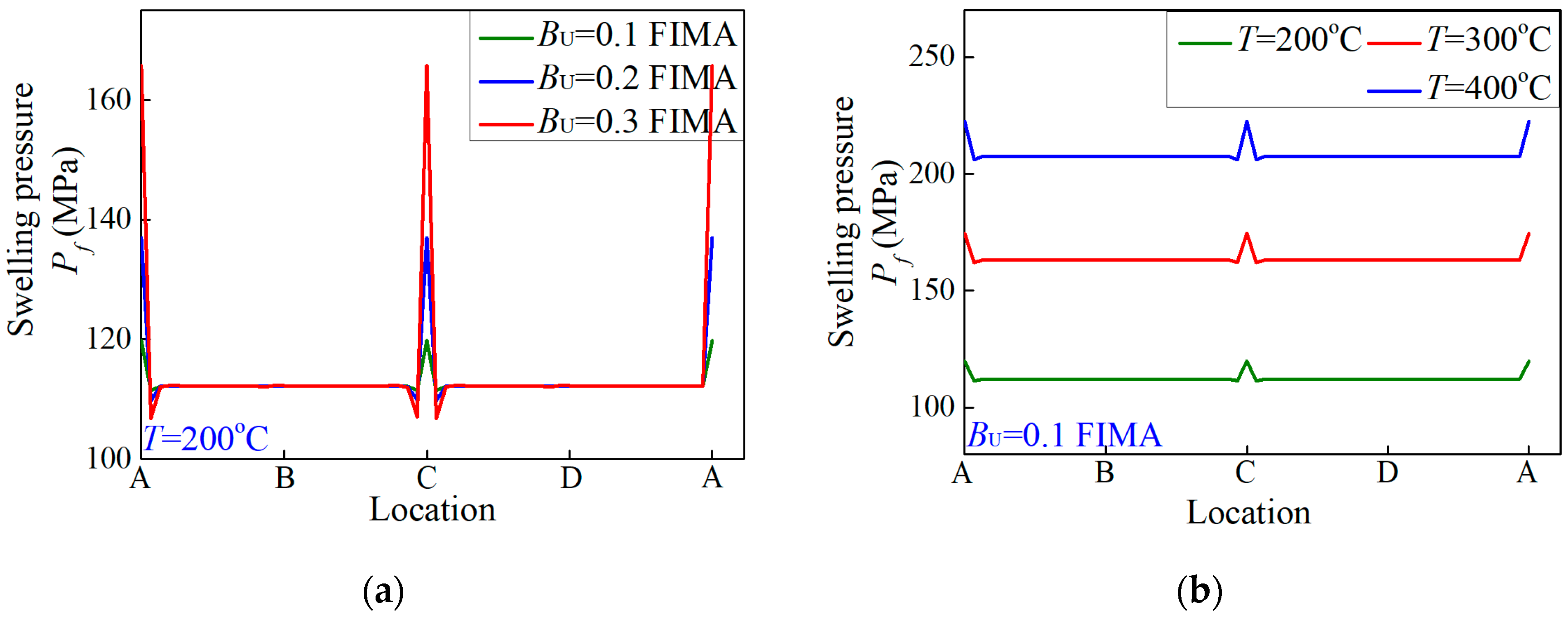
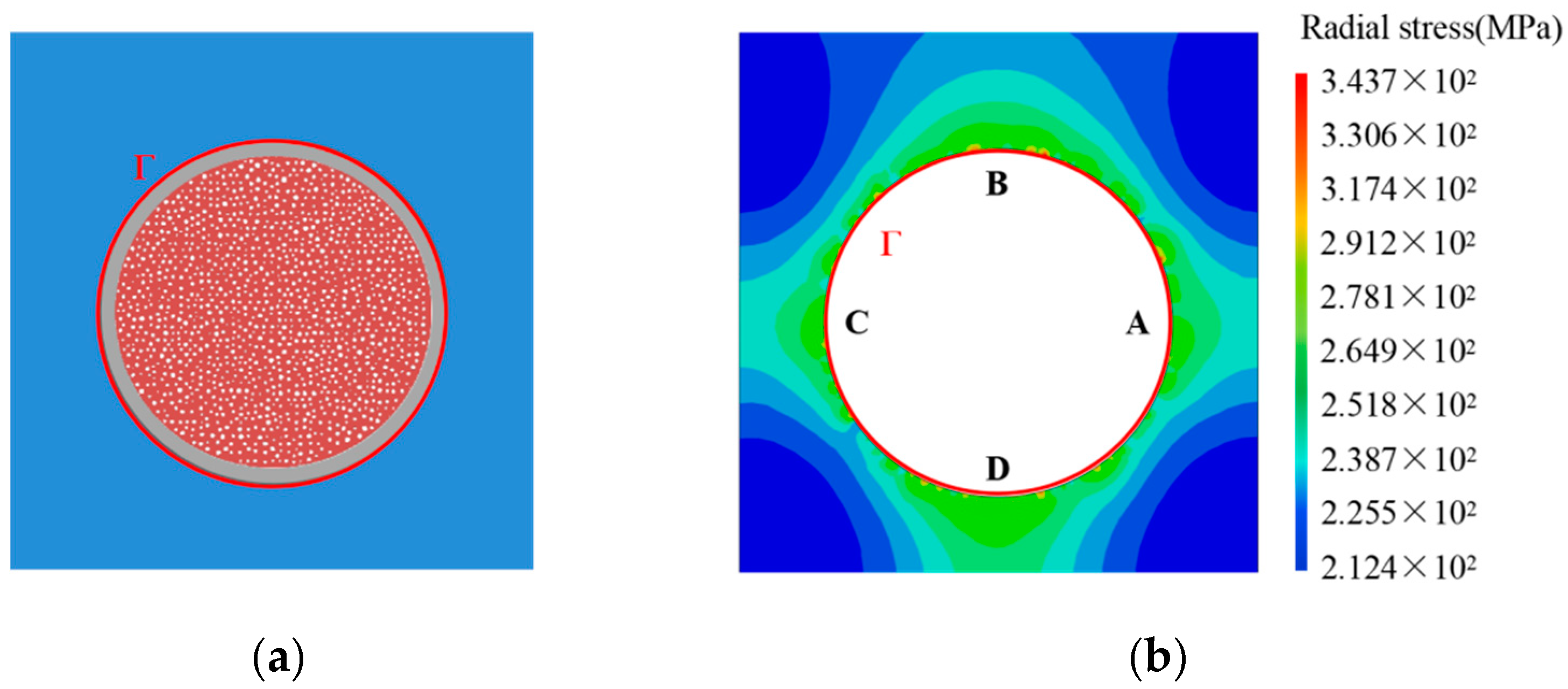
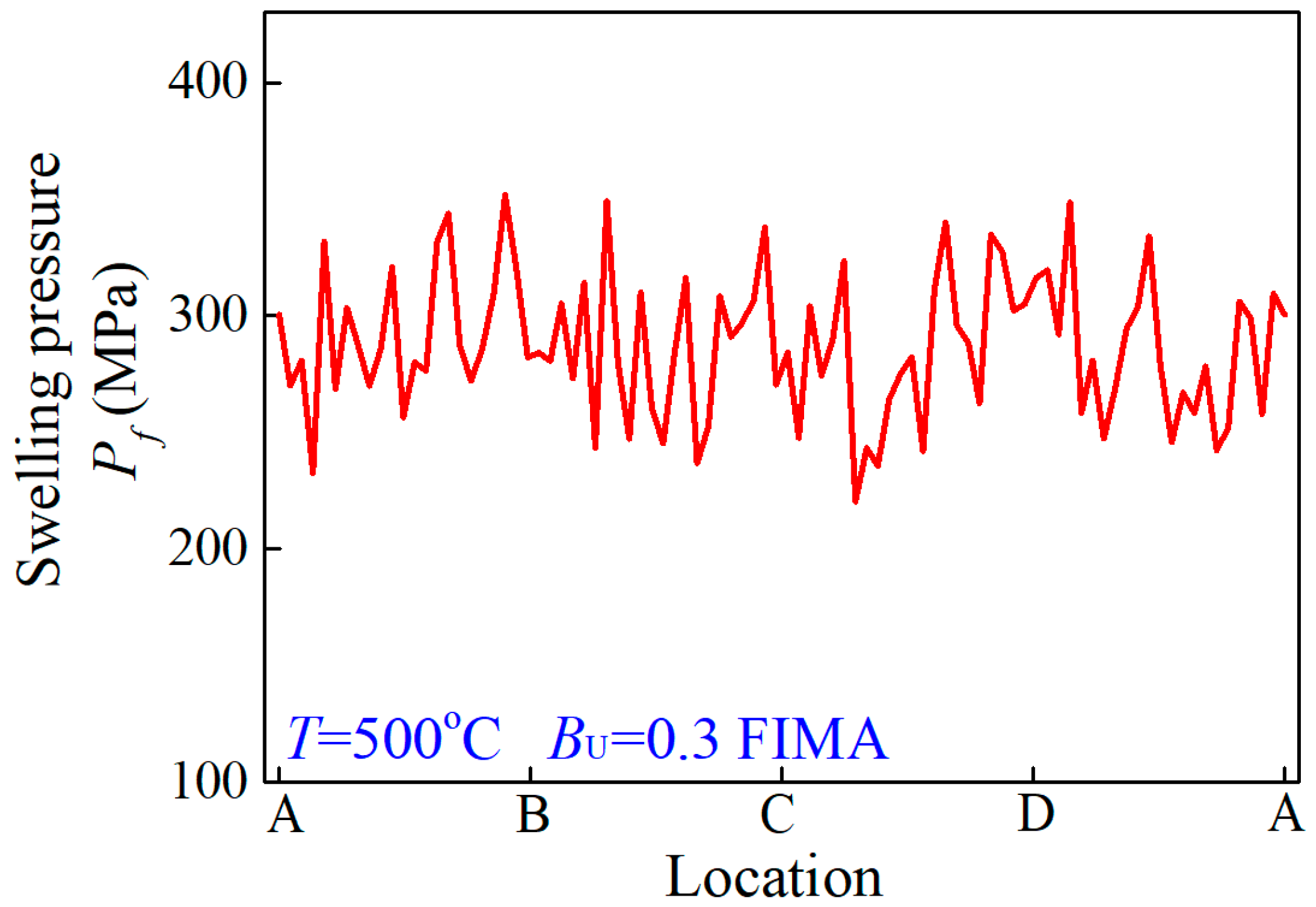
4.2. Numerical Results and Discussions
4.3. The Numerical Analysis of a Porous Fuel Particle
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| The inclusion domain of a fuel particle | |
| The three-dimensional Euclidean space | |
| The interface between metal matrix and interaction layer | |
| The fourth-order elastic tensor | |
| The second-order displacement tensor | |
| The second-order strain tensor | |
| The second-order stress tensor | |
| Superscripts which denote variables of fuel particle and interaction layer, respectively | |
| Superscripts which denote variables of inhomogeneous, fission gaseous fragments and temperature, respectively | |
| The eigenstrain of the first equivalent transformation | |
| The eigenstrain of the second equivalent transformation | |
| The applied strain produced by environmental pressure | |
| The irradiation swelling pressure exerting on matrix | |
| The environmental pressure | |
| The internal pressure in fission pores | |
| The Green’s function | |
| The point set out of a fuel particle | |
| The point set inside a fuel particle | |
| The radial stress |
References
- Wang, H.; Liang, J.; Lu, C.; Huang, H.; Ren, J. Research on the grain growth and the mechanism of (U,Ti)O2 dispersion fuel microspheres. Ceram. Int. 2014, 40, 4421–4427. [Google Scholar] [CrossRef]
- Long, C.S.; Zhao, Y.; Wen, G.; Hongxing, X.; Tianguo, W. A model for cracking of ceramic fuel particles in dispersion fuel. Nucl. Power Eng. 2014, 35, 92–96. [Google Scholar]
- Savchenko, A.; Konovalov, I.; Vatulin, A.; Morozov, A.; Orlov, V.; Uferov, O.; Ershov, S.; Laushkin, A.; Kulakov, G.; Maranchak, S.; et al. Dispersion type zirconium matrix fuels fabricated by capillary impregnation method. J. Nucl. Mater. 2007, 362, 356–363. [Google Scholar] [CrossRef]
- Savchenko, A.; Vatulin, A.; Glagovsky, E.; Konovalov, I.; Morozov, A.; Kozlov, A.; Ershov, S.; Mishunin, V.; Kulakov, G.; Sorokin, V.; et al. Main results of the development of dispersion type IMF at A.A. Bochvar Institute. J. Nucl. Mater. 2010, 396, 26–31. [Google Scholar] [CrossRef]
- Rest, J.; Hofman, L. DART Model for Irradiation-Induced Swelling of Uranium Silicide Dispersion Fuel Elements. Nucl. Technol. 1999, 126, 88–101. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hofman, G.; Cheon, J.S.; Robinson, A.; Wachs, D. Fission induced swelling and creep of U-Mo alloy fuel. J. Nucl. Mater. 2003, 437, 37–46. [Google Scholar] [CrossRef]
- Olander, D.R.; Wongsawaeng, D. Re-solution of fission gas-A review: Part I. Intragranular bubbles. J. Nucl. Mater. 2006, 354, 94–109. [Google Scholar] [CrossRef]
- Olander, D. Growth of the interaction layer around fuel particles in dispersion fuel. J. Nucl. Mater. 2009, 383, 201–208. [Google Scholar] [CrossRef]
- Kim, K. UO2/Zry-4 chemical interaction layers for intact and leak PWR fuel rods. J. Nucl. Mater. 2010, 404, 128–137. [Google Scholar] [CrossRef]
- Gao, L.-J.; Chen, B.-D.; Jiang, S.-Y.; Xiang, Z.; Yu, J.-Y.; Zhang, L.; Li, Y.-M. Analysis of blistering mechanism for dispersion-type fuel plates during irradiation. Atom. Energy Sci. Technol. 2012, 46, 819–825. [Google Scholar]
- Yuan, T.; Huang, K.F.; Wang, J. Solutions to the generalized Eshelby conjecture for anisotropic media: Proofs of the weak version and counter-examples to the high-order and the strong versions. J. Mech. Phys. Solids. 2022, 158, 104648. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. Roy. Soc. Lond. 1957, 241, 376–396. [Google Scholar]
- Moschovidis, Z.A.; Mura, T. Two-ellipsoidal inhomogeneities by the equivalent inclusion method. J. Appl. Mech. 1975, 42, 847–852. [Google Scholar] [CrossRef]
- Mura, T.; Cheng, P.C. The elastic field outside an ellipsoidal inclusion. J. Appl. Mech. 1977, 44, 561–569. [Google Scholar] [CrossRef]
- Rashidinejad, E.; Shodja, H.M. Novel theories on magneto-electro-elastic ellipsoidal multi-inclusions and inhomogeneities and associated impotent fields. Mech. Mater. 2020, 143, 103201. [Google Scholar] [CrossRef]
- Lages, E.N.; Marques, S.P.C. Thermoelastic homogenization of periodic composites using an eigenstrain-based micromechanical model. Appl. Math. Model. 2020, 85, 1–18. [Google Scholar] [CrossRef]
- Ma, L.; Tang, Z.; Bian, Z.; Zhu, J.; Wiercigroch, M. Analytical solution for circular inhomogeneous inclusion problems with non-uniform axisymmetric eigenstrain distribution. Int. J. Mech. Sci. 2021, 194, 106213. [Google Scholar] [CrossRef]
- Ma, L. Fundamental formulation for transformation toughening. Int. J. Solids Struct. 2010, 47, 3214–3220. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Xiang, X.; Ma, L. On the crack-tip stress field due to the presence of isotropic dilatational inclusion: Theoretical and numerical analysis. Arch. Appl. Mech. 2021, 91, 2893–2905. [Google Scholar] [CrossRef]
- Zhang, X.; Sharma, P. Inclusions and inhomogeneities in strain gradient elasticity with couple stresses and related problems. Int. J. Solids Struct. 2005, 42, 3833–3851. [Google Scholar] [CrossRef]
- Ma, L.; Korsunsky, A.M. The principle of equivalent eigenstrain for inhomogeneous inclusion problems. Int. J. Solids Struct. 2014, 51, 4477–4484. [Google Scholar] [CrossRef] [Green Version]
- Eshelby, J.D. The elastic energy-momentum tensor. J. Elast. 1975, 5, 3–4. [Google Scholar] [CrossRef]
- Hongsheng, C.; Chongsheng, L.; Hongxing, X.; Tianguo, W.; Wen, G. Releasing model of fission gas based on dispersion fuel particle cracking. Nucl. Power Eng. 2019, 40, 85–91. [Google Scholar]
- Melnikov, Y.A.; Borodin, V.N. Green’s Functions Potential Fields on Surfaces; Springer International Publishing: Aargau, Switzerland, 2017. [Google Scholar]
- Chen, W.; Liang, X.; Shen, S.P. Forced vibration of piezoelectric and flexoelectric Euler-Bernoulli beams by dynamic Green’s functions. Acta Mech. 2021, 232, 449–460. [Google Scholar] [CrossRef]
- Qin, Q.H. Thermoelectroelastic Green’s function for a piezoelectric plate containing an elliptic hole. Mech. Mater. 1998, 30, 21–29. [Google Scholar] [CrossRef]
- Yoshidal, K.; Arai, M. Prediction of Fatigue Crack Path Based upon Green’s Function Theory. Key Eng. Mater. 2017, 754, 141–144. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Dover Publications: New York, NY, USA, 1944. [Google Scholar]
- Til, S.; Fedorov, A.V.; Magielsen, A.J. Study of ceramic pebble beds in post irradiation examination of the pebble bed assemblies irradiation experiment. Fusion Eng. Des. 2012, 87, 885–889. [Google Scholar]
- Brnić, J.; Niu, J.-T.; Turkalj, G.; Canadija, M.; Lanc, D. Experimental determination of mechanical properties and short-time creep of AISI 304 stainless steel at elevated temperatures. Int. J. Miner. Met. Mater. 2010, 17, 39. [Google Scholar] [CrossRef]
- Spino, J.; Cobos-Sabate, J.; Rousseau, F. Room-temperature micro-indentation Behaviour of LWR-fuels, Part 1: Fuel Micro-hardness. J. Nucl. Mater. 2003, 322, 204–216. [Google Scholar] [CrossRef]
- Katoha, Y.; Snead, L.L.; Parish, P.M.; Hinoki, T. Observation and possible mechanism of irradiation induced creep in ceramics. J. Nucl. Mater. 2013, 434, 141–151. [Google Scholar] [CrossRef]
- Holden, A.N. Dispersion fuel Elements; Gorden and Breach Science Publishers: New York, NY, USA, 1967. [Google Scholar]
- Lyu, J.; Zhao, Y.; Long, C. Mechanical modeling and parameter analysis for mesoscopic failure mechanism of dispersion fuels. Nucl. Power Eng. 2020, 41 (Suppl. S1), 178–182. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Lv, J.; Zuo, H.; Li, Q. Explicit Analysis of Nonuniform Irradiation Swelling Pressure Exerting on Dispersion Fuel Matrix Based on the Equivalent Inclusion Method. Materials 2022, 15, 3231. https://doi.org/10.3390/ma15093231
Dong Y, Lv J, Zuo H, Li Q. Explicit Analysis of Nonuniform Irradiation Swelling Pressure Exerting on Dispersion Fuel Matrix Based on the Equivalent Inclusion Method. Materials. 2022; 15(9):3231. https://doi.org/10.3390/ma15093231
Chicago/Turabian StyleDong, Yingxuan, Junnan Lv, Hong Zuo, and Qun Li. 2022. "Explicit Analysis of Nonuniform Irradiation Swelling Pressure Exerting on Dispersion Fuel Matrix Based on the Equivalent Inclusion Method" Materials 15, no. 9: 3231. https://doi.org/10.3390/ma15093231
APA StyleDong, Y., Lv, J., Zuo, H., & Li, Q. (2022). Explicit Analysis of Nonuniform Irradiation Swelling Pressure Exerting on Dispersion Fuel Matrix Based on the Equivalent Inclusion Method. Materials, 15(9), 3231. https://doi.org/10.3390/ma15093231




