Concentration Quantification of TiO2 Nanoparticles Synthesized by Laser Ablation of a Ti Target in Water
Abstract
:1. Introduction
2. Materials and Methods
3. Results
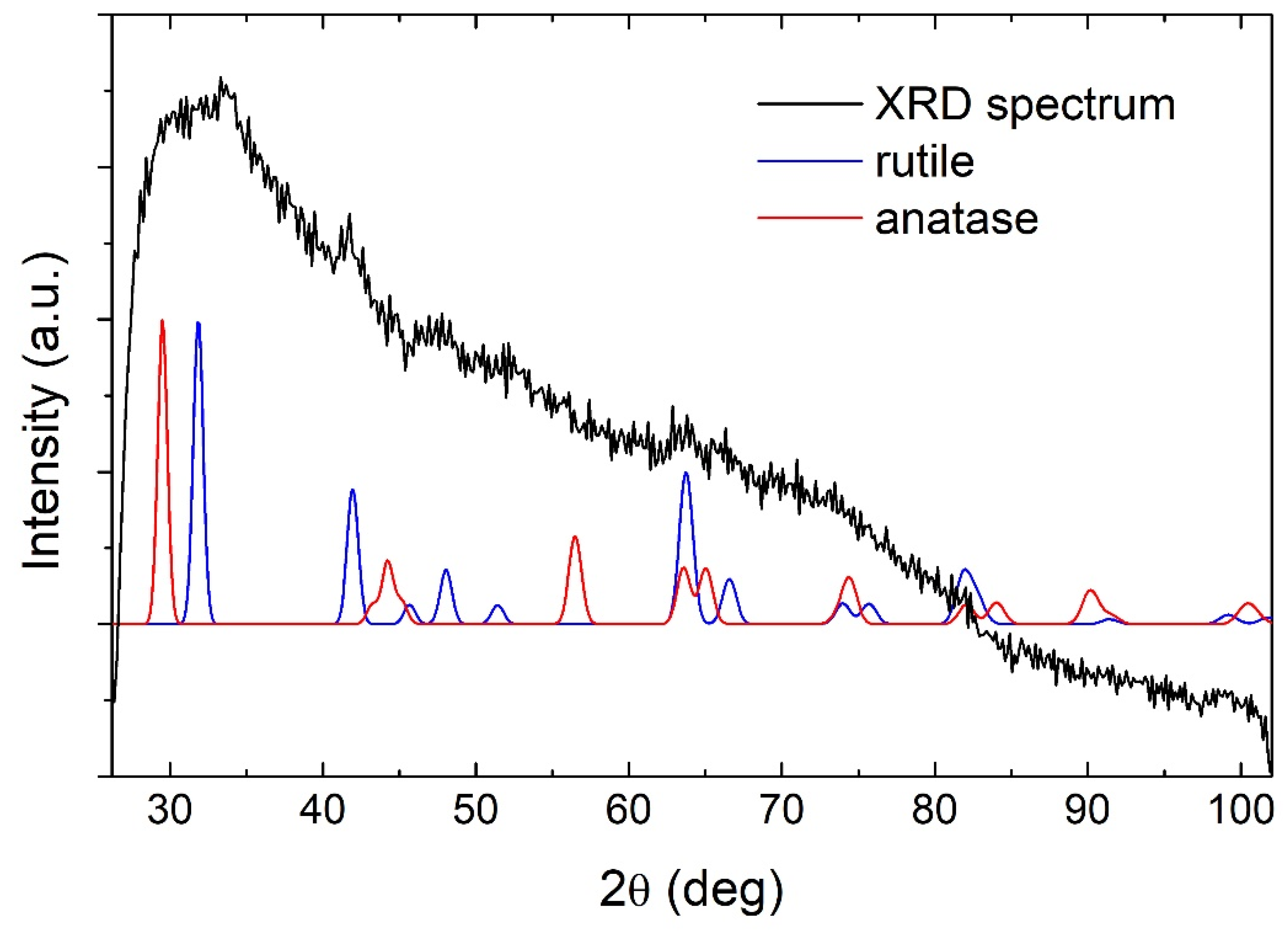
3.1. TiO2 NP Characterization
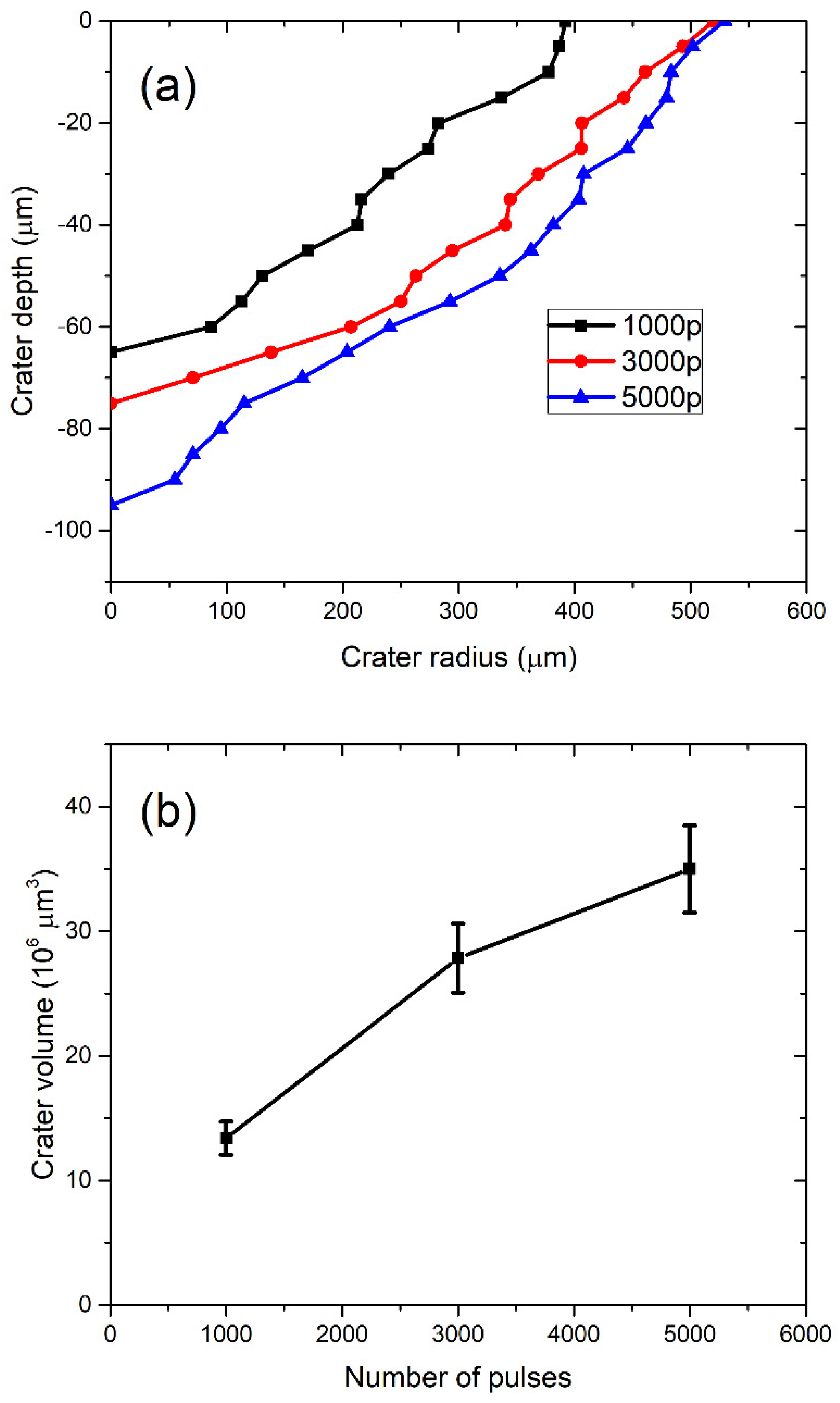
3.2. Calculation of TiO2 NP Concentration from Crater Volume (CV)
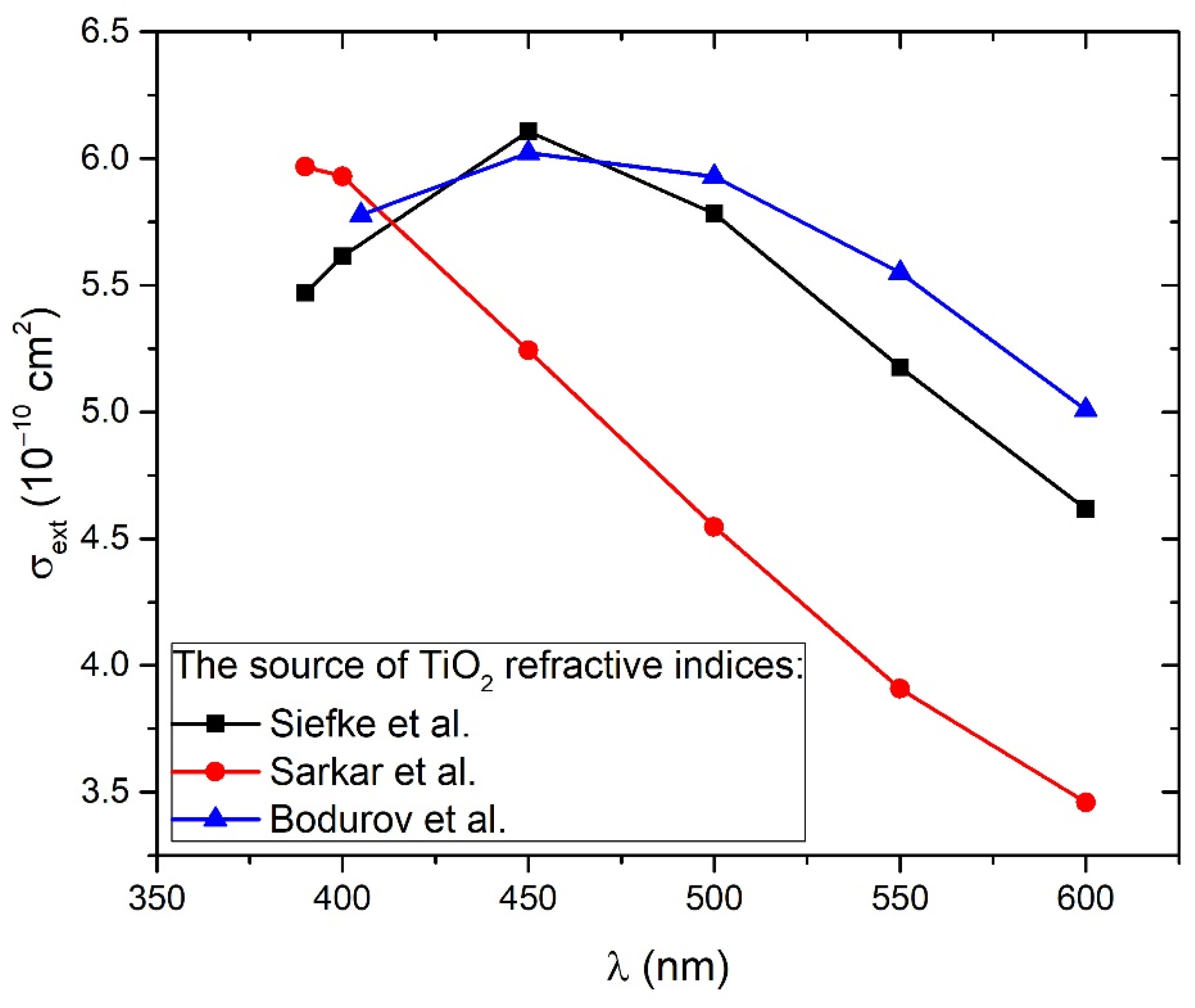
3.3. Calculation of TiO2 NP Concentration from Beer–Lambert Law (CA)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, G. Laser Ablation in Liquids, 1st ed.; Pan Stanford Publishing: Singapore, 2012. [Google Scholar]
- Dell’Aglio, M.; Gaudiuso, R.; De Pascale, O.; De Giacomo, A. Mechanisms and Processes of Pulsed Laser Ablation in Liquids during Nanoparticle Production. Appl. Surf. Sci. 2015, 348, 4–9. [Google Scholar] [CrossRef]
- Semaltianos, N.G. Nanoparticles by Laser Ablation. Crit. Rev. Solid State Mater. Sci. 2010, 35, 105–124. [Google Scholar] [CrossRef]
- Giorgetti, E.; Muniz Miranda, M.; Caporali, S.; Canton, P.; Marsili, P.; Vergari, C.; Giammanco, F. TiO2 Nanoparticles Obtained by Laser Ablation in Water: Influence of Pulse Energy and Duration on the Crystalline Phase. J. Alloys Compd. 2015, 643, S75–S79. [Google Scholar] [CrossRef]
- Gentile, L.; Mateos, H.; Mallardi, A.; Dell’Aglio, M.; De Giacomo, A.; Cioffi, N.; Palazzo, G. Gold Nanoparticles Obtained by Ns-Pulsed Laser Ablation in Liquids (Ns-PLAL) Are Arranged in the Form of Fractal Clusters. J. Nanopart. Res. 2021, 23, 35. [Google Scholar] [CrossRef]
- Hahn, A.; Barcikowski, S.; Chichkov, B.N. Influences on Nanoparticle Production during Pulsed Laser Ablation. J. Laser Micro/Nanoeng. 2007, 3, 73–77. [Google Scholar] [CrossRef]
- Itina, T.E. On Nanoparticle Formation by Laser Ablation in Liquids. J. Phys. Chem. C 2011, 115, 5044–5048. [Google Scholar] [CrossRef]
- Baati, T.; Al-Kattan, A.; Esteve, M.A.; Njim, L.; Ryabchikov, Y.; Chaspoul, F.; Hammami, M.; Sentis, M.; Kabashin, A.V.; Braguer, D. Ultrapure Laser-Synthesized Si-Based Nanomaterials for Biomedical Applications: In Vivo Assessment of Safety and Biodistribution. Sci. Rep. 2016, 6, 25400. [Google Scholar] [CrossRef] [Green Version]
- Shasha, C.; Krishnan, K.M. Nonequilibrium Dynamics of Magnetic Nanoparticles with Applications in Biomedicine. Adv. Mater. 2021, 33, 48–50. [Google Scholar] [CrossRef]
- Iqbal, S.; Fakhar-e-Alam, M.; Akbar, F.; Shafiq, M.; Atif, M.; Amin, N.; Ismail, M.; Hanif, A.; Farooq, W.A. Application of Silver Oxide Nanoparticles for the Treatment of Cancer. J. Mol. Struct. 2019, 1189, 203–209. [Google Scholar] [CrossRef]
- Buccolieri, A.; Serra, A.; Giancane, G.; Manno, D. Colloidal Solution of Silver Nanoparticles for Label-Free Colorimetric Sensing of Ammonia in Aqueous Solutions. Beilstein J. Nanotechnol. 2018, 9, 499–507. [Google Scholar] [CrossRef] [Green Version]
- Lohse, S.E.; Murphy, C.J. Applications of Colloidal Inorganic Nanoparticles: From Medicine to Energy. J. Am. Chem. Soc. 2012, 134, 15607–15620. [Google Scholar] [CrossRef] [PubMed]
- Blažeka, D.; Car, J.; Klobučar, N.; Jurov, A.; Zavašnik, J.; Jagodar, A.; Kovačević, E.; Krstulović, N. Photodegradation of Methylene Blue and Rhodamine b Using Laser-Synthesized Zno Nanoparticles. Materials 2020, 13, 4357. [Google Scholar] [CrossRef]
- Minelli, C.; Bartczak, D.; Peters, R.; Rissler, J.; Undas, A.; Sikora, A.; Sjöström, E.; Goenaga-Infante, H.; Shard, A.G. Sticky Measurement Problem: Number Concentration of Agglomerated Nanoparticles. Langmuir 2019, 35, 4927–4935. [Google Scholar] [CrossRef] [PubMed]
- Shang, J.; Gao, X. Nanoparticle Counting: Towards Accurate Determination of the Molar Concentration. Chem. Soc. Rev. 2014, 43, 7267–7278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vysotskii, V.V.; Uryupina, O.Y.; Gusel’Nikova, A.V.; Roldugin, V.I. On the Feasibility of Determining Nanoparticle Concentration by the Dynamic Light Scattering Method. Colloid J. 2009, 71, 739–744. [Google Scholar] [CrossRef]
- Ribeiro, L.N.D.M.; Couto, V.M.; Fraceto, L.F.; De Paula, E. Use of Nanoparticle Concentration as a Tool to Understand the Structural Properties of Colloids. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Irache, J.M.; Durrer, C.; Ponchel, G.; Duchêne, D. Determination of Particle Concentration in Latexes by Turbidimetry. Int. J. Pharm. 1993, 90, 93–96. [Google Scholar] [CrossRef]
- Xu, X.; Franke, T.; Schilling, K.; Sommerdijk, N.A.J.M.; Cölfen, H. Binary Colloidal Nanoparticle Concentration Gradients in a Centrifugal Field at High Concentration. Nano Lett. 2019, 19, 1136–1142. [Google Scholar] [CrossRef]
- Schmoll, L.H.; Peters, T.M.; O’Shaughnessy, P.T. Use of a Condensation Particle Counter and an Optical Particle Counter to Assess the Number Concentration of Engineered Nanoparticles. J. Occup. Environ. Hyg. 2010, 7, 535–545. [Google Scholar] [CrossRef]
- Tong, M.; Brown, O.S.; Stone, P.R.; Cree, L.M.; Chamley, L.W. Flow Speed Alters the Apparent Size and Concentration of Particles Measured Using NanoSight Nanoparticle Tracking Analysis. Placenta 2016, 38, 29–32. [Google Scholar] [CrossRef]
- Bachurski, D.; Schuldner, M.; Nguyen, P.H.; Malz, A.; Reiners, K.S.; Grenzi, P.C.; Babatz, F.; Schauss, A.C.; Hansen, H.P.; Hallek, M.; et al. Extracellular Vesicle Measurements with Nanoparticle Tracking Analysis–An Accuracy and Repeatability Comparison between NanoSight NS300 and ZetaView. J. Extracell. Vesicles 2019, 8, 1596016. [Google Scholar] [CrossRef] [PubMed]
- Fréchette-Viens, L.; Hadioui, M.; Wilkinson, K.J. Quantification of ZnO Nanoparticles and Other Zn Containing Colloids in Natural Waters Using a High Sensitivity Single Particle ICP-MS. Talanta 2019, 200, 156–162. [Google Scholar] [CrossRef]
- Haiss, W.; Thanh, N.T.K.; Aveyard, J.; Fernig, D.G. Determination of Size and Concentration of Gold Nanoparticles from UV-Vis Spectra. Anal. Chem. 2007, 79, 4215–4221. [Google Scholar] [CrossRef]
- Contreras, E.M.C.; Filho, E.P.B. Heat transfer performance of an automotive radiator with MWCNT nanofluid cooling in a high operating temperature range. Appl. Therm. Eng. 2022, 207, 118149. [Google Scholar] [CrossRef]
- Kozak, D.; Anderson, W.; Vogel, R.; Trau, M. Advances in Resistive Pulse Sensors: Devices Bridging the Void between Molecular and Microscopic Detection. Nano Today 2011, 6, 531–545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Car, J.; Blažeka, D.; Bajan, T.; Krce, L.; Aviani, I.; Krstulović, N. A quantitative analysis of colloidal solution of metal nanoparticles produced by laser ablation in liquids. Appl. Phys. A 2021, 127, 838. [Google Scholar] [CrossRef]
- Lan, Y.; Lu, Y.; Ren, Z. Mini Review on Photocatalysis of Titanium Dioxide Nanoparticles and Their Solar Applications. Nano Energy 2013, 2, 1031–1045. [Google Scholar] [CrossRef]
- Sun, S.; Song, P.; Cui, J.; Liang, S. Amorphous TiO2 Nanostructures: Synthesis, Fundamental Properties and Photocatalytic Applications. Catal. Sci. Technol. 2019, 9, 4198–4215. [Google Scholar] [CrossRef]
- Wiśniewski, M.; Roszek, K. Underestimated Properties of Nanosized Amorphous Titanium Dioxide. Int. J. Mol. Sci. 2022, 23, 2460. [Google Scholar] [CrossRef]
- Vargas, M.A.; Rodríguez-Páez, J.E. Amorphous TiO2 Nanoparticles: Synthesis and Antibacterial Capacity. J. Non-Cryst. Solids 2017, 459, 192–205. [Google Scholar] [CrossRef]
- Liu, X.; Atwater, M.; Wang, J.; Huo, Q. Extinction Coefficient of Gold Nanoparticles with Different Sizes and Different Capping Ligands. Colloids Surf. B Biointerfaces 2007, 58, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Hendel, T.; Wuithschick, M.; Kettemann, F.; Birnbaum, A.; Rademann, K.; Polte, J. In Situ Determination of Colloidal Gold Concentrations with Uv-Vis Spectroscopy: Limitations and Perspectives. Anal. Chem. 2014, 86, 11115–11124. [Google Scholar] [CrossRef]
- Thiele, E.S.; French, R.H. Light-Scattering Properties of Representative, Morphological Rutile Titania Particles Studied Using a Finite-Element Method. J. Am. Ceram. Soc. 2005, 81, 469–479. [Google Scholar] [CrossRef]
- Egerton, T.A. Uv-Absorption-the Primary Process in Photocatalysis and Some Practical Consequences. Molecules 2014, 19, 18192–18214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krstulović, N.; Shannon, S.; Stefanuik, R.; Fanara, C. Underwater-Laser Drilling of Aluminum. Int. J. Adv. Manuf. Technol. 2013, 69, 1765–1773. [Google Scholar] [CrossRef]
- Krstulović, N.; Umek, P.; Salamon, K.; Capan, I. Synthesis of Al-doped ZnO nanoparticles by laser ablation of ZnO:Al2O3 target in water. Mater. Res. Express 2017, 4, 2053–2059. [Google Scholar] [CrossRef]
- Krstulović, N.; Milošević, S. Drilling Enhancement by Nanosecond-Nanosecond Collinear Dual-Pulse Laser Ablation of Titanium in Vacuum. Appl. Surf. Sci. 2010, 256, 4142–4148. [Google Scholar] [CrossRef]
- Mätzler, C. MATLAB Functions for Mie Scattering and Absorption. IAP Res. Rep. 2002, 1139–1151. [Google Scholar]
- Krstulović, N.; Salamon, K.; Budimlija, O.; Kovač, J.; Dasović, J.; Umek, P.; Capan, I. Parameters Optimization for Synthesis of Al-Doped ZnO Nanoparticles by Laser Ablation in Water. Appl. Surf. Sci. 2018, 440, 916–925. [Google Scholar] [CrossRef]
- Mafuné, F.; Kohno, J.Y.; Takeda, Y.; Kondow, T.; Sawabe, H. Formation of Gold Nanoparticles by Laser Ablation in Aqueous Solution of Surfactant. J. Phys. Chem. B 2001, 105, 5114–5120. [Google Scholar] [CrossRef]
- Zeng, H.; Du, X.W.; Singh, S.C.; Kulinich, S.A.; Yang, S.; He, J.; Cai, W. Nanomaterials via Laser Ablation/Irradiation in Liquid: A Review. Adv. Funct. Mater. 2012, 22, 1333–1353. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Li, P.; Tian, Z.; Liang, C. Recent Advances in Surfactant-Free, Surface-Charged, and Defect-Rich Catalysts Developed by Laser Ablation and Processing in Liquids. ChemNanoMat 2017, 3, 512–533. [Google Scholar] [CrossRef]
- Nakamura, T.; Ichitsubo, T.; Matsubara, E.; Muramatsu, A.; Sato, N.; Takahashi, H. On the Preferential Formation of Anatase in Amorphous Titanium Oxide Film. Scr. Mater. 2005, 53, 1019–1023. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kostopoulos, V.; Kontaxis, L.C.; Kollia, E.; Kotrotsos, A. A comparative study between epoxy/Titania micro- and nanoparticulate composites thermal and mechanical behavior by means of particle-matrix interphase considerations. Polym. Eng. Sci. 2017, 58, 1146–1154. [Google Scholar] [CrossRef]
- Naik, V.M.; Haddad, D.; Naik, R.; Benci, J.; Auner, G.W. Optical Properties of Anatase, Rutile and Amorphous Phases of TiO2 Thin Films Grown at Room Temperature by RF Magnetron Sputtering. Mater. Res. Soc. Symp. Proc. 2003, 755, 413–418. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar] [CrossRef] [Green Version]
- Thormählen, I.; Straub, J.; Grigull, U. Refractive Index of Water and Its Dependence on Wavelength, Temperature, and Density. J. Phys. Chem. Ref. Data 1985, 14, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Schiebener, P.; Straub, J.; Sengers, L.J.M.H.; Gallagher, J.S. RI of Water and Steam as a Function of Wavelength, Temperature and Density. J. Phys. Chem. 1990, 19, 677. [Google Scholar]
- Bendavid, A.; Martin, P.J. Review of Thin Film Materials Deposition by the Filtered Cathodic Vacuum Arc Process at CSIRO. J. Aust. Ceram. Soc. 2014, 50, 86–101. [Google Scholar]
- Siefke, T.; Kroker, S.; Pfeiffer, K.; Puffky, O.; Dietrich, K.; Franta, D.; Ohlídal, I.; Szeghalmi, A.; Kley, E.B.; Tünnermann, A. Materials Pushing the Application Limits of Wire Grid Polarizers Further into the Deep Ultraviolet Spectral Range. Adv. Opt. Mater. 2016, 4, 1780–1786. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, V.; Kumar, M.; Schubert, J.; Probst, P.T.; Joseph, J.; König, T.A.F. Hybridized Guided-Mode Resonances via Colloidal Plasmonic Self-Assembled Grating. ACS Appl. Mater. Interfaces 2019, 11, 13752–13760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bodurov, I.; Vlaeva, I.; Viraneva, A.; Yovcheva, T.; Sainov, S. Modified design of a laser refractometer. J. Nanosci. Nanotechnol. 2016, 16, 31–33. [Google Scholar]
- Bodurov, I.; Yovcheva, T.; Sainov, S. Refractive index investigations of nanoparticles dispersed in water. J. Phys. Conf. Ser. 2014, 558, 012062. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://refractiveindex.info (accessed on 21 October 2021).




| No. of Laser Pulses | CV (108 mL−1) | CA (108 mL−1) |
|---|---|---|
| 1000 | 1.9 ± 0.2 | 1.8 ± 0.3 |
| 3000 | 4.0 ± 0.4 | 3.1 ± 0.5 |
| 5000 | 5.0 ± 0.5 | 3.8 ± 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blažeka, D.; Car, J.; Krstulović, N. Concentration Quantification of TiO2 Nanoparticles Synthesized by Laser Ablation of a Ti Target in Water. Materials 2022, 15, 3146. https://doi.org/10.3390/ma15093146
Blažeka D, Car J, Krstulović N. Concentration Quantification of TiO2 Nanoparticles Synthesized by Laser Ablation of a Ti Target in Water. Materials. 2022; 15(9):3146. https://doi.org/10.3390/ma15093146
Chicago/Turabian StyleBlažeka, Damjan, Julio Car, and Nikša Krstulović. 2022. "Concentration Quantification of TiO2 Nanoparticles Synthesized by Laser Ablation of a Ti Target in Water" Materials 15, no. 9: 3146. https://doi.org/10.3390/ma15093146
APA StyleBlažeka, D., Car, J., & Krstulović, N. (2022). Concentration Quantification of TiO2 Nanoparticles Synthesized by Laser Ablation of a Ti Target in Water. Materials, 15(9), 3146. https://doi.org/10.3390/ma15093146







