Analytical Solution of Thermo–Mechanical Properties of Functionally Graded Materials by Asymptotic Homogenization Method
Abstract
:1. Introduction
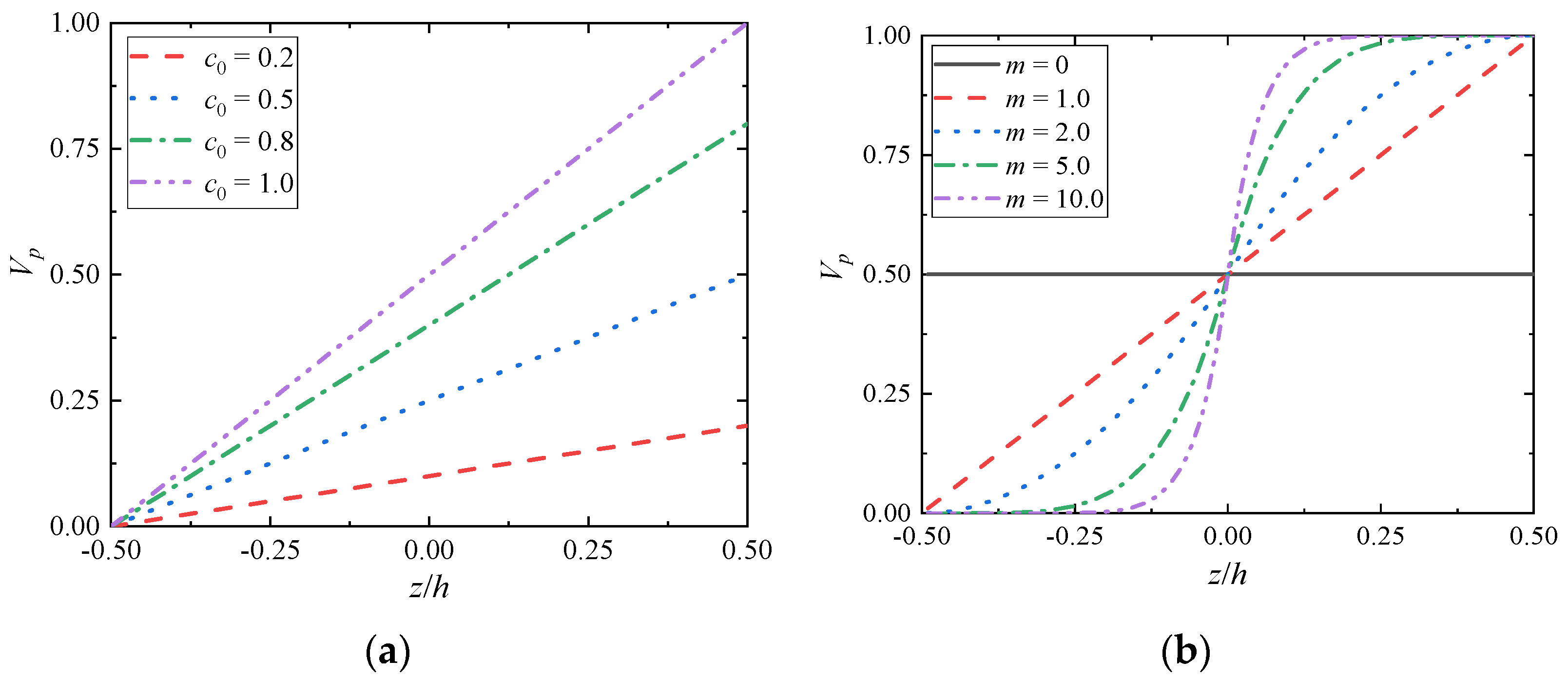
2. The Establishment of the Gradient Microstructure
3. Asymptotic Homogenization Method
3.1. Asymptotic Analysis and Model Development
3.2. Asymptotic Homogenization and Governing Equations
3.3. Determination of Effective Coefficients
4. Numerical Results and Discussion
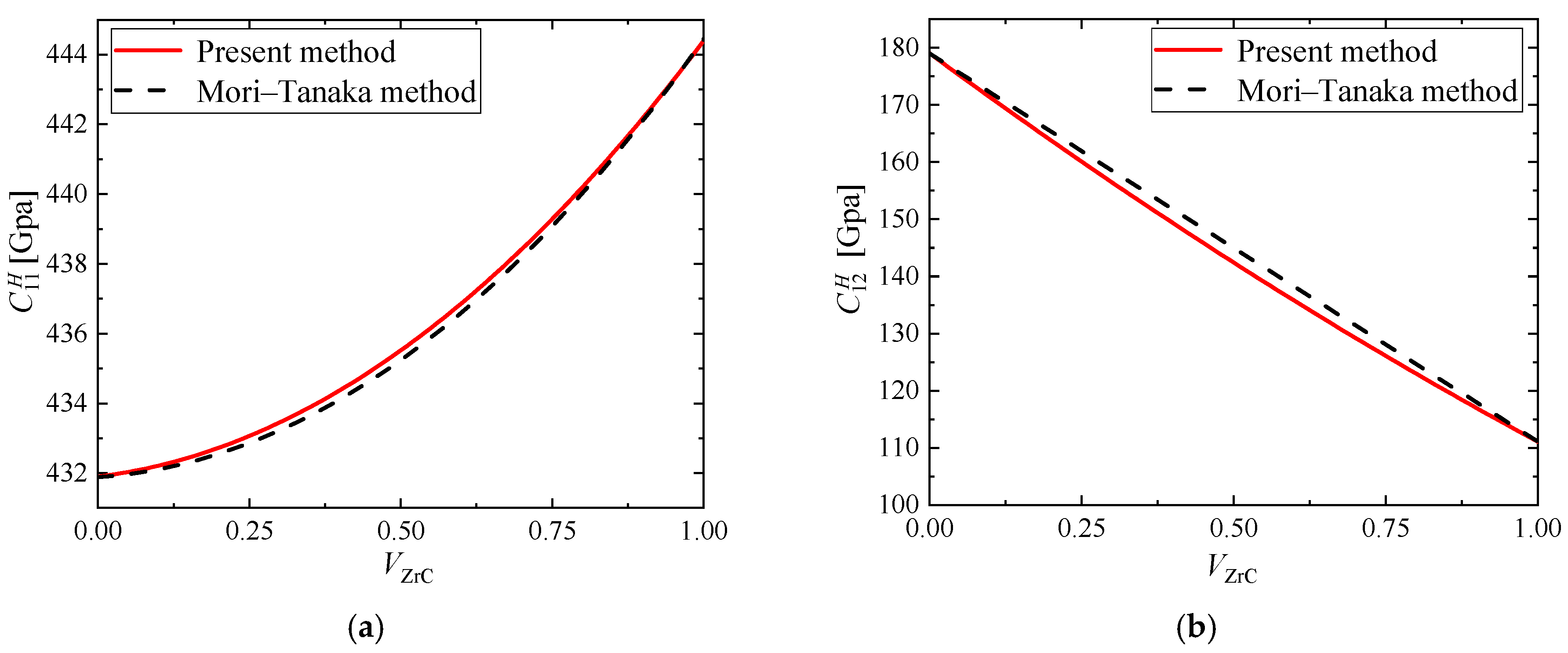
4.1. Validation of the Present Method
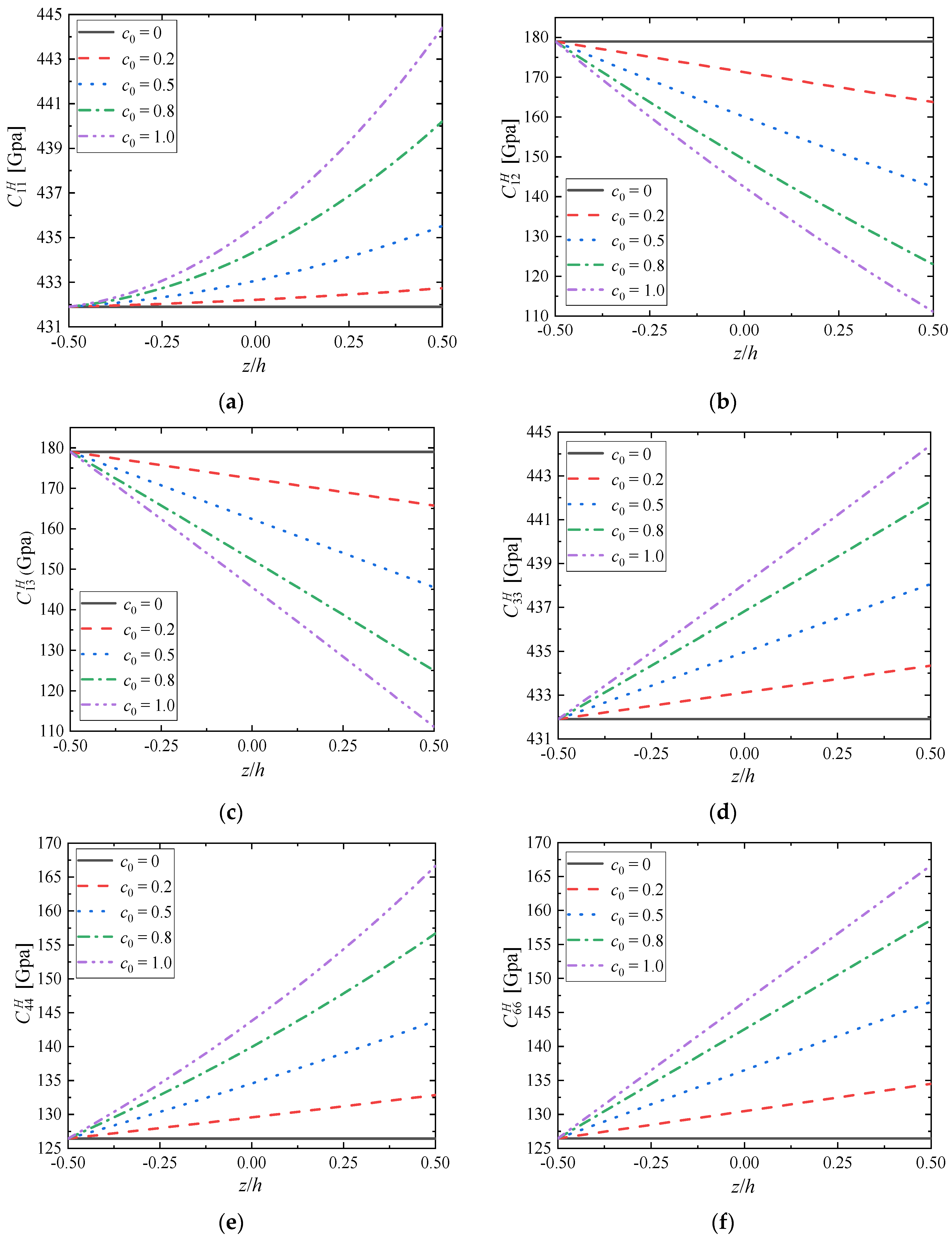
4.2. Effective Elastic Tensor’s Components
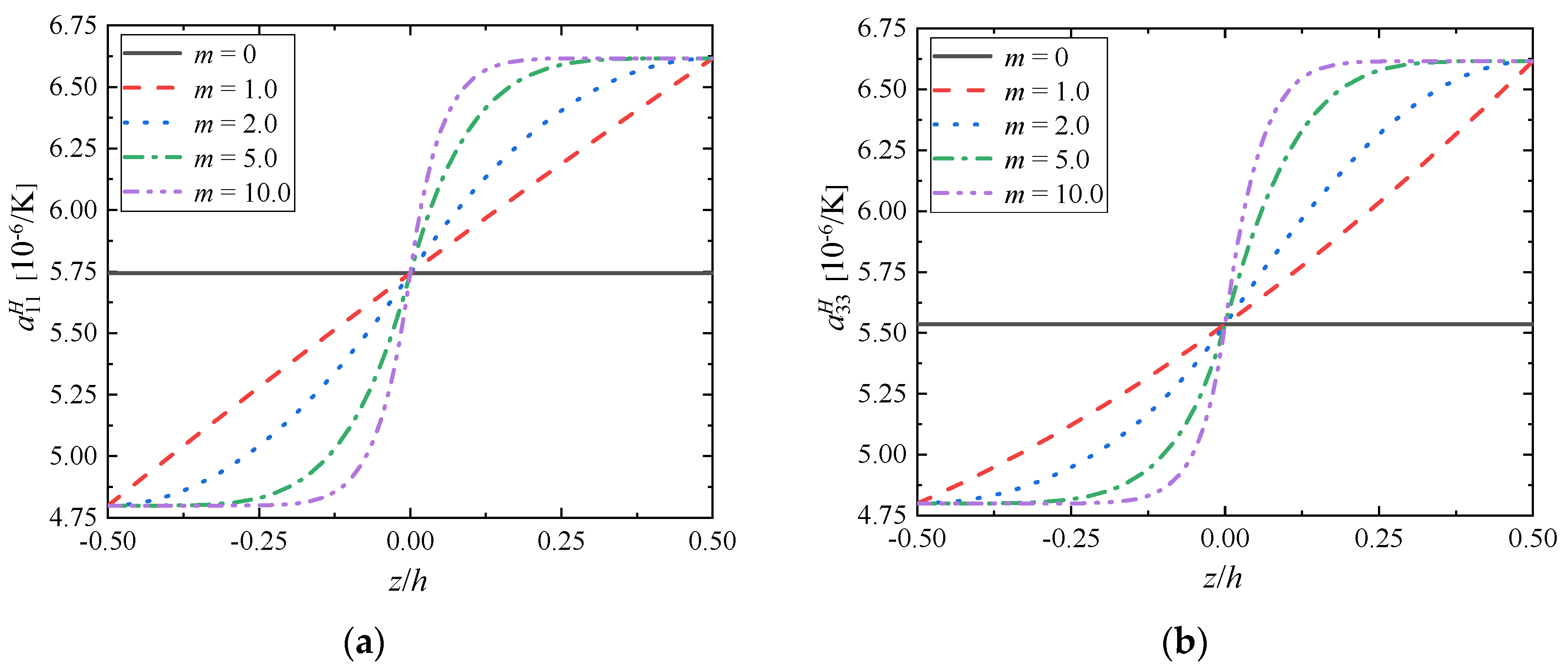
4.3. Effective Thermal Expansion Tensor’s Components
4.4. Effective Thermal Conductivity Tensor’s Components
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sam, M. Microstructural, mechanical and tribological analysis of functionally graded copper composite. Int. J. Cast Met. Res. 2020, 33, 123–133. [Google Scholar]
- Kazemzadeh–Parsi, M.-J.; Francisco, C.; Amine, A. Proper generalized decomposition for parametric study and material distribution design of multi–directional functionally graded plates based on 3D elasticity solution. Materials 2021, 14, 6660. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Xue, K.; Li, Q. Functionally graded rectangular plate with/without cutouts subject to general boundary conditions. Materials 2021, 14, 7088. [Google Scholar] [CrossRef] [PubMed]
- Nejad, M.Z.; Alamzadeh, N.; Hadi, A. Thermoelastoplastic analysis of FGM rotating thick cylindrical pressure vessels in linear elastic–fully plastic condition. Compos. Part B Eng. 2018, 154, 410–422. [Google Scholar] [CrossRef]
- Saleh, B.; Jiang, J.; Ma, A.; Song, D.; Xu, Q. Review on the influence of different reinforcements on the microstructure and wear behavior of functionally graded aluminum matrix composites by centrifugal casting. Met. Mater. Int. 2020, 26, 933–960. [Google Scholar] [CrossRef]
- Birsan, M.; Altenbach, H.; Sadowski, T.; Eremeyev, V.A.; Pietras, D. Deformation analysis of functionally graded beams by the direct approach. Compos. Part B Eng. 2012, 43, 1315–1328. [Google Scholar] [CrossRef] [Green Version]
- Moita, J.S.; Araújo, A.L.; Correia, V.F. Material distribution and sizing optimization of functionally graded plate–shell structures. Compos. Part B Eng. 2018, 142, 263–272. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, R.; Ai, S.; He, R.; Pei, Y.; Fang, D. Load distribution in threads of porous metal–ceramic functionally graded composite joints subjected to thermomechanical loading. Compos. Struct. 2015, 134, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Leon, L.M. Functionally gradient metal matrix composites: Numerical analysis of the microstructure–strength relationships. Compos. Sci. Technol. 2006, 66, 1873–1887. [Google Scholar]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Fan, F.; Lei, B.; Sahmani, S.; Safaei, B. On the surface elastic–based shear buckling characteristics of functionally graded composite skew nanoplates. Thin Wall. Struct. 2020, 154, 106841. [Google Scholar] [CrossRef]
- Fan, F.; Kiani, K. A rigorously analytical exploration of vibrations of arbitrarily shaped multi–layered nanomembranes from different materials. Int. J. Mech. Sci. 2021, 206, 106603. [Google Scholar] [CrossRef]
- Wu, D.; Liu, A.; Huang, Y.; Huang, Y.; Pi, Y.; Gao, W. Mathematical programming approach for uncertain linear elastic analysis of functionally graded porous structures with interval parameters. Compos. Part B Eng. 2018, 152, 282–291. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic–polynomial higher–order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Dutra, T.A.; Ferreira, R.T.L.; Resende, H.B.; Guimaraes, A.; Guedes, J.M. A complete implementation methodology for asymptotic homogenization using a finite element commercial software: Preprocessing and postprocessing. Compos. Struct. 2020, 245, 112305. [Google Scholar] [CrossRef]
- Fernández, M.; Böhlke, T. Hashin–Shtrikman bounds with eigenfields in terms of texture coefficients for polycrystalline materials. Acta Mater. 2019, 165, 686–697. [Google Scholar] [CrossRef]
- Salah, S.B.E.; Nait-Ali, A.; Gueguen, M.; Nadot-Martin, C. Non–local modeling with asymptotic expansion homogenization of random materials. Mech. Mater. 2020, 147, 103459. [Google Scholar] [CrossRef]
- Brown, J.M. Determination of Hashin–Shtrikman bounds on the isotropic effective elastic moduli of polycrystals of any symmetry. Comput. Geosci. 2015, 80, 95–99. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Budiansky, B. On the elastic moduli of some heterogeneous materials. J. Mech. Phys. Solids 1965, 13, 223–227. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. Math. Phy. Eng. Sci. 1957, 241, 376–396. [Google Scholar]
- Hill, R. A self–consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Christensen, R.M.; Lo, K.H. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Yun, G.J.; Zhu, F.Y.; Lim, H.J.; Choi, H. A damage plasticity constitutive model for wavy CNT nanocomposites by incremental Mori–Tanaka approach. Compos. Struct. 2021, 258, 113178. [Google Scholar] [CrossRef]
- Tran, V.P.; Brisard, S.; Guilleminot, J.; Sab, K. Mori–Tanaka estimates of the effective elastic properties of stress–gradient composites. Int. J. Solids Struct. 2018, 146, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Hu, N.; Long, X.; Zheng, H. Extension of combined self–consistent and Mori–Tanaka approach to evaluation of elastoplastic property of particulate composites. Acta Mech. Solida Sin. 2013, 26, 71–82. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Ray, M.C. Effective properties of a novel continuous fuzzy–fiber reinforced composite using the method of cells and the finite element method. Eur. J. Mech.-A/Solids 2012, 36, 191–203. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X. Effective multi–field properties of electro–magneto–thermoelastic composites estimated by finite element method approach. Acta Mech. Solida Sin. 2015, 28, 145–155. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology opimization II–analytical and numerical solution of homogenization equations. Comput. Struct. 1998, 69, 719–738. [Google Scholar] [CrossRef]
- Macedo, R.Q.; Ferreira, R.T.L.; Guedes, J.M.; Donadon, M.V. Intraply failure criterion for unidirectional fiber reinforced composites by means of asymptotic homogenization. Compos. Struct. 2017, 159, 335–349. [Google Scholar] [CrossRef]
- Macedo, R.Q.D.; Ferreira, R.T.L.; Donadon, M.V.; Guedes, J.M. Elastic properties of unidirectional fiber–reinforced composites using asymptotic homogenization techniques. J. Braz. Soc. Mech. Sci. 2018, 40, 255–265. [Google Scholar] [CrossRef]
- Brito-Santana, H.; Medeiros, R.D.; Rodriguez-Ramos, R.; Tita, V. Different interface models for calculating the effective properties in piezoelectric composite materials with imperfect fiber–matrix adhesion. Compos. Struct. 2016, 151, 70–80. [Google Scholar] [CrossRef]
- Medeiros, R.D.; Moreno, M.E.; Marques, F.D.; Tita, V. Effective properties evaluation for smart composite materials. J. Braz. Soc. Mech. Sci. 2012, 34, 362–370. [Google Scholar] [CrossRef] [Green Version]
- Naghdinasab, M.; Farrokhabadi, A.; Madadi, H. A numerical method to evaluate the material properties degradation in composite RVEs due to fiber–matrix debonding and induced matrix cracking. Finite Elem. Anal. Des. 2018, 146, 84–95. [Google Scholar] [CrossRef]
- Rodriguez-Ramos, R.; Medeiros, R.D.; Guinovart-Diaz, R.; Bravo-Castillero, J.; Otero, J.A.; Tita, V. Different approaches for calculating the effective elastic properties in composite materials under imperfect contact adherence. Compos. Struct. 2013, 99, 264–275. [Google Scholar] [CrossRef]
- Montero-Chacon, F.; Zaghi, S.; Rossi, R.; Garcia-Perez, E.; Heras-Perez, I.; Martinez, X.; Oller, S.; Doblare, M. Multiscale thermo–mechanical analysis of multi–layered coatings in solar thermal applications. Finite Elem. Anal. Des. 2017, 127, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Guan, X.; Liu, X.; Jia, X.; Yuan, Y.; Cui, J.; Mang, H.A. A stochastic multiscale model for predicting mechanical properties of fiber reinforced concrete. Int. J. Solids Struct. 2015, 56, 280–289. [Google Scholar] [CrossRef]
- Santana, H.B.; Thiesen, J.L.M.; Medeiros, R.D.; Ferreira, A.; Tita, V. Multiscale analysis for predicting the constitutive tensor effective coefficients of layered composites with micro and macro failures. Appl. Math. Model. 2019, 75, 250–266. [Google Scholar] [CrossRef]
- Nasirov, A.; Gupta, A.; Hasanov, S.; Fidan, I. Three–scale asymptotic homogenization of short fiber reinforced additively manufactured polymer composites. Compos. Part B Eng. 2020, 202, 108269. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, W. Variational asymptotic homogenization of elastoplastic composites. Compos. Struct. 2015, 133, 947–958. [Google Scholar] [CrossRef]
- Han, F.; Cui, J.; Yu, Y. The statistical second–order two–scale method for thermomechanical properties of statistically inhomogeneous materials. Int. J. Numer. Meth. Eng. 2009, 46, 654–659. [Google Scholar] [CrossRef]
- Nasution, M.R.E.; Watanabe, N.; Kondo, A.; Yudhanto, A. Thermomechanical properties and stress analysis of 3–D textile composites by asymptotic expansion homogenization method. Compos. Part B Eng. 2014, 60, 378–391. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.; Cheng, G.; Cai, Y. On predicting the effective elastic properties of polymer nanocomposites by novel numerical implementation of asymptotic homogenization method. Compos. Struct. 2016, 135, 297–305. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, Y.; Cui, J.; Yang, Z. Thermo–mechanical coupling analysis of statistically inhomogeneous porous materials with surface radiation by second–order two–scale method. Compos. Struct. 2017, 182, 346–363. [Google Scholar] [CrossRef]
- Vega, C.R.; Pina, J.C.; Bosco, E.; Flores, E.S.; Guzman, C.; Yaneza, S. Thermo–mechanical analysis of wood through an asymptotic homogenisation approach. Constr. Build. Mater. 2021, 315, 125617. [Google Scholar] [CrossRef]
- Bosco, E.; Claessens, R.J.M.A.; Suiker, A.S.J. Multi–scale prediction of chemo–mechanical properties of concrete materials through asymptotic homogenization. Cem. Concr. Res. 2020, 128, 105929. [Google Scholar] [CrossRef]
- Hennessy, M.G.; Moyles, I.R. Asymptotic reduction and homogenization of a thermo–electrochemical model for a lithium–ion battery. Appl. Math. Model. 2020, 80, 724–754. [Google Scholar] [CrossRef]
- Zhou, L.; Tang, J.; Tian, W.; Xue, B.; Li, X. A multi–physics coupling cell–based smoothed finite element micromechanical model for the transient response of magneto–electro–elastic structures with the asymptotic homogenization method. Thin Wall. Struct. 2021, 165, 107991. [Google Scholar] [CrossRef]
- Zhang, Y.; Shang, S.; Liu, S. A novel implementation algorithm of asymptotic homogenization for predicting the effective coefficient of thermal expansion of periodic composite materials. Acta Mech. Sin. 2017, 33, 368–381. [Google Scholar] [CrossRef]
- Cheng, G.; Cai, Y.; Xu, L. Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech. Sin. 2013, 29, 550–556. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, L.; Cheng, G. Novel numerical implementation of asymptotic homogenization method for periodic plate structures. Int. J. Solids Struct. 2014, 51, 284–292. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xie, Y.M.; Wang, Z.; Li, Q.; Zhou, S. A comparison of fast fourier transform–based homogenization method to asymptotic homogenization method. Compos. Struct. 2020, 15, 111979. [Google Scholar] [CrossRef]
- Qi, L.; Tian, W.; Zhou, J. Numerical evaluation of effective elastic properties of composites reinforced by spatially randomly distributed short fibers with certain aspect ratio. Compos. Struct. 2015, 13, 843–851. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Zhou, J.; Liang, J.; Ma, Y. Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications. Compos. Struct. 2015, 131, 366–373. [Google Scholar] [CrossRef]
- Tian, W.L.; Qi, L.H.; Chao, X.J.; Liang, J.; Fu, M. Periodic boundary condition and its numerical implementation algorithm for the evaluation of effective mechanical properties of the composites with complicated micro–structures. Compos. Part B Eng. 2019, 162, 1–10. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, R.; Otero, J.A.; Cruz-González, O.L.; Guinovart-Díaz, R.; Sevostianov, I. Computation of the relaxation effective moduli for fibrous viscoelastic composites using the asymptotic homogenization method. Int. J. Solids Struct. 2020, 190, 281–290. [Google Scholar] [CrossRef]
- Feng, J.W.; Cen, S.; Li, C.F.; Owen, D.R.J. Statistical reconstruction and Karhunen–Loève expansion for multiphase random media. Int. J. Numer. Meth. Eng. 2015, 105, 3–32. [Google Scholar] [CrossRef]
- Zhang, W.; Song, L.; Li, J. Efficient 3D reconstruction of random heterogeneous media via random process theory and stochastic reconstruction procedure. Comput. Methods Appl. Mech. 2019, 354, 1–15. [Google Scholar] [CrossRef]
- Kuga, Y.; Phu, P. Experimental studies of millimeter–wave scattering in discrete random media and from rough surfaces–summary. J. Electromagn. Wave 1996, 10, 451–453. [Google Scholar] [CrossRef] [Green Version]
- Chu, L.; Dui, G.; Ju, C. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 2018, 186, 39–49. [Google Scholar] [CrossRef]
- Chen, L.; Huang, J.; Yi, M.X.; Xing, Y.F. Physical interpretation of asymptotic expansion homogenization method for the thermomechanical problem. Compos. Struct. 2019, 227, 111200. [Google Scholar] [CrossRef]
- Pierson, H.O. Handbook of Refractory Carbides and Nitrides, 2nd ed.; William Andrew: Hillegom, The Netherlands, 1996; pp. 8–16. [Google Scholar]
- Yao, D.; Li, H.; Wu, H.; Fu, Q.G.; Qiang, X.F. Ablation resistance of ZrC/SiC gradient coating for SiC–coated carbon/carbon composites prepared by supersonic plasma spraying. J. Eur. Ceram. Soc. 2016, 36, 3739–3746. [Google Scholar] [CrossRef]
- Ding, X.; Ma, J.; Zhou, X.; Zhao, X.; Li, G. Fabrication of CeO2–Nd2O3 microspheres by internal gelation process using M(OH)m and [MCit·xH2O] (M = Ce3+, Ce4+, and Nd3+) as precursors. J. Sol-Gel Sci. Techn. 2019, 92, 66–74. [Google Scholar] [CrossRef]
- Flem, M.L.; Allemand, A.; Urvoy, S.; Cédat, D.; Rey, C. Microstructure and thermal conductivity of Mo–TiC cermets processed by hot isostatic pressing. J. Nucl. Mater. 2008, 380, 85–92. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Liu, L.; Chu, L.; Liu, Q. Analytical Solution of Thermo–Mechanical Properties of Functionally Graded Materials by Asymptotic Homogenization Method. Materials 2022, 15, 3073. https://doi.org/10.3390/ma15093073
Chen D, Liu L, Chu L, Liu Q. Analytical Solution of Thermo–Mechanical Properties of Functionally Graded Materials by Asymptotic Homogenization Method. Materials. 2022; 15(9):3073. https://doi.org/10.3390/ma15093073
Chicago/Turabian StyleChen, Dan, Lisheng Liu, Liangliang Chu, and Qiwen Liu. 2022. "Analytical Solution of Thermo–Mechanical Properties of Functionally Graded Materials by Asymptotic Homogenization Method" Materials 15, no. 9: 3073. https://doi.org/10.3390/ma15093073
APA StyleChen, D., Liu, L., Chu, L., & Liu, Q. (2022). Analytical Solution of Thermo–Mechanical Properties of Functionally Graded Materials by Asymptotic Homogenization Method. Materials, 15(9), 3073. https://doi.org/10.3390/ma15093073







