Radiation-Induced Patterning at the Nanometric Scale: A Phase Field Approach
Abstract
:1. Introduction
2. The Rate Theory
2.1. Foundation of the Rate Theory
- Defects produced during the slowing down of incident particles in the medium are produced over a time scale , i.e., the characteristic time of a displacement cascade ( s), much smaller than the time scale associated to the growth or shrink of extended defects (voids, dislocations) which is controlled by mass transport ( s). Such an assumption makes a distinction between point defects (vacancy, interstitials) and extended defects (voids, dislocations, self interstitial tetrahedron ) produced in displacement cascades.
- The flux of incident particle is large enough to neglect the correlation between sub-cascades and the the correlation between produced defects. The production rate of point defects can then be considered as uniform in the irradiated area.
2.2. The Rate Theory Approach
2.3. Limitations of the Rate Theory Approach
3. The Phase Field Approach
3.1. Foundation of the Phase Field
- The initial condition is usually given by an uniform distribution of the order parameter in the integration volume V. Since is an attractor of these equations, a small random variable is added to the uniform value of the order parameter. The mean value of this random variable is null and its variance of the order of [28].
- For close systems, Neumann conditions must be applied to the the order parameter and the driving force, defined by the chemical potential . This implies ad are null over for the conservative Cahn–Hilliard equation. Obviously for the non conservative equation, only the second condition holds.
- Neglecting edge effects, periodic conditions are usually applied for computing microstructures within the framework of the phase field theory. This implies that the order parameter can be expanded in an infinite cosine set. Numerically, a finite set of discrete cosine transform (dct-I) is used to solve these equations for close systems [29].
3.2. Application to Radiation Damage
- Point defects produced during the collision step are assumed to only modify the mobility of species or more precisely the kinetic Onsager coefficients. Their concentration is supposed to evolve rapidly with time and reach a steady state. It may result from the resolution of RT equations. The interest of such an approach lies in the fact that this steady state may evolve with the nano-structure dictated par the solutions of the Phase Field approach. The nano-structure is no more freeze and defined at the beginning of the simulation such as in the RT but can evolve with time. Under this approach, the atomic fraction of point defects is always small and does not modify the value of the thermodynamic potential describing the formation of the nano-structure under equilibrium. For instance, the value of the stiffness coefficient trigging the formation of heterogeneous structures does not depend on the atomic fraction of point defects.
- The motion of atoms under irradiation is dictated by an external dynamics resulting only from the ballistic mixing occurring inside sub-cascades. This ballistic mixing is due to a spatial averaging of atomic collisions occurring inside the sub-cascade. The flux of ejected particles is not proportional to the chemical potential of different species in the material as it is the case in thermal diffusion but depends on the atomic fraction of diffusing species. The key feature of the ballistic mixing lies on the fact that it exhibits a spatial dependence. As clearly pointed out by Sigmund [11], it depends on the nature and the energy of incident particles and can be modeled by a simple diffusion equation. It can be analytically computed [1] or extracted from MD simulations [30].
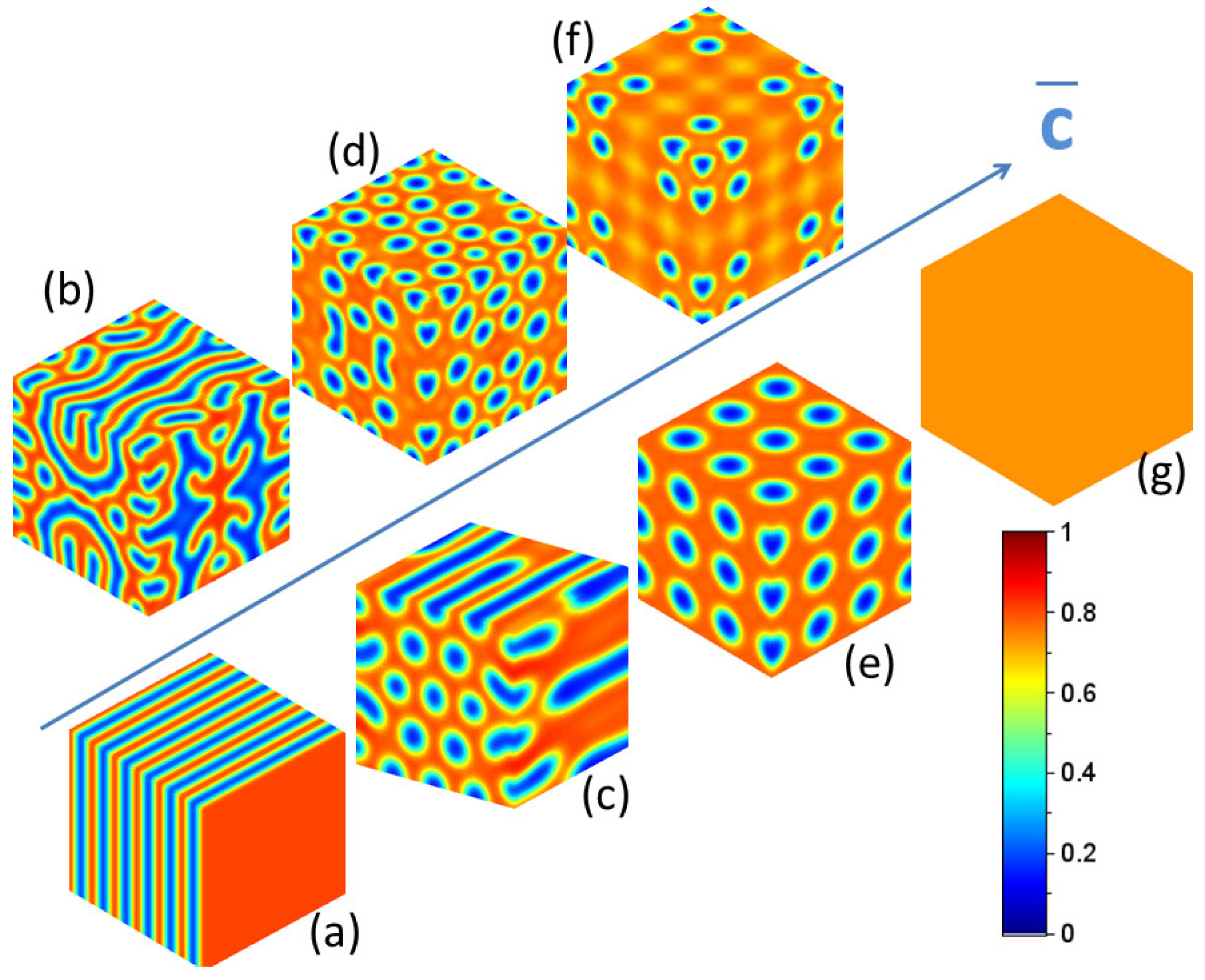
- Low values of implies that ballistic effects induced by irradiation can be neglected and that the system behaves as it does under thermal equilibrium. displays a maximum at as expected for a spinodal decomposition [24].
- High values of implies that ballistic effects dominate the micro-structure of the material under irradiation. As thermal effects are negligible, the large time microstructure results from a random distribution of Cu atoms in an Ag matrix. displays a maximum at .
- When , a competition between thermal and ballistic effects occurs. At large time, displays a maximum at a non null value independent of time [39]. The pattern shows the existence of this non null value of about few . This implies that a nano-patterning occurs under irradiation for given values of temperature T and flux .
3.3. Limitations of the Phase Field Approach
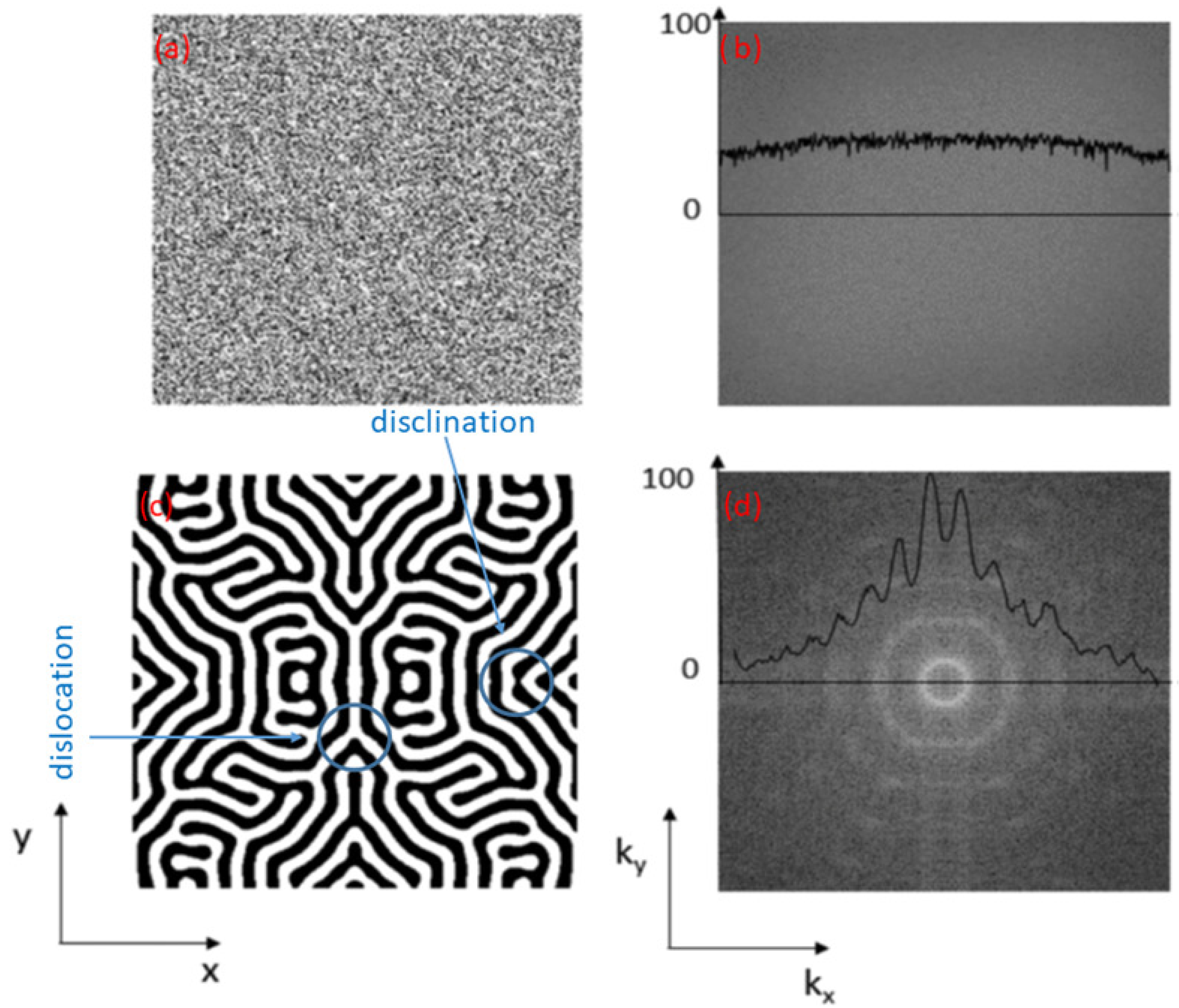
- The theoretical foundations of phase field models lies in the ability to perform a coarse-graining procedure over a length scale small in comparison with the characteristic length of the system L but large enough to neglect fluctuations of the order parameter proportional to under equilibrium. Under irradiation, specific mechanisms of energy deposition may impose larger fluctuations over this length scale and then may be taken into account to define the coarse graining length scale. Whatever the choice of the coarse graining length, this approach is inaccurate to compute for instance the formation of radiation-induced dislocation nor evolution of the short range order.
- The control parameter is the ratio between a-thermal ballistic diffusion term and the radiation-enhanced mobility . This last term is directly related with the concentration of point defects produced under irradiation. This concentration depends on the late time microstructure, resulting from the calculation of the microstructure using the phase field approach, via the numbers and the density of sinks. This feedback effect must be studied in detail.
- Since the dynamics of vacancies and interstitials created under irradiation cannot be described by any free energy functional, the phase field approach is inefficient for computing the evolution of point defects under irradiation.
4. Conclusions and Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sigmund, P. Particle Radiation and Radiation Effects; Springer Series in Solid State Sciences; Springer: Berlin/Heidelberg, Germany, 2006; Volume 151. [Google Scholar]
- Simeone, D.; Ribis, J.; Luneville, L. Continuum approaches for modeling radiation-induced self-organization in materials: From the rate theory to the phase field approach. J. Mat. Res. 2018, 33, 440–454. [Google Scholar] [CrossRef]
- Simeone, D.; Demange, G.; Luneville, L. Disrupted coarsening in complex Cahn-Hilliard dynamics. Phys. Rev. E 2013, 88, 032116. [Google Scholar] [CrossRef]
- Enrique, R.A.; Bellon, P. Self organized Cu-Ag nanocomposites synthesized by intermediate temperature ion-beam mixing. Appl. Phys. Lett. 2001, 78, 4178. [Google Scholar] [CrossRef]
- Ghoniem, N.; Walgraef, D. Instabilities and Self Organization in Materials; Oxford Science Publications: Oxford, UK, 2008; Volume I. [Google Scholar]
- Baldinozzi, G.; Simeone, D.; Gosset, D.; Monnet, I.; Le Caër, S.; Mazerolles, L. Evidence of extended defects in pure zirconia irradiated by swift heavy ions. Phys. Rev. B 2006, 74, 132107. [Google Scholar] [CrossRef]
- Beauford, M.; Vallet, M.; Nicolai, J.; Bardot, J. In situ evolution of He bubbles in SiC under irradiation. J. Appl. Phys. 2015, 118, 205904. [Google Scholar] [CrossRef]
- Turing, A. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. Lond. 1952, B-237, 37–72. [Google Scholar]
- Brailsford, A.D.; Bullough, R. The rate theory of swelling due to void growth in irradiated metals. J. Nucl. Mater. 1972, 44, 121–135. [Google Scholar] [CrossRef]
- Bullough, R.; Hayns, M.R. The temperature dependence of irradiation creep. In Proceedings of the International Conference Organized by the Commission of the European Communities at the Joint Research Centre, Petten, The Netherlands, 5–6 May 1976; Volume 65. [Google Scholar]
- Sigmund, P.; Gras-Marti, A. Theoretical aspects of atomic mixing by ion beams. Nucl. Inst. Methods B 1981, 182, 211–219. [Google Scholar] [CrossRef]
- Karlin, S.; Taylor, H.M. A First Course in Stochastic Processes; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self Organization in Nonequilibrium Systems: From Dissipative Structure to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Van Kampen, G. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Luneville, L.; Sublet, J.C.; Simeone, D. Impact of nuclear transmutations on the primary damage production: The example of Ni based steels. J. Nucl. Mater. 2018, 505, 262–266. [Google Scholar] [CrossRef]
- Sizmann, R. The effect of radiation upon diffusion in metals. J. Nucl. Mater. 1978, 69, 386–412. [Google Scholar] [CrossRef]
- Berge, P.; Pomeau, Y.; Vidal, C. L’ordre dans le Chaos; Hermann: Paris, France, 1984. [Google Scholar]
- Somorjai, R. Physical Chemistry; Academic Press: New York, NY, USA, 1975; Volume XI-B. [Google Scholar]
- Maydet, S.; Russel, K. Precipitate stability under irradiation: Point defect effects. J. Nucl. Mater. 1977, 64, 101. [Google Scholar] [CrossRef]
- Landau, L.; Lifchitz, L. Theoretical Physics; MIR: Moscow, Russia, 1975; Volume 4. [Google Scholar]
- Le Bellac, M.; Mortessagne, F.; Batrouni, G. Equilibrium and Non Equilibrium Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. Sov. Phys. JETP 1950, 20, 1064. [Google Scholar]
- Tolédano, P.; Dmitriev, V. Reconstructive Phase Transitions: In Crystals and Quasicrystals; World Scientific: Singapore, 1996. [Google Scholar]
- Khatchaturyan, A.G. Theory of Structural Transformation in Solids; Wiley Interscience: Hoboken, NJ, USA, 1983. [Google Scholar]
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes I. Phys. Rev. 1931, 37, 405–410. [Google Scholar] [CrossRef]
- Bray, A.; Humayn, K. Scaling and multi scaling in the ordereing kinetics of a conserved order paameter. Phys. Rev. Lett. 1992, 68, 1559. [Google Scholar] [CrossRef]
- Strang, G. The Discrete Cosine Transform. Siam Rev. 1999, 41, 135–147. [Google Scholar] [CrossRef]
- Bukonte, F.; Djurabekova, F.; Samela, J.; Nordlund, K.; Norris, S.A.; Aziz, M.J. Comparison of molecular dynamics and binary collision approximation simulations for atom displacements analysis. Nucl. Instrum. Methods Phys. Res. B 2013, 297, 23–28. [Google Scholar] [CrossRef] [Green Version]
- Simeone, D.; Luneville, L. Concentration profile distortion under ion beam mixing: An example of Levy flight. Phys. Rev. E 2010, 81, 021115. [Google Scholar] [CrossRef]
- Wilkes, P. Phase stability under irradiation—A rev iew of theory and experiment. J. Nucl. Mater. 1979, 83, 166–175. [Google Scholar] [CrossRef]
- Cross, M.; Greenside, H. Pattern Formation and Dynamics in Non Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Luneville, L.; Garcia, P.; Simeone, D. Predicting Nonequilibrium Patterns beyond Thermodynamic Concepts: Application to radiation-induced Microstructures. Phys. Rev. Lett. 2020, 246, 085701. [Google Scholar] [CrossRef] [PubMed]
- Krasnochtchekov, P.; Averback, R.S.; Bellon, P. Phase separation and dynamic patterning in Cu1−xCox films under ion irradiation. Phys. Rev. B 2005, 72, 174102. [Google Scholar] [CrossRef]
- Martin, G. Phase stability under irradiation: Ballistic effects. Phys. Rev. B 1984, 30, 53. [Google Scholar] [CrossRef]
- Enrique, R.A.; Bellon, P. Nonequilibrium fluctuations, effective temperature, and effective interactions 10 driven by irradiation of alloys. Phys. Rev. B 2004, 70, 224106. [Google Scholar] [CrossRef]
- Simeone, D.; Thorogood, G.; Forestier, A.; Garcia, P.; Luneville, L. Radiation-induced micro-structures as ground states of a Swift-Hohenberg Energy functional. J. Appl. Phys. 2019, 125, 065103. [Google Scholar] [CrossRef] [Green Version]
- Luneville, L.; Mallick, K.; Pontikis, V.; Simeone, D. Patterning in systems driven by non local external forces. Phys. Rev. E 2016, 94, 052126. [Google Scholar] [CrossRef] [Green Version]
- Elder, K.; Katakowski, M.; Haataja, M.; Grant, M. Modelling elasticity in crystal growth. Phys. Rev. Lett. 2002, 88, 245701. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, S.V.; Frick, M.; Quitoriano, N.; Ofori-Opoku, N.; Provatas, N.; Bevan, K.H. Capturing Dislocation Half-Loop Formation and Dynamics in Epitaxial Growth Atomistically at Diffusive Time Scales. Materialia 2021, 20, 101253. [Google Scholar] [CrossRef]
- Berry, J.; Grant, M.; Elder, K. Diffusive atomistic dynamics of edge dislocations in two dimensions. Phys. Rev. E 2006, 73, 031609. [Google Scholar] [CrossRef] [Green Version]
- Berry, J.; Provatas, N.; Rottler, J.; Sinclair, C. Defect stability in PFC models: Stacking faults and partial dislocations. Phys. Rev. B 2012, 86, 224112. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Grant, M.; Samajdar, I.; Haldar, A.; Sain, A. Neutron small-angle scattering study of unmixing in feCR alloys. Sci. Rep. 2013, 3, 2728. [Google Scholar] [CrossRef] [PubMed]
- Goldstone, J. Field theories with superconductor solutions. Nuovo Cimento 1961, 19, 154. [Google Scholar] [CrossRef]
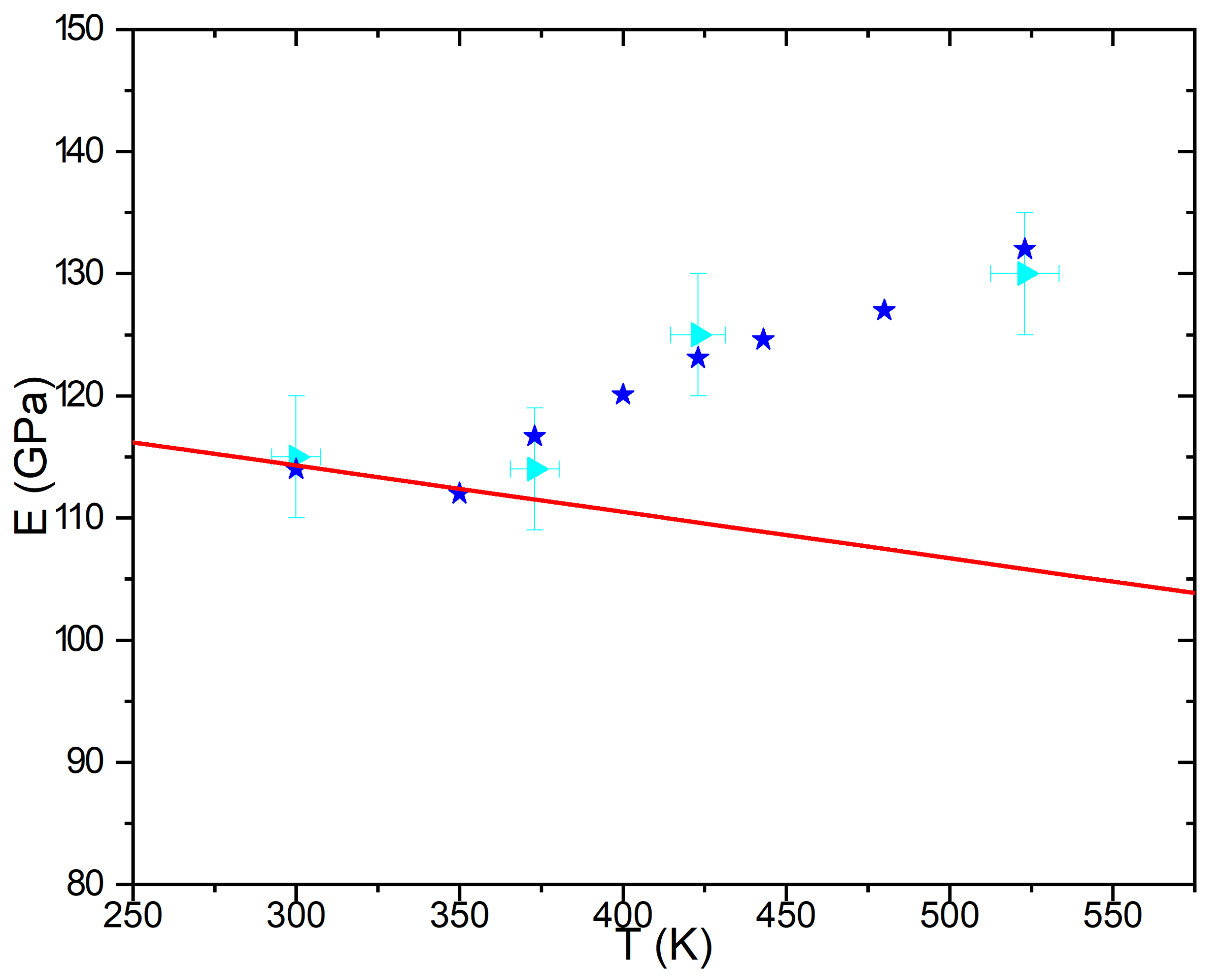
- Simeone, D.; Garcia, P.; Bacri, C.; Luneville, L. Symmetry Breaking Resulting from Long-Range Interactions in Out of Equilibrium Systems: Elastic Properties of Irradiated AgCu. Phys. Rev. Lett. 2020, 125, 246103. [Google Scholar] [CrossRef] [PubMed]
- Chee, S.; Stumphy, B.; Vo, N.; Averback, R.; Bellon, P. Dynamic self-organization in Cu alloys under ion irradiation. Acta Mater. 2010, 58, 4088–4099. [Google Scholar] [CrossRef]
- Katchaturyan, A.; Semenovskaya, S.; Tsakalakos, T. Elastic strain energy in inhomogeneous solids. Phys. Rev. B 1995, 52, 15909. [Google Scholar] [CrossRef] [PubMed]
- Fiscker-Cripps, A. Nanoindentation; Springer Science: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Zhang, Y.; Gao, Y.; Sun, C.; Schewn, D.; Jiang, C.; Gan, J. Symmetry breaking during defect self-organization under irradiation. Mater. Theory 2020, 4, 5–17. [Google Scholar] [CrossRef]
- Li, Y.; Hu, S.; Sun, X.; Stan, M. A review: Applications of the Phase Field methods in predicting microstructure and properties evolution of irradiated nuclear materials. Comput. Mater. 2017, 3, 16. [Google Scholar] [CrossRef]
- Li, Q.; Averback, R.; Bellon, P. Compositional patterning in irradiated alloys: Effective potential and effective interfacial energy. Phys. Rev. B 2021, 103, 104110. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: New York, NY, USA, 1998. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simeone, D.; Garcia, P.; Luneville, L. Radiation-Induced Patterning at the Nanometric Scale: A Phase Field Approach. Materials 2022, 15, 2991. https://doi.org/10.3390/ma15092991
Simeone D, Garcia P, Luneville L. Radiation-Induced Patterning at the Nanometric Scale: A Phase Field Approach. Materials. 2022; 15(9):2991. https://doi.org/10.3390/ma15092991
Chicago/Turabian StyleSimeone, David, Philippe Garcia, and Laurence Luneville. 2022. "Radiation-Induced Patterning at the Nanometric Scale: A Phase Field Approach" Materials 15, no. 9: 2991. https://doi.org/10.3390/ma15092991
APA StyleSimeone, D., Garcia, P., & Luneville, L. (2022). Radiation-Induced Patterning at the Nanometric Scale: A Phase Field Approach. Materials, 15(9), 2991. https://doi.org/10.3390/ma15092991





