Next Article in Journal
Effects of Fiber Orientation on the Coefficient of Thermal Expansion of Fiber-Filled Polymer Systems in Large Format Polymer Extrusion-Based Additive Manufacturing
Next Article in Special Issue
High-Entropy Borides under Extreme Environment of Pressures and Temperatures
Previous Article in Journal
Influence of Modified Epoxy Dian Resin on Properties of Nitrile-Butadiene Rubber (NBR)
Previous Article in Special Issue
Future Study of Dense Superconducting Hydrides at High Pressure
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 15
Issue 8
10.3390/ma15082762
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental and Computational Studies of Compression and Deformation Behavior of Hafnium Diboride to 208 GPa

by
Kaleb Burrage
1,
Chia-Min Lin
2,
Cheng-Chien Chen
2,* and
Yogesh K. Vohra
2,*
1
Neutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA
2
Department of Physics, University of Alabama at Birmingham, Birmingham, AL 35294, USA
*
Authors to whom correspondence should be addressed.
Materials 2022, 15(8), 2762; https://doi.org/10.3390/ma15082762
Submission received: 9 March 2022 / Revised: 5 April 2022 / Accepted: 6 April 2022 / Published: 9 April 2022
(This article belongs to the Special Issue Materials Behavior under Compression)
Browse Figures
Versions Notes

Abstract

The compression behavior of the hexagonal AlB2 phase of Hafnium Diboride (HfB2) was studied in a diamond anvil cell to a pressure of 208 GPa by axial X-ray diffraction employing platinum as an internal pressure standard. The deformation behavior of HfB2 was studied by radial X-ray diffraction technique to 50 GPa, which allows for measurement of maximum differential stress or compressive yield strength at high pressures. The hydrostatic compression curve deduced from radial X-ray diffraction measurements yielded an ambient-pressure volume V0 = 29.73 Å3/atom and a bulk modulus K0 = 282 GPa. Density functional theory calculations showed ambient-pressure volume V0 = 29.84 Å3/atom and bulk modulus K0 = 262 GPa, which are in good agreement with the hydrostatic experimental values. The measured compressive yield strength approaches 3% of the shear modulus at a pressure of 50 GPa. The theoretical strain-stress calculation shows a maximum shear stress τmax~39 GPa along the (1−10) [110] direction of the hexagonal lattice of HfB2, which thereby can be an incompressible high strength material for extreme-environment applications.

1. Introduction

Hafnium diboride (HfB2) belongs to a class of AlB2-type transition metal borides that have exhibited superb physical and thermal properties. The high bulk modulus (K0 = 260–350 GPa [1,2]), low thermal expansion coefficient (7.49 × 10−6 K−1) [3], and high shear to bulk modulus ratio (G0~270 GPa) have brought much attention to HfB2 for applications as a material exposed to extreme environments. The combination of strength and temperature resilience has garnered attention from the field of aerospace engineering for hypersonic and re-entry vehicles into Earth’s atmosphere. HfB2 is special among the refractory metal borides for the applications listed as it has a lower density (10.5 g/cm3) [4] than other ultra-incompressible metal borides such as ReB2 (12.7 g/cm3) and WB2 (10.8 g/cm3) while still retaining similar elastic moduli values [4]. The incorporation of boron into the hexagonal crystal lattice (symmetry group P6/mmm) also enhances neutron absorption capabilities for protection from damaging radiation that can embrittle materials. Relatively recent theoretical studies have shown that these refractory transition metal borides are as efficient as water at moderating neutrons and suggest applications in reactor and future fusion devices [5]. The broad range of application of HfB2 for industrial tool use and other extreme environments has led researchers to study its compression behavior, though only to relatively modest pressures 30–50 GPa compared to the conventional limits of commonly used diamond anvil cells (DAC) that can reach >200 GPa. The compression behavior or equation of state for HfB2 is currently not available in the ultrahigh-pressure region despite the propensity for structural and electronic transitions of Group IV metals with narrow d-bands and broad sp-bands to occur with high pressure [6]. There is also an interest in studying how different pressure states (whether nonhydrostatic or hydrostatic) affect compression behavior. Some previous studies have used pressure mediums such as noble gases to make the sample compression in a DAC more hydrostatic, but this is best classified as quasi-hydrostatic due to crystallization of the gas or fluid with pressure and limited in the applied pressure range (~30 GPa) [7,8]. Theoretically, ab initio evolutionary algorithms have indicated that the AlB2 structure with the transition metal and boron atoms sitting at the origin and the (1/3, 2/3, 1/2) Wyckoff sites can persist to a few hundred GPa in certain diborides such as ZrB2 [9]. However, whether the structure in ZrB2 or HfB2 can be stable at such as high pressure remains experimentally unknown.
In this study, HfB2 is compressed using beveled diamond anvils to 208 GPa to probe volumetric compression in a nonhydrostatic pressure environment, accomplished by an axial X-ray diffraction technique. This is also combined with a separate study using DAC with radial X-ray diffraction (R-XRD) and lattice strain theory (LST) to determine the hydrostatic pressure volume relation, as well as an estimation of its compressive yield strength. Density functional theory (DFT) calculations are also performed, and the theoretical results show good agreement with the experimental results on compression and deformation behavior.

2. Materials and Methods

The nonhydrostatic compression study on HfB2 was conducted using a pair of beveled diamond anvils with a central flat of 30-microns, 8-degree bevel to 300-micron outer diameter. A spring steel gasket was indented to 30-micron thickness and laser drilled for a sample hole of 5-microns for sample placement. The HfB2 sample was in powder form (Alfa Aesar, 99.5% metals basis) and mixed in a 3:1 ratio with platinum powder (Alfa Aesar, 99.97% purity) that was used for pressure calibration. Platinum was chosen as the pressure calibrant as its XRD peaks will not overlap with the sample, while the 3:1 ratio was chosen to ensure the platinum intensity does not overwhelm that of HfB2 for later structural refinement. Given that platinum has a similar shear modulus to the base metal in HfB2, it is not expected that platinum will alter shear strength measurements significantly. This is later addressed in the Discussion section. The axial X-ray diffraction was conducted at the High-Pressure Collaborative Access Team (HPCAT) at Beamline 16-ID-B, Advanced Photon Source, Argonne National Laboratory.
For determination of hydrostatic components of compression, radial X-ray diffraction at beamline 16-BM-D, APS, Argonne National Laboratory was conducted. A pair of 300-micron flat diamond anvils were used for HfB2 sample compression. The same HfB2 and Pt sample mixture from the nonhydrostatic compression study was used for the R-XRD study and was placed in a beryllium gasket on the diamond culet with a sample hole of 70 microns in diameter. The X-ray beam was focused through Double Multilayer Monochromator into a collimating pinhole to a beam size of 3.4 µm (vertical) × 4.7 µm (horizontal) at 30 keV.
The pressure state at the center of a sample in a DAC is defined as nonhydrostatic due to differential stress between the axial and radial directions. The maximum stress lies along the diamond compression axis, while the minimum stress is exerted radially by the gasket material. This differential stress is a measure of compressive yield strength of the sample giving rise to a yielding of the crystallites that can be observed experimentally via R-XRD. To ensure the lattice strain is observed in the R-XRD profiles, a nonhydrostatic pressure state is necessitated, and no pressure medium is used in the sample hole. The lattice strain can be shown using Lattice Strain Theory (LST) produced by Singh et al. [10], where lattice strain from the nonhydrostatic environment will deform the measured d-spacing dm(hkl) by:
dm(hkl) = dp(hkl) [1 + (1 − 3cos2ψ)Q(hkl)],
where dp(hkl) is the hydrostatic component of the d-spacing, ψ is the angle between the cell compression axis and normal to the diffracting plane, and Q(hkl) is the lattice strain. Experimentally, the angle ψ can be determined by the relation ψ = cos(δ)cos(θ), where δ is the azimuthal angle around the XRD image and θ is the diffracting angle. The angle ψ can then be chosen such that 1 − 3cos2(ψ) = 0, in which case the d-spacing measured at this angle is the hydrostatic d-spacing dm(hkl) = dp(hkl). This provides a unique method for determining hydrostatic components of compression while the sample is under nonhydrostatic stress.
The lattice strain term Q(hkl) is also very useful as it can be utilized to derive the differential stress and shear strength of a sample. This is shown in Equation (2):
Q(hkl) = (t/3){α[2 GR(hkl)] − 1+(1 − α)[2 GV] − 1)},
where t is the differential stress, α is a weighted factor between 0 and 1, and GR(hkl) and GV are the shear moduli approximations for the Reuss (iso-stress) and Voigt (iso-strain) conditions. By assuming the Voigt approximation, Equation (2) can be simplified to form a lower bound to compute the differential stress (t) and shear strength (τ):
t = 6G <Q(hkl)> = 2τ.
The measured d-spacing dm(hkl) from Equation (1) and the lattice strain term Q(hkl) were determined in this study by using the Rietveld refinement software MAUD [11]. The collected R-XRD images were integrated into azimuthal sections of δ = 5 degrees to determine the angle ψ, and each section was sequentially refined in MAUD to determine the variation of 1 − 3cos2(ψ) with dm(hkl), which allowed for the calculation of dp(hkl) for both HfB2 sample and Pt pressure marker. The hydrostatic d-spacing dp(hkl) for Pt as well as the d-spacing for the nonhydrostatic experiment to 208 GPa were used in the Birch–Murnaghan equation of state (BM EoS) to determine pressure using Pt equation of state parameters derived by Yokoo et al. [12]:
P(V) = (3/2) K0 [x7/3 − x5/3] [1 + 0.75 (K0′ − 4) x2/3 − 1)], with x = V0/V.
The first-principles calculations were performed using VASP (the Vienna Ab initio Simulation Package, version 5.4.4) [13,14], which is a plane-wave pseudopotential density functional theory (DFT) code [15,16]. The Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) [17] functional and the projector augmented wave (PAW) method [18,19] were employed in our calculations. A plane-wave basis set with an energy cut-off of 600 eV and a fine 33 × 33 × 33 (resolution = 0.01 × 2π/Å) Monkhorst-Pack k-point grid were chosen. Structural relaxation calculations were performed with convergence criteria of 10−3 eV/Å and 10−6 eV/cell for the atomic force and self-consistent electronic steps, respectively. After the structure optimization, we computed the elastic tensor by the strain-stress method [13,14,20,21] in VASP. The bulk modulus K and shear modulus G are derived from the elastic constants using the Voigt–Reuss–Hill approximation [22,23,24], which averages the upper and lower bounds of the moduli.
We also computed the tensile and shear strengths of HfB2 by using the QE (Quantum ESPRESSO, version 6.3) [25,26,27] DFT package. The PAW method and GGA-PBE functional were utilized as well. The same calculation settings and convergence criteria as those in the VASP calculations were considered. We used a fully relaxed crystal structure to construct a 2 × 2 × 2 supercell for computing the strain-stress curves. A k-grid of 11 × 9 × 9 points was used in the supercell calculations. Tensile strains were applied along the [001], [100], [110], and [111] directions, respectively, with a strain value up to 0.4 in a strain step of 0.01. In each step, the lattice constants and atomic positions of the tensile axis were fixed, while the lattice constants and atomic positions of the other two axes were allowed to relax fully. The shear strain-stress curves were obtained in a similar way by considering shear deformation in different directions on various planes. Figure 1 shows an example of shear deformation calculation on the (001) plane along the [1−10] direction with different strain values. In each step of the shear deformation calculation, we fix the lattice constant and atomic positions of the axis perpendicular to the shear plane (a-axis in Figure 1) and completely relax the lattice constants and atomic positions of the other two axes parallel to the shear plane (b and c axes in Figure 1). The structures were visualized by the VESTA software (version 3.4.8) [28].
Since the atoms are located at high-symmetry Wyckoff positions in HfB2, the actual atomic positions along the strain direction will be directly determined by the lattice parameters. We have benchmarked our QE calculations by comparing to results in the literature for ReB2 [29] and Mg2Si [30] using VASP, in which cases the applied strain is fixed, while the other five independent components of the strain tensors and all the atom positions were simultaneously relaxed. The critical strain and maximal stress values determined from these different approaches and software agree at a quantitative level.

3. Results

The hexagonal AlB2 phase of the HfB2 sample was found to be stable to the highest pressure of 208 GPa (V/V0 = 0.7). Figure 2a shows the sample HfB2 and Pt mixture at 0.63 GPa and 208 GPa, while Figure 2b shows the nonhydrostatic compression of HfB2 reaching a maximum pressure of 208 GPa fitted with the 3rd Order BM EoS. The least-square fitting of HfB2 pressure-volume data shows a bulk modulus K0 = 353 GPa with first pressure derivative K0′ = 3.08 and an initial volume V0 = 29.65 Å.
The hydrostatic pressure-volume curve derived from LST and R-XRD is displayed in Figure 3 with the corresponding 3rd Order BM EoS fit and derived elastic parameters. The initial volume from R-XRD hydrostatic parameters gives a slightly higher volume V0 = 29.74 Å with a lower bulk modulus K0 = 282 GPa (with first pressure derivative K0′ = 3.38) compared to the nonhydrostatic case. This decrease in bulk modulus for more hydrostatic environments is also noted in other literature for HfB2 with similar moduli values [1,2]. This is attributed to lattice strain being underestimated under nonhydrostatic stress in axial diffraction geometry [10], i.e., the measured volume for nonhydrostatic cases can be larger with increasing pressure (and strain), rendering a seemingly higher bulk modulus. For HfB2, this effect seems to be profound as the difference in nonhydrostatic and hydrostatic bulk moduli are ~82 GPa for this study and ~79 GPa in Laing et al. for quasi-hydrostatic bulk modulus [1]. This will be discussed further later in the Discussion section.
We next present DFT-GGA calculation results, which can be compared to HfB2 experiments under hydrostatic pressure. The calculated lattice constants, volume, bulk, and shear moduli under ambient conditions are a0 = 3.14 Å, c0 = 3.49 Å, V0 = 29.84 Å3/atom, K0 = 262 GPa, and G0 = 246 GPa, respectively. These calculated values are in good agreement with our experiments (V0 = 29.73 Å3/atom, K0 = 282 GPa) as well as other theoretical and experimental values (V0 = 29.78–29.90 Å3/atom, K0 = 261–395 GPa, G0 = 227–248 GPa) reported in the literature [1,2,31,32,33,34].
Figure 4a shows the calculated hydrostatic axial compression ratios a/a0 and c/c0 up to 210 GPa. The results indicate a slight anisotropic compression behavior of HfB2. The c-axis compresses more easily than the a-axis, and the compression anisotropy decreases gradually with increasing pressure up to 125 GPa. Figure 4b shows the variation of bulk and shear moduli with pressure. The high bulk and shear modulus values under compression suggest highly incompressible and deformation-resistant behavior of HfB2.
The calculated c/a ratio of HfB2 under pressure is plotted in Figure 5a along with the experimental data, including both nonhydrostatic and hydrostatic results. The measured c/a ratio decreases with increasing pressure. The anisotropy between the c and a-axes is noted for the pressure region 0–50 GPa, with the c-axis being the most compressible. Figure 5b shows the calculated volume compression V/V0 under pressure along with the experimental values. Overall, the calculated results are in good agreement with the experiments up to 208 GPa. It is noted that the c/a ratio appears to decrease slightly with pressure in the low-pressure regime, and it starts to increase with pressure in the higher-pressure range.
Figure 6 shows the calculated shear and tensile stress-strain relationships for HfB2. The strain-stress curves show a linear behavior at small strain values (Hooke’s law). At larger strains, a nonlinear behavior follows. The critical value is reached when the stress starts to decrease with strain. When the critical point is exceeded, the structure can become unstable, which leads to deformation or fracture. The maximum stress determines the upper limit of a material’s mechanical strength.
Figure 6a shows the calculated tensile stress as a function of strain along the [001], [100], [110], and [111] directions. The peak tensile stress in the [100] direction corresponds to the ideal tensile strength of HfB2 because it has the lowest value among the four directions. The ideal tensile stress is ~41.31 GPa at a critical strain value of 0.13. Likewise, ideal shear strength occurs at the lowest peak shear stress in all directions. Figure 6b shows that the ideal shear strength of HfB2 is in the (1−10) plane along the [110] direction. The ideal shear stress is ~39.16 GPa at a critical strain value of 0.2. It is noted that the theoretical shear strength of a perfect crystal is approximately equal to the shear modulus G0 divided by 2π. Our calculation results are consistent with this theoretical estimation. Table 1 lists the calculated data for the maximum tensile and shear stresses in each direction and their corresponding critical strain values.

4. Discussion

HfB2 is similar in crystal structure to other AlB2-type transition-metal borides (TMBs) such as TiB2 and ZrB2, and has certain similarities to hexagonal WB2-type TMBs. These materials typically share similar elastic properties, with nonhydrostatic bulk modulus values in the range of 260–400 GPa (e.g., K0 = 263–395 GPa for HfB2 [1,2], K0 = 350–366 GPa for ReB2 [35,36,37,38], and K0 = 358 GPa for Os2B3 [39,40]). However, it is interesting to note the behavior of HfB2 with respect to differing pressure (hydrostatic versus nonhydrostatic) environments as compared to other TMBs. ReB2 has displayed a nonhydrostatic bulk modulus of 360 GPa and a hydrostatic bulk modulus of 366 GPa. This is further replicated by DFT calculations (K0 = 360 GPa) and quasi-hydrostatic compression to 30 GPa (K0 = 360 GPa) [35,36,37,38]. HfB2, however, has shown a ~ 80 GPa difference in bulk modulus between our nonhydrostatic and hydrostatic experiments, as well as in nonhydrostatic and quasi-hydrostatic studies in the literature [1,2]. This suggests the impact of high compressive yield strength of HfB2 on the nonhydrostatic X-ray diffraction measurements. To further illustrate this point, we have analyzed the maximum differential stress (t) obtained from the radial X-ray diffraction data using Equation (3) and average measured lattice strains <Q(hkl)>. Figure 7 shows that the maximum differential stress (t) or compressive yield strength normalized to shear modulus (G) increases with increasing pressure and approaches a limiting value of 3% of the shear modulus (0.03 G).
The lattice strains Q(hkl) for (001), (101), and (002) planes given by Equation (2) for HfB2 as a function of pressure are also shown in Figure 7. The (001) plane shows a considerably higher strain Q and thus higher compressive yield strength than the other planes. This is an interesting result, as the axis of most incompressibility is along the a lattice parameter while maximum strength is along the (001) plane. This is actually opposite to what is seen in WB2-type TMBs, which display higher incompressibility along the c-axis and maximum strength in the (100) plane [36,37]. The WB2-type differs from the AlB2-type in that the interstitial boron layers are puckered, whereas the AlB2 displays a flat plane of boron atoms [41,42]. In a puckered boron layer, the distance between TM and B atoms is shorter than that of the flat boron layer. Therefore, the puckered boron layer has strong covalent hybridization between TM and B atoms. It has been shown in some WB2-type structures that electron density congregates along the c-axis, giving them their characteristic incompressibility [40]. Based on results in the c/a ratio and the lattice-dependent strain Q(hkl) in this study, it is inferred that the orientation of boron atoms in the AlB2-type structure of HfB2 plays a large role in the selection of electronic density along the a-axis as compared to the WB2-type structure. When the applied pressure increases, the Hf-Hf bond along the c-axis becomes shorter, which leads to a more repulsive electron-electron interaction and a stronger hybridization between Hf and B atoms; therefore, the compression of the c-axis can then become comparable to that of the a-axis at higher pressure.
Finally, our DFT calculations show that the weakest tensile strength is along the [100] direction, with a peak tensile stress value of σ~41.3 GPa at critical strain ε~0.13. Moreover, the ideal shear strength of HfB2 occurs along the (1–10) [110] direction, with a peak shear stress value of τ~39.2 GPa at critical strain ε~0.2. Based on the Frenkel model [43], the shear stress τ can be approximated as a sinusoidal stress-strain relationship:
τ= [Ga/2πh] sin(2πx/a),
where G is the shear modulus, a is the spacing between atoms in the direction of shear stress, h is the atomic row spacing, and x is the shear translation. The maximum shear stress value τmax can be obtained by letting sin(2πx/a) = 1. Since h~a, τmax~G/2π~0.16 G, our DFT-calculated shear modulus value of 246.5 GPa will lead to τmax = 246.5 GPa/2π ≈ 39 GPa, which is consistent with the ideal shear strength from the strain-stress curves. Experimentally, the compressive yield strength of 0.03 G is smaller, potentially due to crystal imperfections. The presence of platinum (an elastically weaker material than HfB2) within the sample hole of the DAC poses a natural question to what degree the mechanical properties of HfB2 are altered. Given the excellent agreement in shear modulus, bulk modulus, and lattice parameter in this study with other literature values, it is not expected that the platinum pressure calibrant would cause the large difference in theoretical and experimental shear strength values of HfB2. A further study into fully sintered HfB2 without the presence of platinum would have to be conducted to understand this effect fully.

5. Conclusions

The equation of state of HfB2 was measured up to 208 GPa in a diamond anvil cell employing platinum as an internal pressure standard. The hexagonal AlB2 was found to be stable up to 30% volume compression or V/V0 = 0.7. The c-axis was observed to be more compressible relative to the a-axis below 50 GPa, in agreement with theoretical calculations. The hydrostatic compression curve deduced from radial X-ray diffraction measurements yielded an ambient-pressure volume V0 = 29.73 Å3/atom and a bulk modulus K0 = 282 GPa. Density functional theory calculations showed ambient-pressure volume V0 = 29.84 Å3/atom and bulk modulus K0 = 262 GPa, which are in good agreement with the hydrostatic experimental values. The theoretical strain-stress calculation shows that the weakest deformation direction is along the (1–10) [110] shear direction, and the maximum shear stress is τmax~39 GPa~G0/2π. Our comprehensive experimental and computational studies of the compression and deformation behavior of HfB2 provide new results and understanding of this incompressible high strength material, which has potential applications in extreme environments.

Author Contributions

Conceptualization, Y.K.V.; methodology, K.B. and Y.K.V.; software, C.-M.L. and C.-C.C.; formal analysis, K.B. and C.-M.L.; writing, K.B., C.-M.L., C.-C.C. and Y.K.V.; supervision, C.-C.C. and Y.K.V.; funding acquisition, C.-C.C. and Y.K.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the U.S. National Science Foundation (NSF) under Metals and Metallic Nanostructures program Grant No. DMR-1904164.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The experimental and computational data presented in this study are available upon request to the corresponding authors.

Acknowledgments

Portions of this work were performed at HPCAT (Sector 16), Advanced Photon Source (APS), Argonne National Laboratory. HPCAT operations are supported by DOE-NNSA’s Office of Experimental Sciences. The Advanced Photon Source is a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The calculations were performed on the Frontera computing system at the Texas Advanced Computing Center. Frontera is made possible by NSF award OAC-1818253.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Liang, H.; Sun, W.; Li, X.; Chen, H.; Guan, S.; Liu, P.; Wang, Q.; Li, X.; He, D.; Peng, F. Study of the compression behavior and elastic properties of HfB2 ceramics using experimental method and first-principles calculations. J. Alloy. Compd. 2019, 808, 151764. [Google Scholar] [CrossRef]
  2. Liang, H.; Peng, F.; Guan, S.; Tan, L.; Chen, H.; Lei, L.; He, D.; Lu, C. Abnormal physical behaviors of hafnium diboride under high pressure. Appl. Phys. Lett. 2019, 115, 231903. [Google Scholar] [CrossRef]
  3. Kovalev, D.Y.; Shilkin, S.P.; Konovalikhin, S.V.; Kalinnikov, G.V.; Korobov, I.I.; Kravchenko, S.E.; Khomenko, N.Y.; Andrievskii, R.A. Thermal expansion of micro-and nanocrystalline HfB 2. High Temp. 2019, 57, 32–36. [Google Scholar] [CrossRef]
  4. Carney, C.M. Oxidation resistance of hafnium diboride—Silicon carbide from 1400 to 2000 °C. J. Mater. Sci. 2009, 44, 5673–5681. [Google Scholar] [CrossRef]
  5. Windsor, C.; Astbury, J.O.; Davidson, J.J.; McFadzean, C.J.; Morgan, J.G.; Wilson, C.L.; Humphry-Baker, S.A. Tungsten boride shields in a spherical tokamak fusion power plant. Nucl. Fusion 2021, 61, 086018. [Google Scholar] [CrossRef]
  6. Hao, Y.; Zhu, J.; Zhang, L.; Ren, H.; Qu, J. Structure phase transition and elastic properties of hafnium: First-principles study. Philos. Mag. Lett. 2011, 91, 61–69. [Google Scholar] [CrossRef]
  7. Shu-Jie, Y.; Liang-Chen, C.; Chang-Qing, J. Hydrostaticity of pressure media in diamond anvil cells. Chin. Phys. Lett. 2009, 26, 096202. [Google Scholar] [CrossRef][Green Version]
  8. Klotz, S.; Chervin, J.C.; Munsch, P.; Le Marchand, G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]
  9. Zhang, M.; Wang, H.; Wang, H.; Zhang, X.; Iitaka, T.; Ma, Y. First-Principles Prediction on the High-Pressure Structures of Transition Metal Diborides (TMB2, TM = Sc, Ti, Y, Zr). Inorg. Chem. 2010, 49, 6859–6864. [Google Scholar] [CrossRef] [PubMed]
  10. Singh, A.K.; Balasingh, C.; Mao, H.K.; Hemley, R.J.; Shu, J. Analysis of lattice strains measured under nonhydrostatic pressure. J. Appl. Phys. 1998, 83, 7567–7575. [Google Scholar] [CrossRef]
  11. Lutterotti, L.; Matthies, S.; Wenk, H.R. MAUD: A friendly Java program for material analysis using diffraction. IUCr Newsl. CPD 1999, 21. [Google Scholar]
  12. Yokoo, M.; Kawai, N.; Nakamura, K.G.; Kondo, K.I.; Tange, Y.; Tsuchiya, T. Ultrahigh-pressure scales for gold and platinum at pressures up to 550 GPa. Phys. Rev. B 2009, 80, 104114. [Google Scholar] [CrossRef]
  13. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  14. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
  15. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
  16. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
  17. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
  18. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
  19. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
  20. Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
  21. Wu, X.; Vanderbilt, D.; Hamann, D.R. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105. [Google Scholar] [CrossRef]
  22. Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
  23. Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
  24. Voigt, W. Lehrbuch der Kristallphysik (Leipzig: Teubner); Springer: Berlin/Heidelberg, Germany, 1928. [Google Scholar]
  25. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
  26. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
  27. Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, D.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed]
  28. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  29. Zhang, C.; Sun, H.; John, S.T.; Chen, C. Indentation strength of ultraincompressible rhenium boride, carbide, and nitride from first-principles calculations. Phys. Rev. B 2012, 86, 014108. [Google Scholar] [CrossRef]
  30. Fan, T.-W.; Ke, J.L.; Fu, L.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Ideal strength of Mg2X (X = Si, Ge, Sn and Pb) from first-principles. J. Magnes. Alloy. 2013, 1, 163. [Google Scholar] [CrossRef]
  31. Vajeeston, P.; Ravindran, P.; Ravi, C.; Asokamani, R. Electronic structure, bonding, and ground-state properties of AlB 2-type transition-metal diborides. Phys. Rev. B 2001, 63, 045115. [Google Scholar] [CrossRef]
  32. Zhang, X.; Luo, X.; Han, J.; Li, J.; Han, W. Electronic structure, elasticity and hardness of diborides of zirconium and hafnium: First principles calculations. Comput. Mater. Sci. 2008, 44, 411–421. [Google Scholar] [CrossRef]
  33. Zhang, X.; Luo, X.; Li, J.; Hu, P.; Han, J. The ideal strength of transition metal diborides TMB2 (TM= Ti, Zr, Hf): Plastic anisotropy and the role of prismatic slip. Scr. Mater. 2010, 62, 625–628. [Google Scholar] [CrossRef]
  34. Fahrenholtz, W.G.; Hilmas, G.E.; Talmy, I.G.; Zaykoski, J.A. Refractory diborides of zirconium and hafnium. J. Am. Ceram. Soc. 2007, 90, 1347–1364. [Google Scholar] [CrossRef]
  35. Zhou, W.; Wu, H.; Yildirim, T. Electronic, dynamical, and thermal properties of ultra-incompressible superhard rhenium diboride: A combined first-principles and neutron scattering study. Phys. Rev. B 2007, 76, 184113. [Google Scholar] [CrossRef]
  36. Chung, H.-Y.; Weinberger, M.B.; Levine, J.B.; Kavner, A.; Yang, J.M.; Tolbert, S.H.; Kaner, R.B. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science 2007, 316, 436–439. [Google Scholar] [CrossRef]
  37. Burrage, K.C.; Park, C.; Vohra, Y.K. Shear strength measurements and hydrostatic compression of rhenium diboride under high pressures. J. Appl. Phys. 2021, 129, 205901. [Google Scholar] [CrossRef]
  38. Kavner, A.; Armentrout, M.M.; Rainey, E.S.; Xie, M.; Weaver, B.E.; Tolbert, S.H.; Kaner, R.B. Thermoelastic properties of ReB2 at high pressures and temperatures and comparison with Pt, Os, and Re. J. Appl. Phys. 2011, 110, 093518. [Google Scholar] [CrossRef]
  39. Frotscher, M.; Senyshyn, A.; Albert, B. Neutron diffraction at metal borides, Ru2B3 and Os2B3. Z. Anorg. Allg. Chem. 2012, 638, 2078–2080. [Google Scholar] [CrossRef]
  40. Burrage, K.C.; Lin, C.M.; Chen, W.C.; Chen, C.C.; Vohra, Y.K. Electronic structure and anisotropic compression of Os2B3 to 358 GPa. J. Phys. Condens. Matter 2020, 32, 405703. [Google Scholar] [CrossRef]
  41. Lech, A.T.; Turner, C.L.; Lei, J.; Mohammadi, R.; Tolbert, S.H.; Kaner, R.B. Superhard rhenium/tungsten diboride solid solutions. J. Am. Chem. Soc. 2016, 138, 14398–14408. [Google Scholar] [CrossRef]
  42. Zhang, G.-J.; Ni, D.W.; Zou, J.; Liu, H.T.; Wu, W.W.; Liu, J.X.; Suzuki, T.S.; Sakka, Y. Inherent anisotropy in transition metal diborides and microstructure/property tailoring in ultra-high temperature ceramics—A review. J. Eur. Ceram. Soc. 2018, 38, 371–389. [Google Scholar] [CrossRef]
  43. Frenkel, J.A. Zur theorie der elastizitätsgrenze und der festigkeit kristallinischer körper. Z. Phys. 1926, 37, 572–609. [Google Scholar] [CrossRef]
Materials 15 02762 g001
Figure 1. Schematic of shear deformation in HfB2 along the (001) [1−10] shear direction at strain values 0, 0.2, and 0.4, respectively. The gray and green balls represent the Hf and B atoms, respectively.
Figure 1. Schematic of shear deformation in HfB2 along the (001) [1−10] shear direction at strain values 0, 0.2, and 0.4, respectively. The gray and green balls represent the Hf and B atoms, respectively.
Materials 15 02762 g001
Materials 15 02762 g002
Figure 2. (a) Axial X-ray diffraction patterns of HfB2 and Pt (*) powder at 0.63 GPa and 208 GPa. (b) Pressure volume curve of HfB2 to 208 GPa with the fitted 3rd Order Birch–Murnaghan equation of state. The fitted parameters are shown in the inset.
Figure 2. (a) Axial X-ray diffraction patterns of HfB2 and Pt (*) powder at 0.63 GPa and 208 GPa. (b) Pressure volume curve of HfB2 to 208 GPa with the fitted 3rd Order Birch–Murnaghan equation of state. The fitted parameters are shown in the inset.
Materials 15 02762 g002
Materials 15 02762 g003
Figure 3. (a) R-XRD image of raw and Rietveld refined fits of HfB2 and Pt (*). Beryllium gasket peaks are labelled with beryllium oxide impurity. (b) Hydrostatic pressure volume curve of HfB2 to 50 GPa with the fitted 3rd Order Birch–Murnaghan equation of state. The fitted parameters are shown in the inset.
Figure 3. (a) R-XRD image of raw and Rietveld refined fits of HfB2 and Pt (*). Beryllium gasket peaks are labelled with beryllium oxide impurity. (b) Hydrostatic pressure volume curve of HfB2 to 50 GPa with the fitted 3rd Order Birch–Murnaghan equation of state. The fitted parameters are shown in the inset.
Materials 15 02762 g003
Materials 15 02762 g004
Figure 4. Pressure dependences of (a) axial compression of lattice parameters a/a0 and c/c0, and (b) bulk and shear moduli for HfB2. The density functional theory (DFT) calculations used the generalized gradient approximation (GGA) functional.
Figure 4. Pressure dependences of (a) axial compression of lattice parameters a/a0 and c/c0, and (b) bulk and shear moduli for HfB2. The density functional theory (DFT) calculations used the generalized gradient approximation (GGA) functional.
Materials 15 02762 g004
Materials 15 02762 g005
Figure 5. Pressure dependences of (a) lattice parameter c/a ratio, and (b) unit cell volume V/V0 ratio for HfB2. The density functional theory (DFT) calculations used the generalized gradient approximation (GGA) functional and are plotted together with the experimental data.
Figure 5. Pressure dependences of (a) lattice parameter c/a ratio, and (b) unit cell volume V/V0 ratio for HfB2. The density functional theory (DFT) calculations used the generalized gradient approximation (GGA) functional and are plotted together with the experimental data.
Materials 15 02762 g005
Materials 15 02762 g006
Figure 6. Theoretical stress-strain curves of HfB2 under (a) tensile deformation, and (b) shear deformation, up to strain value of 0.4 with a strain step of 0.1 along various directions.
Figure 6. Theoretical stress-strain curves of HfB2 under (a) tensile deformation, and (b) shear deformation, up to strain value of 0.4 with a strain step of 0.1 along various directions.
Materials 15 02762 g006
Materials 15 02762 g007
Figure 7. (a) Orientation dependent lattice strain Q(hkl) in HfB2 to 50 GPa. (b) The differential stress normalized to shear modulus (t/G ratio) for HfB2 as a function of pressure to 50 GPa.
Figure 7. (a) Orientation dependent lattice strain Q(hkl) in HfB2 to 50 GPa. (b) The differential stress normalized to shear modulus (t/G ratio) for HfB2 as a function of pressure to 50 GPa.
Materials 15 02762 g007
Table 1. Maximum tensile σmax and shear stresses τmax (in GPa) and their corresponding critical strain εmax values along different directions. The results are based on density functional theory (DFT) calculations using the generalized gradient approximation (GGA) functional.
Table 1. Maximum tensile σmax and shear stresses τmax (in GPa) and their corresponding critical strain εmax values along different directions. The results are based on density functional theory (DFT) calculations using the generalized gradient approximation (GGA) functional.
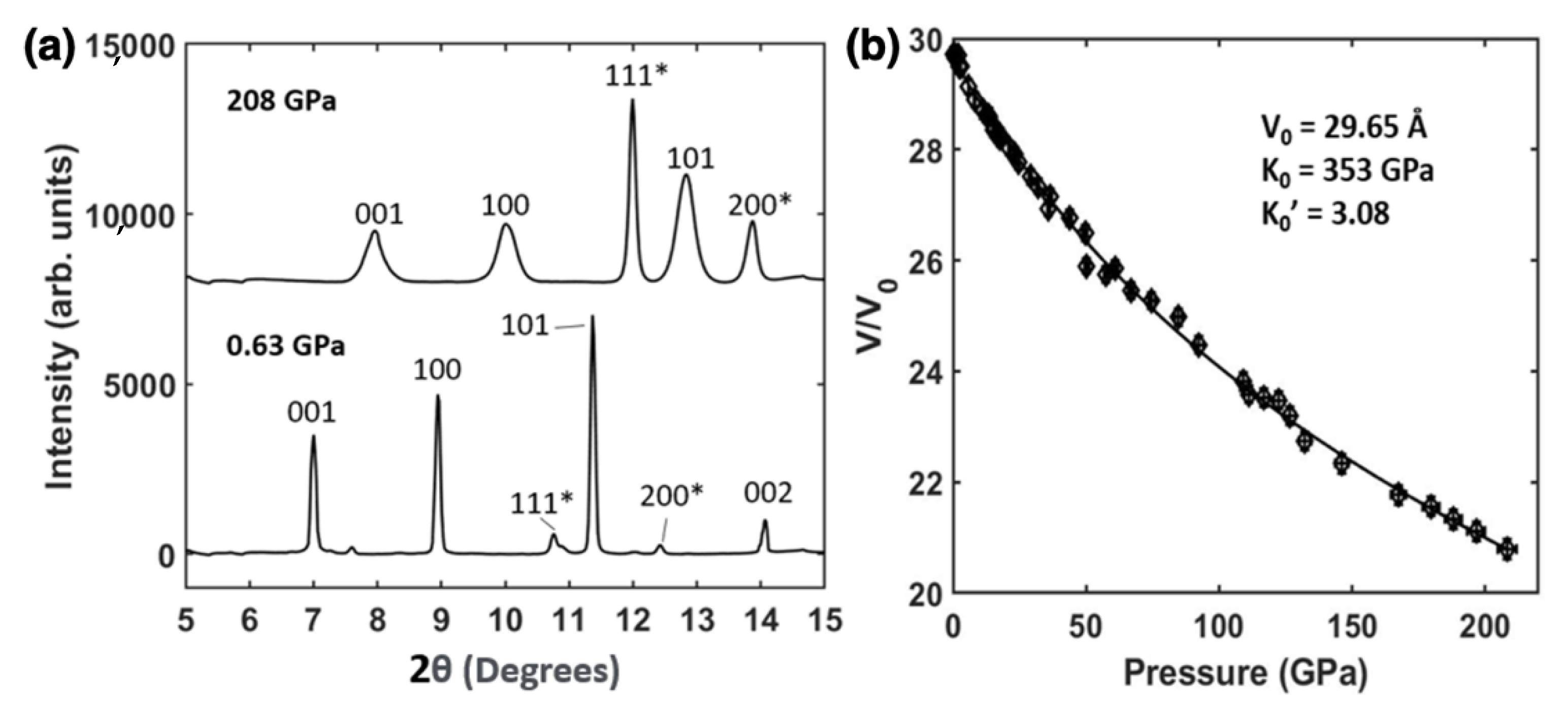
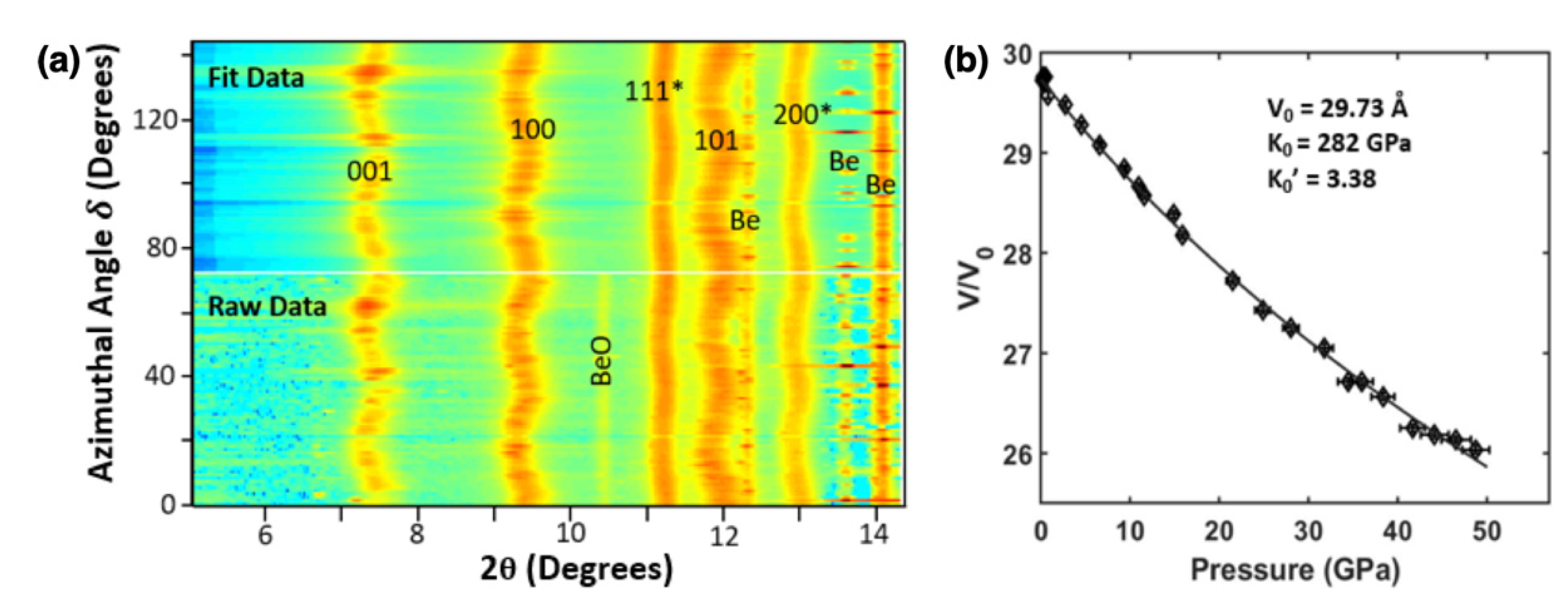
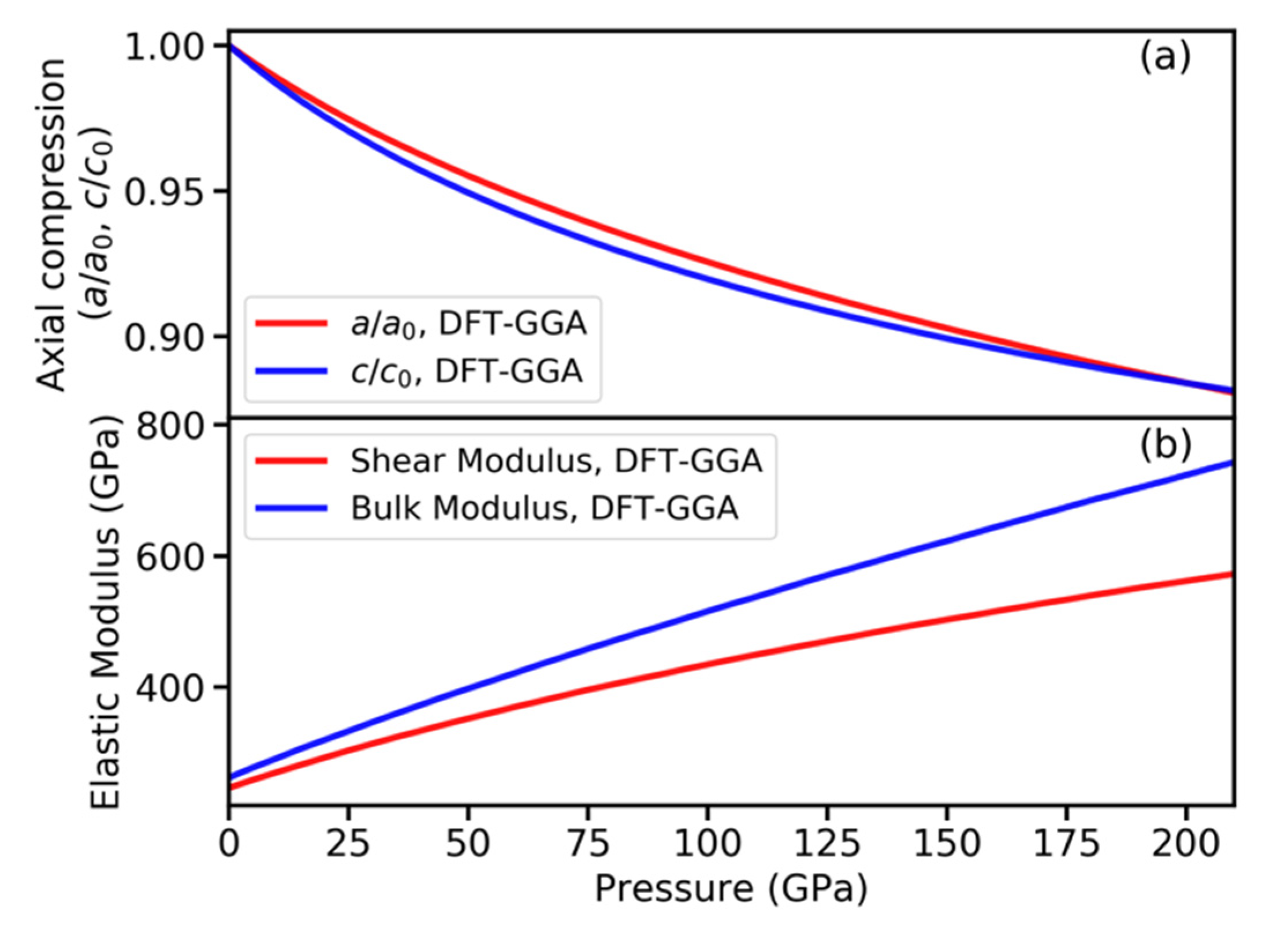
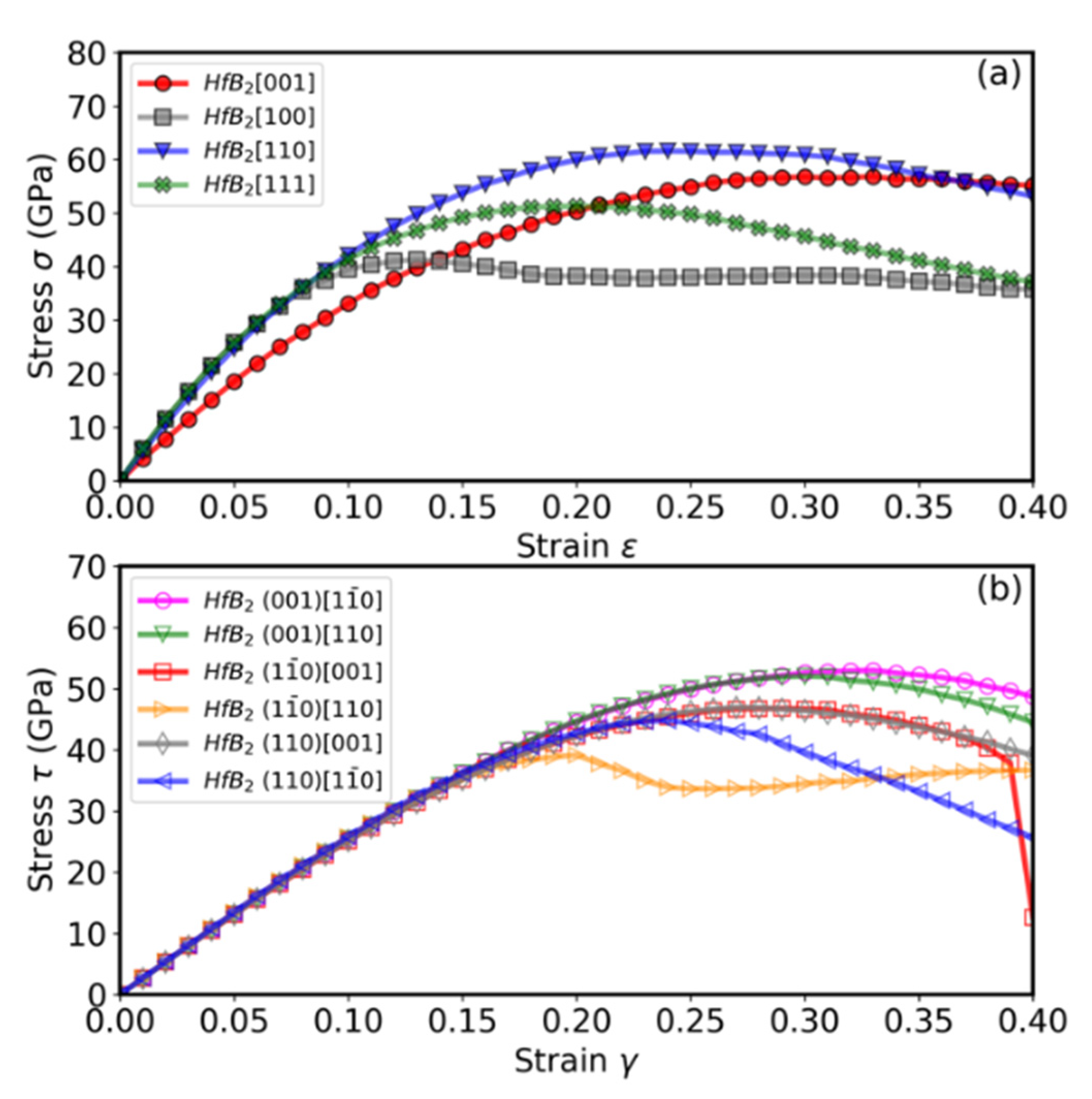
Tensile DeformationShear Deformation
σmaxεmax τmaxεmax
[001]56.840.33(001) [110]52.060.30
[100]41.310.13(001) [1−10]53.010.33
[110]61.590.24(110) [001]46.940.27
[111]51.320.20(110) [1−10]44.820.24
(1−10) [001]46.780.29
(1−10) [110]39.160.20
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Burrage, K.; Lin, C.-M.; Chen, C.-C.; Vohra, Y.K. Experimental and Computational Studies of Compression and Deformation Behavior of Hafnium Diboride to 208 GPa. Materials 2022, 15, 2762. https://doi.org/10.3390/ma15082762

AMA Style

Burrage K, Lin C-M, Chen C-C, Vohra YK. Experimental and Computational Studies of Compression and Deformation Behavior of Hafnium Diboride to 208 GPa. Materials. 2022; 15(8):2762. https://doi.org/10.3390/ma15082762

Chicago/Turabian Style

Burrage, Kaleb, Chia-Min Lin, Cheng-Chien Chen, and Yogesh K. Vohra. 2022. "Experimental and Computational Studies of Compression and Deformation Behavior of Hafnium Diboride to 208 GPa" Materials 15, no. 8: 2762. https://doi.org/10.3390/ma15082762

APA Style

Burrage, K., Lin, C.-M., Chen, C.-C., & Vohra, Y. K. (2022). Experimental and Computational Studies of Compression and Deformation Behavior of Hafnium Diboride to 208 GPa. Materials, 15(8), 2762. https://doi.org/10.3390/ma15082762

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop