Seismic Assessment and Retrofitting of Existing Road Bridges: State of the Art Review
Abstract
:1. Introduction
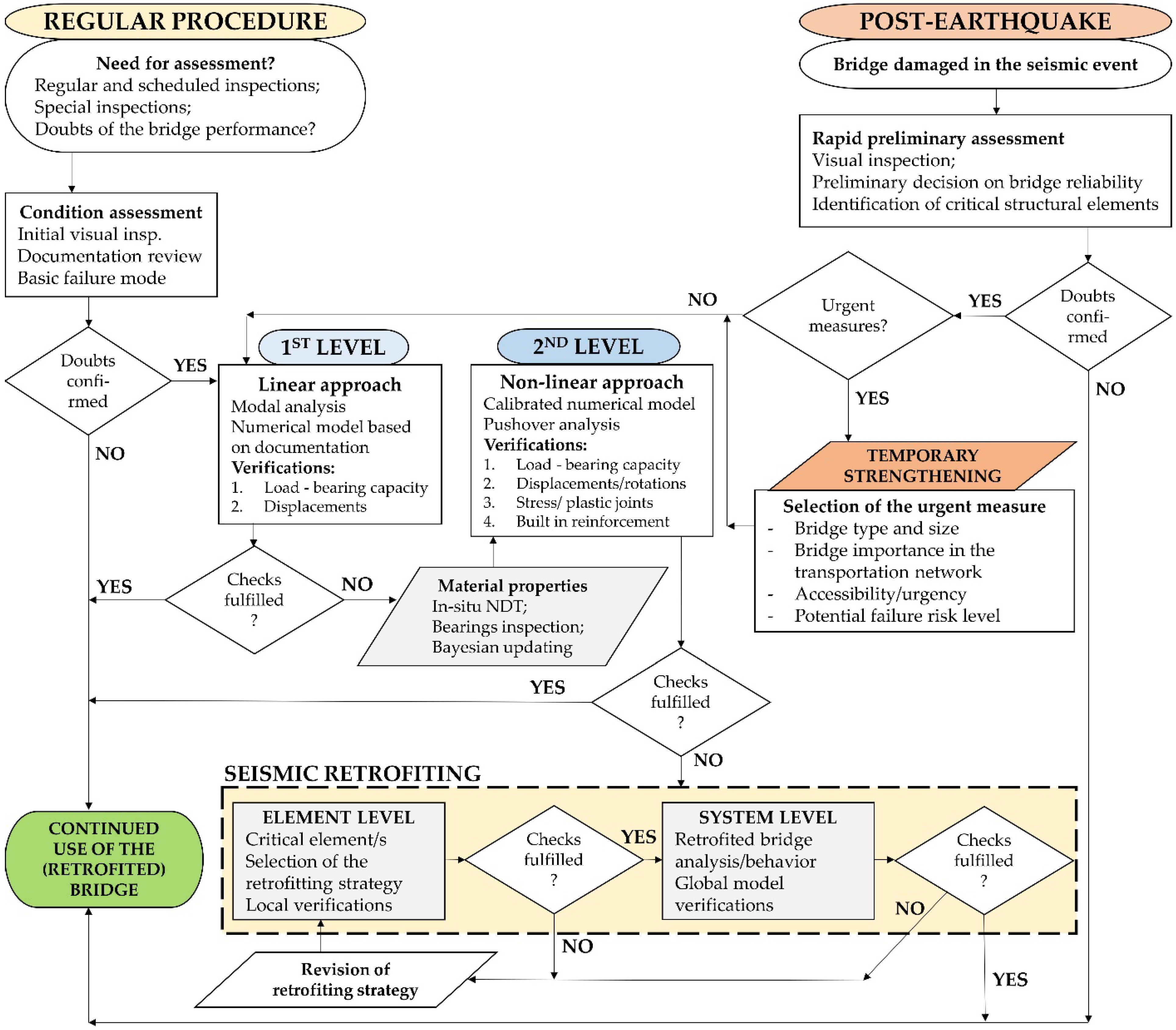
2. Seismic Assessment of Existing Road Bridges
2.1. Analysis Methods
| Analysis Method | Type | Source |
|---|---|---|
| Response spectrum method | Linear analysis | [5,13,27] |
| Fundamental mode method | ||
| Time series analysis | ||
| Time history analysis | Non–linear analysis | [5,28] |
| Pushover analysis | [5,6,13,27,29,30,31] | |
| Probabilistic and sampling methods | Non–linear analysis | [32,33,34,35] |
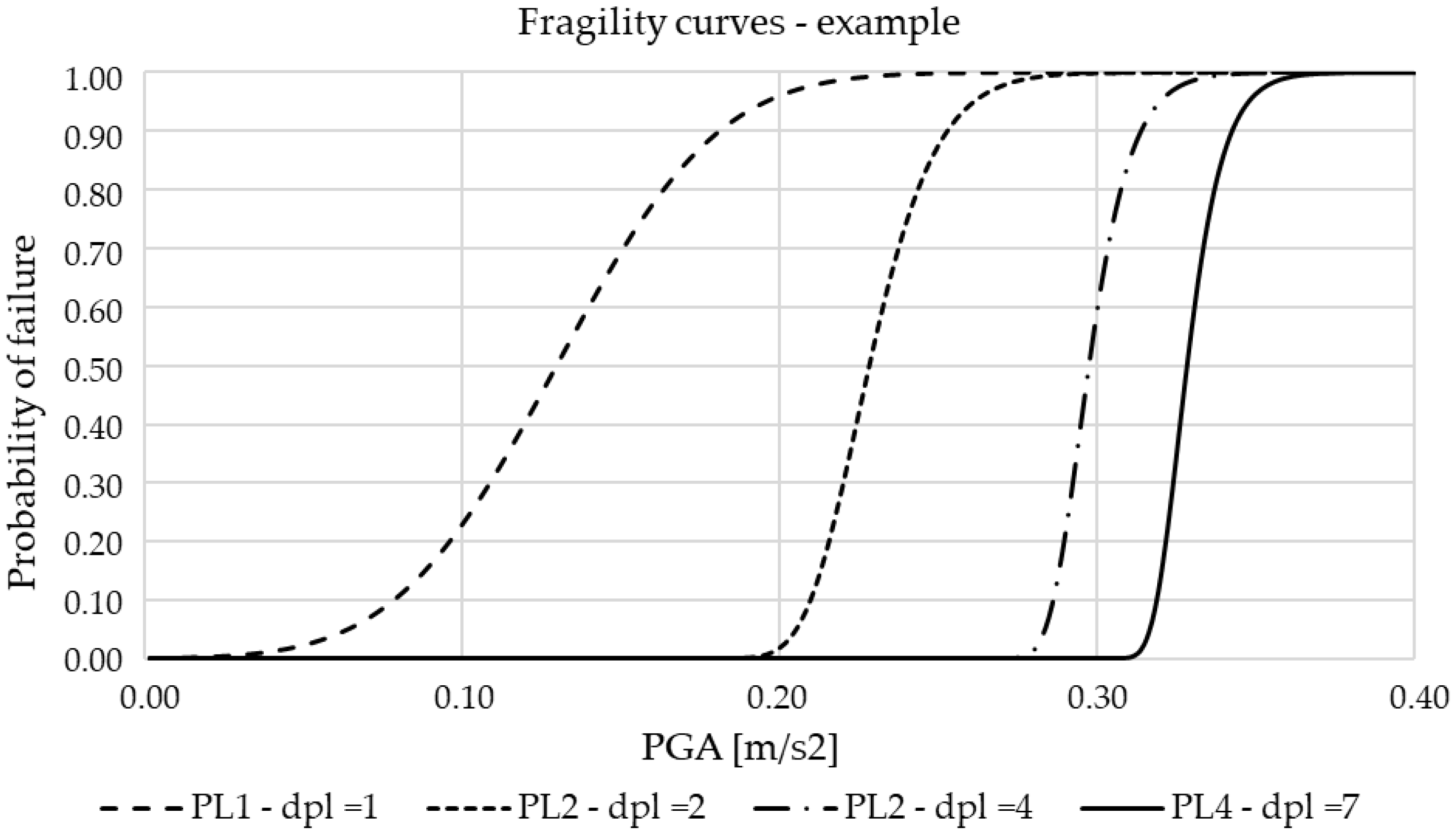
2.2. Fragility Curves
2.3. Literature Review: Seismic Assessment
3. Seismic Retrofitting of Existing Bridges
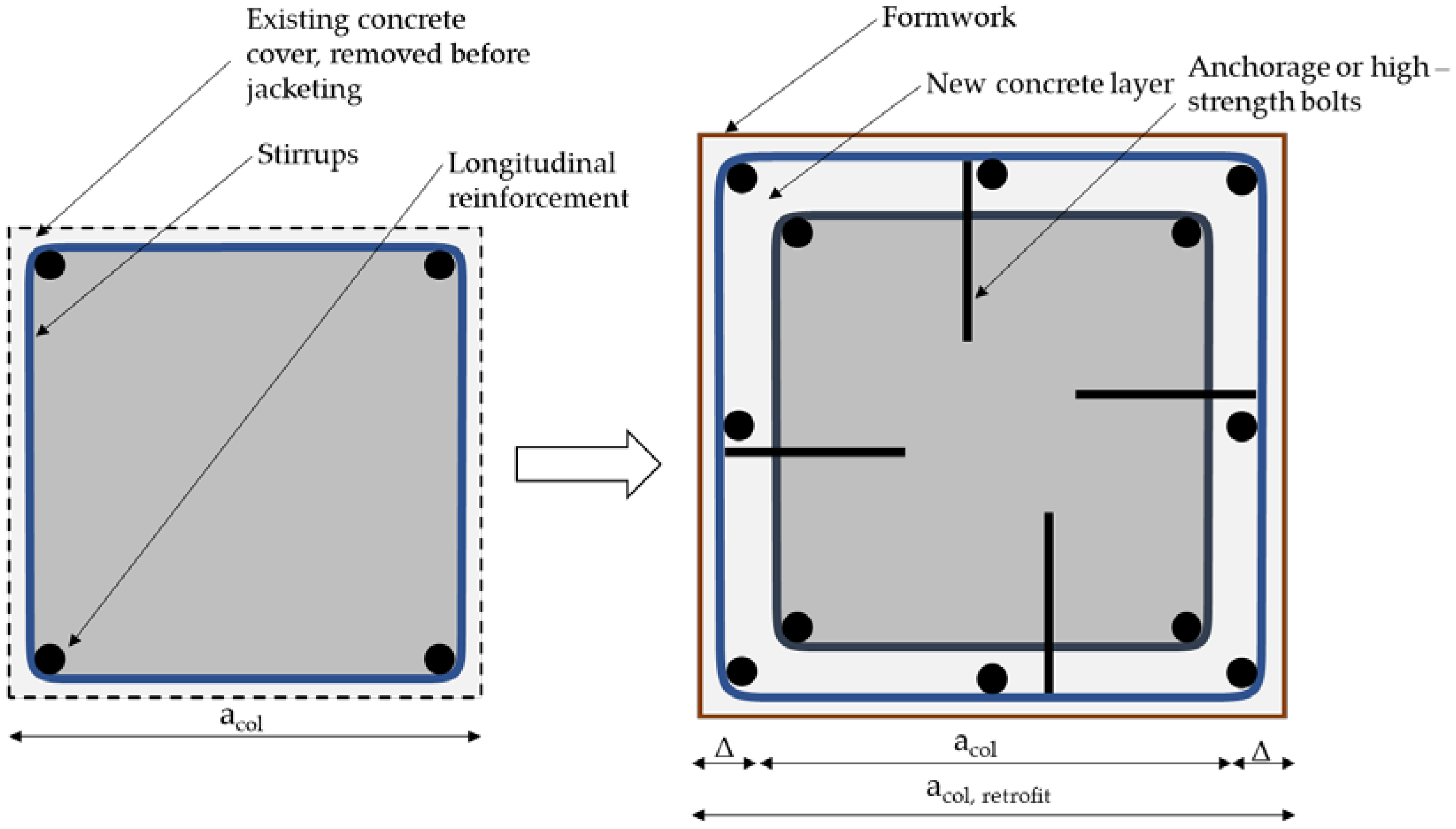
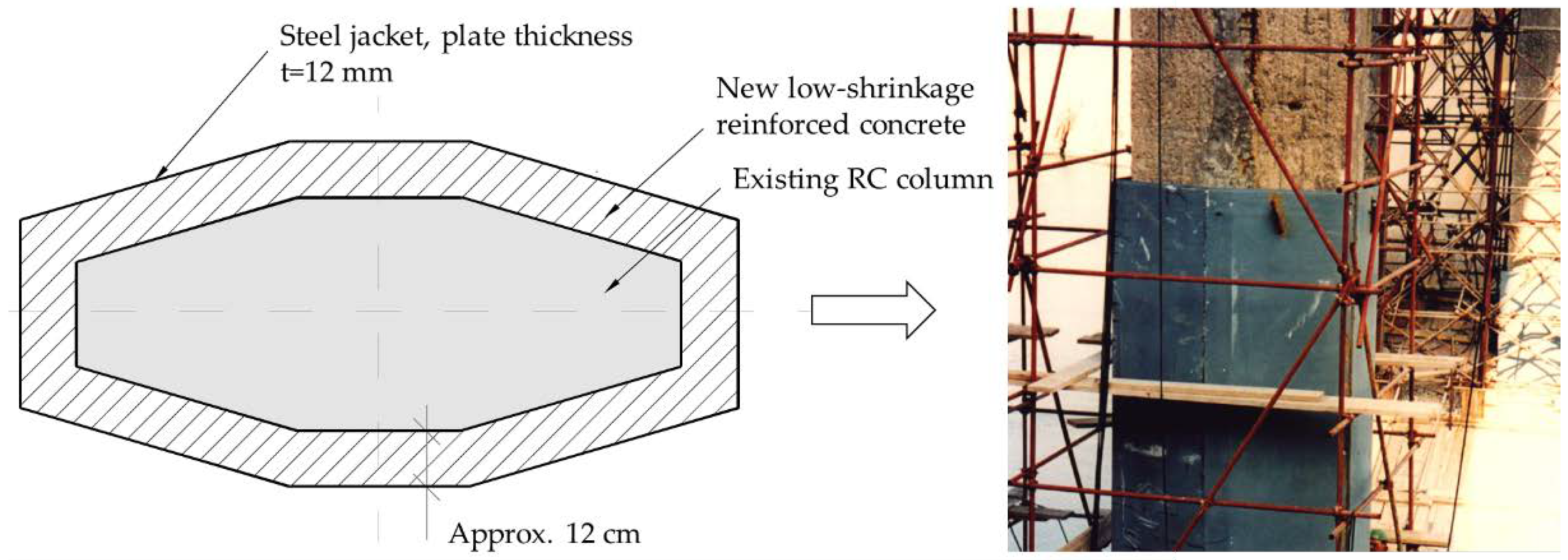
3.1. Bridge Columns/Piers
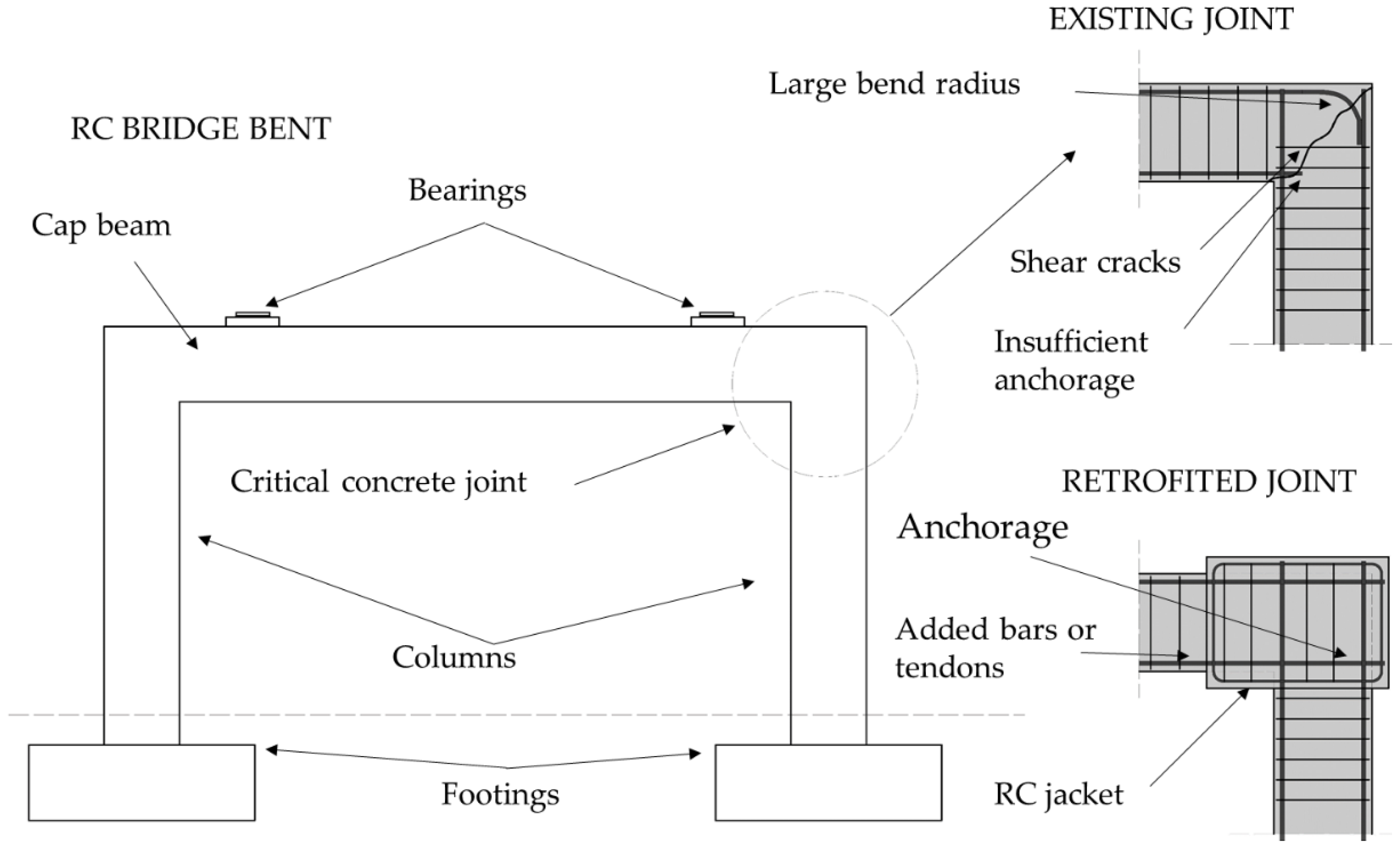
3.2. Cap Beams/Concrete Joints
3.3. Seismic Isolation/Damping
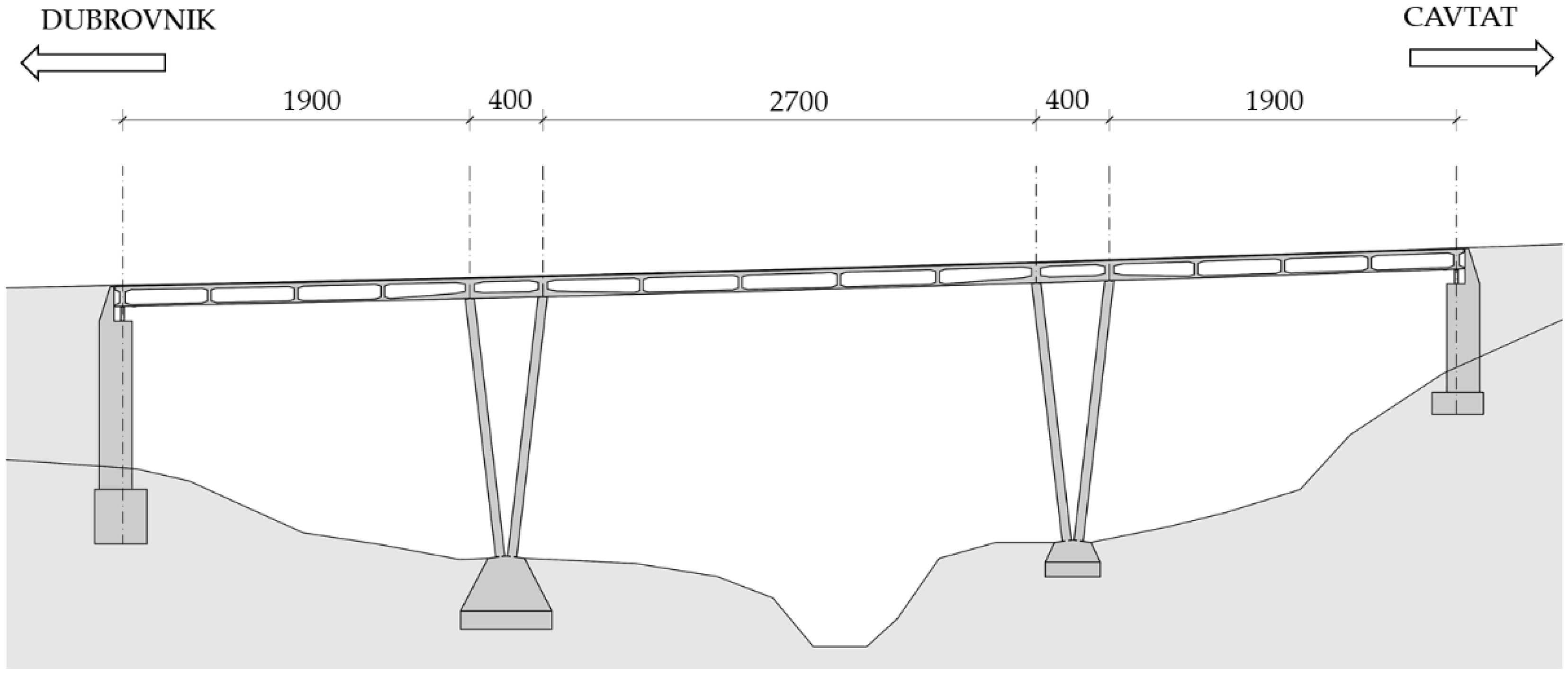
4. First Case Study Bridge
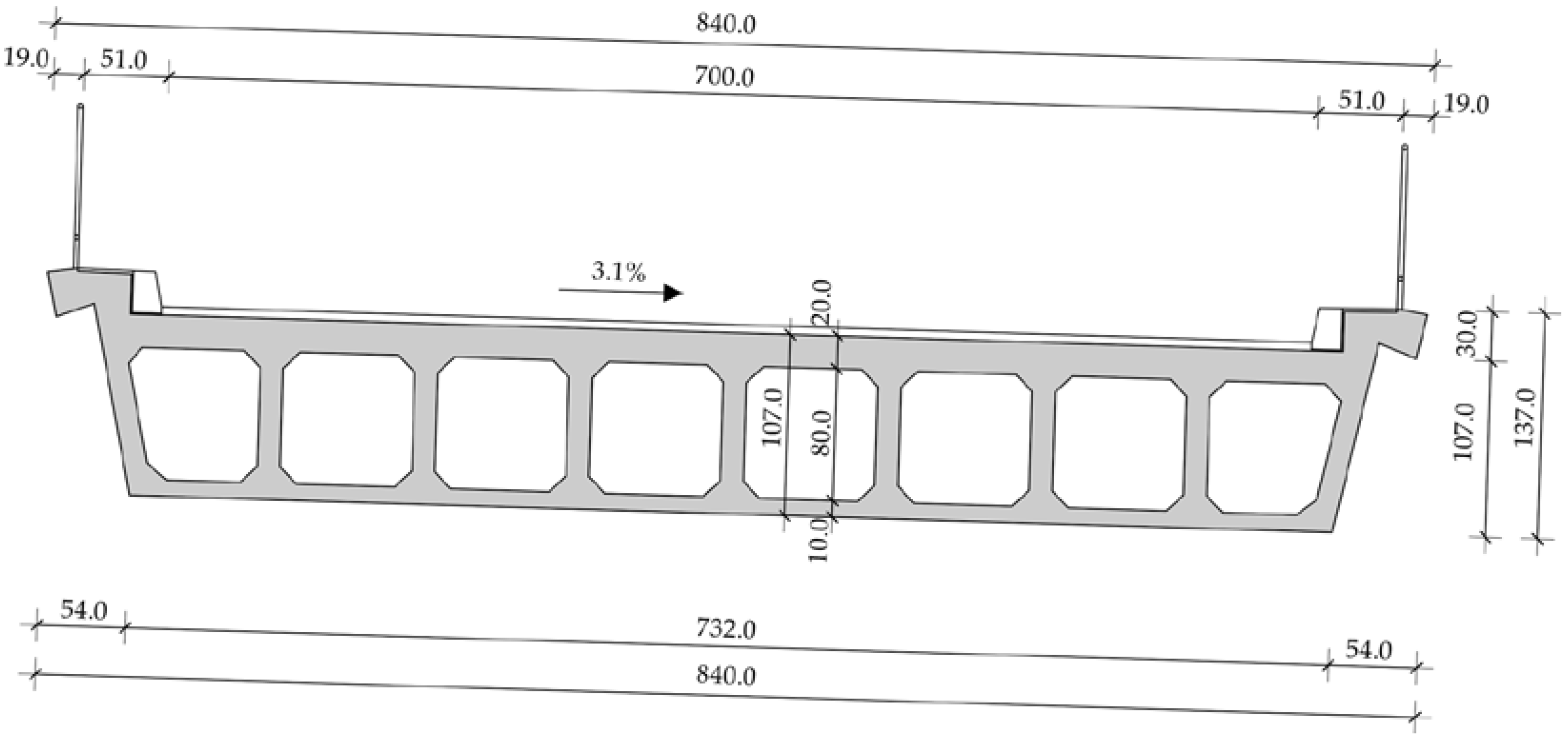
4.1. General Bridge Description
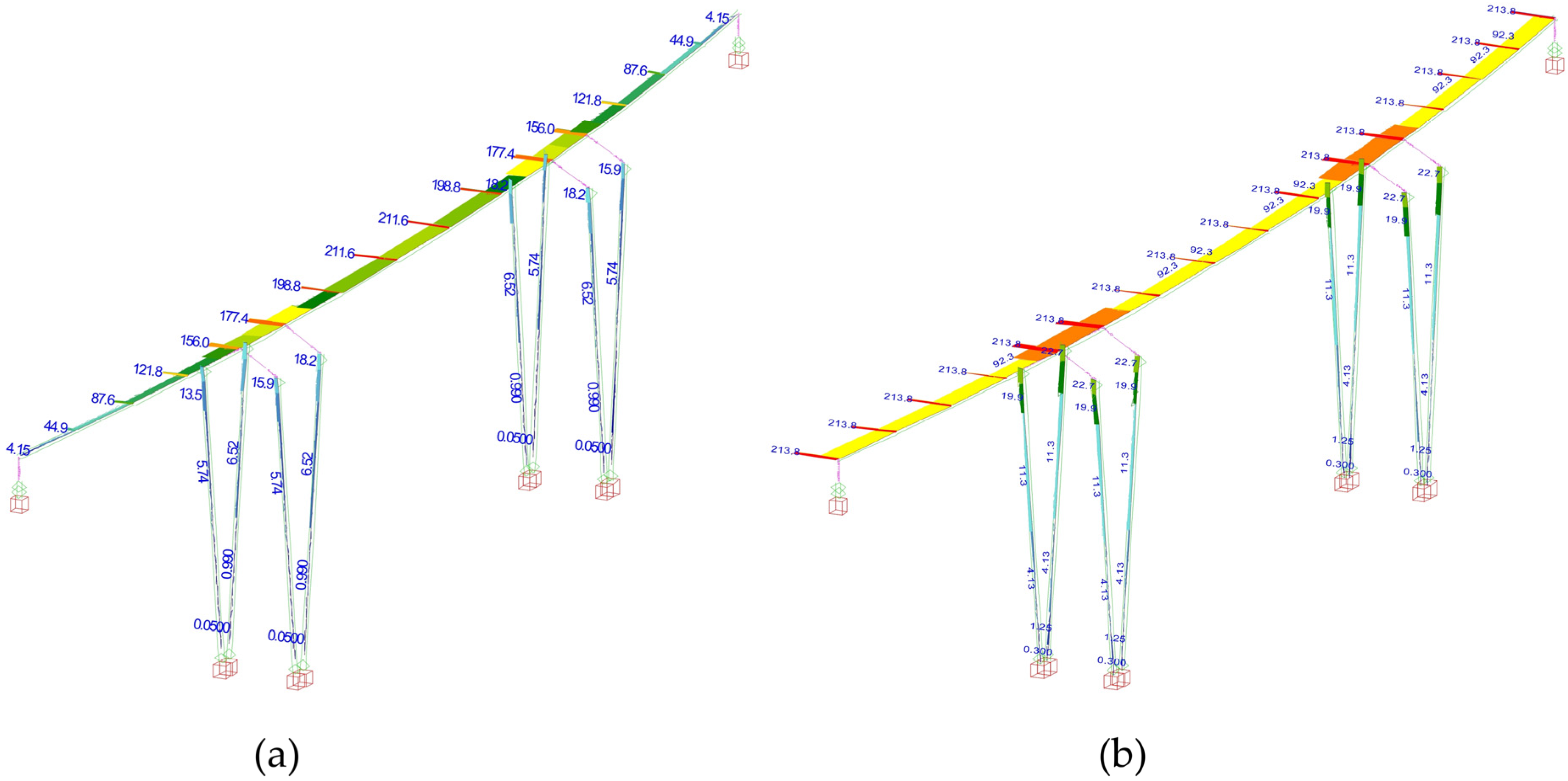
4.2. Assessment Procedure
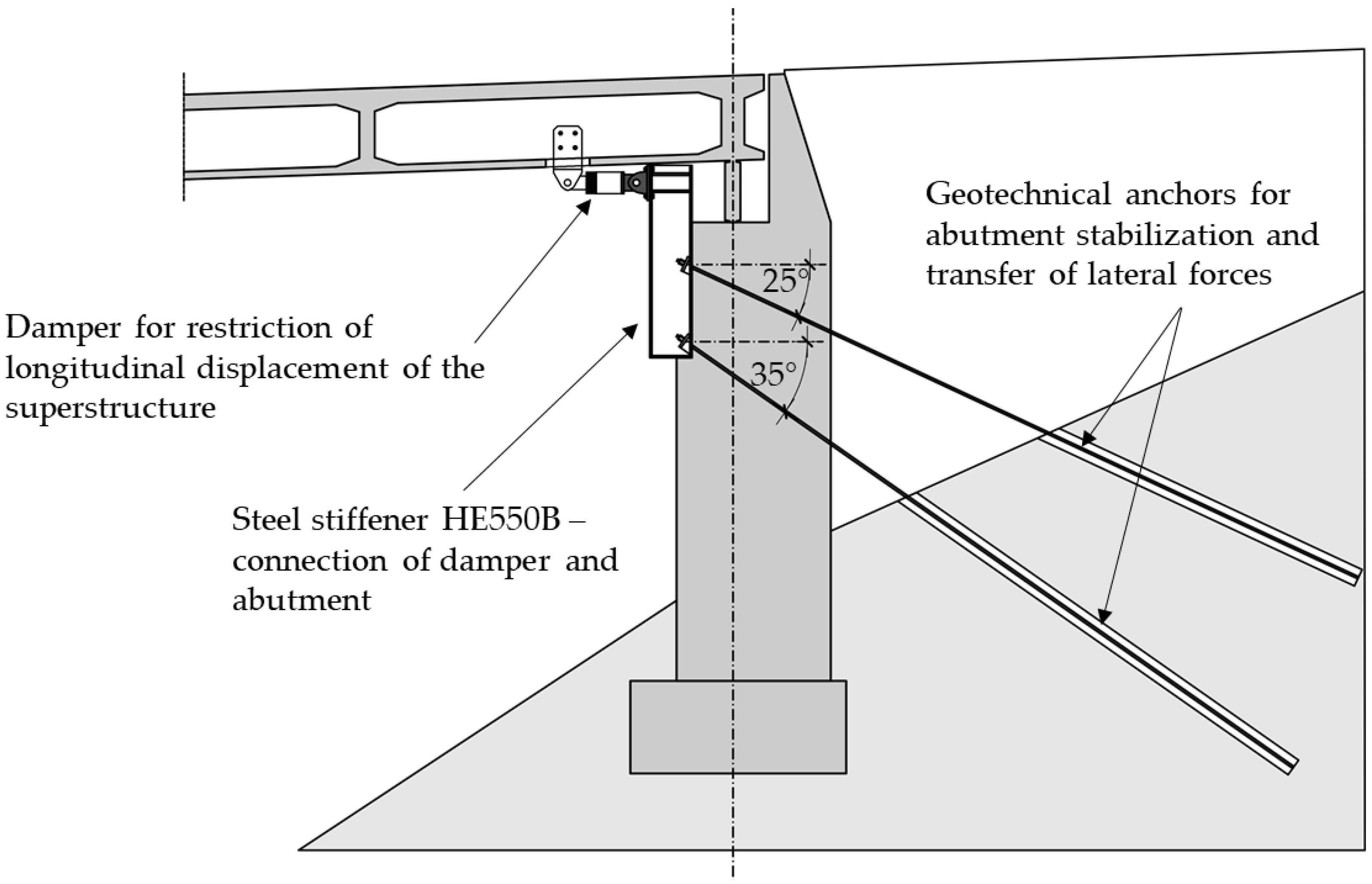
4.3. Retrofitting Proposal
5. Second Case Study Bridge
5.1. Rapid Visual Assessment after the December 2020 Earthquake
5.2. Urgent Retrofitting and Decision for Further Actions on the Bridge
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skokandić, D.; Ivanković, A.M. Value of additional traffic data in the context of bridge service-life management. Struct. Infrastruct. Eng. 2020, 18, 456–475. [Google Scholar] [CrossRef]
- Calvi, G.M.; Moratti, M.; O’Reilly, G.J.; Scattarreggia, N.; Monteiro, R.; Malomo, D.; Calvi, P.M.; Pinho, R. Once upon a Time in Italy: The Tale of the Morandi Bridge. Struct. Eng. Int. 2019, 29, 198–217. [Google Scholar] [CrossRef]
- Ayub, M. Pedestrian Bridge Collapse at University in Miami; US Department of Labor: Washington, DC, USA, 2019.
- Milić, I.; Ivanković, A.M.; Syrkov, A.; Skokandić, D. Bridge failures, forensic structural engineering and recommendations for design of robust structures. J. Croat. Assoc. Civ. Eng. 2021, 73, 717–737. [Google Scholar] [CrossRef]
- CEN: EN 1998-2; Design of Structures for Earthquake Resistance—Part 2: Bridges. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Srbić, M.; Ivanković, A.M.; Vlašić, A.; Kovačević, G.H. Plastic Joints in Bridge Columns of Atypical Cross-Sections with Smooth Reinforcement without Seismic Details. Appl. Sci. 2021, 11, 2658. [Google Scholar] [CrossRef]
- Mitchell, D.; Bruneau, M.; Saatcioglu, M.; Williams, M.; Anderson, D.; Sexsmith, R. Performance of bridges in the 1994 Northridge earthquake. Can. J. Civ. Eng. 1995, 22, 415–427. [Google Scholar] [CrossRef]
- Sakellariadis, L.; Anastasopoulos, I.; Gazetas, G. Fukae bridge collapse (Kobe 1995) revisited: New insights. Soils Found. 2020, 60, 1450–1467. [Google Scholar] [CrossRef]
- Skokandić, D.; Ivanković, A.M.; Žnidarič, A.; Srbić, M. Modelling of traffic load effects in the assessment of existing road bridges. J. Croat. Assoc. Civ. Eng. 2020, 71, 1153–1165. [Google Scholar] [CrossRef]
- Stepinac, M.; Lourenço, P.B.; Atalić, J.; Kišiček, T.; Uroš, M.; Baniček, M.; Novak, M.Š. Damage classification of residential buildings in historical downtown after the ML5.5 earthquake in Zagreb, Croatia in 2020. Int. J. Disaster Risk Reduct. 2021, 56, 102140. [Google Scholar] [CrossRef]
- Lulić, L.; Ožić, K.; Kišiček, T.; Hafner, I.; Stepinac, M. Post-Earthquake Damage Assessment—Case Study of the Educational Building after the Zagreb Earthquake. Sustainability 2021, 13, 6353. [Google Scholar] [CrossRef]
- Government of Croatia. World Bank Report: Croatia Earthquake Rapid Damage and Needs Assessment; Government of Croatia: Zagreb, Croatian, 2020.
- Vlašić, A.; Srbić, M.; Skokandić, D.; Ivanković, A.M. Post-Earthquake Rapid Damage Assessment of Road Bridges in Glina County. Buildings 2022, 12, 42. [Google Scholar] [CrossRef]
- Marin, F.; Darko, M.; Zlatko, Š. Seismic Assessment of Obod Bridge in Croatia//Durability of Concrete Structures. In Proceedings of the 8th Central European Congresses on Concrete Engineering/Radić, Jure, PLitvice Lakes, Croatia, 4–6 October 2012; Marija, K., Ed.; pp. 65–7214. [Google Scholar]
- CEN: EN 1998-1; Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- CEN: EN 1998-3; Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Wiśniewski, D.F.; Casas, J.R.; Ghosn, M. Codes for Safety Assessment of Existing Bridges—Current State and Further Development. Struct. Eng. Int. 2012, 22, 552–561. [Google Scholar] [CrossRef]
- Ivanković, A.M.; Skokandić, D.; Žnidarič, A.; Kreslin, M. Bridge performance indicators based on traffic load monitoring. Struct. Infrastruct. Eng. 2019, 15, 899–911. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Limongelli, M.P.; Ademovic, N.; Anžlin, A.; Gavin, K.; Zanini, M. Structural Health Monitoring for Performance Assessment of Bridges under Flooding and Seismic Actions. Struct. Eng. Int. 2018, 28, 296–307. [Google Scholar] [CrossRef] [Green Version]
- Stepinac, M.; Kisicek, T.; Renić, T.; Hafner, I.; Bedon, C. Methods for the Assessment of Critical Properties in Existing Masonry Structures under Seismic Loads—The ARES Project. Appl. Sci. 2020, 10, 1576. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.; Cai, C.S.; Deng, L.; Zhang, W. Using Dynamic Responses of Moving Vehicles to Extract Bridge Modal Properties of a Field Bridge. J. Bridg. Eng. 2017, 22, 04017018. [Google Scholar] [CrossRef]
- Marić, M.K.; Ivanković, A.M.; Vlašić, A.; Bleiziffer, J.; Srbić, M.; Skokandić, D. Assessment of reinforcement corrosion and concrete damage on bridges using non-destructive testing. J. Croat. Assoc. Civ. Eng. 2019, 71, 843–862. [Google Scholar] [CrossRef]
- Lee, S.; Kalos, N.; Shin, D.H. Non-destructive testing methods in the U.S. for bridge inspection and maintenance. KSCE J. Civ. Eng. 2014, 18, 1322–1331. [Google Scholar] [CrossRef]
- Liu, L.; Guo, T. Seismic non-destructive testing on a reinforced concrete bridge column using tomographic imaging techniques. J. Geophys. Eng. 2005, 2, 23–31. [Google Scholar] [CrossRef]
- Lantsoght, E.; van der Veen, C.; de Boer, A.; Hordijk, D. State-of-the-art on load testing of concrete bridges. Eng. Struct. 2017, 150, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Conde, B.; Ramos, L.F.; Oliveira, D.V.; Riveiro, B.; Solla, M. Structural assessment of masonry arch bridges by combination of non-destructive testing techniques and three-dimensional numerical modelling: Application to Vilanova bridge. Eng. Struct. 2017, 148, 621–638. [Google Scholar] [CrossRef]
- Seismic assessment of existing reinforced concrete arch bridges. J. Croat. Assoc. Civ. Eng. 2014, 66, 691–703. [CrossRef] [Green Version]
- Pelà, L.; Aprile, A.; Benedetti, A. Comparison of seismic assessment procedures for masonry arch bridges. Constr. Build. Mater. 2013, 38, 381–394. [Google Scholar] [CrossRef]
- Mwafy, A.; Kwon, O.-S.; Elnashai, A. Seismic assessment of an existing non-seismically designed major bridge-abutment–foundation system. Eng. Struct. 2010, 32, 2192–2209. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.; Sextos, A. Extension of modal pushover analysis to seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2006, 35, 1269–1293. [Google Scholar] [CrossRef]
- Pelà, L.; Aprile, A.; Benedetti, A. Seismic assessment of masonry arch bridges. Eng. Struct. 2009, 31, 1777–1788. [Google Scholar] [CrossRef]
- Homaei, F.; Yazdani, M. The probabilistic seismic assessment of aged concrete arch bridges: The role of soil-structure interaction. Structures 2020, 28, 894–904. [Google Scholar] [CrossRef]
- Xie, Y.; Zheng, Q.; Yang, C.-S.W.; Zhang, W.; DesRoches, R.; Padgett, J.E.; Taciroglu, E. Probabilistic models of abutment backfills for regional seismic assessment of highway bridges in California. Eng. Struct. 2019, 180, 452–467. [Google Scholar] [CrossRef]
- Monteiro, R.; Delgado, R.; Pinho, R. Probabilistic Seismic Assessment of RC Bridges: Part I—Uncertainty Models. Structures 2016, 5, 258–273. [Google Scholar] [CrossRef]
- MonteiroR Sampling based numerical seismic assessment of continuous span RC bridges. Eng. Struct. 2016, 118, 407–420. [CrossRef]
- Bending moment curvature relationship as an indicator of seismic resistance of older bridge piers. J. Croat. Assoc. Civ. Eng. 2019, 71, 481–488. [CrossRef]
- Stefanidou, S.P.; Kappos, A.J. Bridge-specific fragility analysis: When is it really necessary? Bull. Earthq. Eng. 2018, 17, 2245–2280. [Google Scholar] [CrossRef] [Green Version]
- Kaundinya, I.; Heimbecher, F. Identification and Classification of European Bridge and Tunnel Types. In Proceedings of the Taller, Longer, Lighter—Meeting Growing Demand with Limited Resources, Report of the IABSE IASS 2011 Symposium, IABSE, London, UK, 20–23 September 2011; International Association for Bridge and Structural Engineering (IABSE)/IASS: Zurich, Switzerland, 2011; ISBN 978-0-7079-7122-3. [Google Scholar]
- Choi, E.; DesRoches, R.; Nielson, B. Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 2004, 26, 187–199. [Google Scholar] [CrossRef]
- Saiidi, M. Managing seismic performance of highway bridges—Evolution in experimental research. Struct. Infrastruct. Eng. 2011, 7, 569–586. [Google Scholar] [CrossRef]
- Padgett, J.E.; DesRoches, R. Methodology for the development of analytical fragility curves for retrofitted bridges. Earthq. Eng. Struct. Dyn. 2008, 37, 1157–1174. [Google Scholar] [CrossRef]
- Zanini, M.A.; Pellegrino, C.; Morbin, R.; Modena, C. Seismic vulnerability of bridges in transport networks subjected to environmental deterioration. Bull. Earthq. Eng. 2013, 11, 561–579. [Google Scholar] [CrossRef]
- Sheikh, M.N.; Légeron, F. Performance based seismic assessment of bridges designed according to Canadian Highway Bridge Design Code. Can. J. Civ. Eng. 2014, 41, 777–787. [Google Scholar] [CrossRef] [Green Version]
- Cosenza, E.; Losanno, D. Assessment of existing reinforced-concrete bridges under road-traffic loads according to the new Italian guidelines. Struct. Concr. 2021, 22, 2868–2881. [Google Scholar] [CrossRef]
- Di Sarno, L.; da Porto, F.; Guerrini, G.; Calvi, P.M.; Camata, G.; Prota, A. Seismic performance of bridges during the 2016 Central Italy earthquakes. Bull. Earthq. Eng. 2019, 17, 5729–5761. [Google Scholar] [CrossRef]
- Huang, C.; Huang, S. Seismic resilience assessment of aging bridges with different failure modes. Structures 2021, 33, 3682–3690. [Google Scholar] [CrossRef]
- Alipour, A.; Shafei, B. Seismic Resilience of Transportation Networks with Deteriorating Components. J. Struct. Eng. 2016, 142, 1–12. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Titi, A. Seismic resilience of concrete structures under corrosion. Earthq. Eng. Struct. Dyn. 2015, 44, 2445–2466. [Google Scholar] [CrossRef]
- Zelaschi, C.; Monteiro, R.; Pinho, R.J.S.M. Parametric Characterization of RC Bridges for Seismic Assessment Purposes. Structures 2016, 7, 14–24. [Google Scholar] [CrossRef]
- Modena, C.; Tecchio, G.; Pellegrino, C.; da Porto, F.; Donà, M.; Zampieri, P.; Zanini, M.A. Reinforced concrete and masonry arch bridges in seismic areas: Typical deficiencies and retrofitting strategies. Struct. Infrastruct. Eng. 2014, 11, 415–442. [Google Scholar] [CrossRef]
- Ivanković, A.M.; Skokandić, D.; Marić, M.K.; Srbić, M. Performance-Based Ranking of Existing Road Bridges. Appl. Sci. 2021, 11, 4398. [Google Scholar] [CrossRef]
- Raza, S.; Khan, M.K.I.; Menegon, S.J.; Tsang, H.-H.; Wilson, J.L. Strengthening and Repair of Reinforced Concrete Columns by Jacketing: State-of-the-Art Review. Sustainability 2019, 11, 3208. [Google Scholar] [CrossRef] [Green Version]
- Wright, T.; DesRoches, R.; Padgett, J.E. Bridge Seismic Retrofitting Practices in the Central and Southeastern United States. J. Bridg. Eng. 2011, 16, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Ogata, T.; Osada, K. Seismic retrofitting of expressway bridges in Japan. Cem. Concr. Compos. 2000, 22, 17–27. [Google Scholar] [CrossRef]
- Billah, A.M.; Alam, M.S. Seismic performance evaluation of multi-column bridge bents retrofitted with different alternatives using incremental dynamic analysis. Eng. Struct. 2014, 62–63, 105–117. [Google Scholar] [CrossRef]
- Abdessemed, M.; Kenai, S.; Bali, A.; Kibboua, A. Dynamic analysis of a bridge repaired by CFRP: Experimental and numerical modelling. Constr. Build. Mater. 2011, 25, 1270–1276. [Google Scholar] [CrossRef]
- Del Zoppo, M.; Di Ludovico, M.; Balsamo, A.; Prota, A. Comparative Analysis of Existing RC Columns Jacketed with CFRP or FRCC. Polymers 2018, 10, 361. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Chen, K.; Hu, P.; He, W.; Xiao, L.; Zhang, R. Effect of ECC jackets for enhancing the lateral cyclic behavior of RC bridge columns. Eng. Struct. 2020, 219, 110714. [Google Scholar] [CrossRef]
- Hung, C.-C.; Chen, Y.-S. Innovative ECC jacketing for retrofitting shear-deficient RC members. Constr. Build. Mater. 2016, 111, 408–418. [Google Scholar] [CrossRef]
- Seyhan, E.C.; Goksu, C.; Uzunhasanoglu, A.; Ilki, A. Seismic Behavior of Substandard RC Columns Retrofitted with Embedded Aramid Fiber Reinforced Polymer (AFRP) Reinforcement. Polymers 2015, 7, 2535–2557. [Google Scholar] [CrossRef] [Green Version]
- Zanini, M.A.; Toska, K.; Faleschini, F.; Pellegrino, C. Seismic reliability of reinforced concrete bridges subject to environmental deterioration and strengthened with FRCM composites. Soil Dyn. Earthq. Eng. 2020, 136, 106224. [Google Scholar] [CrossRef]
- Dagenais, M.-A.; Massicotte, B.; Boucher-Proulx, G. Seismic Retrofitting of Rectangular Bridge Piers with Deficient Lap Splices Using Ultrahigh-Performance Fiber-Reinforced Concrete. J. Bridg. Eng. 2018, 23, 04017129. [Google Scholar] [CrossRef]
- Tong, T.; Yuan, S.; Zhuo, W.; He, Z.; Liu, Z. Seismic retrofitting of rectangular bridge piers using ultra-high performance fiber reinforced concrete jackets. Compos. Struct. 2019, 228, 111367. [Google Scholar] [CrossRef]
- Reggia, A.; Morbi, A.; Plizzari, G.A. Experimental study of a reinforced concrete bridge pier strengthened with HPFRC jacketing. Eng. Struct. 2020, 210, 110355. [Google Scholar] [CrossRef]
- Mitchell, D.; Sexsmith, R.; Tinawi, R. Seismic retrofitting techniques for bridges—A state-of-the-art report. Can. J. Civ. Eng. 1994, 21, 823–835. [Google Scholar] [CrossRef]
- Markogiannaki, O.; Tegos, I.; Papadrakakis, M. Seismic Retrofitting of R/C Bridges with the Use of Unbonded Tendons. In Proceedings of the 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Crete, Greece, 25–27 May 2015; pp. 1799–1811. [Google Scholar]
- Recupero, A.; Spinella, N.; Colajanni, P.; Scilipoti, C.D. Increasing the Capacity of Existing Bridges by Using Unbonded Prestressing Technology: A Case Study. Adv. Civ. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Billah, A.M.; Alam, M.S. Performance-based prioritisation for seismic retrofitting of reinforced concrete bridge bent. Struct. Infrastruct. Eng. 2013, 10, 929–949. [Google Scholar] [CrossRef]
- Moustafa, M.A.; Mosalam, K.M. Seismic response of bent caps in as-built and retrofitted reinforced concrete box-girder bridges. Eng. Struct. 2015, 98, 59–73. [Google Scholar] [CrossRef]
- Billah, A.H.M.M.; Alam, M.S.; Bhuiyan, M.A.R. Fragility Analysis of Retrofitted Multicolumn Bridge Bent Subjected to Near-Fault and Far-Field Ground Motion. J. Bridg. Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- ImbsenRA Use of Isolation for Seismic Retrofitting Bridges. J. Bridg. Eng. 2001, 6, 425–438. [CrossRef]
- MakrisN Seismic isolation: Early history. Earthq. Eng. Struct. Dyn. 2019, 48, 269–283. [CrossRef]
- Javanmardi, A.; Ibrahim, Z.; Ghaedi, K.; Khan, N.B.; Ghadim, H.B. Seismic isolation retrofitting solution for an existing steel cable-stayed bridge. PLoS ONE 2018, 13, e0200482. [Google Scholar] [CrossRef] [PubMed]
- Dicleli, M.; Mansour, M.Y.; Constantinou, M.C. Efficiency of Seismic Isolation for Seismic Retrofitting of Heavy Substructured Bridges. J. Bridg. Eng. 2005, 10, 429–441. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J. Design and Optimization of Seismic Isolation and Damping Devices for Highway Bridges Based on Probabilistic Repair Cost Ratio. J. Struct. Eng. 2018, 144, 04018125. [Google Scholar] [CrossRef]
- Castaldo, P.; Priore, R.L. Seismic performance assessment of isolated bridges for different limit states. J. Civ. Struct. Health Monit. 2018, 8, 17–32. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Base Isolation for Seismic Retrofitting of Structures. Prac. Period. Struct. Des. Constr. 2008, 13, 175–185. [Google Scholar] [CrossRef]
- Nguyen, X.-D.; Guizani, L. Optimal seismic isolation characteristics for bridges in moderate and high seismicity areas. Can. J. Civ. Eng. 2021, 48, 642–655. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Palermo, G. Seismic isolation of bridges using isolation systems based on flat sliding bearings. Bull. Earthq. Eng. 2007, 5, 491–509. [Google Scholar] [CrossRef]
- MalekiS Effect of Side Retainers on Seismic Response of Bridges with Elastomeric Bearings. J. Bridg. Eng. 2004, 9, 95–100. [CrossRef]
- Moliner, E.; Museros, P.; Martínez-Rodrigo, M.D. Retrofit of existing railway bridges of short to medium spans for high-speed traffic using viscoelastic dampers. Eng. Struct. 2012, 40, 519–528. [Google Scholar] [CrossRef]
- Martínez-Rodrigo, M.D.; Lavado, J.; Museros, P. Dynamic performance of existing high-speed railway bridges under resonant conditions retrofitted with fluid viscous dampers. Eng. Struct. 2010, 32, 808–828. [Google Scholar] [CrossRef]
- Andrawes, B.; Desroches, R. Comparison between Shape Memory Alloy Seismic Restrainers and Other Bridge Retrofit Devices. J. Bridg. Eng. 2007, 12, 700–709. [Google Scholar] [CrossRef]
- Lian, Q.; Yuan, W.; Yu, J.; Dang, X. Traffic efficiency of post-earthquake road network in fault region retrofitted by friction core rubber bearing. Structures 2021, 33, 54–67. [Google Scholar] [CrossRef]
- Khan, A.K.M.T.A.; Bhuiyan, M.A.R.; Ali, S.B. Seismic Responses of a Bridge Pier Isolated by High Damping Rubber Bearing: Effect of Rheology Modeling. Int. J. Civ. Eng. 2019, 17, 1767–1783. [Google Scholar] [CrossRef]
- Chen, X.; Li, C. Seismic performance of tall pier bridges retrofitted with lead rubber bearings and rocking foundation. Eng. Struct. 2020, 212, 110529. [Google Scholar] [CrossRef]
- Bayraktar, A.; Hökelekli, E. Seismic Performances of Different Spandrel Wall Strengthening Techniques in Masonry Arch Bridges. Int. J. Arch. Herit. 2020, 15, 1722–1740. [Google Scholar] [CrossRef]
- Šavor, Z.; Mujkanovic, N.; Hrelja Kovacevic, G.; Bleiziffer, J. Reconstruction of the Pag Bridge. In Proceedings of the Chinese-Croatian Joint Colloquium-Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Radić, J., Chen, B., Eds.; SECON HDGK: Brijuni Islands, Croatia, 2008; pp. 241–252. [Google Scholar]
- Ghallab, A.; Khafaga, M.; Farouk, M.; Essawy, A. Shear behavior of concrete beams externally prestressed with Parafil ropes. Ain Shams Eng. J. 2013, 4, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, J.; Masroor, A.; Mosqueda, G.; Ryan, K. Static and Dynamic Stability of Elastomeric Bearings for Seismic Protection of Structures. J. Struct. Eng. 2013, 139, 1149–1159. [Google Scholar] [CrossRef]
- Uroš, M.; Šavor Novak, M.; Atalić, J.; Sigmund, Z.; Baniček, M.; Demšić, M.; Hak, S. Post-earthquake damage assessment of buildings-procedure for conducting building inspections. J. Croat. Assoc. Civ. Eng. 2021, 72, 1089–1115. [Google Scholar] [CrossRef]
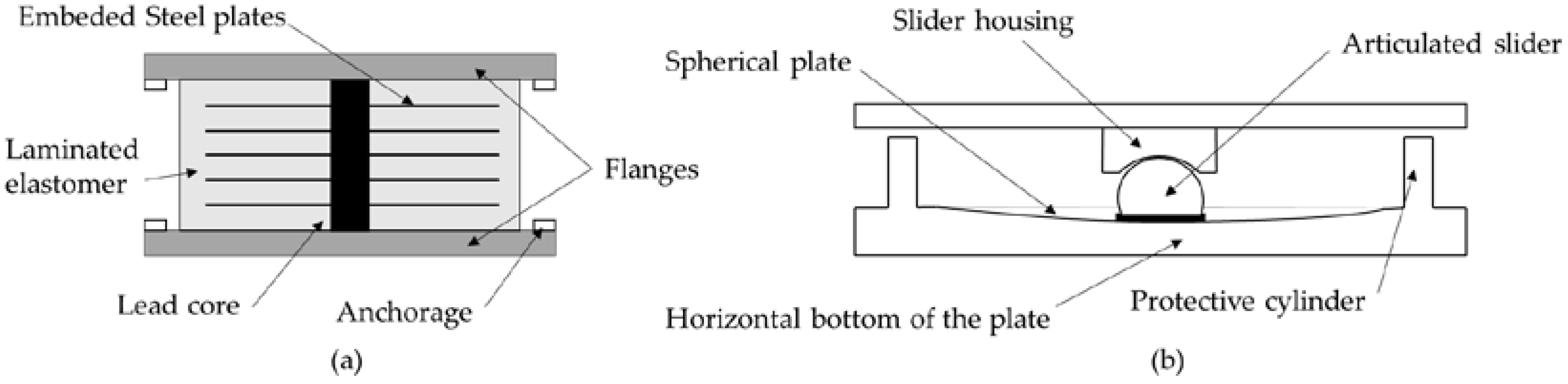





| Retrofit Method | Bridge Element | Bridge Type | Source |
|---|---|---|---|
| Steel jacketing | RC piers | Any bridge with RC piers | [52,53,54,55] |
| Concrete/mortar jacketing | |||
| CFRP jacketing | [52,54,55,56,57] | ||
| ECC jacketing | [58,59] | ||
| AFRP jacketing | [52,60] | ||
| FRCM jacketing | [57,61] | ||
| GFRP jacketing | [52] | ||
| UHPFRC jacketing/repair | [62,63,64] | ||
| Bracing or infill walls between piers in the transverse direction | [65] | ||
| External prestressing with unbonded tendons | Superstructure | girder bridge, cable stayed bridge, slab bridge, box-girder bridge, | [13,66,67] |
| Span restrainers | any bridge with sliding bearings | [53,65] | |
| Reinforced concrete jacking | Cap beams/ RC joints | Any bridge with RC piers/cap beams | [53,65,68,69,70] |
| Transverse external prestressing | [66,67] | ||
| Seat extenders | Cap beams/Abutments | [53,65] | |
| Seismic isolation | Bearings | All bridges | [71,72,73,74,75,76,77,78,79] |
| Foundation cap confinement | [65] | ||
| Restrainers | [65,80] | ||
| Bumper blocks | [4,53] | ||
| Dampers | [13,75,81,82,83] | ||
| Replacement | [76,84,85,86] | ||
| Spandrel wall strengthening | Spandrel walls | Masonry bridges | [50,87] |
| Abutment wing walls stabilization | Abutment | Any bridge with massive abutments | [53] |
| Method | Effect on the Structural Element | Cost | ||
|---|---|---|---|---|
| Strength | Ductility | Stiffness | ||
| RC jacketing | Increase | Increase | Increase | Very high |
| Steel jacketing | Significant increase | Significant increase | Increase | High |
| FRP jacketing | Increase | Significant increase | No effect | Moderate |
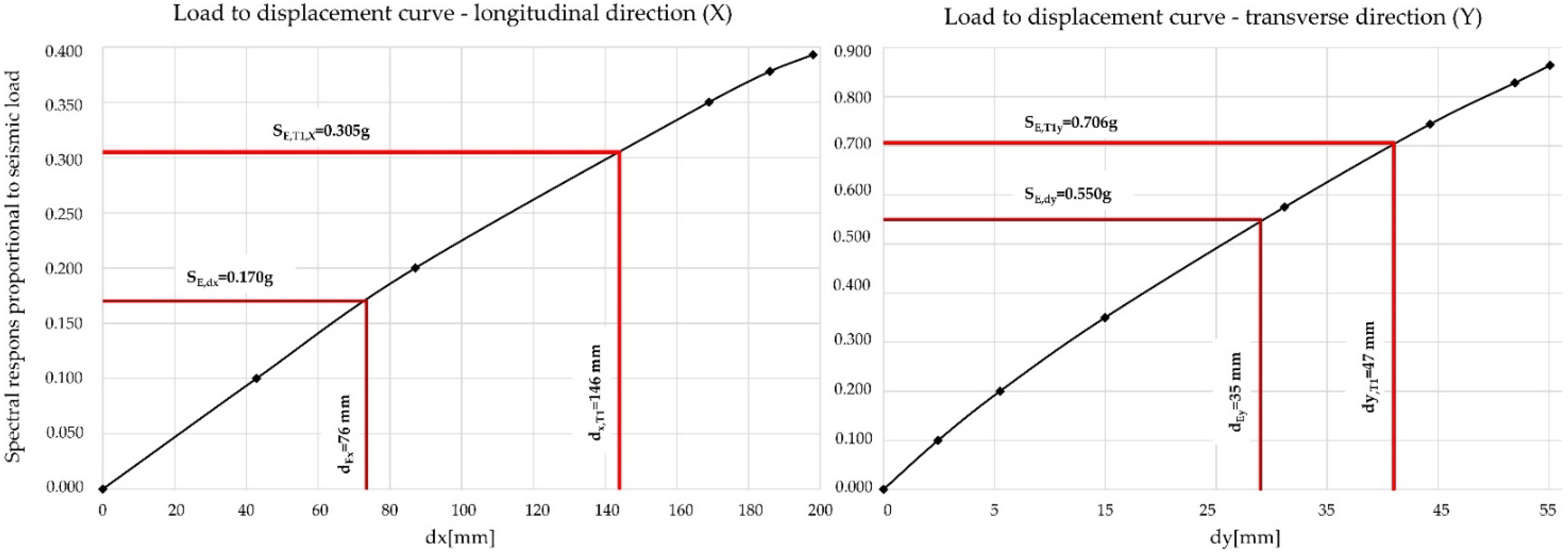
| Modal Shape | Direction | Period | Spectral Response | Target Displacement |
|---|---|---|---|---|
| 1 | Longitudinal (x) | Tx = 0.94 s | S(Tx) = 0.305 g | dE,x = 76 mm |
| 2 | Transverse (y) | Ty = 0.36 s | S(Ty) = 0.706 g | dE,y = 35 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skokandić, D.; Vlašić, A.; Kušter Marić, M.; Srbić, M.; Mandić Ivanković, A. Seismic Assessment and Retrofitting of Existing Road Bridges: State of the Art Review. Materials 2022, 15, 2523. https://doi.org/10.3390/ma15072523
Skokandić D, Vlašić A, Kušter Marić M, Srbić M, Mandić Ivanković A. Seismic Assessment and Retrofitting of Existing Road Bridges: State of the Art Review. Materials. 2022; 15(7):2523. https://doi.org/10.3390/ma15072523
Chicago/Turabian StyleSkokandić, Dominik, Anđelko Vlašić, Marija Kušter Marić, Mladen Srbić, and Ana Mandić Ivanković. 2022. "Seismic Assessment and Retrofitting of Existing Road Bridges: State of the Art Review" Materials 15, no. 7: 2523. https://doi.org/10.3390/ma15072523
APA StyleSkokandić, D., Vlašić, A., Kušter Marić, M., Srbić, M., & Mandić Ivanković, A. (2022). Seismic Assessment and Retrofitting of Existing Road Bridges: State of the Art Review. Materials, 15(7), 2523. https://doi.org/10.3390/ma15072523







