Tribological Properties and 3D Topographic Parameters of Hard Turned and Ground Surfaces
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
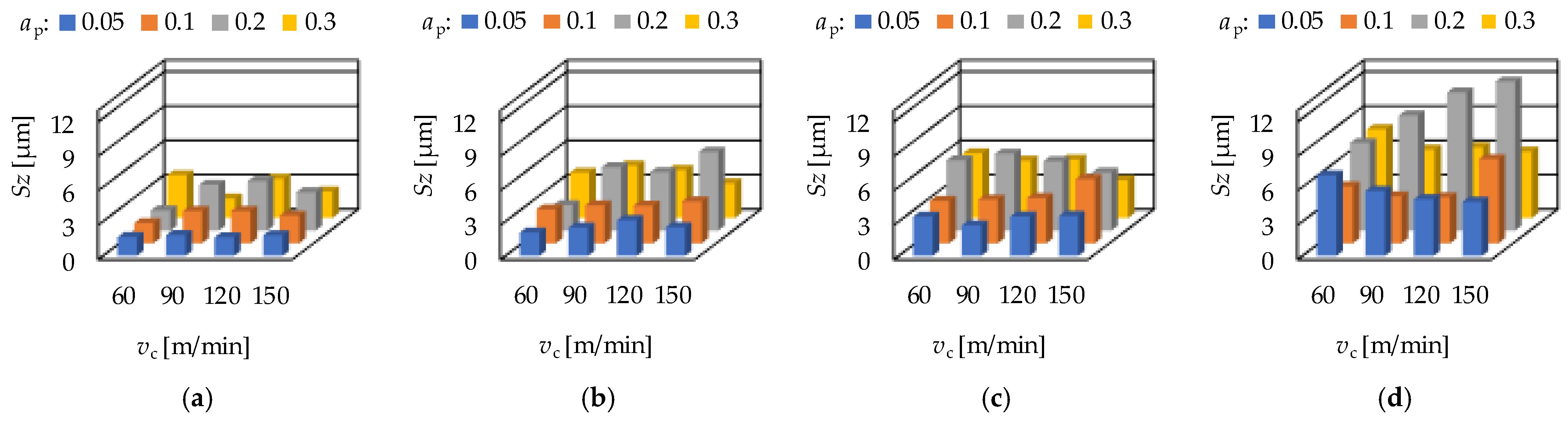
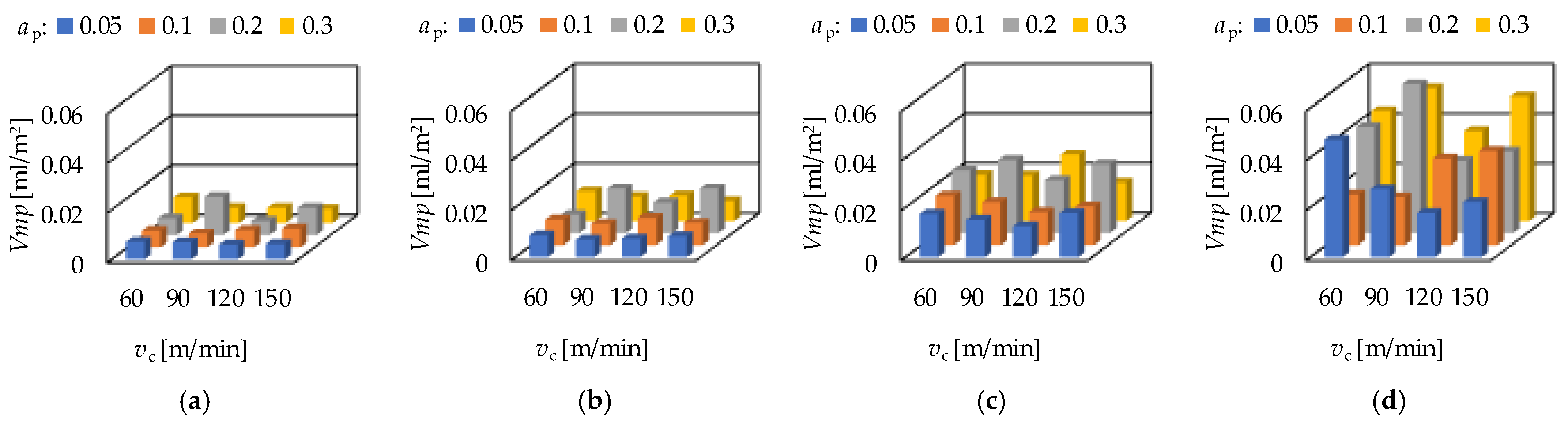
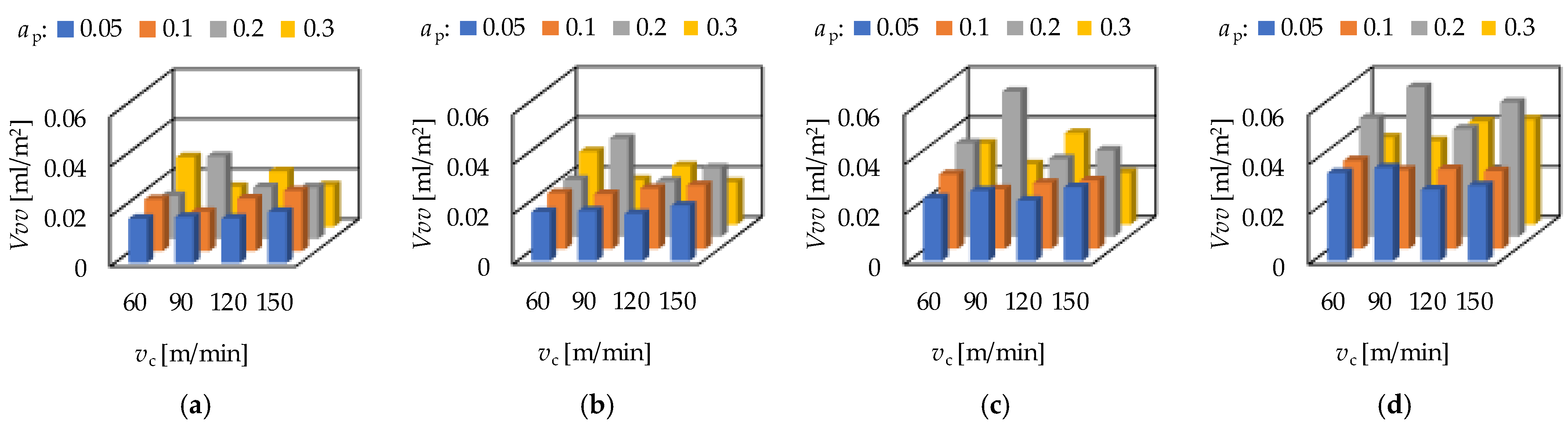
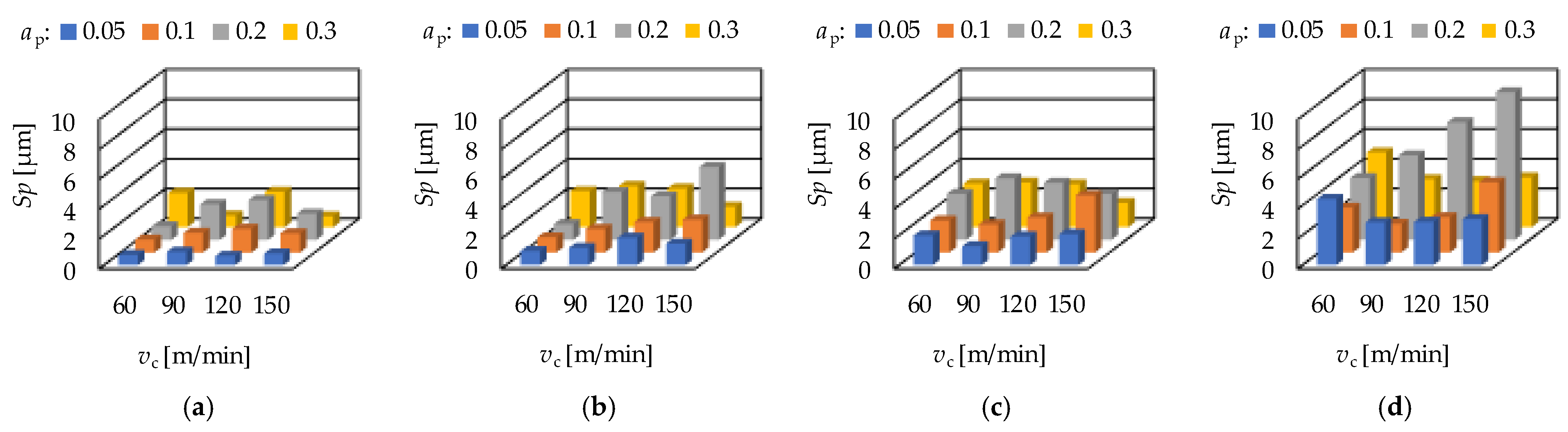
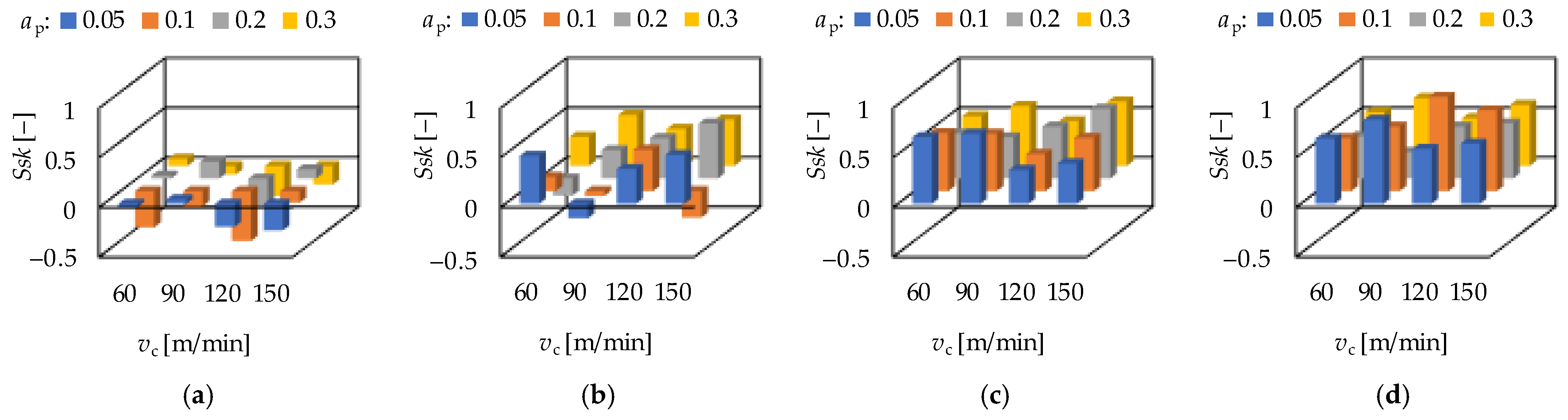
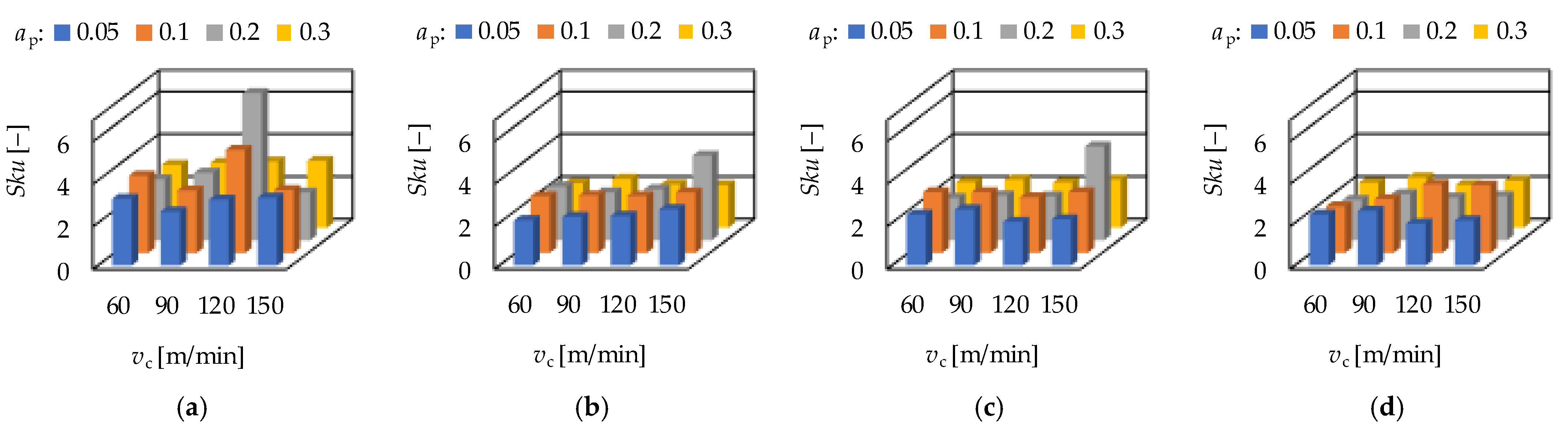
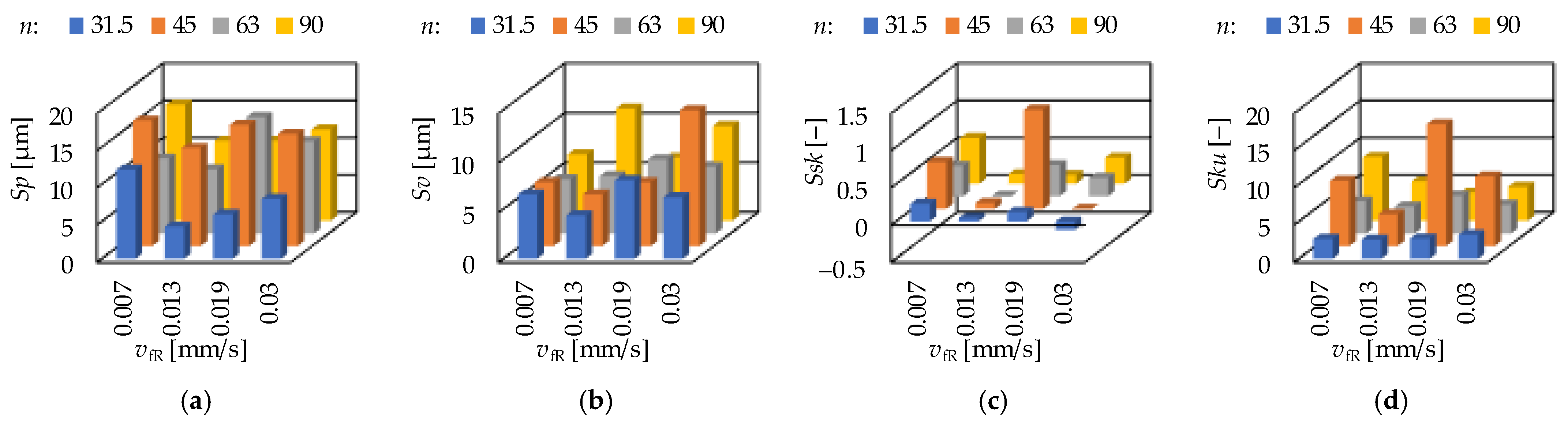
3.1. Roughness Values and Response Functions
3.2. Analysis of Roughness Determining Factors
3.3. Connections between the Analyzed Parameters
4. Conclusions
- For the prediction of the topography parameters a cubic type response function is applicable. The obtained coefficients of determination (R2) varied between 0.48 and 0.91 in the case of hard turning and between 0.46 and 0.84 in the case of grinding.
- The major topography-influencing cutting parameter in hard turning is the feed rate (f) and in grinding the infeed velocity (vfR). The single-factor coefficients of determination vary between 0.2 and 0.65 in hard turning and between 0.05 and 0.27 in grinding. The reason for the relatively low absolute values is the structure of the cubic response function. These values are the highest compared to those of the other components of the response function.
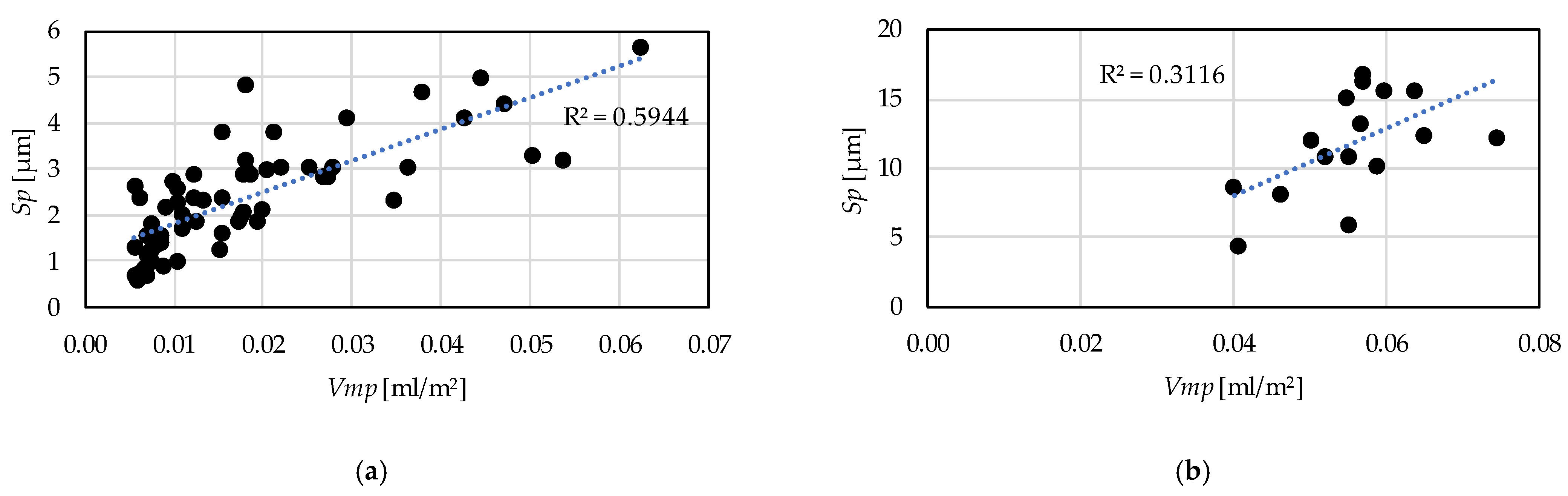
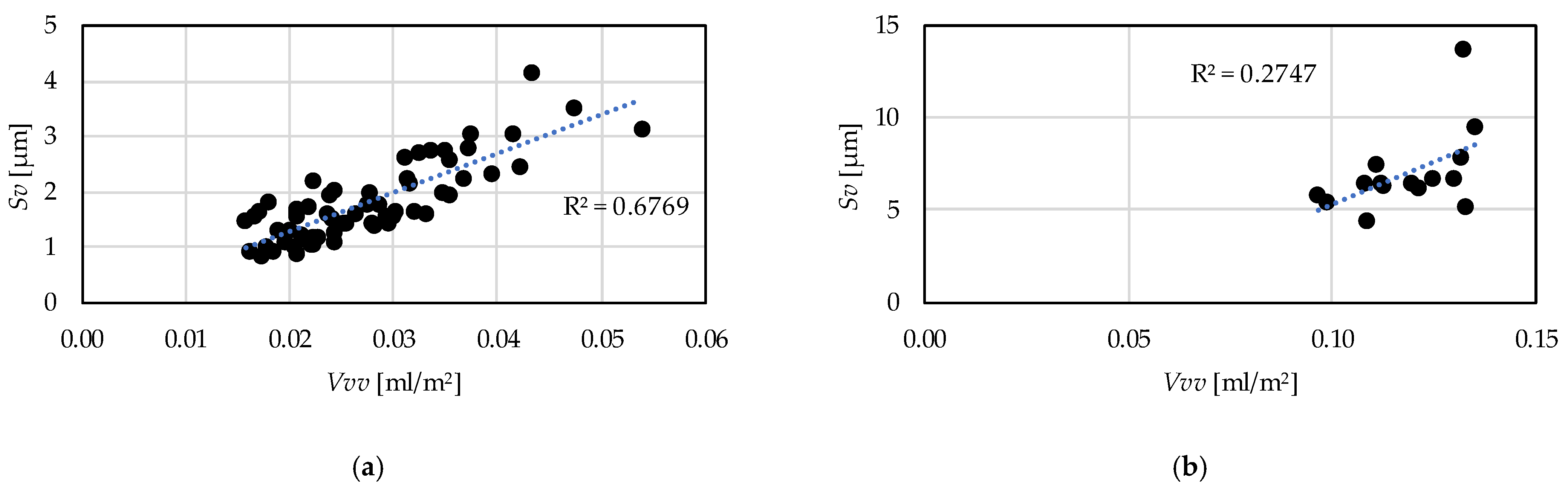
- Based on the hard turning experimental results, there are strong relationships between the peak material volume (Vmp) and maximum peak height (Sp) parameters (R2 = 0.59) and between the valley void volume (Vvv) and maximum valley depth (Sv) parameters (R2 = 0.68). Therefore, both parameters can be reliably used for assessing surface properties. The same is not valid for grinding based on the coefficients of determination 0.31 and 0.27, respectively.
- Based on the grinding experimental results, there is a strong relationship between the skewness (Ssk) and the kurtosis (Sku) parameters. The coefficient of determination is 0.66. This is not valid for the hard turning (R2 = 0.18).
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ap | vc | f | Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 60 | 0.05 | 0.122 | 1.631 | 0.007 | 0.018 | 0.695 | 0.936 | −0.029 | 3.148 |
| 0.05 | 60 | 0.1 | 0.272 | 2.041 | 0.009 | 0.020 | 0.937 | 1.104 | 0.482 | 2.129 |
| 0.05 | 60 | 0.15 | 0.491 | 3.424 | 0.017 | 0.025 | 1.986 | 1.438 | 0.671 | 2.395 |
| 0.05 | 60 | 0.2 | 0.940 | 7.023 | 0.047 | 0.035 | 4.430 | 2.593 | 0.657 | 2.396 |
| 0.05 | 90 | 0.05 | 0.125 | 1.802 | 0.007 | 0.018 | 0.898 | 0.905 | 0.045 | 2.545 |
| 0.05 | 90 | 0.1 | 0.205 | 2.466 | 0.007 | 0.020 | 1.154 | 1.312 | −0.148 | 2.286 |
| 0.05 | 90 | 0.15 | 0.439 | 2.662 | 0.015 | 0.028 | 1.260 | 1.402 | 0.705 | 2.633 |
| 0.05 | 90 | 0.2 | 0.639 | 5.670 | 0.027 | 0.037 | 2.863 | 2.807 | 0.847 | 2.566 |
| 0.05 | 120 | 0.05 | 0.149 | 1.609 | 0.006 | 0.018 | 0.622 | 0.987 | −0.231 | 3.106 |
| 0.05 | 120 | 0.1 | 0.171 | 3.120 | 0.007 | 0.019 | 1.828 | 1.292 | 0.351 | 2.333 |
| 0.05 | 120 | 0.15 | 0.378 | 3.435 | 0.012 | 0.024 | 1.916 | 1.519 | 0.342 | 2.052 |
| 0.05 | 120 | 0.2 | 0.749 | 4.955 | 0.018 | 0.029 | 2.897 | 1.758 | 0.551 | 1.968 |
| 0.05 | 150 | 0.05 | 0.129 | 1.785 | 0.006 | 0.021 | 0.779 | 1.006 | −0.268 | 3.192 |
| 0.05 | 150 | 0.1 | 0.217 | 2.504 | 0.008 | 0.022 | 1.437 | 1.067 | 0.491 | 2.647 |
| 0.05 | 150 | 0.15 | 0.437 | 3.491 | 0.018 | 0.030 | 2.076 | 1.415 | 0.407 | 2.169 |
| 0.05 | 150 | 0.2 | 0.645 | 4.730 | 0.022 | 0.030 | 3.082 | 1.647 | 0.605 | 2.116 |
| ap | vc | f | Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 60 | 0.05 | 0.113 | 1.756 | 0.007 | 0.021 | 0.870 | 0.886 | −0.365 | 3.639 |
| 0.1 | 60 | 0.1 | 0.193 | 2.961 | 0.010 | 0.022 | 1.009 | 1.185 | 0.142 | 2.662 |
| 0.1 | 60 | 0.15 | 0.317 | 3.704 | 0.020 | 0.030 | 2.137 | 1.567 | 0.583 | 2.850 |
| 0.1 | 60 | 0.2 | 0.553 | 4.953 | 0.020 | 0.035 | 3.001 | 1.952 | 0.534 | 2.185 |
| 0.1 | 90 | 0.05 | 0.134 | 2.808 | 0.006 | 0.016 | 1.319 | 1.490 | −0.153 | 2.936 |
| 0.1 | 90 | 0.1 | 0.208 | 3.301 | 0.009 | 0.022 | 1.566 | 1.735 | −0.050 | 2.700 |
| 0.1 | 90 | 0.15 | 0.266 | 3.808 | 0.017 | 0.024 | 1.872 | 1.936 | 0.579 | 2.851 |
| 0.1 | 90 | 0.2 | 0.478 | 4.086 | 0.019 | 0.032 | 1.918 | 2.168 | 0.649 | 2.528 |
| 0.1 | 120 | 0.05 | 0.114 | 2.817 | 0.007 | 0.021 | 1.592 | 1.225 | −0.506 | 4.852 |
| 0.1 | 120 | 0.1 | 0.164 | 3.284 | 0.011 | 0.024 | 2.036 | 1.248 | 0.416 | 2.674 |
| 0.1 | 120 | 0.15 | 0.267 | 3.933 | 0.013 | 0.026 | 2.338 | 1.595 | 0.373 | 2.609 |
| 0.1 | 120 | 0.2 | 0.447 | 4.004 | 0.035 | 0.032 | 2.359 | 1.645 | 0.950 | 3.222 |
| 0.1 | 150 | 0.05 | 0.181 | 2.400 | 0.008 | 0.024 | 1.291 | 1.109 | −0.115 | 2.965 |
| 0.1 | 150 | 0.1 | 0.170 | 3.639 | 0.009 | 0.025 | 2.200 | 1.439 | −0.268 | 2.845 |
| 0.1 | 150 | 0.15 | 0.291 | 5.588 | 0.016 | 0.027 | 3.821 | 1.767 | 0.536 | 2.856 |
| 0.1 | 150 | 0.2 | 0.446 | 7.336 | 0.038 | 0.031 | 4.709 | 2.627 | 0.814 | 3.180 |
| ap | vc | f | Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 60 | 0.05 | 0.270 | 1.754 | 0.007 | 0.017 | 0.910 | 0.844 | 0.031 | 2.875 |
| 0.2 | 60 | 0.1 | 0.432 | 2.231 | 0.007 | 0.023 | 1.046 | 1.185 | −0.172 | 2.525 |
| 0.2 | 60 | 0.15 | 0.878 | 6.130 | 0.025 | 0.037 | 3.074 | 3.056 | 0.453 | 1.983 |
| 0.2 | 60 | 0.2 | 1.494 | 7.644 | 0.043 | 0.048 | 4.138 | 3.506 | 0.425 | 1.896 |
| 0.2 | 90 | 0.05 | 0.346 | 3.987 | 0.015 | 0.033 | 2.387 | 1.600 | 0.170 | 3.175 |
| 0.2 | 90 | 0.1 | 0.479 | 5.526 | 0.018 | 0.039 | 3.200 | 2.326 | 0.285 | 2.246 |
| 0.2 | 90 | 0.15 | 0.581 | 6.704 | 0.029 | 0.058 | 4.123 | 2.581 | 0.414 | 2.100 |
| 0.2 | 90 | 0.2 | 0.965 | 10.049 | 0.062 | 0.127 | 5.659 | 4.390 | 0.267 | 2.163 |
| 0.2 | 120 | 0.05 | 0.128 | 4.332 | 0.006 | 0.021 | 2.673 | 1.659 | −0.283 | 6.930 |
| 0.2 | 120 | 0.1 | 0.195 | 5.100 | 0.012 | 0.022 | 2.916 | 2.184 | 0.406 | 2.390 |
| 0.2 | 120 | 0.15 | 0.837 | 6.056 | 0.021 | 0.031 | 3.825 | 2.231 | 0.522 | 2.062 |
| 0.2 | 120 | 0.2 | 1.412 | 12.051 | 0.029 | 0.043 | 7.887 | 4.164 | 0.524 | 2.009 |
| 0.2 | 150 | 0.05 | 0.333 | 3.324 | 0.011 | 0.021 | 1.757 | 1.567 | 0.093 | 2.246 |
| 0.2 | 150 | 0.1 | 0.115 | 6.860 | 0.018 | 0.028 | 4.881 | 1.979 | 0.554 | 3.982 |
| 0.2 | 150 | 0.15 | 0.667 | 5.067 | 0.028 | 0.035 | 3.068 | 1.999 | 0.702 | 4.410 |
| 0.2 | 150 | 0.2 | 1.046 | 13.034 | 0.033 | 0.054 | 9.900 | 3.134 | 0.556 | 2.072 |
| ap | vc | f | Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 60 | 0.05 | 0.112 | 3.727 | 0.010 | 0.028 | 2.301 | 1.426 | 0.073 | 2.963 |
| 0.3 | 60 | 0.1 | 0.253 | 3.950 | 0.012 | 0.029 | 2.412 | 1.538 | 0.293 | 2.091 |
| 0.3 | 60 | 0.15 | 0.570 | 5.636 | 0.019 | 0.033 | 2.910 | 2.726 | 0.501 | 2.144 |
| 0.3 | 60 | 0.2 | 0.998 | 7.747 | 0.044 | 0.035 | 5.011 | 2.735 | 0.542 | 2.114 |
| 0.3 | 90 | 0.05 | 0.109 | 1.687 | 0.006 | 0.016 | 0.787 | 0.900 | −0.085 | 3.051 |
| 0.3 | 90 | 0.1 | 0.279 | 4.575 | 0.010 | 0.018 | 2.769 | 1.806 | 0.514 | 2.293 |
| 0.3 | 90 | 0.15 | 0.537 | 5.005 | 0.018 | 0.024 | 2.987 | 2.018 | 0.604 | 2.263 |
| 0.3 | 90 | 0.2 | 1.075 | 5.969 | 0.054 | 0.034 | 3.210 | 2.759 | 0.684 | 2.356 |
| 0.3 | 120 | 0.05 | 0.193 | 3.418 | 0.006 | 0.022 | 2.385 | 1.033 | −0.304 | 3.120 |
| 0.3 | 120 | 0.1 | 0.305 | 4.186 | 0.010 | 0.024 | 2.597 | 1.590 | 0.372 | 2.037 |
| 0.3 | 120 | 0.15 | 0.569 | 5.095 | 0.027 | 0.037 | 2.875 | 2.220 | 0.451 | 2.134 |
| 0.3 | 120 | 0.2 | 1.036 | 6.159 | 0.036 | 0.041 | 3.091 | 3.069 | 0.481 | 2.013 |
| 0.3 | 150 | 0.05 | 0.144 | 2.304 | 0.006 | 0.017 | 0.732 | 1.572 | −0.186 | 3.146 |
| 0.3 | 150 | 0.1 | 0.344 | 3.021 | 0.008 | 0.017 | 1.368 | 1.653 | 0.468 | 2.003 |
| 0.3 | 150 | 0.15 | 0.666 | 3.301 | 0.016 | 0.021 | 1.628 | 1.673 | 0.648 | 2.260 |
| 0.3 | 150 | 0.2 | 1.083 | 5.796 | 0.050 | 0.042 | 3.330 | 2.466 | 0.616 | 2.216 |
| n | vfR | Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|
| 31.5 | 0.0069 | 1.106 | 18.463 | 0.050 | 0.120 | 11.987 | 6.476 | 0.237 | 2.670 |
| 45 | 0.0069 | 0.893 | 8.669 | 0.041 | 0.109 | 4.293 | 4.376 | 0.045 | 2.557 |
| 63 | 0.0069 | 1.089 | 13.879 | 0.055 | 0.132 | 5.958 | 7.921 | 0.129 | 2.720 |
| 90 | 0.0069 | 0.810 | 14.270 | 0.046 | 0.121 | 8.075 | 6.195 | −0.110 | 3.231 |
| 31.5 | 0.0130 | 0.762 | 23.286 | 0.057 | 0.108 | 16.868 | 6.417 | 0.630 | 8.785 |
| 45 | 0.0130 | 0.868 | 18.399 | 0.057 | 0.133 | 13.186 | 5.213 | 0.078 | 4.281 |
| 63 | 0.0130 | 0.738 | 22.698 | 0.057 | 0.112 | 16.272 | 6.426 | 1.333 | 16.387 |
| 90 | 0.0130 | 0.771 | 28.778 | 0.055 | 0.132 | 15.079 | 13.699 | −0.003 | 9.385 |
| 31.5 | 0.0193 | 0.727 | 15.550 | 0.059 | 0.099 | 10.070 | 5.480 | 0.407 | 4.342 |
| 45 | 0.0193 | 0.643 | 14.403 | 0.040 | 0.097 | 8.619 | 5.785 | 0.006 | 3.629 |
| 63 | 0.0193 | 0.798 | 23.092 | 0.060 | 0.111 | 15.636 | 7.456 | 0.420 | 5.103 |
| 90 | 0.0193 | 0.942 | 19.109 | 0.065 | 0.130 | 12.377 | 6.732 | 0.248 | 3.865 |
| 31.5 | 0.0302 | 0.752 | 22.328 | 0.064 | 0.125 | 15.628 | 6.699 | 0.616 | 8.584 |
| 45 | 0.0302 | 0.744 | 22.093 | 0.055 | 0.006 | 10.773 | 11.320 | 0.130 | 5.314 |
| 63 | 0.0302 | 0.779 | 17.136 | 0.052 | 0.113 | 10.775 | 6.361 | 0.117 | 3.796 |
| 90 | 0.0302 | 0.967 | 21.828 | 0.075 | 0.135 | 12.269 | 9.558 | 0.350 | 4.561 |
| Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku | |
|---|---|---|---|---|---|---|---|---|
| b0 | 1.37 | −6.75 | 0.04 | 0.07 | −9.61 | 3.13 | −0.77 | −1.18 |
| b1 | −15.53 | −90.97 | −0.08 | 0.08 | −71.76 | −23.91 | −8.07 | 26.96 |
| b2 | −0.02 | 0.27 | 0.00 | 0.00 | 0.35 | −0.08 | 0.02 | 0.19 |
| b3 | −1.45 | 110.72 | −0.11 | −0.34 | 74.11 | 24.05 | 10.36 | −73.80 |
| b11 | 120.34 | 640.51 | 1.17 | 2.35 | 464.84 | 202.58 | 36.86 | −164.53 |
| b22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| b33 | 37.10 | −814.11 | 1.28 | 2.10 | −602.44 | −108.37 | −4.12 | 490.98 |
| b111 | −252.93 | −1237.09 | −3.65 | −8.35 | −889.97 | −385.09 | −60.37 | 249.15 |
| b222 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| b333 | −28.29 | 2269.98 | 2.15 | 0.64 | 1656.12 | 397.07 | −104.12 | −1389.92 |
| b12 | −0.03 | −0.04 | 0.00 | −0.01 | 0.06 | −0.11 | 0.05 | 0.16 |
| b13 | 3.85 | 369.31 | −0.61 | 3.02 | 280.67 | 99.92 | 8.09 | −80.07 |
| b23 | −0.05 | −0.69 | 0.00 | 0.00 | −0.36 | −0.34 | −0.02 | 0.26 |
| b112 | 0.11 | 0.16 | 0.00 | 0.02 | 0.13 | 0.00 | −0.06 | −0.36 |
| b113 | −34.96 | −1016.36 | 0.37 | −9.17 | −771.72 | −270.11 | 42.44 | 317.60 |
| b221 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| b223 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| b331 | 57.43 | 47.81 | 4.90 | 3.49 | 71.17 | −32.99 | −117.26 | 63.09 |
| b332 | −0.10 | 0.80 | −0.01 | −0.02 | 0.56 | 0.07 | 0.29 | 0.86 |
| b123 | 0.07 | 0.05 | 0.00 | 0.00 | −0.16 | 0.21 | −0.01 | −0.53 |
| Sa | Sz | Vmp | Vvv | Sp | Sv | Ssk | Sku | |
|---|---|---|---|---|---|---|---|---|
| b0 | 2.74 | 47.76 | 0.11 | 0.40 | 49.22 | −1.46 | 3.99 | −0.66 |
| b1 | −0.05 | −3.88 | −0.01 | −0.02 | −3.90 | 0.02 | −0.37 | −2.24 |
| b2 | −170.01 | 8045.68 | 8.75 | 15.73 | 6467.88 | 1577.78 | 535.11 | 8856.34 |
| b11 | 0.00 | 0.06 | 0.00 | 0.00 | 0.06 | 0.00 | 0.01 | 0.04 |
| b22 | 7462.72 | −561,230.92 | −346.53 | −512.09 | −426,625.61 | −134,604.82 | −26,412.82 | −506,380.38 |
| b111 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| b222 | −92,984.08 | 10,903,134.74 | 6396.40 | 8736.53 | 7,982,419.09 | 2,920,707.30 | 476,447.27 | 9,328,540.86 |
| b12 | 0.32 | 50.70 | −0.10 | −0.34 | 31.19 | 19.51 | −3.33 | −14.85 |
| b112 | 0.01 | −0.12 | 0.00 | 0.00 | −0.07 | −0.05 | 0.03 | 0.19 |
| b122 | −24.57 | −995.25 | −0.34 | 0.04 | −609.55 | −385.70 | −17.46 | −338.71 |
References
- Mamalis, A.G.; Kundrak, J.; Horvath, M. On a novel tool life relation for precision cutting tools. J. Manuf. Sci. Eng. 2005, 127, 328–332. [Google Scholar] [CrossRef]
- Kundrak, J.; Sztankovics, I.; Lukacs, F. Comparative analysis of hard machined bores based on the roughness and accuracy. Cut. Tools Technol. Syst. 2020, 92, 19–25. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Reverse Problem in Surface Texture Analysis—One-Process Profile Modeling on the Basis of Measured Two-Process Profile after Machining or Wear. Materials 2019, 12, 4169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, B.; Wang, X.; Xu, Y.; Jackson, R.L. Deterministic elastic-plastic modelling of rough surface contact including spectral interpolation and comparison to theoretical models. Tribol. Int. 2019, 135, 246–258. [Google Scholar] [CrossRef]
- El-Tayeb, N.S.M.; Low, K.O.; Brevern, P.V. On the surface and tribological characteristics of burnished cylindrical Al-6061. Tribol. Int. 2009, 42, 320–326. [Google Scholar] [CrossRef]
- Whittaker, R.K.; Hothi, H.S.; Eskelinen, A.; Blunn, G.W.; Skinner, J.A.; Hart, A.J. Variation in Taper Surface Roughness for a Single Design Effects the Wear Rate in Total Hip Arthroplasty. J. Orthop. Res. 2017, 35, 1784–1792. [Google Scholar] [CrossRef]
- Gogolin, A.; Wasilewski, M.; Ligus, G.; Wojciechowski, S.; Gapinski, B.; Krolczyk, J.; Zajac, D.; Krolczyk, G. Influence of geometry and surface morphology of the U-tube on the fluid flow in the range of various velocities. Measurement 2020, 164, 108094. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Karmiris-Obratanski, P.; Kurpiel, S.; Zagorski, K.; Markopoulos, A.P. Investigation on the surface quality obtained during trochoidal milling of 6082 aluminum alloy. Machines 2021, 9, 75. [Google Scholar] [CrossRef]
- Kundrak, J.; Nagy, A.; Markopoulos, A.P.; Karkalos, N.E. Investigation of surface roughness on face milled parts with round insert in planes parallel to the feed at various cutting speeds. Cut. Tools Technol. Syst. 2019, 90, 87–96. [Google Scholar] [CrossRef]
- Elbah, M.; Laouici, H.; Benlahmidi, S.; Nouioua, M.; Yallese, M. Comparative assessment of machining environments (dry, wet and MQL) in hard turning of AISI 4140 steel with CC6050 tools. Int. J. Adv. Manuf. Technol. 2019, 105, 2581–2597. [Google Scholar] [CrossRef]
- Li, S.; Chen, T.; Qiu, C.; Wang, D.; Liu, X. Experimental investigation of high-speed hard turning by PCBN tooling with strengthened edge. Int. J. Adv. Manuf. Technol. 2017, 92, 3785–3793. [Google Scholar] [CrossRef]
- Struzikiewicz, G.; Sioma, A. Evaluation of Surface Roughness and Defect Formation after The Machining of Sintered Aluminum Alloy AlSi10Mg. Materials 2020, 13, 1662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molnar, V. Tribology and Topography of Hard Machined Surfaces. Cut. Tools Technol. Syst. 2021, 94, 49–59. [Google Scholar] [CrossRef]
- Vishwanatha, J.S.; Srinivasa Pai, P. Application of Edge Detection Technique for Surface Roughness Estimation of Ti-6Al-4V Turned Surfaces. Manuf. Technol. 2021, 21, 269–277. [Google Scholar] [CrossRef]
- Podany, J.; Stary, V.; Tomicek, J. 3D Surface Roughness Characteristics for Biological Applications. Manuf. Technol. 2021, 21, 836–841. [Google Scholar] [CrossRef]
- Kundrak, J.; Felho, C. 3D roughness parameters of surfaces face milled by special tools. Manuf. Technol. 2016, 16, 532–538. [Google Scholar] [CrossRef]
- Sagbas, A. Analysis and optimization of surface roughness in the ball burnishing process using response surface methodology and desirability function. Adv. Eng. Softw. 2011, 42, 992–998. [Google Scholar] [CrossRef]
- Zhu, L.; Guan, Y.; Wang, Y.; Xie, Z.; Lin, J.; Zhai, J. Influence of process parameters of ultrasonic shot peening on surface roughness and hydrophilicity of pure titanium. Surf. Coat. Technol. 2017, 317, 38–53. [Google Scholar] [CrossRef]
- Grzesik, W.; Zak, K.; Kiszka, P. Comparison of Surface Textures Generated in Hard Turning and Grinding Operations. Procedia CIRP 2014, 13, 84–89. [Google Scholar] [CrossRef] [Green Version]
- Skoczy, A. Selected Properties of the Surface Layer of C45 Steel Parts Subjected to Laser Cutting and Ball Burnishing. Materials 2020, 13, 3429. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Zelasko, W. Prediction of Parameters of Equivalent Sum Rough Surfaces. Materials 2020, 13, 4898. [Google Scholar] [CrossRef] [PubMed]
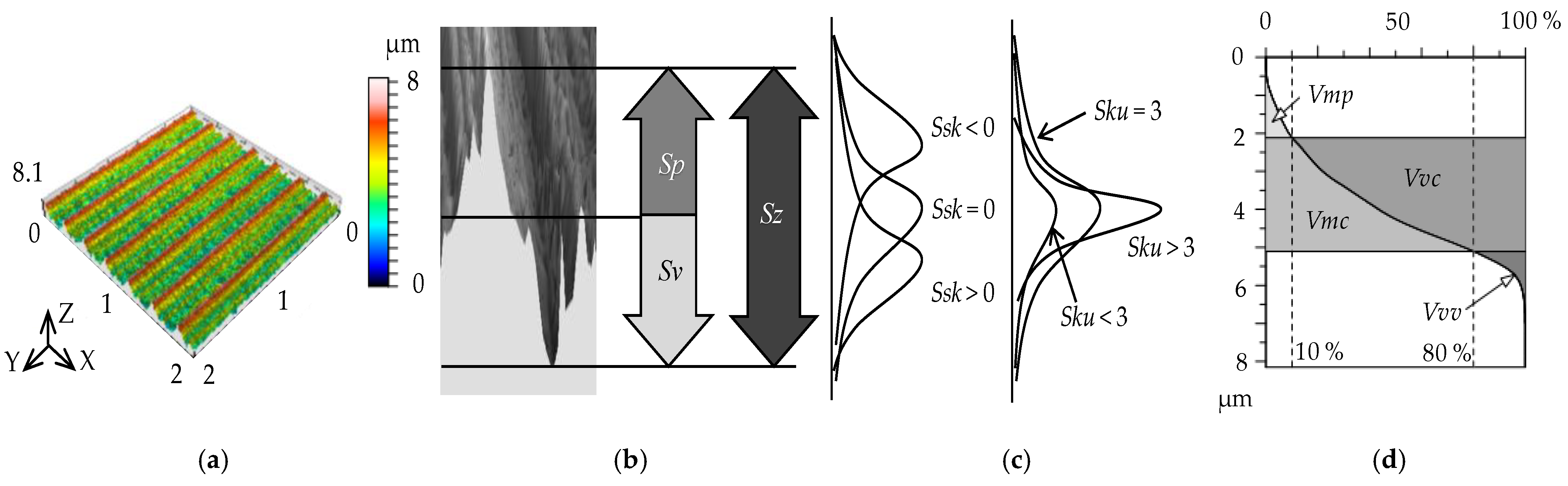
- ISO 25178-2; 2012 Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2012.
- Stout, K.; Blunt, L. Three-Dimensional Surface Topography, 2nd ed.; Penton Press: London, UK, 2000; ISBN 9781857180268. [Google Scholar]
- Hirst, W.; Hollander, A.E. Surface finish and damage in sliding. Proc. Royal Soc. 1974, 337, 379–394. [Google Scholar] [CrossRef]
- Sedlacek, M.; Podgornik, B.; Vizintin, J. Correlation between standard roughness parameters skewness and kurtosis and tribological behaviour of contact surfaces. Tribol. Int. 2012, 48, 102–112. [Google Scholar] [CrossRef]
- Sedlacek, M.; Gregorcic, P.; Podgornik, B. Use of the roughness parameters Ssk and Sku to control friction—A method for designing surface texturing. Tribol. Trans. 2017, 60, 260–266. [Google Scholar] [CrossRef]
- Liang, G.; Schmauder, S.; Lyu, M.; Schneider, Y.; Zhang, C.; Han, Y. An Investigation of the Influence of Initial Roughness on the Friction and Wear Behavior of Ground Surfaces. Materials 2018, 11, 237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naylor, A.; Talwalkar, S.C.; Trail, I.A.; Joyce, T.J. Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters. J. Funct. Biomater. 2016, 7, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Ba, E.C.T.; Dumont, M.R.; Martins, P.S.; Drumond, R.M.; Martins da Cruz, M.P.; Vieira, V.F. Investigation of the effects of skewness Rsk and kurtosis Rku on tribological behavior in a pin-on-disc test of surfaces machined by conventional milling and turning processes. Mater. Res. 2021, 24, e20200435. [Google Scholar] [CrossRef]
- Kovacs, Z.; Viharos, Z.J.; Kodacsy, J. The effects of machining strategies of magnetic assisted roller burnishing on the resulted surface structure. Mater. Sci. Eng. 2018, 448, 012002. [Google Scholar] [CrossRef] [Green Version]
- Aslantas, K.; Danish, M.; Hascelik, A.; Mia, M.; Gupta, M.; Ginta, T.; Ijaz, H. Investigations on Surface Roughness and Tool Wear Characteristics in Micro-Turning of Ti-6Al-4V Alloy. Materials 2020, 13, 2998. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Mendak, M.; Mrozek, K.; Wieczorowski, M. Analysis of Surface Microgeometry Created by Electric Discharge Machining. Materials 2020, 13, 3830. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Hu, L. Study on Scatter of Surface Integrity of Bearing Raceway Grinding. Manuf. Technol. 2021, 21, 781–787. [Google Scholar] [CrossRef]
- Longhai Special Steel. Available online: https://www.steelss.com/Carbon-steel/16mncr5.html (accessed on 17 March 2022).





| Tensile Strength [MPa] | Yield Strength [MPa] | Elongation [%] | HRC Hardness | Thermal Conductivity [N/mK] | Specific Heat [J/kgK] | Melting Temperature [°C] |
|---|---|---|---|---|---|---|
| 1158 | 1034 | 15 | 62–63 | 16 | 500 | 1370–1400 |
| C | Si | Mn | Cr | S | P |
|---|---|---|---|---|---|
| 0.14–0.19 | <0.40 | 1.00–1.30 | 0.80–1.10 | <0.035 | <0.025 |
| Measurement | Workpiece | |||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | |
| 1 | 800 | 760 | 783 | 743 | 771 | 773 | 766 | 778 |
| 2 | 788 | 805 | 723 | 741 | 755 | 789 | 778 | 748 |
| 3 | 776 | 776 | 756 | 766 | 755 | 751 | 766 | 760 |
| 4 | 741 | 776 | 796 | 737 | 789 | 772 | 801 | 726 |
| 5 | 784 | 788 | 780 | 769 | 784 | 754 | 754 | 743 |
| Setup | Depth-of Cut, ap [mm] | Cutting Speed, vc [m/min] | Feed Rate, f [mm/rev] | Setup | Depth-of Cut, ap [mm] | Cutting Speed, vc [m/min] | Feed Rate, f [mm/rev] | Setup | Depth-of Cut, ap [mm] | Cutting Speed, vc [m/min] | Feed Rate, f [mm/rev] | Setup | Depth-of Cut, ap [mm] | Cutting Speed, vc [m/min] | Feed Rate, f [mm/rev] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | 0.05 | 60 | 0.05 | T17 | 0.1 | 60 | 0.05 | T33 | 0.2 | 60 | 0.05 | T49 | 0.3 | 60 | 0.05 |
| T2 | 0.05 | 60 | 0.1 | T18 | 0.1 | 60 | 0.1 | T34 | 0.2 | 60 | 0.1 | T50 | 0.3 | 60 | 0.1 |
| T3 | 0.05 | 60 | 0.15 | T19 | 0.1 | 60 | 0.15 | T35 | 0.2 | 60 | 0.15 | T51 | 0.3 | 60 | 0.15 |
| T4 | 0.05 | 60 | 0.2 | T20 | 0.1 | 60 | 0.2 | T36 | 0.2 | 60 | 0.2 | T52 | 0.3 | 60 | 0.2 |
| T5 | 0.05 | 90 | 0.05 | T21 | 0.1 | 90 | 0.05 | T37 | 0.2 | 90 | 0.05 | T53 | 0.3 | 90 | 0.05 |
| T6 | 0.05 | 90 | 0.1 | T22 | 0.1 | 90 | 0.1 | T38 | 0.2 | 90 | 0.1 | T54 | 0.3 | 90 | 0.1 |
| T7 | 0.05 | 90 | 0.15 | T23 | 0.1 | 90 | 0.15 | T39 | 0.2 | 90 | 0.15 | T55 | 0.3 | 90 | 0.15 |
| T8 | 0.05 | 90 | 0.2 | T24 | 0.1 | 90 | 0.2 | T40 | 0.2 | 90 | 0.2 | T56 | 0.3 | 90 | 0.2 |
| T9 | 0.05 | 120 | 0.05 | T25 | 0.1 | 120 | 0.05 | T41 | 0.2 | 120 | 0.05 | T57 | 0.3 | 120 | 0.05 |
| T10 | 0.05 | 120 | 0.1 | T26 | 0.1 | 120 | 0.1 | T42 | 0.2 | 120 | 0.1 | T58 | 0.3 | 120 | 0.1 |
| T11 | 0.05 | 120 | 0.15 | T27 | 0.1 | 120 | 0.15 | T43 | 0.2 | 120 | 0.15 | T59 | 0.3 | 120 | 0.15 |
| T12 | 0.05 | 120 | 0.2 | T28 | 0.1 | 120 | 0.2 | T44 | 0.2 | 120 | 0.2 | T60 | 0.3 | 120 | 0.2 |
| T13 | 0.05 | 150 | 0.05 | T29 | 0.1 | 150 | 0.05 | T45 | 0.2 | 150 | 0.05 | T61 | 0.3 | 150 | 0.05 |
| T14 | 0.05 | 150 | 0.1 | T30 | 0.1 | 150 | 0.1 | T46 | 0.2 | 150 | 0.1 | T62 | 0.3 | 150 | 0.1 |
| T15 | 0.05 | 150 | 0.15 | T31 | 0.1 | 150 | 0.15 | T47 | 0.2 | 150 | 0.15 | T63 | 0.3 | 150 | 0.15 |
| T16 | 0.05 | 150 | 0.2 | T32 | 0.1 | 150 | 0.2 | T48 | 0.2 | 150 | 0.2 | T64 | 0.3 | 150 | 0.2 |
| Setup | Infeed Velocity vfR [mm/s] | rpm n [1/min] | Setup | Infeed Velocity vfR [mm/s] | rpm n [1/min] | Setup | Infeed Velocity vfR [mm/s] | rpm n [1/min] | Setup | Infeed Velocity vfR [mm/s] | rpm n [1/min] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 31.5 | 0.0069 | G5 | 31.5 | 0.0130 | G9 | 31.5 | 0.0193 | G13 | 31.5 | 0.0302 |
| G2 | 45 | 0.0069 | G6 | 45 | 0.0130 | G10 | 45 | 0.0193 | G14 | 45 | 0.0302 |
| G3 | 63 | 0.0069 | G7 | 63 | 0.0130 | G11 | 63 | 0.0193 | G15 | 63 | 0.0302 |
| G4 | 90 | 0.0069 | G8 | 90 | 0.0130 | G12 | 90 | 0.0193 | G16 | 90 | 0.0302 |
| Analyzed Parameter | Coefficients of Determination of the Influencing Factors | Multifactorial Coefficients of Determination | ||||||
|---|---|---|---|---|---|---|---|---|
| arithmetic mean height | Sa | 0.074 | 0.004 | 0.643 | 0.145 | 0.028 | 0.912 | 0.808 |
| maximum height | Sz | 0.078 | 0.002 | 0.468 | 0.121 | 0.038 | 0.784 | 0.787 |
| peak material volume | Vmp | 0.048 | 0.016 | 0.639 | 0.269 | 0.068 | 0.875 | 0.815 |
| valley void volume | Vvv | 0.022 | 0.018 | 0.292 | 0.120 | 0.121 | 0.741 | 0.574 |
| maximum peak height | Sp | 0.061 | 0.004 | 0.383 | 0.082 | 0.001 | 0.698 | 0.842 |
| maximum valley depth | Sv | 0.104 | 0.001 | 0.519 | 0.073 | 0.196 | 0.826 | 0.457 |
| skewness | Ssk | 0.002 | 0.008 | 0.650 | 0.015 | 0.044 | 0.764 | 0.649 |
| kurtosis | Sku | 0.010 | 0.002 | 0.201 | 0.005 | 0.000 | 0.483 | 0.738 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molnar, V. Tribological Properties and 3D Topographic Parameters of Hard Turned and Ground Surfaces. Materials 2022, 15, 2505. https://doi.org/10.3390/ma15072505
Molnar V. Tribological Properties and 3D Topographic Parameters of Hard Turned and Ground Surfaces. Materials. 2022; 15(7):2505. https://doi.org/10.3390/ma15072505
Chicago/Turabian StyleMolnar, Viktor. 2022. "Tribological Properties and 3D Topographic Parameters of Hard Turned and Ground Surfaces" Materials 15, no. 7: 2505. https://doi.org/10.3390/ma15072505
APA StyleMolnar, V. (2022). Tribological Properties and 3D Topographic Parameters of Hard Turned and Ground Surfaces. Materials, 15(7), 2505. https://doi.org/10.3390/ma15072505





