Analytical Modeling of the Interaction of a Four Implant-Supported Overdenture with Bone Tissue
Abstract
1. Introduction
2. Materials and Methods
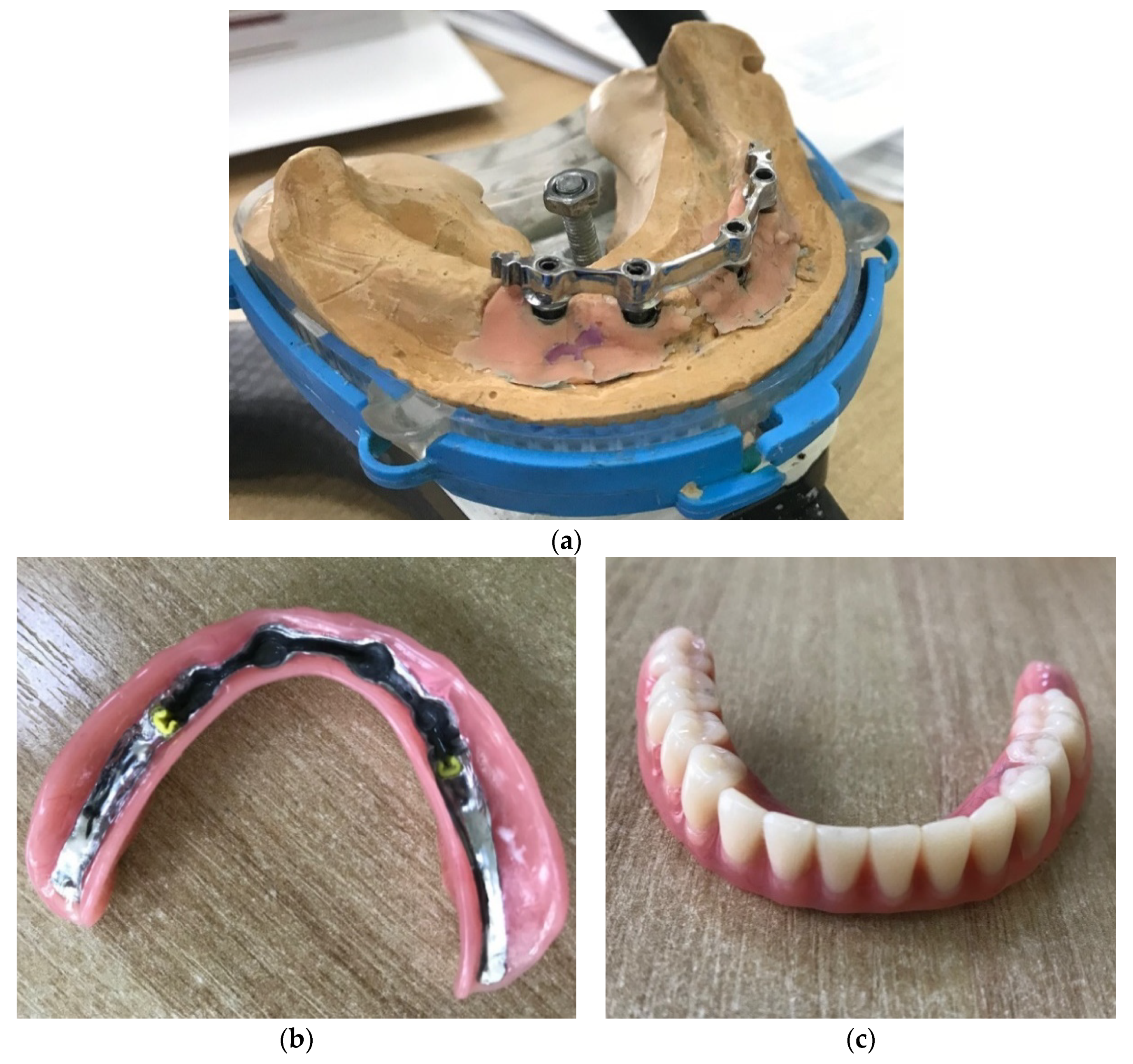
2.1. Formulation of the Problem of the Mechanics of a Four Implant-Supported Overdenture
2.2. Mathematical Model of the Interaction of a Four-Implant Overdenture with Bone Tissue Research Methodology
2.2.1. Basic Assumptions of the Model
- (1)
- The metal structure, including 4 implants, a unifying polygonal bar, and an arched base of the dentition, is a solid and absolutely rigid spatial frame;
- (2)
- (3)
- The mechanical contact between the components is considered perfect.
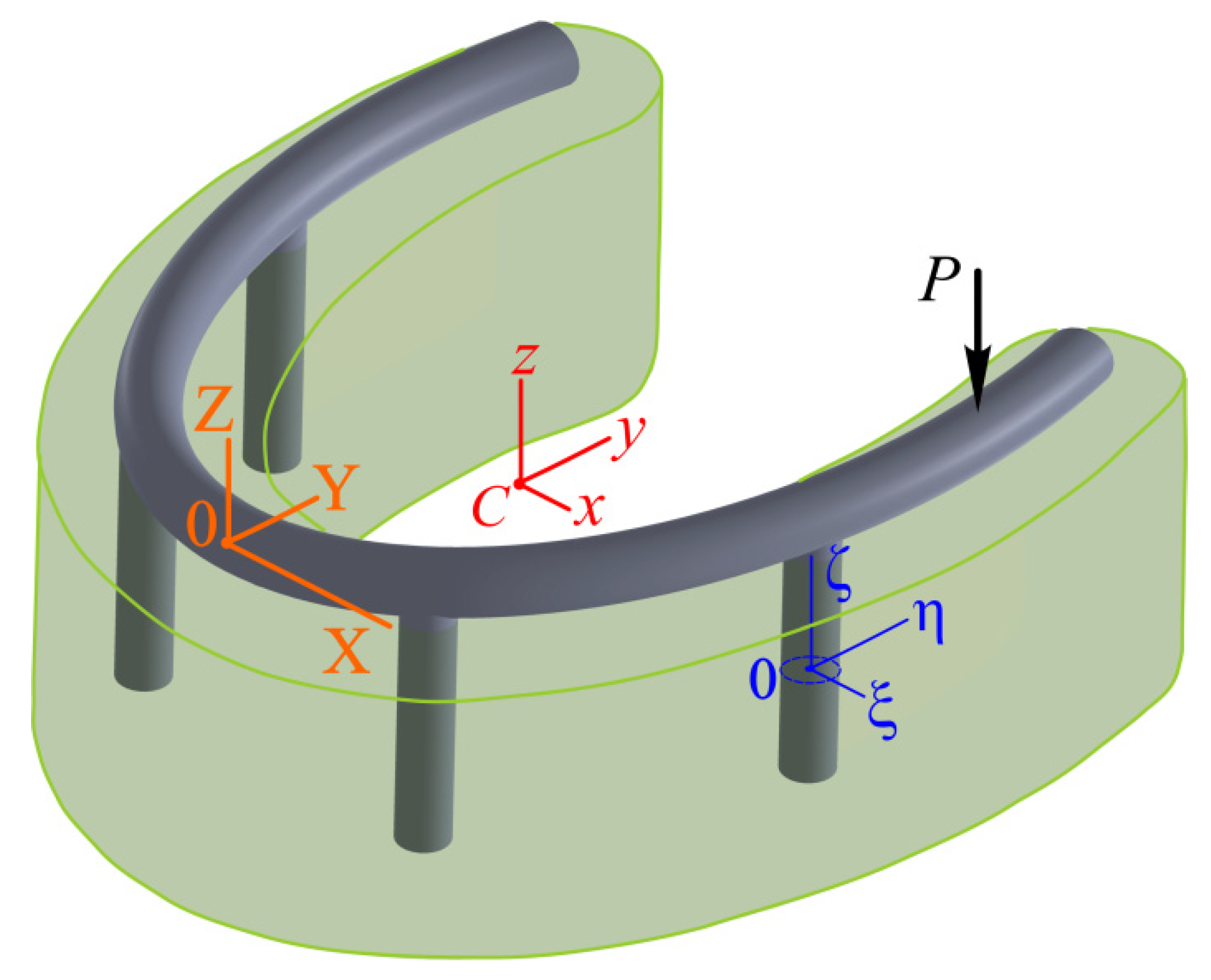
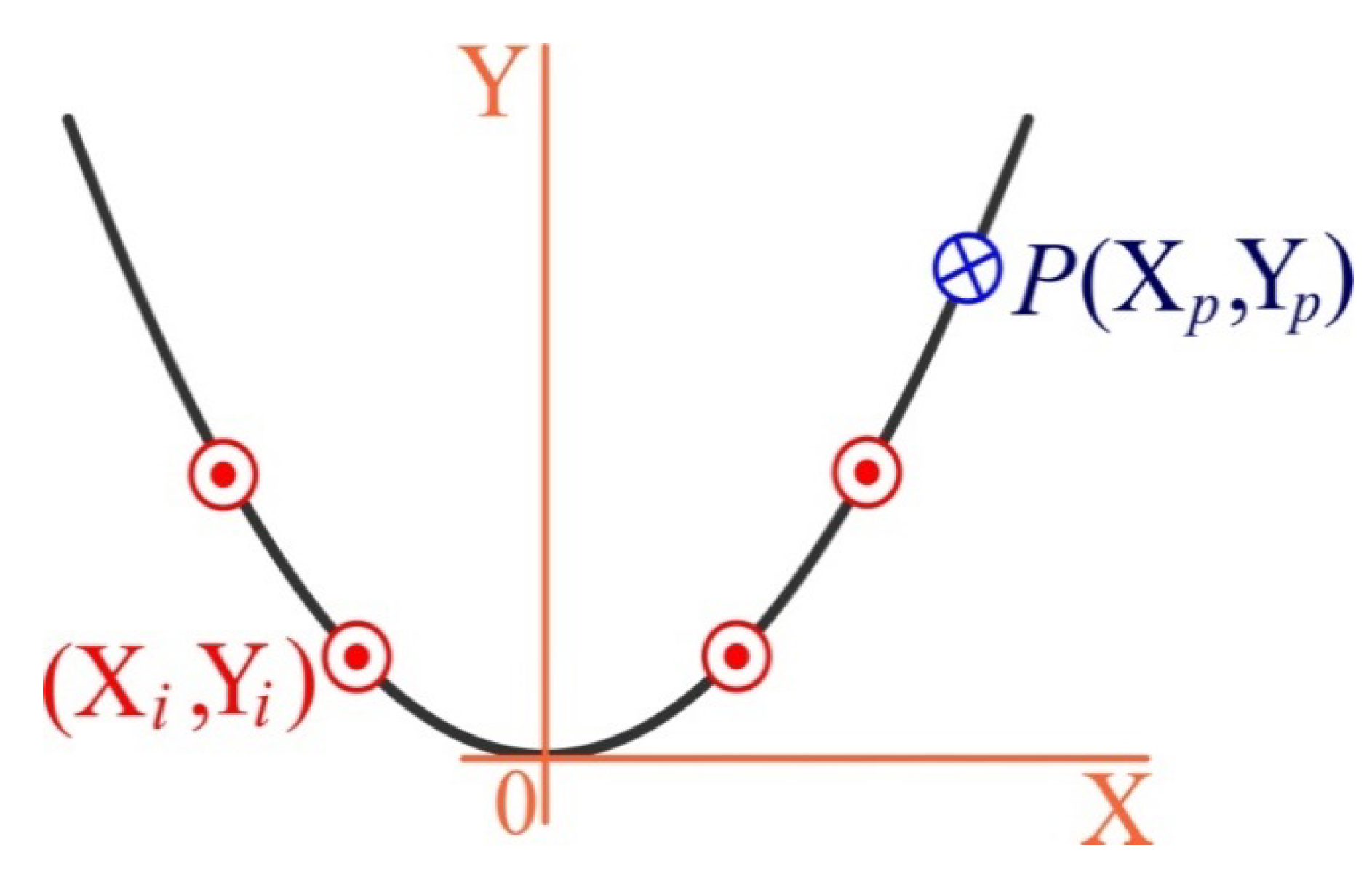
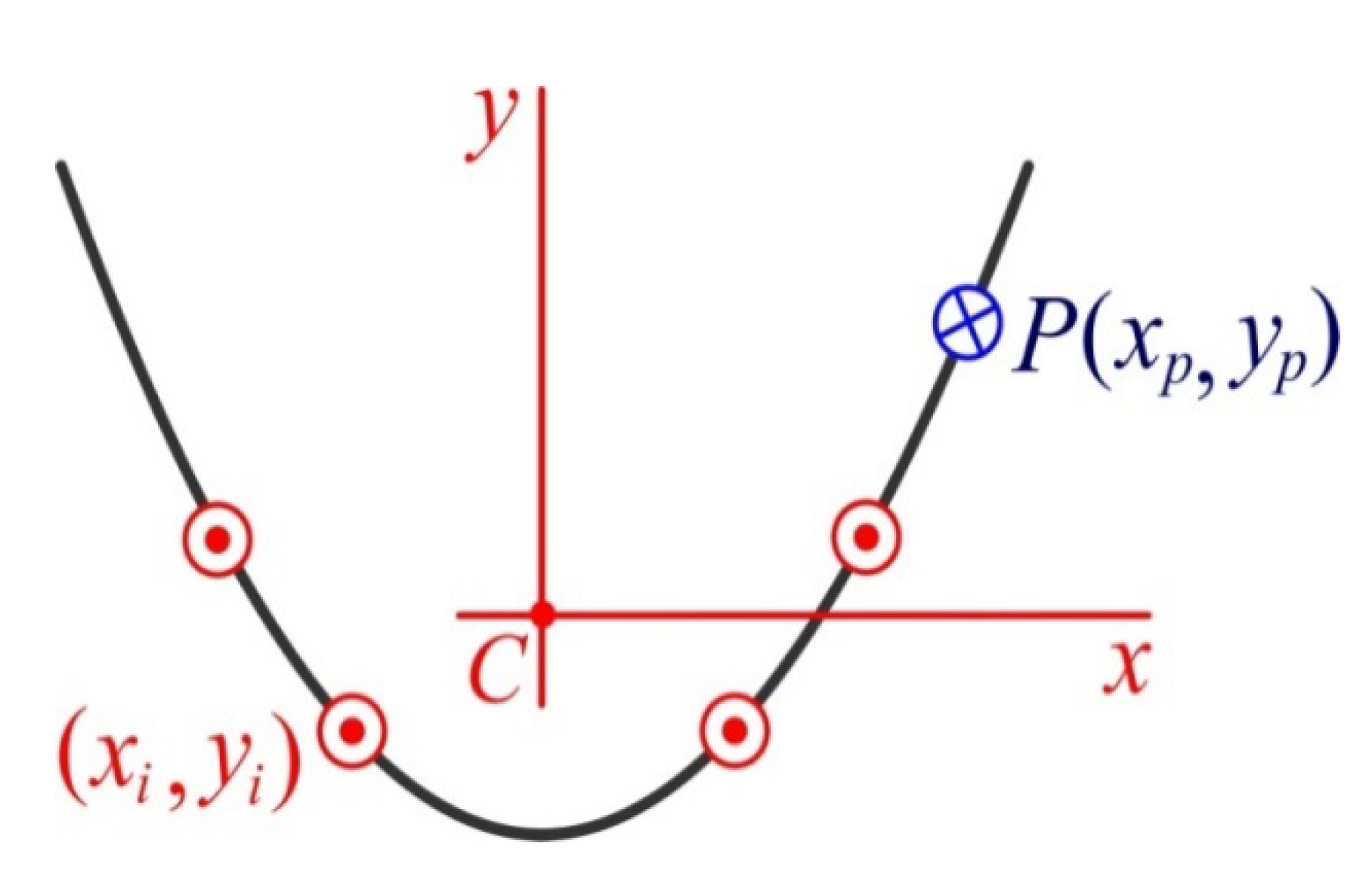
2.2.2. Coordinate Systems and Some Vector Operations
2.2.3. Key Equations of the Model
Kinematics
Statics
Physical Relations
Equation of Statics in Displacement
Stress Calculation Scheme
Strength Conditions
3. Results and Analysis
3.1. Analytical Solution
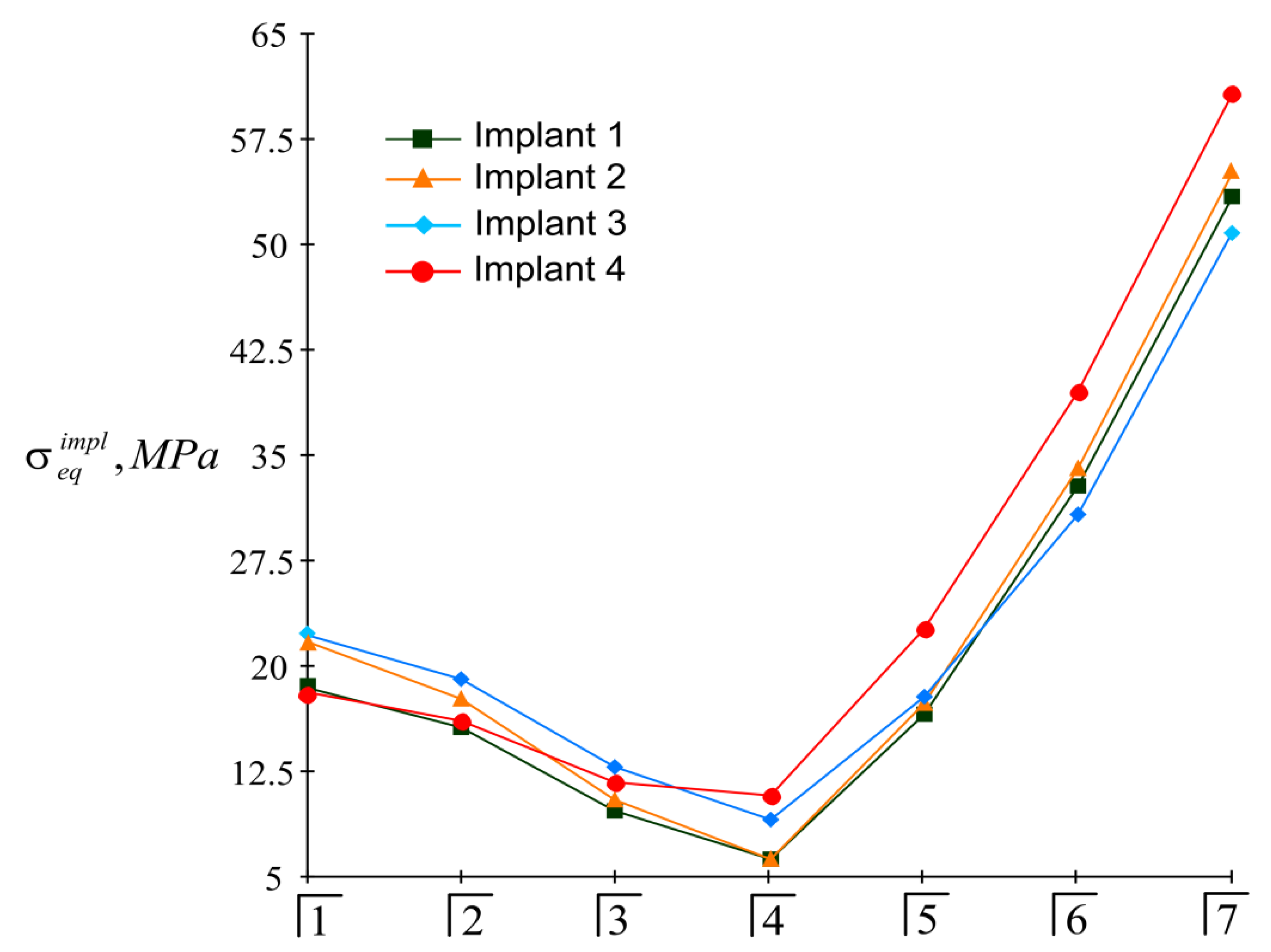
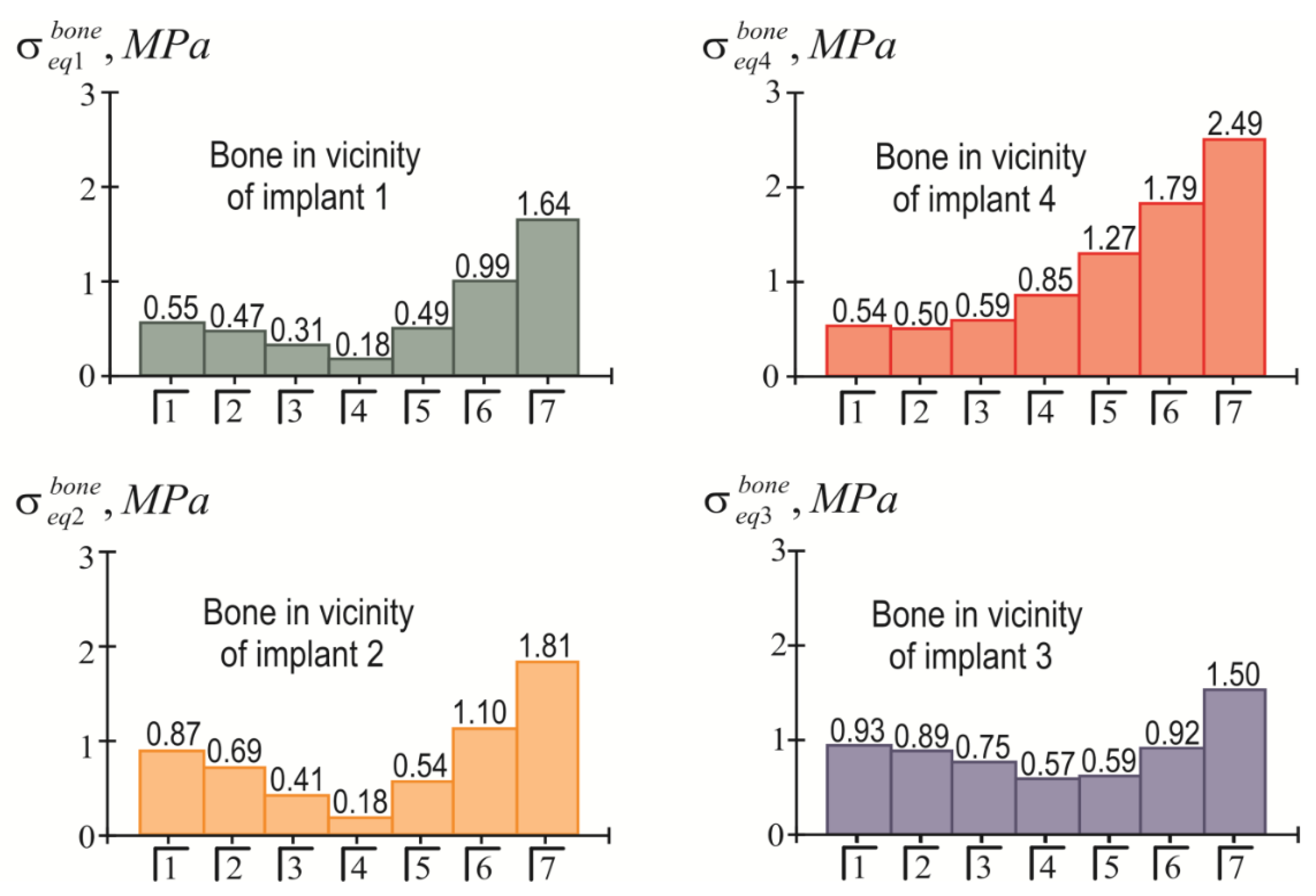
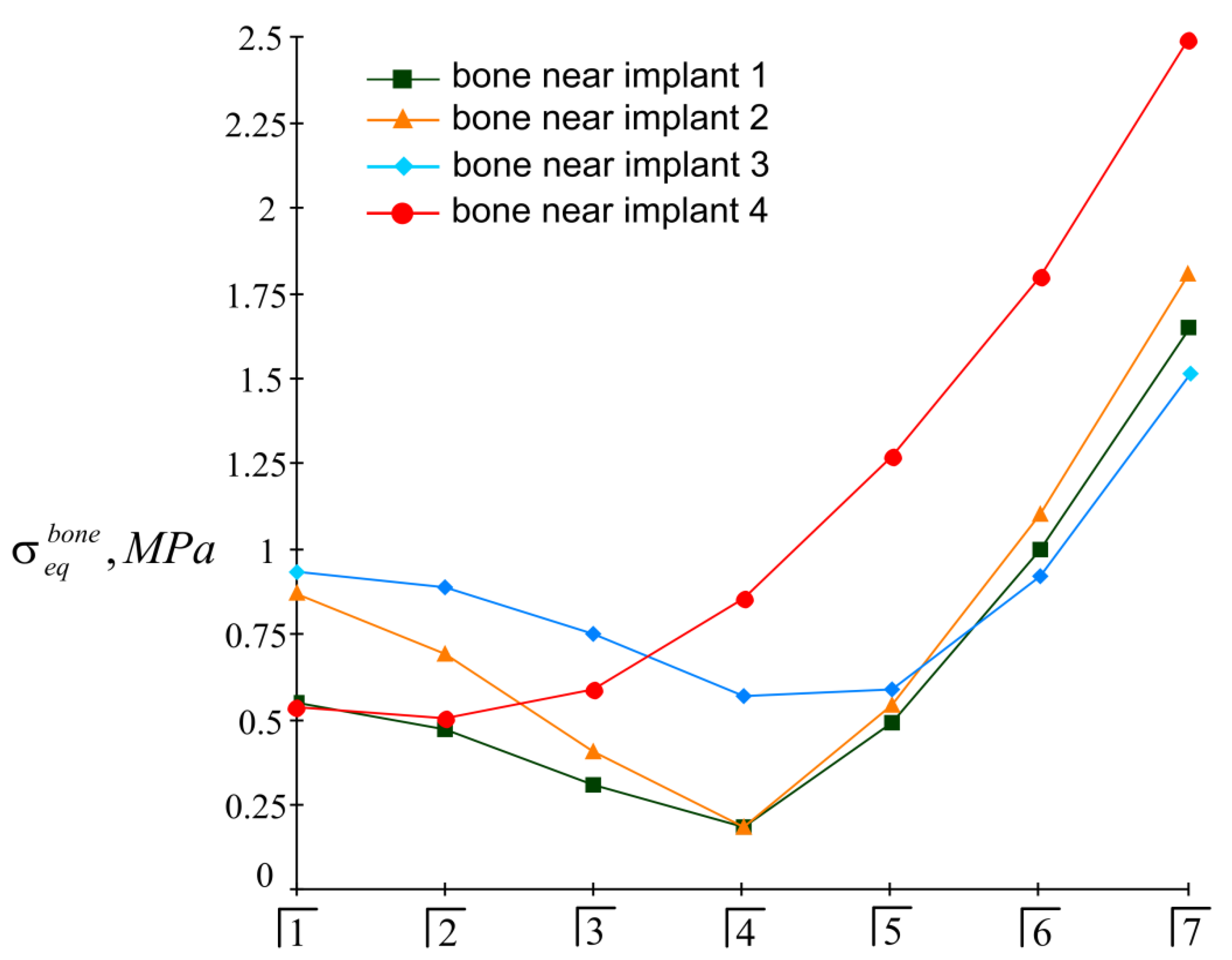
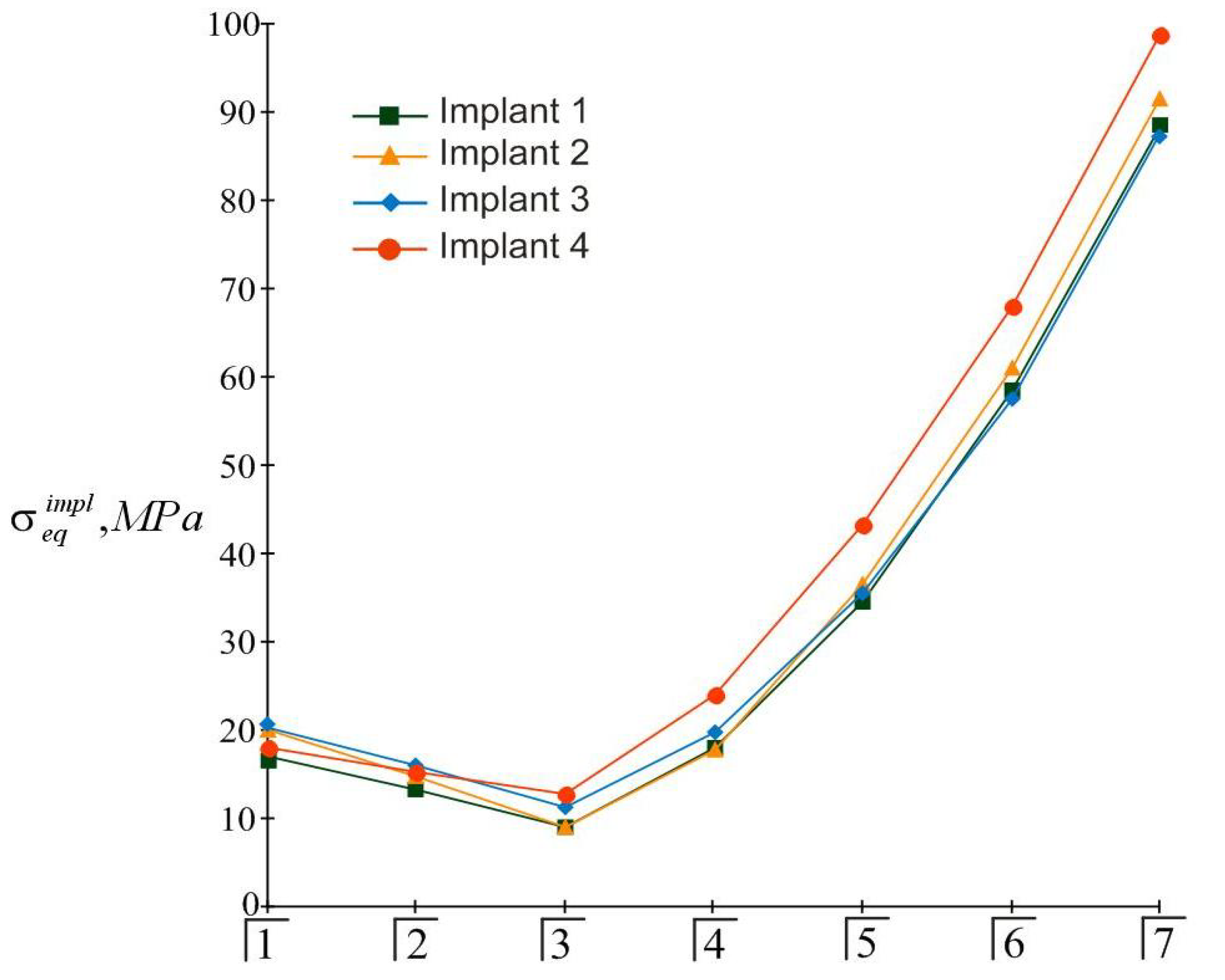
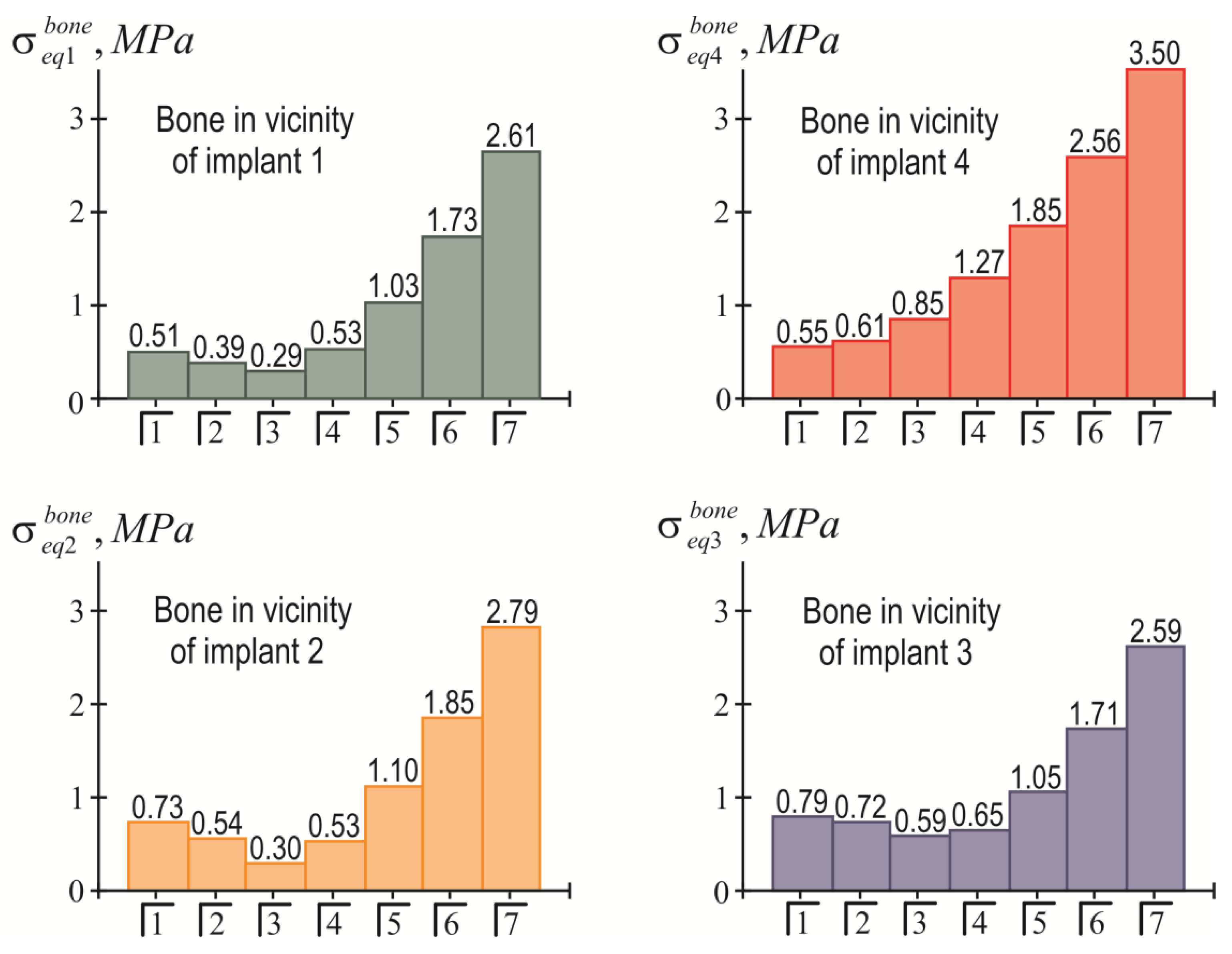
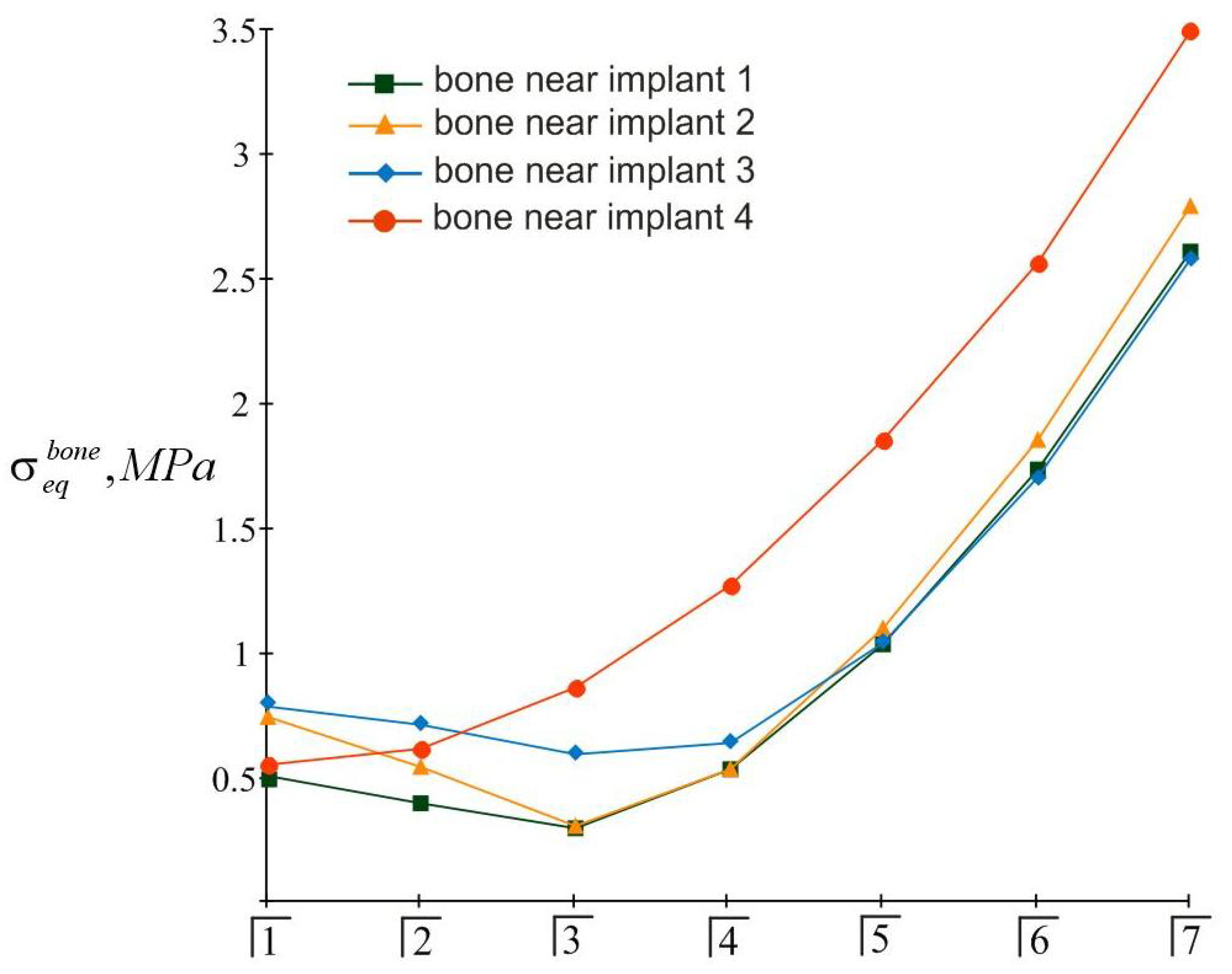
3.2. Examples of Calculation
3.2.1. Example 1
3.2.2. Example 2
4. Discussion
- −
- A computed tomography (CT) analysis of the state of the jaw and dentition;
- −
- The identification of the mechanical properties of bone tissue and teeth according to the established CT density distribution;
- −
- The development of a solution to the problem of jaw interaction with an overdenture variant based on finite element analysis using ANSYS, SolidWorks, or ABACUS software systems;
- −
- Overdenture design based on the results of the numerical analysis.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Cai, M.; Yang, J.; Aldhohrah, T.; Wang, Y. Immediate versus early or conventional loading dental implants with fixed prostheses: A systematic review and meta-analysis of randomized controlled clinical trials. J. Prosthet. Dent. 2019, 122, 516–536. [Google Scholar] [CrossRef] [PubMed]
- Winter, W.; Klein, D.; Karl, M. Micromotion of Dental Implants: Basic Mechanical Considerations. J. Med. Eng. 2013, 2013, 265412. [Google Scholar] [CrossRef] [PubMed]
- Lemos, C.; Verri, F.; Noritomi, P.; Kemmoku, D.; Batista, V.; Cruz, R.; Gomes, J.; Pellizzer, E. Effect of bone quality and bone loss level around internal and external connection implants: A finite element analysis study. J. Prosthet. Dent. 2021, 125, 137.e1–137.e10. [Google Scholar] [CrossRef] [PubMed]
- AlSarhan, M.A.; Alaqeely, R.S.; AlJasser, R.; Otaibi, D.H.; AlOraini, S.; Alshiddi, I.F. Evaluation of complacency about dental implants with shared decision making and satisfaction scores: A cross-sectional study. Saudi Dent. J. 2021, 33, 929–936. [Google Scholar] [CrossRef]
- Li, J.; Jansen, J.; Walboomers, X.; Beucken, J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef]
- Agbaje, J.O.; Casteele, E.V.; Salem, A.S.; Anumendem, D.; Shaheen, E.; Sun, Y.; Politis, C. Assessment of occlusion with the T-Scan system in patients undergoing orthognathic surgery. Sci. Rep. 2017, 7, 5356. [Google Scholar] [CrossRef]
- Bulbuk, O.; Velychkovych, A.; Mazurenko, V.; Ropyak, L.; Pryhorovska, T. Analytical estimation of tooth strength, restored by direct or indirect restorations. Eng. Solid Mech. 2019, 7, 193–204. [Google Scholar] [CrossRef]
- Gowd, M.S.; Shankar, T.; Ranjan, R.; Singh, A. Prosthetic Consideration in Implant-supported Prosthesis: A Review of Literature. J. Int. Soc. Prev. Community Dent. 2017, 7, S1–S7. [Google Scholar] [CrossRef]
- Lakatos, E.; Magyar, L.; Bojtar, I. Material Properties of the Mandibular Trabecular Bone. J. Med. Eng. 2014, 2014, 470539. [Google Scholar] [CrossRef]
- Cicciu, M.; Cervino, G.; Milone, D.; Risitano, G. FEM Investigation of the Stress Distribution over Mandibular Bone Due to Screwed Overdenture Positioned on Dental Implants. Materials 2018, 11, 1512. [Google Scholar] [CrossRef]
- Gherde, C.; Dhatrak, P.; Nimbalkar, S.; Joshi, S. A comprehensive review of factors affecting fatigue life of dental implants. Mater. Today Proc. 2021, 43, 1117–1123. [Google Scholar] [CrossRef]
- Horita, S.; Sugiura, T.; Yamamoto, K.; Murakami, K.; Imai, Y.; Kirita, T. Biomechanical analysis of immediately loaded implants according to the “All-on-Four” concept. J. Prosthodont. Res. 2017, 61, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Cervino, G.; Romeo, U.; Lauritano, F.; Bramanti, E.; Fiorillo, L.; D’Amico, C.; Milone, D.; Laino, L.; Campolongo, F.; Rapisarda, S.; et al. Fem and Von Mises Analysis of OSSTEM® Dental Implant Structural Components: Evaluation of Different Direction Dynamic Loads. Open Dent. J. 2018, 12, 219. [Google Scholar] [CrossRef] [PubMed]
- Lauritano, F.; Runci, M.; Cervino, G.; Fiorillo, L.; Bramanti, E.; Cicciu, M. Three-dimensional evaluation of different prosthesis retention systems using finite element analysis and the Von Mises stress test. Minerva Stomatol. 2016, 65, 353–367. [Google Scholar] [PubMed]
- Chiapasco, M. Early and immediate restoration and loading of implants in completely edentulous patients. Int. J. Oral. Maxillofac. Implant. 2004, 19, 76–91. [Google Scholar]
- Goo, C.L.; Tan, K.B. Fabricating CAD/CAM Implant-Retained Mandibular Bar Overdentures: A Clinical and Technical Overview. Case Rep. Dent. 2017, 2017, 9373818. [Google Scholar] [CrossRef] [PubMed]
- Filipov, I.; Chirila, L.; Cristache, C.M. Rehabilitation of extremely atrophic edentulous mandible in elderly patients with associated comorbidities: A case report and proof of concept. Head Face Med. 2021, 17, 22. [Google Scholar] [CrossRef]
- Pelekhan, B.L.; Rozhko, M.M.; Pelekhan, L.I. The prosthodontic treatment of the mandible edentulousness. Clinical case. Art Med. 2021, 5, 140–146. [Google Scholar] [CrossRef]
- Pelekhan, B.; Rozhko, M.; Pelekhan, L.; Rozhko, O. Compliance with Postoperative Recommendations by Patients with Different Psychological Types after Early Implant Loading Treatment. Galician Med. J. 2021, 28, E202129. [Google Scholar] [CrossRef]
- Shah, F.A.; Thomsen, P.; Palmquist, A. Osseointegration and current interpretations of the bone-implant interface. Acta Biomater. 2019, 84, 1–15. [Google Scholar] [CrossRef]
- Didier, P.; Piotrowski, B.; Le Coz, G.; Joseph, D.; Bravetti, P.; Laheurte, P. Finite Element Analysis of the Stress Field in Peri-Implant Bone: A Parametric Study of Influencing Parameters and Their Interactions for Multi-Objective Optimization. Appl. Sci. 2020, 10, 5973. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar] [CrossRef]
- Barber, J.R.; Ciavarella, M. Contact mechanics. Int. J. Solids Struct. 2000, 37, 29–43. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Shatskyi, I.; Popadyuk, I.; Velychkovych, A. Modelling of energy dissipation in shell dampers. In Proceedings of the 23rd International Conference Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; Brno University of Technology Institute of Solid Mechanics, Mechatronics and Biomechanics: Svratka, Czech Republic, 2017; pp. 870–873. [Google Scholar]
- Shatskyi, I.; Popadyuk, I.; Velychkovych, A. Hysteretic Properties of Shell Dampers. In Dynamical Systems in Applications, Proceedings of the DSTA 2017, Lodz, Poland, 11–14 December 2017; Awrejcewicz, J., Ed.; Springer: Cham, Switzerland, 2018; pp. 343–350. [Google Scholar] [CrossRef]
- Machado, M.R.; Dutkiewicz, M.; Matt, C.; Castello, D.A. Spectral model and experimental validation of hysteretic and aerodynamic damping in dynamic analysis of overhead transmission conductor. Mech. Syst. Signal Process. 2020, 136, 106483. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A. Increase of compliance of shock absorbers with cut shells. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012072. [Google Scholar] [CrossRef]
- Chuzhak, A.; Sulyma, V.; Ropyak, L.; Velychkovych, A.; Vytvytskyi, V. Mathematical Modelling of Destabilization Stress Factors of Stable-Elastic Fixation of Distal Trans- and Suprasyndesmotic Fibular Fractures. J. Healthc. Eng. 2021, 2021, 6607364. [Google Scholar] [CrossRef] [PubMed]
- Velychkovych, A.; Ropyak, L.; Dubei, O. Strength Analysis of a Two-Layer PETF-Concrete Column with Allowance for Contact Interaction between Layers. Adv. Mater. Sci. Eng. 2021, 2021, 4517657. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Shopa, V.M.; Velychkovych, A.S. Development of Full-Strength Elastic Element Section with Open Shell. Strength Mater. 2021, 53, 277–282. [Google Scholar] [CrossRef]
- Bedzir, A.A.; Shatskii, I.P.; Shopa, V.M. Nonideal contact in a composite shell structure with a deformable filler. Int. Appl. Mech. 1995, 31, 351–354. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Dalyak, T.; Shatskyi, I.; Venhrynyuk, T.; Velychkovych, A. Stress Analysis in Damaged Pipeline with Composite Coating. Appl. Sci. 2021, 11, 10676. [Google Scholar] [CrossRef]
- Velychkovych, A.; Bedzir, O.; Shopa, V. Laboratory experimental study of contact interaction between cut shells and resilient bodies. Eng. Solid Mech. 2021, 9, 425–438. [Google Scholar] [CrossRef]
- Golebiowska, I.; Dutkiewicz, M. Application of Friction Pendulum Bearings in Multistory Buildings. In Acoustics and Vibration of Mechanical Structures—AVMS 2019; Herisanu, N., Marinca, V., Eds.; Springer: Cham, Switzerland, 2021; Volume 251, pp. 453–461. [Google Scholar] [CrossRef]
- Berezhnitskii, L.T.; Panasyuk, V.V.; Stashchuk, N.G. Interaction between Rigid Linear Inclusions and Cracks in a Deformable Body; Naukova Dumka: Kyiv, Ukraine, 1983. [Google Scholar]
- Panasyuk, V.V.; Stadnik, M.M.; Silovanyuk, V.P. Stress Concentrations in Three-Dimensional Bodies with Thin Inclusions; Naukova Dumka: Kyiv, Ukraine, 1986. [Google Scholar]
- Grilitsky, D.V.; Opanasovich, V.K.; Shatsky, I.P. Shallow shell with a rigid linear inclusion along the curvature line. Dopovidi Akad. Nauk. Ukr. Rsr Seriya A Fiz. Mat. Ta Tech. Nauk. 1983, 8, 28–30. [Google Scholar]
- Mura, T. Inclusion Problems. Appl. Mech. Rev. 1988, 41, 15–20. [Google Scholar] [CrossRef]
- Kolesov, V.S.; Vlasov, N.M.; Tisovskii, L.O.; Shatskii, I.P. The stress-deformation state of an elastic half-space with a spheroidal thermal inclusion. Int. Appl. Mech. 1992, 28, 426–434. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Kundrat, A.M. Longitudinal shear of a body with mutually immobile rigid collinear inclusions. Mater. Sci. 2004, 40, 376–382. [Google Scholar] [CrossRef]
- Berezhnitskii, L.T.; Kundrat, N.M. Plastic bands at the tip of a linear rigid inclusion. Strength Mater. 1982, 14, 1502–1505. [Google Scholar] [CrossRef]
- Kundrat, N.M. On the initial development of the slip band near an inclusion in the interface. Int. Appl. Mech. 2002, 38, 578–584. [Google Scholar] [CrossRef]
- Kryzhanivs’kyi, E.I.; Rudko, V.P.; Shats’kyi, I.P. Estimation of admissible loads upon a pipeline in the zone of sliding ground. Mater. Sci. 2004, 40, 547–551. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Struk, A.B. Stressed state of pipeline in zones of soil local fracture. Strength Mater. 2009, 41, 548–553. [Google Scholar] [CrossRef]
- Velychkovych, A.S.; Andrusyak, A.V.; Pryhorovska, T.O.; Ropyak, L.Y. Analytical model of oil pipeline overground transitions, laid in mountain areas. Oil Gas Sci. Technol. 2019, 74. [Google Scholar] [CrossRef]
- Aydin, E.; Dutkiewicz, M.; Ozturk, B.; Sonmez, M. Optimization of elastic spring supports for cantilever beams. Struct. Multidiscip. Optim. 2020, 62, 55–81. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Contact interaction of the crack edges in the case of bending of a plate with elastic support. Mater. Sci. 2003, 39, 371–376. [Google Scholar] [CrossRef]
- Martynyak, R.M.; Prokopyshyn, I.A.; Prokopyshyn, I.I. Contact of elastic bodies with nonlinear Winkler surface layers. J. Math. Sci. 2015, 205, 535–553. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Makoviichuk, M.V.; Shatskyi, I.P.; Pritula, I.M.; Gryn, L.O.; Belyakovskyi, V.O. Stressed state of laminated interference-absorption filter under local loading. Funct. Mater. 2020, 27, 638–642. [Google Scholar] [CrossRef]
- Ozhogan, Z.R.; Shatskyi, I.P. Residual deviations of abutment teeth during fixation of bridges. Bull. Dent. 2001, 4, 64–67. [Google Scholar]
- Vytvytskyi, I.I.; Seniushkovych, M.V.; Shatskyi, I.P. Calculation of distance between elastic-rigid centralizers of casing. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2017, 5, 28–35. [Google Scholar]
- Shatskyi, I.; Velychkovych, A.; Vytvytskyi, I.; Seniushkovych, M. Analytical models of contact interaction of casing centralizers with well wall. Eng. Solid Mech. 2019, 7, 355–366. [Google Scholar] [CrossRef]
- Shatskyi, I.; Vytvytskyi, I.; Senyushkovych, M.; Velychkovych, A. Modelling and improvement of the design of hinged centralizer for casing. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 12073. [Google Scholar] [CrossRef]
- Balalayeva, E.; Kukhar, V.; Artiukh, V.; Filatov, V.V.; Simonova, O. Computer Aided Simulation of Behavior of Extrusion Press Ram Jointly with Rotary Elastic Compensator. Adv. Intell. Syst. Comput. 2019, 983, 475–488. [Google Scholar] [CrossRef]
- Shatskii, I.P. Contact of the edges of the slit in the plate in combined tension and bending. Mater. Sci. 1989, 25, 160–165. [Google Scholar] [CrossRef]
- Shatsky, I.P. A cracks closure in combined tension and bending of plates. In Fracture from Defects; Brown, M.W., Ed.; EMAS Publishing: Sheffield, UK, 1998; pp. 733–738. [Google Scholar]
- Shats’kyi, I.P.; Perepichka, V.V. Limiting state of a semi-infinite plate with edge crack in bending with tension. Mater. Sci. 2004, 40, 240–246. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Contact interaction of crack lips in shallow shells in bending with tension. Mater. Sci. 2005, 41, 486–494. [Google Scholar] [CrossRef]
- Dalyak, T. Investigation of the interaction of two parallel shifted cracks in plate bending adjusted for their closure. Theor. Appl. Mech. 2019, 46, 147–155. [Google Scholar] [CrossRef]
- Shatsky, I.P. Bending of the plate weakened by the crack with contacting edges. Dopovidi Akad. Nauk. Ukr. RSR. Seriya A–Fiz. -Mat. Ta Tech. Nauk. 1988, 7, 49–51. [Google Scholar] [CrossRef]
- Young, M.J.; Sun, C.T. Influence of crack closure on the stress intensity factor in bending plates–A classical plate solution. Int. J. Fract. 1992, 55, 81–93. [Google Scholar] [CrossRef]
- Gao, X.; Fraulob, M.; Haiat, G. Biomechanical behaviours of the bone-implant interface: A review. J. R. Soc. Interface 2019, 16, 20190259. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, D. Bite force and dental implant treatment: A short review. Med. Devices 2017, 10, 141–148. [Google Scholar] [CrossRef]
- Matsuzaki, T.; Ayukawa, Y.; Matsushita, Y.; Sakai, N. Effect of post-osseointegration loading magnitude on the dynamics of peri-implant bone: A finite element analysis and in vivo study. J. Prosthodont. Res. 2019, 63, 453–459. [Google Scholar] [CrossRef]
- Aghalovyan, L. Asymptotic Theory of Anisotropic Plates and Shells; National Academy of Sciences: Yerevan, Armenia, 2015. [Google Scholar] [CrossRef]
- Beer, F.; Johnston, E.; DeWolf, J.; Mazurek, D. Mechanics of Materials; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Rashia Begum, S.; Saravana Kumar, M.; Vasumathi, M.; Umar Farooq, M.; Pruncu, C.I. Revealing the compressive and flow properties of novel bone scaffold structure manufactured by selective laser sintering technique. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 09544119211070412. [Google Scholar] [CrossRef]
- Ye, H.; Wang, Z.; Sun, Y.; Zhou, Y. Fully digital workflow for the design and manufacture of prostheses for maxillectomy defects. J. Prosthet. Dent. 2021, 126, 257–261. [Google Scholar] [CrossRef]
- Kaasalainen, T.; Ekholm, M.; Siiskonen, T.; Kortesniemi, M. Dental cone beam CT: An updated review. Phys. Med. 2021, 88, 193–217. [Google Scholar] [CrossRef]
- Kivovics, M.; Penzes, D.; Nemeth, O.; Mijiritsky, E. The Influence of Surgical Experience and Bone Density on the Accuracy of Static Computer-Assisted Implant Surgery in Edentulous Jaws Using a Mucosa-Supported Surgical Template with a Half-Guided Implant Placement Protocol—A Randomized Clinical Study. Materials 2020, 13, 5759. [Google Scholar] [CrossRef] [PubMed]
- Bassi-Junior, L.; Silva, R.; Santos, V.; Lourenço, A.R.; Trevizoli, P.V.; Gaêta-Araujo, H.; Queiroz, P.M.; Gottardo, V.D. Mechanical analysis of prosthetic bars and dental implants in 3 and 4 implant-supported overdenture protocols using finite element analysis. J. Oral Biol. Craniofac. Res. 2021, 11, 438–441. [Google Scholar] [CrossRef] [PubMed]
- Jafariandehkordi, A.; Zahra Jafariandehkordi, Z. A finite element optimization of the design variables of a dental implant screw based on the Mechanostat Theory. Comput. Methods Programs Biomed. Update 2021, 1, 100033. [Google Scholar] [CrossRef]
- Franchina, A.; Stefanelli, L.V.; Maltese, F.; Mandelaris, G.A.; Vantaggiato, A.; Pagliarulo, M.; Pranno, N.; Brauner, E.; Angelis, F.D.; Carlo, S.D. Validation of an Intra-Oral Scan Method Versus Cone Beam Computed Tomography Superimposition to Assess the Accuracy between Planned and Achieved Dental Implants: A Randomized In Vitro Study. Int. J. Environ. Res. Public Health 2020, 17, 9358. [Google Scholar] [CrossRef]
- Brunski, J.; Lemons, J. Chapter 4-Biomedical-Engineering Analyses of Mini Dental Implants. Mini Dent. Implant. 2013, 35–56. [Google Scholar] [CrossRef]
- Bicudo, P.; Reis, J.; Deus, A.; Reis, L.; Vaz, M. Mechanical behaviour of dental implants. Procedia Struct. Integr. 2016, 1, 26–33. [Google Scholar] [CrossRef][Green Version]
- Argatov, I.; Iantchenko, A. A simple mathematical model for the resonance frequency analysis of dental implant stability: Implant clamping quotient. Mech. Res. Commun. 2019, 95, 67–70. [Google Scholar] [CrossRef]
- Zirakashvili, N. Study of the stress–strain state of spongy bone around an implant under occlusal load. Math. Mech. Solids 2020, 25, 1172–1181. [Google Scholar] [CrossRef]
- Baixuan, Y.; Ainara, I.; Peter, H.; Heidi-Lynn, P. Analytical Model for Dental Implant Insertion Torque. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Hussein, M.O. Stress-strain distribution at bone-implant interface of two splinted overdenture systems using 3D finite element analysis. J. Adv. Prosthodont. 2013, 5, 333–340. [Google Scholar] [CrossRef][Green Version]
- El-Anwar, M.; Ghali, R.; Aboelnagga, M. 3D Finite Element Study on: Bar Splinted Implants Supporting Partial Denture in the Reconstructed Mandible. Open Access Maced. J. Med. Sci. 2016, 4, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Reddy, M.S.; Sundram, R.; Eid Abdemagyd, H.A. Application of Finite Element Model in Implant Dentistry: A Systematic Review. J. Pharm. Bioallied Sci. 2019, 11, S85–S91. [Google Scholar] [CrossRef] [PubMed]
- Kayabasi, O. Design methodology for dental implant using approximate solution techniques. J. Stomatol. Oral Maxillofac. Surg. 2020, 121, 684–695. [Google Scholar] [CrossRef] [PubMed]
- Alemayehu, D.B.; Jeng, Y.R. Three-Dimensional Finite Element Investigation into Effects of Implant Thread Design and Loading Rate on Stress Distribution in Dental Implants and Anisotropic Bone. Materials 2021, 14, 6974. [Google Scholar] [CrossRef] [PubMed]
- Johns, R.B. Experimental Studies on Dental Implants. Proc. R. Soc. Med. 1976, 69, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Sadowsky, S.J.; Caputo, A.A. Stress transfer of four mandibular implant overdenture cantilever designs. J. Prosthet. Dent. 2004, 92, 328–336. [Google Scholar] [CrossRef]
- Yasuyuki, M.; Yasuyuki, M.; Mitsugu, T.; Kiyoshi, K. Experimental Study on Displacement and Strain Distributions of Bone Model with Dental Implant. Appl. Mech. Mater. 2011, 83, 73–77. [Google Scholar] [CrossRef]
- Ratnakar, G.; Shailesh, Y. Computational & Experimental Studies in Threaded Dental Implant Research: A Review. E-J. Dent. 2013, 3, 457–465. [Google Scholar]
- Gosavi, S.; Dhatrak, P.N.; Narkar, K. Experimental stress analysis and fea of dentalimplants. Int. J. Res. Eng. Technol. 2016, 5, 328–331. [Google Scholar]
- Wu, A.Y.-J.; Hsu, J.-T.; Fuh, L.-J.; Huang, H.-L. Biomechanical effect of implant design on four implants supporting mandibular full-arch fixed dentures: In vitro test and finite element analysis. J. Formos. Med. Assoc. 2020, 119, 1514–1523. [Google Scholar] [CrossRef]
- Mahantshetty, M.; Thumati, P.; Ayinala, M. The analysis of the stress distribution around angulated and parallelly placed implants based on “all on 4 concept” and four implants placed parallel within the interforaminal distance in an edentulous mandible–An in vitro three-dimensional finite element analysis. J. Dent. Implant. 2021, 11, 44–52. [Google Scholar] [CrossRef]

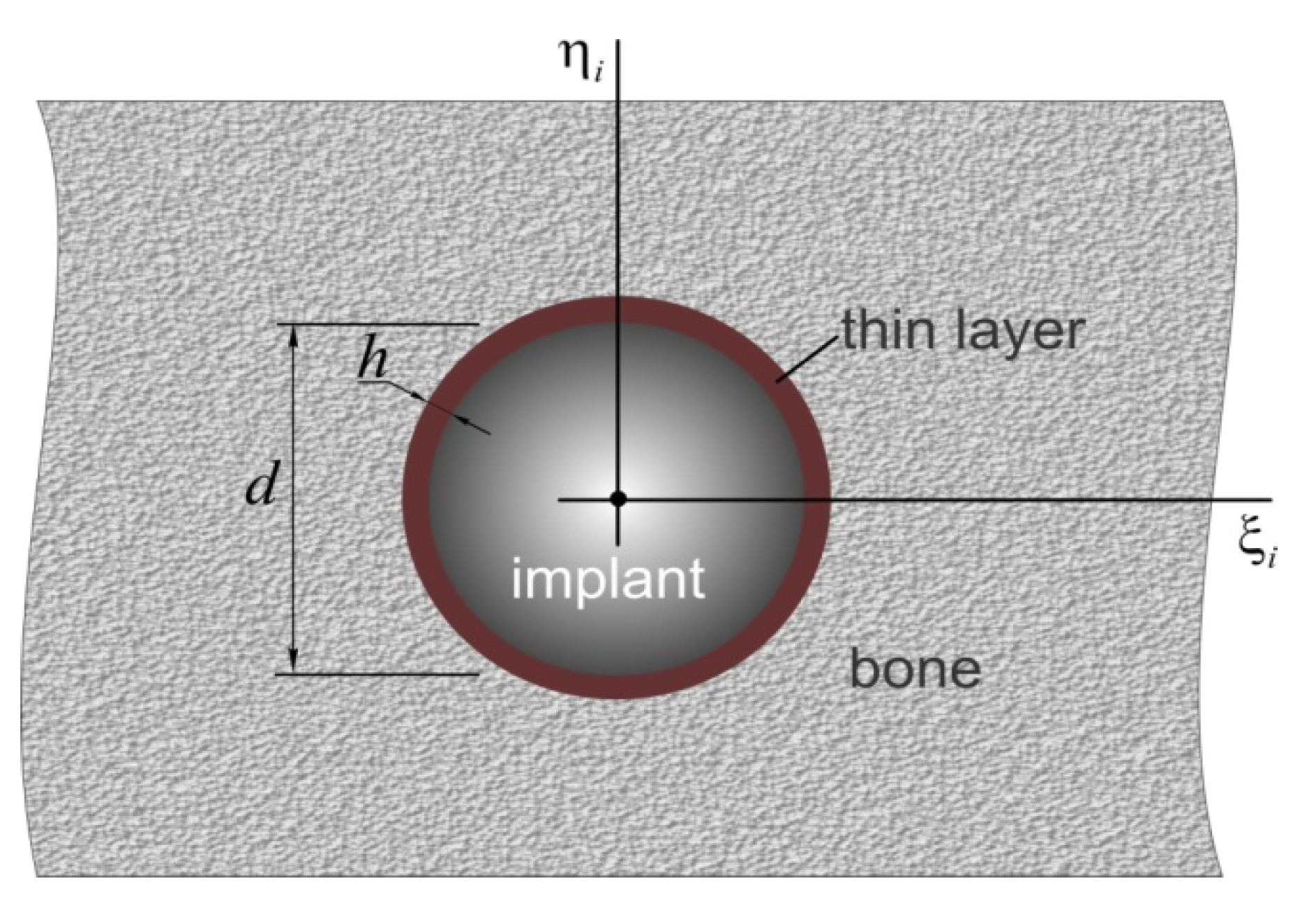


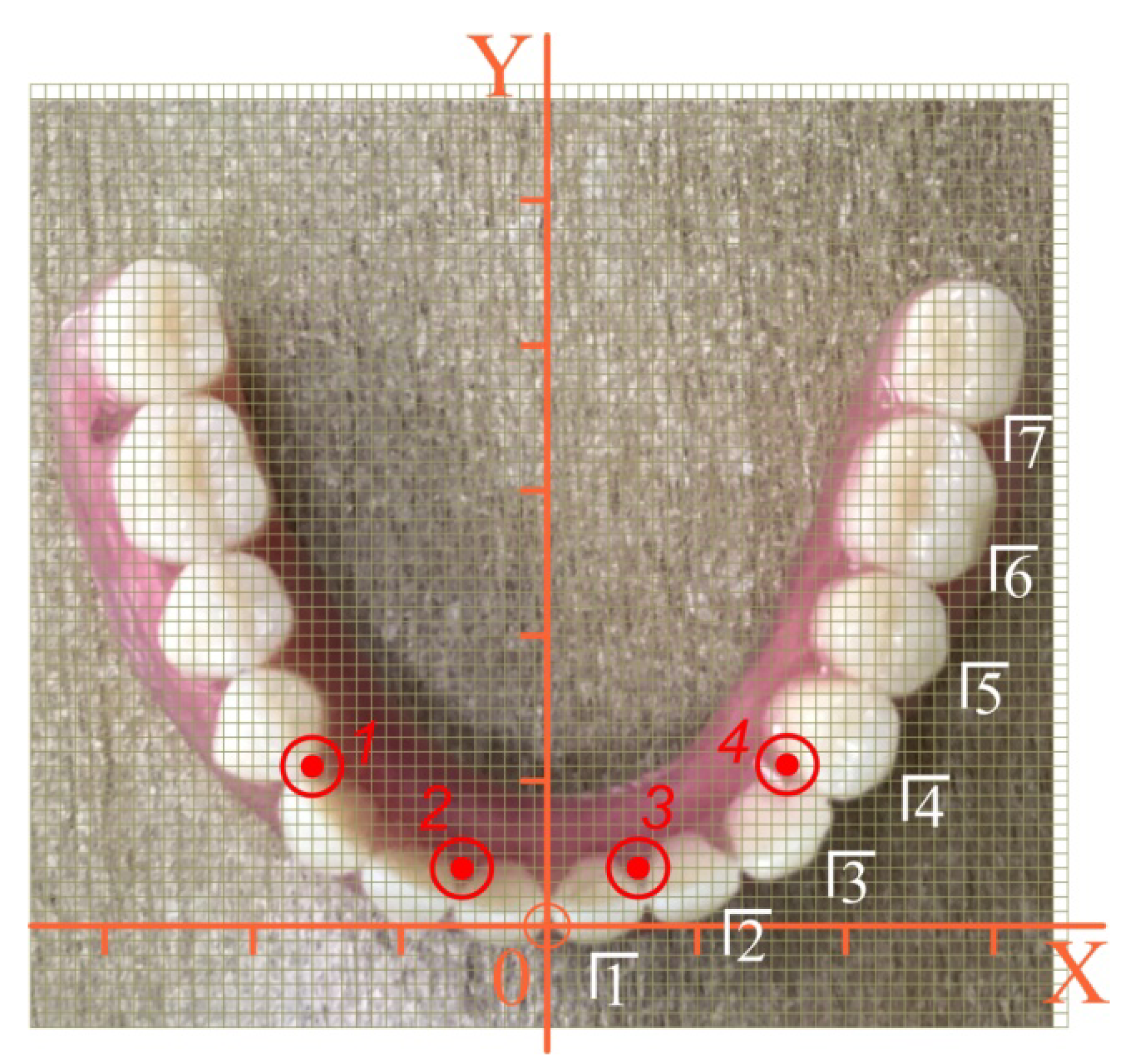

| Implant No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| −21 | −12 | 12 | 21 | |
| 17 | 6 | 6 | 17 | |
| −21 | −12 | 12 | 21 | |
| 5.5 | −5.5 | −5.5 | 5.5 |
| Tooth No. | 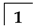 | 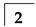 | 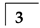 | 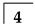 | 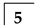 |  | 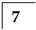 |
|---|---|---|---|---|---|---|---|
| 3 | 9 | 15 | 19 | 23 | 25 | 28 | |
| 1 | 3 | 7 | 13 | 20 | 29 | 40 | |
| 3 | 9 | 15 | 19 | 23 | 25 | 28 | |
| −10.5 | −8.5 | −4.5 | 1.5 | 8.5 | 17.5 | 28.5 |
| No. of Implant | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| −16 | −6 | 6 | 16 | |
| 11 | 4 | 4 | 11 | |
| −16 | −6 | 6 | 16 | |
| 3.5 | −3.5 | –3.5 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelekhan, B.; Dutkiewicz, M.; Shatskyi, I.; Velychkovych, A.; Rozhko, M.; Pelekhan, L. Analytical Modeling of the Interaction of a Four Implant-Supported Overdenture with Bone Tissue. Materials 2022, 15, 2398. https://doi.org/10.3390/ma15072398
Pelekhan B, Dutkiewicz M, Shatskyi I, Velychkovych A, Rozhko M, Pelekhan L. Analytical Modeling of the Interaction of a Four Implant-Supported Overdenture with Bone Tissue. Materials. 2022; 15(7):2398. https://doi.org/10.3390/ma15072398
Chicago/Turabian StylePelekhan, Bohdan, Maciej Dutkiewicz, Ivan Shatskyi, Andrii Velychkovych, Mykola Rozhko, and Liubomyr Pelekhan. 2022. "Analytical Modeling of the Interaction of a Four Implant-Supported Overdenture with Bone Tissue" Materials 15, no. 7: 2398. https://doi.org/10.3390/ma15072398
APA StylePelekhan, B., Dutkiewicz, M., Shatskyi, I., Velychkovych, A., Rozhko, M., & Pelekhan, L. (2022). Analytical Modeling of the Interaction of a Four Implant-Supported Overdenture with Bone Tissue. Materials, 15(7), 2398. https://doi.org/10.3390/ma15072398








