Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles
Abstract
:1. Introduction
2. Methodology
3. Results
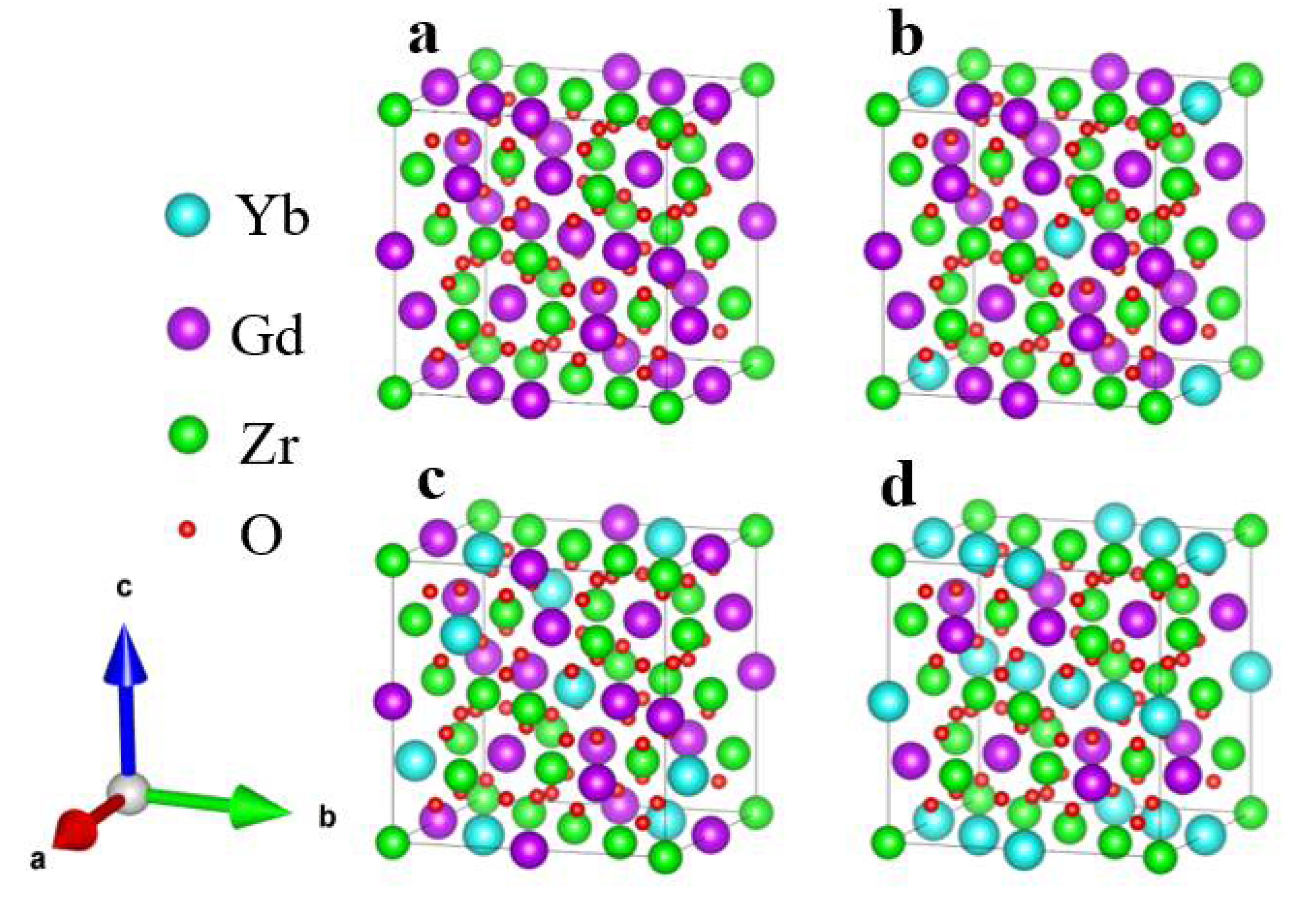
3.1. Yb Doped Gd2Zr2O7 Structure
3.2. Lattice Constant and Elastic Modulus
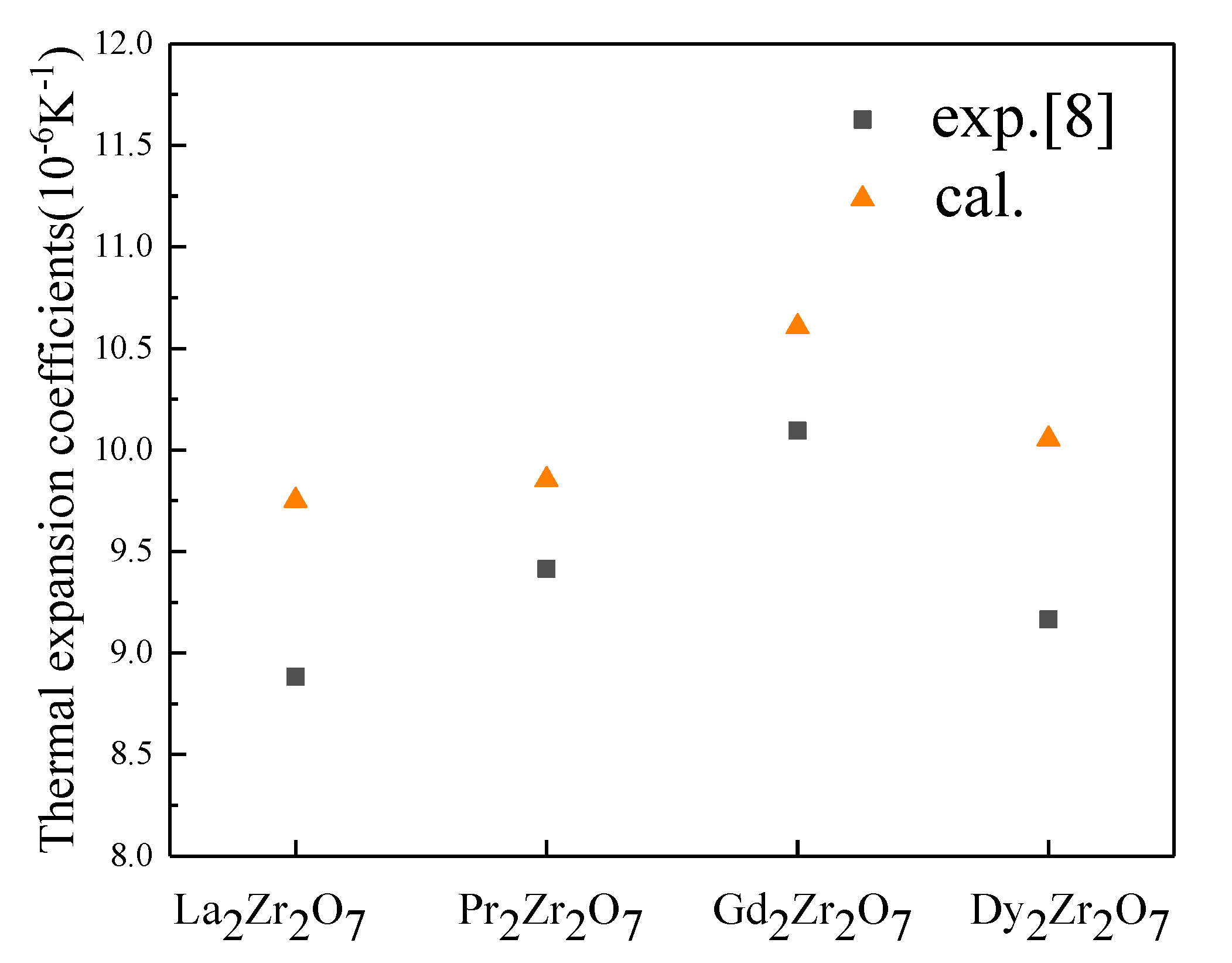
3.3. Thermal Expansion of Rare Earth Zirconates System
3.4. The Validity of α∞ Model
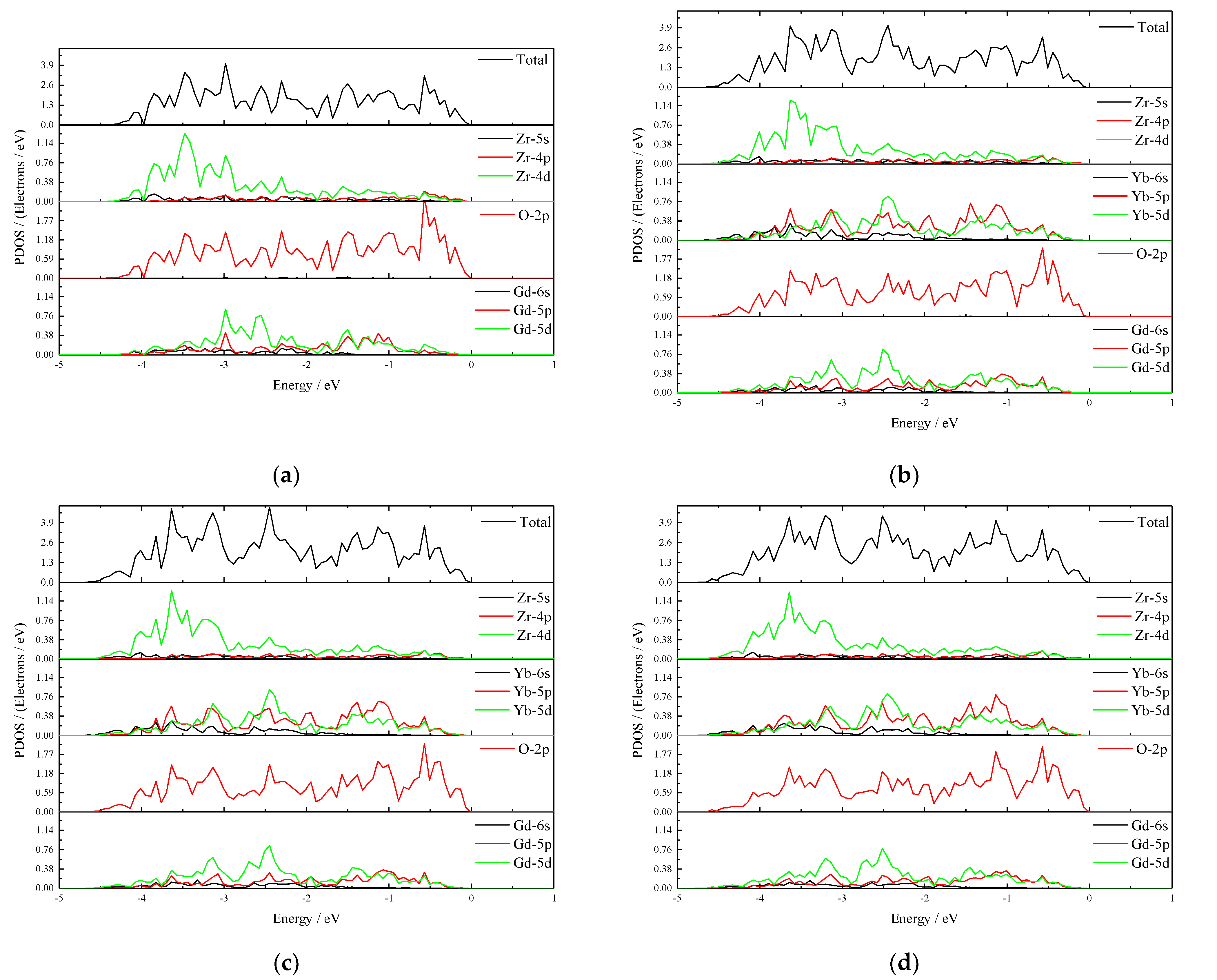
3.5. The Effect of Yb Doping of Gd2Zr2O7 on α∞
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal Barrier Coatings for Gas-Turbine Engine Applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef]
- Clarke, D.R.; Oechsner, M.; Padture, N.P. Thermal-barrier coatings for more efficient gas-turbine engines. MRS Bull. 2012, 37, 891–898. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.X.; Zhou, Y.; Wu, P.; Song, P.; Chong, X.Y.; Feng, J. Thermal properties of Y1−xMgxTaO4−x/2 ceramics via anion sublattice adjustment. Rare Met. 2020, 39, 545–554. [Google Scholar] [CrossRef]
- Clarke, D.R.; Levi, C.G. Materials design for the next generation thermal barrier coatings. Annu. Rev. Mater. Res. 2003, 33, 383–417. [Google Scholar] [CrossRef]
- Cao, X.Q.; Vassen, R.; Stoever, D. Ceramic materials for thermal barrier coatings. J. Eur. Ceram. Soc. 2004, 24, 1–10. [Google Scholar] [CrossRef]
- Zhang, H.S.; Sun, K.; Xu, Q.; Wang, F.; Liu, L.; Wei, Y.; Chen, X.G. Thermophysical properties of Sm2(Zr1−xCex)2O7 ceramics. Rare Met. 2009, 28, 226–230. [Google Scholar] [CrossRef]
- Guo, L.; Li, M.Z.; Zhang, Y.; Ye, F. Improved toughness and thermal expansion of non-stoichiometry Gd2−xZr2+xO7+x/2 ceramics for thermal barrier coating application. J. Mater. Sci. Technol. 2016, 32, 28–33. [Google Scholar] [CrossRef]
- Kawano, T.; Muta, H.; Uno, M.; Ohishi, Y.; Kurosaki, K.; Yamanaka, S. Characterization and thermomechanical properties of Ln2Zr2O7 (Ln = La, Pr, Nd, Eu, Gd, Dy) and Nd2Ce2O7. MRS Online Proc. Libr. 2013, 1514, 139–144. [Google Scholar] [CrossRef]
- Martena, M.; Botto, D.; Fino, P.; Sabbadini, S.; Gola, M.M.; Badini, C. Modelling of TBC system failure: Stress distribution as a function of TGO thickness and thermal expansion mismatch. Eng. Fail. Anal. 2006, 13, 409–426. [Google Scholar] [CrossRef]
- Bacos, M.P.; Dorvaux, J.M.; Lavigne, O.; Mévrel, R.; Poulain, M.; Rio, C.; Vidal-Setif, M.H. Performance and degradation mechanisms of thermal barrier coatings for turbine blades: A review of ONERA activities. Aerospacelab 2011, 3, 1–11. [Google Scholar]
- Liu, Z.G.; Ouyang, J.H.; Zhou, Y. Heat capacities and derived thermodynamic functions of neodymium-gadolinium zirconates from 298.15 to 1050 K. J. Alloy. Compd. 2009, 475, 21–24. [Google Scholar] [CrossRef]
- Ponnilavan, V.; Aravind, A.; Ezhilan, M.; Kannan, S. Titanium substitution in Gd2Zr2O7 for thermal barrier coating applications. Ceram. Int. 2019, 45, 16450–16457. [Google Scholar] [CrossRef]
- Liu, Z.G.; Ouyang, J.H.; Zhou, Y. Structural evolution and thermophysical properties of (SmxGd1-x)2Zr2O7 (0 ≤ x ≤ 1.0) ceramics. J. Alloy. Compd. 2009, 472, 319–324. [Google Scholar] [CrossRef]
- Peczkowski, P.; Kowalik, M.; Zachariasz, P. Synthesis and Physicochemical Properties of Nd-, Sm-, Eu-Based Cuprate High-Temperature Superconductors. Phys. Status Solidi 2018, 215, 1700888. [Google Scholar] [CrossRef]
- Zhao, F.A.; Xiao, H.Y.; Bai, X.M.; Liu, Z.J.; Zu, X.T. Effects of doping Yb3+, La3+, Ti4+, Hf4+, Ce4+ cations on the mechanical properties, thermal conductivity, and electronic structures of Gd2Zr2O7. J. Alloy. Compd. 2019, 776, 306–318. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tanaka, I.; Hug, G. First-principles phonon calculations of thermal expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Phys. Rev. B 2010, 81, 174301. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Xiao, B.; Zhou, R.; Pan, W. Thermal expansions of Ln2Zr2O7 (Ln = La, Nd, Sm, and Gd) pyrochlore. J. Appl. Phys. 2012, 111, 103535. [Google Scholar] [CrossRef]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Ann. Phys. 1912, 344, 257–306. [Google Scholar] [CrossRef] [Green Version]
- Mayer, J.E.; Montroll, E. Molecular distribution. J. Chem. Phys. 1941, 9, 2–16. [Google Scholar] [CrossRef]
- Chen, Y.; Iwata, S.; Mohri, T. First-principles calculation of phase equilibria and phase separation of the Fe-Ni alloy system. Rare Met. 2006, 25, 437. [Google Scholar] [CrossRef]
- Yang, X.Y.; Wang, Z.G.; Zhao, X.S.; Song, J.L.; Zhang, M.M.; Liu, H.D. MatCloud: A high-throughput computational infrastructure for integrated management of materials simulation, data and resources. Comput. Mater. Sci. 2018, 146, 319–333. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Yamada, Y.; Yoshimura, N.; Sakurai, T. Plastic stress-strain matrix and its application for the solution of elastic-plastic problems by the finite element method. Int. J. Mech. Sci. 1968, 10, 343–354. [Google Scholar] [CrossRef]
- Sun, G.; Kürti, J.; Rajczy, P.; Kertesz, M.; Hafner, J.; Kresse, G. Performance of the Vienna ab initio simulation package (VASP) in chemical applications. J. Mol. Struct. 2003, 624, 37–45. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Shimamura, K.; Arima, T.; Idemitsu, K.; Inagaki, Y. Thermophysical properties of rare-earth-stabilized zirconia and zirconate pyrochlores as surrogates for actinide-doped zirconia. Int. J. Thermophys. 2007, 28, 1074–1084. [Google Scholar] [CrossRef]
- Subramanian, M.A.; Aravamudan, G.; Rao, G.V.S. Oxide pyrochlores-a review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Xiong, K.; Wang, B.W.; Sun, Z.P.; Li, W.; Jin, C.C.; Zhang, S.M.; Xu, S.Y.; Guo, L.; Mao, Y. Frist-principles prediction of elastic, electronic, and thermodynamic properties of high entropy carbide ceramic (TiZrNbTa)C. Rare Met. 2022, 41, 1002–1014. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef] [Green Version]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Sanditov, D.S.; Belomestnykh, V.N. Relation between the parameters of the elasticity theory and averaged bulk modulus of solids. Tech. Phys. 2011, 56, 1619–1623. [Google Scholar] [CrossRef]
- Degueldre, C.; Tissot, P.; Lartigue, H.; Pouchon, M. Specific heat capacity and Debye temperature of zirconia and its solid solution. Thermochim. Acta 2003, 403, 267–273. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Kittel’s Introduction to Solid State Physics; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Hisashige, T.; Yamamura, Y.; Tsuji, T. Thermal expansion and Debye temperature of rare earth-doped ceria. J. Alloy. Compd. 2006, 408, 1153–1156. [Google Scholar] [CrossRef]
- Langston, L.S. Fahrenheit 3600. Mech. Eng. 2007, 129, 34–37. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Xiao, B.; Wan, C.L.; Qu, Z.X.; Huang, Z.C.; Chen, J.C.; Pan, W. Electronic structure, mechanical properties and thermal conductivity of Ln2Zr2O7 (Ln = La, Pr, Nd, Sm, Eu and Gd) pyrochlore. Acta Mater. 2011, 59, 1742–1760. [Google Scholar] [CrossRef]
- Lehmann, H.; Pitzer, D.; Pracht, G.; Vassen, R.; Stöver, D. Thermal conductivity and thermal expansion coefficients of the lanthanum rare-earth-element zirconate system. J. Am. Ceram. Soc. 2003, 86, 1338–1344. [Google Scholar] [CrossRef]
- Kutty, K.G.; Rajagopalan, S.; Mathews, C.K.; Varadaraju, U.V. Thermal expansion behaviour of some rare earth oxide pyrochlores. Mater. Res. Bull. 1994, 29, 759–766. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhao, J.; Chen, W.; Yang, J. Theoretical calculation and experimental study on thermal expansion coefficient of inorganic materials. Phys. Eng. 2020, 30, 93–97. [Google Scholar]
- Bakan, E.; Vaßen, R. Ceramic top coats of plasma-sprayed thermal barrier coatings: Materials, processes, and properties. J. Therm. Spray Technol. 2017, 26, 992–1010. [Google Scholar] [CrossRef]
- Hong, Q.J.; Ushakov, S.V.; Kapush, D.; Benmore, C.J.; Weber, R.J.; van de Walle, A.; Navrotsky, A. Combined computational and experimental investigation of high temperature thermodynamics and structure of cubic ZrO2 and HfO2. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Irshad, K.A.; Srihari, V.; Kumar, D.S.; Ananthasivan, K.; Jena, H. High-pressure structural stability, equation of state, and thermal expansion behavior of cubic HfO2. J. Am. Ceram. Soc. 2020, 103, 5374–5381. [Google Scholar] [CrossRef]
- Guo, L.; Guo, H.B.; Peng, H.; Gong, S.K. Thermophysical properties of Yb2O3 doped Gd2Zr2O7 and thermal cycling durability of (Gd0.9Yb0.1)2Zr2O7/YSZ thermal barrier coatings. J. Eur. Ceram. Soc. 2014, 34, 1255–1263. [Google Scholar] [CrossRef]
- Pęczkowski, P.; Łuszczek, M.; Szostak, E.; Muniraju, N.K.C.; Maziopa, A.K.; Gondek, Ł. Superconductivity and appearance of negative magnetocaloric effect in Ba1–xKxBiO3 perovskites, doped by Y, La and Pr. Acta Mater. 2022, 222, 117437. [Google Scholar] [CrossRef]
- Wan, C.; Qu, Z.; Du, A.; Pan, W. Influence of B site substituent Ti on the structure and thermophysical properties of A2B2O7-type pyrochlore Gd2Zr2O7. Acta Mater. 2009, 57, 4782–4789. [Google Scholar] [CrossRef]


| a0/(nm) | C11/(GPa) | C12/(GPa) | C44/(GPa) | B/(GPa) | G/(GPa) | G/B | μ | |
|---|---|---|---|---|---|---|---|---|
| Gd2Zr2O7, cal. | 1.056 | 316.4 | 106.7 | 84.2 | 176.6 | 91.9 | 0.52 | 0.278 |
| Gd2Zr2O7, exp. [26] | 1.054 | 174 | 93 | |||||
| (Gd0.875Yb0.125)2Zr2O7 | 1.055 | 312.3 | 100.2 | 83.4 | 170.6 | 91.7 | 0.54 | 0.272 |
| (Gd0.6875Yb0.3125)2Zr2O7 | 1.052 | 308.4 | 96.7 | 83 | 167.2 | 91.6 | 0.55 | 0.269 |
| (Gd0.5Yb0.5)2Zr2O7 | 1.050 | 310.4 | 96 | 82.5 | 167.7 | 91.7 | 0.55 | 0.269 |
| a0/(nm) | B/(GPa) | G/(GPa) | μ | α∞ (K−1) | |
|---|---|---|---|---|---|
| ZrO2, cal. | 0.512 | 238.5 | 100.6 | 0.316 | 9.72 × 10−6 |
| ZrO2 [a] | 0.515 | 235 | 103 | 0.31 | |
| HfO2, cal. | 0.508 | 253.8 | 112.6 | 0.307 | 9.05 × 10−6 |
| HfO2 [b] | 0.508 | 248 | 115 | 0.3 |
| a0/(nm) | B/(GPa) | G/(GPa) | μ | Thermal Expansion Coefficient/(10−6K−1) | ||
|---|---|---|---|---|---|---|
| α∞ | α/(1073 K) [8] | |||||
| La2Zr2O7 | 1.081 | 176 | 87 | 0.302 | 9.755 | 8.883 |
| Pr2Zr2O7 | 1.072 | 155 | 103 | 0.26 | 9.857 | 9.415 |
| Gd2Zr2O7 | 1.052 | 165 | 63 | 0.284 | 10.61 | 10.094 |
| Dy2Zr2O7 | 1.054 | 164 | 90 | 0.268 | 10.057 | 9.166 |
| ρ/(kg·m−3) | υL/(m·s−1) | υS/(m·s−1) | υm/(m·s−1) | TD/(K) | |
|---|---|---|---|---|---|
| Gd2Zr2O7 | 6868 | 6600 | 3659 | 4075 | 511 |
| (Gd0.875Yb0.125)2Zr2O7 | 6944 | 6496 | 3635 | 4046 | 508 |
| (Gd0.6875Yb0.3125)2Zr2O7 | 7059 | 6402 | 3602 | 4007 | 504 |
| (Gd0.5Yb0.5)2Zr2O7 | 7176 | 6357 | 3574 | 3977 | 502 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Bai, X.; Xiao, W.; Liu, Y.; Li, X.; Wang, J.; Peng, C.; Wang, L.; Wang, X. Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles. Materials 2022, 15, 2264. https://doi.org/10.3390/ma15062264
Wang X, Bai X, Xiao W, Liu Y, Li X, Wang J, Peng C, Wang L, Wang X. Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles. Materials. 2022; 15(6):2264. https://doi.org/10.3390/ma15062264
Chicago/Turabian StyleWang, Xingqi, Xue Bai, Wei Xiao, Yuyang Liu, Xiaoning Li, Jianwei Wang, Cheng Peng, Lijun Wang, and Xingming Wang. 2022. "Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles" Materials 15, no. 6: 2264. https://doi.org/10.3390/ma15062264
APA StyleWang, X., Bai, X., Xiao, W., Liu, Y., Li, X., Wang, J., Peng, C., Wang, L., & Wang, X. (2022). Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles. Materials, 15(6), 2264. https://doi.org/10.3390/ma15062264






