Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response
Abstract
:1. Introduction
2. Materials and Methods
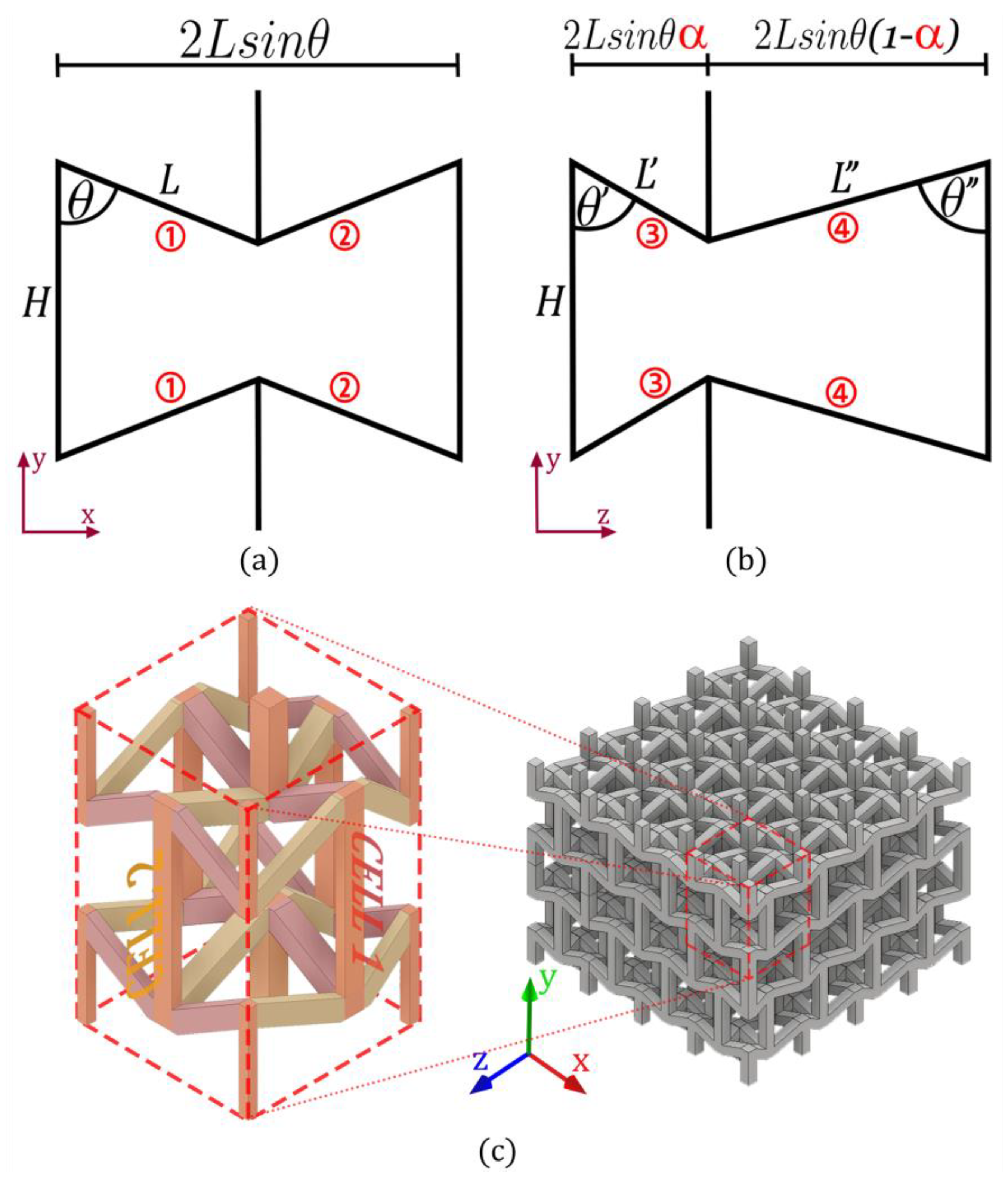
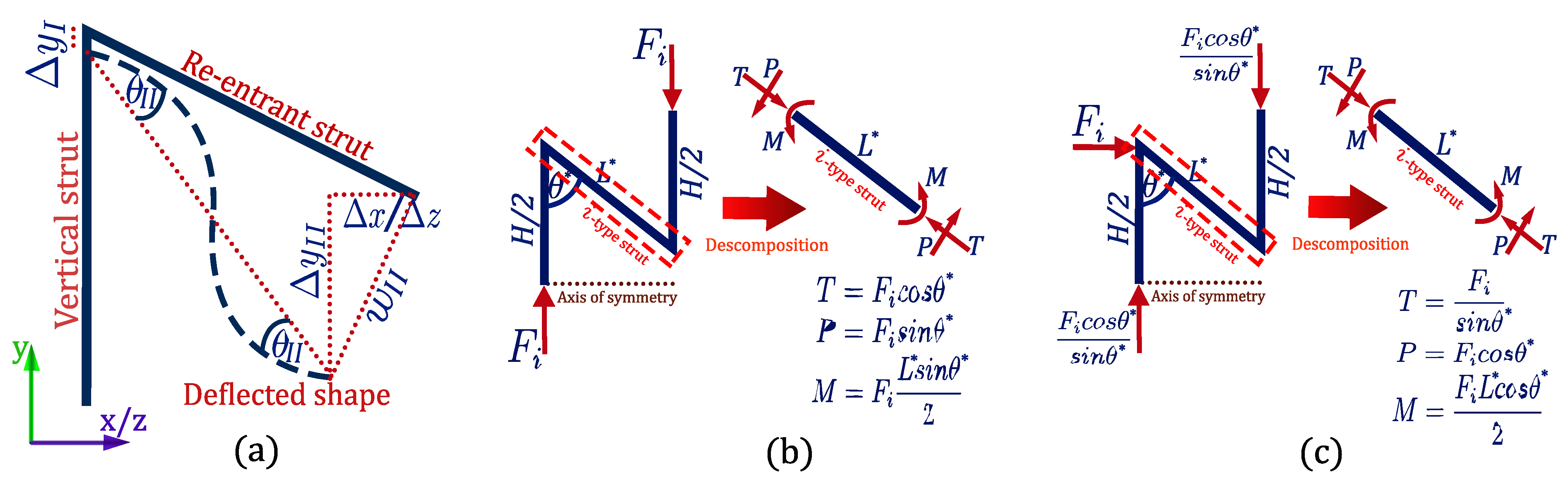
2.1. Orthotropic Mechanical Model of the Cell
2.1.1. x Axis Compression
2.1.2. z Axis Compression
2.1.3. y Axis Compression
2.1.4. Poisson’s Ratio
2.1.5. Young’s Modulus
2.2. Experimental Procedure
3. Results and Discussion
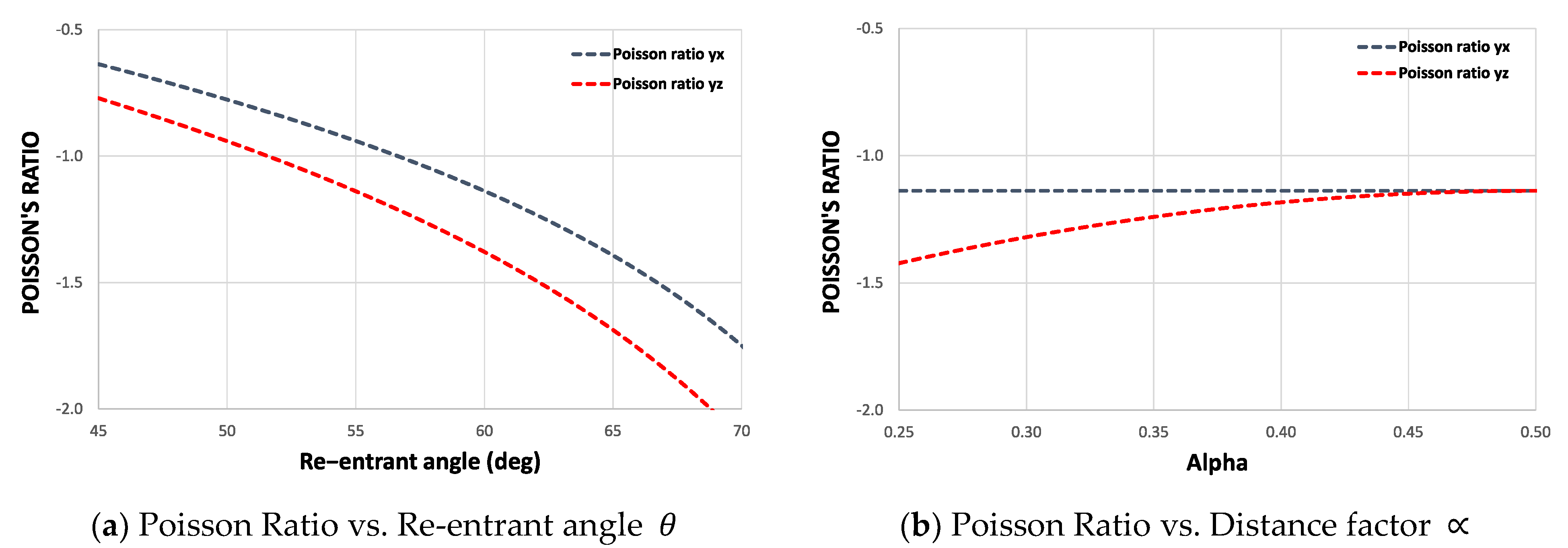
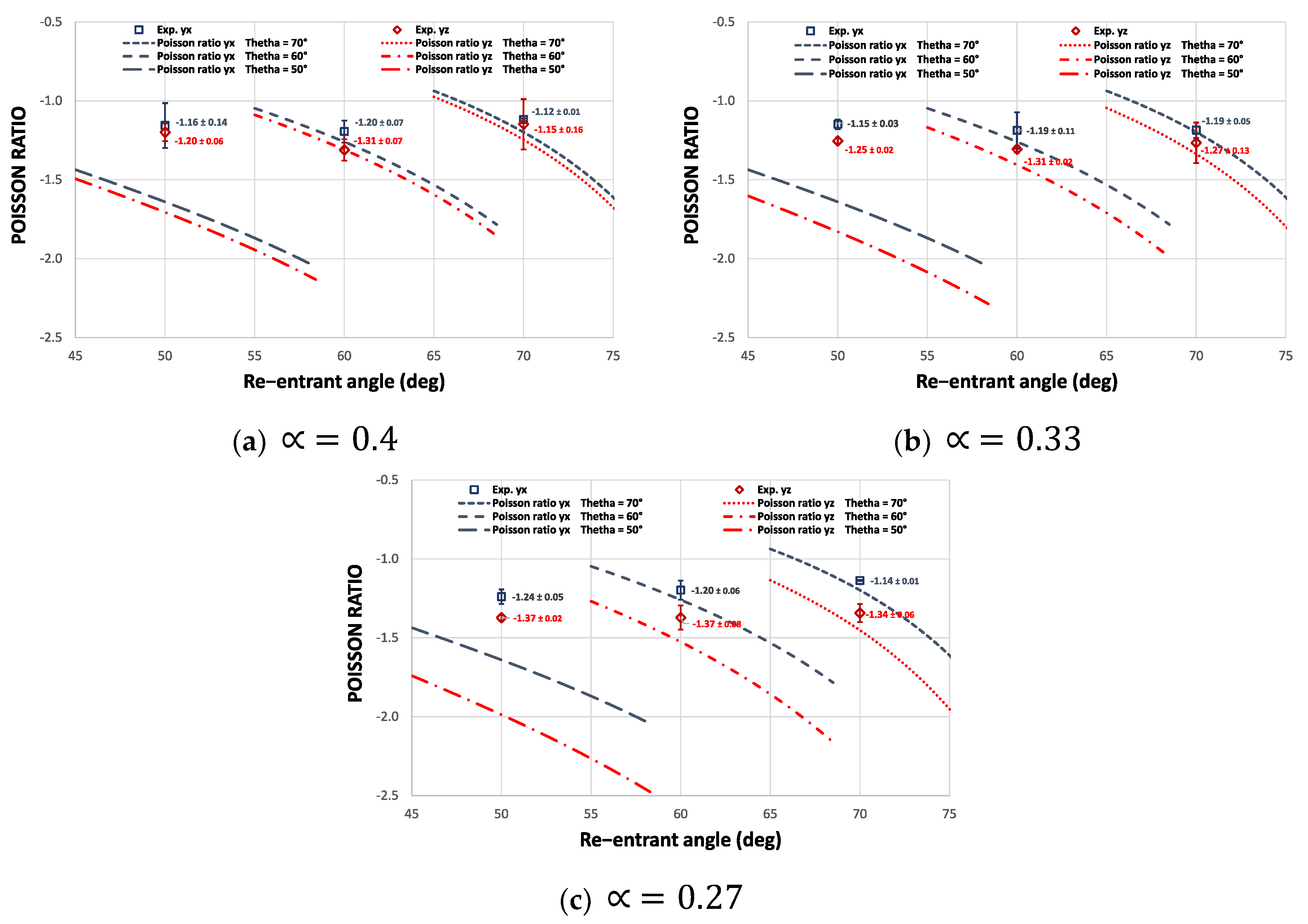
3.1. Poisson’s Ratio
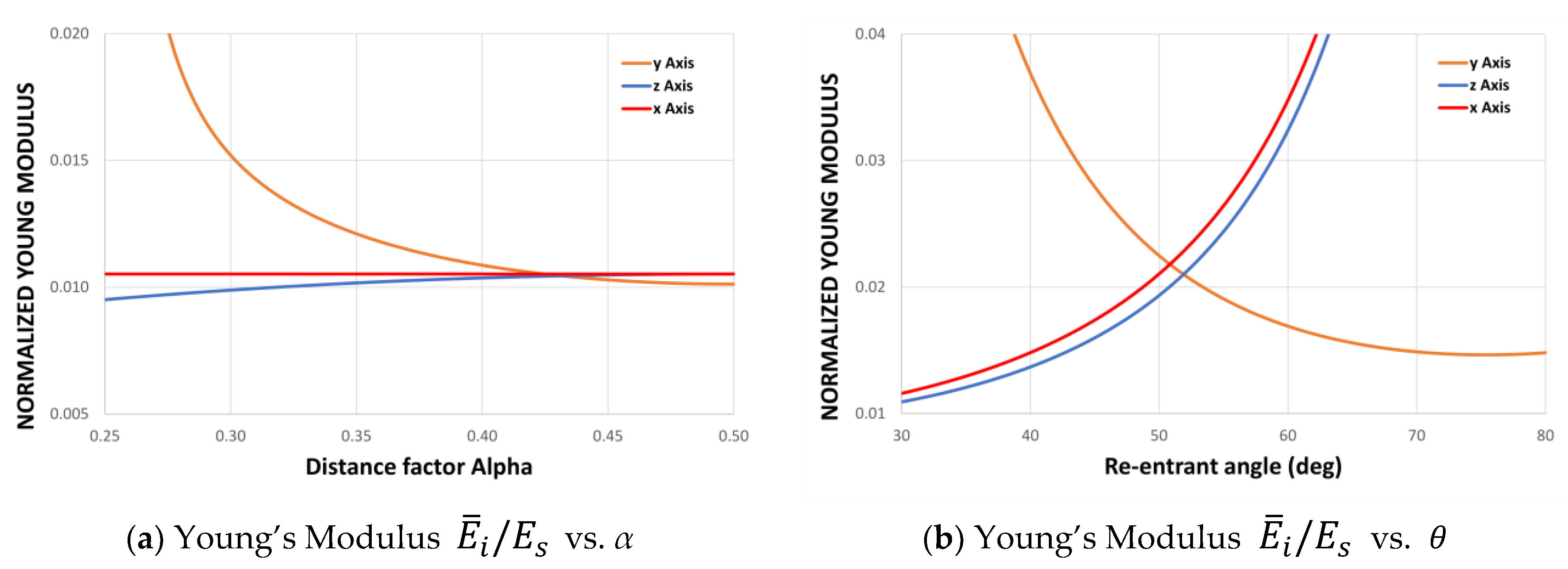
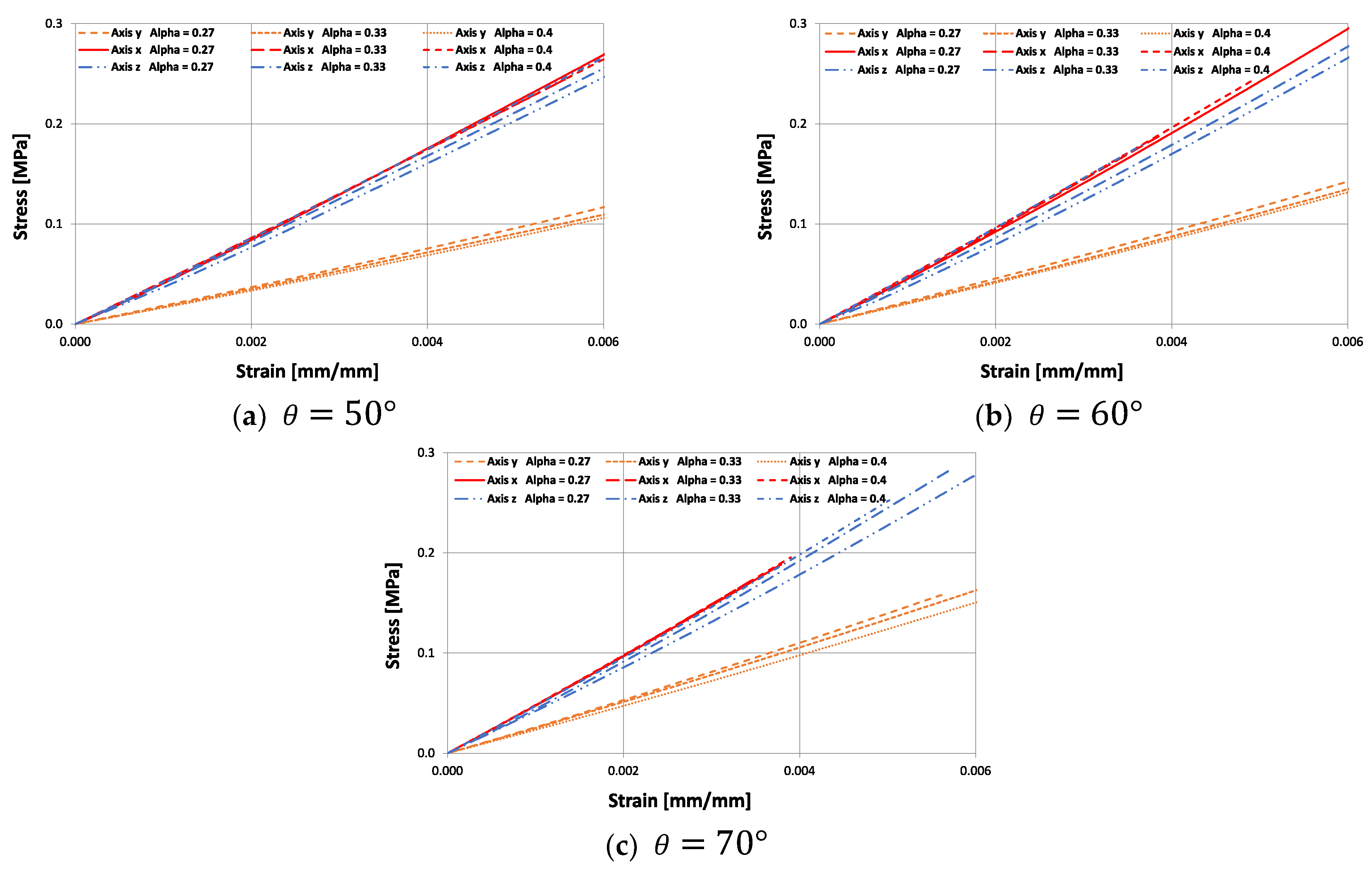
3.2. Young’s Modulus
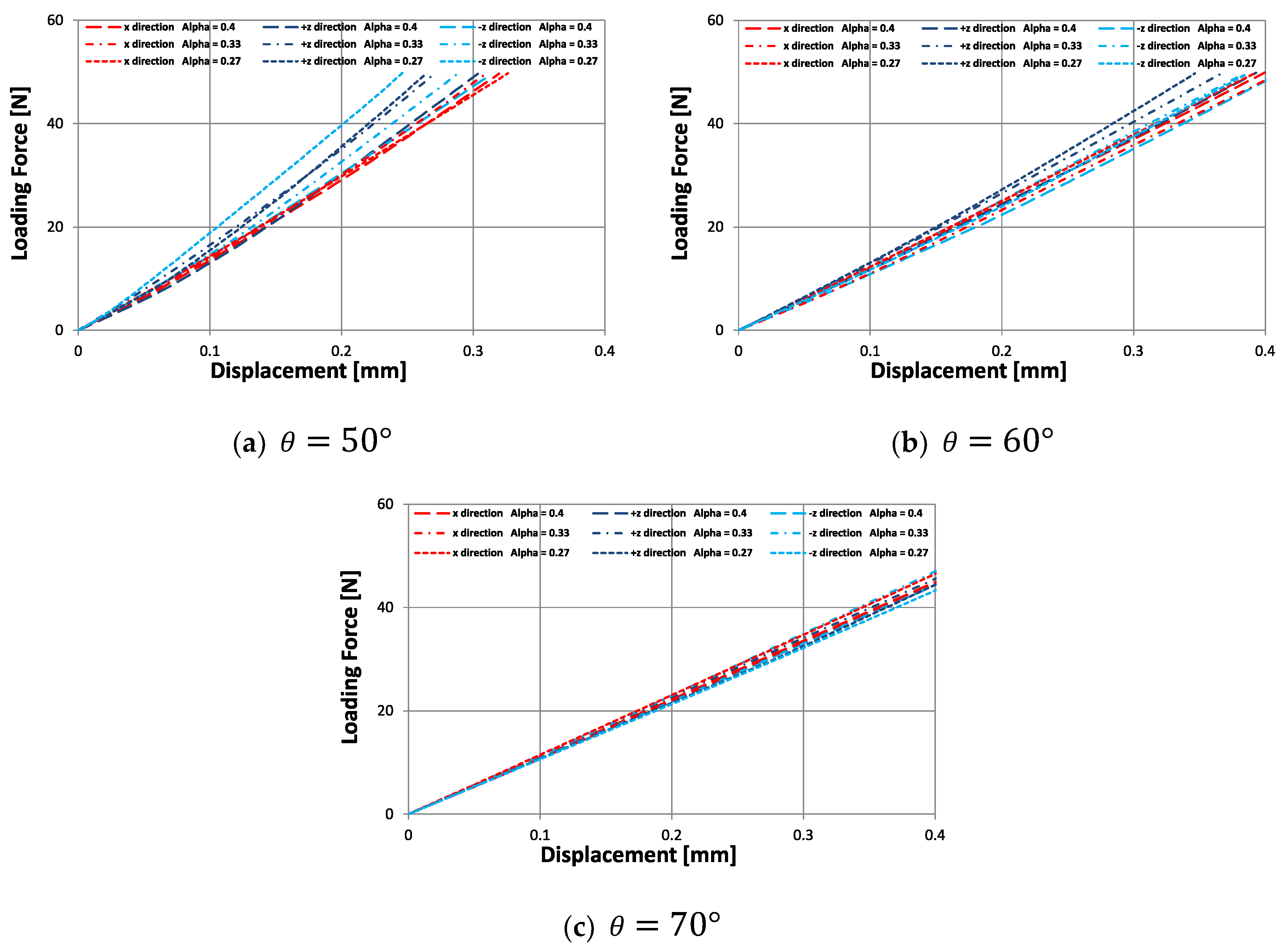
3.3. Flexural Stiffness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef] [Green Version]
- Neff, C.; Hopkinson, N.; Crane, N.B. Experimental and analytical investigation of mechanical behavior of laser-sintered diamond-lattice structures. Addit. Manuf. 2018, 22, 807–816. [Google Scholar] [CrossRef]
- Garner, E.; Kolken, H.M.A.; Wang, C.C.L.; Zadpoor, A.A.; Wu, J. Compatibility in microstructural optimization for additive manufacturing. Addit. Manuf. 2019, 26, 65–75. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.; Wang, L. Enhanced fracture toughness in architected interpenetrating phase composites by 3D printing. Compos. Sci. Technol. 2018, 167, 251–259. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.; Nomura, T.; Dede, E.M.; Yoo, J. Topology optimization for continuous and discrete orientation design of functionally graded fiber-reinforced composite structures. Compos. Struct. 2018, 201, 217–233. [Google Scholar] [CrossRef]
- Weeger, O.; Boddeti, N.; Yeung, S.K.; Kaijima, S.; Dunn, M.L. Digital design and nonlinear simulation for additive manufacturing of soft lattice structures. Addit. Manuf. 2019, 25, 39–49. [Google Scholar] [CrossRef]
- Tan, X.; Wang, B.; Chen, S.; Zhu, S.; Sun, Y. A novel cylindrical negative stiffness structure for shock isolation. Compos. Struct. 2019, 214, 397–405. [Google Scholar] [CrossRef]
- Chen, J.K.; Wu, M.W.; Cheng, T.L.; Chiang, P.H. Continuous compression behaviors of selective laser melting Ti-6Al-4V alloy with cuboctahedron cellular structures. Mater. Sci. Eng. C 2019, 100, 781–788. [Google Scholar] [CrossRef]
- Rahman, H.; Yarali, E.; Zolfagharian, A.; Serjouei, A.; Bodaghi, M. Energy absorption and mechanical performance of functionally graded soft–hard lattice structures. Materials 2021, 14, 1366. [Google Scholar] [CrossRef]
- Rajpal, R.; Lijesh, K.P.; Gangadharan, K.V. Parametric studies on bending stiffness and damping ratio of Sandwich structures. Addit. Manuf. 2018, 22, 583–591. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Mirbolghasemi, A.; Hermenean, K. 3D printed meta-sandwich structures: Failure mechanism, energy absorption and multi-hit capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; He, R.; Bai, X.; Zhang, K.; Ai, S.; Yang, Y.; Fang, D. Bending behavior of lightweight C/SiC pyramidal lattice core sandwich panels. Int. J. Mech. Sci. 2020, 171, 105409. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, K.; Yin, Q.; Zhong, F.; Huang, C. Experimental study on dynamic compressive behaviour of sandwich panel with shear thickening fluid filled pyramidal lattice truss core. Int. J. Mech. Sci. 2018, 138, 467–475. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lin, Y.; Li, X. Plastic crushing failure of bio-inspired cellular hierarchical topological sandwich core. Materials 2021, 14, 5040. [Google Scholar] [CrossRef] [PubMed]
- Quinteros, L.; Meruane, V.; Cardoso, E.L.; Ruiz, R.O. Phononic bandgap optimization in sandwich panels using cellular truss cores. Materials 2021, 14, 5236. [Google Scholar] [CrossRef]
- Ingrole, A.; Hao, A.; Liang, R. Design and modeling of auxetic and hybrid honeycomb structures for in-plane property enhancement. Mater. Des. 2017, 117, 72–83. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-weight shell-lattice metamaterials for mechanical shock absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Malshe, A.P.; Bapat, S.; Rajurkar, K.P.; Haitjema, H. Bio-inspired textures for functional applications. CIRP Ann. 2018, 67, 627–650. [Google Scholar] [CrossRef]
- Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive Manufacturing as a Method to Design and Optimize Bioinspired Structures. Adv. Mater. 2018, 30, 1800940. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Niknam, H.; Hermenean, K. 3D printed architected polymeric sandwich panels: Energy absorption and structural performance. Compos. Struct. 2018, 200, 886–909. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, M.; Wang, C.H.; Sun, G.; Li, G. Out-of-plane crashworthiness of bio-inspired self-similar regular hierarchical honeycombs. Compos. Struct. 2016, 144, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Jia, Z.; Scarpa, F.; Yao, C.W.; Wang, L. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Mater. Des. 2018, 137, 226–234. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Gao, L.; Cao, K.; Zhang, H.; Xu, S.; Jiang, C.; Surjadi, J.U.; Xu, Y.; Lu, Y. Metal-coated hybrid meso-lattice composites and their mechanical characterizations. Compos. Struct. 2018, 203, 750–763. [Google Scholar] [CrossRef]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Han, S.C.; Kang, D.S.; Kang, K. Two nature-mimicking auxetic materials with potential for high energy absorption. Mater. Today 2019, 26, 30–39. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Yang, Z.; Lu, Z.; Liao, B.; He, X. Effective elastic properties and initial yield surfaces of two 3D lattice structures. Int. J. Mech. Sci. 2018, 138–139, 146–158. [Google Scholar] [CrossRef]
- Yang, H.; Wang, B.; Ma, L. Designing hierarchical metamaterials by topology analysis with tailored Poisson’s ratio and Young’s modulus. Compos. Struct. 2019, 214, 359–378. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef] [Green Version]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Cho, H.; Seo, D.; Kim, D.-N. Mechanics of Auxetic Materials. In Handbook of Mechanics of Materials; Schmauder, S., Chen, C.-S., Chawla, K.K., Chawla, N., Chen, W., Kagawa, Y., Eds.; Springer: Singapore, 2019; pp. 733–757. [Google Scholar]
- Wang, T.; Wang, L.; Ma, Z.; Hulbert, G.M. Elastic analysis of auxetic cellular structure consisting of re-entrant hexagonal cells using a strain-based expansion homogenization method. Mater. Des. 2018, 160, 284–293. [Google Scholar] [CrossRef]
- Wang, F. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids 2018, 114, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Ai, L.; Gao, X.L. Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion. Int. J. Mech. Sci. 2018, 135, 101–113. [Google Scholar] [CrossRef]
- Nika, G.; Constantinescu, A. Design of multi-layer materials using inverse homogenization and a level set method. Comput. Methods Appl. Mech. Eng. 2019, 346, 388–409. [Google Scholar] [CrossRef] [Green Version]
- Ai, L.; Gao, X.L. An analytical model for star-shaped re-entrant lattice structures with the orthotropic symmetry and negative Poisson’s ratios. Int. J. Mech. Sci. 2018, 145, 158–170. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 23001. [Google Scholar] [CrossRef]
- Donoghue, J.P.; Alderson, K.L.; Evans, K.E. The fracture toughness of composite laminates with a negative Poisson’s ratio. Phys. Status Solidi Basic Res. 2009, 246, 2011–2017. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Ma, Z.D.; Wang, T. A negative Poisson’s ratio suspension jounce bumper. Mater. Des. 2016, 103, 90–99. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Sumelka, W. The Development of a New Shock Absorbing Uniaxial Graded Auxetic Damper (UGAD). Materials 2019, 12, 2573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Almgren, R. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Gibson, M.F.A.L.L. Cellular solids. Structure & properties. Pergamon Press, Oxford 1988. ISBN 0-08-036607-4. Cryst. Res. Technol. 1990, 25, 1038. [Google Scholar] [CrossRef]
- Evans, K.E. Tensile network microstructures exhibiting negative Poisson’s ratio. J. Phys. D Appl. Phys. 1989, 22, 1870–1876. [Google Scholar] [CrossRef]
- Wang, X.-T.; Chen, Y.-L.; Ma, L. The manufacture and characterization of composite three-dimensional re-entrant auxetic cellular structures made from carbon fiber reinforced polymer. J. Compos. Mater. 2018, 52, 3265–3273. [Google Scholar] [CrossRef]
- Pelinski, K.; Smardzewski, J. Bending Behavior of Lightweight Wood-Based Sandwich Beams with Auxetic Cellular Core. Polymers 2020, 12, 1723. [Google Scholar] [CrossRef]
- Pelinski, K.; Smardzewski, J.; Narojczyk, J. Stiffness of Synclastic Wood Based Auxetic Sandwich Panels. Phys. Status Solidi 2020, 257, 1900749. [Google Scholar] [CrossRef]
- Smardzewski, J. Elastic properties of cellular wood panels with hexagonal and auxetic cores. Holzforschung 2013, 67, 87–92. [Google Scholar] [CrossRef]
- Pflug, J.; Vangrimde, B.; Verpoest, I.; Vandepitte, D.; Britzke, M.; Wagenführ, A. Continuously produced paper honeycomb sandwich panels for furniture applications. In Proceedings of the 5th Global Wood and Natural Fibre Composites Symposium, Kassel, Germany, 25–27 April 2004. [Google Scholar]
- Yang, L.; Harrysson, O.; Cormier, D.; West, H.; Gong, H.; Stucker, B. Additive Manufacturing of Metal Cellular Structures: Design and Fabrication. JOM 2015, 67, 608–615. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69, 475–490. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Modeling of uniaxial compression in a 3D periodic re-entrant lattice structure. J. Mater. Sci. 2013, 48, 1413–1422. [Google Scholar] [CrossRef]
- Yang, L.; Cormier, D.; West, H.; Harrysson, O.; Knowlson, K. Non-stochastic Ti-6Al-4V foam structures with negative Poisson’s ratio. Mater. Sci. Eng. A 2012, 558, 579–585. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Computational Simulation and Optimization of Functionally Graded Auxetic Structures Made From Inverted Tetrapods. Phys. Status Solidi Basic Res. 2017, 254, 1600753. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Heinl, P.; Singer, R.F.; Körner, C. Auxetic cellular structures through selective electron-beam melting. Phys. Status Solidi Basic Res. 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Cansizoglu, O.; Harrysson, O.; Cormier, D.; West, H.; Mahale, T. Properties of Ti-6Al-4V non-stochastic lattice structures fabricated via electron beam melting. Mater. Sci. Eng. A 2008, 492, 468–474. [Google Scholar] [CrossRef]
- Bilski, M.; Wojciechowski, K.W.; Stręk, T.; Kędziora, P.; Grima-Cornish, J.N.; Dudek, M.R. Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties. Materials 2021, 14, 7837. [Google Scholar] [CrossRef]
- Bilski, M.; Pigłowski, P.M.; Wojciechowski, K.W. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]





| ABSplus | |
|---|---|
 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. https://doi.org/10.3390/ma15051841
Valle R, Pincheira G, Tuninetti V, Fernandez E, Uribe-Lam E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials. 2022; 15(5):1841. https://doi.org/10.3390/ma15051841
Chicago/Turabian StyleValle, Rodrigo, Gonzalo Pincheira, Víctor Tuninetti, Eduardo Fernandez, and Esmeralda Uribe-Lam. 2022. "Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response" Materials 15, no. 5: 1841. https://doi.org/10.3390/ma15051841
APA StyleValle, R., Pincheira, G., Tuninetti, V., Fernandez, E., & Uribe-Lam, E. (2022). Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials, 15(5), 1841. https://doi.org/10.3390/ma15051841








