Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density
Abstract
:1. Introduction
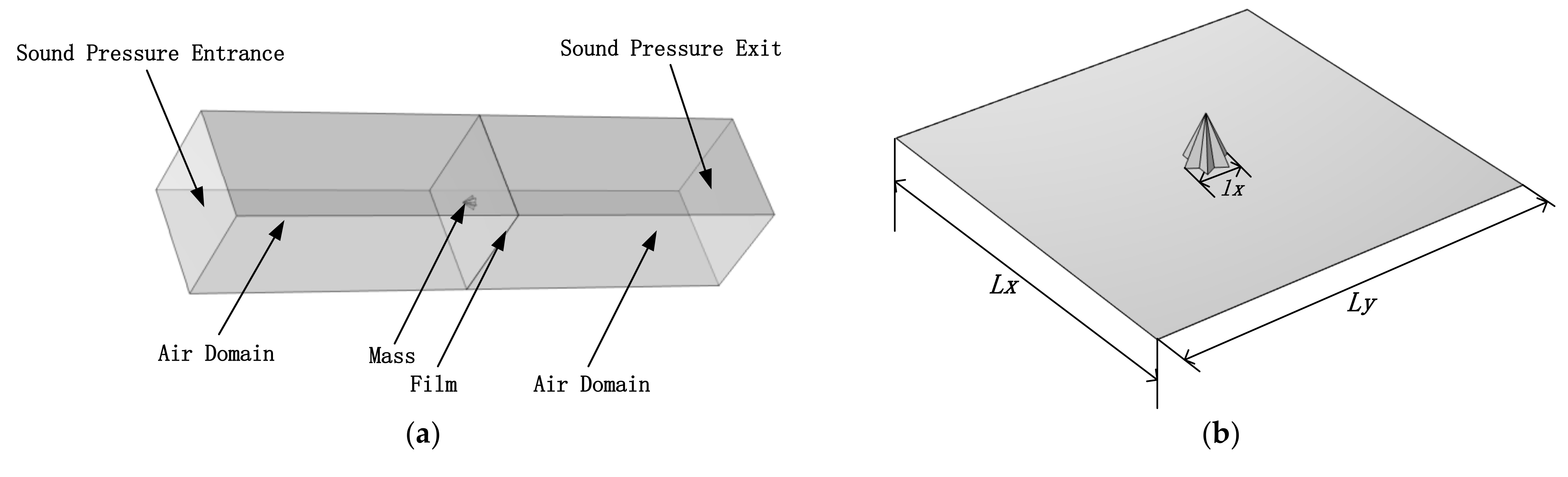
2. Analytical Model and Formulation
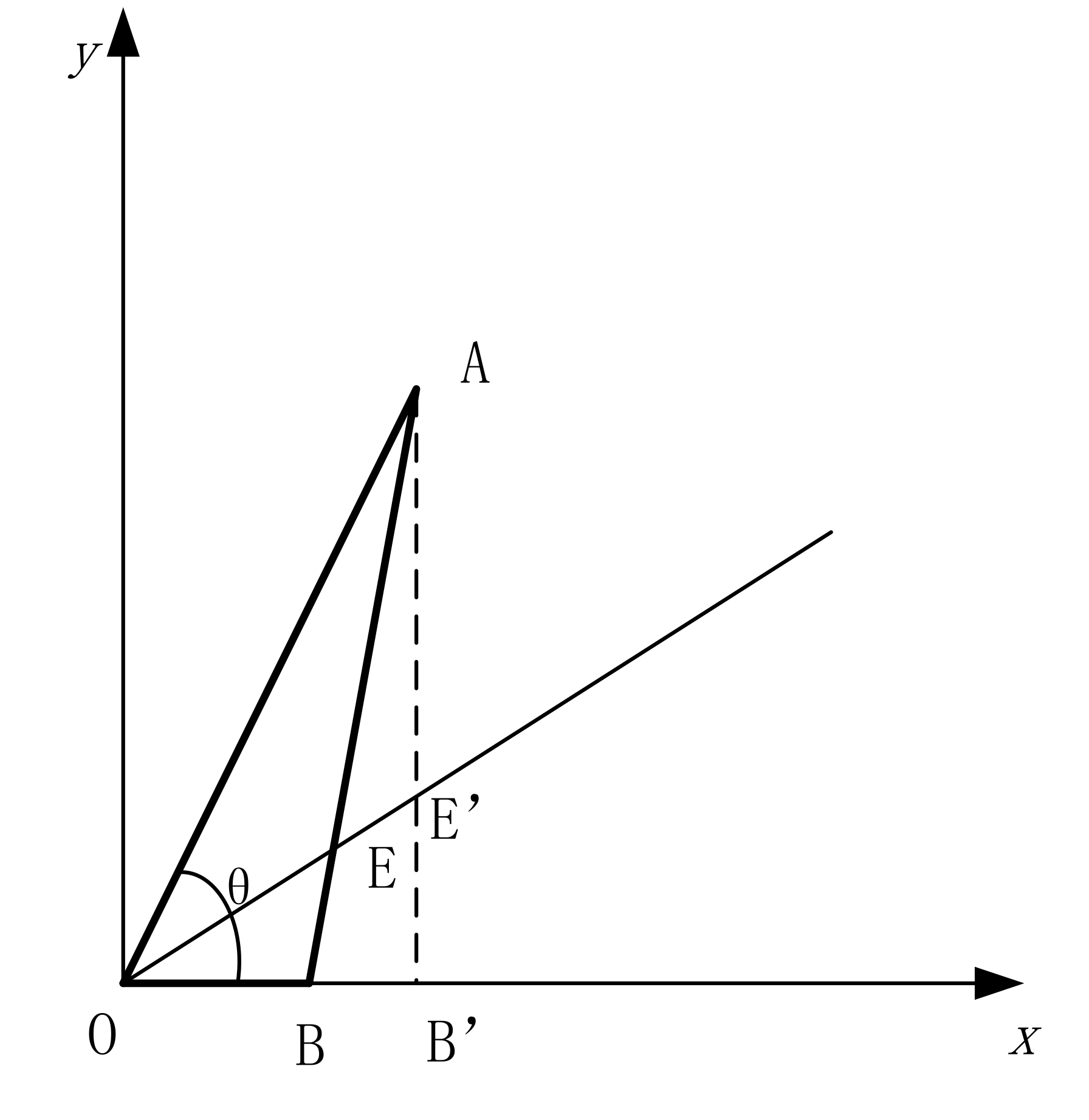
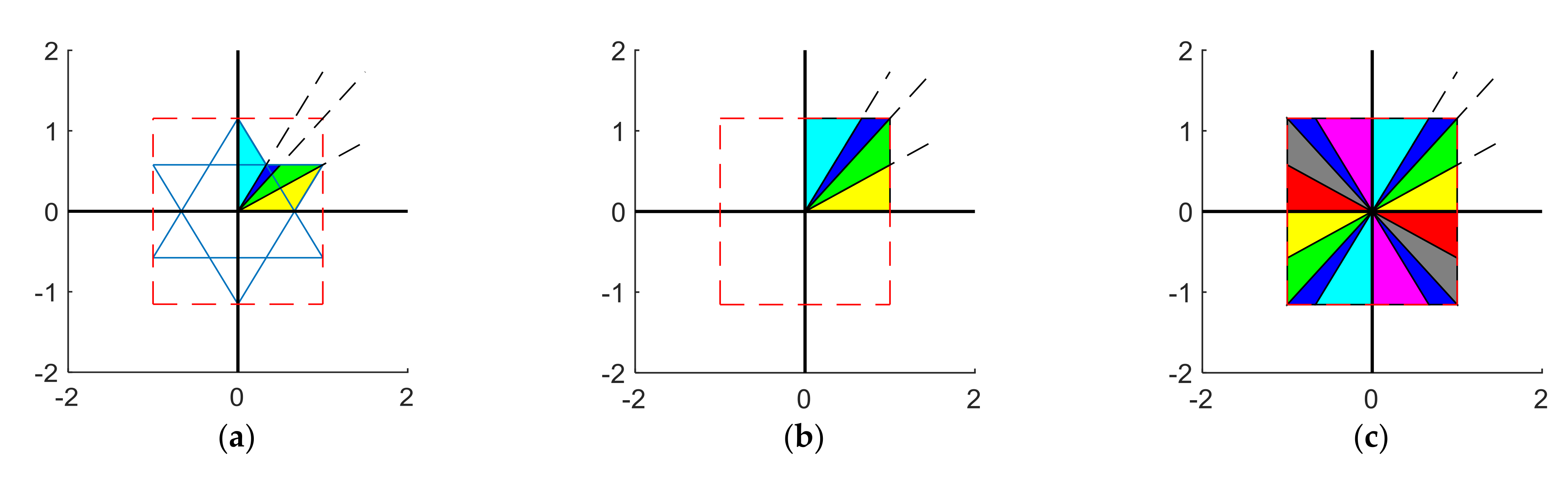
2.1. Loaded Mass Blocks of Any Shape
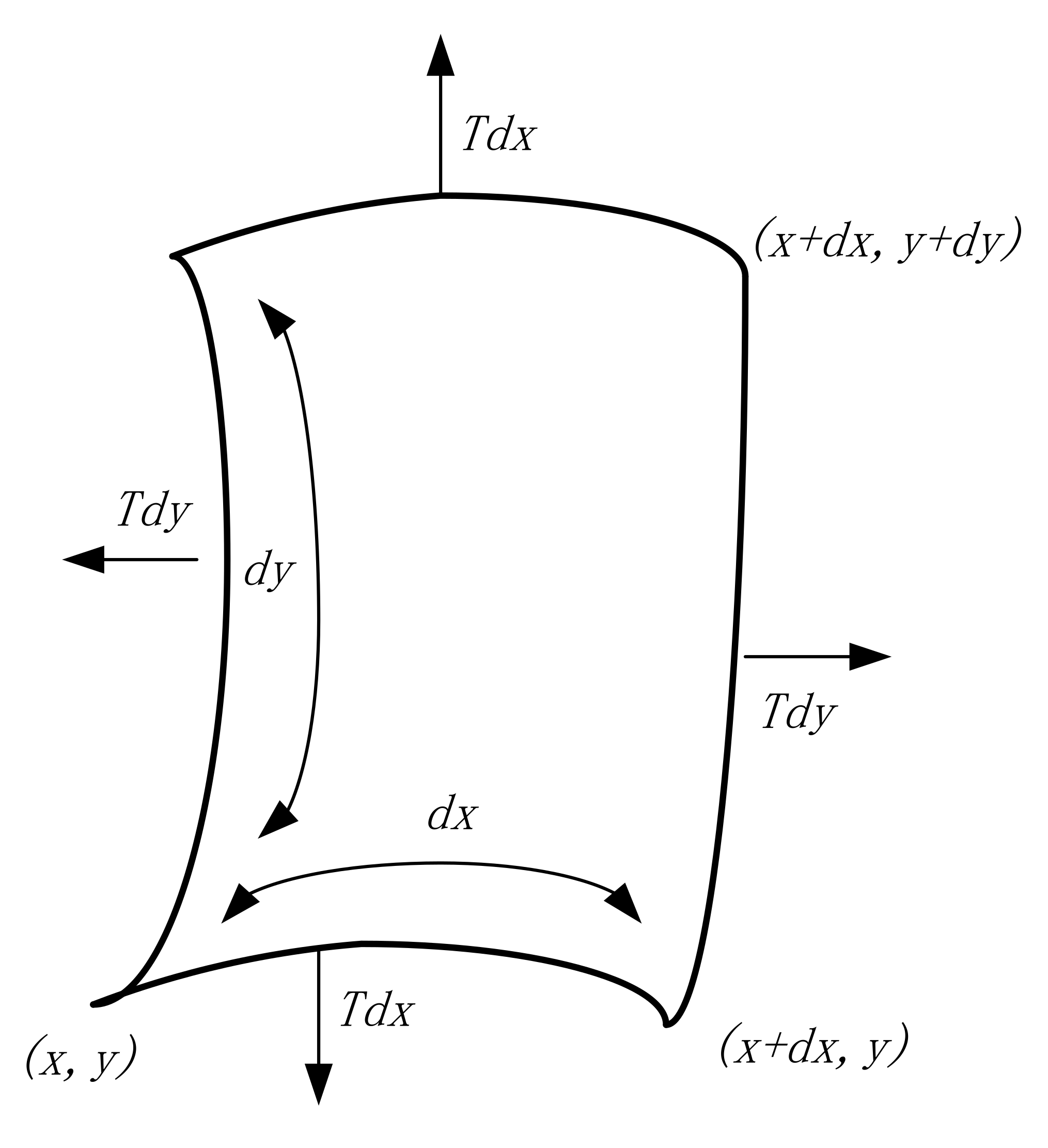
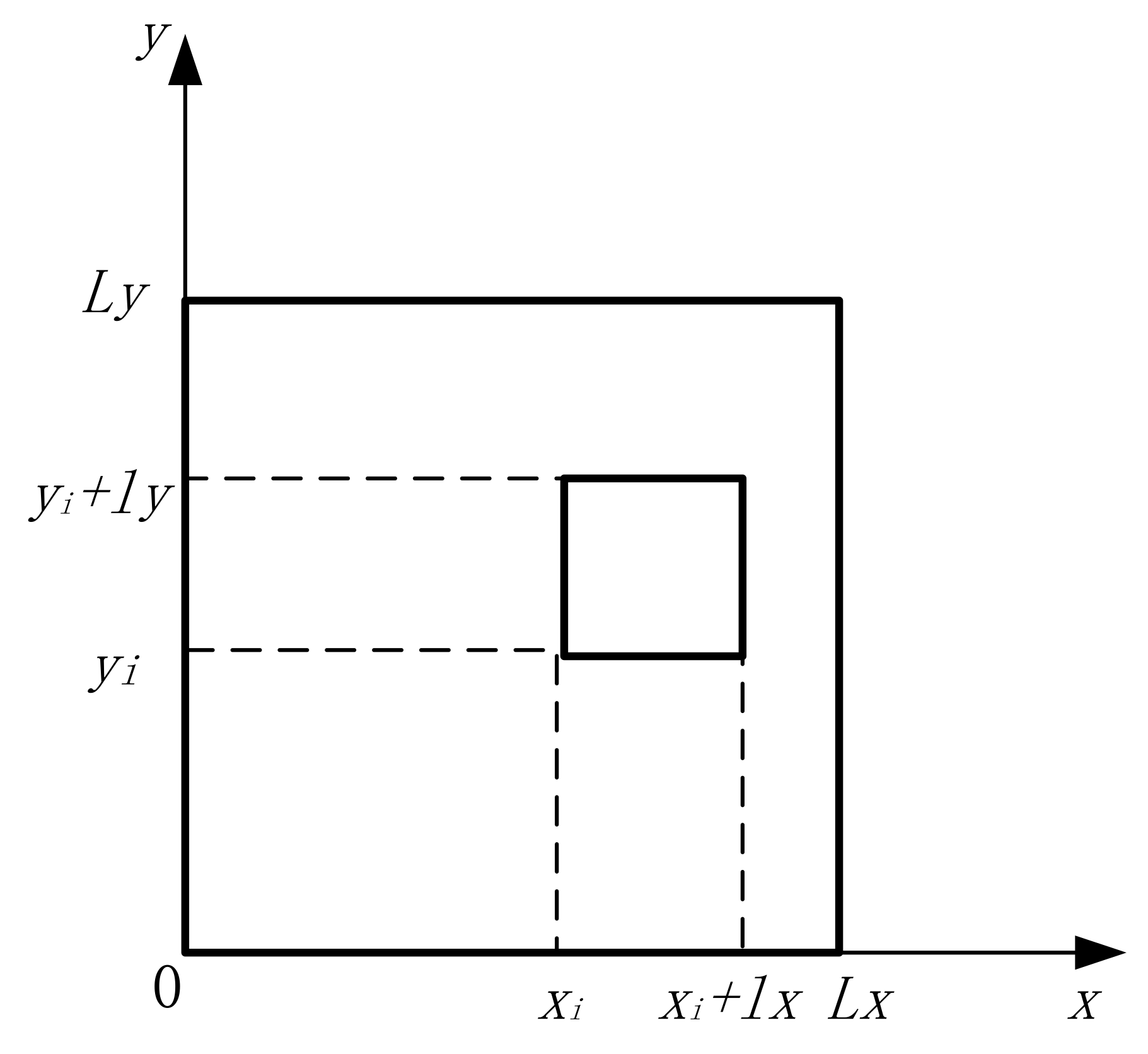
2.2. STL Theory of Membrane-Type Acoustic Metamaterials
2.3. Loading Mass Blocks with Any Area Density
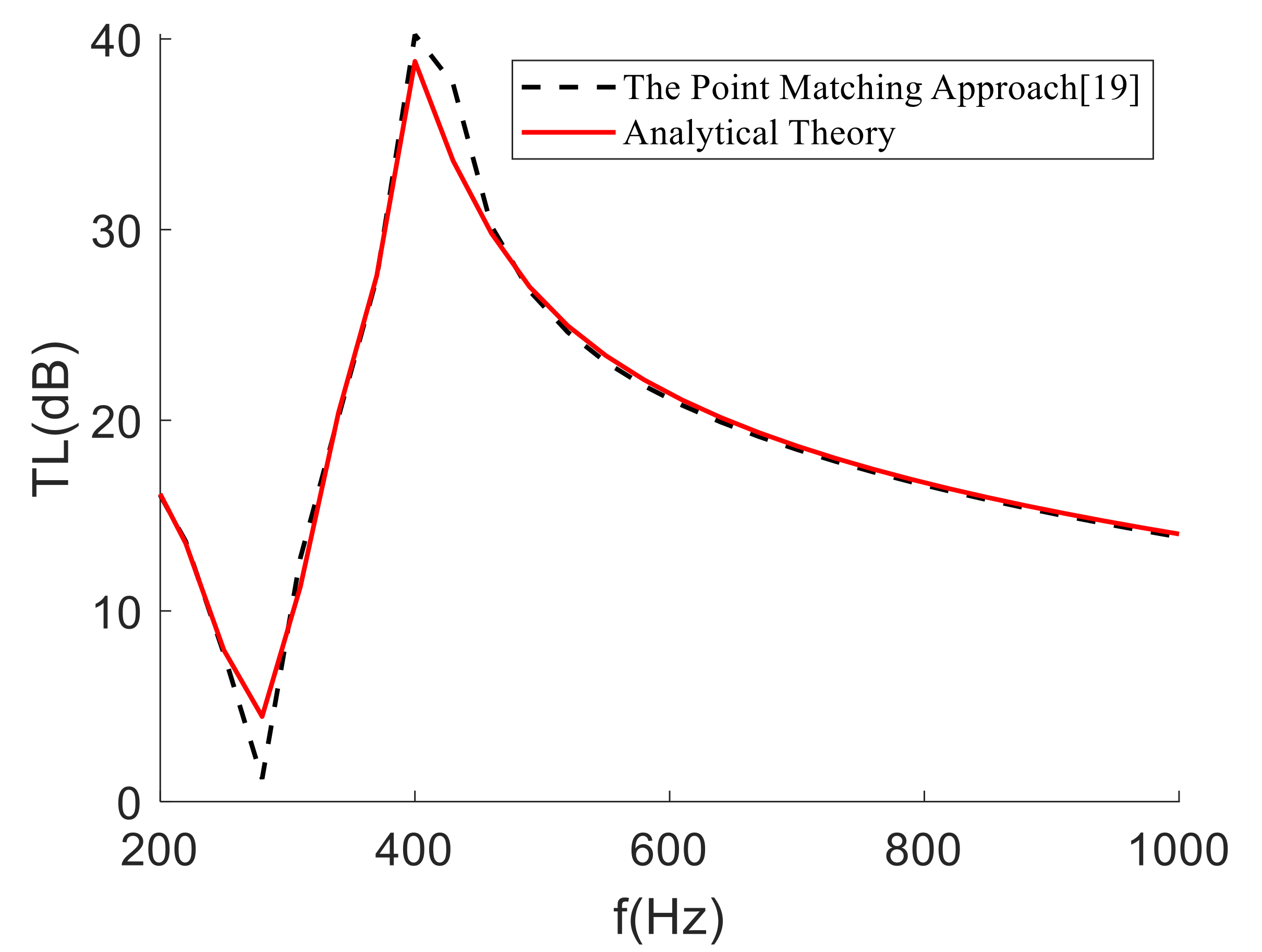
3. Validation of the Method and Discussions
3.1. Cylindrical Mass Block
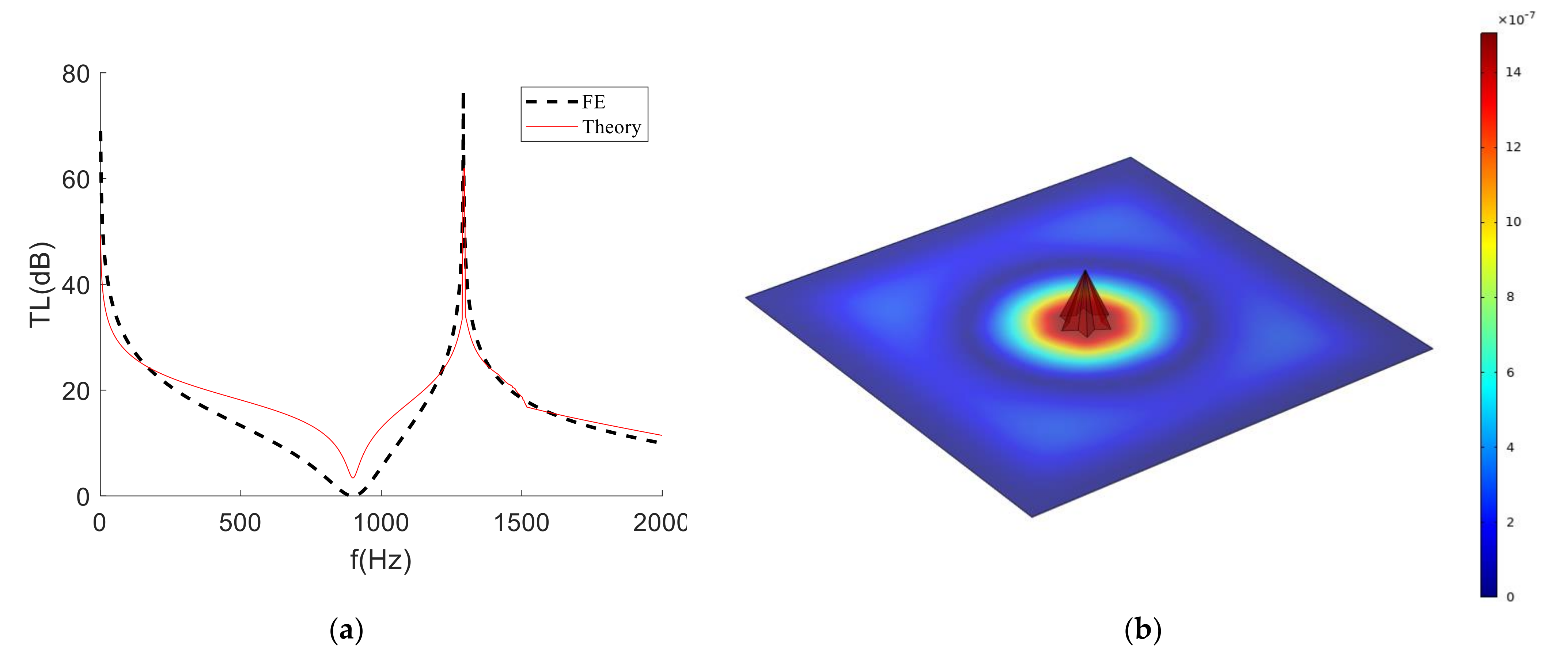
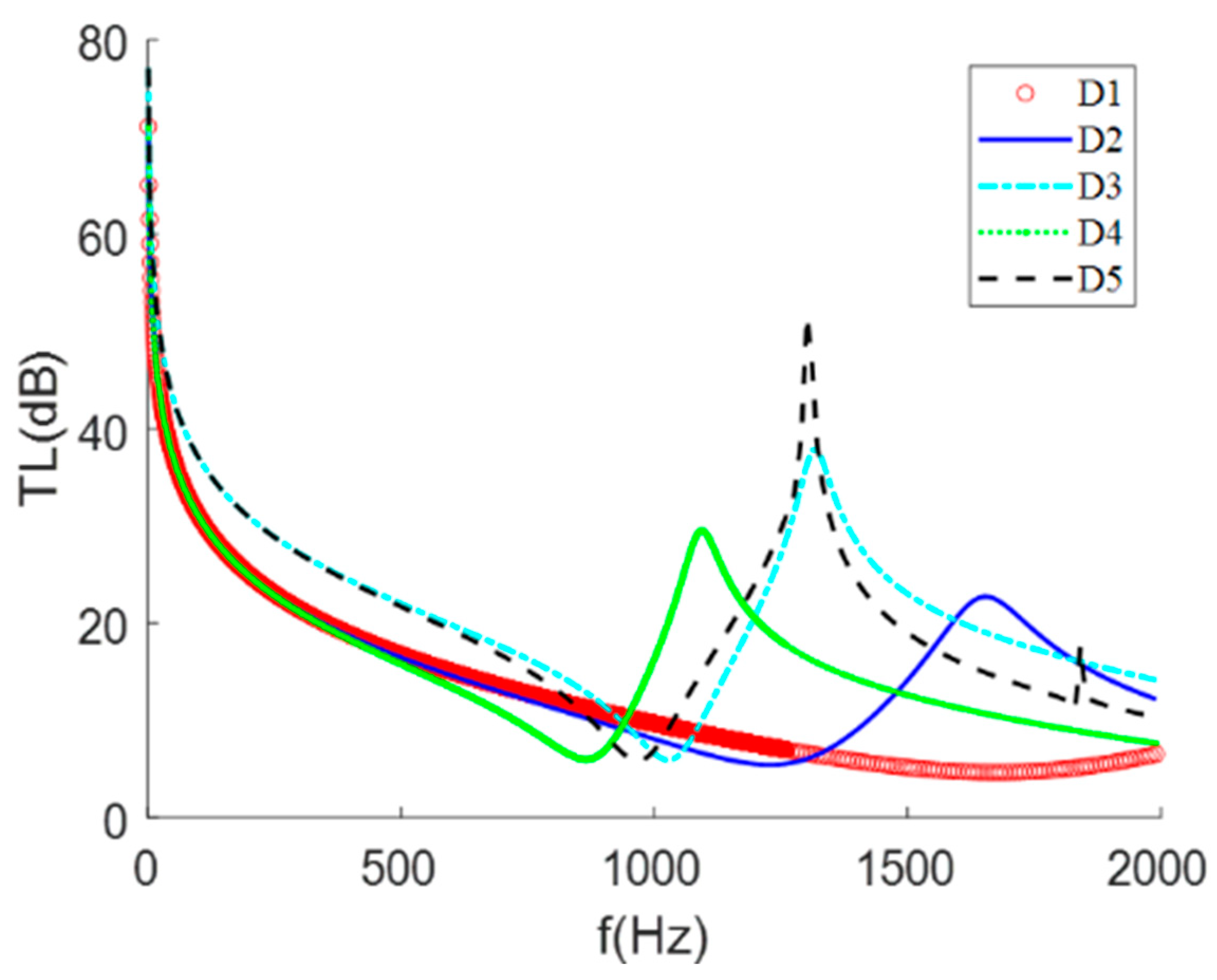
3.2. Hexagonal Pyramid Mass Block
4. Discussion
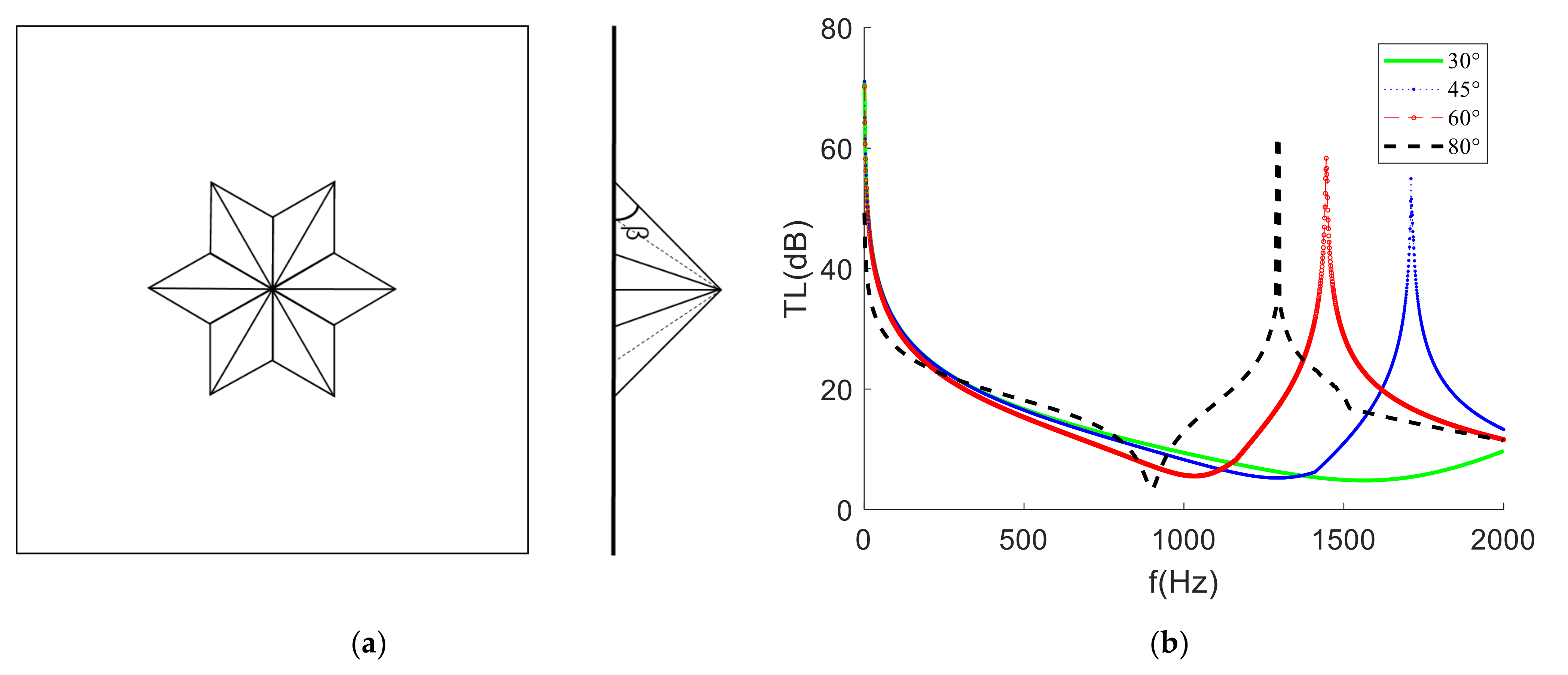
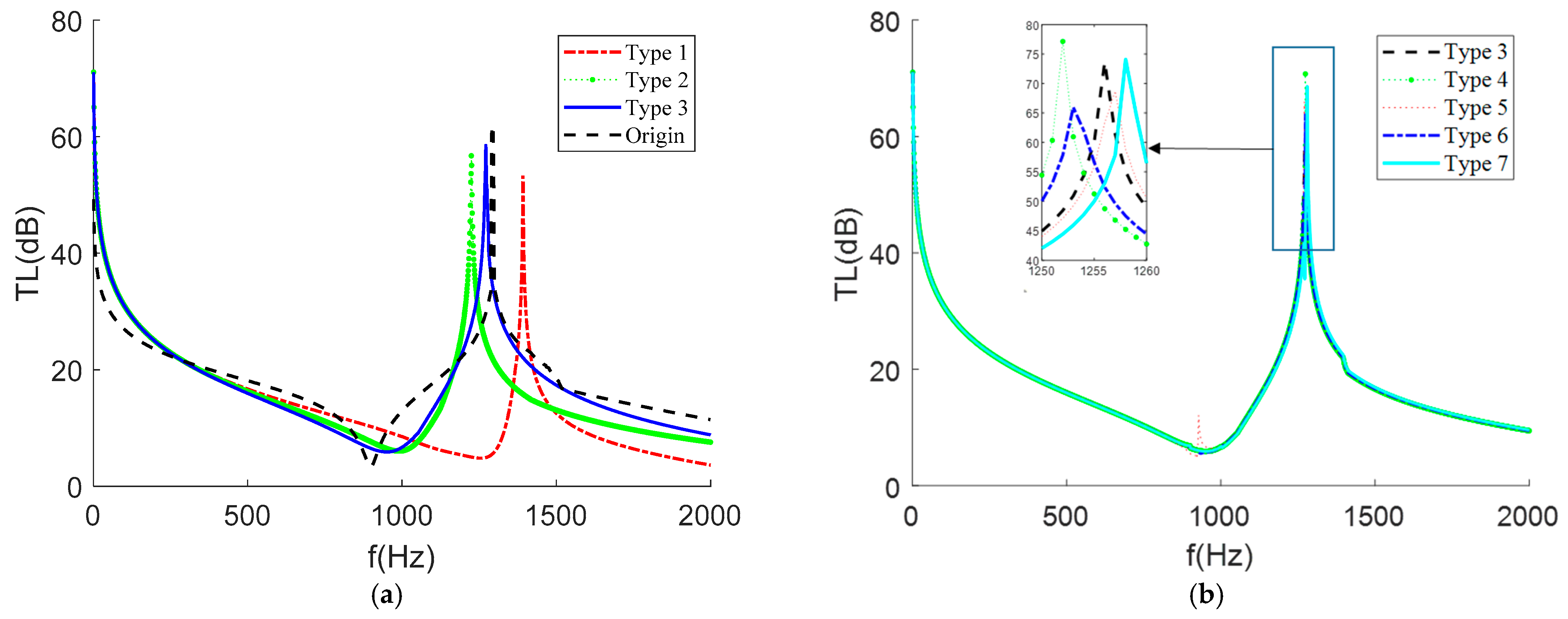
4.1. Longitudinal Inclination Angle
4.2. Different Defect States of Hexagonal Cone
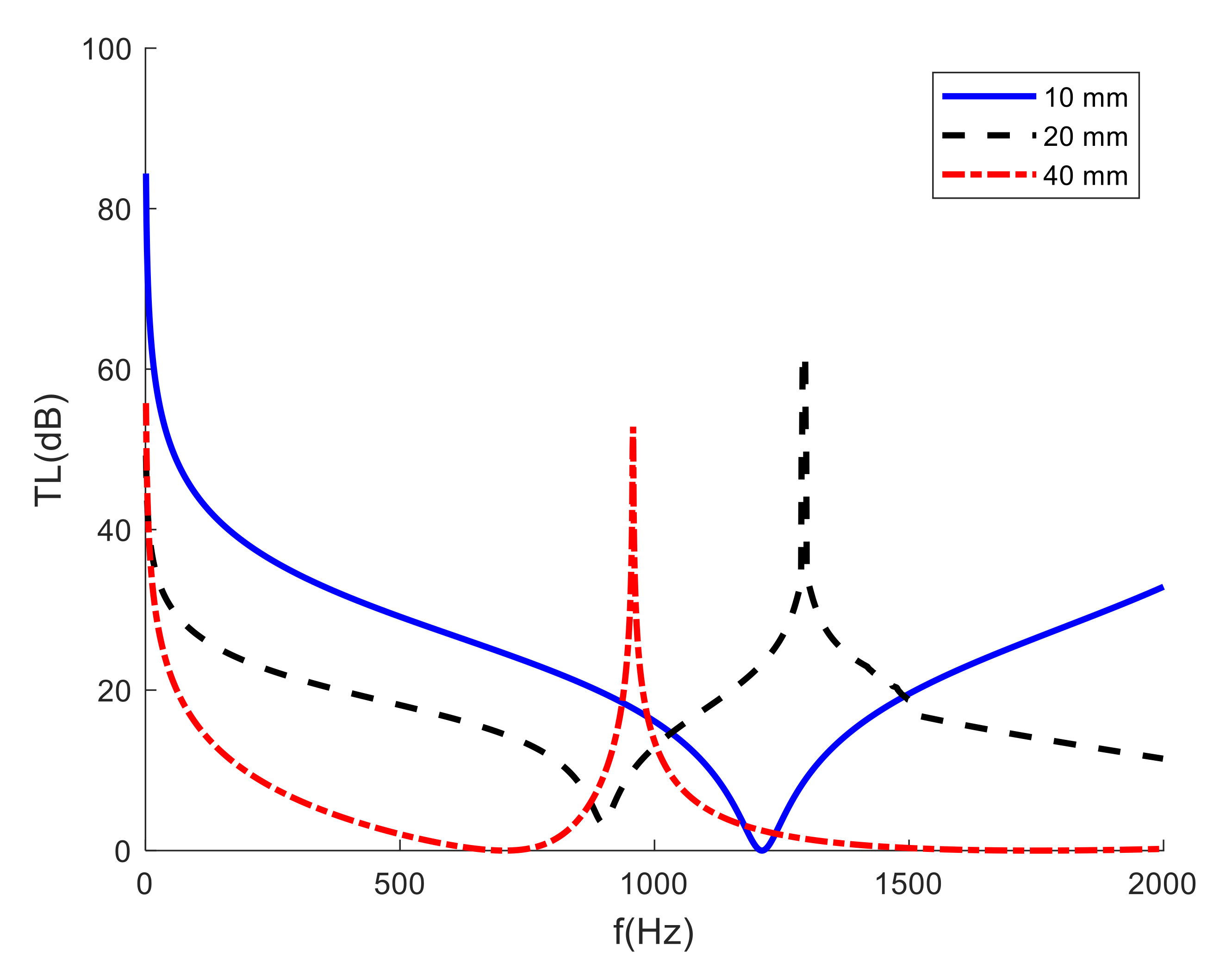
4.3. Films of Different Sizes
5. Conclusions
- (1)
- The more the areal density was concentrated in the middle of the mass block, the greater the peak sound insulation and the lower the frequency of occurrence.
- (2)
- The quality of the mass block affected the size of the sound insulation peak and the position of the center of mass affected the number of peaks of the curve.
- (3)
- The STL of a single mass block membrane-type metamaterial was mainly influenced by the distance between the mass block center of mass and the film center of mass, as well as the distance between the mass block relative to the film boundary, and was basically independent of the angle between the two objects’ centers of mass.
- (4)
- When the mass of the proof mass was constant, the film size controlled the magnitude of STL and the frequency of the peaks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Israilov, M.S. Diffraction of Acoustic Waves on a Half-Plane in the Case of Impedance Boundary Conditions. Applications to Sound Barriers. Mosc. Univ. Mech. Bull. 2020, 75, 7–12. [Google Scholar] [CrossRef]
- Li, D.; Chang, D.; Liu, B. Diffuse Sound Absorptive Properties of Parallel-Arranged Perforated Plates with Extended Tubes and Porous Materials. Materials 2020, 13, 1091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled membranes with doubly negative mass density and bulk modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yao, H.; Du, J.; Sun, Y.; Sun, Y.; Tan, J.; Zhang, X. Analysis of low-frequency sound insulation characteristics of ring-shaped local resonance elastic membrane structure. Bull. Chin. Ceram. Soc. 2017, 36, 7. [Google Scholar]
- Edwards, W.T.; Chang, C.M.; Mcknight, G.; Sorensen, A.; Nutt, R.S. Transmission Loss and Dynamic Response of Hierarchical Membrane-Type Acoustic Metamaterials. J. Vib. Acoust. 2019, 142, 021007. [Google Scholar] [CrossRef]
- Ma, G.; Yang, M.; Xiao, S.; Yang, Z.; Sheng, P. Acoustic metasurface with hybrid resonances. Nat. Mater. 2014, 13, 873–878. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Lv, M.; Luo, W.; Zhang, H.; Geng, D.; Li, Q. Sound Insulation Properties of Membrane-type Acoustic Metamaterials with Petal-like Split rings. J. Phys. D Appl. Phys. 2021, 55, 045104. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, X.; Lau, S.K.; Khoo, B.C.; Cui, F. Membrane-type acoustic metamaterial with eccentric masses for broadband sound isolation. Appl. Acoust. 2019, 157, 107003. [Google Scholar] [CrossRef]
- Zhou, G.; Wu, J.H.; Lu, K.; Tian, X.; Huang, W.; Zhu, K. Broadband low-frequency membrane-type acoustic metamaterials with multi-state anti-resonances. Appl. Acoust. 2020, 159, 107078. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Xie, S. A lightweight multilayer honeycomb membrane-type acoustic metamaterial. Appl. Acoust. 2020, 168, 107427. [Google Scholar] [CrossRef]
- Gao, C.; Halim, D.; Yi, X. Study of bandgap property of a bilayer membrane-type metamaterial applied on a thin plate. Int. J. Mech. Sci. 2020, 184, 105708. [Google Scholar] [CrossRef]
- Cai, M.; Tian, H.; Liu, H.; Qie, Y. Low frequency sound insulation performance of asymmetric coupled-membrane acoustic metamaterials. Multidiscip. Model. Mater. Struct. 2019, 15, 1006–1015. [Google Scholar] [CrossRef]
- Kornhauser, E.T. On the Vibration of Mass-Loaded Membranes. J. Acoust. Soc. Am. 1953, 25, 903–906. [Google Scholar] [CrossRef]
- Cohen, H.; Handelman, G. On the Vibration of a Circular Membrane with Added Mass. J. Acoust. Soc. Am. 1957, 29, 229. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Yong, X.; Xisen, W.; Jianwei, W. Theoretical investigation of the sound attenuation of membrane-type acoustic metamaterials. Phys. Lett. A 2012, 376, 1489–1494. [Google Scholar] [CrossRef]
- Tian, H.; Wang, X.; Zhou, Y.H. Theoretical model and analytical approach for a circular membrane–ring structure of locally resonant acoustic metamaterial. Appl. Phys. A 2014, 114, 985–990. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, G.; Zhou, X.; Hu, G.; Sun, C.T. Analytical coupled vibroacoustic modeling of membrane-type acoustic metamaterials: Membrane model. J. Acoust. Soc. Am. 2014, 136, 2926–2934. [Google Scholar] [CrossRef] [Green Version]
- Langfeldt, F.; Gleine, W.; Estorff, O.V. Analytical model for low-frequency transmission loss calculation of membranes loaded with arbitrarily shaped masses. J. Sound Vib. 2015, 349, 315–329. [Google Scholar] [CrossRef]
- Langfeldt, F.; Gleine, W.; Estorff, O.V. An efficient analytical model for baffled, multi-celled membrane-type acoustic metamaterial panels. J. Sound Vib. 2018, 417, 359–375. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Kopmaz, O.; Telli, S. Free Vibrations of a Rectangular Plate Carrying a Distributed Mass. J. Sound Vib. 2002, 251, 39–57. [Google Scholar] [CrossRef]

| Material | Young’s Modulus (E) | Poisson’s Ratio (nu) | Density (ρ) |
|---|---|---|---|
| PEI | 2.9 GPa | 0.44 | 1270 kg/m3 |
| Structural steel | 210 GPa | 0.30 | 7860 kg/m3 |
| Defect State | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x (mm) | 0 | 0.188 | −0.25 | 0.188 | 0.075 |
| y (mm) | 0.433 | 0.325 | 0.144 | 0 | 0.043 |
| z (mm) | 0.075 | 0.075 | 0.075 | 0.075 | 0.075 |
| Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Angle (°) | 0 | 0 | 0 | 10 | 20 | 30 | 45 |
| Distance (mm) | 7.5 | 5.0 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shi, Y.; Jiang, R.; Zhang, Z.; Huang, Q. Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density. Materials 2022, 15, 1556. https://doi.org/10.3390/ma15041556
Li J, Shi Y, Jiang R, Zhang Z, Huang Q. Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density. Materials. 2022; 15(4):1556. https://doi.org/10.3390/ma15041556
Chicago/Turabian StyleLi, Junyu, Yuanyuan Shi, Renjie Jiang, Zhifu Zhang, and Qibai Huang. 2022. "Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density" Materials 15, no. 4: 1556. https://doi.org/10.3390/ma15041556
APA StyleLi, J., Shi, Y., Jiang, R., Zhang, Z., & Huang, Q. (2022). Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density. Materials, 15(4), 1556. https://doi.org/10.3390/ma15041556







