Cavity Nucleation and Growth in Nickel-Based Alloys during Creep
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Creep Testing
2.3. Density Measurements
2.4. Secondary Electron Microscopy
3. Model Development
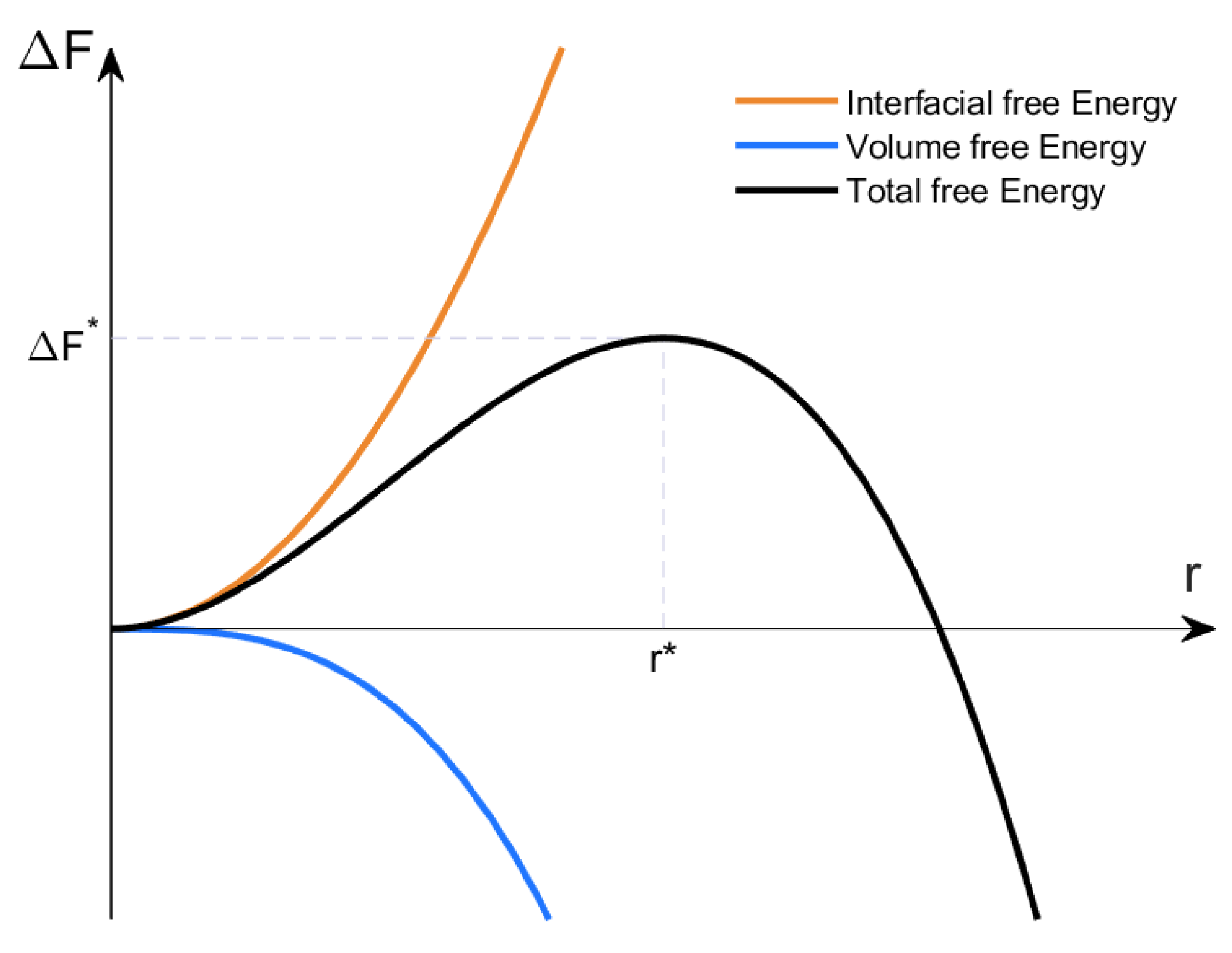
3.1. Classical Nucleation Theory
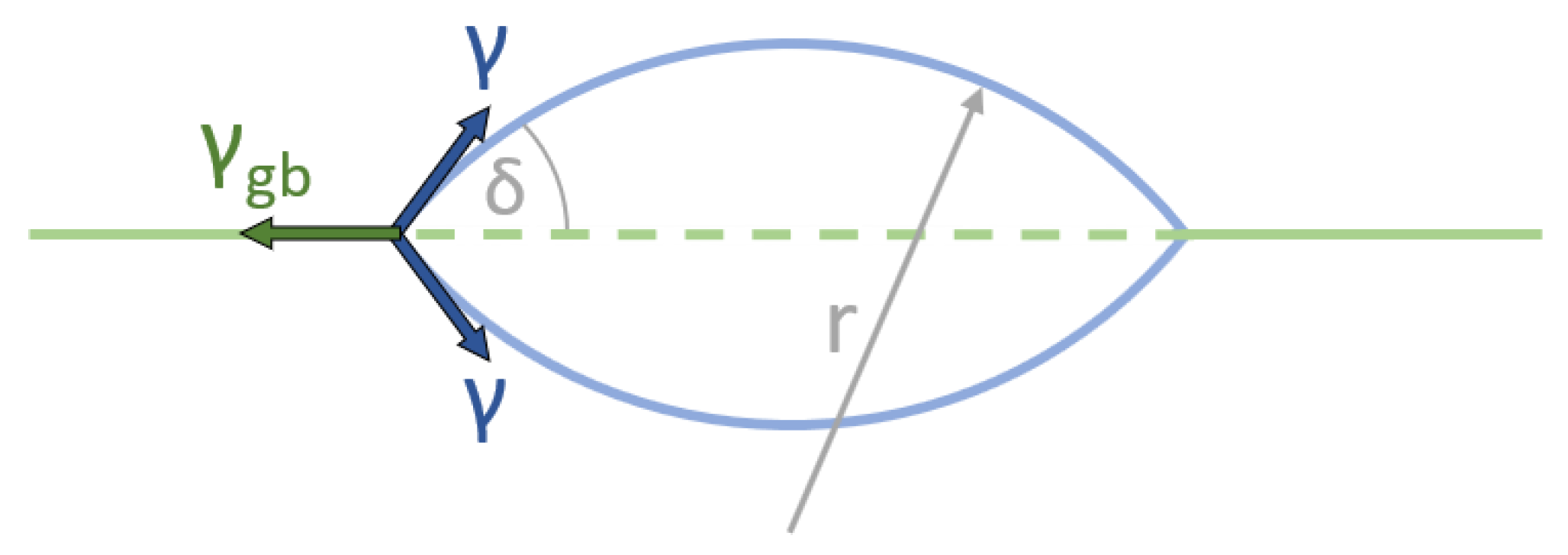
3.2. Heterogenous Nucleation at Grain Boundaries
3.3. Cavity Growth
3.4. Modelling Implementation
4. Results
4.1. Density
4.2. SEM
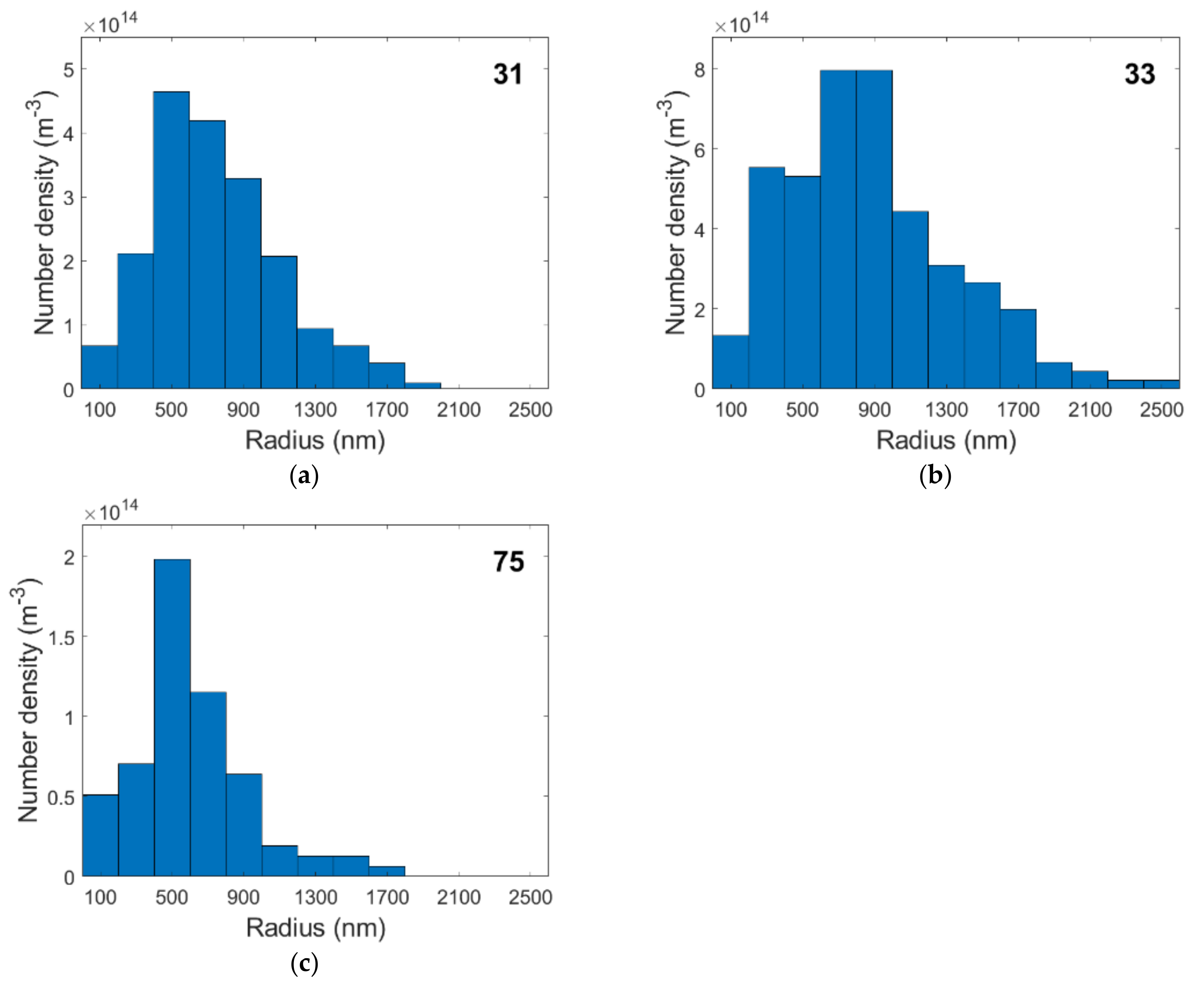
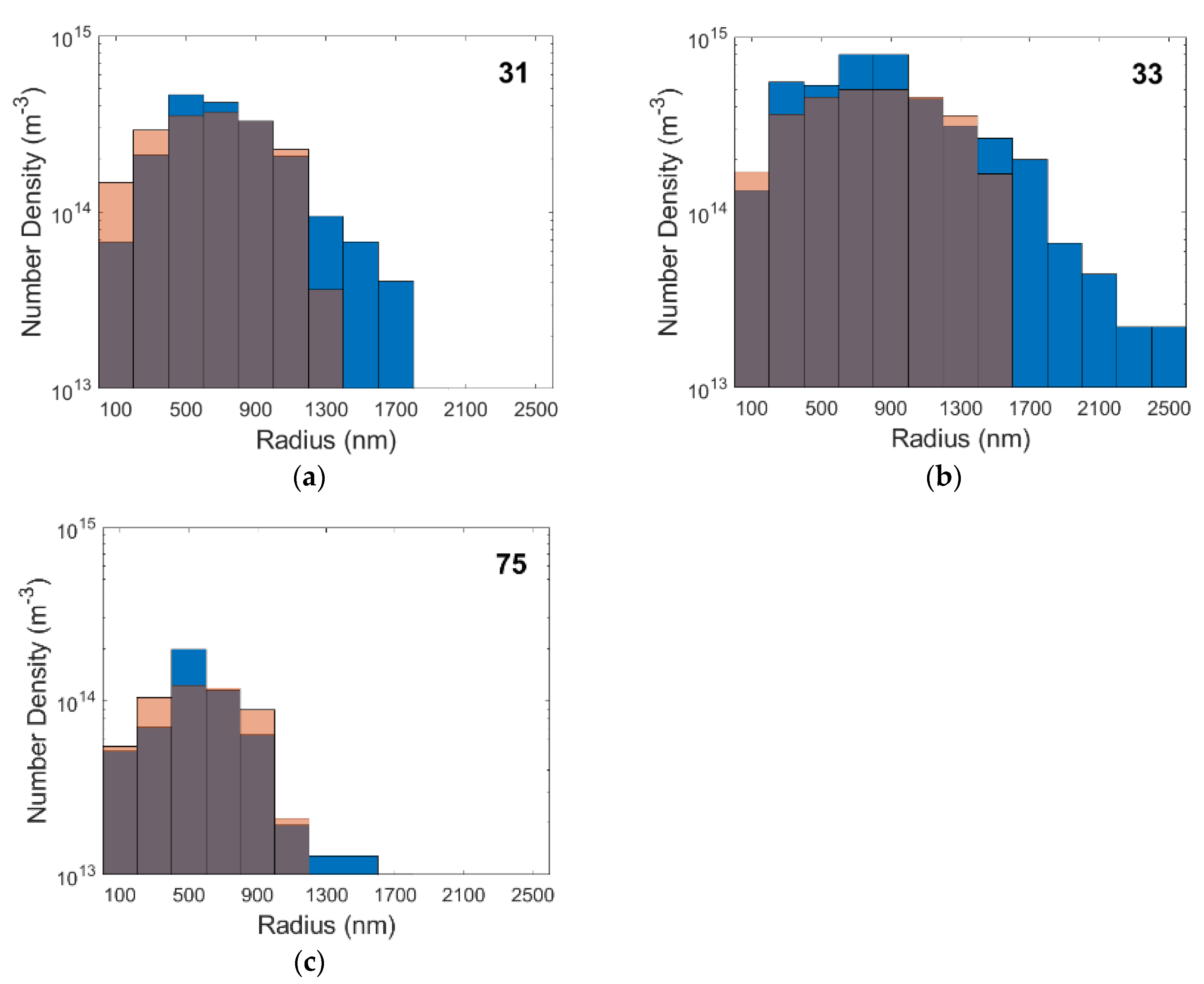
4.3. Cavity Distributions and Number Densities
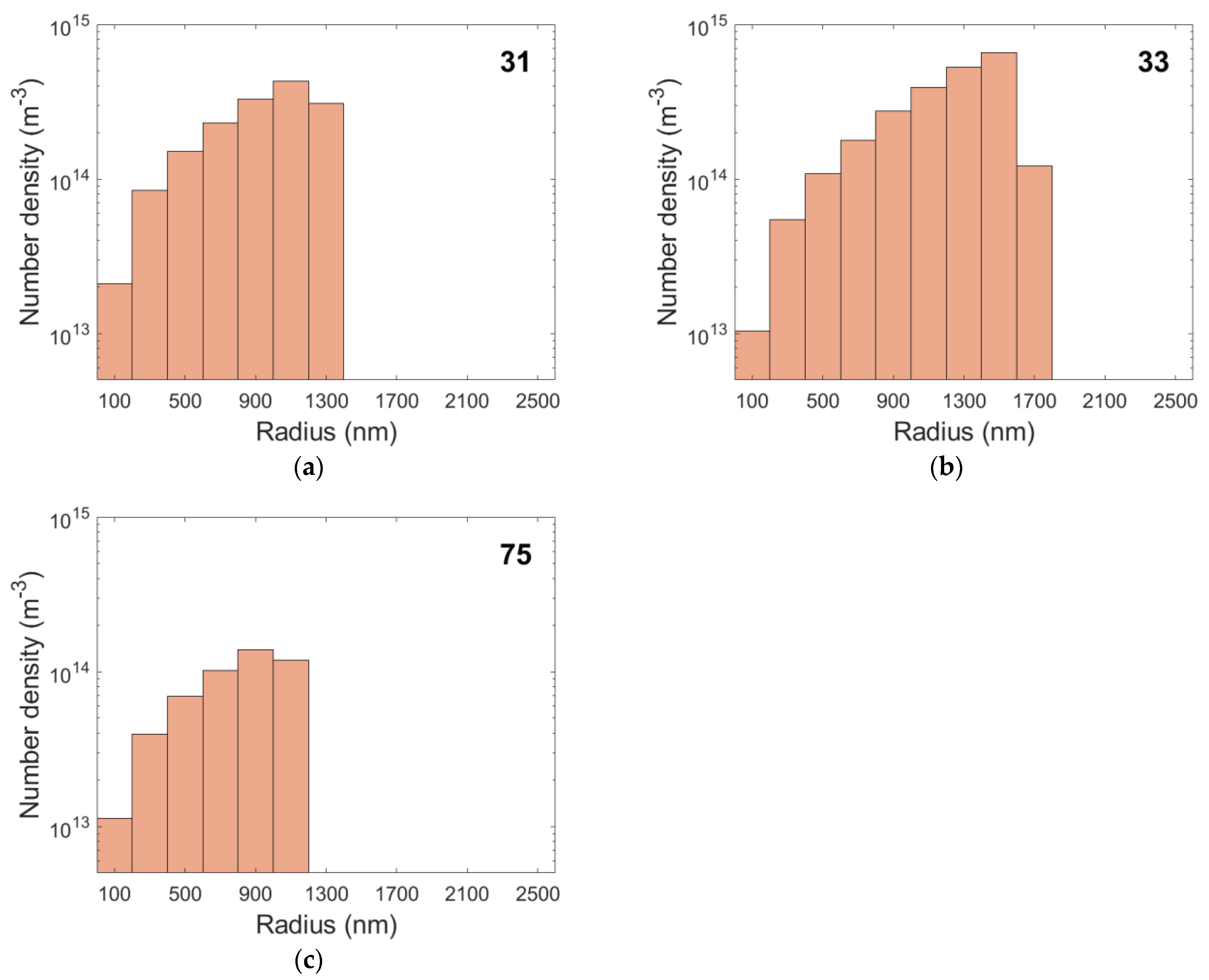
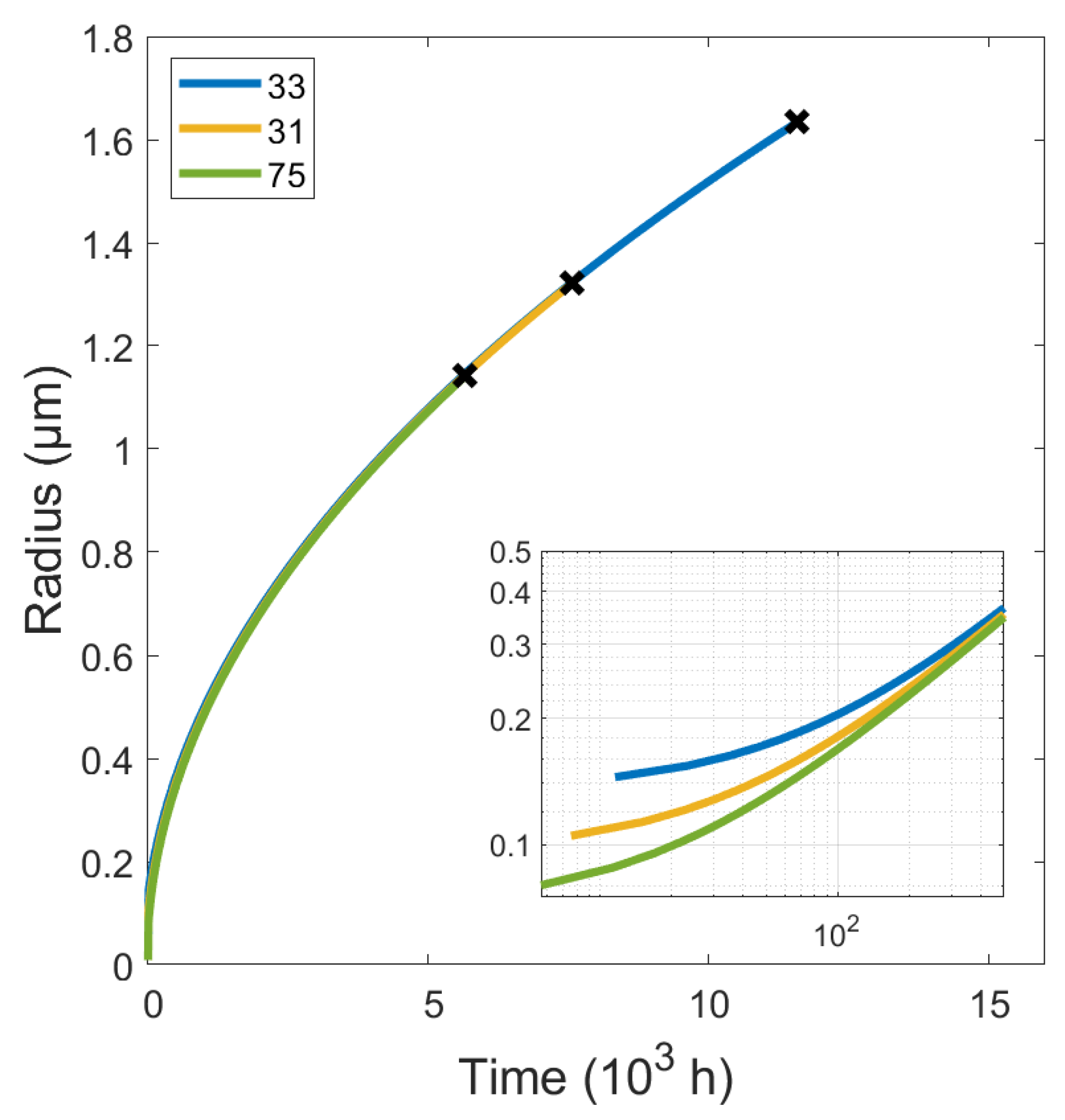
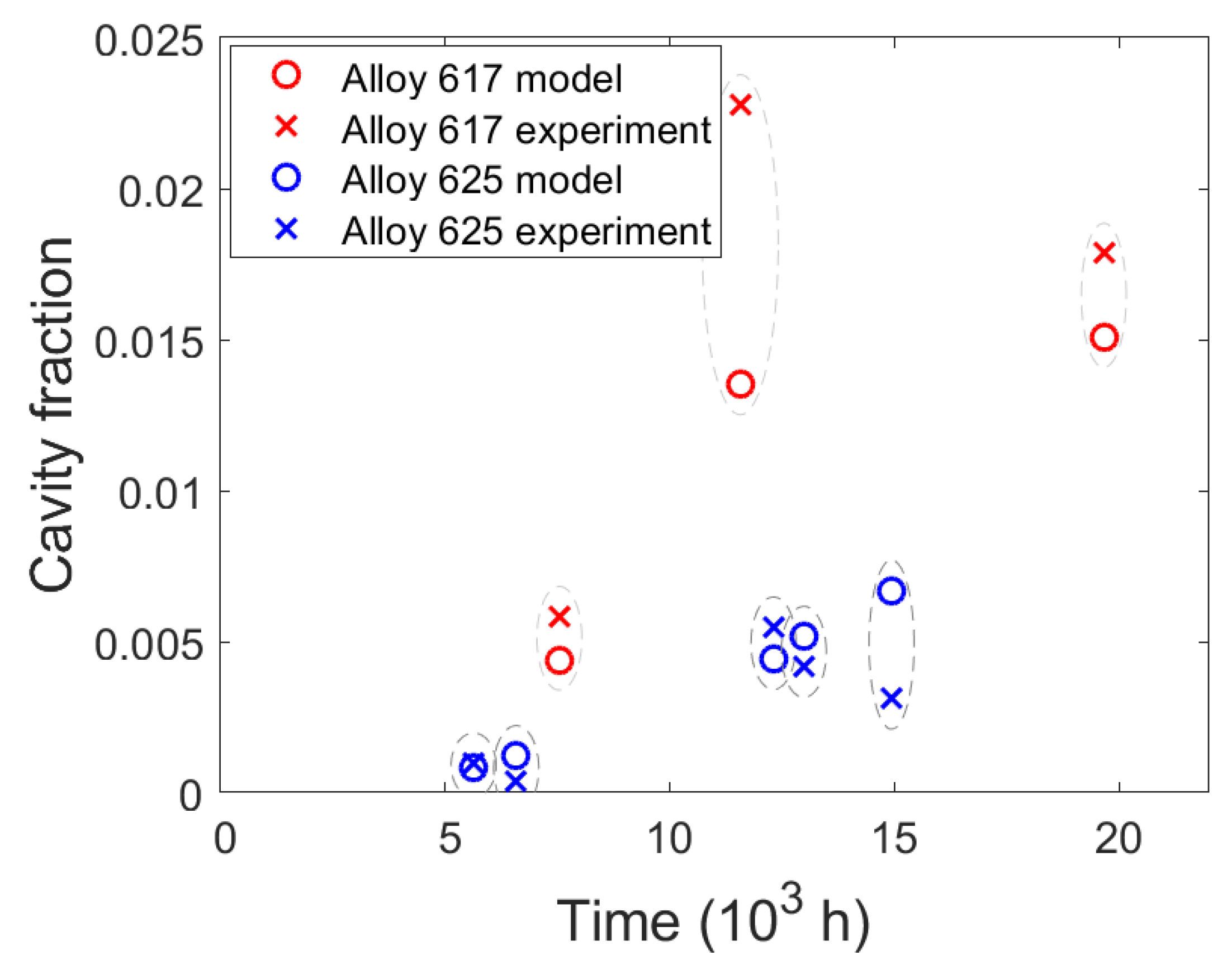
4.4. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sims, C.T. A History of Superalloy Metallurgy for Superalloy Metallurgists. In Proceedings of the Superalloys 1984 (Fifth International Symposium), Champion, PA, USA, 7–11 October 1984; TMS: Champion, PA, USA, 1984; pp. 399–419. [Google Scholar]
- Di Gianfrancesco, A. Materials for Ultra-Supercritical and Advanced Ultra-Supercritical Power Plants; Woodhead Publishing: Sawston, UK, 2016; ISBN 9780081005583. [Google Scholar]
- Ashby, M.F. Mechanisms of Deformation and Fracture. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 23, pp. 117–177. ISBN 0120020238. [Google Scholar]
- Dewa, R.T.; Park, J.H.; Kim, S.J.; Lee, S.Y. High-temperature creep-fatigue behavior of alloy 617. Metals 2018, 8, 103. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira, M.M.; Couto, A.A.; Almeida, G.F.C.; Reis, D.A.P.; De Lima, N.B.; Baldan, R. Mechanical behavior of inconel 625 at elevated temperatures. Metals 2019, 9, 301. [Google Scholar] [CrossRef] [Green Version]
- Utada, S.; Després, L.; Cormier, J. Ultra-high temperature creep of ni-based sx superalloys at 1250 °C. Metals 2021, 11, 1610. [Google Scholar] [CrossRef]
- Resnick, R.; Siegle, L. Nucleation of voids in Metals During Diffusion and Creep. Acta Metall. 1971, 19, 753–758. [Google Scholar] [CrossRef]
- Huang, L.; Sauzay, M.; Cui, Y.; Bonnaille, P. Theoretical and experimental study of creep damage in alloy 800 at high temperature. Mater. Sci. Eng. A 2021, 813, 140953. [Google Scholar] [CrossRef]
- Kassner, M.E.; Hayes, T.A. Creep cavitation in metals. Int. J. Plast. 2003, 19, 1715–1748. [Google Scholar] [CrossRef]
- Needham, N.G.; Wheatley, J.E.; Greenwood, G.W. The creep fracture of copper and magnesium. Acta Metall. 1975, 23, 23–27. [Google Scholar] [CrossRef]
- Davanas, K. Determination of creep cavity nucleation rates. Mater. High Temp. 2020, 37, 75–80. [Google Scholar] [CrossRef]
- He, J.; Sandström, R. Formation of creep cavities in austenitic stainless steels. J. Mater. Sci. 2016, 51, 6674–6685. [Google Scholar] [CrossRef]
- He, J.; Sandström, R. Creep cavity growth models for austenitic stainless steels. Mater. Sci. Eng. A 2016, 674, 328–334. [Google Scholar] [CrossRef]
- He, J.; Sandström, R. Modelling grain boundary sliding during creep of austenitic stainless steels. J. Mater. Sci. 2016, 51, 2926–2934. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Kinetische Behandlung der Keimbildung in übersättigten Dämpfen. Ann. Phys. 1935, 416, 719–752. [Google Scholar] [CrossRef]
- Raj, R.; Ashby, M. Intergranular fracture at elevated temperature. Acta Metall. 1975, 23, 653–666. [Google Scholar] [CrossRef]
- Fernandez-Caballero, A.; Cocks, A.C.F. Creep cavities: Theoretical formulation of cavity nucleation in the presence of dislocation defects. In Proceedings of the Euromat 2021, Graz, Austria, 12–16 September 2021. [Google Scholar]
- Svoboda, J.; Fischer, F.D.; Fratzl, P.; Kozeschnik, E. Modelling of kinetics in multi-component multi-phase systems with spherical precipitates I: Theory. Mater. Sci. Eng. A 2004, 385, 166–174. [Google Scholar] [CrossRef]
- Hull, D.; Rimmer, D.E. The growth of grain-boundary voids under stress. Philos. Mag. 1959, 4, 673–687. [Google Scholar] [CrossRef]
- Wagner, R.; Kampmann, R.; Voorhees, P.W. Homogeneous Second-Phase Precipitation. In Phase Transformations in Metals; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 309–407. ISBN 3527302565. [Google Scholar]
- Meixner, F.; Ahmadi, M.R.; Sommitsch, C. Modeling and Simulation of Pore Formation in a Bainitic Steel During Creep. Metall. Mater. Trans. A 2022, 53, 984–999. [Google Scholar] [CrossRef]
- Ahmadi, M.R.; Sonderegger, B.; Yadav, S.D.; Poletti, C. Modelling and simulation of diffusion driven pore formation in martensitic steels during creep. Mater. Sci. Eng. A 2018, 712, 466–477. [Google Scholar] [CrossRef]
- Clemens, B.M.; Nix, W.D.; Gleixner, R.J. Void nucleation on a contaminated patch. J. Mater. Res. 1997, 12, 2038–2042. [Google Scholar] [CrossRef]
- Inconel Alloy 617. Available online: https://www.specialmetals.com/documents/technical-bulletins/inconel/inconel-alloy-617.pdf (accessed on 28 September 2021).
- Inconel Alloy 625. Available online: https://www.specialmetals.com/documents/technical-bulletins/inconel/inconel-alloy-625.pdf (accessed on 28 September 2021).
- Mathew, M.D.; Parameswaran, P.; Bhanu Sankara Rao, K. Microstructural changes in alloy 625 during high temperature creep. Mater. Charact. 2008, 59, 508–513. [Google Scholar] [CrossRef]
- Krenmayr, B. Mikrostrukturbasierte Kriechmodellierung von martensitischen Stählen und Untersuchung möglicher Abweichungen beim Kriechexperiment. Ph.D. Thesis, Graz University of Technology, Graz, Austria, June 2020. [Google Scholar]
- Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden. Z. Phys. Chem. 1926, 119, 277–301. [Google Scholar] [CrossRef]
- Farkas, L. Keimbildungsgeschwindigkeit in übersättigten Dämpfen. Z. Phys. Chem. 1926, 11, 236–242. [Google Scholar] [CrossRef]
- Kozeschnik, E. Modeling Solid-State Precipitation; Momentum Press: New York, NY, USA, 2012; ISBN 9781606500620. [Google Scholar]
- Slezov, V.V.; Schmelzer, J. Kinetics of formation and growth of a new phase with a definite stoichiometric composition. J. Phys. Chem. Solids 1994, 55, 243–251. [Google Scholar] [CrossRef]
- Fan, Z.; Men, H.; Wang, Y.; Que, Z. A new atomistic mechanism for heterogeneous nucleation in the systems with negative lattice misfit: Creating a 2D template for crystal growth. Metals 2021, 11, 478. [Google Scholar] [CrossRef]
- Hirth, J.P.; Nix, W.D. Analysis of cavity nucleation in solids subjected to external and internal stresses. Acta Metall. 1985, 33, 359–368. [Google Scholar] [CrossRef]
- Riedel, H. Fracture at High Temperatures; Springer: Berlin/Heidelberg, Germany, 1987; ISBN 978-3-642-82963-5. [Google Scholar]
- Zeldovich, Y.B.; Sunyaev, R. 10. On the Theory of New Phase Formation. Cavitation. In Selected Works of Yakov Borisovich Zeldovich, Volume I; Princeton University Press: Princeton, NJ, USA, 1992; pp. 120–137. [Google Scholar]
- Russell, K.C. Nucleation in solids: The induction and steady state effects. Adv. Colloid Interface Sci. 1980, 13, 205–318. [Google Scholar] [CrossRef]
- Lee, J.K.; Aaronson, H. Influence of faceting upon the equilibrium shape of nuclei at grain boundaries—II. Three-dimensions. Acta Metall. 1975, 23, 809–820. [Google Scholar] [CrossRef]
- Anderson, P.M.; Rice, J.R. Constrained creep cavitation of grain boundary facets. Acta Metall. 1985, 33, 409–422. [Google Scholar] [CrossRef]
- Sonderegger, B.; Kozeschnik, E. Generalized nearest-neighbor broken-bond analysis of randomly oriented coherent interfaces in multicomponent Fcc and Bcc structures. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2009, 40, 499–510. [Google Scholar] [CrossRef]
- Vitos, L.; Ruban, A.V.; Skriver, H.L.; Kollár, J. The surface energy of metals. Surf. Sci. 1998, 411, 186–202. [Google Scholar] [CrossRef]
- Benson, G.C.; Shuttleworth, R. The Surface Energy of Small Nuclei. J. Chem. Phys. 1951, 19, 130–131. [Google Scholar] [CrossRef]
- Speight, M.V.; Beere, W. Vacancy Potential and Void Growth on Grain Boundaries. Met. Sci. J. 1975, 9, 190–191. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Rajek, H. Computer Simulation of Precipitation Kinetics in Solid Metals and Application to the Complex Power Plant Steel CB8. 2005. Available online: https://graz.pure.elsevier.com/en/projects/computer-simulation-of-precipitation-kinetics-in-solid-metals-and (accessed on 20 January 2022).
- Prokoshkina, D.; Esin, V.A.; Wilde, G.; Divinski, S.V. Grain boundary width, energy and self-diffusion in nickel: Effect of material purity. Acta Mater. 2013, 61, 5188–5197. [Google Scholar] [CrossRef]
- Janotti, A.; Krčmar, M.; Fu, C.L.; Reed, R.C. Solute Diffusion in Metals: Larger Atoms Can Move Faster. Phys. Rev. Lett. 2004, 92, 085901. [Google Scholar] [CrossRef] [PubMed]
- Arblaster, J.W. Selected Values of the Crystallographic Properties of Elements; ASM International: Geauga County, OH, USA, 2018; ISBN 9781627081542. [Google Scholar]
- Davanas, K.; Solomon, A.A. Theory of intergranular creep cavity nucleation, growth and interaction. Acta Metall. Mater. 1990, 38, 1905–1916. [Google Scholar] [CrossRef]
- Jazaeri, H.; Bouchard, P.J.; Hutchings, M.T.; Spindler, M.W.; Mamun, A.A.; Heenan, R.K. An investigation into creep cavity development in 316h stainless steel. Metals 2019, 9, 318. [Google Scholar] [CrossRef] [Green Version]
- Gupta, C.; Toda, H.; Schlacher, C.; Adachi, Y.; Mayr, P.; Sommitsch, C.; Uesugi, K.; Suzuki, Y.; Takeuchi, A.; Kobayashi, M. Study of creep cavitation behavior in tempered martensitic steel using synchrotron micro-tomography and serial sectioning techniques. Mater. Sci. Eng. A 2013, 564, 525–538. [Google Scholar] [CrossRef]
- Riedlsperger, F.; Krenmayr, B.; Zuderstorfer, G.; Fercher, B.; Niederl, B.; Schmid, J.; Sonderegger, B. Application of an advanced mean-field dislocation creep model to P91 for calculation of creep curves and time-to-rupture diagrams. Materialia 2020, 12, 100760. [Google Scholar] [CrossRef]

| Alloys | Ni | Cr | Mo | Co | Al | Nb | Fe | Mn | Cu | Ti | Si | C | S | P | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alloy 617 | Bal | 21.94 | 8.64 | 11.68 | 1.16 | 1.02 | 0.04 | 0.03 | 0.39 | 0.08 | 0.06 | <0.002 | <0.002 | 0.002 | |
| Alloy 625 | Bal | 20.82 | 8.34 | 0.005 | 0.11 | 3.40 | 3.29 | 0.18 | 0.22 | 0.12 | 0.26 | 0.02 | 0.014 | 0.009 |
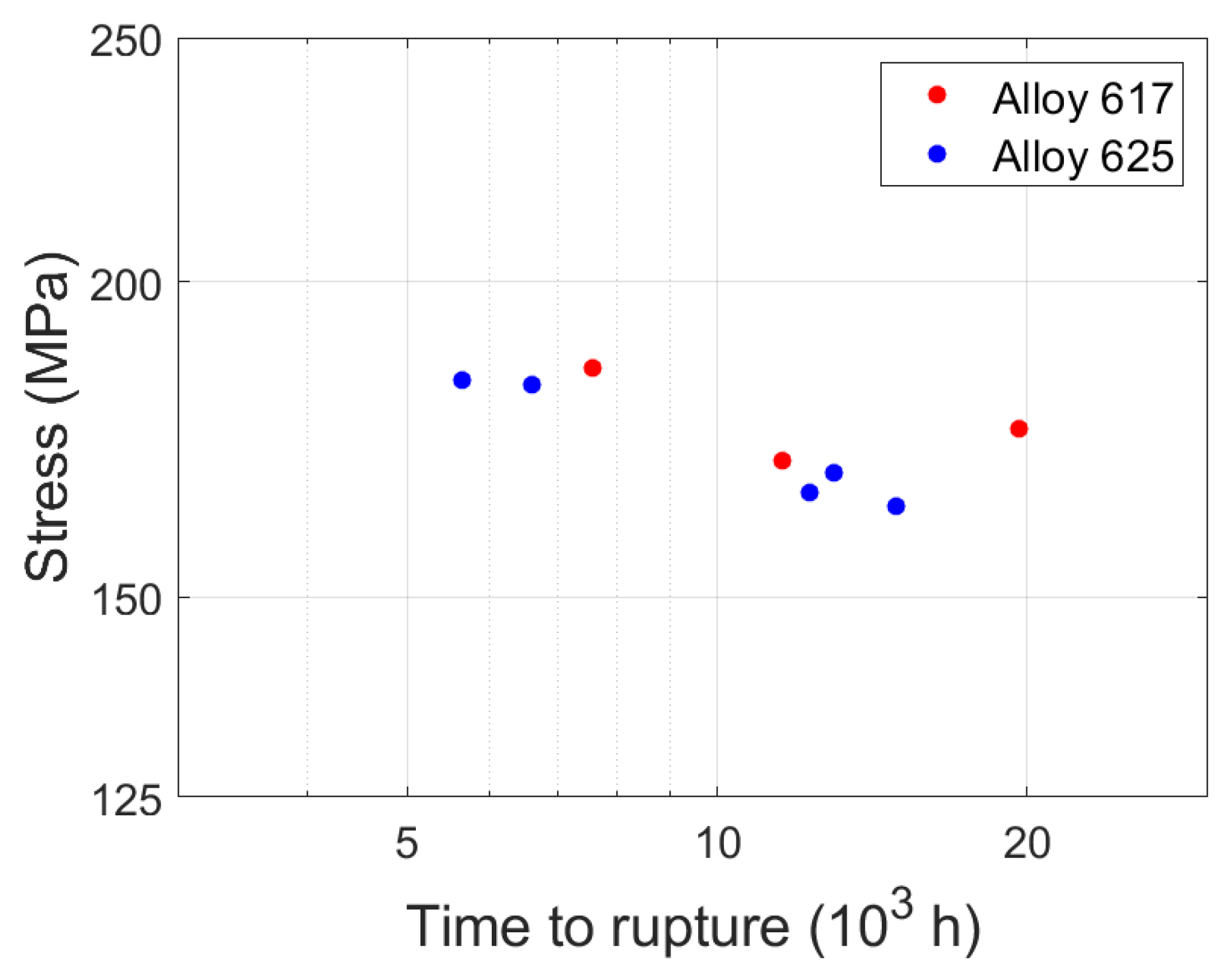
| Specimen ID | Material | Temperature (°C) | Stress (MPa) | Time to Rupture (h) | Neck Diameter (mm) |
|---|---|---|---|---|---|
| 31 | Alloy 617 | 700 | 185 | 7558 | 9.00 |
| 32 | Alloy 617 | 700 | 175 | 19,656 | 9.25 |
| 33 | Alloy 617 | 700 | 170 | 11,577 | 9.39 |
| 71 | Alloy 625 | 700 | 165 | 12,317 | 9.53 |
| 72 | Alloy 625 | 700 | 168 | 12,990 | 9.45 |
| 73 | Alloy 625 | 700 | 163 | 14,940 | 9.59 |
| 74 | Alloy 625 | 700 | 182 | 6600 | 9.07 |
| 75 | Alloy 625 | 700 | 183 | 5652 | 9.05 |
| Parameter | Description | Value |
|---|---|---|
| γ | Free surface energy of Ni | 1.84 J m−1 [39] |
| σ | Stress on specimen | Variable (described in Table 2) |
| Ns | Nucleation sites | Variable (described in Table 7) |
| k | Boltzmann constant | 1.380649 × 10−23 J K−1 |
| T | Temperature | 973 K (700 °C) |
| σD | Driving force of defects | 1.2 × 1010 Pa |
| γgb | Grain boundary energy of Ni | 0.8 J m−1 [45] |
| Qv | Vacancy formation energy in Ni | 1.7 eV [46] |
| DGB | Diffusion coefficient along grain boundaries of Ni | 1.511 × 10−12 m2 s−1 [45] |
| lp | Lattice parameter of fcc nickel | 0.3499 × 10−9 m [47] |
| Ω | Atomic volume | 1.0710 × 10−29 m |
| a | Interatomic spacing (Ω1/3) | 0.204 × 10−9 m |
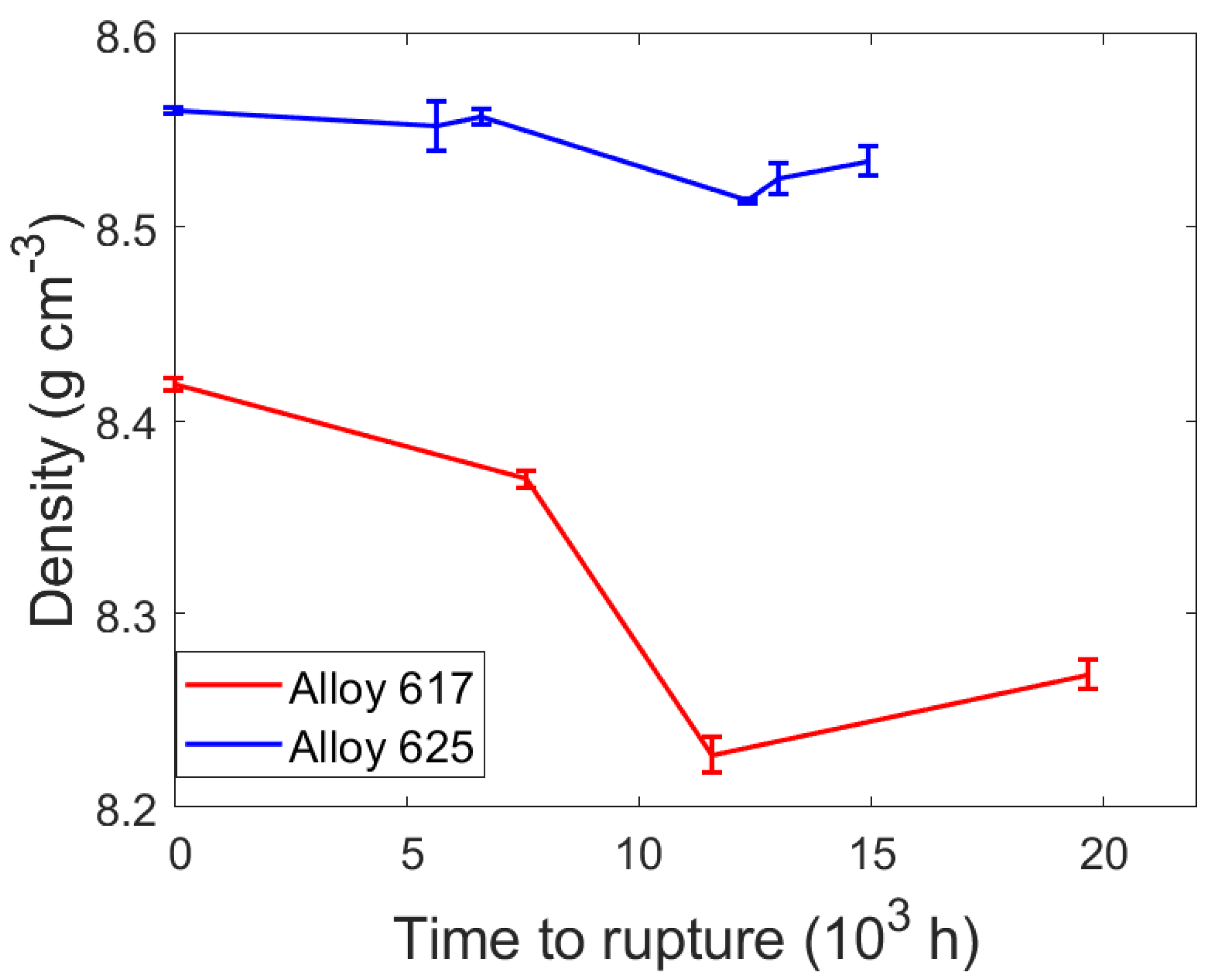
| Specimen | Time to Rupture (h) | Density, Mean ± SE (g/cm3) | Density Decrease (%) |
|---|---|---|---|
| Alloy 617 reference | - | 8.4188 ± 0.003 | - |
| 31 | 7558 | 8.3698 ± 0.004 | 0.58 |
| 32 | 19,656 | 8.2685 ± 0.007 | 1.79 |
| 33 | 11,577 | 8.2271 ± 0.009 | 2.28 |
| Alloy 625 reference | - | 8.5607 ± 0.002 | - |
| 71 | 12,317 | 8.5138 ± 0.001 | 0.55 |
| 72 | 12,990 | 8.5251 ± 0.008 | 0.42 |
| 73 | 14,940 | 8.5341 ± 0.008 | 0.31 |
| 74 | 6600 | 8.5574 ± 0.003 | 0.04 |
| 75 | 5652 | 8.5524 ± 0.012 | 0.10 |
| Specimen | Number of Cavities Measured | Radii Range (nm) |
|---|---|---|
| 31 | 424 | 69–1959 |
| 32 | 3 | 46–121 |
| 33 | 189 | 101–2942 |
| 71 | 17 | 17–234 |
| 72 | 18 | 18–682 |
| 73 | 22 | 20–113 |
| 74 | 55 | 3–712 |
| 75 | 86 | 25–1603 |
| Specimen | Phase Fraction of Cavities (%) | Vmean (µm3) | Number Density of Cavities (m−3) |
|---|---|---|---|
| 31 | 0.58 | 3.05 | 1.91 × 1015 |
| 33 | 2.27 | 5.44 | 4.18 × 1015 |
| 75 | 0.10 | 1.77 | 5.50 × 1014 |
| Specimen | Grain Diameter (m) | Ns (m−3) | Nucleation Rate (m−3s−1) |
|---|---|---|---|
| 31 | 200 × 10−6 | 2.65 × 1023 | 6.43 × 107 |
| 33 | 150 × 10−6 | 3.53 × 1023 | 7.58 × 107 |
| 75 | 500 × 10−6 | 1.06 × 1023 | 2.51 × 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meixner, F.; Ahmadi, M.R.; Sommitsch, C. Cavity Nucleation and Growth in Nickel-Based Alloys during Creep. Materials 2022, 15, 1495. https://doi.org/10.3390/ma15041495
Meixner F, Ahmadi MR, Sommitsch C. Cavity Nucleation and Growth in Nickel-Based Alloys during Creep. Materials. 2022; 15(4):1495. https://doi.org/10.3390/ma15041495
Chicago/Turabian StyleMeixner, Felix, Mohammad Reza Ahmadi, and Christof Sommitsch. 2022. "Cavity Nucleation and Growth in Nickel-Based Alloys during Creep" Materials 15, no. 4: 1495. https://doi.org/10.3390/ma15041495
APA StyleMeixner, F., Ahmadi, M. R., & Sommitsch, C. (2022). Cavity Nucleation and Growth in Nickel-Based Alloys during Creep. Materials, 15(4), 1495. https://doi.org/10.3390/ma15041495







