Next Article in Journal
Mechanical, Thermal, and Fire Properties of Composite Materials Based on Gypsum and PCM
Next Article in Special Issue
Size and Shape’s Effects on the High-Pressure Behavior of WS2 Nanomaterials
Previous Article in Journal
High-Temperature Wear Performance of hBN-Added Ni-W Composites Produced from Combustion-Synthesized Powders
Previous Article in Special Issue
High-Pressure Phases of SnO and PbO: A Density Functional Theory Combined with an Evolutionary Algorithm Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 15
Issue 3
10.3390/ma15031255
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First-Principles Study of High-Pressure Phase Stability and Electron Properties of Be-P Compounds

by
Han Liu
1,2,
Yaqian Dan
1,
Ao Zhang
1,2,
Siyuan Liu
3,
Jincheng Yue
1,
Junda Li
1,
Xuejiao Ma
4,
Yanping Huang
1,
Yanhui Liu
1,* and
Tian Cui
1,*
1
Institute of High Pressure Physics, School of Physical Science and Technology, Ningbo University, Ningbo 315211, China
2
Department of Physics, College of Science, Yanbian University, Yanji 133000, China
3
School of Physics, Southeast University, Nanjing 211189, China
4
Science and Technology on Transient Impact Laboratory, No. 208 Research Institute of Ordnance Industries, Beijing 102202, China
*
Authors to whom correspondence should be addressed.
Materials 2022, 15(3), 1255; https://doi.org/10.3390/ma15031255
Submission received: 23 December 2021 / Revised: 27 January 2022 / Accepted: 1 February 2022 / Published: 8 February 2022
(This article belongs to the Special Issue Advances in Structural Phase Transition and Physical Properties of Nanomaterials under High Pressure)
Browse Figures
Versions Notes

Abstract

:
New, stable stoichiometries in Be-P systems are investigated up to 100 GPa by the CALYPSO structure prediction method. Along with the BeP2-I41/amd structure, we identify two novel compounds of Be3P2-P-421m and Be3P2-C2/m. It should be noted that the Be-P compounds are predicted to be energetically unfavorable above 40 GPa. As can be seen, interesting structures may be experimentally synthesizable at modest pressure. Our results indicate that at 33.2 GPa, the most stable ambient-pressure tetragonal Be3P2-P-421m transitions to the monoclinic Be3P2-C2/m structure. Moreover, the predicted Be3P2-P-421m and Be3P2-C2/m phases are energetically favored compared with the Be3P2-Ia-3 structure synthesized experimentally. Electronic structure calculations reveal that BeP2-I41/amd, Be3P2-P-421m, and Be3P2-C2/m are all semiconductors with a narrow band gap. The present findings offer insight and guidance for exploration toward further fundamental understanding and potential applications in the semiconductor field.

1. Introduction

An important part of computational materials science is predicting novel forms of materials and describing their different characteristics, which are influenced by their electronic structures. Narrow-gap semiconducting substances are an important material with a number of applications, including lasers, infrared detectors, ultrasonic multipliers, and solar cells [1], electrically driven light sources [2], magnetic sensors [3], and thermophotovoltaic cells [4]. Although the III–V group phosphides and nitrides [5] have received the most attention, the II–V group compounds are also being investigated for optoelectronic applications [6,7,8]. Surprisingly, these compounds have abundant semiconductor properties [9,10,11] and crystallize in several phases [12,13]. The electronic structure of Mg3P2, as a II–V group compound, has been investigated by first principles. This compound has a straight bandgap of 1.73 eV, according to researchers [14]. There is ongoing debate over the stoichiometric composition of Ca3P2, and an experimental study on the thermodynamic properties of this compound has been published [15].
However, compared with their calcium and magnesium counterparts, beryllium phosphides have received little theoretical or experimental attention [16,17,18,19,20,21]. It is significant to recognize the crystal structures of any material in order to understand their physical and chemical properties, as well as their practical uses. Up to now, previous studies have demonstrated lattice constants of the anti-bixbyite structure of Be3P2 [20,21]. Regarding the tetragonal structure of Be3P2, based on structural refinements of X-ray and neutron diffraction data, Elmaslout reported lattice constants and structure factors [22]. According to Carvalho et al., Be3P2 microcrystals arise in Be-doped phosphorus-based semiconductor compounds generated by CBE (chemical beam epitaxy) in Be-rich environments and at temperatures over 500 °C [23]. Nevertheless, for semiconductor applications, high pressure phases are paramount. More than 90 percent of the matter in nature is under high pressure. As the pressure increases, the distance between atoms or molecules in condensed matter will gradually decrease, leading to an increase in the number of electron orbitals overlapping between adjacent atoms, which often leads to changes in the physical properties of the material itself. As a result, it is of the utmost importance to perform a thorough investigation of the crystal structure with varied beryllium phosphide stoichiometries and to explore the associated bonding properties under pressure.
In the present paper, utilizing first-principles swarm-intelligence structure search, we explored the binary Be-P phase diagram and built a complete understanding of its crystal structure evolution in the range from 0 to 100 GPa. Under environmental conditions, successfully reproduced BeP2-I41/amd and Be3P2-Ia-3 structures have been reported. In particular, for Be3P2 at ambient pressure, we predict a more favorable Be3P2-P-421m tetragonal structure than the experimentally synthesized structure of Be3P2-Ia-3. On the contrary, it can be discovered from the analysis of the calculation results that Be2P, BeP, and BeP3 are predicted to dissociate into Be and P under the pressure in our scheme. In the subsequent work, we provide a detailed discussion of the methods of our calculations and the results obtained, including structural parameters, electronic band structure, density of states (DOS), and bonding character of the beryllium phosphide systems. Our results are of great significance for the further study of the structures and properties of Be-P system under high pressures.

2. Computational Details

The structure search for the potential BePx (x = 1/2, 2/3, and 1–3) compounds under the pressure range of 0–100 GPa was carried out utilizing the CALYPSO code’’s particle swarm optimization methodology [24,25,26]. Several recent effective uses of this technology include structure predictions on various crystalline systems, as well as determining stable or metastable structures based on chemical composition [27,28,29,30]. The exchange-correlation potentials were handled using the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerh (PBE) [31,32]. The underlying optimizations were carried out utilizing the Vienna ab initio simulation (VASP) 5.4.1 software [33,34] and projector-augmented plane wave (PAW) [35] potentials with a 600 eV energy cutoff. The valence states of the Be and P potentials are 2s2 and 3s23p3, respectively. We employed the Monkhorst-Pack approach for the Brillouin region integral and tested the convergence of the ground state computations using consistently increasing k-point gridding for the considered structures. In order to obtain total energy astringency below 1 meV/atom, Monkhorst-Pack k-point grid is selected as 2π × 0.025 Å−1 [36,37]. Phonon dispersion curves are generated using a finite displacement approach in the PHONOPY program [38] to verify that the structures in the Be-P system are dynamically stable. The projector augmented wave (PAW) pseudopotential employing PBE and the band structures of Be-P phases are computed using the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional, in order to evade the innate weakness of GGA when handling the band structures of semiconducting materials [39].

3. Results

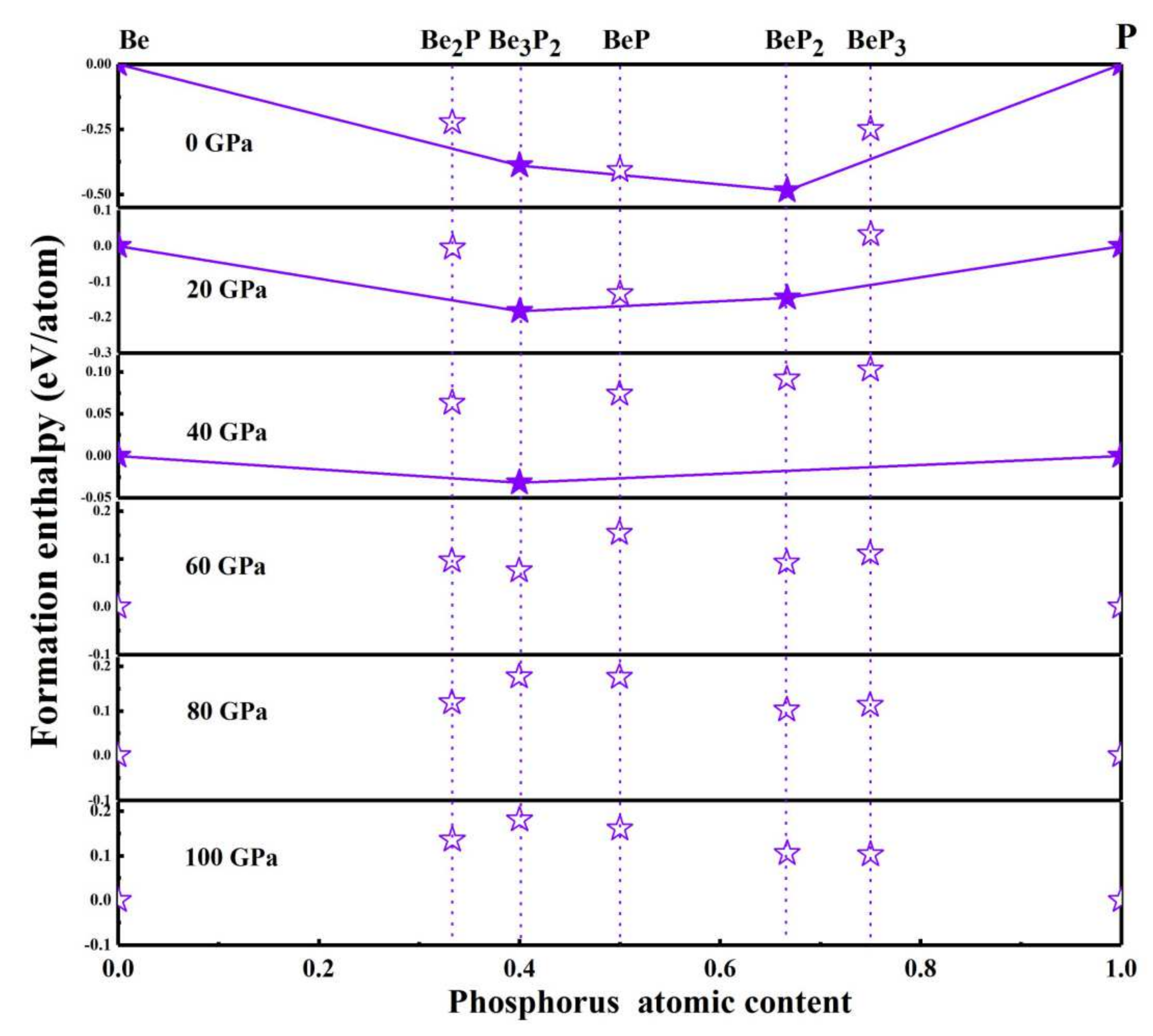
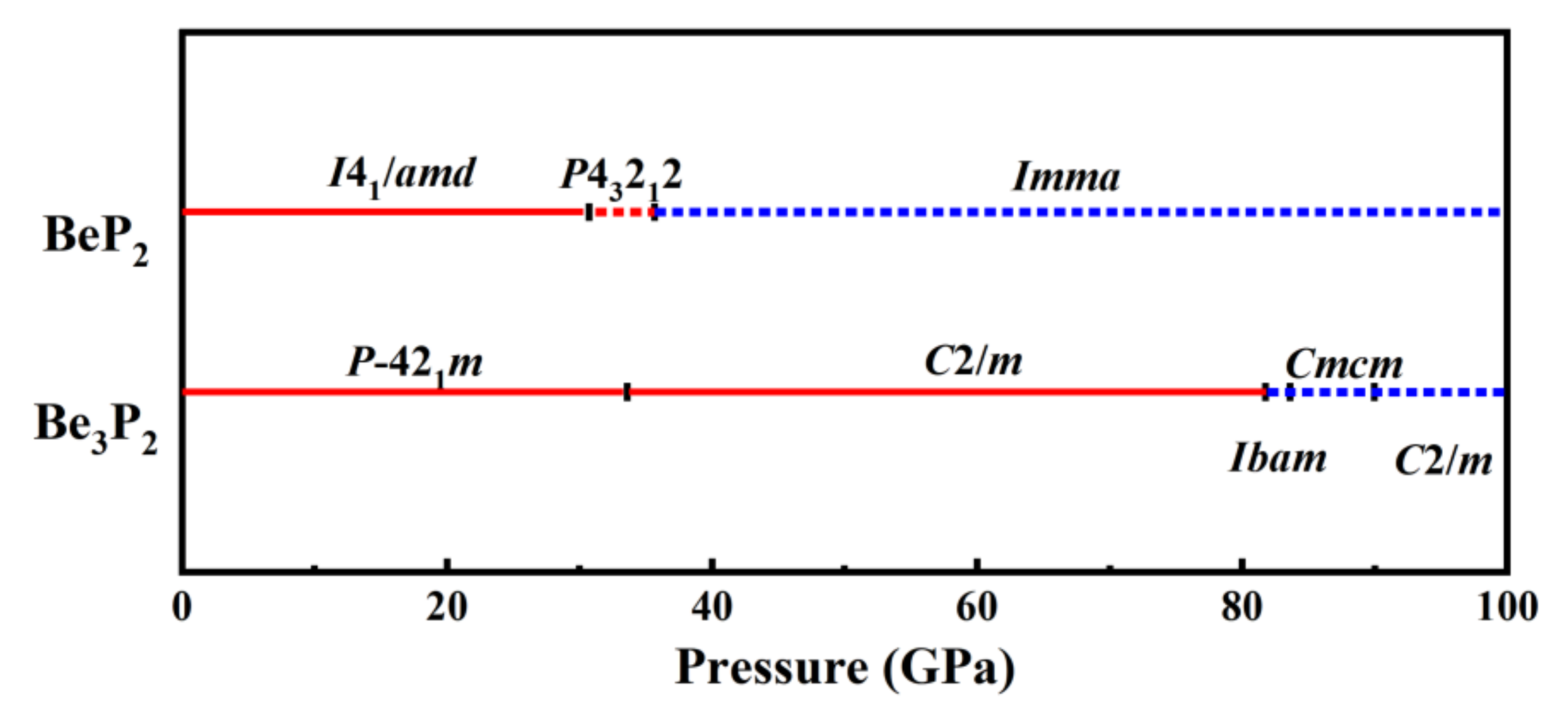
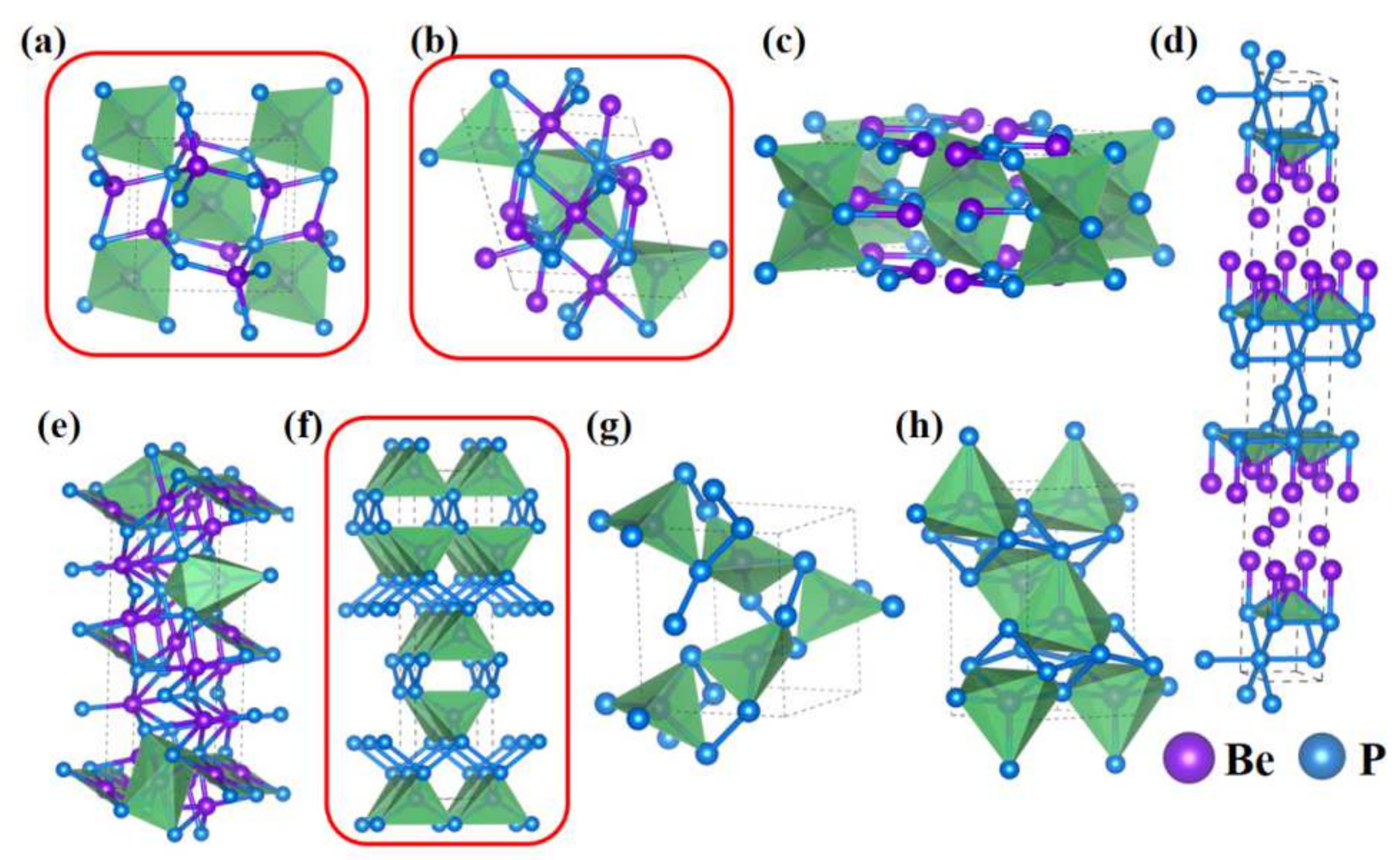
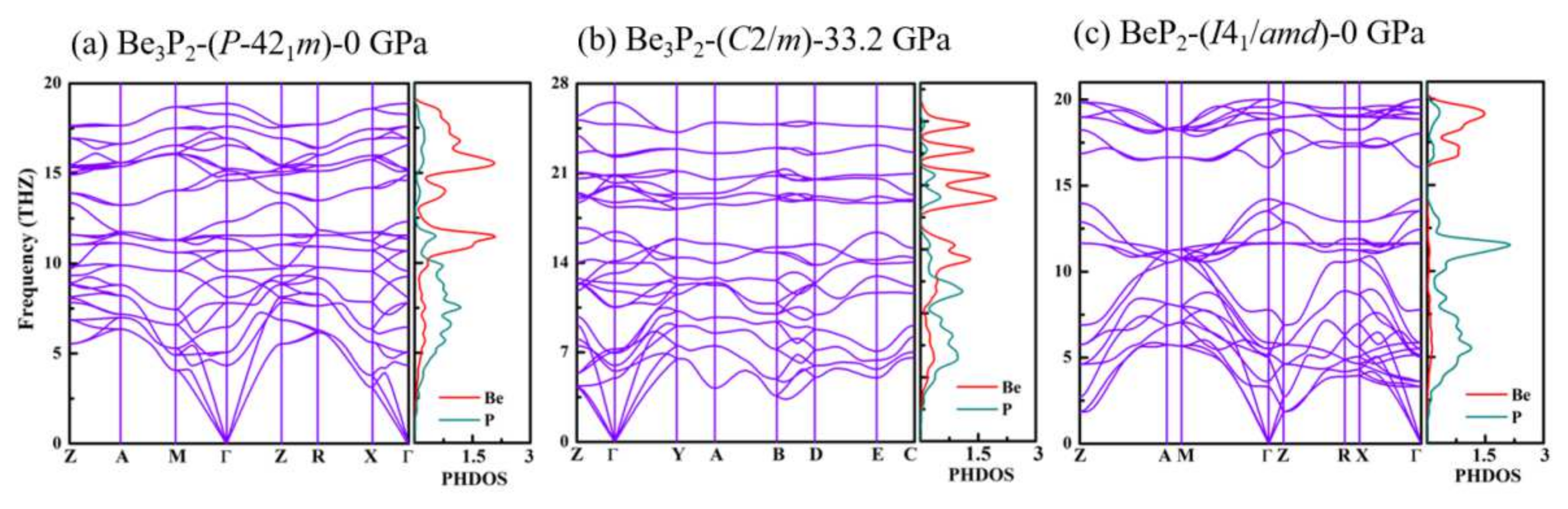
3.1. Crystal Structure

Through the emulation of the variable unit with cell sizes of 1–4 formula units (f.u.), we predicted the structures of BePx (x = 1/2, 2/3, and 1–3) in the range from 0 to 100 GPa. Then, the structures’ relative energetic stabilities are determined by calculating the formation enthalpy (ΔHf) with respect to elementary Be and P solids using the following formula: ΔHf = [H(BePx) − H(Be) − xH(P)]/(x + 1). Here, H(BePx) represents the enthalpy of the predicted compound and H(Be) and H(P) express the enthalpy of elemental Be and P, respectively. ΔHf is the computed formation enthalpy for the energetically advantageous beryllium phosphides. Figure 1 describes the enthalpies of formation of the predicted structure under varied pressures. For reference, the elemental Be solid with P63/mmc symmetry, within their respective stable pressure range and the hexagonal, simple cubic, and triclinic structures for P, were used. The ΔHf for the Be-P compounds was calculated only for the lowest energy obtained structures of each stoichiometry. A Be-P compound was designated to be “stable” (in comparison with the solid elements) only when the lowest formation enthalpy is negative, while a designated “metastable” system was one discovered above the convex hulls. That is to say, it ΔHf value was smaller than the sum of the two elemental products′ ΔHf values. A given compound is stable if it has a positive enthalpy of decomposition when converted into other compounds, as described by the convex hulls. In ambient conditions, it is not difficult to discover that only Be3P2 and BeP2 compounds are stable. In contrast, the calculations show that BePx (x = 1/2, 2/3, and 1–3) are unstable over 40 GPa. Subsequently, we shine a spotlight on the stable compounds.
Figure 2 depicts a complete composition–pressure phase graph of the Be-P system and identifies stable structures by colors and space groups. The Be3P2-P-421m and BeP2-I41/amd are stable compositions at ambient pressure. Then, one more new stoichiometric Be3P2-C2/m becomes stable at 33.2 GPa. This finding for BeP2-I41/amd is consistent with a previous study [40]. Interestingly, for Be3P2 at ambient pressure, the predicted Be3P2-P-421m tetragonal structure is the most stable structure that has not been experimentally synthesized at ambient pressure. Moreover, the enthalpy of Be3P2-Ia-3 synthesized by experiment [18,19] has higher energy than our predicted structures of Be3P2-P-421m, and even higher energy than the Be3P2-C2/m phase under high pressure. To explore the phase behavior of Be3P2 and BeP2 under high pressure, we investigate all the structures in the pressure range.
Here, we present a systematic analysis of atomic arrangements and structural characteristics for Be3P2 and BeP2. In order to describe a phase transition under high pressure, we list all structures for 0–100 GPa, including the metastable structures. For Be3P2, at ambient pressure, the lattice parameters of Be3P2-P-421m are a = b = 5.802 Å, c = 3.830 Å (Figure 3a), which has tetragonal primitive symmetry. In the unit cell, six Be atoms occupy the Wyckoff 4e (0.639, 0.139, 0.247) and 2b (0.500, 0.500, 0.500) sites, and four P atoms are located in the 4e (0.700, 0.270, 0.760) sites. Each Be atom is connected with four P atoms forming a tetrahedron with Be-P distances of 2.22 Å. For the purpose of identifying the sequence of phase transformation for Be3P2, the structures synthesized in experiments must be taken into consideration. Moreover, the calculated lattice parameters of Be3P2-Ia-3 are a = b = c = 10.193 Å at 0 GPa, which is in good agreement with the theoretical (10.19 Å [16,17]) and experimental (10.15 Å [18,19]) values. However, we predicted the structure Be3P2-P-421m to have lower energy. The predicted structure of Be3P2-P-421m is easier to synthesize by experiment due to its lower formation enthalpy.
As the pressure increased to 33.2 GPa, Be3P2-P-421m transforms into a monoclinic Be3P2-C2/m structure, with lattice parameters of a = 5.624 Å, b = 3.283 Å, and c = 5.618 Å (Figure 3b). The volume of the Be3P2-C2/m structure is 98.64 Å3, which demonstrates that the volume decreases by about 23.6% with increasing pressure. Six Be atoms occupy the Wyckoff 4i (0.371, 0.000, 0.114) and 2d (0.000, 0.500, 0.500) sites, and four P atoms lie in the 4i (0.240, 0.000, 0.723) sites in the unit cell. Four Be atoms are coordinated to four P atoms with a Be-P distance of 2.080 Å and two Be atoms are coordinated to six P atoms with a Be-P distance of 2.232 Å. As the pressure increases, three metastable structures, with space groups Ibam (Figure 3c), Cmcm (Figure 3d), and C2/m (Figure 3e) at 81.7 GPa, 82.7 GPa, and 90.4 GPa, have been uncovered. For the BeP2 phase, at ambient pressure, the optimized structure of BeP2 has a tetragonal I41/amd structure, which is agreement with the reported theoretical data [40] in Figure 3f, with lattice constants of a = b = 3.582 Å and c = 14.994 Å. The volume of the BeP2-I41/amd structure is 192.34 Å3, which indicates that the volume increases by about 49.1% compared with the predicted Be3P2-P-421m phase. Four Be atoms occupy the Wyckoff 4a (0.500, −0.500, 0.500) sites, and eight P atoms lie in the 8e (1.000, 0.000, 0.672) sites with four formula units per unit cell. The lattice constant of the c axis is much larger than the a axis and b axis. Each Be atom is coordinated to four P atoms forming a tetrahedron with the Be-P distance of 2.137 Å. Further, these tetrahedrons are interlinked by sharing vertex P atoms that comprise chains with a distance between P and P atoms of 2.283 Å. At higher pressure, BeP2-I41/amd undergoes the phase transition sequence of I41/amd → P43212 → Imma. However, the two novel phases of BeP2-P43212 and BeP2-Imma are metastable structures under high pressure.
It is of great importance to research the dynamical stability of these predicted novel structures. The acquired phonon dispersion curves and projected phonon density of states (PHDOS) of the Be3P2-P-421m, Be3P2-C2/m, and BeP2-I41/amd phases in the pressure range of 0–100 GPa are described in Figure 4. The novel phases are dynamically stable in their accessible pressures since no imaginary vibrational modes are observed in the Brillouin zone. For Be3P2, at ambient pressure, the maximum optical branch frequency of Be3P2-P-421m occurs at 18.8 THz. Under high pressure, the maximum optical branch frequency increases to 26.3 THz in the Be3P2-C2/m phase. For BeP2, the maximum optical branch frequency of BeP2-I41/amd is 20 THz at 0 GPa. The Be atoms are observed to contribute to all medium and high frequencies (10.2–18.8 THz for Be3P2-P-421m, 14.2–26.3 THz for Be3P2-C2/m, and 16.2–20 THz for BeP2-I41/amd). Moreover, the P atoms contribute to the low-frequency region (0–10.2 THz for Be3P2-P-421m, 0–14.2 THz for Be3P2-C2/m, and 0–13.9 THz for BeP2-I41/amd). The relative atomic mass of the Be atom is smaller than that of the P atom, which explains the rationality of the contribution range of Be and P atoms.

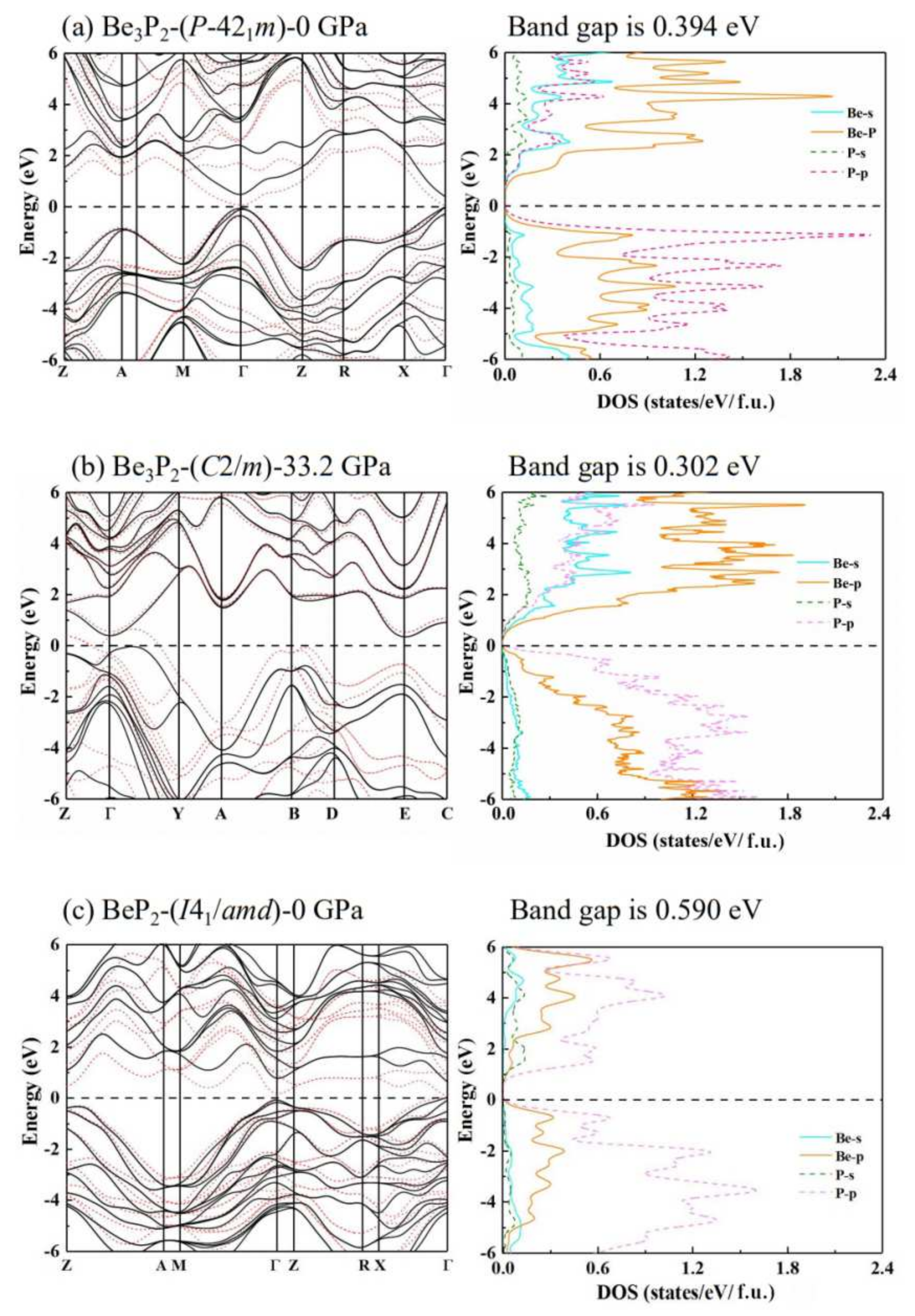
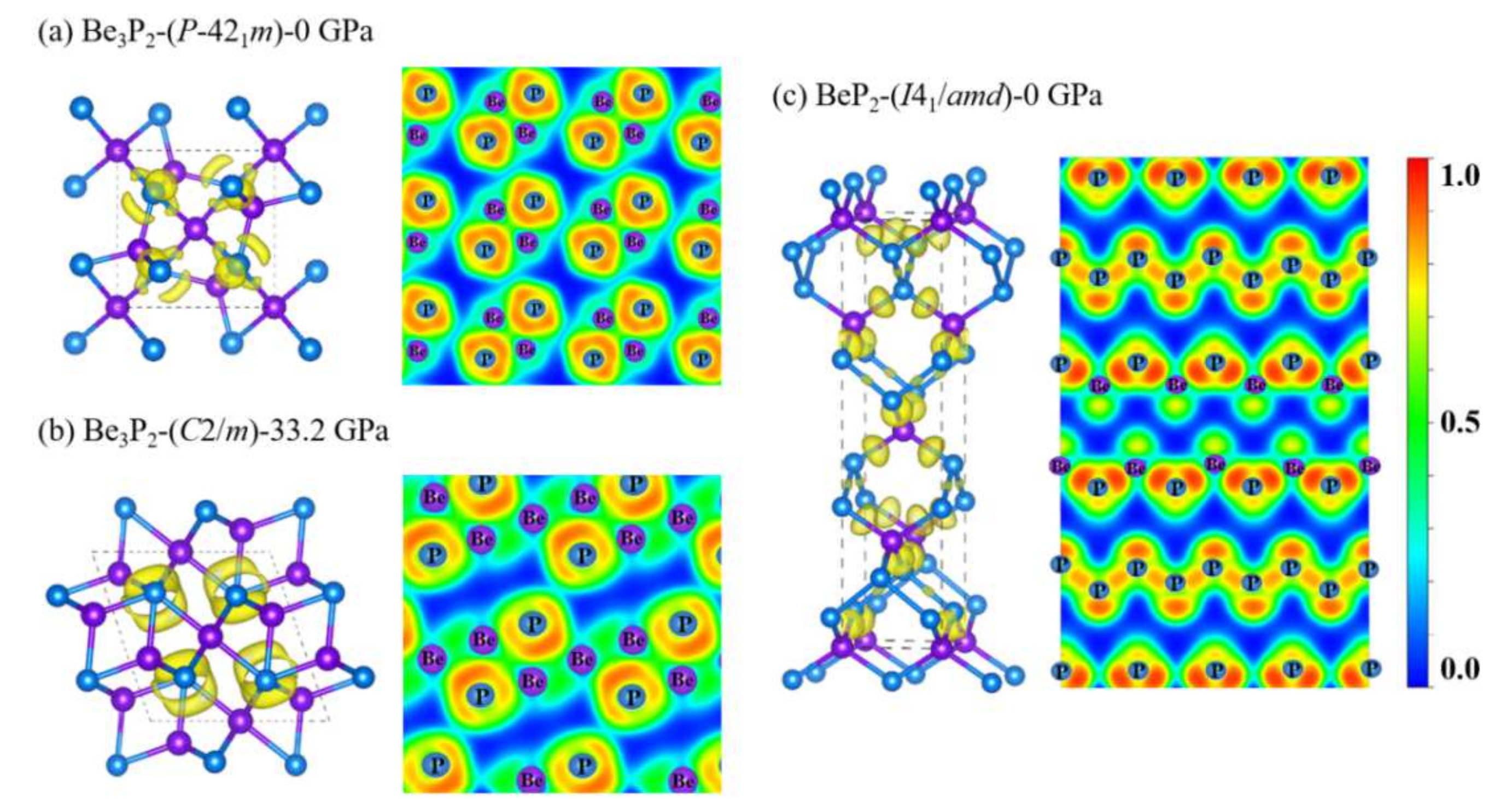
3.2. Electronic Properties

To investigate the potential application of the predicted novel structures of Be3P2-P-421m, Be3P2-C2/m, and BeP2-I41/amd, we have calculated the electronic band structures and projected density of states (PDOS). As we know, the PBE function underestimates the band gap, so we use the hybrid HSE03 functional to get more accurate band structures. The results are presented in Figure 5; in the band structures, the dotted (red) and solid (black) lines indicate the results obtained using the PBE and HSE functions, respectively. The calculations show that the Be3P2-P-421m structure is a semiconductor with a direct bandgap of 0.394 eV at ambient pressure (Figure 5a). With increasing pressure, the bandgap of the Be3P2-C2/m phase decreases to 0.302 eV at 33.2 GPa. Unlike in the Be3P2-P-421m phase, the Be3P2-C2/m phase is an indirect bandgap semiconductor, since the conduction band minimum and valence band maximum are located at the Γ point and between the Γ and Y points in the Brillouin zone, respectively (Figure 5b). For the BeP2-I41/amd phase, it is a semiconductor with a direct bandgap of 0.590 eV at ambient pressure, which is wider than that of the Be3P2-P-421m phase. All three phases are excellent semiconductor materials.
For the Be3P2-P-421m and Be3P2-C2/m phases, the electronic DOS at the Fermi level consists primarily of the p states of Be and P atoms with moderate mixing with the s states of the Be and P atoms. For the results, the orbitals of Be-2s and P-3p as well as Be-2p and P-3s are hybridized formed by covalent bonding. At the Fermi level, the peak value of DOS in the Be3P2-P-421m structure is higher than that of the Be3P2-C2/m phase since the symmetry of Be3P2 decreases with increasing pressure. For the BeP2-I41/amd phase, the P-3s states are located at base of the conduction band, as well as the P-3p and Be-2p states, which make important contributions near the Fermi level. The DOS of these compounds once again proves their semiconducting properties.
The electronic localization functions (ELFs), a measurement of comparative electron localization is computed for the sake of visualization of bonding characteristic of the predicted novel structures of Be3P2-P-421m, Be3P2-C2/m, and BeP2-I41/amd in Figure 6. Large ELF values (>0.5) indicate a strong tendency for electron pairing, manifesting the production of covalent bonds, whereas tiny ELF values (<0.5) indicate non/less electron localization, revealing the existence of ionic bonds between atoms [41]. For the three novel phases, the ELF maximum, which is forcefully towards the P atoms, shows the polar covalent bonding mutual effect of Be and P atoms. In Figure 6c, the strong electron localization between P and P atoms indicates covalent bonding shown in the polymeric chains. At the same time, the layered structure of BeP2-I41/amd can also be proved from the ELF.
To describe the electron transfer circumstances more clearly, the calculation of Bader charge transfer is carried out shown in Table 1. It can be identified that charge is transferred from Be to P in the Be3P2-P-421m, Be3P2-C2/m, and BeP2–I41/amd structures. Our calculations showed that P atoms gained 2.305e in Be3P2-P-421m and 2.344e in Be3P2-C2/m. By contrast, P atoms merely acquired a minor value of 0.765e for BeP2–I41/amd. Generally, the charge transfer is not an integer and the number of charge transfers is significantly less than the normal integer value. The non-integer charge is calculated from its zero-flux surface due to the space in which the charge is separated. Therefore, the chemical valence of Be and P atoms is +2 and −3 in the predicted two phases of Be3P2-P-421m and Be3P2-C2/m, respectively. For the BeP2-I41/amd phase, Bader analysis reveals the chemical valence of Be and P atoms is +2 and −1. The various chemical valences of P are determined by the valence electron configuration of 3s23p3. The calculation results of Bader charge transfer support the above analysis of electron local function and structure.

4. Conclusions

In conclusion, we used first-principles developmental crystal structure forecasting to investigate the crystal structures and probable stoichiometries in the Be-P system. The BeP2-I41/amd structure has been resoundingly duplicated at ambient pressure, confirming the dependability of our calculations regarding binary Be-P compounds. We find that the Be3P2-P-421m and BeP2-I41/amd structures exist at ambient pressure, as well as a new phase that is Be3P2-C2/m at 33.2 GPa. The predicted structures, except for the aforementioned three structures, are unsteady within the range of pressures we investigated. The theoretical phonon dispersion curves prove the dynamical stability of existing expected structures. Electronic structure calculations show that predicted novel structures of Be3P2-P-421m, Be3P2-C2/m, and BeP2-I41/amd are all excellent semiconductor materials, which have bandgaps of 0.394 eV, 0.302 eV, and 0.590 eV, respectively. Moreover, the charge accumulation along the bonding directions between Be and P is an indication of polar covalent bonding. The Bader charge analysis illustrates those electrons obviously transferred from Be to P atoms in these newfangled phases and indicates that the chemical valence of P atom varies with the stoichiometries. Our findings should stimulate further theoretical and experimental research into the high-pressure development of crystal structures and electrical characteristics in Be-P systems.

Author Contributions

Conceptualization, H.L., Y.D. and A.Z.; methodology, X.M., S.L., T.C. and A.Z.; validation, H.L., J.Y. and J.L.; writing—original draft preparation, H.L. and Y.L.; writing—review and editing, S.L., Y.D. and Y.H.; supervision, Y.L. and T.C.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of China (Grant No. 11764043).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ohno, H.; Shen, N.A.; Matsukura, F.; Oiwa, A.; Endo, A.; Katsumoto, S.; Iye, Y. (Ga, Mn) As: A new diluted magnetic semi-conductor based on GaAs. Appl. Phys. Lett. 1996, 69, 363–365. [Google Scholar] [CrossRef]
  2. Khramtsov, I.A.; Fedyanin, D.Y. Superinjection of Holes in Homojunction Diodes Based on Wide-Bandgap Semiconductors. Materials 2019, 12, 1972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Pereira, N.; Lima, A.C.; Correia, V.M.G.; Peřinka, N.; Lanceros-Mendez, S.; Martins, P. Magnetic Proximity Sensor Based on Magnetoelectric Composites and Printed Coils. Materials 2020, 13, 1729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Gamel, M.M.A.; Lee, H.J.; Rashid, W.E.S.W.A.; Ker, P.J.; Yau, L.K.; Hannan, M.A.; Jamaludin, Z. A Review on Thermophotovoltaic Cell and Its Applications in Energy Conversion: Issues and Recommendations. Materials 2021, 14, 4944. [Google Scholar] [CrossRef] [PubMed]
  5. Dietl, T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat. Mater. 2010, 9, 965–974. [Google Scholar] [CrossRef] [Green Version]
  6. L’Haridon, P.; David, J.; Lang, J.; Parthé, E. BeP2: A tetrahedral structure of type order-disorder which obeys a coordination rule for short-range order. J. Solid State Chem. 2020, 19, 287–297. [Google Scholar] [CrossRef]
  7. Gregory, D. Nitride chemistry of the s-block elements. Co-Ord. Chem. Rev. 2001, 215, 301–345. [Google Scholar] [CrossRef]
  8. Orhan, E.; Jobic, S.; Brec, R.; Marchand, R.; Saillard, J.Y. Binary nitrides α-M3N2 (M = Be, Mg, Ca): A theoretical study. J. Mater. Chem. 2020, 12, 2475–2479. [Google Scholar] [CrossRef]
  9. Wang, X.; Lu, Y.; Hu, Z.; Shao, X. Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi). Metals 2021, 11, 971. [Google Scholar] [CrossRef]
  10. Mokhtari, A. Density functional study of the group II phosphide semiconductor compounds under hydrostatic pressure. J. Phys. Condens. Matter 2008, 20, 135224. [Google Scholar] [CrossRef]
  11. Römer, S.R.; Doerfler, T.; Kroll, P.; Schnick, W. Group II element nitrides M3N2 under pressure: A comparative density functional study. Phys. Status Solidi (B) 2020, 246, 1604–1613. [Google Scholar] [CrossRef]
  12. Mokhtari, A.; Akbarzadeh, H. Ab initio calculations of the electronic and structural properties of beryllium-, magnesium-and calcium-nitrides. J. Phys. Condens. Matter 2003, 337, 122–129. [Google Scholar] [CrossRef]
  13. Armenta MG, M.; Reyes-Serrato, A.; Borja, M.A. Ab initio determination of the electronic structure of beryllium-, aluminum-, and magnesium-nitrides: A comparative study. Phys. Rev. B 2020, 62, 4890. [Google Scholar] [CrossRef]
  14. Imai, Y.; Watanabe, A. Electronic structures of Mg3Pn2 (Pn = N, P, As, Sb and Bi) and Ca3N2 calculated by a first-principle pseudopotential method. J. Mater. Sci. 2006, 41, 2435–2441. [Google Scholar] [CrossRef]
  15. Dobrokhotova, Z.V.; Zaitsev, A.I.; Zemchenko, M.A.; Litvina, A.D.; Yaschenko, S.N. Thermodynamic properties of calcium and barium phosphides. J. Therm. Anal. 1992, 38, 1113–1122. [Google Scholar] [CrossRef]
  16. Sa, R.; Zha, W.; Liu, D. First-principles insight into the structural, mechanical, electronic and optical properties of Be3X2 (X = N, P, As). J. Phys. Chem. Solids 2020, 145, 109575. [Google Scholar]
  17. Ullah, M.; Ali, R.; Murtaza, G.; Chen, Y. First principles investigation of Be3X2 (X = N, P, As) and their alloys for solar cell applications. J. Alloy. Compd. 2019, 795, 385–390. [Google Scholar] [CrossRef]
  18. Joshi, K.B.; Paliwal, U. First-principles study of pressure-induced phase transitions and electronic structure of Be3P2 polymorphs. Philos. Mag. 2012, 92, 1159–1169. [Google Scholar] [CrossRef]
  19. Joshi, K.B.; Paliwal, U. Pressure dependent electronic properties of α-Be3P2. J. Phys. Conf. Series. IOP Publ. 2012, 377, 012058. [Google Scholar] [CrossRef]
  20. Stackelberg, Μ.V.; Paulus, R. Untersuchungen über die Kristallstruktur der Nitride und Phosphide zweiwertiger Metalle. Z. Phys. Chem. 1933, 22, 305–322. [Google Scholar] [CrossRef]
  21. Wyckoff, R.W.G. Crystal Structures, 2nd ed.; Krieger: Malabar, FL, USA, 1986. [Google Scholar]
  22. Elmaslout, A.; Motte, J.; Courtois, A.; Protas, J.; Gleitzer, C. Crystal- structure of Be3P2. J. Solid State Chem. 1975, 15, 223–228. [Google Scholar] [CrossRef]
  23. De Carvalho MM, G.; Betinni, J.; Pudenzi, M.A.; Cardoso, L.P.; Cotta, M.A. Evidence of Be3P2 formation during growth of Be-doped phosphorus-based semiconductor compounds. Appl. Phys. Lett. 1999, 74, 3669–3671. [Google Scholar] [CrossRef]
  24. Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef] [Green Version]
  25. Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef] [Green Version]
  26. Wang, H.; Wang, Y.; Lv, J.; Li, Q.; Zhang, L.; Ma, Y. CALYPSO structure prediction method and its wide application. Comput. Mater. Sci. 2016, 112, 406–415. [Google Scholar] [CrossRef]
  27. Zhu, L.; Liu, H.; Pickard, C.J.; Zou, G.; Ma, Y. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nat. Chem. 2014, 6, 644–648. [Google Scholar] [CrossRef] [Green Version]
  28. Li, Y.; Hao, J.; Liu, H.; Li, Y.; Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef] [Green Version]
  29. Zhong, X.; Wang, H.; Zhang, J.; Liu, H.; Zhang, S.; Song, H.; Yang, G.; Zhang, L.; Ma, Y. Tellurium Hydrides at High Pressures: High-Temperature Superconductors. Phys. Rev. Lett. 2016, 116, 057002–057008. [Google Scholar] [CrossRef] [Green Version]
  30. Zhang, S.; Zhu, L.; Liu, H.; Yang, G. Structure and electronic properties of Fe2SH3 compound under high pressure. Inorg. Chem. 2016, 55, 11434–11439. [Google Scholar] [CrossRef] [PubMed]
  31. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  32. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  33. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal--amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  34. Kresse, G.; Hafnerr, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
  35. Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
  36. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
  37. Thirumalai, D.; Hall, R.W.; Berne, B.J. A path integral Monte Carlo study of liquid neon and the quantum effective pair potential. J. Chem. Phys. 1984, 81, 2523–2527. [Google Scholar] [CrossRef]
  38. Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef] [Green Version]
  39. Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
  40. Li, X.; Wang, Q. Prediction of a BeP2 monolayer with a compression-induced Dirac semimetal state. Phys. Rev. B 2018, 97, 085418. [Google Scholar] [CrossRef]
  41. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
Materials 15 01255 g001 550
Figure 1. (color online). In relation to elemental beryllium and phosphorus solids, relative enthalpies of creation of the Be−P phase. Solid lines connect the stable phases to form convex shells (solid stars). Open stars indicate the unstable/meta stable phases.
Figure 1. (color online). In relation to elemental beryllium and phosphorus solids, relative enthalpies of creation of the Be−P phase. Solid lines connect the stable phases to form convex shells (solid stars). Open stars indicate the unstable/meta stable phases.
Materials 15 01255 g001
Materials 15 01255 g002 550
Figure 2. (color online). Be−P compounds composition-pressure phase graph. The metallic and insulating phases are represented by blue and red, respectively. Stable (metastable) phases are represented by solid (dashed) lines.
Figure 2. (color online). Be−P compounds composition-pressure phase graph. The metallic and insulating phases are represented by blue and red, respectively. Stable (metastable) phases are represented by solid (dashed) lines.
Materials 15 01255 g002
Materials 15 01255 g003 550
Figure 3. (color online). Crystal structures of the predicted Be−P system for (a) Be3P2−P−421m, (b) Be3P2−C2/m, (c) Be3P2−Ibam, (d) Be3P2−Cmcm, (e) Be3P2−C2/m, (f) BeP2−I41/amd, (g) BeP2−P43212, and (h) BeP2−Imma. Be atoms and P atoms are represented by the purple and blue spheres, respectively. Inside the red circular region, the structures are stable.
Figure 3. (color online). Crystal structures of the predicted Be−P system for (a) Be3P2−P−421m, (b) Be3P2−C2/m, (c) Be3P2−Ibam, (d) Be3P2−Cmcm, (e) Be3P2−C2/m, (f) BeP2−I41/amd, (g) BeP2−P43212, and (h) BeP2−Imma. Be atoms and P atoms are represented by the purple and blue spheres, respectively. Inside the red circular region, the structures are stable.
Materials 15 01255 g003
Materials 15 01255 g004 550
Figure 4. (color online). Phonon−dispersion contours and PHDOS projected on Be and P atoms for (a) Be3P2−P−421m at 0 GPa, (b) Be3P2−C2/m at 33.2 GPa, and (c) BeP2−I41/amd at 0 GPa.
Figure 4. (color online). Phonon−dispersion contours and PHDOS projected on Be and P atoms for (a) Be3P2−P−421m at 0 GPa, (b) Be3P2−C2/m at 33.2 GPa, and (c) BeP2−I41/amd at 0 GPa.
Materials 15 01255 g004
Materials 15 01255 g005 550
Figure 5. (color online). Electronic band structures and PDOS for (a) Be3P2−P−421m at 0 GPa, (b) Be3P2−C2/m at 33.2 GPa, and (c) BeP2−I41/amd at 0 GPa. Note that zero energy is on the Fermi level. The dotted (red) and solid (black) lines represent results obtained using the PBE and HSE functional, respectively.
Figure 5. (color online). Electronic band structures and PDOS for (a) Be3P2−P−421m at 0 GPa, (b) Be3P2−C2/m at 33.2 GPa, and (c) BeP2−I41/amd at 0 GPa. Note that zero energy is on the Fermi level. The dotted (red) and solid (black) lines represent results obtained using the PBE and HSE functional, respectively.
Materials 15 01255 g005
Materials 15 01255 g006 550
Figure 6. (color online). The ELF graphs for the structures of (a) Be3P2−P−421m, (b) Be3P2−C2/m, and (c) BeP2−I41/amd with isosurface of 0.8.
Figure 6. (color online). The ELF graphs for the structures of (a) Be3P2−P−421m, (b) Be3P2−C2/m, and (c) BeP2−I41/amd with isosurface of 0.8.
Materials 15 01255 g006
Table
Table 1. The Bader charge transfer of Be3P2−P−421m, Be3P2−C2/m, and BeP2−I41/amd.
Table 1. The Bader charge transfer of Be3P2−P−421m, Be3P2−C2/m, and BeP2−I41/amd.
PhasePressure (GPa)AtomNumberCharge Value (e)δ(e)
Be3P2-P-421m0 GPaBe140.466−1.534
--Be220.457−1.543
--P147.3052.305
Be3P2-C2/m33.2 GPaBe140.452−1.548
--Be220.408−1.592
--P147.3442.344
BeP2-I41/amd0 GPaBe140.470−1.530
--P185.7650.765
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Liu, H.; Dan, Y.; Zhang, A.; Liu, S.; Yue, J.; Li, J.; Ma, X.; Huang, Y.; Liu, Y.; Cui, T. First-Principles Study of High-Pressure Phase Stability and Electron Properties of Be-P Compounds. Materials 2022, 15, 1255. https://doi.org/10.3390/ma15031255

AMA Style

Liu H, Dan Y, Zhang A, Liu S, Yue J, Li J, Ma X, Huang Y, Liu Y, Cui T. First-Principles Study of High-Pressure Phase Stability and Electron Properties of Be-P Compounds. Materials. 2022; 15(3):1255. https://doi.org/10.3390/ma15031255

Chicago/Turabian Style

Liu, Han, Yaqian Dan, Ao Zhang, Siyuan Liu, Jincheng Yue, Junda Li, Xuejiao Ma, Yanping Huang, Yanhui Liu, and Tian Cui. 2022. "First-Principles Study of High-Pressure Phase Stability and Electron Properties of Be-P Compounds" Materials 15, no. 3: 1255. https://doi.org/10.3390/ma15031255

APA Style

Liu, H., Dan, Y., Zhang, A., Liu, S., Yue, J., Li, J., Ma, X., Huang, Y., Liu, Y., & Cui, T. (2022). First-Principles Study of High-Pressure Phase Stability and Electron Properties of Be-P Compounds. Materials, 15(3), 1255. https://doi.org/10.3390/ma15031255

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop